Abstract
In this review article, the focus is on partitioned simulation techniques for strongly coupled fluid-structure interaction problems, especially on techniques which use at least one of the solvers as a black box. First, a number of analyses are reviewed to explain why Gauss–Seidel coupling iterations converge slowly or not at all for fluid-structure interaction problems with strong coupling. This provides the theoretical basis for the fast convergence of quasi-Newton and multi-level techniques. Second, several partitioned techniques that couple two black-box solvers are compared with respect to implementation and performance. Furthermore, performance comparisons between partitioned and monolithic techniques are examined. Subsequently, two similar techniques to couple a black-box solver with an accessible solver are analyzed. In addition, several other techniques for fluid-structure interaction simulations are studied and various methods to take into account deforming fluid domains are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fluid-structure interaction (FSI) is the mutual interaction between a fluid flow and a moving or deforming structure. A fluid flow exerts forces on the adjacent structure, which can result in motion or deformation of this structure. Significant structural motion or deformation will, in turn, affect the fluid flow. There are numerous examples of fluid-structure interaction. A selection is presented below to illustrate the above definition.
A notorious example of FSI is the Tacoma Narrows Bridge (see Fig. 1). This suspension bridge collapsed due to aero-elastic fluttering, only two months after being opened to the public. More specifically, an unstable interaction with a frequency of 0.2 Hz developed between the second torsional mode of the bridge and the steady lateral wind of only 68 km/h. By contrast, the von Kármán vortex street had a frequency of approximately 1 Hz for that geometry and wind velocity. Therefore, the cause of the collapse was not forced resonance due to vortex shedding, although the disaster is often explained that way [16]. After this disaster, research on aero-elastic phenomena was increased, which entailed new regulations and improved construction guidelines. Fluid-structure interaction has to be taken into account during the design process of bridges, lightweight membrane structures [201] and large silos [94].
Machines are also susceptible to flutter. For example, the wings of an aircraft [1, 64] and the blades of a turbo-machine [13, 124] can oscillate as a result of a fluid-structure interaction. This can lead to fatigue damage or an aircraft that is hard to handle.
Life-saving examples of fluid-structure interaction are parachutes [176, 180] and air bags [106]. The opening of a parachute is enabled through a complex fluid-structure interaction. An air bag consists of a nylon bag which opens when gas is generated by an electrically ignited pyrotechnic device. Both the deployment of an air bag and the impact of a person on an air bag are fluid-structure interactions.
Also the impact of structures on a liquid surface and other interactions between multi-phase flow and flexible structures have been analyzed extensively [2, 101, 102, 113, 155, 194, 197]. Applications of that research are the design of floating wave energy converters [186] and composite ship hulls [148, 187].
Many fluid-structure interactions occur inside the human body [158]. One of them is the interaction between the elastic wall of large arteries and the blood flow that passes through them [11, 82, 147, 170, 183]. The blood flow also interacts with the heart valves [56, 57, 119, 149, 169] and the muscular heart wall [150, 193]. Accurate fluid-structure interaction simulations are a prerequisite for the improvement of artificial heart valves, stents and other medical devices. Another biomedical application is the prediction of the rupture of aneurysms or the outcome of surgical procedures [178, 200]. Fluid-structure interaction is also present in the pulmonary system [195]. Patient-specific data are used for both material models and geometry to increase the fidelity of the simulations [34, 82, 195].
After this introduction, this review article focuses on numerical simulation of fluid-structure interaction, more specifically partitioned simulations with at least one black-box solver. In Sect. 2, several computational aspects of fluid-structure interaction simulations are discussed, followed by an overview of various simulation techniques in Sect. 3. Then, Sect. 4 reviews stability analyses of a simple partitioned coupling technique. Subsequently, Sects. 5 and 6 compare a number of coupling techniques for respectively two and one black-box solver more in detail. Finally, Sect. 7 presents the conclusions of this review.
2 Fluid-Structure Interaction Simulations
This section begins with a brief description of the governing equations in a fluid-structure interaction problem, followed by a summary of techniques to deal with the deforming fluid domain and interpolation on the fluid-structure interface. Subsequently, numerical effects of different time discretization techniques in the flow solver and the structural solver are explained. Finally, an example illustrates the possibility of numerical instabilities due to the so-called added-mass effect.
2.1 Governing Equations
There are many different ways to discretize the governing equations in space and time and to solve the resulting discrete equations. However, as the focus of this article lies on the interaction, the reader is referred to standard text books for the description of these techniques.
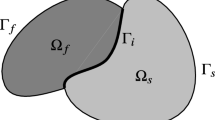
Figure 2 depicts an abstract fluid-structure interaction problem. The subdomains are indicated as Ω f and Ω s and their boundaries as Γ f =∂Ω f and Γ s =∂Ω s , with the subscripts f and s respectively denoting fluid and solid. The fluid-structure interface Γ i =Γ f ∩Γ s is the common boundary of these subdomains.
2.1.1 Flow Equations
The flow of an isothermal fluid is determined by the conservation of mass and the conservation of momentum (Navier–Stokes equation)


for \(\vec {x}\in\varOmega_{f}(t)\). In these equations, ρ f is the fluid density, \(\vec {v}\) the velocity, t the time and \(\vec {f}_{f}\) the body forces per unit of volume on the fluid. For the Newtonian fluids with dynamic viscosity μ f , the stress tensor \(\mathsf{\sigma} _{f}\) is defined as
with p the pressure and I the unit tensor. The rate of strain tensor \(\mathsf{\epsilon} _{f}\) is given by
This article mainly considers incompressible fluids as they prove to be most challenging for the fluid-structure interaction techniques. However, it would be no problem to consider compressible fluids instead. For an incompressible, isothermal fluid, Eqs. (1a) and (1b) simplify to


in conservative form.
2.1.2 Structural Equations
The deformation or displacement \(\vec {u}\) of a structure is determined by the conservation of momentum
for \(\vec {x}\in\varOmega_{s}(t)\) with ρ s the structural density. The notation D2/Dt 2 refers to the second material derivative and \(\vec {f}_{s}\) denotes the body forces per unit volume on the structure. If the current configuration of the structure is represented by \(\vec {x}(\vec {X},t)\) and the reference configuration by \(\vec {X}\), the deformation \(\vec {u}\) is given by
The deformation gradient F is equal to
and its determinant is indicated as J=det(F).
The Cauchy stress tensor \(\mathsf{\sigma} _{s}\) relates forces in the deformed configuration to areas in the deformed configuration, whereas the second Piola–Kirchhoff stress tensor S s links forces in the reference configuration with areas in the reference configuration. The relation between these tensors is given by
In large displacement calculations, the relation between the second Piola–Kirchhoff stress tensor S s and the Green–Lagrange strain tensor \(\mathsf{\epsilon} _{s}\) is imposed by the constitutive equation of the material. The Green–Lagrange strain tensor is given by
for large displacements, which can be linearized as
for small displacements.
2.1.3 Equilibrium Conditions
The equilibrium conditions on a no-slip fluid-structure interface are the equality of velocity (kinematic condition)
and the equality of traction (dynamic condition)
for \(\vec {x}\in\varGamma_{i}(t)\). The vector \(\vec {n}_{f,s}\) is the unit normal vector that points outwards from the domain Ω f,s . Appropriate boundary conditions are imposed on Γ f ∖Γ i and on Γ s ∖Γ i , depending on the problem at hand.
2.2 Deforming Fluid Domain
In a fluid-structure interaction calculation with large displacements, both the fluid domain and the solid domain are deforming. Deformations are common in structural calculations and, therefore, the deformation of the solid domain normally does not cause difficulties. Structural equations are usually solved in a Lagrangian formulation, which means that the grid nodes move at the same velocity as the material. On the other hand, flow equations are traditionally solved in a domain that does not deform using an Eulerian formulation, i.e. a fixed grid. However, there are several techniques to take into account the deforming fluid domain, which are reviewed in the following pages.
2.2.1 Moving Fluid Grid
One approach to calculate the flow in a deforming domain is to use the arbitrary Lagrangian–Eulerian (ALE) formulation of the flow equations [54, 55]. In this formulation, the fluid grid does deform, but at an arbitrary grid velocity (hence the name) and not necessarily at the velocity of the fluid (see Fig. 3). Only the velocity of the fluid grid on the fluid-structure interface is determined by the velocity of the structure at that location. This ensures that the fluid and solid domain do not overlap (except for a small overlap if the grids are non-matching, see Sect. 2.3). The grid velocity \(\vec {w}\) is then extended from the fluid-structure interface to the entire fluid domain to avoid excessive grid distortion.
The comparison between the Eulerian, arbitrary Lagrangian–Eulerian (ALE) and Lagrangian formulation. The lines represent the grid and the shaded grey areas represent a certain amount of material. In the Eulerian formulation, the grid is stationary. In the ALE formulation, the grid and the material can move at the same or at a different velocity. In the Lagrangian formulation, the grid and the material move at the same velocity
There are several possibilities for this extension of the grid velocity to the entire fluid domain. A common technique is to replace the edges between the grid nodes by springs. The initial spacings of the grid nodes before any grid motion constitute the equilibrium state of the springs. A displacement of a node on the fluid-structure interface will generate a force proportional to the displacement along all the springs connected to this node. Using Hooke’s law, the force \(\vec {F}_{i}\) on grid node i is given by
with \(\Delta \vec {x}_{i}\) the displacement of node i. This summation is performed over the n i neighbours of node i. The spring constant k ij between nodes i and j is often chosen to be inversely proportional to the length of the edge
so that short edges become stiffer than long edges [10]. At equilibrium, the net force on each node due to all the springs connected to this node must be zero (\(\vec {F}_{i}=\vec {0}\)). This equilibrium is calculated using an iterative procedure
with the superscript m denoting the iteration. Since displacements are known on the fluid-structure interface and on the fixed boundaries, this equation is solved using a Jacobi sweep on all interior nodes. At convergence, the positions are updated such that
with the superscripts n and n+1 denoting the previous and current time step, respectively. Adding torsional springs increases the robustness of this procedure as they prevent fluid grid cells from overlapping each other [40, 62]. The fluid grid can also be considered as an elastic body instead of as a network of springs [120].
Another technique is to use a Laplace (or diffusion) equation for the grid velocities [117]. In that case, the grid velocities \(\vec {w}\) in the fluid domain are calculated from
with γ the diffusivity. The node positions are updated using
The ratio between interval lengths is preserved by the Laplace equation for the grid velocity with a constant diffusivity. This causes the motion of the fluid-structure interface to diffuse uniformly throughout the fluid domain.
To modify the grid velocity near the fluid-structure interface or for small cells, a spatially varying diffusivity can be calculated based on the distance d to the interface
or the cell volume V
with α>0 a coefficient supplied by the user. Whereas Laplace techniques stipulate either the displacement or the spacing of the grid, biharmonic operators offer the advantage that both the displacement and the normal grid spacing along a boundary can be controlled [93].
All previously mentioned techniques require knowledge of the connectivity between the grid points. An alternative is to interpolate the displacements of the boundary nodes to the whole grid using radial basis functions [18]. For the construction of the interpolation functions, a linear system with dimension proportional to the number of grid points on the boundary of the fluid domain has to be solved. The grid points in the domain are then interpolated one by one, without need for connectivity information. However, the resulting grid quality depends on the selected basis function and its parameters.
Nevertheless, every grid motion technique will yield an unacceptable grid quality when the deformations (translations or rotations) become large or when the topology changes. Large deformations are common if a structure without anchorage moves freely throughout the liquid domain; topology changes occur if a structure breaks or if a valve opens. In that case, a new grid has to be generated for at least part of the domain. Richter [161] uses local grid adaptivity driven by goal-oriented error estimation. The interpolation from the old to the new grid inevitably causes errors. Moreover, the grid generation, followed by load-balancing in a parallel calculation, increases the duration of the simulation. However, the ALE formulation has the advantage that the wall shear stress on the fluid-structure interface can be calculated accurately.
The shear slip mesh update method (SSMUM) is designed for large translations or rotations of rigid bodies [14], but can also be applied to flexible bodies. The cells adjacent to the moving body are rigid and move along with this body; the cells further away are also rigid but have a fixed position. In between, there are one or more layers of cells which deform (see Fig. 4). When the shear deformation of the cells has become to large, they are reconnected to obtain cells with a good quality. An alternative technique to deal with translations or rotations is sliding interfaces. In that case, two grid regions slide along each other. For every edge or face on one side, the overlapping edges or faces on the other side are searched and projected on each other.
The shear slip mesh update method is developed for large translations or rotations. The layer of cells in grey absorbs the shear and is reconnected afterwards. Adapted from [14]
If a no-slip boundary condition is applied on the fluid-structure interface, then both the normal and the tangential material velocity have to be identical in the fluid and structure. By contrast, only the grid velocity normal to the interface has to be the same on both sides of the interface. So, slip of the fluid grid with respect to the structural grid can be allowed, even for a no-slip boundary condition. In the continuous equations, a different domain velocity tangential to the interface has no influence on the physical solution. However, in the discrete equations, a difference in tangential grid velocity will inevitably lead to small changes in shape of the domains.
In several partitioned solution techniques, the flow problem has to be solved repeatedly for slightly different interface positions. Transpiration boundary conditions can be used to avoid the cost of the grid motion and the corresponding update of the fluid matrices (if they are calculated explicitly) each time the flow problem is solved [52, 68]. As long as the displacement is small, this linearized model for the influence of the interface displacement can be used as boundary condition. When the displacement has become too large, a real grid motion has to be performed, followed by the construction of a new linearized model.
2.2.2 Fixed Fluid Grid
Fixed grid approaches are an alternative to the ALE formulation. A class within these fixed grid techniques are the immersed boundary (IB) methods [137]. In the original IB method developed by Peskin [149], the structure was limited to so-called fibres, which consist of a chain of solid nodes [150, 151]. Three-dimensional structures could be created by weaving a net of fibres. However, a fibre-like one-dimensional immersed structure may carry mass, but it occupies no volume in the fluid domain. More recently, the IB method has been extended to allow for structures that occupy finite volumes in the fluid [84, 199, 206]. Figure 5 shows a schematic representation of the IB method for structures with and without volume.
A schematic representation of the immersed boundary (IB) method for structures without (left) and with (right) volume. The vertical and horizontal lines are the fixed fluid grid; the interconnected dots are the Lagrangian solid nodes. The weighting functions for the interpolation of the forces from the solid to the fluid are represented by dashed circles. Adapted from [196]
In the IB methods, the interconnected Lagrangian solid nodes move over the fixed fluid grid, resulting in an overlap of the fluid and solid domain. In the neighbourhood of these solid nodes, a weighting function is defined to interpolate the elastic forces from the Lagrangian solid grid to the Eulerian fluid grid. This interpolation results in a body forces source term \(\vec {f}_{f}\) in the Navier–Stokes equations. Conversely, the velocity of the structural nodes is interpolated from the velocity of the surrounding fluid. The update of the source term and the velocity could be performed explicitly or implicitly. Generally, however, the structural degrees of freedom are eliminated so that the influence of the structure is represented by velocity-dependent source terms in the momentum equations [196].
The main advantage of the IB methods is that the fluid grid does not have to change, whatever the structural displacements are. As a result, the flow solver can be simple and fast, for example by using Cartesian grids. A weakness of these techniques is the loss of accuracy near the interface, caused by the interpolations. Moreover, the accuracy depends on the ratio between the fluid and solid grid size [61, 114]. The interpolation of the velocities from the incompressible fluid to the structure also implies that the structural motion is divergence free, although not all structures behave this way. In addition, the structural equations are never actually solved, which may lead to a restriction of the time step to obtain stability of the calculation. Finally, it is only straightforward to determine the type of the boundary conditions for the fluid grid if the fluid surrounds the structure. Non-physical boundary conditions have to be imposed on the boundaries of the fluid grid where the fluid is surrounded by the structure [150].
Another yet similar class within the fixed grid techniques are the fictitious domain (FD) methods. The distributed Lagrange multiplier fictitious domain (DLM/FD) method was originally developed by Glowinski et al. [85] for the simulation of fluids with immersed rigid bodies [86]. Later, it has been extended to deal with the interaction between a fluid and flexible bodies [204]. In this method, the region in the fluid grid that should be occupied by the structure is filled with the same fluid as the remainder of the fluid domain. Constraints with Lagrange multipliers are used to impose that the velocity of this fictitious fluid is equal to the velocity of the solid in the entire structural domain [204]. Figure 6 is a schematic representation of the DLM/FD method for structures with and without volume. Glowinski et al. [86] refer to the immersed boundary method of Peskin [150] as a non Lagrange multiplier based fictitious domain method.
A schematic representation of the fictitious domain (FD) method for structures without (left) and with (right) volume. The vertical and horizontal lines are the fixed fluid grid; the interconnected dots are the Lagrangian solid nodes. A possible location for the Lagrange multipliers is indicated with crosses. Adapted from [196]
Because the FD methods are similar to the IB methods, they have the same advantages and drawbacks. Furthermore, van Loon et al. [118] have shown that the difficulties with accurate calculation of the tractions on the fluid-structure interface can be reduced by adaptive grid refinement in that region. The DLM/FD method has been employed successfully for heart valve simulations where the fluid domain is divided into separate regions when the valve closes [119].
It is also possible to use a cut-cell method, as demonstrated with two-dimensional calculations by Quirk [160]. With a search algorithm, the cells of the fixed Cartesian fluid grid that are overlapped by the Lagrangian solid grid are detected. If a fluid cell is overlapped completely by the structure, it is disabled. By contrast, if there is only partial overlap, then the overlapped part of the fluid cell is cut off. The fluid-structure interface is thus sharply defined in the fluid domain. Moreover, the accuracy near the interface can be improved by adaptive grid refinement. However, the fluid cells near the interface often have an irregular shape and size, which causes difficulties for many solution techniques. Also, the extension to three dimensions is not straightforward.
Wall et al. [196] combined the extended finite element method (XFEM) with a DLM/FD method [83, 198]. The XFEM originates from the simulation of cracks in finite element calculations of structures, without forcing the cracks to coincide with the element boundaries [15]. Wall et al. [196] found that the fluid-structure interface can be represented in the same way as a crack. To this end, enriched finite element basis functions are added to the elements of the fixed fluid grid that are crossed by the fluid-structure interface. This step is straightforward in a DLM/FD method as the position of the interface is known exactly from the structural grid. The additional basis functions are equal to the standard basis functions, multiplied by a jump function at the interface. The coefficients of these enriched basis functions are additional unknowns in the finite element problem, which represent the discontinuity at the fluid-structure interface on the fixed fluid grid.
The main advantage of combining the XFEM with a DLM/FD method is that the real fluid around the structure and the fictitious fluid overlapped by the structure are decoupled. The structure does not have to be incompressible if the fluid is incompressible, nor does the viscosity of the fictitious fluid influence the motion of the structure.
2.2.3 Moving and Fixed Fluid Grid
Wall et al. [196] also combined the advantages of the ALE formulation and fixed grid techniques in an overlapping domain decomposition/Chimera-like (ODD/C) technique [198]. In this technique, the structure is surrounded by a local, boundary-fitted fluid grid with ALE formulation. Both the structure and this ALE fluid grid move over a fixed fluid grid. The part of this fixed grid that is overlapped by the structure is identified with a quadtree or octree search algorithm and then disabled. Around this disabled region, a Dirichlet boundary condition is imposed for the fixed grid. The boundary condition on the outer boundary of the ALE fluid grid is usually of the Neumann or Robin type. The fluid flow on the fixed grid and on the ALE grid are calculated with a Chimera technique [175]. This means that iterations are performed between the solution of the flow equations on the fixed grid and on the ALE grid. The boundary conditions on the one grid are interpolated from the last solution on the other grid. The iterations have reached convergence when the boundary conditions do no longer change significantly. Figure 7 is a schematic representation of the ODD/C technique.
A schematic representation of the overlapping domain decomposition/Chimera-like (ODD/C) method. The vertical and horizontal lines are the fixed fluid grid; the interconnected dots are the Lagrangian solid nodes. The ALE grid is fitted around the structure. The part of the fixed fluid grid that is overlapped by the structure is disabled (dashed line) and surrounded by a Dirichlet boundary condition (thick line). Adapted from [196]
The main advantages of the ODD/C technique are that the values at the fluid-structure interface can be calculated accurately and that incompressibility of the fluid does not imply incompressibility of the solid. Moreover, the ALE fluid grid is attached only to the structure so its quality will be preserved, even when the structure undergoes large translations or rotations. The iterations between the fluid grids is the price to pay.
2.2.4 Particle Methods
Both smoothed particle hydrodynamics (SPH) [140] and the particle finite element method (PFEM) [100] are particle methods that have been applied to fluid-structure interaction. The PFEM uses a Lagrangian formulation for both the solid and the incompressible fluid [101, 102, 144, 145]. Figure 8 is a schematic representation of the PFEM. Each particle is a material point with the density of either the fluid or the solid. Each time step consists of several actions, starting from the cloud of nodes at t n. First, the boundaries of the fluid and solid domain are identified, for example with the α-shape method [59]. When two clusters of nodes are too far apart, they are considered as separate regions. This approach allows for automatic treatment of topology changes. Then, a grid is created in the fluid and solid domain. Normally, an unstructured grid is generated because the shape of the domain and the distribution of the nodes will be irregular. Because grid generation occurs in each time step, the algorithm has to be automatic and fast. Idelsohn et al. [101] employ the extended Delaunay tessellation [99] for this action. Next, the standard finite element method is used to solve the flow equations and the structural equations, both in Lagrangian formulation, for the velocities, pressure and viscous stresses in the fluid domain and the displacements, stresses and strains in the solid domain, all at t n+1. The Lagrangian formulation of the momentum conservation for both the fluid and the solid is given by
with ρ the density, D/Dt the material derivative and \(\vec {v}\) the velocity. \(\vec {f}\) denotes the body forces per unit volume and \(\mathsf{\sigma} \) is the Cauchy stress tensor. Either explicit or implicit coupling between the flow equations and the structural equations can be used. Oñate et al. [144] suggest implicit coupling with iterations between the fluid and the solid, using a fractional step method for the flow equations. During these iterations, a new grid is generated if the current one is too distorted. The resulting velocities are subsequently used to update the node positions, resulting in a cloud of points at the new time level.
A schematic representation of the particle finite element method (PFEM). Adapted from [102]
2.3 Interpolation on the Fluid-Structure Interface
Due to different grid size requirements for the solution of the flow equations and the structural equations, the cells or elements of the fluid and solid grid are usually non-conforming at the interface. When gaps and overlaps occur, the grids are even non-matching (see Fig. 9). In any case, the displacements and tractions have to be transferred from one side of the interface to the other side.
The simplest approach is to use the data from the nearest point on the other side of the interface, the so-called nearest-neighbour interpolation. Higher accuracy can be obtained by means of projection methods [33, 63]. To obtain the value at some point, it is projected on the other grid, followed by an interpolation to calculate the value at the projected point. Several algorithms exist to find the nearest cell or element on the other side of the interface [122]. Also interpolation with splines and radial basis functions can be applied [19].
2.4 Time Discretization
It is important to keep in mind that differences between the time discretization of the flow equations and the structural equations can have unwanted effects, as demonstrated both analytically and numerically by Vierendeels et al. [191]. When different time integration schemes are used in both domains, the discrete acceleration of the fluid and solid at the interface can be different, even though the displacement or velocity is perfectly matched. As a result, spurious oscillations in time can be present in the acceleration and tractions at the interface, without being visible in the displacement and velocity. Fortunately, these oscillations can often be removed by sufficient numerical damping in the time integration schemes.
A simple example of this difficulty can be found in the discretization of the displacement u with the backward Euler method in the fluid domain
and with the Newmark method in the structure domain
with 0≤β≤1 and 0≤α≤1/2. A dot indicates a time derivative. Assume it is enforced that the displacement is the same on both sides of the interface in every time step
to avoid overlap and gaps. If \(u_{f}^{n+1}=u_{s}^{n+1}\) and \(u_{f}^{n}=u_{s}^{n}\), then it follows from Eqs. (21b) and (22b) that
To obtain \(\dot{u}_{f}^{n+1}=\dot{u}_{s}^{n+1}\), α and β would have to be chosen so that the right-hand sides of Eqs. (22a) and (24) are identical. This is impossible because the linear system
has no solution. As a result, it is impossible to enforce equality of the displacements and velocities at the same time for these two different time discretizations.
The geometric conservation law (GCL) or space conservation law (SCL) is another issue related to the time discretization when moving grids are used [50, 76, 115]. For the discrete equations in a control volume to be conservative in time, the volume swept by the control volume’s boundaries must be calculated in a way that is consistent with the time discretization of the control volume’s change in volume. For a finite volume semi-discretization in space, this gives
with V i and A i respectively the volume and the surface of a finite volume cell. This semi-discrete GCL contains only geometric quantities and is universal for a given semi-discretization in space, independent of the time discretization. The time discretization has to be chosen such that a uniform flow is exactly conserved, resulting in a discrete GCL. This discrete GCL characterizes the time discretization scheme and is thus not universal [115].
2.5 Added-Mass Effect
An important concept in fluid-structure interaction simulations is the added-mass, i.e. the mass of fluid which is accelerated by the structure. This concept can be illustrated by means of a piston with a fluid on one side and a spring and damper on the other side (see Fig. 10).
For an inviscid and incompressible fluid, Eqs. (3a) and (3b) projected on the x-axis simplify to


in Ω f . The boundary conditions for the flow at the outlet Γ o and the fluid-structure interface Γ i are
The boundary condition on the wall Γ w disappears due to the projection on the x-axis. The equation for the structure is given by
The mass of the piston is indicated as m, the damping constant is denoted as c and the spring stiffness factor is b. The pressure on the fluid-structure interface Γ i is given by p i .
The fluid velocity can be eliminated from Eqs. (27a) and (27b), giving



The boundary condition on Γ i is obtained by substituting Eqs. (28b) in (27b). The solution of Eqs. (30a), (30b) and (30c) is given by
Substitution in Eq. (29) results in
which can be rewritten as
with the added-mass m a =ρ f HL. This added-mass reduces the natural frequency of the structure from ω to \(\tilde{\omega}\) with
In a partitioned simulation, the flow equation for the interface pressure
and the structural equation
are solved separately. The damping c is neglected in the remainder of this analysis. As an example, the structural equation is discretized using the Newmark method, giving
with h n a combination of terms at time level n.
To find the solution which satisfies both equations simultaneously, coupling iterations can be performed in each time step. If these coupling iterations are indicated with superscript k and the superscript n+1 is omitted for the changing terms, this yields


Equations (38a) and (38b) are solved consecutively for \({\frac { \mathrm {d} ^{2} u}{ \mathrm {d} {t}^{2}}}\) and p i and the counter k is increased after both equations have been solved. This iteration process can be written as \(p_{i}^{k+1}=g(p_{i}^{k})\), which converges if
For the piston problem, the above condition corresponds with
This means that an added-mass which is too large compared to the structural mass and stiffness causes divergence of the coupling iterations.
3 Overview of Simulation Techniques
3.1 Comparison Between Partitioned and Monolithic Solution
There are two approaches to the numerical simulation of fluid-structure interaction problems. In the monolithic approach, the flow equations and the structural equations are solved simultaneously and, hence, the interaction between the fluid and the structure can be taken into account during the solution process. On the other hand, partitioned techniques solve the flow equations separately from the structural equations. In that case, a coupling algorithm is required to incorporate the interaction between the fluid and the structure. This coupling algorithm stipulates in what order the flow equations and the structural equations have to be solved and what the conditions at the fluid-structure interface have to be. If the interaction between the fluid and the structure is strong, the coupling algorithm generally has to use some kind of coupling iterations between the solution of the flow equations and the solution of the structural equations.
The main advantage of the monolithic approach is that no iterations have to be performed between the solution of the flow equations and the solution of the structural equations. In a partitioned simulation of strong interaction, however, both the flow equations and the structural equations have to be solved in each coupling iteration. So, the duration of such a partitioned simulation increases as the number of coupling iterations per time step increases. If, for a given problem, the coupling iterations of some partitioned technique converge slowly, then the monolithic approach has a distinct advantage over that particular partitioned technique. Moreover, not every coupling algorithm is stable in every situation.
Advantages of the partitioned approach are that it reuses reliable and optimized codes to solve the flow equations and the structural equations. Models that have been developed and implemented over the past decades for either flow problems or structural problems are readily available and can be combined. The partitioned approach is also modular, so the software is easier to maintain. The flow equations and the structural equations can be solved with different techniques, particularly suited for these kind of equations. Conversely, monolithic codes typically solve all equations with the same solution technique.
From the above, it should be clear that both the monolithic and the partitioned approach have their strengths and weaknesses. When both approaches are compared in this article, the aim is not to claim that one is better than the other. Another review which compares partitioned and monolithic techniques can be found in [95].
3.2 Monolithic Approach
As the focus of this review is on partitioned techniques, only a brief overview of the monolithic approach is given. In a monolithic code, the flow equations and the structural equations are first discretized in space and time with a method of choice, which results in a system of coupled discrete equations with the flow variables and the structural variables as unknowns. The discrete flow equations are represented by f, the discrete structural equations by s. The vector v groups the flow variables (velocity, pressure, etc.) for the entire fluid domain; the vector u groups the structural variables (displacement, stress, etc.) in the entire solid domain. Both v and u are at the new time level t n+1; the dependence of the solution on the variables at t n,t n−1,… is hidden.
The interaction between fluid and structure is taken into account by calculating all variables at once. As the equations are generally nonlinear, they are often solved with Newton–Raphson iterations [8, 9, 11, 97, 165]. In each Newton–Raphson iteration, a linear system
has to be solved, with the superscript k denoting the Newton–Raphson iteration, Δv k=v k+1−v k and Δu k=u k+1−u k. The notation ∂ v f refers to the Jacobian matrix containing the partial derivatives of f(v,u) with respect to v. All blocks in the Jacobian are evaluated at (v k,u k).
Several authors simplify or approximate the matrix in Eq. (42) or they fix part of the variables while calculating the others. For example, Heil [92] analyzed the effect of neglecting the block above and/or below the diagonal on the convergence of the Newton–Raphson iterations. He noticed that even the omission of one off-diagonal block causes a significant increase in the number of Newton–Raphson iterations. However, he also observed that a block triangular approximation for the Jacobian is a good preconditioner if the system is solved with an iterative linear solver. To reduce the cost of this preconditioner, the Navier–Stokes block can be replaced by a global pressure Schur complement block. Moreover, as the linear system with the preconditioner does not have to be solved exactly, it can be substituted by a limited number of multi-grid cycles. Multi-grid can also be applied to reduce the cost of solving the linear system in Eq. (42) itself. Hron and Turek [96] use geometric multi-grid, i.e. a hierarchy of grids obtained by successive regular refinement of a given coarse grid [20]. They apply the standard defect-correction framework with a V- or F-type cycle. Gee et al. [79] developed an algebraic multi-grid solver for fluid-structure interaction problems.
The derivatives of the momentum and continuity residuals with respect to the interface displacements are referred to as shape derivatives. There are several ways to compute these shape derivative matrices, required for a consistent linearization of the fluid-structure systems. Balaban et al. [5] use both automatic and manual derivation of the shape derivatives in the reference domain and Bazilevs et al. [12] work with a change of variables. Finite differences [127, 128] can be applied, but the resulting derivatives can lead to slower convergence of the Newton iterations compared to exact derivatives from shape differentiation [69]. Furthermore, van der Zee et al. [205] calculate the shape derivatives by remapping to the reference domain.
The complete fluid-structure interaction problem can also be discretized with space-time finite elements [98, 181, 182]. This method discretizes both the spatial domain and the time with finite element basis functions. Consecutive time steps are called “slabs” of the space-time domain. In each time step, Hübner et al. [98] first solve all governing equations without the nonlinearity due to large displacement of the structure, convection in the fluid and deformation of the fluid grid, followed by an update of the fluid grid. Then, two to four iterations are performed to reach convergence. Tezduyar et al. [182] compare what they call block iterative, quasi-direct and direct coupling. Block iterative coupling means that the off-diagonal blocks are neglected and that the flow equations and the structural equations are solved separately, in a partitioned way. In quasi-direct coupling, the dependence of the off-diagonal block in the flow equations on the grid motion is not taken into account. Finally, direct coupling employs the exact Jacobian matrix. In that case, the authors solve the system with an iterative linear solver using finite differences for part of the matrix-vector product.
3.3 Partitioned Approach
In the partitioned approach, the flow equations and the structural equations are solved separately. The code that solves the flow equations is called the flow solver and the code that solves the structural equations is called the structural solver. The partitioned techniques can be further categorized as explicit, implicit or semi-implicit coupling. Another review of these techniques can be found in [66].
The partitioned techniques will be explained using a moving grid flow solver and a Dirichlet–Neumann (DN) decomposition of the coupled problem, as this is the most common decomposition for fluid-structure interaction problems. In a DN decomposition, the flow equations are solved for a given velocity (or displacement) of the fluid-structure interface (Dirichlet boundary condition), while the structural equations are solved for a given traction distribution on the interface (Neumann boundary condition). The displacement of the interface is represented by the vector x and the traction on the interface by the vector y. With these definitions, the flow solver can be written as
This function represents the steps listed in Algorithm 1. Similarly, the structural solver is given by
which represents the steps in Algorithm 2.
Other decompositions are the Neumann–Dirichlet (ND) [32], Robin–Neumann (RN) and Robin–Robin (RR) [4] decomposition. The names of these decompositions contain the types of boundary conditions that have been applied on respectively the fluid and structure side of the fluid-structure interface. In theory, the ND decomposition could be a useful alternative to the DN decomposition. In practice, however, it is rather involved when using a moving grid flow solver because the flow equations and the equations that govern the deformation of the fluid grid have to be solved simultaneously for the velocity, the pressure and the displacement of the fluid grid.
A disadvantage of the DN decomposition is that an enclosed domain or a domain with only velocity boundary conditions combined with an incompressible fluid causes difficulties. An example of such a problem is a balloon which is being filled with water. If the change in volume of the fluid domain due to the displacement of the structure is not compatible with the net volumetric influx caused by the velocity boundary conditions (if present), the mass conservation cannot be satisfied for the fluid. Moreover, the pressure in the flow problem alone is defined up to an arbitrary constant, whereas the physical pressure level is completely defined in the coupled problem.
The DN decomposition with interface artificial compressibility [46] and the RN decomposition do not suffer from these problems. Küttler et al. [110] solve the problems of the DN decomposition by adding the conservation of the fluid’s volume as a constraint to the structural equations. The Lagrange multiplier for that constraint is the constant that has to be added to the pressure in the fluid domain to obtain the physically correct pressure. As the authors mention themselves, the addition of the volume constraint in the structural equations couples all interface displacements, which is undesired for the solution of the structural equations.
On the following pages, several coupling algorithms are described. They are classified as explicit, implicit or semi-implicit coupling.
3.3.1 Explicit Coupling
Several explicit (also known as loosely or weakly coupled) partitioned techniques exist [64, 65, 116, 153, 154, 209, 210]. These techniques solve the flow equations and the structural equations separately and only once in each time step. Therefore, these techniques do not impose both equilibrium conditions on the fluid-structure interface exactly, which results in restrictions on the time step for stability reasons. It has been shown that the added-mass effect causes this instability of explicit coupling with an incompressible fluid and a rather flexible structure [32, 77]. However, explicit coupling is suitable for aero-elastic simulations [25]. Farhat et al. [64] note that for these simulations, it is not clear that a better computational efficiency cannot be obtained simply by reducing the time step and performing the simulation using a good explicit coupling technique instead of using a technique with coupling iterations, unless no solution can be found with explicit coupling. Typically, explicit coupling requires a smaller time step size but less computational effort per time step due to the absence of coupling iterations within the time step. A smaller time step can be used for the flow solver than for the structural solver, which is called subcycling.
The most basic explicit coupling technique is the conventional serial staggered (CSS) scheme [116]. This technique consists of the steps in Algorithm 3 to go from time level t n to t n+1, with a superscript n to indicate the time level.
This scheme is only first-order accurate in time, whatever the time accuracy of the flow solver and the structural solver is. Moreover, the maximal time step in a CSS simulation is generally much smaller than that of the flow solver and the structural solver alone [64]. In the generalized serial staggered (GSS) scheme, a prediction of the displacement of the interface is added to line 1, based on the displacements in previous time steps. Also, a correction of the fluid traction is added to line 2.
In the improved serial staggered (ISS) scheme of Lesoinne and Farhat [116], the flow equations and the structural equations are not solved at the same time levels. By contrast, the flow variables are calculated at time levels
while the structural variables are calculated at
as shown in Algorithm 4. If both solvers are second-order accurate in time and the flow solver satisfies the geometric conservation law, this ISS scheme is also second-order accurate in time.
Higher-order time accuracy was studied by van Zuijlen and Bijl [207]. They integrate the flow equations and the structural equations in time with an implicit Runge–Kutta scheme, except for the coupling terms, which are integrated in time with an explicit Runge–Kutta scheme of the same order. This implicit/explicit (IMEX) time integration allows for a partitioned solution as well as accuracy in time of arbitrary order. Because multi-step implicit time integration requires more work per time step, the authors also analyzed the time accuracy of the solution as a function of the amount of work to obtain it. For the one-dimensional linear piston problem [17, 154], the third- and fifth-order IMEX scheme were computationally more efficient than a monolithic solution with the second-order backward difference integration.
Later, van Zuijlen et al. [209] investigated the effect of a coarse grid correction or prediction. In their study, only the fluid grid was coarsened. For the correction, the difference between the implicit monolithic solution and the IMEX partitioned solution is restricted to the coarser grid. Subsequently, a calculation on the coarse grid yields the correction, which is then prolongated to the original grid and added to the solution. For the prediction, on the other hand, the difference between a monolithic solution with implicit and explicit time integration is restricted to the coarser grid. The prolongation of the result on the coarse grid is then added to a standard extrapolation based on previous time steps. This sum is used as the starting value for the IMEX partitioned solution on the fine grid. Moreover, the numerical experiments demonstrate that the coarse grid calculations do not have to be performed monolithically; one iteration between the flow solver and the structural solver is sufficient to improve the accuracy of the simulation.
For the explicit partitioned solution of fluid-structure interaction problems with incompressible fluids, finite element techniques based on Nitsche’s principle have been developed [29, 30]. Nitsche’s principle weakly enforces a Dirichlet boundary condition, instead of the more traditional strong enforcement of a Dirichlet boundary condition which imposes that the function spaces satisfy this boundary condition. This principle is only used for the kinematic equilibrium condition on the fluid-structure interface; other Dirichlet boundary conditions can be strongly enforced. The fluid-structure problem with Nitsche’s formulation can then be rewritten in a partitioned way, resulting in a fluid problem with Dirichlet–Nitsche transmission condition and a structure problem with a Robin transmission condition. This Robin boundary condition originates from the Nitsche penalty term. The key to stabilising this scheme is a weakly consistent penalty term in the fluid problem to control the spurious oscillations of the fluid pressure at the interface. A few defect correction iterations are used to recover the time accuracy of the corresponding implicit coupling scheme.
Guidoboni et al. [90] proposed an explicit kinematically coupled time-splitting scheme. As opposed to classical partitioned schemes, which rely on splitting the fluid from the structure, this strategy is based on splitting the structure equation into an elastic and a hydrodynamic part. By treating the elastic part separately, a wide range of structure models can be applied. The hydrodynamic part consists of the fluid stress acting on the interface and viscoelastic terms. This part is solved together with the fluid problem, so the inertia of both fluid and structure are taken into account at the same time, which avoids instabilities due to the added-mass effect. The acceleration term in the structural equation is rewritten in terms of the fluid velocity at the interface using the kinematic coupling condition and the fact that the structure is thin. The splitting error depends on the physical parameters of the solid. This explicit scheme corresponds with using a generalized Robin boundary condition to include the structural inertia and damping into the flow equations [70]. As this non-incremental scheme may lack accuracy, Fernandez [67] extended this approach to incremental schemes. Optimal accuracy is achieved by extrapolating the displacement in a first step and correcting it in a second step. Subsequently, this scheme has been generalized to thick structures with linear elasticity [70]. However, the non-uniformity of the discrete operators only yields quasi-optimal accuracy for thick solids. Stability analysis demonstrated that these explicit Robin–Neumann schemes can be stable, independent of the added-mass.
3.3.2 Implicit Coupling
Implicit (or strongly coupled) partitioned techniques enforce the equilibrium of the traction and velocity (or displacement) on the fluid-structure interface in each time step. This can be achieved with iterations between the solvers or with Newton–Raphson iterations.
Jacobi (see Algorithm 5) and Gauss–Seidel (see Algorithm 6) iterations between the solvers are the most basic implicit coupling techniques. The same notations and definitions as for the explicit coupling are used. However, the superscript n+1 is replaced by a superscript k+1 to indicate the coupling iteration within the time step as all variables are at time level t n+1. The values that are calculated by the solvers are indicated with a tilde, to distinguish them from the values that are provided to the solvers in the same coupling iteration. The notation \({ {\boldsymbol {\mathcal {S}}}\circ {\boldsymbol {\mathcal {F}}}}\) indicates that the result of the function \(\boldsymbol{\mathcal{F}}\) is given as argument to the function \(\boldsymbol{\mathcal{S}}\). The residual \(\boldsymbol{r}^{k}=\tilde{\boldsymbol{x}}^{k}-\boldsymbol{x}^{k}\) has to become smaller than the tolerance ε o to reach convergence.
The Jacobi iteration scheme begins from suitable extrapolations x 0 and y 0, based on previous time steps. On the other hand, Gauss–Seidel iterations only require the extrapolation x 0. In the Jacobi scheme, the flow solver and the structural solver can be executed in parallel. Therefore, this is called an additive or parallel Schwarz procedure in the domain decomposition community [184]. By contrast, the solvers in a Gauss–Seidel scheme have to be executed sequentially, so this is a multiplicative or serial Schwarz procedure [129]. Gauss–Seidel iterations between the flow solver and the structural solver correspond to Richardson iterations on the FSI problem.
In Gauss–Seidel iterations, the displacement at the beginning of the iteration is identical to the one calculated by the structural solver in the previous iteration, so
Consequently, a Gauss–Seidel iteration can be written in fixed-point formulation
Is has frequently been observed that Jacobi and Gauss–Seidel iterations between the flow solver and structural solver within the time step converge slowly, if at all, especially if the fluid is incompressible. However, it has been demonstrated that the convergence of Gauss–Seidel iterations is accelerated if the influence of the flow on the structure is included in the structural solver by means of an approximated added-mass matrix [32]. This added-mass matrix represents the effect of the flow on the structure, reformulated as a mass matrix in the structural equations. As will be explained in Sect. 4, an acceleration can also be obtained if a local, scalar approximation for the structural solver is substituted in the flow solver [42, 142].
Both the interface artificial compressibility (IAC) technique [46, 163, 190] and generalized Robin boundary conditions [4, 142] are based on a local, scalar approximation for the structural solver substituted in the flow solver (see Sect. 6). The former creates a linear approximation for the structural solver and includes this relation in the flow solver as a source term in the continuity equation of the control volumes adjacent to the fluid-structure interface; the latter transforms the structural model into a Robin boundary condition in the flow solver.
The convergence of Gauss–Seidel iterations can also be accelerated by Aitken relaxation [103, 108, 138, 139]. This technique adds a dynamically varying relaxation factor ω k to the Gauss–Seidel iterations
The relaxation factor is adapted based on the result of the previous iterations
More information on Aitken relaxation is provided in Sect. 5. Steepest descent relaxation [108] is another technique with a varying relaxation factor, but it exhibits stepwise or zig-zag convergence, which is well understood and typical of steepest descent methods [143].
Vector extrapolation uses a longer sequence of interface displacements to approximate the correct interface displacement. Vector extrapolation methods can be classified into two families. The first family contains the minimal polynomial extrapolation (MPE) method [31], the reduced rank extrapolation (RRE) method [58, 133] and the modified minimal polynomial extrapolation (MMPE) method [21, 157, 174]. The second class includes the topological ϵ-algorithm (TEA) [21] and the scalar and vector ϵ-algorithm (SEA and VEA) [202]. When applied to linearly generated vector sequences, the MPE, the RRE and the TEA methods are mathematically equivalent to the method of Arnoldi [166], the generalized conjugate residual (GCR) method [60] (which is mathematically equivalent to the generalized minimal residual (GMRES) method [168]) and the method of Lanczos [167], respectively [173].
Küttler and Wall [109] described the application of the first family of vector extrapolation techniques to fluid-structure interaction. Starting from the current interface displacement x k, m Gauss–Seidel iterations are performed to generate the required converging sequence of interface displacements x k,x k+1,…,x k+m. Generally, a fixed relaxation factor should be applied in these iterations to avoid divergence. These iterations also bring about a sequence r k,r k+1,…,r k+m−1, with \(\boldsymbol{r}^{k+i}=\tilde{\boldsymbol{x}}^{k+i}-\boldsymbol{x}^{k+i}\). Based on this second sequence, an extrapolation is constructed for the residual vector
The unknown extrapolation factors α i are calculated by minimizing \(\Vert\hat{\boldsymbol{r}}^{k+m}\Vert_{2}\). The minimization of \(\Vert\hat{\boldsymbol{r}}^{k+m}\Vert_{2}\) is then performed using Eq. (51) with the α i as variables. The difference between the vector extrapolation methods lies in how this minimization is performed. The MPE, RRE, MMPE and TEA method require the solution of the equations
for i=0,…,m−2 under the constraint
The elements of the matrix A are given by
-
A i,j =(r k+i)T(r k+j) for the MPE method,
-
A i,j =(Δr k+i)T(r k+j) for the RRE method,
-
A i,j =(s i)T(r k+j) for the MMPE method,
-
A i,j =(s)T(r k+j) for the TEA method,
for i=0,…,m−2 and j=0,…,m−1 with Δr k+i=r k+i+1−r k+i. The vectors s i (with i=0,…,m−2) are a set of linearly independent vectors and s is an arbitrary fixed vector. Once the coefficients α i are known, the extrapolation for the interface displacement is calculated as
It would be difficult to choose the number of Gauss–Seidel iterations m between two extrapolations of the interface displacement in advance. Therefore, the extrapolation \(\hat{\boldsymbol{r}}\) is calculated after each Gauss–Seidel iteration. The extrapolation of the displacement is only performed when this vector \(\hat{\boldsymbol{r}}\) has become smaller than a predefined tolerance in some norm. Although vector extrapolation seems promising compared to Aitken relaxation because it takes into account a sequence of interface displacements, it turns out to be only slightly faster [109, 111].
Newton–Raphson techniques can also be used in partitioned simulations. These coupling algorithms generally display faster convergence but it is often difficult to obtain the Jacobian needed for Newton–Raphson iterations due to limitations of the flow solver and structural solver [53]. Newton–Raphson iterations can be applied either to the system with all variables in Eq. (41) or to the system condensed on the fluid-structure interface.
The traction on the interface y can be eliminated from Eq. (55), resulting in an equation for the interface displacement only
The introduction of a residual operator
with \({\boldsymbol {\mathcal {I}}}\) the identity operator of appropriate dimension, yields a short equation with x as unknown.
The Jacobian of \({\boldsymbol {\mathcal {R}}}\) with respect to x will further be denoted as \({\boldsymbol {\mathcal {R}}}'\). In each Newton iteration, a linear system
has to be solved, with Δx k=x k+1−x k.
Michler et al. [135] solve Eq. (58) with a Newton–Krylov solver. In particular, they use the generalized minimal residual (GMRES) method [168] as Krylov solver for the linear system in Eq. (59). Because the displacement of the interface is the unknown in Eq. (58), they call this technique Interface-GMRES. In each Newton step, they first perform a number of relaxed Gauss–Seidel iterations to construct a linear approximation to the residual operator \({\boldsymbol {\mathcal {R}}}(\boldsymbol{x})\). With this linear approximation, they calculate the matrix-vector products for the Krylov solver. However, because the solution of a linear system with the Jacobian of the residual operator is circumvented in this way, Küttler and Wall [109] argue that this is not a Newton technique so that the name Newton–Krylov is not appropriate. They refer to this technique as RRE-based, which is equivalent to GMRES for linearly generated vector sequences. Section 5 provides an in-depth analysis of this technique, using the terminology given by the developers.
The matrix-vector products that have to be calculated during the solution of Eq. (59) with a Krylov solver can also be approximated by a finite difference approximation [81, 111]. The product of \({{\boldsymbol {\mathcal {R}}}'}^{k}\) with an arbitrary vector z is then calculated as
In this case, the function \({\boldsymbol {\mathcal {R}}}\) has to be evaluated in each Krylov iteration within each Newton iteration. However, the function \({\boldsymbol {\mathcal {R}}}\) calculates the residual of the coupled problem condensed on the interface, which requires the solution of the flow equations and the structural equations in the entire domain. Hence, this function is very expensive to be evaluated repeatedly inside each Newton iteration. Moreover, this approach is sensitive to the parameter ε when it is set manually by the user [81]. This might be remedied with the techniques to determine an appropriate value for ε automatically as listed by Knoll and Keyes [107].
The most difficult part in the calculation of
is usually the Jacobian of the flow solver \(\boldsymbol{\mathcal{F}}'\). Therefore, Gerbeau and Vidrascu [81] proposed approximating the Jacobian of the flow solver by the Jacobian of a reduced-physics model, indicated as \(\widehat{\pmb{\mathcal{F}}'}\). For the simulation of blood flow in arteries and several other applications, the added-mass effect of the flow on the structure is the most important feature. This mechanism can be reasonably captured with a linear, inviscid model for the incompressible fluid. Such a model is obtained by assuming that the fluid domain is fixed and that the pressure p and velocity \(\vec {v}\) satisfy



with ρ f the fluid density and \(\vec {u}\) the displacement of the structure. Appropriate boundary conditions have to be applied on Γ f /Γ i . After elimination of \(\vec {v}\) by using \(\nabla\cdot \vec {v}=0\), Eqs. (62a), (62b) and (62c) are given by


with ∂p/∂n the normal derivative of the pressure and \(\vec {n}\) the unit normal on the interface. These equations are not used to approximate the flow solver \(\boldsymbol{\mathcal{F}}\); only the Jacobian of the flow solver \(\widehat{\boldsymbol{\mathcal{F}}'}\) is approximated using Eqs. (63a) and (63b). The product of \({\boldsymbol {\mathcal {R}}}'\) with an arbitrary vector z is calculated according to the steps listed in Algorithm 7.
This solution to the Poisson equation on line 1 can be computed quickly. On line 3, a Jacobian K of the structural behaviour appears, but this matrix has normally already been factorized as the structural equations need to be solved to evaluate the residual \({\boldsymbol {\mathcal {R}}}(\boldsymbol{x}^{k})\). This matrix represents the relation between the displacement of the fluid-structure interface and the load on the structure. Hence, also the linear system on line 3 can be solved quickly. With this technique, the propagation of a pressure wave in a cerebral aneurysm and a carotid bifurcation have been simulated [82].
Furthermore, a stability analysis of Gauss–Seidel iterations between a solver for incompressible flow and a structural solver (see Sect. 4) demonstrates that only displacements of the interface with a low wave number are unstable for the flow in a piece of a large artery. Consequently, a low-rank approximation of the Jacobian \({\boldsymbol {\mathcal {R}}}'\) (or \(\boldsymbol{\mathcal{F}}'\) and \(\boldsymbol{\mathcal{S}}'\)) is sufficient to obtain fast convergence of the Newton–Raphson iterations. This principle is implemented by the interface block quasi-Newton technique with least-squares models for the Jacobian of both solvers (IBQN-LS) [192] and by the interface quasi-Newton technique with an approximation for the inverse of the Jacobian of the coupled problem from a least-squares model (IQN-ILS) [43]. The former solves Eq. (55), the latter Eq. (58). Recently, multi-solver [47] and multi-level [48] versions of these techniques have been introduced. Because both techniques only manipulate variables on the fluid-structure interface, they can be used to couple black-box commercial codes. Section 5 describes these techniques in detail.
Two solvers can also be coupled with a block Newton method. Many variants of the block Newton method exist [112]. Artlich and Mackens [3] refer to Keller [105] for the block elimination (BE) method which solves Eq. (42) in a partitioned way. The approximate Newton (AN) method of Chan [35] is a variation of the block elimination method that is only suitable for systems with a small number of equations in s. However, both the block elimination method and the approximate Newton method require knowledge of ∂ v f,∂ u f,∂ v s and ∂ u s.
Starting from the AN method, Artlich and Mackens [3] developed the iterative approximate Newton (IAN) method to couple two iterative solvers without knowing the Jacobian blocks. This method was later named approximate tangential block Newton (ATBN) method by Mackens et al. [121] and Menck [131]. Matthies and Steindorf [127] applied this method to fluid-structure interaction simulations [128, 129, 177]. They assume that an iterative solver is available for both the flow problem
and the structural problem
The superscript i denotes the iteration within the solvers. Of course, the structural variables are constant during the iterations in the flow solver and vice versa. If one of the solvers is a direct solver, it is considered as an iterative solver that finds the solution in one iteration. However, in that case this approach can become very expensive unless the matrices in the direct solver do not have to be factorized again for each calculation. Yeckel et al. [203] analyzed the special case where the iterative solvers are Newton solvers and developed the approximate block Newton (ABN) method and variations on the ATBN method with block diagonal preconditioners.
In the paragraphs below, the implementation of Matthies and Steindorf [128] is summarized. To calculate the solution of Eqs. (66a) and (66b) with a block Newton scheme, a linear system
has to be solved in each Newton iteration, with Δv k=v k+1−v k and Δu k=u k+1−u k. ∂ v F denotes the Jacobian of F with respect to v and I is the unit matrix of appropriate dimension. Because the linear system is solved within a Newton iteration, the superscript k remains constant during the solution of the linear system and therefore it is dropped in the remainder of this explanation. The system in Eq. (67) is first reformulated as an equation in Δu only. Therefore, the change of the flow variables Δv is isolated symbolically from the first row, giving
with
The expression for Δv from Eq. (68) is then substituted in the second row of Eq. (67), which yields the equation in Δu only
with
The matrix S is the Schur complement of I−∂ v F in the block Jacobian of Eq. (67). Once Δu has been calculated from Eq. (71), the result is inserted into Eq. (68) to obtain Δv. The procedure to calculate Δv and Δu consists of four steps, listed in Algorithm 8.
On line 1, a Newton iteration is performed to solve the flow problem (Eq. (66a)) with u fixed. The solution is (v+δ v,u) and the following steps are linearized around this point. The residual of the structural problem (Eq. (66b)) at this point is calculated on line 2 by means of linearization. On line 3, a Newton iteration is performed to solve the structural problem for u, while taking into account the effect of u on v due to the flow problem in a linearized way. Finally, δ v, i.e. the change of v to solve the flow problem with fixed u, is corrected for the influence of Δu, which results in Δv. This process is depicted in Fig. 11 for two dimensions. The method was called approximate tangential block Newton because the step on line 3 is parallel to the curve v=F(v,u), albeit in a linearized way.
The approximate tangential block Newton method in two dimensions. Adapted from [121]
The equation
on line 1 can be interpreted as a Newton linearization around δ v=0 to solve
for δ v with fixed v and u. Instead of using the Newton linearization from Eq. (74) to solve Eq. (75), δ v is calculated approximately with the iterative flow solver. To this end, v+δ v is replaced by w, followed by m>1 iterations with the flow solver
with i=0,…,m−1. These iterations start from w 0=v and they yield δ v≈w m−v.
For the calculation of r on line 2, the second and third term in Eq. (73) are considered as a linearization of −S(v+δ v,u) around δ v=0. As a result, r can be calculated with one iteration of the structural solver
The solution to the linear system
for Δu on line 3 is calculated with an iterative linear solver. Such a solver only requires a procedure to multiply the system matrix by an arbitrary vector. Therefore, the system matrix S does not have to be known explicitly, which also implies that it does not have to be stored in the computer’s memory. The product of S with some arbitrary vector z is approximated by finite differences with a small step size ε.
In the previous equation, the product C(ε z) appears, which is further denoted as c. To calculate c, the system
has to be solved. The right-hand side of Eq. (80) is approximated with finite differences, giving
This last system is solved by considering it as a Newton linearization around c=0 for
As on line 1, Eq. (82) is solved by replacing v+c by w, followed by m′>1 iterations with the flow solver
with i=0,…,m′−1. These iterations start from w 0=v and they yield c≈w m−v.
As Δu is now known, Δv is calculated on line 4 using
The product CΔu is calculated in the same way as C(ε z) on line 3.
3.3.3 Semi-Implicit Coupling
To overcome the stability problems of explicit coupling without the cost of implicit coupling, Fernandez et al. [71] developed a partially implicit, partially explicit coupling technique. This semi-implicit technique does not impose the equality of tractions and velocity on the fluid-structure interface exactly but remains stable in several cases that cannot be solved with explicit coupling. Only the fluid pressure is coupled implicitly to the structure to make the calculation stable. All other terms in the flow equations are coupled explicitly to reduce the duration of the calculation. This splitting of the flow equations is straightforward if they are solved with a Chorin-Temam projection scheme [37, 179].
In the description of the time semi-discrete version of this technique, the Navier–Stokes equations are discretized in time with the backward Euler scheme. Assuming that everything is known at time t n, the steps in Algorithm 9 are performed to compute the values at time t n+1.
To calculate the position of the fluid grid on line 1, the structural displacement is extrapolated as \(\tilde{\vec {u}}^{n+1}\), based on previous time steps. This grid velocity at the interface is extended to the rest of the fluid domain using Eq. (11), followed by an update of the grid position using Eq. (17).
In the explicit ALE-advection-diffusion sub-step on line 2, \(\vec {v}^{*}\) is calculated from
in Ω f and on Γ i , respectively. Although this is the explicit step of the coupling, the flow solver itself can be implicit. In the second term of Eq. (85a), \(\vec {v}^{n}\) is used in order to obtain a linear problem but this can be replaced by \(\vec {v}^{*}\) without influencing the coupling strategy.
On line 3, the fluid projection sub-step is coupled with the structure using one of the implicit coupling techniques (see Sect. 3.3.2). If the Dirichlet–Neumann decomposition of the coupled problem is used, the fluid projection sub-step is given by


in Ω f with a known velocity on Γ i
This Darcy problem can be reformulated as a Poisson equation
which can be solved quickly. Afterwards, the velocity is corrected as
Subsequently, the structural equations are solved for a given traction on the interface.
The update of the fluid grid (line 1) and the expensive ALE-advection-diffusion sub-step (line 2) are performed only once in each time step, which reduces the computational cost significantly. For the calculation of a pressure wave in a straight, flexible 3D tube, this semi-implicit scheme is 25 times faster than Aitken relaxation and 5 times faster than a partitioned Newton solver with exact Jacobian or approximate Jacobian from a reduced-physics model [71]. In the semi-implicit simulations of this case, the implicit coupling between the structure and the projection sub-step has been performed with Newton iterations using exact Jacobians. As the projection sub-step is performed on a fixed grid, the Jacobian of the flow problem can be calculated more easily than in the case of implicit coupling because no shape-derivatives have to be calculated. However, numerical experiments by Fernandez et al. [71] indicate that when the implicit coupling between the projection sub-step and the structure is performed with Gauss–Seidel iterations, the semi-implicit scheme might be slower than the implicit coupling with Newton iterations.
3.4 Other Coupled Problems
Most coupling algorithms described in this section can be used for coupled problems in general. Some applications in fields other than fluid-structure interaction are listed below.
Yeckel et al. [203] solve conjugate heat transfer problems that represent melt crystal growth processes. Therefore, they couple a furnace radiation model with a melt crystal growth model using the ABN method. The partitioned spatial regions are each modelled by independent heat transfer codes and linked by temperature and flux matching conditions at the common boundaries.
Jahromi et al. [104] analyze the effect of excavations on the frame of a building. A code that models the behaviour of the soil during excavations is coupled with a code for nonlinear structural dynamics using a variation of the IBQN-LS technique [192]. The interaction between the models occurs at a relatively small number of points.
Artlich and Mackens [3] calculate the combustion in a fluidized bed reactor under pressure. Their model takes into account the exothermic chemical reaction between C and O2 to form CO2. The calculation of the carbon and oxygen concentrations is performed separately from the calculation of the temperature field.
In the last example, there is only one domain and data are exchanged throughout the domain. In the other examples, the domains do not overlap and data are exchanged at the common boundary of the domains. The following sections will only discuss coupling algorithms applied to fluid-structure interaction.
4 Stability Analysis of Gauss–Seidel Coupling Iterations
The previous section illustrates that a partitioned simulation of strong interaction between a fluid and a structure requires a coupling algorithm with some kind of iteration between the solvers. These iterations within the time step are necessary to calculate the value of the degrees of freedom for which the flow equations, the structural equations and the equilibrium conditions on the interface are satisfied simultaneously.
The convergence of Gauss–Seidel iterations depends on several parameters, such as the geometry, the time step, the structural stiffness and the ratio of the fluid density to the solid density. The exact relation between these parameters and the convergence of the coupling iterations is different for every coupling technique.
A stability analysis is the obvious means to gain a clear understanding of a coupling technique’s behaviour. Such a stability analysis has been performed by Förster et al. [77] who analyzed the effect of the aforementioned parameters on algorithms without coupling iterations. Causin et al. [32] studied algorithms with and without coupling iterations using Dirichlet–Neumann and Neumann–Dirichlet decomposition. They derived the maximal relaxation factor that leads to convergence of the coupling iterations as a function of these parameters for a simplified model of blood flow in an artery and then validated the formulas with numerical experiments. Badia et al. [4] derived the relaxation factor for the same case but with Robin–Dirichlet and Robin–Neumann decomposition.
Vierendeels et al. [191] analyzed the stability of coupling iterations for the one-dimensional motion of a rigid object in a channel as a function of the density ratio and the size of the gap between the object and the channel. In their model, the structure only has inertia and no stiffness. Consequently, the inertia of the fluid and of the structure are balancing each other out, which results in an error amplification factor of the coupling iterations that is independent of the time step. The difference between compressible and incompressible fluids is analyzed by van Brummelen [25] for the partitioned simulation of the flow over a flexible panel.
In this section, a von Neumann stability analysis on Gauss–Seidel coupling iterations is reviewed, also for a simplified model of blood flow in an artery. This analysis results in a modal decomposition of the error on the interface’s displacement during Gauss–Seidel coupling iterations and the error amplification factor that corresponds with each mode. Such a modal decomposition provides more information than a single relaxation factor and explains the fast convergence of the quasi-Newton techniques with a Jacobian from a least-squares model that will be introduced in the following section.
The stability analysis of the Gauss–Seidel iterations is first performed with a simple structural model that consists of independent segments without structural inertia such that a linearized model for the structure can be substituted in the flow solver [42]. Subsequently, an extension of this analysis is reviewed with a more complex structural model that includes both the interaction between the segments of the tube and the structural inertia but without a substitution of the structural model in the flow solver [44].
4.1 Independent Tube Segments Without Structural Inertia
4.1.1 Description of the Model
The flow in an artery is simplified to the unsteady, incompressible flow in a straight, flexible tube with a circular cross-section and length L, depicted in Fig. 12. The model is one-dimensional and gravity and viscosity are not taken into account. The flow is governed by the continuity and momentum equation which can be written in conservative form as


with z the coordinate along the axis of the tube, a=πr 2 the cross-sectional area of the tube and r the inner radius. t is the time, v the velocity along the axis of the tube, p′ the pressure and ρ f the density of the fluid.
The behaviour of the elastic tube wall is described with a Hookean constitutive relation. The structure contains no mass, as the inertia of the tube wall is neglected with regard to that of the fluid. An axisymmetric model is used in the coordinate system (r,φ,z), with φ the angle in the cross-sectional plane as indicated in Fig. 12. The stress in the tube wall in circumferential direction σ φφ is approximated as
with E the Young’s modulus and r o the radius for which σ φφ =σ φφo . As other stress components are neglected, this model only allows for radial motion of the tube wall. The force balance on the fluid-structure interface is
with h the thickness of the tube wall.
By substituting the constitutive equation (Eq. (90)) and the kinematic pressure p=p′/ρ f in Eq. (91), the following relation holds
with \(r_{o} p'_{o}=\sigma_{\varphi\varphi o}h\). This can be rewritten as
by using a=πr 2 and by introducing the Moens–Korteweg wave speed
The kinematic pressure p=p′/ρ f is referred to as the pressure in the remainder of this section.
The tube wall thus has a constitutive law of the form a=a(p), with the cross-sectional area only a function of the local pressure. The wave speed c is defined as
and with Eq. (93), it is given by
The straight tube with circular cross-section and length L is discretized with a one-dimensional grid with N cells of length Δz, as indicated in Fig. 12. The fluid velocity and pressure are stored in the cell centres. Central discretization is used for all terms in the continuity and momentum equation, except for the convective term in the momentum equation which is discretized with a first-order upwind scheme. The time discretization scheme is backward Euler and the time step is indicated with Δt. The conservation of mass and momentum in a control volume around cell centre i is expressed by the following system of equations
for v i ≥0. The subscripts i, i+1 and i−1 indicate the cell centres (i=1,…,N) and the subscript i±1/2 signifies the values calculated at the cell interfaces, v i−1/2=(v i−1+v i )/2 and v i+1/2=(v i +v i+1)/2. The superscript n denotes the previous time level; the superscript n+1 for the new time level is omitted. A pressure stabilization term with coefficient α=a o /(v o +Δz/Δt) has been added in the continuity equation to prohibit pressure wiggles due to central discretization of the pressure in the momentum equation, with v o the reference flow velocity. This stabilization term can be written as
on Cartesian grids. In Eq. (97a), the first term and the combination of the second and the third term are proportional to Δz but they do not scale with Δt. For large Δt, the stabilization term is proportional to Δz 2 so it scales with Δz with respect to the other terms in Eq. (97a); for small Δt, the stabilization term is proportional to ΔtΔz so it scales with Δt with respect to the other terms. Thus, the stabilization term does not affect the accuracy of the scheme because the other terms are also first-order accurate [189].
The geometrical discretization of the elastic problem is identical to that of the flow problem to avoid errors in the data transfer between the flow and the structure. Equation (93) is discretized as
and linearization of this equation around the reference state (subscript o) results in
For Gauss–Seidel coupling iterations, Eqs. (97a) and (97b) are solved for \(\tilde{v}^{k+1}\) and \(\tilde{p}^{k+1}\) with a fixed geometry \(a^{k+1}=\tilde{a}^{k}\). Similarly, the cross sectional area \(\tilde{a}^{k+1}\) is calculated from Eqs. (99a) and (99b) with a fixed pressure \(p^{k+1}=\tilde{p}^{k+1}\). As in the previous sections, the tilde indicates a value which is calculated in the current coupling iteration.
The analyze the influence on the convergence of the Gauss–Seidel iterations, the linearized elastic relation (Eq. (99b)) is included in the flow equations. Therefore, \(a^{k+1}=\tilde{a}^{k}\) is substituted by \(\tilde{a}^{k}+\gamma_{j} a_{o}/c_{o}^{2}(\tilde{p}^{k+1}-p^{k})\) in Eqs. (97a) and (97b), which is an approximation for \(\tilde{a}^{k+1}\). These substitution terms can be activated or deactivated by setting the parameters γ j (j=1,…,4) to 1 or to 0, which allows to identify the terms that prevent the instability of the Gauss–Seidel coupling iterations. Quadratic terms in p are omitted. Irrespective of this linear substitution, the structure equation itself can be linear or nonlinear.
The substitution terms are useful because various coupling schemes ranging from monolithic to partitioned can be studied. If all the coupling terms are enabled (γ j =1, j=1,…,4) and the linear elastic relation (Eq. (99b)) is used, then the modified coupling scheme is in reality a monolithic code. The importance of the different coupling terms is investigated in the following paragraphs.
4.1.2 Von Neumann Stability Analysis
The stability of the Gauss–Seidel coupling scheme with extra coupling terms in the flow equations is now investigated with von Neumann stability analysis, which does not take into account the boundary conditions. The velocity, pressure and cross-sectional area at the new time level in Eqs. (97a), (97b), (99a) and (99b) are written as the sum of the coupled solution and the remaining error in the coupling iteration (indicated with an overbar). The coupled solution at both time level n and n+1 is in turn linearized as the sum of the reference value (subscript o) and a perturbation (indicated with a hat). For the velocity, this gives
for i=1,…,N and analogously for the pressure and the cross-sectional area. Subsequently, the equations are linearized by neglecting all nonlinear combinations of the error terms and the perturbations. Because the equations linearized around v o , p o and a o are also satisfied by the coupled solution, all perturbations from the current and previous time step cancel out.
The error terms are expanded as the sum of N Fourier modes, giving
for the error on the velocity (i=1,…,N) with \(\jmath=\sqrt{-1}\) and \(\omega_{\ell}=\frac{2\pi\ell}{L}\) the (angular) wave number.
The amplification of each wave number can be studied separately since the equations are linear in \(\bar{v}\), \(\bar{a}\) and \(\bar{p}\). Therefore, \(\bar{v}_{i}^{k+1}\) is substituted by \(\check{v}_{\ell}^{k+1}\exp(\jmath\omega_{\ell}i\Delta z)\) (ℓ=0,1,…,N/2 if N is even and ℓ=0,1,…,(N−1)/2 if N is odd) and analogously for the error on the pressure and the cross-section. The dimensionless product ω ℓ Δz=2πℓ/N is further denoted as the wave number ϑ ℓ . For clarity, the inverted hat and the subscript ℓ are omitted. This results in the following equations, with \(a^{k+1}=\tilde{a}^{k}\) and \(p^{k+1}=\tilde{p}^{k+1}\).
By combining Eqs. (102a) and (102b), the amplification factor of each mode in the error can be calculated. In each coupling iteration, the error on the interface’s position with wave number ϑ is amplified by
with
which is a function of ϑ and the parameters v o , a o , c o , Δz and Δt. The iteration scheme will converge for given values of the parameters if the error amplification factor μ is less than one for all ϑ.
To study the stability of the coupling iterations as a function of the structural stiffness, the time step Δt and the space step Δz, the following combinations of the relevant parameters are defined.
In this article, mainly the Young’s modulus E and the time step Δt are varied so κ represents the dimensionless structural stiffness and τ the dimensionless time step. The effect of the reference flow velocity v o can be seen by modifying κ and τ such that κτ remains constant. The radius r o and the length L of the tube can be influenced through κ and τ, respectively. Approximate values of κ and τ for a simulation of a piece of a large human artery are κ≈60 and τ≈0.01 [32].
The error amplitude reduction of the coupling scheme with Gauss–Seidel iterations is now studied for different values of the parameters κ and τ and for the most significant combinations of the coupling terms (indicated by the values of γ 1, γ 2, γ 3 and γ 4). The following conclusions can be drawn from the study of the error amplification factor.
If γ 1=γ 2=γ 3=γ 4=1, the coupling is monolithic and the error amplification factor μ is zero for all wave numbers ϑ, irrespective of κ, τ and N. Only one coupling iteration will be required.
If γ 1=γ 2=γ 3=γ 4=0, the coupling is completely partitioned and the amplification factor μ in Eqs. (103a) and (103b) simplifies to
The coefficient α of the pressure stabilization term in the continuity equation has been substituted by
in the previous equation because α cannot be altered independently.
Figures 13 and 14 show the error amplification as a function of ϑ. The dimensionless wave number ϑ ℓ is equal to 2πℓ/N (ℓ=0,1,…,N/2 if N is even and ℓ=0,1,…,(N−1)/2 if N is odd) and hence it changes discretely with steps of 2π/N. Nevertheless, continuous curves are shown for clarity. The lowest wave numbers have the largest error amplification so that the corresponding Fourier modes are the most unstable ones during coupling with Gauss–Seidel iterations without extra coupling terms. Van Brummelen [26] comes to the same conclusion using a semi-infinite open fluid domain bounded by a string or a beam, which demonstrates that this conclusion is not model-dependent. From Eq. (106), it is clear that the mode with ϑ=0 is always unstable if γ 1=0.
As can be seen in Fig. 13 and Eq. (106), the error amplification increases quadratically when the dimensionless stiffness κ decreases. For v o =0, κ is infinite and τ=0, but limits show that μ is still well defined and given by
in that case. Figure 14 illustrates that a smaller dimensionless time step τ makes higher wave numbers unstable if no coupling terms are used. The error amplification thus increases when the time step or the structural stiffness decreases without coupling terms. The effect of κ is generally greater than that of τN. The parameter κ determines the vertical position of the curve while τN modifies both its shape and position. In Fig. 14, the range of ϑ for which μ>1 grows as τN decreases.
According to Eq. (106), the relation between ϑ and μ in a completely partitioned simulation only depends on the parameter κ and the product τN=v o Δt/Δz; the length of the tube does not appear in this equation. However, the fact that the length has no influence on the error amplification factor does not mean that the length has no influence on the stability of the coupling iterations. On the contrary, the determining factor for the convergence of the quasi-Newton coupling algorithms in the following section is not the evolution of the error amplification as a function of the wave number as such but the number of Fourier modes that have an error amplification larger than one. As κ and τN remain constant while the length increases, the relation between ϑ and μ will not change. Consequently, the fraction of the modes for which μ>1 will be invariant. However, the total number of modes and thus the number of modes for which μ>1 will increase.
The increase in the number of unstable Fourier modes as κ decreases is depicted in Fig. 15(a). An increase in N by some factor has the same effect on the error amplification as an increase in τ by the same factor, namely the maximal ϑ for which μ>1 decreases, which is a stabilizing effect. On the other hand, the number of Fourier modes rises for increasing N as the difference 2π/N between the discrete values of the wave number ϑ decreases, which is a destabilizing effect because there will be more unstable modes. Together these influences cause a variation in the number of unstable Fourier modes with N as shown in Fig. 15(b). The number of unstable modes only varies significantly with N for small N, a flexible structure and a small time step. For κ=10 and τ=0.001, all wave numbers are unstable as long as N≤51. For values of N which are of practical interest, the number of unstable Fourier modes is almost independent of N.
Figure 16(a) shows the reduction in the error amplification factor due to the coupling term premultiplied with γ 1. When γ 1=1, κ influences both the shape and the vertical position of the curve. This coupling term is referred to as the artificial compressibility term [123, 162, 190]. It includes a local, linear approximation for the structural behaviour into the continuity equation of the flow solver (see Sect. 6). Figure 16(b) shows that with artificial compressibility (γ 1=1), the error amplification factor remains nearly constant when τN decreases, as opposed to Fig. 14 where a smaller τN causes an increase in the error amplification factor.
The error amplification factor as a function of the wave number with coupling parameters γ 1=1, γ 2=γ 3=γ 4=0. (a) τN=1. (b) κ=100. The error amplification factor remains nearly constant when τN is decreased, as opposed to Fig. 14
In Fig. 17(a), two configurations are shown for which the term premultiplied with γ 1 is not sufficient to stabilize the Gauss–Seidel iterations. This situation can appear when κ<1 while τ>1. This extreme case means that the convective speed is larger than the critical speed in an iteration where the solution is sought for a time step which is too large to follow the convective phenomena accurately. As can be seen in Fig. 17(b), the only way to stabilize this extreme case is to add the convective coupling term premultiplied by γ 2 in the continuity equation. It can also be noticed that the coupling term premultiplied by γ 3 cannot stabilize this case.
4.2 Interacting Tube Segments with Structural Inertia
The structural model described in Sect. 4.1 disregards the mass of the structure. Moreover, it is a so-called independent-rings model [159] because the interaction between the segments of the tube is not taken into account. Therefore, the model of the tube’s wall is improved in [44] by including the structural mass and the interaction between the segments. This leads to additional insights, among others with regard to the effect of the time step.
The backward Euler scheme and the Newmark scheme [141] are used for the time discretization of the flow equations and the structural equations, respectively. It has been shown in several studies [32, 42, 77] that the instability of the coupling iterations within the time step has a physical cause. Consequently, the time discretization schemes are not expected to have much influence on the stability of the coupling iterations although they can influence the final result of the coupling iterations. This expectation is confirmed by Degroote et al. [44] who performed the same analysis with the composite time discretization scheme [6] for both the flow equations and the structural equations.
4.2.1 Description of the Model
The flow equations and the boundary conditions are identical to those in the previous section. The structural deformation in the radial direction is determined by
with ρ s the solid density and h the thickness of the tube’s wall [159]. Axial deformations of the structure are not considered so the length of a tube segment remains constant. The parameters A and B (A,B≥0) account for the inner action of the bending and the tension in the tissue, and they depend on the properties of the structure. The parameter C is defined as
with E the Young’s modulus and ν the Poisson coefficient. This expression for C corresponds to a thin-walled tube that is clamped in the axial direction. The radius r o corresponds to a uniform pressure p o if the structure is at rest.
Equation (109) for the structure is discretized in space with the central difference method and in time with the Newmark method [141], giving
for cell i (i=1,…,N). An overdot signifies a time derivative. Once the coupling iterations within time step n+1 have converged, the corresponding acceleration and velocity are calculated as
The Newmark parameters β and γ are chosen so that \(\gamma\geq\frac{1}{2}\) and \(\beta\geq\frac{1}{4} (\frac{1}{2}+\gamma )^{2}\), which results in an unconditionally stable integration scheme.
4.2.2 Von Neumann Stability Analysis
The stability of the Gauss–Seidel coupling algorithm is now determined with von Neumann stability analysis on the flow equations and the structural equations. As opposed to Sect. 4.1, the inner radius and not the cross-sectional area is considered as a variable. Therefore, the velocity, pressure and inner radius of the tube in Eqs. (97a), (97b), (111a), (111b) and (111c) are substituted by the sum of the coupled solution and the remaining error in the coupling iteration (indicated with an overbar). The coupled solution at both time level n and n+1 is in turn linearized as the sum of the reference value (subscript o) and a perturbation (indicated with a hat) as shown in Eq. (100). Subsequently, a is replaced by πr 2 and all equations are linearized by neglecting the nonlinear combinations of the error terms and the perturbations. Because the equations linearized around v o , p o and r o are satisfied by the coupled solution, all perturbations from the current and previous time step cancel out. Because Eqs. (111b) and (111c) are only used at the end of the time step, they are not important for the stability of the coupling iterations within the time step. This means that γ is not a parameter in these iterations.
The error terms are expanded as the sum of N Fourier modes, shown in Eq. (101). The amplification of each wave number can be studied separately. Therefore, \(\bar{v}_{i}^{k+1}\) is substituted by \(\check{v}_{\ell}^{k+1}\exp (\jmath\omega_{\ell}i\Delta z )\) and analogously for the error on the pressure and the radius. The product ω ℓ Δz is again denoted as the dimensionless wave number ϑ ℓ . For clarity, the inverted hat and the subscript ℓ are omitted. This results in the following equations, with α′=α/π, \(r^{k+1}=\tilde{r}^{k}\) and \(p^{k+1}=\tilde{p}^{k+1}\).
For the error amplification factor, dimensionless parameters are used. The parameters κ and τ have the same meaning as in the previous section. An additional dimensionless parameter ϕ accounts for the structural inertia, giving
with
The interaction between the segments is determined by the parameters
By combining Eqs. (112a), (112b) and (112c), the amplification factor μ of each mode in the error on the radius is then calculated as
with
and μ 2 determined by Eq. (106). The structural model in Eq. (109) with interaction between the segments and with structural inertia results in additional contributions to the error amplification which are all grouped in a term μ 1. Consequently, the complete error amplification factor is obtained as the product of μ 1 and μ 2.
Because (1−cos(ϑ)) is never negative and \((\frac{\phi}{\tau N} )^{2}+1\) is always positive, the second and third term in the denominator of μ 1 never increase the error amplification (χ,ψ≥0). The error amplification will thus always be mitigated by increasing the parameters χ and ψ which account for the interaction between the tube segments. Taking into account the interaction between the tube segments in the structural model should therefore facilitate the convergence of the coupling iterations compared to a simulation with an independent-rings model. Because both χ and ψ appear only once in the expression for μ, it is easy to understand their effect and consequently they can be set to zero in the remainder of the analysis. With χ=ψ=0, μ 1 is independent of the wave number.
The effect of the time step on the stability is important in many cases and it is more complex. The factor μ 1 is proportional to (τN)2 if τN≪ϕ and if the relative contribution of the terms due to the interaction between the tube segments is small. If τN≪1 then μ 2 is proportional to (τN)−2; otherwise τN only influences μ 2 for the lowest and highest wave numbers (ϑ≈0 or π). Apart from τN≈1 and τN≈ϕ which are difficult to analyze, there are three possibilities for the effect of the time step on the stability of the coupling iterations in this particular case:
-
μ∼(τN)2: if τN≪ϕ and τN≫1;
-
μ≈constant: if both τN≪ϕ and τN≪1 or if both τN≫ϕ and τN≫1;
-
μ∼(τN)−2: if τN≫ϕ and τN≪1.
If the time step is varied over a wide range, its effect on μ might change throughout that variation as the time step determines which of the above situations is appropriate. The time step will have no significant influence on the error amplification factor μ if τN is sufficiently far outside the range
If ϕ<1 then μ is proportional to (τN)−2 when τN lies in the range given above. By contrast, if ϕ>1 then μ is proportional to (τN)2 for τN in that range.
The physical meaning of the previous paragraph can be explained as follows. If τN≪1, the inertia is dominant in the flow while if τN≫1, the flow almost reaches steady state in each time step. For the structure, the inertia is dominant if τN≪ϕ while the stiffness is dominant if τN≫ϕ. Hence, the inertia in the fluid and in the structure are balancing each other out if τN≪1 and τN≪ϕ. For τN≪1 and τN≫ϕ, an equilibrium between the inertia in the fluid and the structural stiffness has to be found. By contrast, τN≫1 and τN≪ϕ results in an equilibrium between the structural inertia and the fluid which can be considered to be at steady state. Finally, if τN≫1 and τN≫ϕ, then inertia is insignificant in both the fluid and the structure. So, if inertia is important in either the fluid or the structure, then the error amplification factor μ is proportional to (τN)−2 or (τN)2, respectively.
Figure 18 shows μ as a function of the wave number for four different values of τN. The parameters ϕ≈0.1 and κ≈60 approximate the flow in a piece of a large artery (see Table 1). An increase in μ can be noticed for decreasing τN as long as τN∈[0.1,1] and much smaller changes for τN outside that range.
When τN≪ϕ, μ 1 is proportional to ϕ −2 and μ 2 always holds a factor κ −2 such that μ is proportional to (ϕκ)−2, which contains the ratio of the fluid density to the solid density ρ f /ρ s . As expected, increasing this ratio increases the error amplification factor.
The number of unstable modes as a function of the dimensionless time step is depicted in Fig. 19 for N=100. While the error amplification factor μ as a function of ϑ depends on τN, the number of modes with μ>1 is mainly a function of τ alone but the boundaries of the region τN=[0.1,1] in which the number of unstable modes increases for decreasing τ depend on N.
The findings of this analysis are compared to those of Causin et al. [32] in the following paragraphs. With a two-dimensional fluid model and a structural model that takes into account inertia but not the interaction between the segments (A=B=0), Causin et al. [32] calculate the maximal relaxation factor of Gauss–Seidel iterations with Dirichlet–Neumann decomposition as
with C the structural stiffness parameter as defined in Eq. (110). λ max is the maximal eigenvalue of the added-mass operator, given by
which increases as L increases and decreases as r o increases. The amplification factor of the Gauss–Seidel iterations with ω=1 according to Causin et al. [32] can be rewritten as
by introducing the dimensionless parameters from Eqs. (113a), (113b) and (113c). Equation (117) is similar to Eq. (114b), yet it does not represent the difference between the Fourier modes.
The model of Causin et al. [32] also predicts that for very small τN the maximal relaxation factor does not depend on τN. However, for large τN, the amplification factor varies as (τN)−2. The transition between the different regimes also depends on the ratios between structural stiffness, structural inertia and fluid inertia as described above.
If the first three terms in the denominator of μ 1 are large compared to the last term, then μ 1 is proportional to \(r_{o}^{-2}\). By contrast, μ 2 is proportional to r o as κ is proportional to \(r_{o}^{-1/2}\). As a result, μ=μ 1 μ 2 decreases for increasing r o , predicting less instability. As opposed to the analysis of independent tube segments without structural inertia, the analysis of interacting tube segments with structural inertia predicts the same tendency due to an increase of r o as Eq. (117).
4.2.3 Numerical Experiments
Nonlinear simulations of the flow in a flexible tube are used in [44] to verify the conclusions of the linear analysis, especially with regard to the effect of the time step as this effect is the most important one.
A fluid velocity of
has been applied at the inlet of the tube and zero pressure is imposed at the outlet of the tube (p out =0). The structure is initially at rest and both χ and ψ have been set to zero. The tube is discretized in N=100 segments with the same length. The values from Table 1 have been used again for the geometry and for the properties of the materials.
Simulations with 100 time steps have been performed for different values of τ and with different coupling algorithms. The L 2-norm of the residual is reduced by three orders of magnitude with respect to its initial value in the time step. In Fig. 20, the average number of coupling iterations per time step is depicted for different sizes of the dimensionless time step τ and the range [0.1/N,1/N] is indicated with vertical dotted lines.
The number of coupling iterations per time step (averaged over 100 time steps) for different values of τ with N=100. As predicted by the stability analysis, the average number of IQN-ILS coupling iterations per time step increases as τ decreases for τ in the range [10−3,10−2] while it is constant for τ sufficiently far outside that range. Reuse of information from the 4 previous time steps (IQN-ILS(4)) mitigates the increase of the average number of coupling iterations as τ decreases
Figure 18 shows that the error amplification is smaller than one for all wave numbers if the time step is large (τ≈1), except for ϑ=0. As a result, Fig. 19 indicates one unstable mode for τ≈1. Although Gauss–Seidel iterations are expected to diverge if μ>1 for at least one mode, they converge quickly for a large time step (τ≈1). This discrepancy is caused by the boundary conditions which are not taken into account in the stability analysis. By imposing the pressure at the outlet and with a wall model a=a(p), the components of the error on p and a with ϑ=0 are also determined, so this unstable mode is stabilized by the boundary conditions. When the time step decreases, the convergence of the Gauss–Seidel iterations becomes slow; for example, on average 28 Gauss–Seidel coupling iterations per time step were required for a dimensionless time step of τ=2×10−2. The Gauss–Seidel iterations diverged in the first time step when τ was less than or equal to 10−2.
It is thus impossible to verify the conclusions of the stability analysis over a wide range of time steps by performing simulations with the Gauss–Seidel coupling algorithm because the error amplification factor for the low wave numbers would be larger than one in the simulations with a small time step, which would cause divergence of the Gauss–Seidel coupling iterations. Other coupling algorithms, such as IQN-ILS, have to be used for the partitioned simulations with small time steps. More information on this technique can be found in the following section. The number of IQN-ILS coupling iterations per time step (averaged over the 100 time steps in the simulation) is a measure for the number of unstable modes.
Figure 20 shows that the number of IQN-ILS coupling iterations per time step is almost constant for τ=6×10−1 to 6×10−2 and for τ=2×10−4 to 2×10−5. Between τ=6×10−2 and 2×10−4, the number of IQN-ILS iterations increases steadily with decreasing time step. Consequently, the number of IQN-ILS coupling iterations per time step (Fig. 20) and the number of unstable modes (Fig. 19) display a similar behaviour.
The increase in the number of IQN-ILS coupling iterations with a decreasing time step can be mitigated by using information from the coupling iterations in the previous time steps as well, instead of only information from the current time step. Figure 20 illustrates that the number of coupling iterations per time step is reduced significantly if the information from the four previous time steps, denoted as IQN-ILS(4), is also used. This reuse will be explained in detail in the following section.
5 Coupling of two Black-Box Solvers
In this section, the focus lies on partitioned methods that couple a black-box flow solver with a black-box structural solver. When the solvers are black boxes, it is difficult or even impossible to obtain the exact Jacobian matrices which are required in Newton–Raphson methods that solve the root-finding problem in Eq. (58).
Several coupling algorithms are discussed, namely IQN-ILS, IBQN-LS, Aitken relaxation, Interface-GMRES(R), multi-solver techniques and multi-level techniques. The performance of these partitioned techniques is compared, both in terms of how often the flow problem and structural problem have to be solved within a time step and in terms of the total simulation time. The performance of IQN-ILS is also compared with a monolithic Newton solver.
5.1 IQN-ILS
The previous section described a stability analysis of the Gauss–Seidel iterations between the flow solver and the structural solver in a partitioned simulation of the unsteady flow in a straight, flexible tube. Figure 13 depicts the amplification of the error as a function of the wave number. Even for a very flexible tube and a small time step, only some wave numbers are unstable.
The physical meaning of these curves is shown in Fig. 21. The position of the wall of a tube, which initially has a constant cross-section and contains a fluid at rest, is perturbed with two different wave numbers. At the inlet and outlet, a zero pressure is imposed. Because the fluid is incompressible, a displacement of the interface with a low wave number requires that the fluid is accelerated globally, which causes large pressure variations throughout the fluid. On the other hand, a displacement with the same amplitude and a high wave number only generates local fluid motion and hence smaller pressure gradients. The pressure differences in the case of the high wave number can barely be seen since the same scale has been used for both wave numbers. The displacement of the structure will be largest when the first pressure distribution is applied. If the fluid were compressible, a local displacement of the interface would lead to a local compression/expansion of the fluid instead of a global acceleration/deceleration for an incompressible fluid.
The pressure contours (in Pa) in an axisymmetric tube due to two displacements of the tube’s wall with the same amplitude but a different wave number. Initially, the fluid is at rest and the tube has a constant cross-section. A displacement of the tube’s wall with a low wave number (top) creates much larger pressure variations than a displacement with a high wave number (bottom). Only the difference between the two calculations and not the values as such are important
Only the modes of the error which are unstable (μ>1) or which disappear slowly (μ≈1) in the Gauss–Seidel iterations have to be removed by another technique. Thus, for the quasi-Newton iterations to converge quickly, the approximate Jacobian has to describe the reaction to only a limited number of modes in the error on the interface’s displacement, namely the unstable and slowly converging modes. For the modes which are not included in the approximate Jacobian, the quasi-Newton iterations correspond to Gauss–Seidel iterations, as will be explained below.
In the remainder of this section, approximations are indicated with a hat. The output of the solvers \(\boldsymbol{\mathcal{F}}\) and \(\boldsymbol{\mathcal{S}}\) is indicated with a tilde because this is only an intermediate value that is not always passed on to the next coupling iteration.
All coupling algorithms begin a time step from an extrapolation of the interface’s displacement based on the previous time steps, for example
Lower-order extrapolations are used for the first two time steps.
The FSI problem reformulated as a set of nonlinear equations in the interface’s displacement
can be solved by means of Newton–Raphson iterations


with the residual calculated as
The notation \({{\boldsymbol {\mathcal {R}}}'}^{k}\) denotes the Jacobian of \({\boldsymbol {\mathcal {R}}}\), evaluated at x k. The Newton–Raphson iterations in the time step have converged when ∥r k∥2≤ε o with ε o the convergence tolerance. However, the exact Jacobian of \({\boldsymbol {\mathcal {R}}}\) is unknown as the Jacobians of the black-box solvers \(\boldsymbol{\mathcal{F}}\) and \(\boldsymbol{\mathcal{S}}\) are unavailable. Moreover, the linear system in Eq. (121a) with as dimension the number of degrees of freedom in the displacement of the fluid-structure interface has to be solved in each Newton–Raphson iteration. Although the number of degrees of freedom in the interface’s displacement is generally smaller than that in the entire fluid and structure domain, the Jacobian matrix \({\boldsymbol {\mathcal {R}}}'\) is normally dense. As a result, the solution of the linear system in Eq. (121a) would correspond to a significant computational cost in simulations with a high number of degrees of freedom on the interface if a direct solver were used.
If the Jacobian \({\boldsymbol {\mathcal {R}}}'\) is approximated and quasi-Newton iterations are performed, black-box solvers can be used. However, the linear system in Eq. (121a) still needs to be solved. As will be explained below, it is more advantageous to approximate the inverse of the Jacobian. The quasi-Newton iterations with the approximation for the inverse of the Jacobian can be written as
It can be seen from Eq. (123) that the approximation for the inverse of the Jacobian does not have to be created explicitly; a procedure to calculate the product of this matrix with the vector −r k is sufficient. The vector −r k is the difference between the desired residual, i.e. 0, and the current residual r k and it is further denoted as Δr=0−r k=−r k. The matrix-vector product is calculated from information obtained during the previous quasi-Newton iterations. Equation (122) shows that the flow equations and structural equations are solved in quasi-Newton iteration k, resulting in \(\tilde{\boldsymbol{x}}^{k}={ {\boldsymbol {\mathcal {S}}}\circ {\boldsymbol {\mathcal {F}}}}(\boldsymbol{x}^{k})\) and the corresponding residual r k. The vectors \(\tilde{\boldsymbol{x}}\) and r from all previous coupling iterations are also available, giving a set of known residual vectors

and the corresponding set of vectors \(\tilde{\boldsymbol{x}}\)

After each coupling iteration, the difference between the vectors from the current coupling iteration and the vectors from the previous coupling iteration is calculated
This yields a set of differences Δr i
and the corresponding set of differences \(\Delta\tilde{\boldsymbol{x}}^{i}\)
which both grow in each coupling iteration. Numerical experiments show that the convergence of the coupling iterations is often similar if all differences Δr i and \(\Delta\tilde{\boldsymbol{x}}^{i}\) (i=0,…,k−1) are calculated with respect to fixed references, for example Δr i=r i+1−r 0 and \(\Delta\tilde{\boldsymbol{x}}^{i}=\tilde{\boldsymbol{x}}^{i+1}-\tilde{\boldsymbol{x}}^{0}\) or Δr i=r i−r k and \(\Delta\tilde{\boldsymbol{x}}^{i}=\tilde{\boldsymbol{x}}^{i}-\tilde{\boldsymbol{x}}^{k}\). However, calculation of the vectors Δr i and \(\Delta\tilde{\boldsymbol{x}}^{i}\) as the difference between two consecutive coupling iterations facilitates the comparison between the IQN-ILS method and Aitken relaxation in Sect. 5.3.
Each Δr i corresponds to a \(\Delta\tilde{\boldsymbol{x}}^{i}\) and these vectors are stored as the columns of the matrices
and
Due to the similarity between consecutive time steps, the information from the previous time steps can be reused. The matrices \(\underline{\boldsymbol {V}}^{k}\) and \(\underline{\boldsymbol {W}}^{k}\) are then combined with those from q previous time steps (if at least q time steps have already been performed), giving
and
No differences between the first vectors r and \(\tilde{\boldsymbol{x}}\) in a time step and the last vectors in the previous time step should be added to the matrices V k and W k as will be explained below. By including the information from q previous time steps, the convergence of the coupling iterations is remarkably accelerated. However, if information from too many time steps is reused, the convergence can slow down again as information from time step n−q+1 might no longer be relevant in time step n+1. The optimal value of q is problem-dependent but the convergence of the coupling iterations does not change significantly near the optimum; consequently, the performance of the method is robust with respect to the parameter q.
The number of columns in V k and W k is indicated with v which is generally much smaller than the number of rows u. Nevertheless, in simulations with a low number of degrees of freedom on the interface, it is possible that the number of columns has to be limited to u by discarding the rightmost columns.
The vector Δr=0−r k is approximated as a linear combination of the known Δr i
with \(\boldsymbol{c}^{k}\in\mathbb{R}^{v\times 1}\) the coefficients of the decomposition. Because v≤u, Eq. (129) is an overdetermined set of equations for the elements of c k and hence the least-squares solution to this linear system is calculated. In [192], the solution to the least-squares problem is calculated using the normal equations
However, this implementation becomes unstable if the number of columns in the matrix V k is rather high, which especially occurs when information from previous time steps is reused. For that reason, the so-called economy-size QR-decomposition of V k is calculated using Householder transformations [88]
with \(\boldsymbol {Q}^{k}\in\mathbb{R}^{u\times v}\) an orthogonal matrix and \(\boldsymbol {R}^{k}\in\mathbb{R}^{v\times v}\) an upper triangular matrix. Because new vectors are added to the left-hand side of the matrices \(\underline{\boldsymbol {V}}^{k}\) and \(\underline{\boldsymbol {W}}^{k}\) in Eqs. (127a) and (127b), the QR-decomposition cannot be updated but it has to be recalculated in each quasi-Newton iteration. However, the cost of the QR-decomposition is small compared to the cost of \(\boldsymbol{\mathcal{F}}\) and \(\boldsymbol{\mathcal{S}}\).
The coefficient vector c k is then determined by solving the triangular system
using back substitution. If a Δr i vector is (almost) a linear combination of other Δr j vectors, one of the diagonal elements of R k will (almost) be zero. Therefore, the equation corresponding to that row of R k cannot be solved during the back substitution. If a small diagonal element is detected, the corresponding columns in V k and W k are removed. Subsequently, the QR-decomposition (Eq. (131)) is performed again. This procedure is repeated until none of the diagonal elements is too small.
The tolerance ε s for the detection of small diagonal elements depends on how accurately the flow equations and structural equations are solved. An appropriate value for ε s can be determined by analyzing the change of the vector \(\tilde{\boldsymbol{x}}\) due to a small perturbation of the vector x. If the perturbation is too small, the resulting change will be numerical noise. The value of ε s should be chosen so that the change of \(\tilde{\boldsymbol{x}}\) has a physical meaning if the perturbation of x has an L 2-norm larger than ε s . If the solution of the flow equations and the structural equations is calculated with more significant digits, for example by using stricter convergence criteria inside the solvers, then a smaller value of ε s can be used.
As the coupling iterations converge, the L 2-norm of the most recent differences Δr k−1 and \(\Delta\tilde{\boldsymbol{x}}^{k-1}\) decreases during the coupling iterations. Because \(\tilde{\boldsymbol{x}}^{k}\) is calculated with the same accuracy in each coupling iteration, the number of significant digits in Δr k−1 and \(\Delta\tilde{\boldsymbol{x}}^{k-1}\) decreases if their norm decreases. Numerical experiments indicate that the coupling iterations converge fastest if the new Δr k−1 and \(\Delta\tilde{\boldsymbol{x}}^{k-1}\) are added to the left-hand side of V k and W k. Fewer operations are performed on the columns on the left-hand side during the QR-decomposition. However, all columns in V k and W k have not been ordered depending on their L 2-norm. In that case, columns of the current time step could be located to the right of older columns so they would be eliminated if they were considered as a linear combination of older columns (instead of the other way around).
The \(\Delta\tilde{\boldsymbol{x}}\) that corresponds to Δr is subsequently calculated as a linear combination of the previous \(\Delta\tilde{\boldsymbol{x}}^{i}\), analogous to Eq. (129), giving
From Eq. (122), it follows that
and substitution of Eq. (133) in Eq. (134) results in
Because the coefficients c k are a function of Δr, Eq. (135) shows how Δx can be approximated for a given Δr. Hence, Eq. (135) can be seen as a procedure to calculate the product of the approximation for the inverse of the Jacobian and a vector Δr=−r k
The amount of memory required by this matrix-free procedure is proportional to the number of rows and columns in V k, so u×v instead of u 2. It is also faster than the explicit creation of the approximation for the inverse of the Jacobian as
with I the unity matrix in \(\mathbb{R}^{u\times u}\). This is a significant advantage for simulations with a high number of degrees of freedom on the interface compared to the least-squares technique with explicit construction of the matrices [192].
The relation between Δr and Δx is thus found by means of the \(\Delta\tilde{\boldsymbol{x}}\) values. One might try to relate the residual r directly to x instead of to \(\tilde{\boldsymbol{x}}\), but this obviously will not work as the new input for \({ {\boldsymbol {\mathcal {S}}}\circ {\boldsymbol {\mathcal {F}}}}\) would be a linear combination of the previous inputs. The only new information in the input of \({ {\boldsymbol {\mathcal {S}}}\circ {\boldsymbol {\mathcal {F}}}}\) would originate from numerical errors and the coupling iterations would not converge.
In Eqs. (127a) and (127b), the columns of V k can be considered as linearly independent. If a column were a linear combination of the other columns, this would be detected as a small or zero diagonal element in R k. Consequently, that column and the corresponding column of W k would be removed. In the following paragraphs, it is demonstrated what the product of the approximation for the inverse of the Jacobian with a vector Δr is for Δr either in the subspace spanned by the columns of V k or orthogonal to that subspace.
If Δr is equal to one of the columns in V k, say Δr=Δr 0, then the least-squares solution
to the overdetermined problem Δr≈V k c k in Eq. (129) is
This value of c k yields zero error for the least-squares problem. Any other value of c k would increase the least-squares error, unless linearly dependent columns would be present in V k but this was excluded in the first place. According to Eq. (133), \(\Delta\tilde{\boldsymbol{x}}=\boldsymbol {W}^{k}\boldsymbol{c}^{k}\) and thus in this specific case \(\Delta\tilde{\boldsymbol{x}}=\Delta\tilde{\boldsymbol{x}}^{0}\). Equation (135) states that Δx=W k c k−Δr. For Δr=Δr 0 and using the definitions of r k, Δr k−1 and \(\Delta\tilde{\boldsymbol{x}}^{k-1}\) in Eqs. (122), (125a) and (125b), this becomes
So, Δr 0=r 1−r 0 yields Δx=x 1−x 0, which is a finite difference approximation for the product with the inverse of the Jacobian. The same is true for any other column in V k and linear combinations thereof. As a result, Newton iterations are performed for all Δr in the span of the columns of V k.
By contrast, if Δr is orthogonal to all of the columns in V k, then the least-squares solution
to the overdetermined problem Δr≈V k c k in Eq. (129) is
This can easily be seen in Eq. (132) where the coefficients are calculated as R k c k=Q k TΔr. As the columns of Q k span the same subspace as the columns of V k, Q k TΔr=0 if Δr is orthogonal to all columns in V k. According to Eq. (133), \(\Delta\tilde{\boldsymbol{x}}=\boldsymbol {W}^{k}\boldsymbol{c}^{k}\) and thus in this specific case \(\Delta\tilde{\boldsymbol{x}}=\boldsymbol{0}\). Equation (135) states that Δx=W k c k−Δr, which gives
Using the definition of r k in Eq. (122), the new displacement is given by
So, Gauss–Seidel iterations are performed for all Δr orthogonal to the span of the columns of V k.
IQN-ILS thus uses a low-rank approximation for the inverse of the Jacobian. The convergence behaviour of this technique can be explained using Fig. 13. In that figure, it can be observed that only a fraction of the Fourier modes is unstable during Gauss–Seidel coupling iterations. The reason for this instability is that Gauss–Seidel iterations treat the interaction between the fluid and the structure explicitly during a coupling iteration because they solve the flow equations with all structural degrees of freedom fixed and vice versa. Thus only this fraction of unstable modes needs to be treated implicitly during the coupling iterations. For the other modes, Gauss–Seidel iterations are an acceptable solutions strategy. It can thus be concluded that no full-rank Jacobian is needed to obtain fast convergence. Only a low-rank approximation for the Jacobian is required, as long as it represents the behaviour of the small fraction of unstable and slowly converging modes.
Above, it was mentioned that no differences between the first vectors r and \(\tilde{\boldsymbol{x}}\) in a time step and the last vectors in the previous time step should be added to the matrices V k and W k. In that respect, it should be noted that \({{\boldsymbol {\mathcal {R}}}'}^{k}\) is the Jacobian of r k as a function of x k, all at time level n+1. So, \({{\boldsymbol {\mathcal {R}}}'}^{k}\) is the relation between a given Δx between two vectors x at time level n+1 and the resulting Δr, also at time level n+1. To approximate the product of the inverse of \({{\boldsymbol {\mathcal {R}}}'}^{k}\) with a vector, the product of \({ \mathrm {d} \tilde{\boldsymbol{x}}/ \mathrm {d} \boldsymbol{r}}\) with that same vector is approximated as a linear combination of known \(\Delta\tilde{\boldsymbol{x}}^{i}\). Hence, the \(\Delta\tilde{\boldsymbol{x}}^{i}\) in this linear combination must be differences between two vectors \(\tilde{\boldsymbol{x}}\) at the same time level; preferably from time level n+1 but also from previous time levels. However, if differences between vectors from different time levels are used, then a time derivative is included while \({{\boldsymbol {\mathcal {R}}}'}^{k}\) relates differences within a time step.
The complete IQN-ILS technique is shown in Algorithm 10. Because the matrices V k and W k have to contain at least one column, a relaxation with factor ω (line 6) is performed in the second coupling iteration of the first time step if information from the previous time steps is reused (q>0) and in the second coupling iteration of each time step without reuse (q=0). Recently, this algorithm has been applied to couple an adjoint flow solver with an adjoint structural solver [49].
From a mathematical point of view, \({\boldsymbol {\mathcal {R}}}(\boldsymbol{x})=\boldsymbol{0}\) is a set of nonlinear equations in \(\boldsymbol{x}\in\mathbb{R}^{u\times 1}\). Such a system is commonly solved using Newton–Raphson iterations (see Eqs. (121a) and (121b)). The construction of a finite difference approximation for \({{\boldsymbol {\mathcal {R}}}'}^{k}\) requires the evaluation of the black-box function \({\boldsymbol {\mathcal {R}}}\) for u perturbations of x, which is expensive in practice.
with
In the equations above, the amplitude of the perturbation in the ith direction is given by ε i and \(\boldsymbol{e}^{i}\in\mathbb{R}^{u\times 1}\) is a vector with a ‘one’ on row i and a ‘zero’ on all other rows. However, it is probably possible to use the same finite difference approximation for a number of Newton iterations or even a number of time steps but this requires manual fine-tuning to find the optimal reuse parameter.
Solving Eq. (121a) with a matrix-free Krylov solver is possible but also expensive. Such a linear solver does not require that \({{\boldsymbol {\mathcal {R}}}'}^{k}\) is known explicitly. It only needs a procedure to calculate the product of \({{\boldsymbol {\mathcal {R}}}'}^{k}\) with a vector δ, which can be approximated by means of a finite difference approximation.
Therefore, the function \({\boldsymbol {\mathcal {R}}}\) has to be evaluated in each Krylov iteration within each Newton iteration. By contrast, IQN-ILS only needs one evaluation of \({\boldsymbol {\mathcal {R}}}\) in each quasi-Newton iteration. The function \({\boldsymbol {\mathcal {R}}}\) calculates the residual of the coupled problem condensed on the interface, which requires the solution of the flow equations and the structural equations in the entire domain. Hence, this black-box function is expensive to be evaluated repeatedly inside each Newton iteration. Again, the Krylov vectors from one Newton iteration can probably be reused for the following Newton iterations or even time steps but this also requires manual fine-tuning. Moreover, this approach is sensitive to the parameter ε, which has to be set by the user [81].
All of the above indicates that the Jacobian \({{\boldsymbol {\mathcal {R}}}'}^{k}\) (or the procedure to calculate the product of \({{\boldsymbol {\mathcal {R}}}'}^{k}\) with a vector) has to be approximated, resulting in a quasi-Newton scheme


with M k the approximation for the Jacobian. As already explained for the IQN-ILS method, also the inverse of the Jacobian can be approximated so that no linear system (Eq. (147a)) has to be solved, giving
with N k the approximation for the inverse of the Jacobian. However, the construction of M k or N k should not require additional evaluations of \({\boldsymbol {\mathcal {R}}}\). By contrast, the approximation has to be constructed and updated with the information that is generated in each quasi-Newton iteration.
If the updates of M k or N k are performed so that the secant equation
or
is satisfied, the method belongs to the secant methods, which is a subclass of the quasi-Newton methods [51]. Because Eqs. (149) and (150) only impose u constraints on the u×u matrix elements, the matrices can be updated in different ways, resulting in various updating methods. Haelterman [91] provides an overview of these methods and an analysis of their properties.
A quasi-Newton method is a rank-one update method if the update of M k or N k can be written as a rank-one matrix
or
with \(\boldsymbol{a},\boldsymbol{b}\in\mathbb{R}^{u\times 1}\). Examples of rank-one update methods are Broyden’s first and second method [22], the (inverse) column-updating method [125, 126], the symmetric rank-one update method [39], Pearson’s method [146] and McCormick’s method [130]. However, Pearson’s method and McCormick’s method are only applicable to problems where \({\boldsymbol {\mathcal {R}}}'\) is symmetric positive definite at the solution of \({\boldsymbol {\mathcal {R}}}(\boldsymbol{x})=\boldsymbol{0}\).
An advantage of a rank-one update is that the inverse of the updated matrix M k+1=M k+ab T can easily be computed from the inverse of the previous matrix M k with the Sherman-Morrison theorem [172].
The conditions for this theorem are that M k is an invertible square matrix and that b T(M k)−1 a≠−1.
Typically, the matrix M or N is not calculated explicitly. By contrast, if the initial matrix is for example the identity matrix (M 0=I), then the approximate matrix can be stored as two series of column vectors and reconstructed symbolically as a sum of dyadic products
with \(\boldsymbol{a}^{i},\boldsymbol{b}^{i}\in\mathbb{R}^{u\times 1}\) for i=1,…,k. Because generally k≪u, it is much faster to compute the product of M k with a vector when M k is stored as a sum of dyadic products than when it is stored as a dense matrix.
Rank-two update methods add a matrix of rank two in each iteration. Well-known rank-two update methods of M k are the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method [23, 24, 73, 87, 171], the Davidon–Fletcher–Powell (DFP) method [38, 74] and the Powell–Symmetric–Broyden (PSB) method [156]. For rank-two update methods, the inverse of M k+1 can be calculated from the inverse of M k by applying the Sherman-Morrison theorem (Eq. (153)) twice. However, all of the above rank-two update methods are only applicable to problems where \({\boldsymbol {\mathcal {R}}}'\) is symmetric positive definite at the solution of \({\boldsymbol {\mathcal {R}}}(\boldsymbol{x})=\boldsymbol{0}\). Finally, Greenstadt’s method [89] performs a rank-two update on N k.
The quasi-Newton methods which require symmetric positive definiteness are useful in optimization problems. However, only the quasi-Newton methods which do not require that the matrix is symmetric positive definite can be used for FSI simulations because \({\boldsymbol {\mathcal {R}}}'\) does not have this property. Well-known quasi-Newton methods like PSB and BFGS are thus not applicable in this case because they enforce symmetry of the approximate Jacobian. Therefore, the approximate symmetric Jacobian calculated by these techniques can be quite different from the real unsymmetric Jacobian. Nevertheless, FSI problems have been solved with BFGS [129]. This approach requires two times more coupling iterations than a Gauss–Seidel scheme and ten times more iterations than a normal Newton scheme [128]. Despite the symmetric approximate Jacobian, the quasi-Newton iterations do converge in that case, albeit slowly.
Haelterman [91] proves that the IQN-ILS method can also be formulated as a rank-one update quasi-Newton method. The method is different from all the methods listed above. Moreover, the IQN-ILS method respects the secant equation (Eq. (150)) and even the generalized secant equation
for i=1,2,…,min(k,u). The IQN-ILS method is also a least change secant update method because N k+1 minimizes the Frobenius norm ∥N k+1−N k∥ F .
with
The notation \(\mathbb{A}(\boldsymbol {A},\boldsymbol {B})\) defines a set of “interpolating” matrices
with \(\boldsymbol {A}\in\mathbb{R}^{a\times b}\), \(\boldsymbol {B}\in\mathbb{R}^{c\times b}\), b≤a and A of rank b. Hence, all matrices in \(\mathbb{A}(\boldsymbol {A},\boldsymbol {B})\) project A on B. The square brackets \([\Delta\boldsymbol{a}]_{i}^{j}\) denote that the set of column vectors Δa i,…,Δa j are concatenated to a matrix as
The subscript max(0,k−u+1) together with the superscript k avoids that more than u columns are combined, because in that case the matrices would no longer satisfy the requirements for the set of interpolating matrices.
Moreover, for a general affine function \({\boldsymbol {\mathcal {R}}}(\boldsymbol{x})=\boldsymbol {A}\boldsymbol{x}+\boldsymbol{b}\) (\(\boldsymbol {A}\in\mathbb{R}^{u\times u}\) and \(\boldsymbol{x},\boldsymbol{b}\in\mathbb{R}^{u\times 1}\)) and with exact arithmetic, IQN-ILS converges in u+1 iterations while Broyden’s method needs 2u iterations [91]. However, for fluid-structure interaction problems, even u+1 iterations would be unacceptable as generally u≫k. For affine functions with exact arithmetic, the approximation for the inverse of the Jacobian converges to the true inverse of the true Jacobian in a monotonous way [91].
Haelterman [91] has used the IQN-ILS method, Broyden’s methods and the column-updating methods to simulate the unsteady, incompressible flow in a one-dimensional flexible tube (see Sect. 4). In these simulations, the IQN-ILS method is faster compared to Broyden’s methods and the column-updating methods. The difference between the methods is larger when the problem is more difficult to solve, which means that more iterations are needed. For other nonlinear problems which only require a small number of coupling iterations, the differences between the methods are small.
5.2 IBQN-LS
Vierendeels et al. [192] rewrite the FSI problem as a system of equations with both the interface’s displacement and the traction distribution on the interface as unknowns. This system is solved with block quasi-Newton iterations of the Gauss–Seidel type. The Jacobians of the flow solver and structural solver are approximated by means of least-squares models, constructed with the displacement of the fluid-structure interface and the traction distribution on the interface in all previous quasi-Newton iterations in the time step [188, 192]. This method will be referred to as IBQN-LS, meaning interface block quasi-Newton with approximate Jacobians from least-squares models.
The IBQN-LS method is explained in detail in Algorithm 11. This coupling technique solves the FSI problem written as
with block Newton–Raphson iterations of the Gauss–Seidel type. The linear system
is thus first solved for Δx, followed by an update of x and the right-hand side. Subsequently, the modified system is solved for Δy and afterwards y is updated. As a consequence, the IBQN-LS method modifies the traction distribution that is calculated by the flow solver before transferring it to the structural solver, as opposed to the other techniques described in this section. In agreement with the notation for intermediate values, the input and output of the flow solver are denoted as x k+1 and \(\tilde{\boldsymbol{y}}^{k+1}\) and the input and output of the structural solver as y k+1 and \(\tilde{\boldsymbol{x}}^{k+1}\). For this algorithm, the residual vector \(\boldsymbol{r}^{k+1}=\tilde{\boldsymbol{x}}^{k+1}-\boldsymbol{x}^{k+1}\) is not equal to \({ {\boldsymbol {\mathcal {S}}}\circ {\boldsymbol {\mathcal {F}}}}(\boldsymbol{x}^{k+1})-\boldsymbol{x}^{k+1}\) when the linear system in Eq. (160) is solved because then \(\boldsymbol{y}^{k+1}\neq\tilde{\boldsymbol{y}}^{k+1}\).
Starting from the displacement x k that was given as input to the flow solver in the previous coupling iteration, the displacement x k+1=x k+Δx k is calculated by solving the system
for Δx k. The prime denotes the Jacobian matrix of a function. In the original approach of Vierendeels et al. [192], this linear system is solved with a direct solver and explicit construction of the matrices \(\widehat{\boldsymbol{\mathcal{F}}'}\) and \(\widehat{\boldsymbol{\mathcal{S}}'}\). By contrast, a matrix-free implementation is presented by Degroote et al. [45], using an iterative Krylov solver like the generalized conjugate residual (GCR) method [60] or the mathematically equivalent generalized minimal residual (GMRES) method [168]. The matrix on the left-hand side of Eq. (161) and thus the approximate Jacobians \(\widehat{{\boldsymbol{\mathcal{F}}'}^{k}}\) and \(\widehat{{\boldsymbol{\mathcal{S}}'}^{k}}\) do not have to be calculated explicitly; a procedure to calculate the product of these matrices with a vector is sufficient.
The procedure to calculate the product of the approximate Jacobian \(\widehat{{\boldsymbol{\mathcal{F}}'}^{k}}\) or \(\widehat{{\boldsymbol{\mathcal{S}}'}^{k}}\) with a vector is similar to the procedure described in Sect. 5.1. The matrix-vector product with \(\widehat{{\boldsymbol{\mathcal{F}}'}^{k}}\) is calculated from the previous inputs
and the corresponding outputs
of the flow solver. After each coupling iteration, the difference between the vectors from the current coupling iteration and the vectors from the previous coupling iteration is calculated.
All Δx i and \(\Delta\tilde{\boldsymbol{y}}^{i}\) (i=0,…,k−1) from the current time step (and possibly from previous time steps) are stored as columns of the matrices \(\boldsymbol {V}^{k}_{f}\) and \(\boldsymbol {W}^{k}_{f}\), with the subscript f referring to the flow solver. Subsequently, the economy-size QR-decomposition of \(\boldsymbol {V}^{k}_{f}\) is calculated. To determine the product of \(\widehat{{\boldsymbol{\mathcal{F}}'}^{k}}\) with a vector Δx, the triangular system
is solved for \(\boldsymbol{c}^{k}_{f}\), after which the matrix-vector product is calculated as
The product of \(\widehat{{\boldsymbol{\mathcal{S}}'}^{k}}\) with a vector is calculated analogously, based on the inputs and outputs of the structural solver.
Once x k+1 has been obtained, the corresponding traction distribution \(\tilde{\boldsymbol{y}}^{k+1}=\boldsymbol{\mathcal{F}}(\boldsymbol{x}^{k+1})\) is calculated and the matrices V f , W f , Q f and R f are updated. To calculate the traction distribution y k+1=y k+Δy k that has to be applied on the structure, the system
is solved, again with the matrix-free iterative solver. Each time the solution to either the flow problem or the structural problem has been calculated, the procedure for the product of the corresponding solver’s approximate Jacobian with a vector is improved by means of that solver’s latest input and output.
Analogous to the IQN-ILS technique, the matrices \(\boldsymbol {V}^{k}_{s,f}\) and \(\boldsymbol {W}^{k}_{s,f}\) have to contain at least one column to calculate the quasi-Newton update; otherwise a relaxation with factor ω is used for the interface’s displacement (line 8 in Algorithm 11) and the traction distribution is passed on without modification (line 17).
5.3 Aitken Relaxation
Aitken relaxation [108, 138, 139] (Algorithm 12) determines a dynamically varying scalar relaxation factor ω k for the Gauss–Seidel iterations within a time step.
The next input for \({ {\boldsymbol {\mathcal {S}}}\circ {\boldsymbol {\mathcal {F}}}}\) is thus a linear combination of the last output and the previous input. Moreover, the update of the interface’s displacement is in the direction of the residual vector, as opposed to the update from the IQN-ILS method on line 11 of Algorithm 10. The first relaxation in a time step is executed with the relaxation factor from the end of the previous time step, but limited to ω max, so ω n+1,0=sign(ω n)min(|ω n|,ω max) and ω 0,0=ω max. The value of ω k is obtained as
which is interpreted in [108] as the secant method for scalars directly applied to vectors and projected on r k−r k−1. By combining Eqs. (167) and (168), it can be seen that the update of the interface’s displacement is given by
for k>0. The previous equation is similar to line 11 of Algorithm 10. If the Jacobian were created explicitly in the IQN-ILS algorithm, if the normal equations were used to solve the least-squares problem in Eq. (129) and if the matrices V k and W k were limited to their newest column, line 11 of Algorithm 10 would give
Equations (169) and (170) are, however, not identical because the coefficient of −r k is a scalar in the first equation and a matrix in the second one. This proves that Aitken relaxation is fundamentally different from the IQN-ILS method. On the other hand, it demonstrates that implementing the IQN-ILS method is hardly more complex than implementing Aitken relaxation. However, Aitken relaxation can also be seen as an interface quasi-Newton technique: if the inverse of the Jacobian in Eq. (123) is approximated by −ω k I, the Aitken relaxation method is retrieved.
The Gauss–Seidel iterations with Aitken relaxation [108]
5.4 Interface-GMRES(R)
Interface-GMRES (Algorithm 13) uses the Newton–Raphson method to solve the nonlinear equation \({\boldsymbol {\mathcal {R}}}(\boldsymbol{x})=\boldsymbol{0}\) for the interface’s displacement. The Newton–Raphson update Δx is obtained by approximating the solution to the linear system in Eq. (121a) with an iterative solver. To be able to calculate the Jacobian-vector product, Gauss–Seidel iterations are first performed on lines 7 to 22, which results in a sequence of interface displacements x i and the corresponding residuals r i with i=1,…,j. From these sequences, differences Δx i=x i−x 0 and Δr i=r i−r 0 are calculated and stored as columns of V j and W j. It has been proved by induction that the Krylov space corresponding to the linear system in Eq. (121a) is asymptotically similar to \(\mathrm{span}\{\Delta\boldsymbol{x}^{i}\}_{i=1}^{j}\) and the Gauss–Seidel iterations thus serve as a preconditioner to the GMRES solution of Eq. (121a) [27, 135, 136]. The residual at \(\boldsymbol{x}^{0}+\sum_{i=1}^{j}c_{i}\Delta\boldsymbol{x}^{i}\) is approximated as
which can be considered as a finite difference approximation. When the minimization problem in the residual space
has converged sufficiently, the corresponding Newton–Raphson update is calculated as
The coefficient vector c is calculated in the same way as in the IQN-ILS method, as shown on line 20 of Algorithm 13. The expression \(\min_{\boldsymbol{c}}\Vert\boldsymbol{r}^{k}+\sum_{i=1}^{j} c_{i}\Delta\boldsymbol{r}^{i}\Vert_{2}\) is called the linearized residual ζ, as opposed to the true residual ∥r k∥2.
The interface generalized minimal residual method (Interface-GMRES) [27]
For FSI with strong interaction, the relaxation on line 13 of Algorithm 13 is imperative as the inner loop consists of Gauss–Seidel iterations which diverge fast without relaxation. The optimal value of the relaxation factor ω is problem-dependent. The lower bound for ω is determined by the finite accuracy and the solution tolerance of the solvers and the upper bound has to avoid divergence of the solvers or grid distortion.
The orthonormalization of the Δx i on lines 10 to 12 is recommended in [27] to improve the accuracy of the solution of Eq. (172). Due to this orthonormalization, however, the displacement of the interface on line 14 is significantly different from the solution so that the flow solver and structural solver converge slowly. As a result, each evaluation of the residual operator \({\boldsymbol {\mathcal {R}}}\) takes longer than for the other techniques. Hence, the comparison with other techniques is different when the number of residual evaluations is considered than when the total duration of the simulation is the criterion. This is shown by the numerical experiments and is also mentioned by Küttler and Wall [109].
Algorithm 13 can be conceived as the construction of a model with the residual as input and the interface’s displacement as output. Instead of using the model to update the interface’s displacement in the inner loop, relaxed Gauss–Seidel iterations are performed until the model meets the user-defined tolerance ε 1. To prevent Eq. (172) from being solved too accurately during the first few Newton–Raphson iterations, ε 1 is set to a fraction λ of the current residual ∥r k∥.
Instead of discarding the x i and r i from the previous Newton–Raphson iterations, they can be reused in the next Newton–Raphson iteration, which is called Interface-GMRESR. Algorithm 14 shows how Algorithm 13 has to be altered to reuse the Gauss–Seidel iterations from previous Newton–Raphson iterations.
The interface generalized minimal residual method with reuse (Interface-GMRESR) [27]
The inner loop is executed at least once before going to the Newton–Raphson update; otherwise no additional Δr and Δx are known with respect to the previous Newton–Raphson update and the Newton–Raphson update would be ineffective. Each time a Newton–Raphson update is performed on line 23, the reference x 0 is modified and the solvers are evaluated. However, this solver evaluation does not result in an additional difference Δx and Δr, whereas IBQN-LS and IQN-ILS modify the reference in each iteration and obtain a difference of the input and output in each iteration except for the first one.
Due to the relaxation on line 13, the Δx j in Algorithm 13 all have the same norm, regardless of whether it is the first or the final iteration in the time step. However, the step size is adapted to the initial residual. If the problem is nonlinear, the Δx and Δr can be inaccurate because this finite difference step size is suboptimal. As the norm of the differences in IBQN-LS and IQN-ILS is equal to the step size, the norm automatically decreases during the coupling iterations as they converge so these methods do not require a preset step size.
Michler et al. [135] introduced reuse of differences from the previous time steps and not only from the previous Newton–Raphson iterations. They mention that reuse increases the efficiency, but that it comes at the expense of robustness and therefore has to be applied cautiously. They present results for only 25 time steps in a simulation with a compressible fluid. To enable reuse in Interface-GMRESR, j should not be reset to 0 at the beginning of the time step. The convergence plots in [135] demonstrate that with reuse from the previous time steps, there is a large discrepancy between the linearized residual and the true residual. The inner loop with Gauss–Seidel iterations converges after one iteration because the linearized residual is already very small. Consequently, the algorithm repeatedly performs one Gauss–Seidel iteration followed by a Newton–Raphson update. In this regime, an additional Δx and Δr are obtained at the cost of two solver evaluations.
There are several similarities between IQN-ILS (Algorithm 10) and Interface-GMRES (Algorithm 13), as both algorithms use changes in interface data from one coupling iteration to another and as both solve a least-squares problem. However, the major difference is that IQN-ILS calculates Δx k (see Eq. (135)) using \(\Delta\tilde{\boldsymbol{x}}{}^{j}\), while Interface-GMRES uses Δx j (see Eqs. (173a) and (173b)). Hence, the interface displacement resulting from a quasi-Newton step is a linear combination of previous inputs for the flow solver in the case of Interface-GMRES, whereas it is a linear combination of outputs of the structural solver in the case of IQN-ILS.
As x 0 is a linear combination of previous inputs of the flow solver x j, the dimension of the basis spanned by the Δx j is not increased in the quasi-Newton steps of Interface-GMRES. The least-squares model thus improves in the quasi-Newton steps of IQN-ILS but not in those of Interface-GMRES. Therefore, Interface-GMRES needs a number of Gauss–Seidel iterations between two quasi-Newton steps in order to improve the least-squares model. Furthermore, it can be seen from Eqs. (132) and (173a and (173b)) that if r k is orthogonal to the basis spanned by the Δr j (j=0,…,k−1), then all decomposition coefficients c k are zero. In that case, the quasi-Newton step of IQN-ILS is actually a Gauss–Seidel step (\(\boldsymbol{x}^{k+1}=\boldsymbol{x}^{k}+\boldsymbol{r}^{k}=\tilde{\boldsymbol{x}}{}^{k}\)), while Interface-GMRES performs no step.
5.5 Multi-Solver IQN-ILS
Fluid-structure interaction simulations are often executed on clusters, consisting of a large number of cluster nodes. Each node contains a small number of multi-core processors and an amount of memory. By running a solver in parallel, i.e. on more than one core of the cluster, a calculation can generally be accelerated. Optimally, doubling the number of cores should halve the calculation’s duration. However, mostly, the speed-up is only near-linear until a certain numbers of cores and flattens out or even decreases for larger numbers of cores.
Once the fluid-structure interaction simulation can no longer be accelerated by increasing the number of cores per solver, the multi-solver algorithms can be applied for an additional speed-up. These multi-solver algorithms reduce the calculation time by increasing the number of flow solvers and structural solvers, while keeping the number of cores per solver constant. In [47], multi-solver (MS) versions of both IQN-ILS and IBQN-LS are presented. Here, only MS-IQN-ILS is discussed as MS-IBQN-LS works in a similar way.
In Eqs. (127a) and (127b), each column of the matrix \(\underline{\boldsymbol {V}}^{k}\) is a difference in residual that is related to a difference in output of the structural solver in the corresponding column of matrix \(\underline{\boldsymbol {W}}^{k}\). As explained in Sect. 5.1, data from previous time steps can be reused in the least-squares model of the current time step, if consecutive time steps are sufficiently similar. However, the relation between the columns of V n and W n is only approximate at t n+1. So, this reuse has to be applied with caution [135].
Therefore, the multi-solver quasi-Newton coupling algorithms first recalculate the data from the previous time steps at the current time level, before including that data in a least-squares model. Consequently, only data from the current time step is present in the least-squares model. The columns of the matrix V n contain specific combinations of the degrees-of-freedom on the interface that accelerated the convergence of the coupling iterations in the previous time step. Hence, it is expected that knowing the difference of the output at t n+1 due to the same difference of the input as used at time level t n will improve the least-squares model for the approximate Jacobian. Moreover, the recalculation of differences from previous time steps can be done in parallel with normal coupling iterations if g>1 flow solvers and h>1 structural solvers are used.
In the following paragraphs, a subscript i or j distinguishes the different solvers and their respective input and output. Algorithm 15 describes the Multi-Solver IQN-ILS (MS-IQN-ILS) algorithm with parallel recalculation of differences from the previous time step. Solvers \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) calculate the solution of the coupled problem, while solvers \(\boldsymbol{\mathcal{F}}_{i}\) (i=2,…,g) and \(\boldsymbol{\mathcal{S}}_{j}\) (j=2,…,h) recalculate differences from previous time steps. Lines 5 to 14 describe the standard IQN-ILS algorithm, with the exception of the ‘start’ that has been added on line 13. This command means that the calculation has to be started, without waiting for the result to continue the execution of the coupling algorithm. On line 4, the coupling algorithm checks whether \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) have completed the previous calculation, i.e. whether they are ‘ready’, before starting the following calculation. The check of the convergence tolerance on line 3 evaluates to false while the calculation of \(\boldsymbol{r}^{k}_{1}\) is ongoing.
As opposed to other coupling algorithms, the multi-solver algorithm does not wait on line 13 until the calculations by \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) are ready. Consequently, it can control the other solvers \(\boldsymbol{\mathcal{F}}_{i}\) (i=2,…,g) and \(\boldsymbol{\mathcal{S}}_{j}\) (j=2,…,h) in the meantime. On line 16 and line 23, the coupling algorithm loops over these additional solvers. In a first step of the recalculation of differences by solver \(\boldsymbol{\mathcal{F}}_{i}\) and \(\boldsymbol{\mathcal{S}}_{j}\), a column Δr of V n and the corresponding column \(\Delta\tilde{\boldsymbol{x}}\) of W n are selected. Different selection procedures are also possible: newest first, oldest first, largest ∥Δr∥2 first, largest \(\Vert\Delta\tilde{\boldsymbol{x}}\Vert_{2}/\Vert\Delta\boldsymbol{r}\Vert_{2}\) first, etc.
In the MS-IQN-ILS, Δr k−1 and \(\Delta\tilde{\boldsymbol{x}}^{k-1}\) are calculated as
instead of using Eqs. (125a) and (125b). So, the selected Δr and \(\Delta\tilde{\boldsymbol{x}}\) from t n are differences with respect to the reference vectors \(\boldsymbol{r}_{1}^{n,0}\) and \(\tilde{\boldsymbol{x}}{}_{1}^{n,0}\) which originate from the first coupling iteration at t n. To be recalculated at t n+1, the vectors Δr and \(\Delta\tilde{\boldsymbol{x}}\) have to be added to a value of r and \(\tilde{\boldsymbol{x}}\) at t n+1, namely \(\boldsymbol{r}^{0}_{i}\) and \(\tilde{\boldsymbol{x}}^{0}_{i}\). By using extrapolated values \(\boldsymbol{r}^{0}_{i}=\boldsymbol{0}\) and \(\tilde{\boldsymbol{x}}{}^{0}_{i}=\boldsymbol{x}^{0}_{1}\) as references at t n+1, the recalculation of differences from the previous time step can begin immediately at the start of the new time step, simultaneously with the first coupling iteration between \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\). The input x i for \(\boldsymbol{\mathcal{F}}_{i}\) is then calculated using Eq. (122) and the calculation by \(\boldsymbol{\mathcal{F}}_{i}\) starts on line 20. The coupling algorithm does not wait until this calculation is complete, but checks on line 17 whether \(\boldsymbol{\mathcal{F}}_{i}\) has finished its calculation. When this is the case, x i and the corresponding \(\tilde{\boldsymbol{y}}{}_{i}\) are added to an intermediate first in, first out (FIFO) queue.
When the coupling algorithm detects that a structural solver \(\boldsymbol{\mathcal{S}}_{j}\) is ready (line 24) and the intermediate FIFO queue is not empty, then it takes the oldest x j and the corresponding \(\tilde{\boldsymbol{y}}{}_{j}\) from this queue. It subsequently starts a structural calculation \(\tilde{\boldsymbol{x}}{}_{j}=\boldsymbol{\mathcal{S}}_{j}(\boldsymbol{y}{}_{j})\) with \(\boldsymbol{y}_{j}=\tilde{\boldsymbol{y}}{}_{j}\) and determines the corresponding residual \(\boldsymbol{r}_{j}=\tilde{\boldsymbol{x}}{}_{j}-\boldsymbol{x}_{j}\). This intermediate FIFO queue thus decouples the flow solvers \(\boldsymbol{\mathcal{F}}_{i}\) (i=2,…,g) from the structural solvers \(\boldsymbol{\mathcal{S}}_{j}\) (j=2,…,h) and enables a different number of flow solvers and structural solvers (g≠h). If, for example, a flow calculation takes significantly longer than a structural calculation, then more flow solvers than structural solvers can be used as the additional flow solvers and additional structural solvers have to recalculate the same number of modes.
At the end of the calculation by \(\boldsymbol{\mathcal{S}}_{j}\), both the residual r j and the structural displacement \(\tilde{\boldsymbol{x}}{}_{j}\) are known. By subtracting the first residual \(\boldsymbol{r}_{1}^{0}\) and the first displacement \(\tilde{\boldsymbol{x}}{}_{1}^{0}\) calculated by \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) as references, a new Δr and \(\Delta\tilde{\boldsymbol{x}}\) in the current time step become available. It should be emphasized that these Δr and \(\Delta\tilde{\boldsymbol{x}}\) should not be calculated using the extrapolated values as references. As long as the correct reference vectors are unknown because the first calculation of \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) at t n+1 is ongoing, the data calculated by \(\boldsymbol{\mathcal{F}}_{i}\) (i=2,…,g) and \(\boldsymbol{\mathcal{S}}_{j}\) (i=j,…,h) are stored in a second queue. Once the reference values have been calculated, the differences corresponding to the data in this second queue are calculated. All differences that have been recalculated are then combined with \(\underline{\boldsymbol {V}}^{k}\) and \(\underline{\boldsymbol {W}}^{k}\) to form V k and W k.
At the end of each time step, the values of the degrees of freedom inside the fluid and solid domain have to be the same in all solvers because the solution at t n,t n−1,… influences the solution at t n+1. Therefore, the additional solvers \(\boldsymbol{\mathcal{F}}_{i}\) (i=2,…,g) and \(\boldsymbol{\mathcal{S}}_{j}\) (j=2,…,h) have to be synchronized with \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) (see lines 31 to 36). This can be implemented either by copying all variables from \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) to all other flow solvers and structural solvers or by solving the equations once more in \(\boldsymbol{\mathcal{F}}_{i}\) (i=2,…,g) and \(\boldsymbol{\mathcal{S}}_{j}\) (j=2,…,h) with \(\boldsymbol{x}^{last}_{1}\) and \(\boldsymbol{y}^{last}_{1}\) as input.
5.6 Multi-Level IQN-ILS
In Sect. 5.1, it has been explained that only a low-rank approximation to the inverse of the Jacobian is required by IQN-ILS because only a fraction of the Fourier modes is unstable according to the stability analysis of Sect. 4. In addition, it can be noticed in Fig. 13 that the unstable Fourier modes have a low wave number. Due to their low wave number, the behaviour of these unstable modes can thus be determined on a relatively coarse grid. Therefore, the multi-level IQN-ILS (ML-IQN-ILS) technique uses more than one grid level, each with a different number of grid points [48]. ML-IQN-ILS is particularly developed for problems with fine grids where the phenomena that determine the stability of the partitioned fluid-structure interaction simulation can be described on a coarser grid.
ML-IQN-ILS first calculates the coupled solution on the coarsest grid level and constructs the low-rank approximation for the inverse of the Jacobian as present in standard IQN-ILS while doing so. Subsequently, coupling iterations are performed on the second, finer grid level, during which the approximation for the inverse of the Jacobian obtained on the coarsest grid level is further improved by performing coupling iterations. This procedure is then repeated until the solution on the finest grid level has been found, as explained in detail below. Here, only ML-IQN-ILS is discussed as ML-IBQN-LS works in a similar way.
The goal of the multi-level IQN-ILS technique is thus to obtain the low-rank approximation for the inverse of the Jacobian required for the convergence of the coupling iterations on the finest grid level at a lower cost, by constructing it partly on coarser grid levels. As this reduces the number of coupling iterations on the finest grid level and as the cost of the coupling iterations on the coarser grid levels is low, the total time required to solve the coupled problem decreases. This multi-level approach is depicted in Fig. 22 for two grid levels. As only data on the fluid-structure interface is exchanged, this partitioned multi-level coupling technique can couple black-box solvers.
The coarse and fine fluid grid (left) and the coarse and fine structural grid (right), together with the unique coupling grid (centre) in a multi-level simulation with two grid levels. Adapted from [48]
The multi-level IQN-ILS algorithm is not called a multi-grid technique because there are significant differences. Multi-grid refers to a solution technique [20], which has been used for fluid-structure interaction simulations in for example [28, 79, 97, 208, 210]. A major difference is that in the multi-grid technique, the coarse grids provide a correction for the smooth error components on the fine grids. By contrast, the ML-IQN-ILS technique uses the coarse grids to generate an approximation for the inverse of the Jacobian on the fine grids. Accordingly, the ML-IQN-ILS technique begins each time step on the coarsest grid and proceeds towards the finest grid, without returning towards the coarser grids.
The solution techniques used in the flow solver and structural solver are not interfering with the ML-IQN-ILS coupling technique, which allows both solvers to be black-box solvers. Although not required, the calculation in the fluid and/or structure subdomains on each grid level could be performed with a multi-grid solver. In that case, however, the coarse grids used in the multi-grid solver would be independent of and totally unrelated to the coarse grids used on the different levels by the ML-IQN-ILS coupling technique.
As the multi-level coupling techniques use several grid levels for the flow equations and the structural equations, data has to be interpolated between different discretizations of the fluid-structure interface. However, even though the discretization of the interface inside the flow solver and the structural solver depends on the grid level, all operations of the coupling algorithm are performed on a unique grid, the so-called ‘coupling grid’ (see Fig. 22).
In the explanation of this coupling algorithm, the grid level is indicated with a subscript i. The first grid level is the coarsest grid level and the gth grid level is the finest one. Algorithm 16 shows the ML-IQN-ILS technique in detail. Lines 7 to 17 are the standard IQN-ILS algorithm as described above. Around the standard algorithm, an additional loop over the grid levels is added (line 4). First, the coupled solution is calculated on the coarsest grid level. Then, starting from that solution, coupling iterations on the following, finer grid level are performed. These steps are subsequently repeated for all grid levels until the solution on the finest grid has been found. The variable ℓ ensures that at least one coupling iteration is performed on each grid level.
The displacement and the residual are not changed when the grid level i changes, as both are defined on the coupling grid. The coupling algorithm itself works with the unique coupling grid, which determines the dimension of the approximation for the inverse of the Jacobian. The solvers have to interpolate the data from the boundary of their grid to the coupling grid. The interpolation on the fluid-structure interface is thus the responsibility of the solvers (or a layer around the actual solvers). In this way, the acceleration of the coupling iterations and the interpolation of the data on the fluid-structure interface are completely separated, which facilitates the implementation.
Because the coupling algorithm operates on the coupling grid, the difference between r and \(\tilde{\boldsymbol{x}}\) in consecutive coupling iterations is always interpolated to a fixed number of grid points, regardless of the current grid level. As a result, the modes that have been generated on a coarse grid level can be used to accelerate the coupling iterations on the finer grid levels. The same least-squares model is used for all grid levels so the number of columns in the matrices V k and W k increases on each grid level. The counter k is only set to zero at the beginning of the time step (line 1) and not when the coupling iterations on a following grid level start. Lines 21 to 23 show that synchronization of the solvers is necessary at the end of the time step. Once the solution has been found on the finest grid level, all degrees of freedom on the coarser grid levels have to be corrected.
It should be noted that the difference between r and \(\tilde{\boldsymbol{x}}\) in the last coupling iteration on a certain grid level i and the first coupling iteration on the following grid level i+1,
should not be added to V k and W k. Otherwise, the approximation for the inverse of \({\boldsymbol {\mathcal {R}}}'\) would not only relate a change of the residual to a change of the interface’s displacement, but would also represent the additional features that become visible due to a change of the grid level.
5.7 Comparison Between Partitioned Techniques
Gallinger and Bletzinger [78] compared the performance of Aitken relaxation, IQN-ILS and a finite-difference Newton–Krylov solver for the 2D benchmark consisting of a flexible beam behind a rigid cylinder [185]. For both the FSI2 and FSI3 tests, IQN-ILS with reuse of information from previous time steps is approximately 3 times faster than Aitken relaxation, which in turn outperforms the Newton–Krylov solver, even with reuse of Krylov vectors.
In [45], a comparison is presented between Aitken relaxation, IQN-ILS, IBQN-LS and Interface-GMRES for two different cases, namely the 2D benchmark with a flexible beam behind a rigid cylinder [185] and the propagation of a pressure wave in a 3D flexible tube [69, 75, 81].
For the first case, the steady FSI1 test and the unsteady FSI2 test are performed. The iterative flow solver begins the calculation in coupling iteration k+1 from the solution in coupling iteration k. As a result, the computational cost of a calculation with the flow solver decreases during the coupling iterations as the difference between the displacements of the interface decreases. The structural solver begins each calculation from the solution in the previous time step. Table 2 shows the number of calculations by the solvers and the relative duration of the simulations. The number between brackets behind the name of an algorithm indicates from how many time steps information is reused. The number of solver calculations per time step in the unsteady simulation has been averaged over the last period of the oscillation.
Interface-GMRESR has been used with λ=0.01 because this resulted in the lowest number of solver evaluations. In the unsteady FSI2 test, Interface-GMRESR requires more coupling iterations than Interface-GMRES, especially when the deformation within a time step is large. Reuse of information from 3 time steps reduces the number of coupling iterations by approximately 30 % for both IQN-ILS and IBQN-LS. For this unsteady simulation, the duration of the simulation is similar for IQN-ILS(3) and IBQN-LS(3), which are significantly faster than Aitken relaxation and Interface-GMRES(R).
For the second case, Table 3 gives the number of solver calculations in a time step, averaged over the entire simulation, and the relative duration of the simulations. The number of solver calculations per time step has been averaged over the entire simulation. These results demonstrate that the performance of the coupling methods is different with respect to number of solver calculations and CPU time. The reason for this difference is that if the coupling algorithm predicts an irregular displacement of the interface or pressure distribution on the interface, it will take the flow solver and structural solver longer to converge. For this case, the duration of the simulation is again similar for IBQN-LS(10) and IQN-ILS(10), which are faster than the other methods.
Furthermore, it has been observed that the number of Krylov iterations required for solving the linear systems (Eqs. (161) and (166)) in each IBQN-LS iteration is more or less identical to the number of columns in \(\boldsymbol {V}^{k}_{f,s}\) and \(\boldsymbol {W}^{k}_{f,s}\). The convergence criterion for the residual of these linear systems has been set to 10−10 times their initial residual, measured in L 2-norm. The low number of Krylov iterations combined with the cheap matrix-vector product results in a quick solution of these linear systems.
In [47], the performance of the standard and the multi-solver version of the IQN-ILS and IBQN-LS algorithms is compared using three cases. First, a 1D model is considered for the unsteady, incompressible flow in a straight, flexible tube [42]. The speed-up of a simulation as a result of the multi-solver approach can be observed in the average number of coupling iterations between \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) per time step. The additional solvers \(\boldsymbol{\mathcal{F}}_{i}\) (i=2,…,g) and \(\boldsymbol{\mathcal{S}}_{j}\) (j=2,…,h) help \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) to find the solution of the coupled problem more quickly. Table 4 lists the average number of coupling iterations between \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) per time step for the MS-IQN-ILS algorithm. As the number of solvers increases from g=1 to g=8 (with g=h), the average number of coupling iterations per time step decreases from 8 to 2.9 for MS-IQN-ILS. With a negligible duration of the communication and synchronization compared to the duration of the calculation, this will result in a reduction of the run time by at least 50 %.
The second case is a 2D rolling tank, presented by Idelsohn et al. [102]. This case consists of a rectangular tank, filled with oil and air, and a flexible beam which is clamped to bottom of this tank. An electric motor imposes a harmonic rolling motion of the tank around the midpoint of its bottom. With g=4 and h=2 or h=4, the average number of coupling iterations of MS-IQN-ILS decreased by respectively 35 % and 40 % compared to IQN-ILS. It could be remarked that reuse of information from previous time steps by the IQN-ILS algorithm can result in a similar acceleration of the simulation, without the cost of the additional solvers. However, this case cannot be simulated robustly with simple reuse (i.e. no recalculation) of data from previous time steps in the least-squares model.
The third case is again the propagation of a pressure wave in the 3D flexible tube. The MS-IQN-ILS algorithm uses 4 solvers of each type (g=h=4) as the duration of a flow calculation and a structural calculation is approximately the same. The average number of coupling iterations reduces by more than 40 % compared to IQN-ILS.
A remark on the performance of the multi-solver algorithms is that they will need a slightly different number of coupling iterations each time the same simulation is performed, as opposed to most other coupling algorithms. The reason is that the order of the various calculations can change because the multi-solver algorithms involve ‘start’ and ‘ready’ commands. Depending on whether a recalculated difference becomes available before or after \(\boldsymbol{\mathcal{F}}_{1}\) and \(\boldsymbol{\mathcal{S}}_{1}\) start a new calculation, the convergence will be slightly faster or slower. Therefore, the simulations have been performed several times and the number of coupling iterations per time step has been averaged over all runs.
The performance of the standard and multi-level version of the IQN-ILS algorithm is compared in [48]. The first case is again the 1D model for the unsteady, incompressible flow in a straight, flexible tube. Table 5 demonstrates that if a coarse grid level with 103 points and a fine grid level with 104 points are used, ML-IQN-ILS leads to a reduction in the overall simulation time by approximately 35 % compared to IQN-ILS. The average number of coupling iterations per time step on the fine grid level is approximately half of that in a simulation with a fine grid only. If a coarse grid level with 4×103 points and a fine grid level with 104 points are used, the reduction of the simulation time obtained by using the multi-level techniques is smaller. Therefore, it can be concluded that the ratio of the number of degrees of freedom on the fine grid level to the number of degrees of freedom on the coarse grid level has to be sufficiently large. If an intermediate grid level with 4×103 grid points is added between the coarse grid level with 103 points and the fine grid level with 104 points, the additional coupling iterations on the intermediate grid level more or less outweigh the small reduction of the number of coupling iterations on the fine grid. Nevertheless, more than two grid levels might reduce the duration of the simulation significantly compared to two grid levels in other cases.
The second case is the propagation of a pressure wave in a 3D flexible tube. The coarse grid level contains 34944+1824 degrees of freedom for the flow and the structure, respectively. For the fine grid level, each direction is refined, giving 2247168+28032 degrees of freedom. In the simulation with two grid levels, the number of coupling iterations on the fine grid is reduced by approximately 50 % compared to a simulation with a fine grid only. As the cost of the coupling iterations on the coarse grid level is relatively small, the duration of the simulation also decreases by approximately 50 %.
5.8 Comparison Between IQN-ILS and a Monolithic Technique
Partitioned solution techniques are often compared with other partitioned techniques but the difference with monolithic techniques in terms of the duration of the simulation usually remains unclear. Nevertheless, there are some exceptions, for example the comparison by Michler et al. [134] using 1D problems. Furthermore, Küttler et al. [111] presented a comparison between a monolithic technique and several partitioned techniques on three 3D biomechanical cases. One of the cases was the propagation of a pressure wave in a 3D tube, which is also considered in the comparison presented here. They came to the conclusion that the computational time was lowest using a monolithic Newton–Krylov solver with block Gauss–Seidel preconditioning [92], followed by a matrix-free Newton–Krylov solver with calculation of the matrix-vector product by the solvers. Both of these techniques require access to the solver internals. A matrix-free Newton–Krylov solver with finite difference approximation of the matrix-vector product was the third best technique in the comparison, followed by vector extrapolation [109] and Aitken relaxation [108, 138, 139]. However, these last three techniques treat the solvers as black boxes.
Degroote et al. [43] compare the performance of the partitioned IQN-ILS method with a monolithic Newton method (MN, see Eq. (42)). To analyze the difference in performance between both solution techniques without other causes for differences, ADINA (Adina R&D Inc., Watertown, MA, USA) has been used as this programme is capable of both monolithic Newton–Raphson iterations and partitioned Gauss–Seidel iterations between the flow solver and the structural solver. Only a small modification of the partitioned technique in ADINA was necessary to implement the IQN-ILS algorithm. As a result, both the mathematical model and the solver for the resulting discrete equations are identical in the monolithic and the partitioned simulations. To ensure that both techniques solve the coupled problem to the same accuracy, the convergence of the FSI problem is also controlled by ADINA. Several 2D and 3D cases with incompressible fluids from different authors [7, 69, 139] are investigated. The results of this comparison are briefly described below.
The first case is the propagation of a pressure wave in a straight, three-dimensional elastic tube [69, 75, 81]. The simulation with IQN-ILS takes approximately twice as long as that with the MN method, regardless of the grid size. Nevertheless, the partitioned simulation becomes more difficult as the tube length increases. This has been explained by the stability analysis in the previous section. The number of quasi-Newton iterations in the first time step increases significantly with increasing length of the tube. Due to the reuse from previous time steps, however, the ratio of the time for the IQN-ILS simulation to the time for the MN simulation increases more slowly. The partitioned simulation requires 20 to 30 % less memory than the monolithic simulation.
Because the deformations in the previous case are small, a similar case with large deformations is performed. In this so-called mass conservation test [7], the pressure at the inlet and outlet of a tube is increased in 16 equal steps and the steady solution is calculated in each step. The simulation with IQN-ILS takes 33 % longer than the simulation with the MN method but both algorithms are capable of calculating the response. No information from the previous steps is reused by the IQN-ILS method because the boundary conditions of subsequent steps are significantly different.
The strong coupling test case [7, 98] is an unsteady test which is difficult to perform due to the strong interaction between fluid and solid. This test consists of an elastic piston in a channel which is filled with an incompressible fluid. The piston is located at the left-hand side of the channel and the velocity on its left-hand side is prescribed such that the acceleration has a constant value. At the right-hand side of the channel, an outflow boundary condition with zero normal traction is imposed. The simulation continues until the fluid domain has almost zero thickness. The channel walls are defined as free-slip boundaries, yielding a one-dimensional behaviour. Therefore, the coupled system can be conceived as a linear oscillator, with the piston as linear spring and the fluid as mass. However, as the fluid mass varies from its initial value to almost zero, the properties of the oscillator change significantly during the simulation. For this test, Gauss–Seidel iterations diverge quickly, even with strong relaxation [98]. The IQN-ILS method passes this strong coupling test, but it is 2 to 3 times more expensive than the monolithic simulation, depending on the grid size.
The shell in steady cross-flow is a benchmark case with large displacements [7]. It consists of a rectangular, thin structure clamped at one edge to the wall of a fluid domain with a brick shape. The cross-flow velocity is increased in several steps and the steady solution is calculated in each step. The IQN-ILS method is 30 % to 50 % faster for this simulation, especially as the grid is refined. The IQN-ILS algorithm requires on average 3.22 iterations per step and reuses information from the previous steady step to accelerate the convergence.
The last case is a flexible flap in a converging channel [139]. The structure has a density of 1500 kg/m3 and the fluid density is varied from 250 kg/m3 to 1750 kg/m3. As the fluid density increases, the ratio of the time for the IQN-ILS simulation to the time for the MN simulation increases from 1.32 to 2.33. This effect of the fluid/solid density ratio is expected and has been explained by the stability analysis in the previous section.
In conclusion, the ratio of the time for the IQN-ILS simulation to the time for the MN simulation is between 1/2 and 4 for each of these cases. Furthermore, the partitioned simulation requires 20 to 30 % less memory than the monolithic simulation. Finally, the time spent on the IQN-ILS algorithm is negligible compared to the time spent on the flow and structural equations.
The conclusions of any comparison with only a limited number of cases are difficult to generalize. First, while problems of various characteristics have been solved, still, only specific and rather small problems have been considered. Second, the solutions of the structural equations and the flow equations inside the residual operator (Eq. (122)) of the partitioned approach have been obtained with full Newton–Raphson iterations using a direct sparse solver. Typically, however, different solver schemes are used, in particular schemes that are much more efficient for the fluid equations when the number of elements becomes very large. This means that the partitioned approach has been put at a disadvantage in this comparison.
6 Coupling of a black-box solver and an accessible solver
When two strongly interacting problems are simulated with coupling iterations between two solvers, at least partially implicit treatment of the interaction has to be used to avoid divergence (or slow convergence) of these coupling iterations. Implicit treatment of the interaction means that while one problem is solved, the influence of the other problem is taken into account. This influence can be approximated and a better approximation will result in faster convergence of the coupling iterations.
In the previous section, both the flow solver and the structural solver are used as a black box. Gauss–Seidel iterations treat the interaction explicitly when both solvers are black boxes and therefore they are unsuitable in that case. However, if one solver is accessible, then an approximation model for the black-box solver can be included into this accessible solver. For example, Causin et al. [32] rewrote the flow equations as an added-mass operator in the structural equations. Substitution of a linear reduced-physics model of the flow into the structural equations approximates this added-mass operator, thus accelerating the convergence of the Gauss–Seidel coupling iterations [81]. In Sect. 4, the substitution of a linearized structural model into the continuity equation of the flow problem proved to stabilize the Gauss–Seidel iterations. This is the main idea of the interface artificial compressibility (IAC) technique, which is explained below and subsequently compared with IBQN-LS and Robin boundary conditions.
6.1 IAC
The IAC technique first constructs an approximate, local and linear model for the behaviour of the black-box structural solver. To this end, the displacement of the structure is calculated for two different pressure distributions on the fluid-structure interface. This model is then included in the flow solver by rewriting it as a pressure-dependent source term in the continuity equation of the cells adjacent to the fluid-structure interface. The addition of a source term in the continuity equation is possible in most commercial flow solvers by means of user-defined functions without access to the complete source code. However, a source term has to be added and therefore the solver has to be “accessible”. Due to this source term, Gauss–Seidel coupling iterations between the solvers converge quickly.
The construction of the approximate model for the structure corresponds with determining the suitable amount of compressibility, which consists of several steps. First, the deformation of the structure is calculated for two different pressure distributions on the fluid-structure interface. This requires two calculations by the black-box structural solver, in the same way as a normal time step, with the same time step size and the corresponding inertia forces.
y 1,a and y 1,b can be either a spatially varying pressure or a uniform pressure on the entire interface. If a spatially varying pressure is applied, y 1,a and y 1,b refer to pressure distributions \(p^{a}_{i}\) and \(p^{b}_{i}=p^{a}_{i}+\Delta p_{i}\) on the fluid-structure interface, with i running over all grid cells adjacent to the interface. If uniform pressures \(p^{a}_{i}=p^{a}\) and \(p^{b}_{i}=p^{b}\) are used, p a and p b can be estimations for the lowest and highest pressure during the entire simulation.
Subsequently, the displacements x 1,a and x 1,b are transferred to the flow solver, which results in two different deformations of the grid cells adjacent to the fluid-structure interface. The volume ΔV i swept by the fluid-structure interface as the interface is displaced from x 1,a to x 1,b is calculated for each grid cell i adjacent to the fluid-structure interface. The artificial compressibility coefficient \(c^{k}_{i}\) is then calculated as
with \(V^{k}_{i}\) the current volume of grid cell i. This definition is similar to the Bramwell–Hill equation for the wave speed c BH in a straight elastic tube with cross-sectional area a
The values ΔV i /Δp i are only valid in some range around the pressure for which they have been calculated. If the behaviour of the structure changes significantly during the simulation, it is possible that this linearization has to be recalculated after a number of time steps.
If Eq. (3a) is integrated over an arbitrary, deforming control volume V i , the continuity equation is given by
with ∂V i the control volume’s boundary and \(\vec {A}\) the area vector pointing outward. The compressibility of the fluid near the fluid-structure interface is achieved by adding a source term in this equation
for each grid cell i adjacent to the fluid-structure interface with Δt the time step. p i denotes the pressure on the fluid-structure interface in grid cell i. The flow equations are solved for p k+1 and \(\vec {v}^{k+1}\) and the additional source term is treated implicitly during the solution of the flow equations.
Substitution of Eqs. (177) in (180) gives
The first term in the previous equation thus represents a linear approximation for
If a first-order differencing scheme is used for the second term in Eq. (181)
then the first two terms of this equation can be combined as
Consequently, the continuity equation in the flow solver with the IAC term is given by
This demonstrates that the time derivative of V i due to the displacement of the interface is now treated implicitly during the solution of the flow equations, albeit in an approximate, linearized way with a finite difference approximation.
The effect of substituting a linearized structural model in the continuity equation of the flow problem can be interpreted as compressibility. However, when the coupling iterations converge, p k+1 is equal to p k so that the source term disappears. As a result, the solution of the last coupling iteration in a time step corresponds to an incompressible fluid. Hence, this technique was named ‘artificial compressibility’ method and it has been applied to two- and three-dimensional problems with simple geometries [162, 164, 190]. Subsequently, this method has been improved by limiting the compressibility to the fluid cells adjacent to the fluid-structure interface, which is called ‘interface artificial compressibility’ [46, 163].
It is important to limit the artificial compressibility to the grid cells adjacent to the fluid-structure interface. This corresponds to mimicking the displacement of the structure due to the current pressure while the flow equations are solved. When the pressure on the interface changes, the source term mimics how much the structure will move due to that change. The fluid mass that will be displaced by the motion of the structure is temporarily produced by or stored in the source term in the continuity equation of the grid cells adjacent to the interface. This causes a modification of the remainder of the flow field so that it already corresponds to the approximated future displacement of the structure. For the grid cells which are not adjacent to the interface, it seems as if the interface has already moved by the approximated displacement.
The concept of the artificial compressibility method for fluid-structure interaction bears resemblance to the artificial compressibility method of Chorin [36] and Témam [179] who introduced compressibility in pseudo-time to calculate the steady flow of incompressible fluids. This concept was later extended to unsteady simulations by Peyret [152] and Merkle and Athavale [132] who used a calculation in a pseudo-time within each time step. The similarity between IAC and artificial compressibility methods for the simulation of incompressible flows is that the different coupling iterations can be conceived as steps in a pseudo-time. From that point of view, Eq. (182) is a time derivative in the pseudo-time (with pseudo-time step equal to Δt) which is added to the continuity equation.
6.2 Comparison Between IAC and IBQN-LS
In [46], the IAC method and the IBQN-LS method have both been used to simulate the propagation of a pressure wave in a 3D flexible tube. In this simulation, the rate of change of the tube’s volume is between −2×10−5 m3/s and 2×10−5 m3/s. In comparison, the maximal difference between the rate of change of the tube’s volume and the net volumetric influx for the IAC method is 1.85×10−9 m3/s, which proves that the artificially added compressibility has disappeared to a sufficient level once the coupling iterations have converged. For this case, different uniform values for p a and p b have been used.
The number of coupling iterations per time step averaged over an entire simulation is given in Table 6 for both the IAC method and the IBQN-LS method with a convergence tolerance of ε o =10−3∥r 0∥2. The number of iterations per time step has been averaged over the entire simulation. Even though the IBQN-LS method is greatly accelerated by reusing information from the previous time steps, the IAC method required the least CPU time.
The second case is the FSI2 test with the oscillating beam attached to a rigid cylinder. For this case, the parameters p a and p b of the IAC method should not be uniform on the fluid-structure interface. With uniform p a and p b, the compressibility coefficient would approximate the behaviour of the structure due to a compression loading. However, this is not an important displacement mode during the simulation. By contrast, the most important displacement modes of the beam are its first bending modes. To ensure that the compressibility coefficient approximates the bending behaviour of the structure, p a is set to zero everywhere and p b depends on the position
with x and y the horizontal and vertical coordinates. x=0.25 m is the left end of the beam and x=0.60 m is the right end; y=0.20 m is the vertical middle of the beam. By applying a positive pressure on the top of the beam and a negative pressure on the bottom, the beam will bend. The difference between p a and p b on the right end of the beam is zero; therefore the compressibility coefficient c is set to a very large value in the cells adjacent to the right end of the beam.
The average number of coupling iterations per time step is listed in Table 7 for a convergence tolerance of ε o =10−3∥r 0∥2. The number of iterations per time step has been averaged over the entire simulation. For this case, the IBQN-LS method with reuse is twice as fast as the IAC method. So, although it is possible to solve this problem with the IAC method, IBQN-LS and IQN-ILS (not shown in Table 7) are preferred. With regard to the number of iterations, the difference between the IAC method and the IBQN-LS(3) simulation is even larger. However, the flow solver converges faster when the IAC method is used because the difference between the displacement in subsequent iterations is smaller.
The examples above demonstrate that a local (scalar) approximation of the structural behaviour inside the flow solver can accelerate the convergence of the Gauss–Seidel coupling iterations. By contrast, a local approximation of the flow behaviour inside the structural solver would not be useful. Instead, a global (matrix) approximation of the fluid added-mass would have to be included in the structural solver. For the flow in a flexible tube, this can be explained as follows. An increase in pressure at some point on the interface will only influence the structure in the neighbourhood of that point. On the other hand, due to the incompressibility, the displacement of the interface at some point will influence the entire fluid domain.
Furthermore, fast convergence with the IAC method requires that the local, linear relation between the pressure on the interface and the displacement of the structure is a good approximation of the reality. This condition is satisfied for the flexible tube, but not really for the clamped beam. For the latter, a difference in pressure between the top and the bottom near the free end of the beam will cause a deflection of the entire beam, so not a local relation.
6.3 Comparison Between IAC and Robin Boundary Conditions
When solving the flow equations, Gauss–Seidel iterations with Robin–Neumann decomposition (GS-RN) [4, 72, 142] use a Robin boundary condition for the fluid, given by
with the coefficient α changing along the fluid-structure interface. As the fluid velocity does not have to match the structural velocity in this boundary condition, some fluid is allowed to cross the interface. Conversely, Gauss–Seidel coupling iterations with Dirichlet–Neumann decomposition and IAC (GS-DN-IAC) [46] use a Dirichlet boundary condition.
Degroote [41] demonstrates that GS-RN and GS-DN-IAC are different implementations of the same underlying idea, being to include an approximation for the structural behaviour in the flow solver. In this analysis, a finite volume discretization is applied. Additionally, they mention that only GS-DN-IAC neglects the viscous tractions on the fluid-structure interface in the linearized structural model (but not in the result). Furthermore, GS-DN-IAC uses the cell velocity whereas GS-RN uses the face velocity, which converge towards each other as the cell size decreases. Under those conditions, they demonstrate that GS-RN and GS-DN-IAC are equal if
for face m of cell i. So, GS-RN includes an approximation for the structural behaviour in the flow solver by means of a Robin boundary condition whereas GS-DN-IAC uses a pressure-dependent source term to achieve this.
For the flow in a straight flexible tube, Sect. 4 demonstrated that only the source term in the continuity equation is required for fast convergence of the GS-DN-IAC iterations as long as the fluid velocity is lower than the wave speed. Hence, only the source term is added to the continuity equation in [46, 162, 163] whereas both the continuity and the momentum equations are modified in [4, 72, 142].
The choice of the technique to calculate the coefficients is independent of the choice between GS-RN and GS-DN-IAC. In [4], an analytical expression for the coefficient α is obtained by considering a membrane so that the structural equations can be written in the same form as the Robin boundary condition. Moreover, an optimal value for α derived from a von Neumann analysis has been proposed in [80]. Conversely, the structural equations are solved twice in [46], each time with a different pressure on the interface, followed by a finite difference approximation.
7 Overall Conclusion
This review article focuses on partitioned simulation techniques for strongly coupled fluid-structure interaction problems, especially techniques which use black-box solvers. In addition, a review is presented of many different techniques to take into account the deforming fluid domain (Sect. 2) and other techniques to perform fluid-structure interaction simulations (Sect. 3).
The von Neumann stability analysis (Sect. 4) on a one-dimensional model of the unsteady flow in a straight flexible tube demonstrates that error modes with a low wave number in the displacement of the interface are most unstable during the coupling iterations. Only a limited number of the Fourier modes are unstable or badly damped if the model parameters are chosen to approximate the flow in a piece of a large artery. Only these modes need to be treated implicitly during the coupling iterations to achieve fast convergence. As a result, quasi-Newton coupling techniques quickly yield the coupled solution as long as the behaviour of these unstable or badly damped modes is captured by the approximate Jacobian(s).
Different techniques to couple two black-box solvers are analyzed, including IQN-ILS, IBQN-LS, Aitken relaxation and Interface-GMRES. Furthermore, multi-solver and multi-level versions of IQN-ILS are discussed. Both the algorithms and the performance of all these techniques are compared. For the cases considered, both IQN-ILS and IBQN-LS require fewer coupling iterations than Interface-GMRES and Aitken relaxation. Furthermore, the IQN-ILS technique has been compared to a monolithic Newton solver for several two- and three-dimensional cases. For these cases, the ratio of the partitioned simulation’s duration to the monolithic simulation’s duration is between 1/2 and 4.
If only one of the two solvers is a black box, the interaction between the solvers can be taken into account implicitly during the coupling iterations by including an approximate model for the behaviour of the black-box solver in the accessible solver. A local, scalar model for the behaviour of a black-box structural solver can be constructed by means of finite differencing. This model can be included in a flow solver by reformulating it as a source term in the continuity equation of the cells adjacent to the fluid-structure interface or, alternatively, as a Robin boundary condition at the fluid-structure interface.
References
Amsallem D, Farhat C, Lieu T (2007) Aeroelastic analysis of F-16 and F-18/A configurations using adapted CFD-based reduced-order models. In: 48th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and materials conference, Honolulu, HI, USA, pp 1–20. AIAA 2007-2364
Antoci C, Gallati M, Sibilla S (2007) Numerical simulation of fluid-structure interaction by SPH. Comput Struct 85(11–14):879–890
Artlich S, Mackens W (1995) Newton-coupling of fixed point iterations. In: Hackbusch W, Wittum G (eds) 11th GAMM-seminar: numerical treatment of coupled systems. Notes on numerical fluid mechanics, vol 51. Vieweg, Braunschweig, pp 1–10
Badia S, Nobile F, Vergara C (2008) Fluid-structure partitioned procedures based on Robin transmission conditions. J Comput Phys 227(14):7027–7051
Balaban G, Logg A, Rognes M (2012) A Newton method for fluid-structure interaction using full Jacobians based on automatic form differentiation. In: 6th European Congress on computational methods in applied sciences and engineering, Vienna, Austria, pp 1–14
Bathe KJ (2007) Conserving energy and momentum in nonlinear dynamics: a simple implicit time integration scheme. Comput Struct 85(7–8):437–445
Bathe KJ, Ledezma G (2007) Benchmark problems for incompressible fluid flows with structural interactions. Comput Struct 85(11–14):628–644
Bathe KJ, Zhang H (2004) Finite element developments for general fluid flows with structural interactions. Int J Numer Methods Eng 60(1):213–232
Bathe KJ, Zhang H, Wang M (1995) Finite element analysis of incompressible and compressible fluid flows with free surfaces and structural interactions. Comput Struct 56(2–3):193–213
Batina J (1990) Unsteady Euler airfoil solutions using unstructured dynamic meshes. AIAA J 28(8):1381–1388
Bazilevs Y, Calo V, Zhang Y, Hughes T (2006) Isogeometric fluid-structure interaction analysis with applications to arterial blood flow. Comput Mech 38(4–5):310–322
Bazilevs Y, Calo V, Hughes T, Zhang Y (2008) Isogeometric fluid-structure interaction: theory, algorithms, and computations. Comput Mech 43(1):3–37
Bazilevs Y, Hsu MC, Kiedl J, Wüchner R, Bletzinger KU (2011) 3D simulation of wind turbine rotors at full scale. Part II: Fluid-structure interaction modeling with composite blades. Int J Numer Methods Fluids 65:236–253
Behr M, Tezduyar T (1999) The shear-slip mesh update method. Comput Methods Appl Mech Eng 174(3–4):261–274
Belytschko T, Black T (1999) Elastic crack growth in finite elements with minimal remeshing. Int J Numer Methods Eng 45(5):601–620
Billah K, Scanlan R (1991) Resonance, Tacoma Narrows bridge failure, and undergraduate physics textbooks. Am J Phys 59(2):118–124
Blom F (1998) A monolithical fluid-structure interaction algorithm applied to the piston problem. Comput Methods Appl Mech Eng 167(3–4):369–391
de Boer A, van der Schoot M, Bijl H (2007) Mesh deformation based on radial basis function interpolation. Comput Struct 85(11–14):784–795
de Boer A, van Zuijlen A, Bijl H (2007) Review of coupling methods for non-matching meshes. Comput Methods Appl Mech Eng 196(8):1515–1525
Brandt A (1977) Multilevel adaptive solutions to boundary-value problems. Math Comput 31(138):333–390
Brezinski C (1975) Généralisations de la transformation de Shanks, de la table de Padé et de l’ϵ-algorithme. Calcolo 12(4):317–360
Broyden C (1965) A class of methods for solving nonlinear simultaneous equations. Math Comput 19(92):577–593
Broyden C (1970) The convergence of a class of double-rank minimization algorithms. Part I. IMA J Appl Math 6(1):76–90
Broyden C (1970) The convergence of a class of double-rank minimization algorithms. Part II. IMA J Appl Math 6(3):222–231
van Brummelen E (2009) Added mass effects of compressible and incompressible flows in fluid-structure interaction. J Appl Mech 76(2):021206
van Brummelen E (2011) Partitioned iterative solution methods for fluid-structure interaction. Int J Numer Methods Fluids 65(1–3):3–27
van Brummelen E, Michler C, de Borst R (2005) Interface-GMRES(R) acceleration of subiteration for fluid-structure-interaction problems. Report DACS-05-001. Available from: http://www.em.lr.tudelft.nl/downloads/DACS-05-001.pdf
van Brummelen E, van der Zee K, de Borst R (2008) Space/time multigrid for a fluid-structure-interaction problem. Appl Numer Math 58(12):1951–1971
Burman E, Fernandez M (2007) Stabilized explicit coupling for fluid–structure interaction using Nitsche’s method. C R Math 345(8):467–472
Burman E, Fernandez M (2009) Stabilization of explicit coupling in fluid-structure interaction involving fluid incompressibility. Comput Methods Appl Mech Eng 198(5–8):766–784
Cabay S, Jackson L (1976) A polynomial extrapolation method for finding limits and antilimits for vector sequences. SIAM J Numer Anal 13(5):734–752
Causin P, Gerbeau JF, Nobile F (2005) Added-mass effect in the design of partitioned algorithms for fluid-structure problems. Comput Methods Appl Mech Eng 194(42–44):4506–4527
Cebral J, Löhner R (1997) Conservative load projection and tracking for fluid-structure problems. AIAA J 35(4):687–692
Cebral J, Löhner R, Soto O, Choyke P, Yim P (2001) Patient-specific simulation of carotid artery stenting using computational fluid dynamics. In: 4th international conference on medical image computing and computer-assisted intervention. Lecture notes in computer science, vol 2208. Springer, London, pp 153–160
Chan T (1985) An approximate Newton method for coupled nonlinear systems. SIAM J Numer Anal 22(5):904–913
Chorin A (1967) A numerical method for solving incompressible viscous flow problems. J Comput Phys 2(1):12–26
Chorin A (1968) Numerical solution of Navier–Stokes equations. Math Comput 22(104):745–762
Davidon W (1959) Variable metric methods for minimization. AEC Research and Development Report ANL-5990
Davidon W (1968) Variance algorithms for minimization. Comput J 10(4):406–410
Degand C, Farhat C (2002) A three-dimensional torsional spring analogy method for unstructured dynamic meshes. Comput Struct 80(3–4):305–316
Degroote J (2011) On the similarity between Dirichlet–Neumann with interface artificial compressibility and Robin–Neumann schemes for the solution of fluid-structure interaction problems. J Comput Phys 230(17):6399–6403
Degroote J, Bruggeman P, Haelterman R, Vierendeels J (2008) Stability of a coupling technique for partitioned solvers in FSI applications. Comput Struct 86(23–24):2224–2234
Degroote J, Bathe KJ, Vierendeels J (2009) Performance of a new partitioned procedure versus a monolithic procedure in fluid-structure interaction. Comput Struct 87(11–12):793–801
Degroote J, Annerel S, Vierendeels J (2010) Stability analysis of Gauss–Seidel iterations in a partitioned simulation of fluid-structure interaction. Comput Struct 88(5–6):263–271
Degroote J, Haelterman R, Annerel S, Bruggeman P, Vierendeels J (2010) Performance of partitioned procedures in fluid-structure interaction. Comput Struct 88(7–8):446–457
Degroote J, Swillens A, Bruggeman P, Haelterman R, Segers P, Vierendeels J (2010) Simulation of fluid-structure interaction with the interface artificial compressibility method. Commun Numer Methods Eng 26(3):276–289
Degroote J, Annerel S, Vierendeels J (2011) Multi-solver algorithms for the partitioned simulation of fluid-structure interaction. Comput Methods Appl Mech Eng 200(25–28):2195–2210
Degroote J, Annerel S, Vierendeels J (2012) Multi-level algorithms for the partitioned simulation of fluid-structure interaction. Comput Methods Appl Mech Eng 225–228:14–27
Degroote J, Hojjat M, Stavropoulou E, Wüchner R, Bletzinger KU (2013) Partitioned solution of an unsteady adjoint for strongly coupled fluid-structure interactions and application to parameter identification of a one-dimensional problem. Struct Multidiscip Optim 47(1):77–94
Demirdzic I, Peric M (1988) Space conservation law in finite volume calculations of fluid flow. Int J Numer Methods Fluids 8(9):1037–1050
Dennis J, Schnabel R (1983) Numerical methods for unconstrained optimization and nonlinear equations, 6th edn. Prentice Hall, Englewood Cliffs
Deparis S, Fernandez M, Formaggia L (2003) Acceleration of a fixed point algorithm for fluid-structure interaction using transpiration conditions. Modél Math Anal Numér 37(4):601–616
Dettmer W, Perić D (2006) A computational framework for fluid-structure interaction: finite element formulation and applications. Comput Methods Appl Mech Eng 195(41–43):5754–5779
Donea J, Guiliani S, Halleux J (1982) An arbitrary Lagrangian–Eulerian finite-element method for transient dynamic fluid structure interactions. Comput Methods Appl Mech Eng 33(1–3):689–723
Donea J, Huerta A, Ponthot JP, Rodriguez-Ferran A (2004) Arbitrary Lagrangian–Eulerian methods. In: Encyclopedia of computational mechanics: fundamentals, vol 1. Wiley, New York, pp 1–25. Chap 14
Dumont K, Vierendeels J, Segers P, Van Nooten G, Verdonck P (2005) Predicting ATS open pivot (TM) heart valve performance with computational fluid dynamics. J Heart Valve Dis 14(3):393–399
Dumont K, Vierendeels J, Kaminsky R, Van Nooten G, Verdonck P, Bluestein D (2007) Comparison of the hemodynamic and thrombogenic performance of two bileaflet mechanical heart valves using a CFD/FSI model. J Biomech Eng 129(4):558–565
Eddy R (1979) Extrapolation to the limit of a vector sequence. In: Wang P (ed) Information linkage between applied mathematics and industry. Academic Press, New York, pp 387–396
Edelsbrunner H, Mücke E (1994) Three-dimensional alpha shapes. ACM Trans Graph 13(1):43–72
Eisenstat S, Elman H, Schultz M (1983) Variational iterative methods for nonsymmetric systems of linear equations. SIAM J Numer Anal 20(2):345–357
Fadlun E, Verzicco R, Orlandi P, Mohd-Yusof J (2000) Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J Comput Phys 161(1):35–60
Farhat C, Degand C, Koobus B, Lesoinne M (1998) Torsional springs for two-dimensional dynamic unstructured fluid meshes. Comput Methods Appl Mech Eng 163(1–4):231–245
Farhat C, Lesoinne M, Le Tallec P (1998) Load and motion transfer algorithms for fluid/structure interaction problems with non-matching discrete interfaces: momentum and energy conservation, optimal discretization and application to aeroelasticity. Comput Methods Appl Mech Eng 157(1–2):95–114
Farhat C, van der Zee K, Geuzaine P (2006) Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity. Comput Methods Appl Mech Eng 195(17–18):1973–2001
Felippa C, Park K, Farhat C (2001) Partitioned analysis of coupled mechanical systems. Comput Methods Appl Mech Eng 190(24–25):3247–3270
Fernandez M (2011) Coupling schemes for incompressible fluid-structure interaction: implicit, semi-implicit and explicit. Bol Soc Esp Mat Apl 55:59–108
Fernandez M (2011) Incremental displacement-correction schemes for the explicit coupling of a thin structure with an incompressible fluid. C R Math 349(7–8):473–477
Fernandez M, Le Tallec P (2003) Linear stability analysis in fluid-structure interaction with transpiration. Part II: Numerical analysis and applications. Comput Methods Appl Mech Eng 192(43):4837–4873
Fernandez M, Moubachir M (2005) A Newton method using exact Jacobians for solving fluid-structure coupling. Comput Struct 83(2–3):127–142
Fernandez M, Mullaert J (2011) Displacement-velocity correction schemes for incompressible fluid-structure interaction. C R Math 349(17–18):1011–1015
Fernandez M, Gerbeau JF, Grandmont C (2007) A projection semi-implicit scheme for the coupling of an elastic structure with an incompressible fluid. Int J Numer Methods Eng 69(4):794–821
Figueroa C, Vignon-Clementel I, Jansen K, Hughes T, Taylor C (2006) A coupled momentum method for modeling blood flow in three-dimensional deformable arteries. Comput Methods Appl Mech Eng 195(41–43):5685–5706
Fletcher R (1970) A new approach to variable metric algorithms. Comput J 13(3):317–322
Fletcher R, Powell M (1963) A rapidly convergent descent method for minimization. Comput J 6(2):163–168
Formaggia L, Gerbeau JF, Nobile F, Quarteroni A (2001) On the coupling of 3D and 1D Navier–Stokes equations for flow problems in compliant vessels. Comput Methods Appl Mech Eng 191(6–7):561–582
Förster C, Wall W, Ramm E (2006) On the geometric conservation law in transient flow calculations on deforming domains. Int J Numer Methods Fluids 50(12):1369–1379
Förster C, Wall W, Ramm E (2007) Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Comput Methods Appl Mech Eng 196(7):1278–1293
Gallinger T, Bletzinger KU (2010) Comparison of algorithms for strongly coupled partitioned fluid-structure interaction—efficiency versus simplicity. In: Pereira J, Sequeira A (eds) 5th European conference on computational fluid dynamics, Lisbon, Portugal, pp 1–20
Gee M, Küttler U, Wall W (2011) Truly monolithic algebraic multigrid for fluid-structure interaction. Int J Numer Methods Eng 85(8):987–1016
Gerardo-Giorda L, Nobile F, Vergara C (2010) Analysis and optimization of Robin–Robin partitioned procedures in fluid-structure interaction problems. SIAM J Numer Anal 48(6):2091–2116
Gerbeau JF, Vidrascu M (2003) A quasi-Newton algorithm based on a reduced model for fluid-structure interaction problems in blood flows. Modél Math Anal Numér 37(4):631–648
Gerbeau JF, Vidrascu M, Frey P (2005) Fluid-structure interaction in blood flows on geometries based on medical imaging. Comput Struct 83(2–3):155–165
Gerstenberger A, Wall W (2008) An eXtended Finite Element Method/Lagrange multiplier based approach for fluid-structure interaction. Comput Methods Appl Mech Eng 197(19–20):1699–1714
Gilmanov A, Sotiropoulos F (2005) A hybrid Cartesian/immersed boundary method for simulating flows with 3D, geometrically complex, moving bodies. J Comput Phys 207(2):457–492
Glowinski R, Pan TW, Périaux J (1994) A fictitious domain method for Dirichlet problem and applications. Comput Methods Appl Mech Eng 111(3–4):283–303
Glowinski R, Pan TW, Hesla T, Joseph D, Périaux J (1999) A distributed Lagrange multiplier/fictitious domain method for particulate flows. Int J Multiph Flow 25(5):755–794
Goldfarb D (1970) A family of variable metric methods derived by variational means. Math Comput 24(109):23–26
Golub G, Van Loan C (1996) Matrix computations, 3rd edn. Johns Hopkins University Press, Baltimore
Greenstadt J (1970) Variations on variable-metric methods. Math Comput 24(109):1–22
Guidoboni G, Glowinski R, Cavallini N, Canic S, Lapin S (2009) A kinematically coupled time-splitting scheme for fluid–structure interaction in blood flow. Appl Math Lett 22(5):684–688
Haelterman R (2009) Analytical study of the least squares quasi-Newton method for interaction problems. PhD Thesis, Ghent University
Heil M (2004) An efficient solver for the fully coupled solution of large-displacement fluid-structure interaction problems. Comput Methods Appl Mech Eng 193(1–2):1–23
Helenbrook B (2003) Mesh deformation using the biharmonic operator. Int J Numer Methods Eng 56(7):1007–1021
Hillewaere J, Dooms D, Van Quekelberghe B, Degroote J, Vierendeels J, De Roeck G, Degrande G (2012) Unsteady Reynolds averaged Navier–Stokes simulation of the post-critical flow around a closely spaced group of silos. J Fluids Struct 30:51–72
Hou G, Wang J, Layton A (2012) Numerical methods for fluid-structure interaction—a review. Commun Comput Phys 12(2):337–377
Hron J, Turek S (2006) A monolithic FEM solver for an ALE formulation of fluid-structure interaction with configuration for numerical benchmarking. In: Wesseling P, Oñate E, Périaux J (eds) 4th European conference on computational fluid dynamics. Egmond aan Zee, Bergen
Hron J, Turek S (2006) A monolithic FEM/multigrid solver for ALE formulation of fluid structure interaction with application in biomechanics. In: Bungartz HJ, Schäfer M (eds) Fluid-structure interaction—modelling, simulation, optimisation. Lecture notes in computational science and engineering, vol 53. Springer, Berlin, pp 146–170
Hübner B, Walhorn E, Dinkler D (2004) A monolithic approach to fluid-structure interaction using space-time finite elements. Comput Methods Appl Mech Eng 193(23–26):2087–2104
Idelsohn S, Calvo N, Oñate E (2003) Polyhedrization of an arbitrary 3D point set. Comput Methods Appl Mech Eng 192(22–24):2649–2667
Idelsohn S, Oñate E, Del Pin F (2003) A Lagrangian meshless finite element method applied to fluid-structure interaction problems. Comput Struct 81(8–11):655–671
Idelsohn S, Marti J, Limache A, Oñate E (2008) Unified Lagrangian formulation for elastic solids and incompressible fluids: application to fluid-structure interaction problems via the PFEM. Comput Methods Appl Mech Eng 197(19–20):1762–1776
Idelsohn S, Marti J, Souto-Iglesias A, Oñate E (2008) Interaction between an elastic structure and free-surface flows: experimental versus numerical comparisons using the PFEM. Comput Mech 43(1):125–132
Irons B, Tuck R (1969) A version of the Aitken accelerator for computer iteration. Int J Numer Methods Eng 1(3):275–277
Jahromi H, Izzuddin B, Zdravkovic L (2009) A domain decomposition approach for coupled modelling of nonlinear soil-structure interaction. Comput Methods Appl Mech Eng 198(33–36):2738–2749
Keller H (1977) Numerical solution of bifurcation and nonlinear eigenvalue problems. In: Rabinowitz P (ed) Applications of bifurcation theory. Academic Press, San Diego, pp 359–384
Khan M, Moatamedi M, Souli M, Zeguer T (2008) Multiphysics out of position airbag simulation. Int J Crashworthiness 13(2):159–166
Knoll D, Keyes D (2004) Jacobian-free Newton–Krylov methods: a survey of approaches and applications. J Comput Phys 193(2):357–397
Küttler U, Wall W (2008) Fixed-point fluid-structure interaction solvers with dynamic relaxation. Comput Mech 43(1):61–72
Küttler U, Wall W (2009) Vector extrapolation for strong coupling fluid-structure interaction solvers. J Appl Mech 76(2):021205
Küttler U, Förster C, Wall W (2006) A solution for the incompressibility dilemma in partitioned fluid-structure interaction with pure Dirichlet fluid domains. Comput Mech 38(4–5):417–429
Küttler U, Gee M, Förster C, Comerford A, Wall W (2010) Coupling strategies for biomedical fluid-structure interaction problems. Int J Numer Methods Biomed Eng 26(3–4):305–321
Lanzkron P, Rose D, Wilkes J (1996) An analysis of approximate nonlinear elimination. SIAM J Sci Comput 17(2):538–559
Lee C, Noguchi H, Koshizuka S (2007) Fluid-shell structure interaction analysis by coupled particle and finite element method. Comput Struct 85(11–14):688–697
Lee J, LeVeque R (2003) An immersed interface method for incompressible Navier–Stokes equations. SIAM J Sci Comput 25(3):832–856
Lesoinne M, Farhat C (1996) Geometric conservation laws for flow problems with moving boundaries and deformable meshes and their impact on aeroelastic computations. Comput Methods Appl Mech Eng 134(1–2):71–90
Lesoinne M, Farhat C (1998) A higher-order subiteration free staggered algorithm for non-linear transient aeroelastic problems. AIAA J 36(9):1754–1756
Löhner R, Yang C (1996) Improved ALE mesh velocities for moving boundaries. Commun Numer Methods Eng 12(10):599–608
van Loon R, Anderson P, de Hart J, Baaijens F (2004) A combined fictitious domain/adaptive meshing method for fluid-structure interaction in heart valves. Int J Numer Methods Fluids 46(5):533–544
van Loon R, Anderson P, van de Vosse F (2006) A fluid-structure interaction method with solid-rigid contact for heart valve dynamics. J Comput Phys 217(2):806–823
Lynch D (1982) Unified approach to simulation of deforming elements with applications to phase-change problems. J Comput Phys 47(3):387–411
Mackens W, Menck J, Voss H (1999) Coupling iterative subsystem solvers. In: Keil F, Mackens W, Voss H, Werther J (eds) Scientific computing in chemical engineering II. Simulation, image processing, optimization, and control. Springer, Berlin, pp 184–191
Maman N, Farhat C (1995) Matching fluid and structure meshes for aeroelastic computations: a parallel approach. Comput Struct 54(4):779–785
Manno V, Reitsma S (1993) Developing numerical techniques for solving low Mach number fluid-acoustic problems. AIAA J 31(11):1984–1991
Marshall J, Imregun M (1996) A review of aeroelasticity methods with emphasis on turbomachinery applications. J Fluids Struct 10(3):237–267
Martinez J (1984) A quasi-Newton method with modification of one column per iteration. Computing 33(3–4):353–362
Martinez J, Zambaldi M (1992) An inverse column-updating method for solving large-scale nonlinear systems of equations. Optim Methods Softw 1(2):129–140
Matthies H, Steindorf J (2002) Partitioned but strongly coupled iteration schemes for nonlinear fluid-structure interaction. Comput Struct 80(27–30):1991–1999
Matthies H, Steindorf J (2003) Partitioned strong coupling algorithms for fluid-structure interaction. Comput Struct 81(8–11):805–812
Matthies H, Niekamp R, Steindorf J (2006) Algorithms for strong coupling procedures. Comput Methods Appl Mech Eng 195(17–18):2028–2049
McCormick G, Pearson J (1969) Variable metric methods and unconstrained optimization. In: Fletcher R (ed) Optimization. Academic Press, London, pp 307–325
Menck J (2002) An approximate Newton-like coupling of subsystems. J Appl Math Mech 82(2):101–114
Merkle C, Athavale M (1987) Time-accurate unsteady incompressible flow algorithm based on artificial compressibility. In: 8th AIAA computational fluid dynamics conference, Honolulu, HI, USA, pp 397–407. AIAA 1987-1137
Mešina M (1977) Convergence acceleration for the iterative solution of the equations x=ax+f. Comput Methods Appl Mech Eng 10(2):165–173
Michler C, van Brummelen E, Hulshoff S, de Borst R (2003) The relevance of conservation for stability and accuracy of numerical methods for fluid-structure interaction. Comput Methods Appl Mech Eng 192(37–38):4195–4215
Michler C, van Brummelen E, de Borst R (2005) An interface Newton–Krylov solver for fluid-structure interaction. Int J Numer Methods Fluids 47(10–11):1189–1195
Michler C, van Brummelen E, de Borst R (2006) Error-amplification analysis of subiteration-preconditioned GMRES for fluid-structure interaction. Comput Methods Appl Mech Eng 195(17–18):2124–2148
Mittal R, Iaccarino G (2005) Immersed boundary methods. Annu Rev Fluid Mech 37:239–261
Mok D, Wall W (2001) Partitioned analysis schemes for the transient interaction of incompressible flows and nonlinear flexible structures. In: Schweizerhof K, Wall W, Bletzinger KU (eds) Trends in computational structural mechanics, Barcelona
Mok D, Wall W, Ramm E (2001) Accelerated iterative substructuring schemes for instationary fluid-structure interaction. In: Bathe KJ (ed) Computational fluid and solid mechanics. Elsevier, Amsterdam, pp 1325–1328
Monaghan J (1994) Simulating free surface flows with SPH. J Comput Phys 110(2):399–406
Newmark N (1959) A method of computation for structural dynamics. J Eng Mech Div 85(3):67–94
Nobile F, Vergara C (2008) An effective fluid-structure interaction formulation for vascular dynamics by generalized Robin conditions. SIAM J Sci Comput 30(2):731–763
Nocedal J, Wright S (1999) Numerical optimization. Springer series in operations. Springer, Berlin
Oñate E, Idelsohn S, Del Pin F, Aubry R (2004) The particle finite element method. An overview. Int J Comput Methods 1(2):267–307
Oñate E, Idelsohn S, Celigueta M, Rossi R (2008) Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comput Methods Appl Mech Eng 197(19–20):1777–1800
Pearson J (1969) Variable metric methods of minimization. Comput J 12(2):171–178
Perktold K, Rappitsch G (1995) Computer simulation of local blood flow and vessel mechanics in a compliant carotid artery bifurcation model. J Biomech 28(7):845–856
Peseux B, Gornet L, Donguy B (2005) Hydrodynamic impact: numerical and experimental investigations. J Fluids Struct 21(3):277–303
Peskin C (1972) Flow patterns around heart valves: a numerical method. J Comput Phys 10(2):252–271
Peskin C (1977) Numerical analysis of blood flow in the heart. J Comput Phys 25(3):220–252
Peskin C (2002) The immersed boundary method. Acta Numer 11:479–517
Peyret R (1976) Unsteady evolution of a horizontal jet in a stratified fluid. J Fluid Mech 78(1):49–63
Piperno S, Farhat C (2001) Partitioned procedures for the transient solution of coupled aeroelastic problems. Part II: Energy transfer analysis and three-dimensional applications. Comput Methods Appl Mech Eng 190(24–25):3147–3170
Piperno S, Farhat C, Larrouturou B (1995) Partitioned procedures for the transient solution of coupled aeroelastic problems. Part I: Model problem, theory and two-dimensional application. Comput Methods Appl Mech Eng 124(1–2):79–112
Potapov S, Maurel B, Combescure A, Fabis J (2009) Modeling accidental-type fluid-structure interaction problems with the SPH method. Comput Struct 87(11–12):721–734
Powell M (1970) A new algorithm for unconstrained optimization. In: Roosen J, Mangasarian O, Ritter K (eds) Nonlinear programming. Academic Press, London, pp 31–65
Pugachev B (1977) Acceleration of the convergence of iterative processes and a method for solving systems of nonlinear equations. USSR Comput Math Math Phys 17(5):199–207
Quarteroni A (2006) Cardiovascular mathematics. In: Sanz-Solé M, Soria J, Varona J, Verdera J (eds) International Congress of mathematicians, vol 1. Eur. Math. Soc., Madrid, pp 479–512
Quarteroni A, Tuveri M, Veneziani A (2000) Computational vascular fluid dynamics: problems, models and methods. Comput Vis Sci 2(4):163–197
Quirk J (1994) An alternative to unstructured grids for computing gas-dynamic flows around arbitrarily complex 2-dimensional bodies. Comput Fluids 23(1):125–142
Richter T (2012) Goal-oriented error estimation for fluid-structure interaction problems. Comput Methods Appl Mech Eng 223–224:28–42
Riemslagh K, Vierendeels J, Dick E (1998) Coupling of a Navier–Stokes solver and an elastic boundary solver for unsteady problems. In: Papailiou K, Tsahalis D, Périaux J, Hirsch C, Pandolfi M (eds) 2nd European computational fluid dynamics conference. Wiley, Athens, pp 1040–1045
Riemslagh K, Vierendeels J, Dick E (2000) An efficient coupling procedure for flexible wall fluid-structure interaction. In: 3th European Congress on computational methods in applied sciences and engineering, Barcelona, Spain, p 13
Råback P, Ruokolainen J, Lyly M, Järvinen E (2001) Fluid-structure interaction boundary conditions by artificial compressibility. In: 3rd European conference on computational fluid dynamics, Swansea, Wales, UK
Rugonyi S, Bathe KJ (2001) On the finite element analysis of fluid flows fully coupled with structural interactions. Comput Model Eng Sci 2(2):195–212
Saad Y (1981) Krylov subspace methods for solving large unsymmetric linear-systems. Math Comput 37(155):105–126
Saad Y (1982) The Lanczos biorthogonalization algorithm and other oblique projection methods for solving large unsymmetric linear systems. SIAM J Numer Anal 19(3):485–506
Saad Y, Schultz M (1986) GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J Sci Stat Comput 7(3):856–869
dos Santos N, Gerbeau JF, Bourgat JF (2008) A partitioned fluid-structure algorithm for elastic thin valves with contact. Comput Methods Appl Mech Eng 197(19):1750–1761
Scotti C, Finol E (2007) Compliant biomechanics of abdominal aortic aneurysms: a fluid-structure interaction study. Comput Struct 85(11–14):1097–1113
Shanno D (1970) Conditioning of quasi-Newton methods for function minimization. Math Comput 24(111):647–656
Sherman A, Morrison W (1950) Adjustment of an inverse matrix corresponding to changes in the elements of a given column or a given row of the original matrix. Ann Math Stat 21(1):124–127
Sidi A (1988) Extrapolation vs projection methods for linear-systems of equations. J Comput Appl Math 22(1):71–88
Sidi A, Ford W, Smith D (1986) Acceleration of convergence of vector sequences. SIAM J Numer Anal 23(1):178–196
Steger J, Benek J (1987) On the use of composite grid schemes in computational aerodynamics. Comput Methods Appl Mech Eng 64(1–3):301–320
Stein K, Benney R, Kalro V, Tezduyar T, Leonard J, Accorsi M (2000) Parachute fluid-structure interactions: 3-D computation. Comput Methods Appl Mech Eng 190(3–4):373–386
Steindorf J (2002) Partitionierte Verfahren für Probleme der Fluid-Struktur Wechselwirkung. PhD Thesis, Technische Universität Braunschweig, Brunswick
Taylor C, Draney M, Ku J, Parker D, Steele B, Wang K, Zarins C (1999) Predictive medicine: computational techniques in therapeutic decision-making. Comput Aided Surg 4(5):231–247
Témam R (1969) Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Arch Ration Mech Anal 33(5):377–385
Tezduyar T, Osawa Y (2001) Fluid-structure interactions of a parachute crossing the far wake of an aircraft. Comput Methods Appl Mech Eng 191(6–7):717–726
Tezduyar T, Sathe S, Keedy R, Stein K (2006) Space-time finite element techniques for computation of fluid-structure interactions. Comput Methods Appl Mech Eng 195(17–18):2002–2027
Tezduyar T, Sathe S, Stein K (2006) Solution techniques for the fully discretized equations in computation of fluid-structure interactions with the space-time formulations. Comput Methods Appl Mech Eng 195(41–43):5743–5753
Tezduyar T, Sathe S, Schwaab M, Conklin B (2008) Arterial fluid mechanics modeling with the stabilized space-time fluid-structure interaction technique. Int J Numer Methods Fluids 57(5):601–629
Toselli A (2005) Domain decomposition methods—algorithms and theory. Computational mathematics, vol 34. Springer, Berlin
Turek S, Hron J (2006) Proposal for numerical benchmarking of fluid-structure interaction between an elastic object and laminar incompressible flow. In: Bungartz HJ, Schäfer M (eds) Fluid-structure interaction—modelling, simulation, optimisation. Lecture notes in computational science and engineering, vol 53. Springer, Berlin, pp 371–385
Van Paepegem W, Blommaert C, De Baere I, Degrieck J, De Backer G, De Rouck J, Degroote J, Vierendeels J, Matthys S, Taerwe L (2011) Slamming wave impact of a composite buoy for wave energy applications: design and large scale testing. Polym Compos 32(5):700–713
Varyani K, Gatiganti R, Gerigk M (2000) Motions and slamming impact on catamaran. Ocean Eng 27(7):729–747
Vierendeels J (2006) Implicit coupling of partitioned fluid-structure interaction solvers using reduced-order models. In: Bungartz HJ, Schäfer M (eds) Fluid-structure interaction—modelling, simulation, optimisation. Lecture notes in computational science and engineering, vol 53. Springer, Berlin, pp 1–18
Vierendeels J, Riemslagh K, Dick E (1999) A multigrid semi-implicit line-method for viscous incompressible and low-Mach-number flows on high aspect ratio grids. J Comput Phys 154(2):310–341
Vierendeels J, Riemslagh K, Dick E, Verdonck P (2000) Computer simulation of intraventricular flow and pressure gradients during diastole. J Biomech Eng 122(6):667–674
Vierendeels J, Dumont K, Dick E, Verdonck P (2005) Analysis and stabilization of fluid-structure interaction algorithm for rigid-body motion. AIAA J 43(12):2549–2557
Vierendeels J, Lanoye L, Degroote J, Verdonck P (2007) Implicit coupling of partitioned fluid-structure interaction problems with reduced order models. Comput Struct 85(11–14):970–976
Vierendeels J, Dumont K, Verdonck P (2008) A partitioned strongly coupled fluid-structure interaction method to model heart valve dynamics. J Comput Appl Math 215(2):602–609
Walhorn E, Kölke A, Hübner B, Dinkler D (2005) Fluid-structure coupling within a monolithic model involving free surface flows. Comput Struct 83(25–26):2100–2111
Wall W, Rabczuk T (2008) Fluid-structure interaction in lower airways of CT-based lung geometries. Int J Numer Methods Fluids 57(5):653–675
Wall W, Gerstenberger A, Gamnitzer P, Förster C, Ramm E (2006) Large deformation fluid-structure interaction—advances in ALE methods and new fixed grid approaches. In: Bungartz HJ, Schäfer M (eds) Fluid-structure interaction—modelling, simulation, optimisation. Lecture notes in computational science and engineering, vol 53. Springer, Berlin, pp 195–228
Wall W, Genkinger S, Ramm E (2007) A strong coupling partitioned approach for fluid-structure interaction with free surfaces. Comput Fluids 36(1):169–183
Wall W, Gamnitzer P, Gerstenberger A (2008) Fluid-structure interaction approaches on fixed grids based on two different domain decomposition ideas. Int J Comput Fluid Dyn 22(6):411–427
Wang X, Liu W (2004) Extended immersed boundary method using FEM and RKPM. Comput Methods Appl Mech Eng 193(12–14):1305–1321
Wilson N, Arko F, Taylor C (2005) Predicting changes in blood flow in patient-specific operative plans for treating aortoiliac occlusive disease. Comput Aided Surg 10(4):257–277
Wüchner R, Kupzok A, Bletzinger KU (2007) A framework for stabilized partitioned analysis of thin membrane-wind interaction. Int J Numer Methods Fluids 54(6–8):945–963
Wynn P (1962) Acceleration technique for iterated vector and matrix problems. Math Comput 16(79):301–322
Yeckel A, Lun L, Derby J (2009) An approximate block Newton method for coupled iterations of nonlinear solvers: theory and conjugate heat transfer applications. J Comput Phys 228(23):8566–8588
Yu Z (2005) A DLM/FD method for fluid/flexible-body interactions. J Comput Phys 207(1):1–27
van der Zee K, van Brummelen E, de Borst R (2010) Goal-oriented error estimation and adaptivity for free-boundary problems: the domain-map linearization approach. SIAM J Sci Comput 32(2):1064–1092
Zhang L, Gerstenberger A, Wang X, Liu W (2004) Immersed finite element method. Comput Methods Appl Mech Eng 193(21–22):2051–2067
van Zuijlen A, Bijl H (2005) Implicit and explicit higher order time integration schemes for structural dynamics and fluid-structure interaction computations. Comput Struct 83(2–3):93–105
van Zuijlen A, Bijl H (2009) Multi-level acceleration for sub-iterations in partitioned fluid-structure interaction. AIP Conf Proc 1168:1347–1350
van Zuijlen A, de Boer A, Bijl H (2007) Higher-order time integration through smooth mesh deformation for 3D fluid-structure interaction simulations. J Comput Phys 224(1):414–430
van Zuijlen A, Bosscher S, Bijl H (2007) Two level algorithms for partitioned fluid-structure interaction computations. Comput Methods Appl Mech Eng 196(8):1458–1470
Acknowledgements
I greatly appreciate the support and guidance by my Ph.D. supervisor, Prof. Jan Vierendeels.
Author information
Authors and Affiliations
Corresponding author
Additional information
Joris Degroote gratefully acknowledges funding by a Ph.D. fellowship and a post-doctoral fellowship of the Research Foundation—Flanders (FWO).
Rights and permissions
About this article
Cite this article
Degroote, J. Partitioned Simulation of Fluid-Structure Interaction. Arch Computat Methods Eng 20, 185–238 (2013). https://doi.org/10.1007/s11831-013-9085-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-013-9085-5