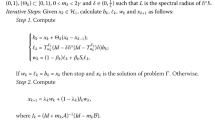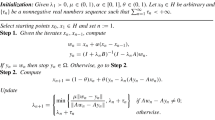An inertial forward–backward splitting method for solving inclusion problems in Hilbert spaces

Abstract

In this work, our interest is in investigating the monotone inclusion problems in the framework of real Hilbert spaces. For solving this problem, we propose an inertial forward–backward splitting algorithm involving an extrapolation factor. We then prove its strong convergence under some mild conditions. Finally, we provide some applications including the numerical experiments for supporting our main theorem.

1 Introduction

In this work, we study the following inclusion problem: find $\hat{x}$ in a Hilbert space H such that

$$\begin{aligned} 0\in A\hat{x}+B\hat{x} \end{aligned}$$

(1.1)

where $A:H\rightarrow H$ is an operator and $B:H\rightarrow 2^{H}$ is a set-valued operator. We denote the solution set of (1.1) by $(A+B)^{-1}(0)$. This problem includes, as special cases, convex programming, variational inequalities, split feasibility problem and minimization problem. To be more precise, some concrete problems in machine learning, image processing and linear inverse problem can be modeled mathematically as this formulation.

For solving the problem (1.1), the forward–backward splitting method [11, 18, 28, 29, 33, 41] is usually employed and is defined by the following manner: $x_{1}\in H$ and

$$\begin{aligned} x_{n+1}=(I+rB)^{-1}(x_{n}-rAx_{n}),\quad n\ge 1, \end{aligned}$$

(1.2)

where $r>0$. In this case, each step of iterates involves only with A as the forward step and B as the backward step, but not the sum of operators. This method includes, as special cases, the proximal point algorithm [14, 38] and the gradient method. In [27], Lions and Mercier introduced the following splitting iterative methods in a real Hilbert space:

$$\begin{aligned} x_{n+1}=(2J^{A}_{r}-I)(2J^{B}_{r}-I)x_{n},\quad n\ge 1 \end{aligned}$$

(1.3)

and

$$\begin{aligned} x_{n+1}=J^{A}_{r}(2J^{B}_{r}-I)x_{n}+(I-J^{B}_{r})x_{n},\quad n\ge 1, \end{aligned}$$

(1.4)

where $J^{T}_{r}=(I+rT)^{-1}$ with $r > 0$. The first one is often called Peaceman–Rachford algorithm [34] and the second one is called Douglas–Rachford algorithm [21]. We note that both algorithms are weakly convergent in general [10, 12, 27].

In particular, if $A:=\nabla f$ and $B:=\partial g$, where $\nabla f$ is the gradient of f and $\partial g$ is the subdifferential of g which is defined by $\partial g (x) := \big \{ s\in H : g(y) \ge g(x) + \langle s, y-x \rangle , \ \ \forall y\in H \big \}$, then problem (1.1) becomes the following minimization problem:

$$\begin{aligned} \underset{x \in H}{\min }f(x)+g(x) \end{aligned}$$

(1.5)

and (1.2) also becomes

$$\begin{aligned} x_{n+1}=\mathrm{prox}_{rg}(x_n-r \nabla f(x_n)),\quad n\ge 1, \end{aligned}$$

(1.6)

where $r > 0$ is the stepsize and $\mathrm{prox}_{rg}=(I+r\partial g)^{-1}$ is the proximity operator of g.

In [2], Alvarez and Attouch employed the heavy ball method which was studied in [35, 36] for maximal monotone operators by the proximal point algorithm. This algorithm is called the inertial proximal point algorithm and it is of the following form:

$$\begin{aligned} \left\{ \begin{array}{llll} y_n = x_n+\theta _n(x_n-x_{n-1})\\ x_{n+1} =(I+r_nB)^{-1}y_n,~~n \ge 1. \end{array} \right. \end{aligned}$$

(1.7)

It was proved that if $\{r_{n}\}$ is non-decreasing and $\{\theta _{n}\}\subset [0,1)$ with

$$\begin{aligned} \sum _{n=1}^{\infty } \theta _n\Vert x_n-x_{n-1}\Vert ^2<\infty , \end{aligned}$$

(1.8)

then algorithm (1.7) converges weakly to a zero of B. In particular, condition (1.8) is true for $\theta _{n}<1/3$. Here, $\theta _{n}$ is an extrapolation factor and the inertia is represented by the term $\theta _n(x_{n}-x_{n-1})$. It is remarkable that the inertial methodology greatly improves the performance of the algorithm and has a nice convergence properties [22, 23, 32].

In [31], Moudafi and Oliny proposed the following inertial proximal point algorithm for solving the zero-finding problem of the sum of two monotone operators:

$$\begin{aligned} \left\{ \begin{array}{llll} y_n = x_n+\theta _n(x_n-x_{n-1})\\ x_{n+1} =(I+r_nB)^{-1}(y_n-r_nAx_n),~~n \ge 1, \end{array} \right. \end{aligned}$$

(1.9)

where $A:H\rightarrow H$ and $B:H\rightarrow 2^{H}$. They obtained the weak convergence theorem provided $r_{n}<2/L$ with L the Lipschitz constant of A and the condition (1.8) holds. It is observed that, for $\theta _n>0$, the algorithm (1.9) does not take the form of a forward–backward splitting algorithm, since operator A is still evaluated at the point $x_n$.

Recently, Lorenz and Pock [29] proposed the following inertial forward–backward algorithm for monotone operators:

$$\begin{aligned} \left\{ \begin{array}{llll} y_n = x_n+\theta _n(x_n-x_{n-1})\\ x_{n+1} =(I+r_nB)^{-1}(y_n-r_nAy_n),~~n \ge 1, \end{array} \right. \end{aligned}$$

(1.10)

where $\{r_{n}\}$ is a positive real sequence. It is observed that algorithm (1.10) differs from that of Moudafi and Oliny insofar that they evaluated the operator B as the inertial extrapolate $y_{n}$. The algorithms involving the inertial term mentioned above have weak convergence, and however, in some applied disciplines, the norm convergence is more desirable that the weak convergence [10]. An abundant literature has been devoted to the asymptotic hierarchical minimization property which results from the introduction of a vanishing viscosity term (in our context the Tikhonov approximation) in gradient-like dynamics. For first-order gradient systems and subdifferential inclusions, see also [1, 2, 4]. In parallel way, there is also a vast literature on convex minimization algorithms that combine different descent methods (gradient, Prox, forward–backward) with Tikhonov and more general penalty and regularization schemes. The historical evolution can be traced back to Fiacco and McCormick [24], and the interpretation of interior point methods with the help of a vanishing logarithmic barrier. Some more specific references for the coupling of Prox and Tikhonov can be found in Cominetti [19]. The resulting algorithms combine proximal-based methods (for example forward–backward algorithms), with the viscosity of penalization methods, see also [6, 7, 13]. For second-order gradient systems involving inertial features, the introduction of a vanishing Tikhonov regularization was first considered by Attouch–Czarnecki [5] for the heavy ball with friction method. More recently, Attouch–Chbani–Riahi [8] examined this question for continuous inertial dynamics with asymptotic vanishing damping coefficient.

In this work, our interest is to establish a modified forward–backward algorithm involving the inertial technique for solving the inclusion problems such that the strong convergence is obtained in the framework of Hilbert spaces. The rest of this paper is organized as follows. In Sect. 2, we recall some basic concepts and lemmas. In Sect. 3, we prove the strong convergence theorem of our proposed method. Finally, in Sect. 4, we provide some applications for our obtained results in various ways. In Sect. 5, we provide a comparison between the standard forward–backward algorithm and the proposed inertial method.

2 Preliminaries and lemmas

Let C be a nonempty, closed and convex subset of a Hilbert space H. The nearest point projection of H onto C is denoted by $P_{C}$, that is, $\Vert x-P_{C}x\Vert \le \Vert x-y\Vert$ for all $x\in H$ and $y\in C$. Such $P_{C}$ is called the metric projection of H onto C. It is known that $\langle x-P_{C}x,y-P_{C}x\rangle \le 0$ holds for all $x\in H$ and $y\in C$; see also [25, 40].

We next state some results in real Hilbert spaces.

Lemma 2.1

[40] Let H be a real Hilbert space. Then, the following equations hold:

• (1)   $\Vert x-y\Vert ^{2}=\Vert x\Vert ^{2}-\Vert y\Vert ^{2}-2\langle x-y,y\rangle$ for all $x,y \in H$;

• (2)   $\Vert x+y\Vert ^{2}\le \Vert x\Vert ^{2}+2\langle y,x+y\rangle$ for all $x,y \in H$;

• (3)   $\Vert tx+(1-t)y\Vert ^{2}=t\Vert x\Vert ^{2}+(1-t)\Vert y\Vert ^{2}-t(1-t)\Vert x-y\Vert ^{2}$ for all $t\in [0,1]$ and $x,y \in H$.

Recall that a mapping $T: H\rightarrow H$ is said to be nonexpansive if, for all $x,y\in H$,

$$\begin{aligned} \Vert Tx-Ty\Vert \le \Vert x-y\Vert . \end{aligned}$$

(2.1)

A mapping $T : H\rightarrow H$ is said to be firmly nonexpansive if, for all $x, y\in H$,

$$\begin{aligned} \Vert Tx-Ty\Vert ^{2}\le \Vert x-y\Vert ^{2}-\Vert (I-T)x-(I-T)y\Vert ^{2}, \end{aligned}$$

(2.2)

or equivalently

$$\begin{aligned} \langle Tx-Ty,x-y\rangle \ge \Vert Tx-Ty\Vert ^{2} \end{aligned}$$

(2.3)

for all $x,y\in H$. We denote F(T) by the fixed point set of T. It is known that T is firmly nonexpansive if and only if $I-T$ is firmly nonexpansive. We know that the metric projection $P_{C}$ is firmly nonexpansive [25].

An operator $A:C\rightarrow H$ is called $\alpha$-inverse strongly monotone if there exists a constant $\alpha >0$ with

$$\begin{aligned} \langle Ax-Ay, x-y\rangle \ge \alpha \Vert Ax-Ay\Vert ^{2},\quad \forall x,y\in C. \end{aligned}$$

(2.4)

We see that if A is $\alpha$-inverse strongly monotone, then it is $\frac{1}{\alpha }$-Lipschitzian continuous.

A set-valued mapping $B:H\rightarrow 2^{H}$ is called monotone if for all $x,y\in H,f\in B(x),$ and $g\in B(y)$ imply $\langle x-y,f-g\rangle \ge 0$. A monotone mapping B is maximal if its graph $G(B):=\big \{(f,x)\in H\times H:f\in B(x)\big \}$ of B is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping B is maximal if and only if for $(x,f)\in H\times H, \langle x-y, f-g\rangle \ge 0$ for all $(y,g)\in G(B)$ imply $f\in B(x)$. Let $J_{r}^{B}=(I+r B)^{-1}$, $r>0$ be the resolvent of B. It is well known that $J_{r}^{B}$ is single-valued, $D(J_{r}^{B})=H$ and $J_{r}^{B}$ is firmly nonexpansive for all $r>0$.

Theorem 2.2

[37] Let H be a real Hilbert space and let $T:C\rightarrow C$ be a nonexpansive mapping with a fixed point. For each fixed $u\in C$ and every $t\in (0,1)$, the unique fixed point $x_t\in C$ of the contraction $C\ni x\mapsto tu+(1-t)Tx$ converges strongly as $t\rightarrow 0$ to a fixed point of T.

In what follows, we shall use the following notation:

$$\begin{aligned} T_r^{A,B}=J_r^B(I-rA)=(I+rB)^{-1}(I-rA),\quad r>0. \end{aligned}$$

(2.5)

Lemma 2.3

[28] Let H be a real Hilbert space. Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator and $B:H\rightarrow 2^H$ a maximal monotone operator. Then, we have

• (i) For $r>0$, $F(T_r^{A,B})=(A+B)^{-1}(0)$;

• (ii) For $0<s\le r$ and $x\in H, \Vert x-T_s^{A,B}x\Vert \le 2\Vert x-T_r^{A,B}x\Vert$.

Lemma 2.4

[28] Let H be a real Hilbert space. Assume that A is an $\alpha$-inverse strongly monotone operator. Then, given $r>0$, we have

$$\begin{aligned} \Vert T^{A,B}_rx-T^{A,B}_ry\Vert ^2\le & {} \Vert x-y\Vert ^2-r(2\alpha -r)\Vert Ax-Ay\Vert ^2\nonumber \\&-\ \Vert (I-J_r^B)(I-rA)x-(I-J_r^B)(I-rA)y\Vert ^{2}, \end{aligned}$$

(2.6)

for all $x,y\in B_{r}=\{z\in H: \Vert z\Vert \le r\}$.

Lemma 2.5

[30] Let $\{a_n\}$ and $\{c_n\}$ be sequences of nonnegative real numbers such that

$$\begin{aligned} a_{n+1}\le (1-\delta _n)a_n+b_n+c_n, \ \ n\ge 1, \end{aligned}$$

(2.7)

where $\{\delta _n\}$ is a sequence in (0, 1) and $\{b_n\}$ is a real sequence. Assume $\sum _{n=1}^\infty c_n<\infty$. Then, the following results hold:

• (i) If $b_n\le \delta _n M$ for some $M\ge 0$, then $\{a_n\}$ is a bounded sequence.

• (ii) If $\sum _{n=1}^\infty \delta _n=\infty$ and $\limsup _{n\rightarrow \infty }\frac{b_n}{\delta _n}\le 0$, then $\lim _{n\rightarrow \infty }a_n=0$.

Lemma 2.6

[26] Assume $\{s_n\}$ is a sequence of nonnegative real numbers such that

$$\begin{aligned} s_{n+1}\le (1-\delta _n)s_n+\delta _n\tau _n, \quad n\ge 1 \end{aligned}$$

(2.8)

and

$$\begin{aligned} s_{n+1}\le s_n-\eta _n+\rho _n, \quad n\ge 1. \end{aligned}$$

(2.9)

where $\{\delta _n\}$ is a sequence in (0, 1), $\{\eta _n\}$ is a sequence of nonnegative real numbers and $\{\tau _n\}$, and $\{\rho _n\}$ are real sequences such that

• (i) $\sum _{n=1}^\infty \delta _n=\infty$,

• (ii) $\lim _{n\rightarrow \infty }\rho _n=0$,

• (iii) $\lim _{k\rightarrow \infty }\eta _{n_k}=0$ implies $\limsup _{k\rightarrow \infty }\tau _{n_k}\le 0$ for any subsequence of real numbers $\{n_k\}$ of $\{n\}$. Then $\lim _{n\rightarrow \infty }s_n=0$.

Proposition 2.7

[20] Let H be a real Hilbert space. Let $m\in \mathbb {N}$ be fixed. Let $\{x_i\}_{i=1}^m\subset X$ and $t_i\ge 0$ for all $i=1,2,...,m$ with $\sum _{i=1}^mt_i\le 1$. Then, we have

$$\begin{aligned} \left\| \sum _{i=1}^mt_ix_i\right\| ^2\le \frac{\sum _{i=1}^mt_i\Vert x_i\Vert ^2}{2-(\sum _{i=1}^mt_i)}. \end{aligned}$$

(2.10)

3 Strong convergence results

In this section, we are in position to prove the strong convergence of a Halpern-type forward–backward method involving the inertial technique in Hilbert spaces.

Theorem 3.1

Let H be a real Hilbert space. Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator and $B:H\rightarrow 2^H$ a maximal monotone operator such that $S=(A+B)^{-1}(0)\ne \emptyset$. Let $\{x_{n}\}$ be a sequence generated by $u,x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{ll} y_{n}=x_{n}+\theta _{n}(x_{n}-x_{n-1}),\\ x_{n+1}=\alpha _{n}u+\beta _{n}y_{n}+\gamma _{n}J^{B}_{r_{n}}(y_{n}-r_{n}Ay_{n}),\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(3.1)

where $J^{B}_{r_{n}}=(I+r_{n}B)^{-1}$, $0<r_{n}\le 2\alpha$, $\{\theta _{n}\}\subset [0,\theta ]$ with $\theta \in [0,1)$ and $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\gamma _{n}\}$ are sequences in [0, 1] with $\alpha _{n}+\beta _{n}+\gamma _{n}=1$. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$;

• (ii) $\lim _{n\rightarrow \infty }\alpha _{n}=0$, $\sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (iii) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _{n\rightarrow \infty }r_{n}<2\alpha$;

• (iv) $\liminf _{n\rightarrow \infty }\gamma _{n}>0$.

Then, the sequence $\{x_{n}\}$ converges strongly to $P_{S}u.$

Proof

For each $n\in \mathbb {N}$, we put $T_{n}=J^{B}_{r_{n}}(I-r_nA)$ and let $\{z_{n}\}$ be defined by

$$\begin{aligned} z_{n+1}=\alpha _{n}u+\beta _{n}z_{n}+\gamma _{n}T_{n}z_{n}. \end{aligned}$$

(3.2)

Using Lemma 2.4, we see that

$$\begin{aligned} \Vert x_{n+1}-z_{n+1}\Vert\le & {} \beta _{n}\Vert y_{n}-z_{n}\Vert +\gamma _{n}\Vert T_{n}y_{n}-T_{n}z_{n}\Vert \nonumber \\\le & {} (1-\alpha _{n})\Vert y_{n}-z_{n}\Vert \nonumber \\= & {} (1-\alpha _{n})\Vert x_{n}+\theta _{n}(x_{n}-x_{n-1})-z_{n}\Vert \nonumber \\\le & {} (1-\alpha _{n})\Vert x_{n}-z_{n}\Vert +\theta _{n}\Vert x_{n}-x_{n-1}\Vert . \end{aligned}$$

(3.3)

By our assumptions and Lemma 2.5 (ii), we conclude that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_{n}-z_{n}\Vert =0. \end{aligned}$$

(3.4)

Let $z=P_{S}u$. Then

$$\begin{aligned} \Vert z_{n+1}-z\Vert\le & {} \alpha _{n}\Vert u-z\Vert +\beta _{n}\Vert z_{n}-z\Vert +\gamma _{n}\Vert T_{n}z_{n}-z\Vert \nonumber \\\le & {} \alpha _{n}\Vert u-z\Vert +(1-\alpha _{n})\Vert z_{n}-z\Vert . \end{aligned}$$

(3.5)

This shows that $\{z_{n}\}$ is bounded by Lemma 2.5 (i) and hence $\{x_{n}\}$ and $\{y_{n}\}$ are also bounded. We observe that

$$\begin{aligned} \Vert y_{n}-z\Vert ^2= & {} \Vert x_{n}-z+\theta _{n}(x_{n}-x_{n-1})\Vert ^2\nonumber \\\le & {} \Vert x_{n}-z\Vert ^2+2\theta _{n}\langle x_{n}-x_{n-1},y_{n}-z\rangle \end{aligned}$$

(3.6)

and

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2= & {} \Vert \alpha _{n}u+\beta _{n}y_{n}+\gamma _{n}T_{n}y_{n}-z\Vert ^2\nonumber \\\le & {} \Vert \beta _{n}(y_{n}-z)+\gamma _{n}(T_{n}y_{n}-z)\Vert ^2+2\alpha _{n}\langle u-z,x_{n+1}-z\rangle .\qquad \quad \end{aligned}$$

(3.7)

On the other hand, by Proposition 2.7 and Lemma 2.4, we obtain

$$\begin{aligned} \Vert \beta _{n}(y_{n}-z)+\gamma _{n}(T_{n}y_{n}-z)\Vert ^2\le & {} \frac{1}{1+\alpha _{n}}\left( \beta _{n}\Vert y_{n}-z\Vert ^2+\gamma _{n}\Vert T_{n}y_{n}-z\Vert ^2 \right) \nonumber \\\le & {} \frac{\beta _{n}}{1+\alpha _{n}}\Vert y_{n}-z\Vert ^2+\frac{\gamma _{n}}{1+\alpha _{n}}\left( \Vert y_{n}-z\Vert ^2\right. \nonumber \\&-\,r_{n}(2\alpha -r_{n})\Vert Ay_{n}-Az\Vert ^2\nonumber \\&-\,\left. \Vert y_{n}-r_{n}Ay_{n}-T_{n}y_{n}+r_{n}Az\Vert \right) \nonumber \\= & {} \frac{1-\alpha _{n}}{1+\alpha _{n}}\Vert y_{n}-z\Vert ^2-\frac{\gamma _{n}r_{n}(2\alpha -r_{n})}{1+\alpha _{n}}\Vert Ay_{n}-Az\Vert ^2\nonumber \\&-\, \frac{\gamma _{n}}{1+\alpha _{n}}\Vert y_{n}-r_{n}Ay_{n}-T_{n}y_{n}+r_{n}Az\Vert . \end{aligned}$$

(3.8)

Replacing (3.6) and (3.8) into (3.7), it follows that

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le & {} \frac{1-\alpha _{n}}{1+\alpha _{n}}\left( \Vert x_{n}-z\Vert ^2+2\theta _{n}\langle x_{n}-x_{n-1},y_{n}-z\rangle \right) \nonumber \\&-\,\frac{\gamma _{n}r_{n}(2\alpha -r_{n})}{1+\alpha _{n}}\Vert Ay_{n}-Az\Vert ^2\nonumber \\&-\, \frac{\gamma _{n}}{1+\alpha _{n}}\Vert y_{n}-r_{n}Ay_{n}-T_{n}y_{n}+r_{n}Az\Vert +2\alpha _{n}\langle u-z,x_{n+1}-z\rangle \nonumber \\= & {} \left( 1-\frac{2\alpha _{n}}{1+\alpha _{n}} \right) \Vert x_{n}-z\Vert ^2+\frac{2\alpha _{n}}{1+\alpha _{n}}\left( (1+\alpha _{n})\langle u-z,x_{n+1}-z\rangle \nonumber \right. \\&+\,\left. \frac{1-\alpha _{n}}{\alpha _{n}}\theta _{n}\langle x_{n}-x_{n-1},y_{n}-z\rangle \right) -\frac{\gamma _{n}r_{n}(2\alpha -r_{n})}{1+\alpha _{n}}\Vert Ay_{n}-Az\Vert ^2\nonumber \\&-\, \frac{\gamma _{n}}{1+\alpha _{n}}\Vert y_{n}-r_{n}Ay_{n}-T_{n}y_{n}+r_{n}Az\Vert . \end{aligned}$$

(3.9)

We can check that $\frac{2\alpha _{n}}{1+\alpha _{n}}$ is in (0, 1). From (3.9), we then have

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le & {} \left( 1-\frac{2\alpha _{n}}{1+\alpha _{n}} \right) \Vert x_{n}-z\Vert ^2+\frac{2\alpha _{n}}{1+\alpha _{n}}\left( (1+\alpha _{n})\langle u-z,x_{n+1}-z\rangle \right. \nonumber \\&+\,\left. \frac{1-\alpha _{n}}{\alpha _{n}}\theta _{n}\langle x_{n}-x_{n-1},y_{n}-z\rangle \right) \end{aligned}$$

(3.10)

and also

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le & {} \Vert x_{n}-z\Vert ^2-\frac{\gamma _{n}r_{n}(2\alpha -r_{n})}{1+\alpha _{n}}\Vert Ay_{n}-Az\Vert ^2\nonumber \\&-\, \frac{\gamma _{n}}{1+\alpha _{n}}\Vert y_{n}-r_{n}Ay_{n}-T_{n}y_{n}+r_{n}Az\Vert \nonumber \\&+\, 2\alpha _{n}\langle u-z,x_{n+1}-z\rangle +\frac{2(1-\alpha _{n})}{1+\alpha _{n}} \theta _{n}\langle x_{n}-x_{n-1},y_{n}-z\rangle .\nonumber \\ \end{aligned}$$

(3.11)

For each $n\ge 1$, we get

$$\begin{aligned} s_n= & {} \Vert x_{n}-z\Vert ^2, \ \delta _n=\frac{2\alpha _{n}}{1+\alpha _{n}} \\ \tau _n= & {} (1+\alpha _n)\langle u-z,x_{n+1}-z\rangle +\frac{1-\alpha _{n}}{\alpha _{n}}\theta _{n}\langle x_{n}-x_{n-1},y_{n}-z\rangle ,\\ \eta _n= & {} \frac{\gamma _{n}r_{n}(2\alpha -r_{n})}{1+\alpha _{n}}\Vert Ay_{n}-Az\Vert ^2+\frac{\gamma _{n}}{1+\alpha _{n}}\Vert y_{n}-r_{n}Ay_{n}-T_{n}y_{n}+r_{n}Az\Vert \\ \rho _n= & {} 2\alpha _{n}\langle u-z,x_{n+1}-z\rangle +\frac{2(1-\alpha _{n})}{1+\alpha _{n}}\theta _{n}\langle x_{n}-x_{n-1},y_{n}-z\rangle . \end{aligned}$$

Then, (3.10) and (3.11) are reduced to the following:

$$\begin{aligned} s_{n+1}\le (1-\delta _n)s_n+\delta _n\tau _n, \quad n\ge 1 \end{aligned}$$

(3.12)

and

$$\begin{aligned} s_{n+1}\le s_n-\eta _n+\rho _n, \quad n\ge 1. \end{aligned}$$

(3.13)

Since $\sum _{n=1}^{\infty }\alpha _{n}=\infty$, it follows that $\sum _{n=1}^{\infty }\delta _n=\infty$. By the boundedness of $\{y_n\}$ and $\{x_n\}$, and $\lim _{n\rightarrow \infty }\alpha _n=0$, we see that $\lim _{n\rightarrow \infty }\rho _n=0$. In order to complete the proof, using Lemma 2.6, it remains to show that $\lim _{k\rightarrow \infty }\eta _{n_{k}}=0$ implies $\limsup _{k\rightarrow \infty }\tau _{n_{k}}\le 0$ for any subsequence $\{\eta _{n_{k}}\}$ of $\{\eta _n\}$. Let $\{\eta _{n_{k}}\}$ be a subsequence of $\{\eta _n\}$ such that $\lim _{k\rightarrow \infty }\eta _{n_{k}}=0$. So, by our assumptions, we can deduce that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert Ay_{n_k}-Az\Vert =\lim _{k\rightarrow \infty } \Vert y_{n_k}-r_{n_k}Ay_{n_k}-T_{n_k}y_{n_k}+r_{n_k}Az\Vert =0. \end{aligned}$$

(3.14)

This gives, by the triangle inequality, that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert T_{n_k}y_{n_k}-y_{n_k}\Vert =0. \end{aligned}$$

(3.15)

Since $\liminf _{n\rightarrow \infty }r_n>0$, there is $r>0$ such that $r_n\ge r$ for all $n\ge 1$. In particular, $r_{n_k}\ge r$ for all $k\ge 1$. Lemma 2.3 (ii) yields that

$$\begin{aligned} \Vert T_{r}^{A,B}y_{n_k}-y_{n_k}\Vert \le 2\Vert T_{n_k}y_{n_k}-y_{n_k}\Vert . \end{aligned}$$

(3.16)

Then, by (3.15), we obtain

$$\begin{aligned} \limsup _{k\rightarrow \infty }\Vert T_{r}^{A,B}y_{n_k}-y_{n_k}\Vert \le 0. \end{aligned}$$

(3.17)

This implies that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert T_{r}^{A,B}y_{n_k}-y_{n_k}\Vert =0. \end{aligned}$$

(3.18)

On the other hand, we have

$$\begin{aligned} \Vert T_{r}^{A,B}y_{n_k}-x_{n_k}\Vert\le & {} \Vert T_{r}^{A,B}y_{n_k}-y_{n_k}\Vert +\Vert y_{n_k}-x_{n_k}\Vert \nonumber \\\le & {} \Vert T_{r}^{A,B}y_{n_k}-y_{n_k}\Vert +\theta _{n_k}\Vert x_{n_k}-x_{n_k-1}\Vert . \end{aligned}$$

(3.19)

By condition (i) and (3.18), we get

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert T_{r}^{A,B}y_{n_k}-x_{n_k}\Vert =0. \end{aligned}$$

(3.20)

Let $z_t=tu+(1-t)T_r^{A,B}z_t$, $t\in (0,1)$. Employing Theorem 2.2, we have $z_t\rightarrow P_Su=z$ as $t\rightarrow 0$. So, we obtain

$$\begin{aligned} \Vert z_t-x_{n_k}\Vert ^2= & {} \Vert t(u-x_{n_k})+(1-t)(T_{r}^{A,B}z_t-x_{n_k})\Vert ^2\nonumber \\\le & {} (1-t)^2\Vert T_{r}^{A,B}z_t-x_{n_k}\Vert ^2+2t\langle u-x_{n_k},z_t-x_{n_k}\rangle \nonumber \\= & {} (1-t)^2\Vert T_{r}^{A,B}z_t-x_{n_k}\Vert ^2+2t\langle u-z_t,z_t-x_{n_k}\rangle +2t\Vert z_t-x_{n_k}\Vert ^2\nonumber \\\le & {} (1-t)^2\left( \Vert T_{r}^{A,B}z_t-T_{r}^{A,B}y_{n_k}\Vert +\Vert T_{r}^{A,B}y_{n_k}-x_{n_k}\Vert \right) ^2 \nonumber \\&+\ 2t\langle u-z_t,z_t-x_{n_k}\rangle +\ 2t\Vert z_t-x_{n_k}\Vert ^2\nonumber \\\le & {} (1-t)^2\left( \Vert z_t-y_{n_k}\Vert +\Vert T_{r}^{A,B}y_{n_k}-x_{n_k}\Vert \right) ^2 \nonumber \\&+\ 2t\langle u-z_t,z_t-x_{n_k}\rangle +2t\Vert z_t-x_{n_k}\Vert ^2\nonumber \\\le & {} (1-t)^2 \left( \Vert z_t-x_{n_k}\Vert +\theta _{n_k}\Vert x_{n_k}-x_{n_k-1}\Vert +\Vert T_{r}^{A,B}y_{n_k}-x_{n_k}\Vert \right) ^2\nonumber \\&+\ 2t\langle u-z_t,z_t-x_{n_k}\rangle +2t\Vert z_t-x_{n_k}\Vert ^2. \end{aligned}$$

(3.21)

This shows that

$$\begin{aligned} \langle z_t-u,z_t-x_{n_k}\rangle\le & {} \frac{(1-t)^2}{2t}\left( \Vert z_t-x_{n_k}\Vert +\theta _{n_k}\Vert x_{n_k}-x_{n_k-1}\Vert \right. \nonumber \\&\left. +\ \Vert T_{r}^{A,B}y_{n_k}-x_{n_k}\Vert \right) ^2+\,\frac{(2t-1)}{2t}\Vert z_t-x_{n_k}\Vert ^2.\qquad \end{aligned}$$

(3.22)

From condition (i), (3.20) and (3.22), we obtain

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle z_t-u,z_t-x_{n_k}\rangle\le & {} \frac{(1-t)^2}{2t}M^2+\frac{(2t-1)}{2t}M^2\nonumber \\= & {} \frac{t}{2}M^2 \end{aligned}$$

(3.23)

for some $M>0$ large enough. Taking $t\rightarrow 0$ in (3.23), we obtain

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle z-u,z-x_{n_k}\rangle \le 0. \end{aligned}$$

(3.24)

On the other hand, we have

$$\begin{aligned} \Vert x_{n_k+1}-x_{n_k}\Vert\le & {} \alpha _{n_k}\Vert u-x_{n_k}\Vert +\beta _{n_k}\Vert y_{n_k}-x_{n_k}\Vert +\gamma _{n_k}\Vert T_{n_k}y_{n_k}-x_{n_k}\Vert \nonumber \\\le & {} \alpha _{n_k}\Vert u-x_{n_k}\Vert +(1-\alpha _{n_k})\Vert y_{n_k}-x_{n_k}\Vert \nonumber \\&+\ \gamma _{n_k}\Vert T_{n_k}y_{n_k}-y_{n_k}\Vert \nonumber \\\le & {} \alpha _{n_k}\Vert u-x_{n_k}\Vert +(1-\alpha _{n_k})\theta _{n_k}\Vert x_{n_k}-x_{n_k-1}\Vert \nonumber \\&+\ \gamma _{n_k}\Vert T_{n_k}y_{n_k}-y_{n_k}\Vert . \end{aligned}$$

(3.25)

By (i), (ii), (3.15) and (3.25), we see that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k+1}-x_{n_k}\Vert =0. \end{aligned}$$

(3.26)

Combining (3.24) and (3.26), we get that

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle z-u,z-x_{n_k+1}\rangle \le 0. \end{aligned}$$

(3.27)

It also follows from (i) that $\limsup _{k\rightarrow \infty }\tau _{n_k}\le 0$. We conclude that $\lim _{n\rightarrow \infty }s_n=0$ by Lemma 2.6. Hence, $x_n\rightarrow z$ as $n\rightarrow \infty$. We thus complete the proof.$\square$

Remark 3.2

We remark here that the condition (i) is easily implemented in numerical computation since the value of $\Vert x_n-x_{n-1}\Vert$ is known before choosing $\theta _{n}$. Indeed, the parameter $\theta _{n}$ can be chosen such that $0\le \theta _n\le \bar{\theta }_{n}$, where

$$\begin{aligned} \bar{\theta }_{n}= \left\{ \begin{array}{ll} \min \left\{ \frac{\omega _n}{\Vert x_n-x_{n-1}\Vert }, \theta \right\} &{}\quad \hbox {if }\; x_n\ne x_{n-1},\\ \theta &{}\quad \hbox {otherwise}, \end{array} \right. \end{aligned}$$

where $\{\omega _n\}$ is a positive sequence such that $\sum _{n=1}^{\infty } \omega _n<\infty$.

4 Applications and numerical experiments

In this section, we discuss various applications in the variational inequality problem, the split feasibility problem, the convex minimization problem and the constrained linear inverse problem.

4.1 Variational inequality problem

The variational inequality problem (VIP) is to find a point $\hat{x}\in C$ such that

$$\begin{aligned} \langle A\hat{x},x-\hat{x}\rangle \ge 0, \quad \forall x\in C \end{aligned}$$

(4.1)

where $A:C\rightarrow H$ is a nonlinear monotone operator. The solution set of (4.1) will be denoted by S. The extragradient method is used to solve the VIP (4.1). It is also known that the VIP is a special case of the problem of finding zeros of the sum of two monotone operators. Indeed, the resolvent of the normal cone is nothing but the projection operator. So we obtain immediately the following results.

Theorem 4.1

Let C be nonempty closed convex subset of a real Hilbert space H. Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator such that $S\ne \emptyset$. Let $\{x_{n}\}$ be a sequence generated by $u,x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{ll} y_{n}=x_{n}+\theta _{n}(x_{n}-x_{n-1}),\\ x_{n+1}=\alpha _{n}u+\beta _{n}y_{n}+\gamma _{n}P_C(y_{n}-r_{n}Ay_{n}),\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(4.2)

where $r_{n}\in (0,2\alpha )$, $\{\theta _{n}\}\subset [0,\theta ]$ with $\theta \in [0,1)$, and $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\gamma _{n}\}$ are sequences in [0, 1] with $\alpha _{n}+\beta _{n}+\gamma _{n}=1$. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$;

• (ii) $\lim _{n\rightarrow \infty }\alpha _{n}=0$, $\sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (iii) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _{n\rightarrow \infty }r_{n}<2\alpha$;

• (iv) $\liminf _{n\rightarrow \infty }\gamma _{n}>0$.

Then, the sequence $\{x_{n}\}$ converges strongly to $P_{S}u.$

4.2 Convex minimization problem

Let $F:H\rightarrow \mathbb {R}$ be a convex smooth function and $G:H\rightarrow \mathbb {R}$ be a convex, lower-semicontinuous and nonsmooth function. We consider the problem of finding $\hat{x}\in H$ such that

$$\begin{aligned} F(\hat{x})+G(\hat{x})\le F(x)+G(x) \end{aligned}$$

(4.3)

for all $x\in H$. This problem (4.3) is equivalent, by Fermat’s rule, to the problem of finding $\hat{x}\in H$ such that

$$\begin{aligned} 0\in \nabla F(\hat{x})+\partial G(\hat{x}) \end{aligned}$$

(4.4)

where $\nabla F$ is a gradient of F and $\partial G$ is a subdifferential of G. We know that if $\nabla F$ is $\frac{1}{L}$-Lipschitz continuous, then it is L-inverse strongly monotone [9, Corollary 10]. Moreover, $\partial G$ is maximal monotone [39, Theorem A]. If we set $A=\nabla F$ and $B=\partial G$ in Theorem 3.1, then we obtain the following result.

Theorem 4.2

Let H be a real Hilbert space. Let $F:H\rightarrow \mathbb {R}$ be a convex and differentiable function with $\frac{1}{L}$-Lipschitz continuous gradient $\nabla F$ and $G:H\rightarrow \mathbb {R}$ be a convex and lower semi-continuous function which $F+G$ attains a minimizer. Let $\{x_{n}\}$ be a sequence generated by $u,x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{ll} y_{n}=x_{n}+\theta _{n}(x_{n}-x_{n-1}),\\ x_{n+1}=\alpha _{n}u+\beta _{n}y_{n}+\gamma _{n}J^{\partial G}_{r_{n}}\left( y_{n}-r_{n}\nabla F(y_{n}) \right) ,\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(4.5)

where $J^{\partial G}_{r_{n}}=(I+r_{n}\partial G)^{-1}$, $0<r_{n}\le 2\alpha$, $\{\theta _{n}\}\subset [0,\theta ]$ with $\theta \in [0,1)$, and $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\gamma _{n}\}$ are sequences in [0, 1] with $\alpha _{n}+\beta _{n}+\gamma _{n}=1$. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$;

• (ii) $\lim _{n\rightarrow \infty }\alpha _{n}=0$, $\sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (iii) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _{n\rightarrow \infty }r_{n}<2\alpha$;

• (iv) $\liminf _{n\rightarrow \infty }\gamma _{n}>0$.

Then, the sequence $\{x_{n}\}$ converges strongly to a minimizer of $F+G$.

4.3 Split feasibility problem

The split feasibility problem (SFP) [17] is to find a point $\hat{x}$ such that

$$\begin{aligned} \hat{x}\in C, \quad T\hat{x}\in Q, \end{aligned}$$

(4.6)

where C and Q are, respectively, closed convex subsets of Hilbert spaces $H_1$ and $H_2$ and $T:H_1\rightarrow H_2$ is a bounded linear operator with its adjoint $T^*$. For solving the SFP (4.6), Byrne [15] proposed the following CQ algorithm:

$$\begin{aligned} x_{n+1}=P_C(x_n-\lambda T^*(I-P_Q)Tx_n), \end{aligned}$$

(4.7)

where $0<\lambda <2\alpha$ with $\alpha =1/\Vert T\Vert ^2$. Here, $\Vert T\Vert ^2$ is the spectral radius of $T^{*}T$. We know that $T^*(I-P_Q)T$ is $1/\Vert T\Vert ^2$-inverse strongly monotone [16]. So we now obtain immediately the following strong convergence theorem for solving the SFP (4.6).

Theorem 4.3

Let C and Q be nonempty closed convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. Let $T:H_1\rightarrow H_2$ be a bounded linear operator. Let $\{x_{n}\}$ be a sequence generated by $u,x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{ll} y_{n}=x_{n}+\theta _{n}(x_{n}-x_{n-1}),\\ x_{n+1}=\alpha _{n}u+\beta _{n}y_{n}+\gamma _{n}P_C\left( y_{n}-r_{n}T^*(I-P_Q)Ty_{n}\right) ,\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(4.8)

where $0<r_{n}\le \frac{2}{\Vert T\Vert ^2}$, $\{\theta _{n}\}\subset [0,\theta ]$ with $\theta \in [0,1)$, and $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\gamma _{n}\}$ are sequences in [0, 1] with $\alpha _{n}+\beta _{n}+\gamma _{n}=1$. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$;

• (ii) $\lim _{n\rightarrow \infty }\alpha _{n}=0$, $\sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (iii) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _{n\rightarrow \infty }r_{n}<\frac{2}{\Vert T\Vert ^2}$;

• (iv) $\liminf _{n\rightarrow \infty }\gamma _{n}>0$.

Then, the sequence $\{x_{n}\}$ converges strongly to a solution of the SFP (4.6).

The constrained linear system: find $x\in C$ such that

$$\begin{aligned} Tx=b, \end{aligned}$$

(4.9)

where $T:H\rightarrow H$ is a bounded linear operator and $b\in H$ is fixed. We see that the SFP includes as special case the linear inverse problem (4.9). So we obtain, in particular, the following result.

Corollary 4.4

Let H be a real Hilbert space. Let $T:H\rightarrow H$ be a bounded linear operator and $b\in H$ with K the largest eigenvalue of $T^tT$. Let $\{x_{n}\}$ be a sequence generated by $u,x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{ll} y_{n}=x_{n}+\theta _{n}(x_{n}-x_{n-1}),\\ x_{n+1}=\alpha _{n}u+\beta _{n}y_{n}+\gamma _{n}P_{C}\left( y_{n}-r_{n}T^t(Ty_n-b) \right) ,\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(4.10)

where $0<r_{n}\le \frac{2}{K}$, $\{\theta _{n}\}\subset [0,\theta ]$ with $\theta \in [0,1)$, and $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\gamma _{n}\}$ are sequences in [0, 1] with $\alpha _{n}+\beta _{n}+\gamma _{n}=1$. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$;

• (ii) $\lim _{n\rightarrow \infty }\alpha _{n}=0$, $\sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (iii) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _{n\rightarrow \infty }r_{n}<\frac{2}{K}$;

• (iv) $\liminf _{n\rightarrow \infty }\gamma _{n}>0$.

If (4.9) is consistent, then the sequence $\{x_{n}\}$ converges strongly to its solution.

Table 1 Comparison of Algorithm 3.1 and Algorithm 3.1 with $\theta _{n}=0$ in Example 5.1

5 Numerical experiments

In this section, we provide the numerical examples to illustrate its performance and to compare our Algorithm 3.1 with Algorithm 3.1 that defined without the inertial term (i.e. $\theta _{n}=0$) for solving the SFP in an infinite dimensional space $L_{2}[0,1]$.

Example 5.1

Let $H_{1}=H_{2}=L_{2}[0,1]$ with the inner product given by

$$\begin{aligned} \langle x,y\rangle =\int _{0}^{1}x(t)y(t)\mathrm{d}t. \end{aligned}$$

Let $C=\{x(t)\in L_{2}[0,1]:\langle x(t),3t^2\rangle =0\}$ and $Q=\{x(t)\in L_{2}[0,1]:\langle x(t),\frac{t}{3}\rangle \ge -1\}$. Find $x(t)\in C$ such that $(Ax)(t)\in Q$, where $(Ax)(t)=\frac{x(t)}{2}$.

Fig. 1

Error plotting of $E_{n}$ for Choice 1

Fig. 2

Error plotting of $E_{n}$ for Choice 2

Fig. 3

Error plotting of $E_{n}$ for Choice 3

Fig. 4

Error plotting of $E_{n}$ for Choice 4

Let $\alpha _n=\frac{1}{100n+1}$, $\beta _n=0.5-\frac{1}{100n}$, $\gamma _n=1-\alpha _{n}-\beta _{n}$, $r_{n}=0.01$ and

$$\begin{aligned} \theta _{n}= \left\{ \begin{array}{ll} \min \left\{ \frac{1}{n^{2}\Vert x_n(t)-x_{n-1}(t)\Vert _{L_2}}, 0.5\right\} &{} \quad \hbox {if }\; x_n\ne x_{n-1},\\ 0.5 &{} \quad \hbox {otherwise}. \end{array} \right. \end{aligned}$$

The stoping criterion is defined by

$$\begin{aligned} E_{n}=\frac{1}{2}\Vert x_{n}(t)-P_{C}x_{n}(t)\Vert _{L_2}^{2}+\frac{1}{2}\Vert (Ax_{n})(t)-P_{Q}(Ax_{n})(t)\Vert _{L_2}^{2}. \end{aligned}$$

We now provide a comparison of the convergence of Algorithm 3.1 and Algorithm 3.1 with $\theta _{n}=0$ in terms of the number of iterations and the cpu time with different choices of u, $x_0$ and $x_1$ as reported in Table 1.

The error plotting of $E_n$ of Algorithm 3.1 and Algorithm 3.1 with $\theta _{n}=0$ for each choice is shown in Figs. 1, 2, 3 and 4, respectively.

Remark 5.2

In numerical experiment, it is revealed that the sequence generated by our proposed Algorithm 3.1 involving the inertial technique converges more quickly than by Algorithm 3.1 without the inertial term does.