Viscosity approximation methods for solving fixed-point problems and split common fixed-point problems

Abstract

In this paper, we introduce the strong convergence theorem for the viscosity approximation methods for solving the split common fixed-point problem in Hilbert spaces. As a consequence, we obtain strong convergence theorems for split variational inequality problems for Lipschitz continuous and monotone operators and split common null point problems for maximal monotone operators. Our results improve and extend the corresponding results announced by many others.

1 Introduction

Let C and Q be nonempty closed convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. The split feasibility problem (SFP) is formulated as finding a point x satisfying the property

$$\begin{aligned} x\in C \text { such that } Ax\in Q, \end{aligned}$$

where $A: H_1\rightarrow H_1$ is a bounded linear operator. Recently, the SFP has been widely studied by many authors (see [1, 14, 16, 17, 19]), due to its application in signal processing [2]. In particular, Byrne [1] introduced the so-called CQ algorithm. For $x_0\in H_1$ and define the iteration $\{x_n\}$ as

$$\begin{aligned} x_{n+1}=P_{C}(I-\gamma A^*(I-P_Q)A)x_n, \end{aligned}$$

(1.1)

where $0<\gamma < \dfrac{2}{\rho (A^*A)}$ and where $P_C$ denotes the projector onto C and $\rho (A^*A)$ is the spectral radius of the operator $A^*A.$ It is known that the CQ algorithm converges weakly to a solution of the SFP if such a solution exists.

In the case, where both C and Q consist of fixed-point sets of some nonlinear operators, the SFP is known as the split common fixed-point problem (SCFP). More specifically, the SCFP is to find

$$\begin{aligned} x\in Fix(U) \text { such that } Ax\in Fix(T), \end{aligned}$$

where Fix(U) and Fix(T) are the fixed-point sets of $U: H_1\rightarrow H_1$ and $T: H_2\rightarrow H_2$, respectively. We denote the solution set of the SCFP by

$$\begin{aligned} \varGamma :=\{x\in H_1: x\in Fix(U) \text { and } Ax\in Fix(T)\}. \end{aligned}$$

When U and T are directed operators, Censor and Segal [5] proposed and proved the convergence of the following algorithm in the setting of the finite-dimensional spaces:

$$\begin{aligned} x_{n+1}=U(I-\gamma A^*(I-T)Ax_n). \end{aligned}$$

(1.2)

Note that a class of directed operators includes the metric projection. Therefore, the results of Censor and Segal recover Byrne’s CQ algorithm. Moudafi [11] introduced the following algorithm:

$$\begin{aligned} {\left\{ \begin{array}{ll}u_n=x_n-\gamma A^*(I-T)Ax_n,\\ x_{n+1}=(1-\alpha _n)u_n+\alpha _nUu_n \end{array}\right. } \end{aligned}$$

(1.3)

to solve the SCFP for demicontractive operators and he obtained the weak convergence. It is known that demicontractive operators include the directed operators. Hence, Moudafi’s algorithm is an extension of the algorithm (1.2).

Recently, Moudafi [12] and Zhao and He [20] proposed the viscosity approximation methods for solving the SCFP for quasi-nonexpansive operators. Motivated by their work, in this paper, we introduce a generalized algorithm to solve the SCFP and their results are as our consequences.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty closed convex subset of H. The weak convergence of $\{x_n\}_{n=1}^{\infty }$ to x is denoted by $x_{n}\rightharpoonup x$ as $n\rightarrow \infty$, while the strong convergence of $\{x_n\}_{n=1}^{\infty }$ to x is written as $x_n\rightarrow x$ as $n\rightarrow \infty .$

For every point $x\in H$, there exists a unique nearest point in C, denoted by $P_Cx$, such that $\Vert x-P_Cx\Vert \le \Vert x-y\Vert \ \forall y\in C$. $P_C$ is called the metric projection of H onto C. It is known that $P_C$ is nonexpansive.

Lemma 2.1

[6] Let C be a nonempty closed convex subset of a real Hilbert space H. Given $x\in H$ and $z\in C$. Then, $z=P_Cx\Longleftrightarrow \langle x-z,z-y\rangle \ge 0 \ \ \forall y\in C.$

Definition 2.2

[6] Assume that $T:H\rightarrow H$ is a nonlinear operator. Then, $I-T$ is said to be demiclosed at zero if for any $\{x_n\}$ in H, the following implication holds:

$$\begin{aligned} x_n\rightharpoonup x \text { and } (I-T)x_n\rightarrow 0 \Longrightarrow x\in Fix(T). \end{aligned}$$

Definition 2.3

Let $T:H\rightarrow H$ be an operator with $Fix(T)\ne \emptyset .$ Then

• $T:H\rightarrow H$ is called firmly nonexpansive if

  $$\begin{aligned} \Vert Tx-Ty\Vert ^2\le \langle Tx-Ty,x-y\rangle , \end{aligned}$$

  or equivalently

  $$\begin{aligned} \Vert Tx-Ty\Vert ^2\le \Vert x-y\Vert ^2-\Vert (I-T)x-(I-T)y\Vert ^2; \end{aligned}$$

• $T:H\rightarrow H$ is called directed if

  $$\begin{aligned} \langle z-Tx,x-Tx\rangle \le 0 \ \ \ \forall z\in Fix(T), x\in H, \end{aligned}$$

  or equivalently

  $$\begin{aligned} \Vert Tx-z\Vert ^2\le \Vert x-z\Vert ^2-\Vert x-Tx\Vert ^2 \ \ \ \forall z\in Fix(T), x\in H; \end{aligned}$$

• $T:H\rightarrow H$ is called $\alpha$-strongly quasi-nonexpansive with $\alpha >0$ if

  $$\begin{aligned} \Vert Tx-z\Vert ^2\le \Vert x-z\Vert ^2-\alpha \Vert x-Tx\Vert ^2 \ \ \ \forall z\in Fix(T), x\in H, \end{aligned}$$

  or equivalently

  $$\begin{aligned} \langle Tx-x,x-z\rangle \le \dfrac{-1-\alpha }{2}\Vert x-Tx\Vert ^2 \ \ \ \forall z\in Fix(T), x\in H; \end{aligned}$$

• $T:H\rightarrow H$ is called quasi-nonexpansive if

  $$\begin{aligned} \Vert Tx-z\Vert \le \Vert x-z\Vert \ \ \ \forall z\in Fix(T), x\in H; \end{aligned}$$

• $T:H\rightarrow H$ is called $\beta$-demicontractive with $0\le \beta <1$ if

  $$\begin{aligned} \Vert Tx-z\Vert ^2\le \Vert x-z\Vert ^2+\beta \Vert (I-T)x\Vert ^2\ \ \ \forall z\in Fix(T), x\in H, \end{aligned}$$

  or equivalently

  $$\begin{aligned} \langle x-z,Tx-x\rangle \le \dfrac{\beta -1}{2}\Vert x-Tx\Vert ^2 \ \ \ \forall z\in Fix(T), x\in H. \end{aligned}$$

  (2.1)

To prove its convergence, we will need the two following lemmas.

Lemma 2.4

[9] Let $\{a_n\}$ be a sequence of non-negative real numbers, such that there exists a subsequence $\{a_{n_j}\}$ of $\{a_n\}$, such that $a_{n_{j}}<a_{n_{j}+1}$ for all $j\in \mathbb {N}$. Then, there exists a nondecreasing sequence $\{m_k\}$ of $\mathbb {N}$, such that $\lim _{k\rightarrow \infty }m_k=\infty$, and the following properties are satisfied by all (sufficiently large) number $k\in \mathbb {N}$:

$$\begin{aligned} a_{m_k}\le a_{m_{k}+1}\quad \text {and}\quad a_k\le a_{m_k+1}. \end{aligned}$$

In fact, $m_k$ is the largest number n in the set $\{1,2,\ldots ,k\}$, such that $a_n<a_{n+1}$.

Lemma 2.5

[13, 15] Let $\{a_n\}$ be sequences of non-negative real numbers, such that

$$\begin{aligned} a_{n+1}\le (1-\alpha _n)a_n+\alpha _n b_n, \end{aligned}$$

where $\{\alpha _n\}\subset (0,1)$ and $\{b_n\}$ are a sequence, such that

• (a) $\sum _{n=0}^\infty a_n=\infty$;

• (b) $\limsup _{n\rightarrow \infty }b_n=0.$

Then, $\lim _{n\rightarrow \infty }a_n=0.$

Lemma 2.6

[18] If $U:H\rightarrow H$ is $\beta _1$-strongly quasi-nonexpansive and $T:H\rightarrow H$ is $\beta _2$-strongly quasi-nonexpansive with $Fix(U)\cap Fix(T)\ne \emptyset$, then UT is $\dfrac{\beta _1\beta _2}{\beta _1+\beta _2}$-strongly quasi-nonexpansive and $Fix(UT)=Fix(U)\cap Fix (T).$

Lemma 2.7

Let $U:H\rightarrow H$ be a $\beta$-demicontractive operator and $T:H\rightarrow H$ be a $\alpha _1$-strongly quasi-nonexpansive operator with $\beta <\alpha _1$. Then, the operator UT is $\dfrac{\alpha _1\beta }{\alpha _1-\beta }$ demicontractive and $Fix(U)\cap Fix(T)=Fix(UT).$

Proof

It is suffices to show that $Fix(UT)\subset Fix(U)\cap Fix(T).$ Let $p\in Fix(UT)$, it is enough to show that $p\in Fix(T)$. We take $z\in Fix(U)\cap Fix(T)$, we have

$$\begin{aligned} \Vert p-z\Vert ^2&=\Vert UTp-z\Vert ^2\\&\le \Vert Tp-z\Vert ^2+\beta \Vert UTp-Tp\Vert ^2\\&\le \Vert p-z\Vert ^2-\alpha _1\Vert Tp-p\Vert ^2+\beta \Vert UTp-Tp\Vert ^2\\&=\Vert p-z\Vert ^2-\alpha _1\Vert Tp-p\Vert ^2+\beta \Vert Tp-p\Vert ^2\\&=\Vert p-z\Vert ^2-(\alpha _1-\beta )\Vert Tp-p\Vert ^2. \end{aligned}$$

This implies that $Tp=p$, that is, $p\in Fix(T).$ Therefore, $Fix(U)\cap Fix(T)=Fix(UT).$

Take $z\in Fix(U)\cap Fix(T) ,x\in H$, let $a:=\Vert x-z\Vert$, $b:=\Vert Tx-z\Vert$, $c:=\Vert UTx-z\Vert$, we have $\Vert a-c\Vert =\Vert UTx-x\Vert , \Vert a-b\Vert =\Vert Tx-x\Vert ,\Vert b-c\Vert =\Vert UTx-Tx\Vert .$ Since the definition of U and T, we obtain $\Vert b\Vert ^2\le \Vert a\Vert ^2-\alpha _1\Vert a-b\Vert ^2$ and $\Vert c\Vert ^2\le \Vert b\Vert ^2+\beta \Vert b-c\Vert ^2.$ This implies

$$\begin{aligned} -2\alpha _1\langle a,b\rangle\le & {} (1-\alpha _1)\Vert a\Vert ^2-(1+\alpha _1)\Vert b\Vert ^2,\\ 2\beta \langle b,c\rangle\le & {} (1-\beta )\Vert b\Vert ^2-(1-\beta )\Vert c\Vert ^2. \end{aligned}$$

On the other hand

$$\begin{aligned} 0&\le \Vert \alpha _1a-(\alpha _1-\beta )b-\beta c\Vert ^2\\&=\alpha ^2_1\Vert a\Vert ^2+(\alpha _1-\beta )^2\Vert b\Vert ^2+\beta ^2\Vert c\Vert ^2-2\alpha _1 (\alpha _1-\beta )\langle a,b\rangle \\&\quad +2\beta (\alpha _1-\beta )\langle b,c\rangle -2\alpha _1\beta \langle a,c\rangle \\&=\alpha ^2_1\Vert a\Vert ^2+(\alpha _1-\beta )^2\Vert b\Vert ^2+\beta ^2\Vert c\Vert ^2\\&\quad +(\alpha _1-\beta )\left[ (1-\alpha _1)\Vert a\Vert ^2-(1+\alpha _1)\Vert b\Vert ^2\right] \\&\quad +(\alpha _1-\beta )\left[ (1-\beta )\Vert b\Vert ^2-(1-\beta )\Vert c\Vert ^2\right] -2\alpha _1\beta \langle a,c\rangle \\&=(\alpha _1+\alpha _1\beta -\beta )\Vert a\Vert ^2+(-\alpha _1+\alpha _1\beta +\beta ) \Vert c\Vert ^2-2\alpha _1\beta \langle a,c\rangle \\&=(\alpha _1-\beta )(1+\dfrac{\alpha _1\beta }{\alpha _1-\beta }) \Vert a\Vert ^2-(\alpha _1-\beta )(1-\dfrac{\alpha _1\beta }{\alpha _1-\beta }) \Vert c\Vert ^2-2\alpha _1\beta \langle a,c\rangle \\&=(\alpha _1-\beta )\left( \Vert a\Vert ^2-\Vert c\Vert ^2+\dfrac{\alpha _1\beta }{\alpha _1-\beta }\Vert a-c\Vert ^2\right) . \end{aligned}$$

Thus

$$\begin{aligned} \Vert c\Vert ^2\le \Vert a\Vert ^2+\dfrac{\alpha _1\beta }{\alpha _1-\beta }\Vert a-c\Vert ^2, \end{aligned}$$

that is, the operator UT is $\dfrac{\alpha _1\beta }{\alpha _1-\beta }$-demicontractive. $\square$

Lemma 2.8

Let $U:H \rightarrow H$ is $\beta$ demicontractive with $F(U)\ne \emptyset$ and set $U_\lambda =(1-\lambda )I+\lambda U$, $\lambda \in (0,1-\beta )$ then

• (a) $Fix(U)=Fix(U_\lambda );$

• (b) $\Vert U_\lambda x-z\Vert ^2\le \Vert x-z\Vert ^2-\dfrac{1}{\lambda }(1-\beta -\lambda )\Vert (I-U_\lambda )x\Vert ^2 \ \ \forall x\in H, z\in Fix(U);$

• (c) F(U) is a closed convex subset of $H_1.$

Proof

• (a) It is obvious.

• (b) We have

  $$\begin{aligned} \Vert U_\lambda x-z\Vert ^2&=\Vert (1-\lambda )x+\lambda Ux-z\Vert ^2\\&=\Vert (x-z)+\lambda (Ux-x)\Vert ^2\\&=\Vert x-z\Vert ^2+2\lambda \langle x-z, Ux-x\rangle +\lambda ^2 \Vert Ux-x\Vert ^2\\&\le \Vert x-z\Vert ^2+ \lambda (\beta -1)\Vert Ux-x\Vert ^2+\lambda ^2 \Vert Ux-x\Vert ^2\\&=\Vert x-z\Vert ^2-\lambda (1-\beta -\lambda )\Vert (I-U)x\Vert ^2\\&=\Vert x-z\Vert ^2-\dfrac{1}{\lambda }(1-\beta -\lambda )\Vert (I-U_\lambda )x\Vert ^2. \end{aligned}$$

• (c) It is a consequence of Proposition 1 in [18]. $\square$

Lemma 2.9

Let $T:H_2\rightarrow H_2$ be a $\mu$-demicontractive operator, $A: H_1\rightarrow H_2$ be a linear bounded operator with $L=\Vert A^*A\Vert$. For a positive real number $\gamma ,$ define the operator $V: H_1\rightarrow H_1$ by

$$\begin{aligned} V: =I+\gamma A^*(T-I)A. \end{aligned}$$

Then:

• (a) for all $x\in H_1$ and $z\in A^{-1}(Fix(T))$,

  $$\begin{aligned} \Vert Vx-z\Vert ^2\le \Vert x-z\Vert ^2-\dfrac{1}{\gamma L}(1-\mu -\gamma L)\Vert (I-V)x\Vert ^2. \end{aligned}$$

• (b) for all $x\in H_1$ and $z\in A^{-1}(Fix(T))$,

  $$\begin{aligned} \Vert Vx-z\Vert ^2\le \Vert x-z\Vert ^2-\gamma (1-\mu -\gamma L)\Vert (I-T)Ax\Vert ^2. \end{aligned}$$

• (c) $x\in Fix(V)$ if $Ax\in Fix(T)$ provided that $\gamma \in (0,\dfrac{1-\mu }{L})$.

Proof

• (a) Given $x\in H_1$ and $z\in A^{-1}(Fix(T))$, we have

  $$\begin{aligned} \langle A^*(I-T)Ax,x-z\rangle&=\langle (I-T)Ax,Ax-Az\rangle \\&\ge \dfrac{1-\mu }{2}\Vert (I-T)Ax\Vert ^2. \end{aligned}$$

  On the other hand

  $$\begin{aligned} \Vert A^*(I-T)Ax\Vert ^2&=\langle A^*(I-T)Ax,A^*(I-T)Ax\rangle \\&=\langle (I-T)Ax,AA^*(I-T)Ax\rangle \\&\le L \Vert (I-T)Ax\Vert ^2. \end{aligned}$$

  Thus

  $$\begin{aligned} \langle A^*(I-T)Ax,x-z\rangle \ge \dfrac{1-\mu }{2L}\Vert A^*(I-T)Ax\Vert ^2. \end{aligned}$$

  We have

  $$\begin{aligned} \Vert Vx-z\Vert ^2&=\Vert x-\gamma A^*(I-T)Ax-z\Vert ^2\\&=\Vert x-z\Vert ^2-2\gamma \langle x-z,A^*(I-T)Ax\rangle +\gamma ^2\Vert A^*(I-T)Ax\Vert ^2\\&\le \Vert x-z\Vert ^2-2\gamma \dfrac{1-\mu }{2L}\Vert A^*(I-T)Ax\Vert ^2+\gamma ^2\Vert A^*(I-T)Ax\Vert ^2\\&=\Vert x-z\Vert ^2-\dfrac{\gamma }{L}(1-\mu -\gamma L)\Vert A^*(I-T)Ax\Vert ^2\\&=\Vert x-z\Vert ^2-\dfrac{1}{\gamma L}(1-\mu -\gamma L)\Vert \gamma A^*(I-T)Ax\Vert ^2\\&= \Vert x-z\Vert ^2-\dfrac{1}{\gamma L}(1-\mu -\gamma L)\Vert (I-V)x\Vert ^2. \end{aligned}$$

• (b) Given $x\in H_1$ and $z\in A^{-1}(Fix(T))$, we have

  $$\begin{aligned} \Vert Vx-z\Vert ^2&=\Vert x+\gamma A^*(T-I)Ax-z\Vert ^2\\&=\Vert x-z\Vert ^2+2\gamma \langle x-z,A^*(T-I)Ax\rangle +\gamma ^2\Vert A^*(T-I)Ax\Vert ^2\\&=\Vert x-z\Vert ^2+2\gamma \langle Ax-Az,(T-I)Ax\rangle \\&+\gamma ^2\langle A^*(T-I)Ax,A^*(T-I)Ax\rangle \\&\le \Vert x-z\Vert ^2+\gamma (-1+\mu )\Vert (T-I)Ax\Vert ^2\\&+\gamma ^2\langle AA^*(T-I)Ax,(T-I)Ax\rangle \\&\le \Vert x-z\Vert ^2+\gamma (-1+\mu )\Vert (T-I)Ax\Vert ^2+\gamma ^2\Vert AA^*\Vert \Vert (T-I)Ax\Vert ^2\\&=\Vert x-z\Vert ^2-\gamma (1-\mu -\gamma L)\Vert (T-I)Ax\Vert ^2. \end{aligned}$$

• (c) It is obvious that $Ax\in Fix(T)$ then $x\in Fix(V)$. We show the converse, let $x\in Fix(V)$ and $z\in A^{-1}(Fix(T))$, we have

  $$\begin{aligned} \Vert x-z\Vert ^2=\Vert Vx-z\Vert ^2\le \Vert x-z\Vert ^2-\gamma (1-\mu -\gamma L)\Vert (T-I)Ax\Vert ^2. \end{aligned}$$

  Since $\gamma \in (0,\dfrac{1-\mu }{L})$, we obtain $(T-I)Ax=0$, that is, $Ax\in Fix(T).$

3 Main results

Theorem 3.1

Let $U:H\rightarrow H$ be a $\alpha$-strongly quasi-nonexpansive operator such that $I-U$ is demiclosed at zero. Suppose that $f:H\rightarrow H$ is a contraction with constant $\rho \in (0,1)$. Let $\{x_n\}$ be a sequence in H defined by

$$\begin{aligned} x_0\in H, \ \ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U x_n, \end{aligned}$$

(3.1)

where the sequence $\{\alpha _n\}$ satisfies the following conditions:

$$\begin{aligned} \alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0 \quad \text {and}\quad \sum _{n=0}^\infty \alpha _n=\infty . \end{aligned}$$

Then $\{x_n\}$ strongly converges to an element $q\in Fix(U)$, where $q=P_{Fix(U)}\circ f(q).$

Proof

First, we note that Fix(U) is a closed convex subset by Lemma 2.8. Thus, the mapping $P_{Fix(U)}\circ f: H\rightarrow H$ is a contraction. By Banach’ s contraction principle that there exists a unique element $q\in H$, such that $q=P_{Fix(U)}\circ f(q).$ In particular, $q\in Fix(U)$ and

$$\begin{aligned} \langle (I-f)(q),q-z\rangle \le 0 \ \ \forall z\in Fix(U). \end{aligned}$$

(3.2)

Now, we show that $\{x_n\}$ is bounded. Indeed, we have

$$\begin{aligned} \Vert x_{n+1}-q\Vert&=\Vert \alpha _n f(x_{n})+(1-\alpha _n)Ux_n-q\Vert \\&=\Vert \alpha _n (f(x_{n})-x_{n})+(1-\alpha _n)(Ux_n-q)\Vert \\&\le \alpha _n\Vert f(x_n)-q\Vert +(1-\alpha _n)\Vert U x_n-q\Vert \\&\le \alpha _n\Vert f(x_n)-f(q)\Vert +\alpha _n\Vert f(q)-q\Vert +(1-\alpha _n)\Vert U x_n-q\Vert \\&\le \alpha _n \rho \Vert x_n-q\Vert +\alpha _n\Vert f(q)-q\Vert +(1-\alpha _n)\Vert x_n-q\Vert \\&=[1-\alpha _n(1-\rho )] \Vert x_n-q\Vert +\alpha _n\Vert f(q)-q\Vert \\&=[1-\alpha _n(1-\rho )] \Vert x_n-q\Vert +\alpha _n\dfrac{\Vert f(q)-q\Vert }{1-\rho }\\&\le \max \left\{ \Vert x_n-q\Vert ,\dfrac{\Vert f(q)-q\Vert }{1-\rho }\right\} \\&\le \cdots \le \max \left\{ \Vert x_0-q\Vert ,\dfrac{\Vert f(q)-q\Vert }{1-\rho }\right\} . \end{aligned}$$

This implies that the sequence $\{x_n\}$ is bounded and $\{f(x_n)\}, \{Ux_n\}$ are bounded.

On the other hand, we get

$$\begin{aligned} x_{n+1}-x_n=\alpha _n(f(x_n)-x_n)+(1-\alpha _n)(U x_n-x_n). \end{aligned}$$

This implies that

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert ^2= & {} \alpha ^2_n\Vert f(x_n)-x_n\Vert ^2+(1-\alpha _n)^2\Vert U x_n-x_n\Vert ^2\nonumber \\&+\,2\alpha _n(1-\alpha _n)\langle f(x_n)-x_n, Ux_n-x_n\rangle \nonumber \\\le & {} \alpha ^2_n\Vert f(x_n)-x_n\Vert ^2+(1-\alpha _n)\Vert U x_n-x_n\Vert ^2\nonumber \\&+\,2\alpha _n(1-\alpha _n)\langle f(x_n)-x_n, Ux_n-x_n\rangle \end{aligned}$$

(3.3)

and

$$\begin{aligned} \Vert x_{n+1}-q\Vert ^2-\Vert x_n-q\Vert ^2-\Vert x_{n+1}-x_n\Vert ^2= & {} 2\langle x_{n+1}-x_n,x_n-q\rangle \nonumber \\= & {} 2\alpha _n \langle f(x_n)-x_n,x_n-q\rangle \nonumber \\&+2(1-\alpha _n)\langle U x_n-x_n,x_n-q\rangle \nonumber \\\le & {} 2\alpha _n \langle f(x_n)-x_n,x_n-q\rangle \nonumber \\&-(1-\alpha _n)(1+\alpha )\Vert x_n-Ux_n\Vert ^2.\nonumber \\ \end{aligned}$$

(3.4)

From (3.3) and (3.4), we obtain

$$\begin{aligned} \Vert x_{n+1}-q\Vert ^2-\Vert x_n-q\Vert ^2&\le \alpha ^2_n\Vert f(x_n)-x_n\Vert ^2+2\alpha _n \langle f(x_n)-x_n,x_n-q\rangle \\&\quad +2\alpha _n(1-\alpha _n)\langle f(x_n)-x_n, Ux_n-x_n\rangle \\&\quad -\alpha (1-\alpha _n)\Vert x_n-Ux_n\Vert ^2. \end{aligned}$$

Therefore

$$\begin{aligned} \alpha (1-\alpha _n)\Vert x_n-Ux_n\Vert ^2&\le \alpha ^2_n\Vert f(x_n)-x_n\Vert ^2+2\alpha _n \langle f(x_n)-x_n,x_n-q\rangle \nonumber \\&\quad +\Vert x_n-q\Vert ^2-\Vert x_{n+1}-q\Vert ^2. \end{aligned}$$

(3.5)

Let us consider the following two cases.

Case 1 There exists $N\in {\mathbb N}$, such that $\Vert x_{n+1}-q\Vert ^2\le \Vert x_n-q\Vert ^2$ for all $n\ge N.$ This implies that $\lim _{n\rightarrow \infty }\Vert x_n-q\Vert ^2$ exists. Since (3.5), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n-Ux_n\Vert =0. \end{aligned}$$

(3.6)

Now, we show that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_n-q,f(q)-q\rangle \le 0. \end{aligned}$$

(3.7)

Indeed, we take a subsequence $\{x_{n_j}\}$ of $\{x_n\}$, such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_n-p,f(p)-p\rangle =\lim _{j\rightarrow \infty }\langle x_{n_j}-q,f(q)-q\rangle . \end{aligned}$$

We may assume that $x_{n_j}\rightharpoonup x^*$. By (3.6), we have $x^*\in Fix(U)$. Thus

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_n-q,f(q)-q\rangle =\lim _{j\rightarrow \infty }\langle x_{n_j}-q,f(q)-q\rangle =\langle x^*-q,f(q)-q\rangle \le 0. \end{aligned}$$

Next, we will show that $x_n\rightarrow q$. we get

$$\begin{aligned} \Vert x_{n+1}-q\Vert ^2&=\Vert \alpha _n(f(x_n)-q)+(1-\alpha _n)(U x_n-q)\Vert ^2\\&=(1-\alpha _n)^2\Vert U x_n-q)\Vert ^2+\alpha ^2_n\Vert f(x_n)-q\Vert ^2\\&\quad +2\alpha _n(1-\alpha _n)\langle U x_n-q,f(x_n)-q\rangle \\&\le (1-\alpha _n)^2\Vert x_n-q\Vert ^2+\alpha ^2_n\Vert f(x_n)-q\Vert ^2\\&\quad +2\alpha _n(1-\alpha _n)\langle U x_n-q,f(x_n)-f(q)\rangle \\&\quad + 2\alpha _n(1-\alpha _n)\langle U x_n-q,f(q)-q\rangle \\&\le (1-\alpha _n)^2\Vert x_n-q\Vert ^2+\alpha ^2_n\Vert f(x_n)-q\Vert ^2\\&\quad +2\alpha _n(1-\alpha _n)\rho \Vert x_n-q\Vert ^2+2\alpha _n(1-\alpha _n)\langle U x_n-p,f(q)-q\rangle \\&=[1-\alpha _n(2-\alpha _n-2\rho (1-\alpha _n))]\Vert x_n-q\Vert ^2+\alpha ^2_n\Vert f(x_n)-q\Vert ^2\\&\quad + 2\alpha _n(1-\alpha _n)\langle U x_n-q,f(q)-q\rangle \\&=(1-\gamma _n)\Vert x_n-q\Vert ^2+\gamma _n \delta _n, \end{aligned}$$

where

$$\begin{aligned} \gamma _n= & {} \alpha _n(2-\alpha _n-2\rho (1-\alpha _n)),\\ \delta _n= & {} \dfrac{\alpha _n\Vert f(x_n)-q\Vert ^2+ 2(1-\alpha _n)\langle U x_n-q,f(q)-q\rangle }{2-\alpha _n-2\rho (1-\alpha _n)}. \end{aligned}$$

We have $\gamma _n\rightarrow 0, \sum _{n=1}^\infty \gamma _n=\infty$, and by (3.7), we get $\limsup _{n\rightarrow \infty }\delta _n\le 0.$ By Lemma 2.5, we conclude that $x_n\rightarrow q.$

Case 2 There exists a subsequence $\{\Vert x_{n_j}-q\Vert ^2\}$ of $\{\Vert x_{n}-q\Vert ^2\}$, such that $\Vert x_{n_j}-q\Vert ^2 < \Vert x_{n_j+1}-q\Vert ^2$ for all $j\in \mathbb {N}$. In this case, it follows from Lemma 2.4 that there exists a nondecreasing sequence $\{m_k\}$ of $\mathbb {N}$, such that $\lim _{k\rightarrow \infty }m_k=\infty$, and the following inequalities hold for all $k\in \mathbb {N}$:

$$\begin{aligned} \Vert x_{m_k}-q\Vert ^2\le \Vert x_{m_k+1}-q\Vert ^2 \quad \text {and}\quad \Vert x_{k}-q\Vert ^2\le \Vert x_{m_k}-q\Vert ^2. \end{aligned}$$

(3.8)

Similarly, we get

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_{m_k}-Ux_{m_k}\Vert =0, \end{aligned}$$

(3.9)

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle x_{m_k}-q,f(q)-q\rangle \le 0, \end{aligned}$$

(3.10)

and

$$\begin{aligned} \Vert x_{m_k+1}-q\Vert ^2\le (1-\gamma _{m_k})\Vert x_{m_k}-q\Vert ^2+\gamma _{m_k} \delta _{m_k}, \end{aligned}$$

(3.11)

where

$$\begin{aligned} \gamma _{m_k}= & {} \alpha _{m_k}(2-\alpha _{m_k}-2\rho (1-\alpha _{m_k})),\\ \delta _{m_k}= & {} \dfrac{\alpha _{m_k}\Vert f(x_{m_k})-q\Vert ^2+ 2(1-\alpha _{m_k})\langle Ux_{m_k}-q,f(q)-q\rangle }{2-\alpha _{m_k}-2\rho (1-\alpha _{m_k})}. \end{aligned}$$

By Lemma 2.5, we obtain $x_{m_k}\rightarrow q.$ By (3.8), we get $\Vert x_k-q\Vert \le \Vert x_{m_k}-q\Vert \ \forall k\in \mathbb {N}$. Therefore, $x_k\rightarrow q.$ $\square$

Corollary 3.2

Let $U:H\rightarrow H$ be a $\beta$ demicontractive, such that $I-U$ is demiclosed at zero. Suppose that $f:H\rightarrow H$ is a contraction with constant $\rho \in (0,1)$. Let $\{x_n\}$ be a sequence in H defined by

$$\begin{aligned} x_0\in H, \ \ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U_\lambda x_n, \end{aligned}$$

(3.12)

where the parameter $\lambda$ and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\lambda \in (0,1-\beta )$;

• (b) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $\{x_n\}$ strongly converges to an element $q\in Fix(U)$, where $q=P_{Fix(U)}\circ f(q).$

Proof

By Lemma 2.8, we have $U_\lambda$ is $\alpha$-strongly quasi- nonexpansive with $\alpha =\dfrac{1}{\lambda }(1-\beta -\lambda )$. Since $\lambda \in (0,1-\beta )$, we get $\alpha >0$. On the other hand, $Fix(U)=Fix(U_\lambda )$ and $\lambda (I-U)=I-U_\lambda$, and thus, $I-U_\lambda$ is demiclosed at zero. The remaining of the proof is followed from Theorem 3.1. $\square$

Corollary 3.3

Let $U:H\rightarrow H$ be a quasi-nonexpansive operator, such that $I-U$ is demiclosed at zero. Suppose that $f:H\rightarrow H$ is a contraction with constant $\rho \in (0,1)$. Let $\{x_n\}$ be a sequence in H defined by

$$\begin{aligned} x_0\in H, \ \ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U_\lambda x_n, \end{aligned}$$

(3.13)

where the parameter $\lambda \in (0,1)$ and the sequence $\{\alpha _n\}$ satisfy the following conditions: $\alpha _n\in (0,1),$ $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty =\infty .$ Then, $\{x_n\}$ strongly converges to an element $q\in Fix(U)$, where $q=P_{Fix(U)}\circ f(q).$

Corollary 3.3 extends Maingé’s result in [10] from $\lambda \in (0,\dfrac{1}{2})$ to $\lambda \in (0,1)$.

Theorem 3.4

Let $U:H_1\rightarrow H_1$ be a $\alpha _2$-strongly quasi-nonexpansive operator and $T:H_2\rightarrow H_2$ be a $\mu$-demicontractive operator that both $I-U$ and $I-T$ are demiclosed at zero. Let $A: H_1\rightarrow H_2$ be a bounded linear operator with $L=\Vert A^*A\Vert$, and $f:H_1\rightarrow H_1$ be a contraction with constant $\rho \in (0,1)$. Suppose $\varGamma \ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U(I+\gamma A^*(T-I)A)x_n, \end{array}\right. } \end{aligned}$$

(3.14)

where the parameters $\gamma$ and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\gamma \in (0,\dfrac{1-\mu }{L})$;

• (b) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $x_n\rightarrow q$, where $q=P_\varGamma \circ f(q).$

Proof

We will show as follows:

• (a) The operator UV is $\alpha$-strongly quasi-nonexpansive, where $V:=I+\gamma A^*(T-I)A$;

• (b) The operator $I-UV$ is demiclosed at zero.

By Lemma 2.9, then $V:=I+\gamma A^*(T-I)A$ is $\alpha _1$-strongly quasi-nonexpansive with $\alpha _1=\dfrac{1}{\gamma L}(1-\mu -\gamma L)$. By Lemma 2.6, then UV is $\alpha$-strongly quasi-nonexpansive and $Fix(U)\cap Fix(V)=Fix(UV)$, where $\alpha =\dfrac{\alpha _1\alpha _2}{\alpha _1+\alpha _2}$.

First, we show that $\varGamma =Fix(U)\cap Fix(V)=Fix(UV).$ Indeed, it follows from Lemma 2.9 that

$$\begin{aligned} \varGamma&=\{x\in H_1: x\in Fix(U) \text { and } Ax\in Fix(T) \}\\&=\{x\in H_1: x\in Fix(U) \text { and } x\in Fix(V) \}\\&=Fix(U)\cap Fix(V)\\&=Fix(UV). \end{aligned}$$

Let $\{x_n\}$ be a sequence such that $x_n-U Vx_n\rightarrow 0$ and $x_n\rightharpoonup x$. We have $\Vert x_n-q\Vert \le \Vert x_n-U Vx_n\Vert +\Vert U Vx_n-q\Vert$, that is $\Vert x_n-q\Vert -\Vert UVx_n-q\Vert \le \Vert x_n-UVx_n\Vert \rightarrow 0$. This implies that

$$\begin{aligned} \Vert x_n-q\Vert ^2-\Vert U Vx_n-q\Vert ^2\rightarrow 0. \end{aligned}$$

We have

$$\begin{aligned} \Vert UVx_n-q\Vert ^2&\le \Vert Vx_n-q\Vert ^2-\alpha _2\Vert U Vx_n-Vx_n\Vert ^2\\&\le \Vert x_n-q\Vert ^2-\alpha _1\Vert Vx_n-x_n\Vert ^2-\alpha _2\Vert U Vx_n-Vx_n\Vert ^2. \end{aligned}$$

It follows

$$\begin{aligned} Vx_n-x_n\rightarrow 0\quad \text {and}\quad U Vx_n-Vx_n\rightarrow 0 . \end{aligned}$$

This implies that $Vx_n\rightharpoonup x$, and by the demiclosedness of $I-U$, we get $x\in Fix(U)$.

On the other hand, by Lemma 2.9, we get

$$\begin{aligned} \Vert UVx_n-q\Vert ^2&\le \Vert Vx_n-q\Vert ^2-\alpha _2\Vert U_\lambda Vx_n-Vx_n\Vert ^2\\&\le \Vert x_n-q\Vert ^2-\gamma (1-\mu -\gamma L)\Vert (T-I)Ax_n\Vert ^2\\&\quad -\alpha _2\Vert U_\lambda Vx_n-Vx_n\Vert ^2. \end{aligned}$$

It follows

$$\begin{aligned}&\gamma (1-\mu -\gamma L)\Vert (T-I)Ax_n\Vert ^2\le \Vert x_n-q\Vert ^2- \Vert U Vx_n-q\Vert ^2\\&\quad -\alpha _2\Vert U Vx_n-Vx_n\Vert ^2\rightarrow 0. \end{aligned}$$

Since $Ax_n\rightharpoonup Ax$ and the demiclosedness of $I-T$, we get $Ax\in Fix(T)$, that is $x\in Fix(V)$. Therefore, $x\in Fix(U)\cap Fix(V)=Fix(UV).$ That is, $I-UV$ is demiclosed at zero. $\square$

Corollary 3.5

Let $U:H_1\rightarrow H_1$ be a $\beta$-demicontractive operator and $T:H_2\rightarrow H_2$ be a $\mu$-demicontractive operator that both $I-U$ and $I-T$ are demiclosed at zero. Let $A: H_1\rightarrow H_2$ be a bounded linear operator with $L=\Vert A^*A\Vert$ and $f:H_1\rightarrow H_1$ be a contraction with constant $\rho \in (0,1)$. Suppose $\varGamma \ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U_\lambda (I+\gamma A^*(T-I)A)x_n, \end{array}\right. } \end{aligned}$$

(3.15)

where the parameters $\lambda$, $\gamma$, and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\lambda \in (0,1-\beta )$;

• (b) $\gamma \in (0,\dfrac{1-\mu }{L})$;

• (c) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $x_n\rightarrow q$, where $q=P_\varGamma \circ f(q).$

Proof

By Lemma 2.9, then $V:=I+\gamma A^*(T-I)A$ is $\alpha _1$-strongly quasi-nonexpansive with $\alpha _1=\dfrac{1}{\gamma L}(1-\mu -\gamma L)$, and by Lemma 2.8, then $U_\lambda$ is $\alpha _2$-strongly quasi-nonexpansive with $\alpha _2=\dfrac{1}{\lambda }(1-\beta -\lambda ).$ The remaining of the proof is followed from Theorem 3.4. $\square$

Corollary 3.6

Let $U:H_1\rightarrow H_1$ be a quasi-nonexpansive operator and $T:H_2\rightarrow H_2$ be a quasi-nonexpansive operator that both $I-U$ and $I-T$ are demiclosed at zero. Let $A: H_1\rightarrow H_2$ be a bounded linear operator with $L=\Vert A^*A\Vert$ and $f:H_1\rightarrow H_1$ be a contraction with constant $\rho \in (0,1)$. Suppose $\varGamma \ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U_\lambda (I+\gamma A^*(T-I)A)x_n, \end{array}\right. } \end{aligned}$$

(3.16)

where the parameters $\lambda$, $\gamma$, and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\lambda \in (0,1)$;

• (b) $\gamma \in (0,\dfrac{1}{L})$;

• (c) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $x_n\rightarrow q$, where $q=P_\varGamma \circ f(q).$

Theorem 3.7

Let $S:H_1\rightarrow H_1$ be a $\beta$-demicontractive operator and $T:H_2\rightarrow H_2$ be a $\mu$-demicontractive operator. Let $A: H_1\rightarrow H_2$ be a bounded linear operator with $L=\Vert A^*A\Vert$ and $f:H_1\rightarrow H_1$ be a contraction with constant $\rho \in (0,1)$. Suppose $\varGamma \ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U_\lambda x_n, \end{array}\right. } \end{aligned}$$

(3.17)

where $U:=S(I+\gamma A^*(T-I)A)$. Assume that $I-U$ is demiclosed at zero and the parameters $\beta , \lambda$, $\gamma$, and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\gamma \in (0,\dfrac{1-\mu }{L})$;

• (b) $\beta <\alpha _1$, where $\alpha _1:=\dfrac{1}{\gamma L}(1-\mu -\gamma L)$;

• (c) $\lambda \in (0,1-\dfrac{\alpha _1\beta }{\alpha _1+\beta })$;

• (d) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $x_n\rightarrow q$, where $q=P_\varGamma \circ f(q).$

Proof

Let $V:=I+\gamma A^*(T-I)A$, by Lemma 2.9, then the operator V is $\alpha _1$-strongly quasi-nonexpansive. Therefore, by Lemma 2.7, then the operator SV is $\dfrac{\alpha _1\beta }{\alpha _1-\beta }$ demicontractive and $Fix(S)\cap Fix(V)=Fix(SV)$. We show that $\varGamma =Fix(S)\cap Fix(V)=Fix(SV).$ Indeed, it follows from Lemma 2.9 that

$$\begin{aligned} \varGamma&=\{x\in H_1: x\in Fix(S) \text { and } Ax\in Fix(T) \}\\&=\{x\in H_1: x\in Fix(S) \text { and } x\in Fix(V) \}\\&=Fix(S)\cap Fix(V). \end{aligned}$$

The remaining of the proof is followed by Corollary 3.2. $\square$

Corollary 3.8

Let $S:H_1\rightarrow H_1$ be a quasi-nonexpansive operator $T:H_2\rightarrow H_2$ be a $\mu$-demicontractive operator that both $I-S$ and $I-T$ are demiclosed at zero. Let $A: H_1\rightarrow H_2$ be a bounded linear operator with $L=\Vert A^*A\Vert$ and $f:H_1\rightarrow H_1$ be a contraction with constant $\rho \in (0,1)$. Suppose $\varGamma \ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)U_\lambda x_n, \end{array}\right. } \end{aligned}$$

(3.18)

where $U:=S(I+\gamma A^*(T-I)A)$ and the parameters $\lambda$, $\gamma$ and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\lambda \in (0,1)$;

• (b) $\gamma \in (0,\dfrac{1-\mu }{L})$;

• (c) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $x_n\rightarrow q$, where $q=P_\varGamma \circ f(q).$

Proof

We will show that $I-SV$ is demiclosed at zero.

To prove (b), let $\{x_n\}$ be a sequence, such that $x_n-SVx_n\rightarrow 0$ and $x_n\rightharpoonup x$. We have $\Vert x_n-q\Vert \le \Vert x_n-SVx_n\Vert +\Vert SVx_n-q\Vert$, that is, $\Vert x_n-q\Vert -\Vert SVx_n-q\Vert \le \Vert x_n-SVx_n\Vert \rightarrow 0$. This implies that

$$\begin{aligned} \Vert x_n-q\Vert ^2-\Vert SVx_n-q\Vert ^2\rightarrow 0. \end{aligned}$$

On the other hand

$$\begin{aligned} \Vert SVx_n-q\Vert ^2&\le \Vert Vx_n-q\Vert ^2\\&\le \Vert x_n-q\Vert ^2-\alpha _1 \Vert Vx_n-x_n\Vert ^2. \end{aligned}$$

It follows

$$\begin{aligned} Vx_n-x_n\rightarrow 0. \end{aligned}$$

This implies that $Vx_n\rightharpoonup x$. Since $\Vert SVx_n-Vx_n\Vert \le \Vert SVx_n-x_n\Vert +\Vert x_n-Vx_n\Vert \rightarrow 0$ and by the demiclosedness of $I-S$ we get $x\in Fix(S)$. On the other hand, by Lemma 2.9, we have

$$\begin{aligned} \Vert SVx_n-q\Vert ^2&\le \Vert Vx_n-q\Vert ^2\\&\le \Vert x_n-q\Vert ^2-\gamma (1-\mu -\gamma L)\Vert (T-I)Ax_n\Vert ^2. \end{aligned}$$

It follows $\gamma (1-\mu -\gamma L)\Vert (T-I)Ax_n\Vert ^2\le \Vert x_n-q\Vert ^2-\Vert SVx_n-q\Vert ^2\rightarrow 0$. Since $Ax_n\rightharpoonup Ax$ and$(I-T)Ax_n\rightarrow 0$, by the demiclosedness of $I-T$, we get $Ax\in Fix(T)$, that is $x\in Fix(V)$. Therefore, $x\in Fix(S)\cap Fix(V)=Fix(SV).$

$\square$

Corollary 3.8 extends Zhao’s and He’s result in [20] from $\lambda \in (0,\dfrac{1}{2})$ to $\lambda \in (0,1)$ and Corollary 3.8 answers the question’s Moudafi in [12].

4 The split variational inequality problem

Given operators $f: H_1\rightarrow H_1$, $g: H_2\rightarrow H_2$, and a bounded linear operator $A: H_1\rightarrow H_2$ and nonempty closed convex subsets $C\subset H_1$ and $Q\subset H_2$, the split variational inequality problem (SVIP) is the problem of finding a point $x^*\in VIP(C,f)$, such that $Ax^*\in VIP(Q,g)$, that is

$$\begin{aligned} {\left\{ \begin{array}{ll} x^*\in C \text { such that } \langle f(x^*),x-x^*\rangle \ge 0 &{}\quad \text { for all } x\in C,\\ Ax^*\in Q \text { such that } \langle g(Ax^*),y-Ax^*\rangle \ge 0 &{}\quad \text { for all } y\in Q. \end{array}\right. } \end{aligned}$$

This is equivalent to the problem of finding $x^*\in Fix(P_C(I-\eta f))$, such that $Ax^*\in Fix(P_Q(I-\eta g))$, where $\eta >0$. We denote the set of solutions by SVIP(A, C, Q, f, g). Therefore, SVIP can be viewed as SCFP. Under appropriate conditions of the operators f and g, we can apply our results for SVIP.

Lemma 4.1

[4, 8] Let $f: H_1\rightarrow H_1$ be a monotone and k-Lipschitz continuous on C. Let $S: =P_C(I-\eta f)$, where $\eta >0$. If ${x_n}$ is a sequence in C satisfying $x_{n}\rightharpoonup x^*$ and $x_n-Sx_n\rightarrow 0$, then $x^*\in VIP(C,f).$

Lemma 4.2

[9] Let $f: H_1\rightarrow H_1$ be a monotone and k-Lipschitz operator on C and $\eta >0$. Let $W:=P_C(I-\eta f)$ and $S:=P_C(I-\eta fW)$. Then, for all $z\in VIP(C,f)$, we have

$$\begin{aligned} \Vert Sx-z\Vert ^2\le \Vert x-z\Vert ^2-(1- k^2\eta ^2)\Vert x-Wx\Vert ^2. \end{aligned}$$

In particular, if $k\eta <1$, S is a quasi-nonexpansive operator and $Fix(S)=Fix(W)=VIP(C,f).$

Corollary 4.3

Let C and Q be nonempty closed convex subsets of Hilbert spaces $H_1$ and $H_2$, respectively. Let $f:H_1\rightarrow H_1$ and $g:H_2\rightarrow H_2$ be monotone and k-Lipschitz continuous operators on C and Q, respectively, and $A: H_1\rightarrow H_2$ a bounded linear operator with $\Vert A^*A\Vert =L.$ Suppose $SVIP(A,C,Q,f,g)\ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _n x_0+(1-\alpha _n)U_\lambda x_n, \end{array}\right. } \end{aligned}$$

(4.1)

where $U=ST, S:=P_C(I-\eta f P_C(I-\eta f)), T:=P_Q(I-\eta g P_Q(I-\eta g))$, and the parameters $\lambda$, $\gamma , \eta$, and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\eta \in (0,\dfrac{1}{k})$;

• (b) $\lambda \in (0,1)$;

• (c) $\gamma \in (0,\dfrac{1}{L})$;

• (d) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$, and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $\{x_n\}$ converges strongly to $x^*\in SVIP(A,C,Q,f,g).$

Proof

Since Lemma 4.2, we obtain that both operators S and T are two quasi-nonexpansive operators. Next, we show that $I-S$ is demiclosed at zero. Let $\{x_n\}$ be a sequence in $H_1$, such that $x_n-Sx_n\rightarrow 0$ and $x_n\rightharpoonup x$ as $n\rightarrow \infty .$ For some $q\in VIP(C,f)$ we have $\Vert x_n-q\Vert ^2-\Vert Sx_n-q\Vert ^2\rightarrow 0$ as $n\rightarrow \infty$. By Lemma 4.2, we get

$$\begin{aligned} (1-\eta ^2 k^2)\Vert x_n-P_C(I-\eta f)x_n\Vert ^2\le \Vert x_n-q\Vert ^2-\Vert Sx_n-q\Vert ^2. \end{aligned}$$

This implies $x_n-P_C(I-\eta f)x_n\rightarrow 0$. By Lemma 4.1, we obtain $x\in VIP(C,f)=Fix(S)$. Similarly, $I-T$ is also demiclosed at zero. The result implies from Corollary 3.8. $\square$

5 The split common null point problem

Given two set-valued operators $B_1: H_1\rightarrow 2^{H_1}$ and $B_2: H_2\rightarrow 2^{H_2}$ and a bounded linear operator $A:H_1\rightarrow H_2$, the split common null point problem (SCNP) is the problem of finding

$$\begin{aligned} x\in H_1 \text { such that } 0\in B_1(x) \text{ and } 0\in B_2(Ax). \end{aligned}$$

(5.1)

Recently, Byrne et al.[3] and Kazmi et al. [7] proposed a strong convergence theorem for finding such a solution x when $B_1$ and $B_2$ are maximal monotone. Recall that $B: H\rightarrow 2^H$ is said to be monotone if

$$\begin{aligned} \langle x-y,u-v\rangle \ge 0 \ \ \forall x,y\in D(B), u\in Bu, v\in By, \end{aligned}$$

where $B(D):=\{x\in H, Bx\ne \emptyset \}.$

A monotone operator is said to be maximal if its graph is not properly contained in the graph of any other monotone operator.

For a maximal monotone operator $B: H\rightarrow 2^H$ and $\lambda >0$, we can define a single-valued operator:

$$\begin{aligned} J^B_\lambda :=(I+\lambda B)^{-1}:H\rightarrow H. \end{aligned}$$

It is known that $J^B_\lambda$ is firmly nonexpansive and $0\in B(x)$ iff $x\in Fix(J^B_\lambda ).$

Therefore, the problem (5.1) is equivalently to the problem of finding

$$\begin{aligned} x\in H_1 \text { such that } x\in Fix(J^{B_1}_\lambda ) \text{ and } Ax\in Fix(J^{B_2}_\lambda ), \end{aligned}$$

where $\lambda >0$, that is, the SCNP reduces to the SCFP.

Theorem 5.1

Let $B_1:H_1\rightarrow 2^{H_1}$ and $B:H_2\rightarrow B_2^{H_2}$ be two set-valued maximal monotone operators. Let $A: H_1\rightarrow H_2$ be a bounded linear operator with $L=\Vert A^*A\Vert$ and $f:H_1\rightarrow H_1$ be a contraction with constant $\rho \in (0,1)$. Suppose $\varGamma \ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)J^{B_1}_\lambda (I+\gamma A^*(J^{B_2}_\lambda -I)A)x_n, \end{array}\right. } \end{aligned}$$

(5.2)

where the parameters $\gamma$ and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\gamma \in (0,\dfrac{1}{L})$;

• (b) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $x_n\rightarrow q$, where $q=P_\varGamma \circ f(q).$

Proof

We have $J^{B_1}_\lambda$ and $J^{B_2}_\lambda$ are two firmly nonexpansive operators and hence nonexpansive. Therefore, $I-J^{B_1}_\lambda$ and $I-J^{B_2}_\lambda$ are demiclosed at zero. $J^{B_1}_\lambda$ is 1-strongly quasi-nonexpansive and $J^{B_2}_\lambda$ is 0 demicontractive. Therefore, the remaining of the proof is followed from Theorem 3.4. $\square$

Table 1 With $\alpha _n=\dfrac{1}{n+1}$

Fig. 1

Figure for Case 1

The result of Byrne et al. [3] is a consequence of our Theorem 5.1.

Corollary 5.2

Let $B_1:H_1\rightarrow 2^{H_1}$ and $B:H_2\rightarrow B_2^{H_2}$ be two set-valued maximal monotone operators. Let $A: H_1\rightarrow H_2$ be a bounded linear operator with $L=\Vert A^*A\Vert$. Suppose $\varGamma \ne \emptyset$. Let $\{x_n\}\subset H_1$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H_1,\\ x_{n+1}=\alpha _n x_0+(1-\alpha _n)J^{B_1}_\lambda (I+\gamma A^*(J^{B_2}_\lambda -I)A)x_n, \end{array}\right. } \end{aligned}$$

(5.3)

where the parameters $\gamma$ and the sequence $\{\alpha _n\}$ satisfy the following conditions:

• (a) $\gamma \in (0,\dfrac{1}{L})$;

• (b) $\alpha _n\in (0,1), \lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=0}^\infty \alpha _n=\infty .$

Then, $x_n\rightarrow x_0$, where $x_0=P_\varGamma x_0.$

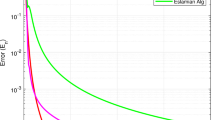
6 Numerical example

In this section, let us show numerical example to demonstrate the convergence of our algorithm.

Let $H_1= \mathbb {R}^2$ and $H_2=\mathbb {R}^2$. Let $U:\mathbb {R}^2\rightarrow \mathbb {R}^2$ be defined $Ux=(\dfrac{1}{2}t,\dfrac{1}{2}z)^t$ and $T: \mathbb {R}^2\rightarrow \mathbb {R}^2$ be defined by $Tx=(0,z)^t$, where $x=(t,z)^t$. It is easy to see that U is 1-strongly quasi-nonexpansive mapping and T is 0-demicontractive mapping.

Table 2 With $\alpha _n=\dfrac{1}{(n+1)^{0.1}}$

Fig. 2

Figure for Case 2

Choose $\gamma =0.3$ and $x_0=(1,2)^t$. The stopping criterion for our testing method is taken as: $\Vert x_{n+1}-x^*\Vert <10^{-10}$, where $x_n=(t_n,z_n)^t$ and $x^*$ are a solution problem. Let assume that $f(x)=\dfrac{1}{3}x$ and $A=\left[ \begin{matrix} 1 &{}0 \\ 0 &{} 2\\ \end{matrix} \right]$. We set $L=\Vert A^*A\Vert _2$ and $\gamma \in (0,\dfrac{1}{L})$, where $\Vert .\Vert _2$ is the matrix 2-norm.

• Case 1: Take $\alpha _n=\dfrac{1}{n+1}$. Then, using (3.14), we have Table 1 and Fig. 1.

• Case 2: Take $\alpha _n=\dfrac{1}{(n+1)^{0.1}}$. Then, using (3.14), we have Table 2 and Fig. 2.