Weighted aggregation for guided image filtering

Abstract

As a local filter, the guided image filtering (GIF) suffers from halo artifacts. To address this issue, a novel weighted aggregating strategy is proposed in this paper. By introducing the weighted aggregation to GIF, the proposed method called WAGIF can achieve results with sharp edges and avoid/reduce halo artifacts. More specifically, compared to the weighted guided image filtering and the gradient domain guided image filtering, the proposed method can achieve both fine and coarse smoothing results in the flat areas while preserving edges. In addition, the complexity of the proposed approach is O(N) for an image with N pixels. It is demonstrated that the GIF with weighted aggregation performs well in the fields of computational photography and image processing, including single image detail enhancement, tone mapping of high-dynamic-range images, single image haze removal, etc.

1 Introduction

Edge-preserving image filtering is the most fundamental operation in the fields of image processing, computer vision and computer graphics. Most popular edge-preserving image filtering techniques can be classified into two categories: regularization algorithms with global optimization (i.e., $L_0$ norm gradient minimization [26], total variation (TV) [13, 16], propagated guided image filtering (PGIF) [18] and weighted least squares (WLS) [5, 17]) and local algorithms (i.e., bilateral filtering (BF) [4, 22, 25], domain transform filtering (DTF) [19], wavelet-based Filtering [1, 20, 27] and guided image filtering (GIF) [9, 12, 15, 21]). Regularization algorithms optimize a cost function which consists of a data fidelity term and a regularization term globally. The data fidelity term measures fidelity of the filtered image and the input image. On the other hand, the regularization term essentially enforces a soft constraint on the global structure and smoothness of the filtered image. Generally speaking, the regularization techniques are often outstanding and computationally expensive. On the contrary, the local algorithms efficiently predict the intensity of each interest pixel in a small spatial range (patch) around the underlying pixel. It is indicated in [9] that halo artifacts are inevitably produced in local filters because of edge blurring. The mechanism of halo artifacts was discussed in [4, 14, 15, 26].

The GIF, which is one of the fastest local edge-preserving filters, is widely used in image enhancement [6, 10], tone mapping of high-dynamic-range (HDR) images [5, 7], haze removal [8], etc. As a local filter, GIF suffers from halo artifacts. To optimize the edge-preserving performance, several improved GIF algorithms have been proposed in recent years. The weighted guided image filter (WGIF) [15] incorporates an edge-aware weighting into the regularization parameter of GIF. As such, the regularization parameter in WGIF is adaptive to a specified edge-aware weighting instead of a fixed one in GIF. The gradient domain guided image filter (GDGIF) [12] incorporates an explicit first-order edge-aware constraint into the GIF. The key ideas of the WGIF and the GDGIF are similar, i.e., the regularization parameter (smoothing factor) is small in an edge patch and big in a flat patch. The edge-aware strategy makes edges to be preserved better in WGIF and GDGIF than the ones obtained by GIF and thus reduces halo artifacts. However, it is noted that while the edge-aware weighting is introduced, textures may be treated as edges and cannot be smoothed. Besides the edge-aware methods, the multi-scale idea described in [24] is also selectable for solving the halo problem.

In this paper, the halo problem is analyzed from a new perspective, i.e., we argue that the halo artifacts are caused by inaccurate estimation of pixel intensities. The average aggregation employed in GIF, WGIF, GDGIF, etc. is indiscriminate for all patches. For a pixel located on the edges, the estimations of this pixel in some patches are close to the means, which are far from the true value, and yield blurring edges. To solve this problem, we propose to estimate a specific pixel from patches with different weights. Then, a novel weighted aggregation strategy, in which weights are measured by the mean square errors (MSE), is proposed to yield final output. It is shown in experiments that the proposed aggregation not only preserves edges effectively, but also achieves good smoothing results in strong texture regions.

2 The proposed method

Before the weighted aggregation strategy is proposed, the GIF, WGIF and GDGIF techniques are briefly reviewed.

2.1 Guided image filtering

The principle of the GIF is that the input image I is filtered with a given guidance image G. It is assumed that the filtering output $\hat{I}$ is a linear transform of the guidance image G in a small patch $w_k$, and the filtered output $(\hat{I}_k(p))$ at pixel p is expressed as:

$$\begin{aligned} \hat{I}_k(p) = a_kG(p)+b_k,\quad \forall p \in w_k, \end{aligned}$$

(1)

where $a_k$ and $b_k$ are linear coefficients assumed to be constant in the patch $w_k$ centered at pixel k. A solution to determine the linear coefficients $a_k$ and $b_k$ is proposed by minimizing the following cost function:

$$\begin{aligned} E(a_k, b_k) = \sum _{p\in w_k}\left[ (a_kG(p) + b_k - I(p))^2 + \epsilon a_k^2\right] , \end{aligned}$$

(2)

where $\epsilon$ is a fixed regularization parameter penalizing large $a_k$. More specifically, the effect of $\epsilon$ in the GIF is similar to the range variance $\delta _r^2$ in the BF [25]. A big value of $\epsilon$ leads to the resultant images which are visually smooth and edges are blurred, and vise versa.

Accordingly, the WGIF [15] and the GDGIF [12] have been proposed by employing an adaptive regularization parameter instead of a fixed one. First, an edge-aware weighting is introduced in WGIF [15], which is defined as follows:

$$\begin{aligned} \varGamma _p=\frac{1}{M}\sum _{i \in G}{\frac{\tilde{\delta }_{G,p} + \beta }{\tilde{\delta }_{G,i} + \beta }}, \end{aligned}$$

(3)

where $\beta$ is a small positive constant, M is the number of pixels in the guided image G and $\tilde{\delta }_{G,i}$ and $\tilde{\delta }_{G,p}$ are the variances of G in $3 \times 3$ patches centered at the pixels i and p, respectively. Then, the $\epsilon$ is modified as $\epsilon _p=(0.001\times L)^2/\varGamma _p$, where L is the dynamic range of the guided image G. Instead of the fixed regularization parameter in GIF, the values of $\epsilon _p$ in WGIF are different at different pixels. The value of $\varGamma _p$ is always large ($\varGamma _p > 1$), while the pixel p locates in an edge region and is small ($\varGamma _p < 1$) when p is in a flat region. As such, a small $\epsilon _p$ is adopted in edge regions, while a big $\epsilon _p$ is used in flat regions. A similar idea is introduced in GDGIF [12]. The edge-aware weighting in GDGIF is also formulated similarly as Eq. (3), but $\tilde{\delta }_{G,p}$ and $\tilde{\delta }_{G,i}$ terms are multiplied separately by the variance of the guided image in $w_p$ (Eq. (9) in [12]). The GDGIF claims that the edges are detected more accurately than WGIF with the new edge-aware weighting.

Equation (2) is a linear ridge regression model and coefficients ($a_k$, $b_k$) can be solved by minimizing the cost function and expressed as:

$$\begin{aligned} a_k= & {} \frac{\hbox {cov}_k(G, I)}{\delta _{G, k}^2 + \epsilon },\nonumber \\ b_k= & {} \bar{I}_k - a_k\bar{G}_k, \end{aligned}$$

(4)

where $\hbox {cov}_k(G, I)$ is the covariance of the guided image G in $w_k$, $\delta _{G, k}^2$ is the variance of the guided image in $w_k$, and $\bar{G}_k$ and $\bar{I}_k$ are the means of G and I in $w_k$, respectively. With the values of $a_k$ and $b_k$, the filtered output of the pixel p is computed by Eq. (1). It is highlighted that the pixel p is involved in all patches $w_k$ that cover p. The value of $\hat{I}_k(p)$ is not identical when the pixel p is computed in different patches. A commonly used aggregating strategy in several algorithms (i.e., GIF [9], WGIF [15], GDGIF [12], etc.) is to average all the possible prediction values of the pixel p:

$$\begin{aligned} \hat{I}(p)= & {} \frac{1}{N}\sum _{k|\forall w_k,p\in w_k}\hat{I}_k(p) = \bar{a}_p G(p) + \bar{b}_p, \end{aligned}$$

(5)

in which N is the number of pixels in $w_k$, $\hat{I}_k(p)$ is the linear prediction of the pixel p in the $w_k$ (Eq. 1) and $\bar{a}_p = \frac{1}{N}\sum _{k\in w_p}a_k$ and $\bar{b}_p = \frac{1}{N}\sum _{k\in w_p}b_k$ are means of a and b in the patch $w_p$ centered at the pixel p (Eqs. (9) and (10) in [9]), respectively.

As described in [9], the output $\hat{I}(p)$ of the pixel p approximates to the input I(p) when $\bar{a}_p$ is close to 1. Meanwhile, the $\hat{I}(p)$ approximates to the mean of the pixels in $w_p$ when $\bar{a}_p$ is close to 0. Moreover, the conditions of $a_k \approx 1$ and $b_k \approx 0$ are held in regions with high variances ($\delta _{G, k}^2 \gg \epsilon$), and the conditions of $a_k \approx 0$ and $b_k \approx 1$ are held in regions with low variances ($\delta _{G, k}^2 \ll \epsilon$). Considering a simple case that the patch $w_p$ centered at a single step edge, each pixel in $w_p$ is involved in one or more flat patches where $a_k$ approximates to 0. Therefore, the value of $\bar{a}_p$ in $w_p$ is smaller than 1 evidently. Thus, the edge is blurred and halo artifacts may arise. Hence, it is reasonable to prevent halo artifacts in GIF method by improving the aggregating method as introduced in the following section.

2.2 GIF with weighted aggregation

To further illustrate the effect of the average aggregation on the edge blurring, some experimental results of GIF are shown in Fig. 1 visually. For a pixel near an edge (e.g., p in Fig. 1c), it should be involved in some patches (e.g., $w_i$ (red) in Fig. 1c) which are on the same side and others on the different side (e.g., $w_j$ (green) in Fig. 1c). Within the GIF algorithm framework, it is easily derived that the output $\hat{I}_i(p)$ in $w_i$ is closer to the expected result than the $\hat{I}_j(p)$ in $w_j$. In other words, the estimation error of p in $w_j$ is bigger than the one in $w_i$. With the average aggregation, big errors in those patches like $w_j$ are introduced in the final result averagely. Thus, edges are blurred especially when big smoothing parameters ($r,\epsilon$) are selected (Fig. 1c). As analyzed in [5, 9, 24], these blurred edges result in halo artifacts (Fig. 1b). It is obvious that the final aggregated result becomes more accurate if big weightings are assigned to the patches whose estimation errors are small. Meanwhile, the halo artifacts can be alleviated. In this study, the mean square error (MSE) is adopted to measure the estimation accuracy in each patch.

Fig. 1

Average aggregation results. The parameters of GIF are $\epsilon =0.4^2$ and $r=16$ (r is the radius of the filtering patch). a and b Input image and filtered result, respectively. c Profiles of input signal and filtered result (color figure online)

Fig. 2

Curves of the MSE. a Curve of $e_k$ on the condition of $\epsilon = 0.15^2$. b Values of $e_k$ while a 1D square signal is corrupted with a white Gaussian noise ($r = 3$)

Considering the estimation processing in a $w_k$, the mean square error (MSE) of the GIF can be expressed as:

$$\begin{aligned} e_k = \frac{1}{N}\sum _{i\in w_k}\left[ (a_kG(i) + b_k) - I(i)\right] ^2. \end{aligned}$$

(6)

Assuming that the estimation with low MSE has high confidence and a high weight is assigned accordingly. An aggregating weight $\gamma _k$ of the patch $w_k$ is introduced, and the aggregation step of the GIF is reformulated as:

$$\begin{aligned} \hat{I}(p)=\frac{1}{||\gamma _k||}\sum _{k|\forall w_k,p\in w_k}\gamma _k\left[ a_kG(p)+b_k\right] , \end{aligned}$$

(7)

where $\gamma _k=\exp (-e_k/\eta )$ ($\eta > 0$ is a small constant scalar) is the aggregating weight of the patch $w_k$ and $||\gamma _k||= \sum _{j\in w_k}\gamma _j$ is a normalization coefficient.

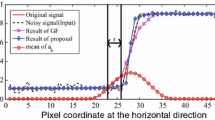
Figure 2 provides an intuitive understanding of the proposed aggregation in one-dimensional signal. Putting $G \equiv I$ and formulations of $a_k$ and $b_k$ (Eq. 4) to Eq. (6), we have $e_k = \epsilon ^2 \delta _{I,k}^2/(\delta _{I,k}^2 + \epsilon )^2$ where $\delta _{I,k}^2$ is variance of I in $w_k$. Figure 2a shows the curve of $e_k$ ($\epsilon = 0.15^2$). Figure 2b indicates values of $e_k$ (red), while a 1D square signal is corrupted with a white Gaussian noise ($r = 3$). As illustrated in Fig. 2a, the value of $e_k$ decreases monotonically with $\delta _{I,k}^2$ increasing when $\delta _{I,k}^2$ is bigger than $\epsilon$ and varies inversely when $\delta _{I,k}^2$ is smaller than $\epsilon$. In the case that a pixel p locates on an edge area, variances of all patches covering p are much bigger than $\epsilon$ ($\delta _{I,k}^2 \gg \epsilon$), and a patch with high variance has a low MSE, which means that the prediction $\hat{I}_k(p)$ in this patch $w_k$ is much close to the input I(p). Accordingly, a high aggregating weight $\gamma _k$ is assigned to this patch. On the contrary, when a pixel p locates on a flat area, $\delta _{I,k}^2 \ll \epsilon$ is tenable for all patches ($w_k$) covering the specific pixel p. In this case, aggregating weights in patches which have low variance are big and the final results approximate to the mean. As illustrated in Fig. 2b, the values of MSE in edge patches are higher than ones in flat patches. Moreover, the curve of MSE achieves local minimum value when the patch center locates at edges, which reveals that the predictions in these patches are close to the true values.

Fig. 3

1D signal processing. The input (blue) is a square step signal with a white Gaussian noise whose mean is zero and variance is 0.001 (color figure online)

Figure 3 demonstrates the results of the proposed method and the relevant GIF-based methods in one-dimensional signal. In order to illustrate the differences among selected methods, two sets of smooth factors (r, $\epsilon$) are selected: ($4, 0.15^2$) (Fig. 3a) and ($16, 0.4^2$) (Fig. 3b). It is observed that the GIF with the proposed weighted aggregation (green) achieves much better results than other methods. The result by the proposed method on large smooth factors, which is almost the same as the ground truth, reveals that the proposed method is robust to smooth parameters r and $\epsilon$. Figure 3 shows that both WGIF and GDGIF are helpful in edge preserving, but both methods yield oscillations in flat regions, which implies that the WGIF and GDGIF are sensitive to signal oscillation. Hence, the WGIF and GDGIF methods are only good to the images with weak textures. On the contrary, the proposed algorithm not only preserves edges well, but also removes signal oscillations in flat areas. To verify the performance of the proposed method on 2D images, one more example, which is originated from [5], is adopted for analysis as shown in Fig. 4. For the BF method, the parameters are chosen as $\delta _s = 12, \delta _r=0.8$. Since the parameters r and $\epsilon$ in GIF play similar roles in $\delta _s$ and $\delta ^2_r$ in BF, r and $\epsilon$ in GIF-based methods are selected as 12 and $0.8^2$, respectively. The guided image for GIF-based approaches is the input image itself. It is observed that BF and GIF methods remove the fine-scale noise, and the step edges are blurred accordingly. While the edge-aware weighting is introduced by WGIF and GDGIF, oscillations caused by noise cannot be removed because they are treated as edges. On the contrary, by applying weighed aggregation to GIF, it is possible to achieve both fine and coarse smoothing results, i.e., preserves the step edges sharply without introducing obvious artifacts (Fig. 4g) and removes oscillations in flat regions. In summary, the proposed method significantly outperforms GIF, WGIF, GDGIF, BF and WLS.

Fig. 4

2D image filtering. a Input image by courtesy of [5]. b Base layer of BF [25]. c Result of WLS optimization ($\alpha = 1.8$, $\lambda = 0.35$). d–f Results of GIF [9], WGIF [15] and GDGIF [12], respectively. g Base layer decomposed by proposed method ($\eta = 0.005$). (b)–(f) Obtained by original codes

Substituting Eq. (4) into Eq. (6), we obtain

$$\begin{aligned} e_k= & {} \frac{1}{N}\sum _{i\in w_k}\left( a_kG(i) + \bar{I}_k - a_k\bar{G}_k - I(i)\right) ^2 \nonumber \\= & {} \frac{1}{N}\sum _{i\in w_k}\left[ a_k(G(i) - \bar{G}_k) - (I(i) - \bar{I}_k)\right] ^2 \nonumber \\= & {} a_k^2{\delta ^2_{G,k}} - 2a_k \hbox {cov}_k(G,I) + {\delta ^2_{I,k}}, \end{aligned}$$

(8)

where ${\delta ^2_{G,k}}$ and ${\delta ^2_{I,k}}$ are variances of the guided image G and the input image I in $w_k$, respectively, and $\hbox {cov}_k(G,I)$ is the covariance of G and I in $w_k$. This is the expression of the MSE $e_k$. With some simplifications, the weighted aggregation (Eq. 7) can be reformulated as:

$$\begin{aligned} \hat{I}(p)=G(p)\sum _{k\in w_p}\frac{\gamma _k}{||\gamma _k||}a_k + \sum _{k\in w_p}\frac{\gamma _k}{||\gamma _k||}b_k. \end{aligned}$$

(9)

According to Eqs. (9) and (8), the pseudo-code of the proposed weighed aggregation GIF, namely WAGIF, is described by Algorithm 1. It is noted that the symbol mean in Algorithm 1 is an average filtering operator within a box window of radius r.

Fig. 5

Image detail enhancement. a Input images. b Enhanced images of GIF. c Results of WGIF. d Enhanced images of GDGIF. e Enhanced images of PGIF. f Results of the proposed method. The detail layers are boosted by 5 times for all algorithms

2.3 Analysis on computational complexity

The main computational burden of either step 1 described in [9] or steps 2–4 in Algorithm 1 is the average filter mean. Besides that, the rest operators in Algorithm 1 are pixel-wise operations. Furthermore, the average filter mean can be efficiently computed in O(N) by using integral image technique [3] or moving sum method described in [9]. Therefore, the proposed WAGIF naturally has linear computational complexity (O(N)) and is independent of the filtering radius r. Experiments demonstrate that the C++-based implementation achieves a steady running time when different filtering radii r are selected. By working on a PC platform with Intel Xeon E5 2.1 GHz CPU and 128 GB RAM, the operation time is about 285 ms/MP. Moreover, the proposed WAGIF can be easily extended to the GPU platform for high performance and the running time in GPU implementation is about 48 ms/MP.

3 Applications and experiments

In this section, the WAGIF is applied to several applications including single image enhancement [4, 23], HDR tone mapping [4, 11] and single image haze removal [8]. The experiments are performed on MATLAB platform. In order to verify the contribution of the weighted aggregation to GIF, only GIF-based algorithms (e.g., GIF [9], WGIF [15], GDGIF [12] and PGIF [18]) are employed for comparison, and the codes of the GIF, WGIF and GDGIF are provided by the corresponding authors. The parameters used in all experiments are selected as follows: $r = 15$, $\epsilon =0.15^2$. Moreover, $\eta = 0.005$ is selected for single image enhancement and HDR tone mapping, and $\eta$ is set to 0.0015 for single image haze removal.

Single image enhancement In this work, the input image is decomposed into a base layer and a detail layer, where the base layer is a reconstructed image formed by homogeneous regions with sharp edges and the detail layer represents image texture. Generally, the edge-preserving filters are performed on the base layer. Then, the output image is reconstructed by combining the smoothed base layer and magnified detail layer. A detailed description of the image detail enhancement can be found in [4].

Fig. 6

HDR tome mapping via different filters. a–e Results via GIF, WGIF, GDGIF, PGIF and the proposed method, respectively (color figure online)

Fig. 7

Haze removal via different filters. a Input images. b–d Results via GIF, WGIF and GDGIF, respectively. e Result via the proposed method

Figure 5 illustrates enhanced images by different methods. As shown in zoom-in patches in Fig. 5b, e, halo artifacts are obvious in outputs of GIF and PGIF (i.e., the black shadow near the petal in the first row and the purple halo around the stamen in the second row). Halo artifacts are reduced significantly in the enhanced images via WGIF, but they are still perceived (see the first result in Fig. 5c). As claimed in [12], GDGIF reduces halos better than WGIF (Fig. 5d). Compared with other results shown in Fig. 5, halo artifact reduction by the proposed method is comparable to GDGIF and WGIF, but the enhanced images of the proposed method have clearest details and are perceived naturally and pleasurably.

HDR tone mapping Tone mapping [4, 11], which converts a high-dynamic-range (HDR) image into a conventional low-dynamic-range (LDR) image, is a popular application in digital photography. This work can be viewed as a type of image detail enhancement in which an HDR image is also decomposed into a base layer and a detail layer. Different from single image enhancement, in which the detail layer is magnified, the base layer in HDR tone mapping is compressed. Hence, HDR tone mapping is also referred to as HDR image compressing.

In these experiments, a popular HDR tone mapping framework introduced in [4] is applied, i.e., an HDR image is decomposed into a base layer and a detail layer by an edge-preserving filter in log domain. Then the base layer is compressed by a specific scale factor. The LDR images after tone mapping by various methods including GIF, WGIF, GDGIF, PGIF and the proposed method are shown in Fig. 6. The zoom-in patches illustrated in Fig. 6 show that the proposed approach achieves results in which the halo artifacts and the gradient reversals are avoided or alleviated in the resultant LDR images. Furthermore, the proposed method preserves details better than WGIF [15], GDGIF [12] and PGIF [18] and display vivid color (see Fig. 6b–d).

Single image haze removal A haze transmission map was estimated via the dark channel prior and an effective single image dehaze framework was proposed in [8]. In [9], a refinement of the transmission was presented by simply filtering the raw transmission map under the guidance of the hazy image. In this example, the dehazing framework in [8] is applied and the raw transmission map is filtered by GIF [9], WGIF [15], GDGIF [12] and the proposed method, respectively. The dehazed images via different filters are shown in Fig. 7. It is seen that the proposed method is greatly superior to GIF, WGIF and GDGIF methods in terms of haze removal and detail preserving.

Next, the fog-aware density evaluator (FADE), a non-reference prediction of perceptual fog density proposed in [2], is employed to evaluate the dehazed image quality. The fog densities of images in Fig. 7 are listed in Table 1.

A low FADE value indicates a low perceptual fog density. Experimental results performed on nine fog images tested in [8] show that the FADE by the proposed WAGIF is 1.3640, which is the lowest average value among all GIF-based algorithms (GIF: 1.3736, WGIF: 1.4209 and GDGIF: 1.4198).

4 Conclusion

As edges are of critical importance to the visual appearance of images, one significant work in image processing is to achieve edge-preserving image filtering. In this paper, the aggregation step of GIF [9] is analyzed and a novel weighted aggregating guided image filtering, i.e., WAGIF, is proposed. Different from the aggregation which is applied by GIF [9] and its variants [12, 15], predictions of the interested pixel are aggregated by weighting instead of averaging. Moreover, the weight of each prediction is specified according to the estimation confidence in the corresponding patch. The proposed weighted aggregation contributes GIF-based algorithms in two aspects: improving edge-preserving effect significantly and smoothing flat areas finely and coarsely. Experiments performed on image detail enhancement, HDR tone mapping and single image haze removal show that the proposed method achieves excellent visual quality in comparison with state-of-the-art algorithms.

Table 1 Fog densities of the images in Fig. 7

Limitation With a small scaling parameter ($\eta$), over-sharpening sometimes exists in filtered images and gradient reversal artifacts arise. In the example shown in Fig. 5, inconspicuous gradient reversals can be found somewhere near the edges of petals and these gradient reversals will be more obvious when $\eta$ is set to a smaller value.