1 Introduction

In image processing and computer vision literature, segmentation refers to the process of dividing an image into multiple disjoint segments. It is a key preliminary vision task used by various high level image and videos analysis techniques such as: content-based image retrieval [1,2,3,4,5,6], image compression [7,8,9,10], object detection [11,12,13,14,15,16,17] and activity recognition [18,19,20,21,22,23]. There are two main types of image segmentation: interactive segmentation and automated segmentation. Interactive segmentation [24,25,26,27] extracts an object of interest with the help of human interaction, while automated segmentation partitions an image into a set of disjoint regions without any human interaction [28,29,30,31,32,33,34]. A large number of image segmentation algorithms have been reported in the literature. However, these can be divided into four categories: (1) image based, (2) feature-based, (3) physics-based and (4) hybrid approaches.

The physics-based approaches [35,36,37,38,39] utilize the reflectance property of the objects for segmentation. These methods can better handle the chromatic changes caused by shadows and highlights. However, in most cases, no prior information about the object’s reflectance is available. Therefore, physics-based methods are only useful for some specific cases, where the reflectance of objects is known.

The hybrid approaches [28, 29, 40,41,42,43,44,45] try to combine the strengths of each approach. However, how to combine the strengths of different approaches and avoid their weaknesses? Still remains an open question.

Feature-based approaches treat the segmentation process as a clustering problem [30,31,32, 46,47,48,49,50]. As in any clustering problem, determining the exact number of clusters is a principal shortcoming of these approaches.

The quality of data partitioning and clustering can be assessed by a clustering validity index (CVI) [51, 52]. Such an index quantify the extent to which the given clusters reflect the actual structure present in the data. In this paper, we propose a new clustering validity index which combines the compactness, separation and overlap to improve the accuracy of segmentation. The concept of aggregation (t-norms and t-conorms) is used to build a new measure of overlap. The optimal clusters centroids and the optimal number of clusters are estimated by using a genetic algorithm-based optimizer. Additionally, the super-pixels are used for reducing the computational complexity to get well-defined segments.

Section 2 presents the proposed method in detail, while Sect. 3 contains the experimental results followed by conclusion.

2 The proposed method

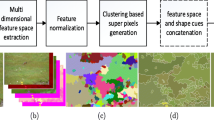
The proposed method has three key processes. The first is super-pixel segmentation to reduce the search space and computational cost of the clustering process. The second is a new clustering validity index (CVI) which is proposed to get the best possible arrangement of data partitioning. Finally, the genetic algorithm is used to optimize the cluster centroids and find the optimal number of clusters.

2.1 Super-pixels generation and features extraction

Perceptually uniform regions in image are called super-pixels. It exponentially reduces the image primitives regions and helps to extract rich spatial features [53,54,55,56]. In this work, the procedure of [56] is used for the super-pixel segmentation. Figure 1 shows the result of super-pixel segmentation [56].

Let \(\chi ^i\) represents the ith super-pixel, then its feature vector, \(\mathbf {x}^{i}\in \mathfrak {R}^{n\times 1}\), is computed as follows:

$$\begin{aligned} \mathbf {x}^{i}&=\left[ \dfrac{\sum \nolimits _{j=1}\chi ^i_j}{|\chi ^i|}\in \hbox {RGB},\dfrac{\sum \nolimits _{j=1}\chi ^i_j}{|\chi ^i|}\in \hbox {HSV},\nonumber \right. \\&\quad \left. \dfrac{\sum \nolimits _{j=1}\chi ^i_j}{|\chi ^i|}\in \hbox {Lab},\hbar \right] ^\mathrm{T} \end{aligned}$$
(1)

where the first, second and third components of the feature vector represent the means of super-pixel in RGB, HSV and Lab color spaces respectively, while \(\hbar \) represents the normalized histogram of oriented gradients (HoG) of \(8\times 8\) window centered on the super-pixel.

Fig. 1
figure 1

The first row contain images taken from BSD [61] while the second row show the results of super-pixel segmentation [56]

Full size image

2.2 Clustering validity index (CVI)

Let \(\mathbf {v}^{1}\), \(\mathbf {v}^{2}, \ldots , \mathbf {v}^{K}\in \mathfrak {R}^{n\times 1}\) represent the clusters centroids and \(X=\{\mathbf {x}^{1}, \mathbf {x}^{2}, \mathbf {x}^{3}, \ldots \mathbf {x}^{N}\}\) denote the data points. Then, the membership values \({{u}^{ij}}\), \(i = 1, 2,\ldots , K\) and \(j = 1, 2,\ldots , N\) can be determined as [57]:

$$\begin{aligned} u^{ij}&=\left[ {\sum \limits _{l=1}^{K}\left( \frac{||\mathbf {v}^{i}-\mathbf {x}^{j}||_2}{||\mathbf {v}^{l}-\mathbf {x}^{j}||_2}\right) ^\frac{2}{m-1}}\right] ^{-1},\, \nonumber \\&\quad \hbox {for} \quad 1\le i\le K, \ 1 \le j\le N \end{aligned}$$
(2)

where m is a parameter used to control the fuzziness of the membership values. The membership \(u^{ij}\) demonstrates the relationship of a point \(\mathbf {x}^{j}\) to a centroid \(\mathbf {v}^i\). The t-conorm is normally used to assign a data point \(\mathbf {x}^{j}\) to the most matching element of the membership vector \(\mathbf {u}^{j} =[u^{1j}; \ldots ;u^{K j}]^T\). However, a data point \(\mathbf {x}^{j}\) may be a member of multiple centroids with different degree of similarity. Thus, the aggregate value of \(\mathbf {u}^{j}\) is better to evaluate the overlap of a particular data point, \(\mathbf {x}^{j}\). The fuzzy OR operator \((\hbox {fOR}-l)\) [58] uses the combination of t-norms with a given order (l) to estimate the extent of similarity. Suppose a \(\rho \) represents the power set of \(C= {1,2, \ldots ,K}\) and \(\rho _{l} =\{S \in \rho :|S|=l \}\), where |S| represents the cardinality of the subset S. Then \((\hbox {fOR}-l)\) maps \(u^{j}\) to a scalar value .i.e., \(\overset{l}{\bot }(\mathbf {u}^{j})\in [0; 1]\),

$$\begin{aligned} \overset{l}{\bot }(\mathbf {u}^{j})=\underset{S\in \rho _{l-1}}{\top }\left( \underset{j\in C\backslash S}{\bot }u^{ij}\right) . \end{aligned}$$
(3)

The above equation demonstrates that the standard t-norms, \(\overset{l}{\bot }(\mathbf {u}^{j})\) give us the lth highest value of \(\mathbf {u}^{j}\).

Then, for a particular point \(\mathbf {x}^{j}\in X\), the degree of overlap among l fuzzy clusters can be determined by its membership vector \(\mathbf {u}^{j}\), as given in Eq. (3). For a point \(\mathbf {x}^{j}\) the total degree of overlap is determined by the order which induces minimum overlap. The K-order overlap measure is adopted to explore the most probable order(s) that induces minimum overlap. Thus, for a given point \(\mathbf {x}^{j}\) the overall overlap can be given by Eq. (4).

$$\begin{aligned} O_{\bot }(\mathbf {u}^{j},K)=\frac{\overset{\lceil K/2\rceil }{\bot }\mathbf {u}^{j}+\overset{K}{\bot }\mathbf {u}^{j}}{2} \end{aligned}$$
(4)

Thus, the commutative overlap for K-order is given by:

$$\begin{aligned} O_{\bot }(K)=\frac{\sum \nolimits _{j=1}^{N}O_{\bot }(\mathbf {u}^j,K)}{N} \end{aligned}$$
(5)

Illustration of Overlap\(O_{\bot }(K)\) Consider the following fuzzy membership matrix U:

$$\begin{aligned} \left[ \begin{array}{llllll} 0.200 &{}\quad 0.185 &{}\quad 0.091 &{}\quad 0.120 &{}\quad 0.241 &{}\quad 0.080 \\ 0.080 &{}\quad 0.074 &{}\quad 0.227 &{}\quad 0.160 &{}\quad 0.231 &{}\quad 0.227 \\ 0.240 &{}\quad 0.111 &{}\quad 0.182 &{}\quad 0.080 &{}\quad 0.154 &{}\quad 0.091 \\ 0.040 &{}\quad 0.121 &{}\quad 0.048 &{}\quad 0.200 &{}\quad 0.039 &{}\quad 0.273 \\ 0.120 &{}\quad 0.148 &{}\quad 0.046 &{}\quad 0.070 &{}\quad 0.031 &{}\quad 0.136 \end{array} \right] \end{aligned}$$

where \(K=5\) and number of data points are six. In this case the \(\overset{\lceil K/2\rceil }{\bot }\mathbf {u}^{j} \) and \(\overset{K}{\bot }\mathbf {u}^{j}\) give us the third and fifth maximum values in each column, respectively, where \(j=1,2, \ldots ,6\).

$$\begin{aligned}&\overset{3}{\bot }\mathbf {u}^{j} \\&\quad = \left[ \begin{array}{llllll} 0.120&0.121&0.91&0.120&0.154&0.136 \end{array} \right] \\&\overset{5}{\bot }\mathbf {u}^{j}\\&\quad =\left[ \begin{array}{llllll} 0.040&0.074&0.046&0.070&0.031&0.080 \end{array} \right] \end{aligned}$$

Thus, \(\frac{\overset{3}{\bot }\mathbf {u}^{j}+\overset{5}{\bot }\mathbf {u}^{j}}{2}\) becomes: \(\big [ 0.080 \; 0.098 \; 0.478 \; 0.095 \; 0.093 \; 0.108 \big ]\). So the total overlap \(O_{\bot }(5)\) becomes 0.1587.

The commutative normalized fuzzy deviation of data points [59] is used as a compactness measure,

$$\begin{aligned} \Omega = \sum \limits _{i=1}^{K} \left( \frac{\sum \nolimits _{j=1}^{N}{u^{ij}||\mathbf {v}^{i}-\mathbf {x}^{j}||_2}}{\sum \nolimits _{j=1}^{N}{u}^{ij}}\right) \end{aligned}$$
(6)

The separation is defined in term of clusters centroids diversity. Let \(V=[\mathbf {v}^1,\mathbf {v}^2,\ldots \mathbf {v}^K]^\mathrm{T}\) represent the K clusters centroids then a symmetric matrix \(A\in \mathfrak {R}^{K\times K}\) is constructed:

$$\begin{aligned} A=V^\mathrm{T}V \end{aligned}$$
(7)

The clusters separation \(\Psi \) can be computed by the following equation:

$$\begin{aligned} \Psi =\frac{\max (\lambda )}{\sum _{i=1}^{K} A_{ii}} \end{aligned}$$
(8)

where \(\lambda \) represent the eigenvalues of A. The compactness ‘\(\Omega \)’ needs to be minimized in order to maximize the intra-cluster similarities. Similarly, we need smaller overlap \(O_{\bot }(\cdot )\) to ensure the maximum disjointness. To increase inter-clusters deviation, we need to maximize the fuzzy separation \(\Psi \). So, the final clustering validity index (CVI) is given by:

$$\begin{aligned} \hbox {CVI}=\frac{\Omega }{\Psi }\cdot O_{\bot }(\kappa ) \end{aligned}$$
(9)

The smaller CVI represents the best clustering and vice versa.

2.3 Genetic algorithm-based super-pixels clustering

We consider the clustering of super-pixels as a maximization case of optimization problem. The main purpose of genetic algorithm is to decide the optimal number of clusters, K, and estimate optimal centroids.

Let \(\mathbf {v^i\in \mathfrak {R}^{n\times 1}},i=1\dots K\) represent the clusters centroids then a chromosome is represented by string of real numbers, \([(\mathbf {v}^1)^\mathrm{T},(\mathbf {v}^2)^\mathrm{T},\dots (\mathbf {v}^K)^\mathrm{T}]\in \mathfrak {R}^{1\times nK}\), where n is the dimension of centroid and K denote the number of centroids.

In case of genetic algorithm, one need to have a fitness function to evaluate the quality of chromosome (solution). Here, we consider clustering as a maximization optimization problem and define a fitness function by incorporating the new clustering validity index (CVI),

$$\begin{aligned} f=\frac{1}{\hbox {CVI}}. \end{aligned}$$
(10)

The given fitness function is the reciprocal of the clustering validity index (CVI), as given in Eq. 9. Note that the highest fitness value means the best chromosome and low fitness value means the bad chromosome.

figure a
Table 1 Genetic algorithm parameters
Full size table

Algorithm 1 demonstrates the genetic algorithm in detail. A container \(B_\mathrm{s}\) is used to store the best solution found so far. An initial population is selected form \(\{ \bar{P}\cup P\}\), where P is randomly generated from the set of super-pixels X and \(\bar{P}\) represents its opposition [60]. For each individual, i, its opposition is computed,

$$\begin{aligned} \bar{P}_{i,j}=a_j+b_j-P_{i,j}, \end{aligned}$$
(11)

where \(P_{i,j}\) and \(\bar{P}_{i,j}\) represent the jth component of the ith individual of the current population and its opposition respectively. The details of parameters setting of GA are given in Table 1. The binary tournament selection is used to select the candidates for reproduction. Subsequently, the chromosomes that are being selected are put into the mating pool for reproduction. New offsprings are produced on the basis of single point crossover with random cut point. The crossover rate \(\rho _\mathrm{c}\) is set to 0.8. Initially, the mutation rate \(\rho _\mathrm{m}\) is kept high for the sake of better exploration and decreased with time to ensure exploitation. The initial mutation probability \(\rho _\mathrm{m}\) is set to 0.18 (as given in line 3). In the successive iterations, the mutation rate is decreased by factor of \(\hbox {e}^{-g/\eta }\), where \(\eta =20\) (line 13). The lines 14–15, set the lower bound of the mutation rate \(\rho _\mathrm{m}\). To ensure elitism the best individuals among the parent population and newly generated offspring are retained in the new population. The stopping criteria, (\(g\le G \Vert \delta \ne \hbox {true}\)) is used to terminate the execution. Note that G represents the maximum epochs while \(\delta \), \(f_{g,\mathrm{best}}\), and \(f_{g-1,\mathrm{best}}\) represent the flag, best solutions in the current generation and previous generation respectively. Lines 18 and 19 of the Algorithm 1 demonstrate that the old best solution, which is stored in container \(B_\mathrm{s}\), is replaced by the new best solution if \(f(P_k)>f(B_\mathrm{s})\), where \(f(\cdot )\) represent the fitness of a chromosome. We run the algorithm for different number of clusters, K, with \(K\in \{2,3,\dots , K_{\max }\}\). Thus, the algorithm returns the best possible number of clusters, K, with optimized centroids.

3 Experimental results

The experimentation is performed on Berkeley image segmentation database (BSD) [61]. The results of proposed algorithm are compared with six well-known image segmentation methods: Segmentation via Lossy Data Compression (LDC) [62], Efficient Graph-based Image Segmentation (EG) [63], Describing Reflectance’s for Color Segmentation Robust to Shadows, Highlights, and Textures (also called Ridge-based Analysis of Distributions physics-based) (RADp) [35], Statistical Region Merging (SRM) [64], A Level Set Method for Image Segmentation in the Presence of Intensity Inhomogeneities with Application to MRI (LS) [65] and Multi-region Image Segmentation by Parametric Kernel Graph Cuts (KGC) [66].

3.1 Qualitative comparisons

Here, the results of the proposed algorithm are visually compared with six algorithms: SRM, LDC, RADp, KGC, LS, and EG. For qualitative analysis, 11 images are selected from Berkeley Segmentation Database (BSD) [61] which include Coastal (321 \(\times \) 481), Night (481 \(\times \) 321), Building (481 \(\times \) 321), Bear (321 \(\times \) 481), Flower (321 \(\times \) 481), Cow (321 \(\times \) 481), Men (321 \(\times \) 481), Boat (4811 \(\times \) 321), Bird (481 \(\times \) 321), Lady (481 \(\times \) 321) and Ship (481 \(\times \) 321).

Figure 2 visually presents the results of the above-mentioned algorithms for 11 BSD images. The first row demonstrate the results of the mentioned algorithms for Coastal image. The Coastal image contain rocks, water, sky and a small boat. For Coastal image, the proposed method performs best and accurately segment out the water, sky, rock and the boat. Similarly, SRM also performs better for the Coastal image and generate results near to human perception. The LDC over-segments the water and rock regions, while the RADp is unable to perform any segmentation. The KGC, LS, EG and NC perform poor and tend to produce over-segmentation. The second row of Fig. 2 shows the results for Night image. It is clear that the proposed method outperforms the other methods and achieve results near to the corresponding human subject. For the same image, SRM and RADp perform better and segment forest region but fail to detect the moon area. Although KGC detects the moon but divides the sky region into undesirable segments. The LS, EG and NC fail to detect the actual boundaries of the objects and lead to undesirable results. Note that the proposed method also outperform the other techniques in case of Building (third row), Bear (fourth row), Flower (fifth row) and Cow (sixth row) and produce results which nearly matching corresponding human segmentations. Seventh row demonstrates the results for Men image. It can be observed that the proposed method performs better than other stated methods. For the Men image, the SRM, RADp, and KGC perform comparatively good but LDC and LS makes over-segmentation. In case of Boat (eight row), the proposed method performs best, while the rest of methods perform over-segmentation of water, sky and boat regions. For Boat, the RADp is unable to perform any segmentation. It is clear form Fig. 2 that the proposed algorithm perform better compared to other stated methods in case of Bird (ninth row), Lady (tenth row) and Ship (eleventh row).

The proposed algorithm uses the RGB, HSV and Lab color spaces to encode the color information and histogram of oriented gradients (HoG) to encode the texture information. Thus, the proposed algorithm fails when two different segments have nearly the same textures and colors. It can be noted from Fig. 3 that the spider and rock region (non-fungus region) have nearly the same colors and textures and hence the proposed algorithm fails to separate them out.

Generally, the SRM faces the problem of under segmentation, while the LDC is unable to achieve the actual contours and hence produce over-segmented results. Normally, RADp fails to get the segments boundaries and tends to under segmentation, while in some cases it over-segment the uniform regions and makes noisy segmentation. The KGC generally leads to over-segmentation but for some instances, it performs better comparatively. The LS perform poorly to detect the segments boundaries. For many images, the performance of EG is good enough but generally leads to over-segmentation. The results show that the proposed method comparatively performs better than other stated methods.

3.2 Quantitative comparison

We have used the variation of information (VoI) [67] and probabilistic rand index (PRI) [68] to quantitatively evaluate the performance of the proposed method.

Variation of information (VoI) relates two segmentation in term of information contents and returns a score in the range \([0, \infty )\). The smaller value of VoI denotes the high degree of similarity between the different setup of segmentations and vice versa.

The Probabilistic Rand Index (PRI) matches the given segmentation with underlying ground truth segmented images. It assigns variable weights to pixels pairs to incorporate the human-induced variability among ground truths. PRI generates a score in the range of [0, 1]. The larger PRI score means the better segmentation and vice versa.

Fig. 2
figure 2

Qualitative comparison of the proposed method with other algorithms. The first column contains the ground truth human segmented images, while second to seventh column present the results of proposed method, SRM, LDC, RADp, KGC, LS, and EG respectively

Full size image
Table 2 PRI score for 11 selected BSD images
Full size table
Table 3 VoI score for 11 selected BSD images
Full size table
Table 4 Average PRI and VoI scores for 500 BSD images
Full size table

Table 2 shows the PRI score of each algorithm for the 11 selected BSD images. The last column of the Table 2 contains the average PRI score of each algorithm for the 11 images. It is clear from the given table that the proposed algorithm outperforms the rest of the algorithms in term of PRI score. Similarly, Table 3 presents the VoI score of each algorithm for the given 11 BSD images. It can be noted from Table 3 that the proposed algorithm perform better than the other algorithms in term of VoI score. Table 4 show the mean PRI and VoI scores of the seven algorithms for 500 BSD images. It is clear from Table 4 that the proposed method perform better compared to other stated methods in term of VoI and PRI scores.

Fig. 3
figure 3

Fail case

Full size image
Table 5 Average running time in second for an image of size (481 \(\times \) 321)
Full size table

Running time analysis It is difficult to compute the running time complexity of Genetic Algorithm (GA) analytically, in term of Big Oh notation, due to its stochastic and randomized nature. Therefore, the running time of the proposed algorithm is measured and compared with other algorithms in terms of CPU time. The simulations are performed in MATLAB R2014a with Windows 7 operating system on a Laptop machine having the processor, Intel(R) Core(TM) i3-2350M CPU@ 2.30 GHz, and installed memory of 8 GB. The detail of the running time (in seconds) of different algorithms is given in Table 5.

4 Conclusion

In this paper, a new clustering validity index (CVI) is proposed. The proposed CVI combines the clusters overlap, global compactness and fuzzy separation. The clusters overlap determines that how much a particular data point belongs to the other clusters centroids. The global compactness determines that how much the points in a particular cluster are similar while the fuzzy separation looks for the difference among different clusters centroids. The better clustering/segmentation needs minimum overlap and minimum compactness while maximum separation. Furthermore, a genetic algorithm is applied to optimize the clusters/segments centroids. The clustering of super-pixels is performed in order to reduce the computational complexity. The proposed dynamic genetic algorithm automatically converges to the optimal number of clusters/segments, which have minimum overlap and compactness, and maximum separation. The algorithm runs for a different number of clusters K in the range [\(K_{\min }\), \(K_{\max }\)]. The number of clusters K, which best maximize the objective function is considered the optimal segmentation. For initialization, the opposition-based strategy is used in order to have a better start. Performance of the proposed algorithm is compared with six state-of-the-art image segmentation algorithms. The qualitative and quantitative results demonstrate that the proposed algorithm performs better compared to other state-of-the-art image segmentation methods. In future work, the image segmentation may be extended to semantic segmentation by incorporating saliency and attention networks [69, 70].