Heuristic optimization-based wave kernel descriptor for deformable 3D shape matching and retrieval

Abstract

This paper presents an optimized wave kernel signature (OWKS) using a modified particle swarm optimization (MPSO) algorithm. The variance parameter and its setting mode play a central role in this kernel. In order to circumvent a purely arbitrary choice of the internal parameters of the WKS algorithm, we present a four-step feature descriptor framework in an effort to further improve the classical wave kernel signature (WKS) by acting on its variance parameter. The advantage of the enhanced method comes from the tuning of the variance parameter using MPSO and the selection of the first vector from the constructed OWKS at its first energy scale, thus giving rise to substantially better matching and retrieval accuracy for deformable 3D shape. The special choice of this vector is to extremely reinforce the stability for efficient salient features extraction method from the 3D meshes. Experimental results demonstrate the effectiveness of our proposed shape classification and retrieval approach in comparison with state-of-the-art methods. For instance, in terms of the nearest neighbor (NN) metric, the OWKS achieves a 96.9% score, with performance improvements of 83.5 and 90.4% over the baseline methods WKS and heat kernel signature, respectively.

1 Introduction

A shape descriptor should be discriminative and insensitive to deformations and noises. Most of them are constructed from the spectral decomposition of the Laplace–Beltrami operator (LBO) associated with the shape [1,2,3,4]. These descriptors accomplish state-of-the-art performances in many shape analysis tasks, such as segmentation, registration, shape matching, and retrieval [5,6,7].

An example of spectral shape analysis is the global point signature (GPS) of a point on a shape, as proposed by Rustamov [8], which computed by associating each point with the scaled eigenfunctions of the LBO. The GPS signature is invariant under isometric deformations, but is limited by the eigenvalues “switching” when the involved eigenvalues are close to each other.

A different approach was suggested by Sun et al. [1] who introduced the heat kernel signature (HKS), and independently by Gebal et al in [9]. It is based on the solution of the heat equation. The HKS is invariant to inelastic deformations, insensitive to topological transformations and robust under perturbations of the shape. The two main disadvantages of HKS are the lack of scale invariance and its excessive sensitivity to low-frequency information. As a remedy to these drawbacks, Bronstein and Kokkinos [10] introduced a scale-invariant version of HKS (SI-HKS). The SI-HKS descriptor is obtained by sampling the time scales logarithmically leading to a shape scaling that corresponds to a translation, and therefore it is characterized by the scale invariance.

Aubry et al. exhibited in [2] another physically inspired descriptor, which is called the wave kernel signature (WKS). It was proposed as a solution to rectify the poor feature localization of HKS, as well as to resolve the severe sensitivity of the HKS to low-frequency information. However, the capability of the WKS for features classification and matching accuracy between shapes depends on its parameters. Apart from the fact that the parameters could affect the features of the descriptor, they are also related to the sensitivity of the signature to global or local properties around an interest point [11].

A discriminative 3D shape descriptor needs to be robust, and its internal parameters require proper tuning. For this reason, stochastic methods like the genetic algorithm (GA) [12], the particle swarm optimization (PSO) [13, 14], the ant colony optimization (ACO) [15] and the shuffled frog leaping algorithm (SFLA) [16] could be used. In fact, a popular and a widely used algorithm is PSO, where it is used as a solution of optimization problems. Then it is so-called standard PSO (SPSO). SPSO is an evolutionary algorithm that is based on swarm intelligence, as it is inspired by the birds’ foraging behavior. Lately, a modified particle swarm optimization (MPSO) [17, 18] has obtained increasing attention due to its simple implementation, solution’s accuracy and excellence in performance. Moreover, the MPSO variant provides particular qualities in terms of reliability and speed convergence than SPSO and GA [18], since it uses an adaptive inertia weight. MPSO can be applied in several domains, such as combinational optimization, neural network training and pattern recognition.

1.1 Contributions

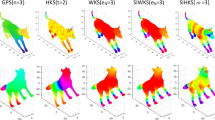
This paper focuses on the construction of an optimized wave kernel signature (OWKS) to improve classification results and obtain reliable feature points across a collection of shapes, to improve the retrieval accuracy rate and to enhance robustness under unfavorable circumstances. In our case, OWKS is done by invoking MPSO, for searching and selecting the optimized value of the variance parameter for the WKS. This enables us to obtain a beneficial shape feature and to make the shape signature as significant as possible. The algorithm improves the solution according to a fitness function. The objective function to minimize is the mean square error (MSE). The OWKS is then used as local shape descriptor for shapes classification, recognition and point matching. We observe, as exemplified in Fig. 1, that the gap between two signatures of the same point on the two nearly isometric shapes becomes marginal as soon as we use OWKS. Note that while remaining nearly stable under perturbations and robust to deformations of the shape, the OWKS remains informative over the energy scale e.

The rest of the paper is structured as follows. After a short overview of the WKS descriptor and the modified particle swarm optimization in Sect. 2, we introduce the OWKS-based shape recognition and matching concept in Sect. 3. The superiority of the proposed framework is shown experimentally for several tasks on 3D shapes analysis in Sect. 4. Finally, the conclusion is in Sect. 5.

Fig. 1

Comparison of the wave kernel signature (second column) and the optimized wave kernel signature (third column) on two different poses of an animal shape (first column) at three different points (marked in red, green, and blue). Solid and dotted lines represent the shape on the top and bottom, respectively (color figure online)

2 Background

2.1 The Laplace–Beltrami operator (LBO)

Given a real function f defined on a Riemannian manifold ${\mathcal {M}}$, the LBO [19] is defined as

$$\begin{aligned} \Delta _{{\mathcal {M}}} f=\text {div}\left( \text {grad} f\right) , \end{aligned}$$

(1)

where grad f is the gradient vector field of f and divf is the divergence operator of f on the manifold. The LBO is a linear differential operator and can be calculated in local coordinates. The Laplacian eigenvalue equation is considered as follows

$$\begin{aligned} \Delta _{{\mathcal {M}}}{\varvec{\phi }}=\lambda {\varvec{\phi }}, \end{aligned}$$

(2)

where $\lambda$ representing the eigenvalues of $\Delta$, these values constitute a discrete non-negative set and they are ordered as $\lambda _0=0<\lambda _1<\lambda _2<\cdots <\lambda _{n-1}$; the solution is called eigenfunctions of $\Delta$ corresponding to the scalars $\lambda$. For each normalized eigenfunction $\Phi _i$ corresponds one eigenvalue $\lambda _i$.

For all the n vertices ${\mathcal {S}}=\left( s_1,s_2,\ldots ,s_n\right)$ of a mesh, the Laplace–Beltrami matrix L is symmetric, semi-positive definite and its spectral decomposition is given by

$$\begin{aligned} L=\Phi \Lambda \Phi ^\mathrm{T}, \end{aligned}$$

(3)

where $\Lambda$ is the matrix of eigenvalues with $\lambda _n=\mathrm{diag}\left( \Lambda \right)$.

Fig. 2

Wave distribution over time scale. The colors range from blue (low values) to red (high values). The wave values on every point on the shape change according to the energy parameter in WKS$\left( s,e\right)$ (color figure online)

2.2 Wave kernel signature

The wave kernel process over the surface ${\mathcal {M}}$ is governed by the Schrödinger equation defined as

$$\begin{aligned} \frac{\partial {u}}{\partial {t}}\left( s,t\right) =i\Delta _{\mathcal {M}}\psi _E\left( s,t\right) , \end{aligned}$$

(4)

where $\Delta _{\mathcal {M}}$ is the LBO of ${\mathcal {M}}$ and $\psi _E\left( s,t\right)$ is the solution of Schrödinger equation. $\psi _E\left( s,t\right)$ describes the evolution of a quantum particle with unknown position on the surface ${\mathcal {M}}$ that can expressed in the spectral domain by

$$\begin{aligned} \psi _E\left( s,t\right) =\sum _{k=0}^{\infty }{e}^{i\lambda _{k}t}{\varvec{\phi }}_{k}f_E\left( \lambda _k\right) , \end{aligned}$$

(5)

where E denotes the energy of the particle at time $t=0$, $f_E$ expresses the initial distribution of energy, $\lambda _k$ is the kth eigenvalue and ${\varvec{\phi }}_k$ is the kth eigenvector’s entry associated to one point. $|\psi _E\left( s,t\right) |^2$ is the probability to find a particle of energy level E at point $s\in {\mathcal {M}}$ [2, 20]. The energies are directly related to the eigenvalues of the LBO, which implies $\lambda _k=E_k$. The reason is simply behind the replacement of the time parameter in (5) by energy. The wave kernel signature at a point s on the mesh is then defined in the logarithmic scale $e_k$ by

$$\begin{aligned} \mathrm{WKS}\left( s,e\right) =C_e\sum _k{\varvec{\phi }}_{k}^2\left( s\right) e^\frac{-\,\left( e-\mathrm{log}\left( {E}_k\right) \right) ^2}{2\sigma ^2}, \end{aligned}$$

(6)

with $C_e=\frac{1}{\sum _{k}e^\frac{-\left( e-\mathrm{log}\left( {E}_k\right) \right) ^2}{2\sigma ^2}}$ is a normalization constant, while $\sigma$ is the variance of the wave distribution.

Fig. 3

Wave kernel signatures at three different points. Note that the wave distribution over time corresponds to the behavior shown in Fig. 2

Fig. 4

Displacement of swarms in particle swarm optimization

By confining the wave kernel into a logarithmic energy scale domain and fixing the spatial variables, we can obtain the wave propagation in energy scale for each point s on the manifold by computing WKS$\left( s,e\right)$. We present in Fig. 2 an example of wave propagation over energy scale on the right hand shape, as well as the wave distribution for three different points on the mesh in Fig. 3. Aubry et al. [2] formally proved that the wave kernel signature is isometric invariant, scale invariant, informative, multi-scale, and stable against perturbations of the surface, but at the same time tends to generate noisier matches [20].

Fig. 5

Flowchart of the proposed method

2.3 Introduction to SPSO and MPSO

A graphical explanation of SPSO’s operation is depicted in Fig. 4. Let N be the number of particles in a swarm population. Each individual particle $\mathbf{X } _i$ may represent a possible solution for optimization problems in a d-dimensional space carrying position vector ${\varvec{x}}_i=\lbrace {x}_{i1},x_{i2},\ldots ,x_{id}\rbrace$ and velocity vector ${\varvec{v}}_i=\lbrace {v}_{i1},v_{i2},\ldots ,v_{id}\rbrace$, where $i=1,2,\ldots ,N$, randomly initialized in the search space. During the tth iteration, the next velocity and direction vector of the ith particle ${\varvec{v}}_i\left( t\right)$ are determined by its current vector ${\varvec{v}}_i\left( t-1\right)$, its best previous position ${\varvec{p}}_i$, and the global best position ${\varvec{p}}_g$ obtained by any other particles in the population at iteration t, updating by formula (7) and position vector is updated by formula (8)

$$\begin{aligned} \begin{aligned} {\varvec{v}}_i\left( t+1\right)&=\omega \cdot {\varvec{v}}_i \left( t\right) +c_1\cdot {\varvec{\varphi }}_{1}\left( t\right) \left( {\varvec{p}}_i-{\varvec{x}}_i\left( t\right) \right) ^\mathrm{T}\\ {}&\quad +\,c_2\cdot {\varvec{\varphi }}_2\left( t\right) \left( {\varvec{p}}_g-{\varvec{x}}_i\left( t\right) \right) ^\mathrm{T}, \end{aligned} \end{aligned}$$

(7)

$$\begin{aligned} {\varvec{x}}_i\left( t+1\right) ={\varvec{x}}_i\left( t\right) +{\varvec{v}}_i\left( t+1\right) , \end{aligned}$$

(8)

where $\omega$ is the fixed inertia weight and controls the exploration search, $c_1$ and $c_2$ are the acceleration factors, t is the current iteration number, ${\varvec{\varphi }}_1\left( t\right)$ and ${\varvec{\varphi }}_2\left( t\right)$ are random vectors in the range [0, 1], formulated by

$$\begin{aligned} \begin{aligned} {\varvec{\varphi }}_1\left( t\right) =\lbrace \varphi _{11}\left( t\right) ,\varphi _{12}\left( t\right) ,\ldots ,\varphi _{1d}\left( t\right) \rbrace \\ {\varvec{\varphi }}_2\left( t\right) =\lbrace \varphi _{21}\left( t\right) ,\varphi _{22}\left( t\right) ,\ldots ,\varphi _{2d}\left( t\right) \rbrace \end{aligned} \end{aligned}$$

(9)

The personal best position is defined using formula

$$\begin{aligned} {\varvec{p}}_i\left( t+1\right) =\left\{ \begin{array}{ll} {\varvec{p}}_i\left( t\right) &{}\quad \mathrm{if}\quad f\left( {\varvec{x}}_i\right) >f\left( {\varvec{p}}_i\left( t\right) \right) \\ {\varvec{x}}_i\left( t+1\right) &{}\quad \mathrm{if}\quad f\left( {\varvec{x}}_i\right) \le {f}\left( {\varvec{p}}_i\left( t\right) \right) , \end{array}\right. \end{aligned}$$

(10)

and the global best position is defined as

$$\begin{aligned} {\varvec{p}}_g\left( t+1\right) =\arg \min _{{\varvec{p}}_i}f\left( {\varvec{p}}_i\left( t+1\right) \right) ,\quad 1\le {i}\le {N}. \end{aligned}$$

(11)

Interestingly in MPSO, the fixed inertia weight, which was used in SPSO, has been replaced by another evolutionary parameter. In fact, during initial exploration, a large inertia weight factor is used and gradually reduced as the search progresses. We define the concept of time-varying process of this inertial weight by $\omega ^\mathrm{iter}=\left( \omega _\mathrm{max}-\omega _\mathrm{min}\right) \times \frac{\mathrm{iter}_\mathrm{max}-\mathrm{iter}_\mathrm{min}}{\mathrm{iter}_\mathrm{max}}+\omega _\mathrm{min}$, where $\mathrm{iter}_\mathrm{max}$ is the number of maximum iterations.

3 OWKS-based shape recognition concept

In this section, we introduce the idea of optimizing the wave kernel signature using MPSO. The overall illustration of our framework is presented in Fig. 5 and is detailed in the following steps:

• Step 1 Computation of the Laplacian matrix L, using [21].

• Step 2 Spectral decomposition of L.

• Step 3 Invoking MPSO to search a new value instead of the considered fixed value $\alpha =7$ as done in [2]. This is equivalent to finding the global optimum value of the variance $\sigma _\mathrm{opt}$ along all iterations so that $\sigma _\mathrm{opt}=\alpha _j\delta$, where the linear increment $\delta$ in e is $\delta =\frac{e_\mathrm{max}-e_\mathrm{min}}{M}$. The values of e ranging from $e_\mathrm{min}=\mathrm{log}\left( E_1\right)$ to $e_\mathrm{max}=\frac{\mathrm{log}\left( E_k\right) }{1.02}$; $k=300$ eigen-decomposition pairs of L and $M=100$ is the number of evaluated values of WKS.

• Step 4 Let $S_{1}$ and $S_2$ be two shapes to be compared. Two matrices WKS$_{S_1}$ and WKS$_{S_2}$, each one is of size equal to $\left( n\times {M}\right)$, are constructed. These two matrices are the descriptors that are being optimized. At this stage, we are merely interested to extract the first finite-dimensional vector from each matrix for representing and characterizing each shape in a compact and in an intelligent way. WKS$_{S_1}\left( s_n,e_1\right)$ and WKS$_{S_2}\left( s_n,e_1\right)$ are these vectors both of size equal to $\left( n\times {1}\right)$. This means, in particular, that we consider the necessity of extracting them from the first energy scale $e=e_1$ over M aiming to identify a few significant salient points on the shape. Because the first feature vector extracted from each OWKS corresponds to the low frequencies of the mesh, whose small energy corresponds to properties induced by the global geometry. Note that the extrema of this vector are considered as main salient points. On the other side, when we choose $e>e_1$, the interest points detection’s algorithm creates scatter and insignificant salient points on the mesh. $H_{1}$ and $H_2$ represent the normalized histograms of those vectors, and they have $b=10$ bins. Let i be the index of bins into the histograms. We are now ready to compare these histograms; we calculate the global best solution, on minimizing a certain objective function. The fitness function proposed for MPSO algorithm is the mean square error (MSE) between two shapes distributions and that expresses, via a corresponding value, how well both of them match. The above insights in this step have to be reiterated in a systematic way to finally find the optimized value of the variance parameter that yields to obtain the proper OWKS descriptor for a class of shapes. MSE is calculated by the following equation

  $$\begin{aligned} \hbox {MSE}=\hbox {Fitness}=\dfrac{1}{b}\sum _{i=1}^b{\mathcal {H}}_i^2, \end{aligned}$$

  (12)

  where ${\mathcal {H}}\left( i\right) =H_{1}\left( i\right) -H_2\left( i\right)$ is the difference between two distributions on the shape converted into histograms. This fitness function is thus proposed to find the better solution in a minimum computation time (to accelerate the convergence of MPSO) and accuracy.

Still referring to Fig. 5, we briefly detail the bottom part of the remain flowchart. Once OWKS of two shapes are computed (this instruction would be repeated for the whole database by considering a chosen reference model), files are registered such that each one contains only the first vector for the corresponding optimized shape descriptor. These files are then loaded automatically to the workspace of MATLAB by coupling C++ with MATLAB environment. The data vectors are now available to be assessed relying on the computation of a dissimilarity measure between pairs of 3D shapes in the database. $\ell _1$-distance, also known as city-block metric or Manhattan, which gives numerical results that express how well each pair of 3D shapes match.

Unlike WKS, our optimized descriptor can be applied to better identify, distinguish and differentiate between the salient feature points detected on the shape under condition that we choose the first vector of OWKS descriptor which corresponds to the first energy scale $e=e_1$. We thus adopt the OWKS method proposed in this paper to detect a set of key-points on a 3D shape as the local maxima of the function OWKS$\left( s,e_1\right)$. In practice, to find the feature points on the mesh, we proclaim a point s as a key-point if OWKS$\left( s,e_1\right) >\hbox {OWKS}\left( s_n,e_1\right)$ for all $s_n$ in the two ring neighborhood of s. Almost a similar observation is mentioned in [1].

To summarize, our OWKS descriptor encompasses highly valuable properties which are: as local shape descriptor, the OWKS is isometry-invariant (two isometric shapes have equal OWKS), and thus captures local features since its vector-mapping on the shape is selected at the first energy scale $e_1$ to pick up only sharp edges.

4 Experimental results

To evaluate the performance of our OWKS framework, we present qualitative and quantitative extensive results for non-rigid shape classification, matching and retrieval. The effectiveness of our approach is validated by carrying out a comprehensive comparison with several state-of-the-art methods.

4.1 Experimental settings

MPSO depends on factors such as the swarm size, number of iterations, inertia weight factor and some other parameters that determine its behavior. The recommended parameters values of MPSO are tabulated in Table 1. These values were selected and validated through several trials in reference to several works focusing on the convergence analysis of the MPSO variants and are then fine-tuned considering few shaded conditions. This is also in order to speed up the convergence, to reach the best possible solution and to give result in faster CPU time [18]. Then, they are involved within MPSO to find the globally optimized parameter for WKS. It means that the precise choice of MPSO parameters allows MPSO itself to achieve its satisfactory performance and, thereafter, for readily obtaining the OWKS descriptor. As a result, Table 2 compares the average computational time of the OWKS against WKS for some models shown in the paper.

Table 1 Recommended parameter values for MPSO

Table 2 Time for WKS and OWKS computations on a computer with 2 GHz 2 Duo CPU and 3G RAM

4.1.1 Dataset

The performance of the proposed framework is tested for three different tasks, i.e., for features classification, shapes classification and shapes matching; as well as it is evaluated on a recent challenging SHREC: we use SHREC 2015 3D shape database [22], which contains 1200 3D watertight triangle meshes that are derived from 50 categories, where each category contains 24 objects with distinct postures. Each shape in the dataset has approximately n = 9400 vertices. Sample shapes from this benchmark are shown in Fig. 6. This large-scale database is also freely available at http://www.icst.pku.edu.cn/zlian/shrec15-non-rigid/.

Fig. 6

Sample shapes from SHREC-2015 dataset

4.2 Features classification

We emphasize the superiority of our proposed OWKS over the non-optimized WKS in features classification. When constructing OWKS, we refer to MPSO as described in Sect. 3, in order to pick up the suitable value ${\widehat{\alpha }}_\mathrm{opt}$. In fact, this value is obtained on an average of many experiments. We note from Fig. 7a that this algorithm converges rapidly to an optimal mean value ${\widehat{\alpha }}_\mathrm{opt}$ for the Armadillo class from the 28th generation with a mean square error rate nearly equal to $10^{-3}$ as plotted in Fig. 7b. The algorithm tends to minimize the fitness function and therefore the distance between histograms and then to increase the matching accuracy. In the case of changing the model, the parameter is likewise changed as shown in Table 3.

Fig. 7

Top: Feature points detected on the four poses of the Armadillo. a, b Evolution of MPSO to determine a precise value of ${\widehat{\alpha }}_\mathrm{opt}$ , and the attempts to minimize the distance between the shapes to be effectively recognized. c, d Classical MDS embedding of the feature points based on their OWKS at the first time scale. The color of each point projected on the 2D plan corresponds to the pose from which it is taken. a Searching for ${\widehat{\alpha }}_\mathrm{opt}$, b fitness function evolution, c $\alpha =7$, d ${\widehat{\alpha }}_\mathrm{opt}=14.03$ (color figure online)

The method of detecting the salient feature points is likewise adopted to obtain the key-points on the shapes. It can be seen from the top of Fig. 7 that the same number of interest points is detected equal to 7, for each pose. This figure proves the effectiveness, the precision and the consistency of our method to detect repeated structure within a collection of poses belonging to the same class of shapes, such as the head, the hands and the feet. Figure 7c, d presents a comparative example between the classification of all 28 feature points embedded in ${\mathbb {R}}^2$ which are derived from the first vector of the classical WKS and the OWKS, respectively. This latter descriptor tends not only to maximize large between-class scatter but also to minimize the within-class scatter and therefore is well suited for handling features.

Table 3 Evaluation of the recognition parameters

4.3 Shapes classification

The classification for six selected shape classes from the database is also illustrated in Fig. 8, which clearly illustrates the OWKS’s ability to maximize extra-class distances, thus ensuring a better separability. Remarkably, the WKS descriptor failed to make an accurate classification, almost all models are clustered together. Differently, we observe that our method can distinguish models belonging to different categories well. OWKS-based shape classification is likewise an asset to approximate between the shapes that nearly having the same features. For instance, the classical MDS embedding shows that the classification result is almost alike for the Man and the Woman class against the Centaur’s class. In other words, since the Centaur is a half human shape, it is very logical that both classes of the Man and the Woman are the closest to the Centaur’s class, and vice versa. To validate our method further, all these observations and findings are confirmed by the calculation of the extra- and intra-class distances in Table 4.

Fig. 8

Shapes classification result. Classical MDS embedding of shape similarities as computed using, from left to right, the standard WKS and the OWKS, respectively

Table 4 Comparaison between intra-class and extra-class distances before and after the invocation of MPSO for the woman category

4.4 Global shape matching and retrieval

4.4.1 Matching performance

We propose to use the $\ell _1$-distance to compare a reference shape to all the objects in the database. The performance of the proposed framework is also evaluated on the challenging benchmark SHREC-2015 database. Actually, each given query is compared to the other shapes that exist in the database in an effort to find the most closest shapes to the query. To validate our method, an example of the top 6 matches returned for a complete Spectacle and Octopus query by OWKS, WKS, GPS and HKS methods is shown in Table 5. Remarkably in this table, except our approach that returns correct results, the WKS, GPS, and HKS methods yield poor retrieval results.

Table 5 Retrieval results for a complete query-shaped spectacle and octopus models by our algorithm, WKS, GPS and HKS

Table 6 Matching results under SHREC-2015 dataset before and after optimizing WKS. Each shape is matched against all the other shapes in the database. Each cell shows the dissimilarity measure between two shapes selected from the database. The smallest value corresponds to the correct match

As shown in Table 6, the proposed approach is effective and yields correct matching results. The matching performance of the proposed approach is evaluated by performing a pairwise comparison between the OWKS$\left( s,e_1\right)$ vector of a given query and all the OWKS$\left( s,e_1\right)$ vectors of the shapes in the SHREC-2015 dataset using the $\ell _1$-distance, and then finding the closest shape to the query. Shapes belonging to the same category have very weak values for the OWKS descriptor, where a low value (displayed in boldface) corresponds to the correct match when compared to the WKS. Again we show that the proposed approach decreases the value of the $\ell _1$-distance between the Centaur class and the Woman class. However, it increases this value between the Woman class and the two classes of Hand and Bird. It means, in particular, that the use of MPSO beside WKS tends to rearrange classes such that the distance between the most similar classes takes the smallest value of the $\ell _1$-distance. Let us take the example of the Women-Centaurs classes before the introduction of MPSO: they are very far apart although they should be more similar because when using OWKS, these two classes come closer, which better corresponds to reality.

4.4.2 Retrieval evaluation results

We adopt the standard measures for shape retrieval using code from [22]. The proposed OWKS descriptor is comprehensively evaluated using six commonly used evaluation metrics: we show Precision/Recall (P/R) curves, and tabled values for nearest neighbor (NN), First-Tier (FT), Second-Tier (ST), E-Measure (E) and Discounted Cumulative Gain (DCG).

Firstly, to evaluate the retrieval performance of the proposed method, we computed the dissimilarity matrix between all the first feature vectors extracted from each OWKS of the shapes in the SHREC-2015 dataset using $\ell _1$-distance. We portrayed P/R curves of OWKS against several baseline methods in Fig. 9. It can be seen that the OWKS descriptor outperforms the baseline approaches (see [22] and references therein) for surface area (SA), HKS, WKS, multi-feature, time series analysis for shape retrieval (TSASR), sphere intersection descriptor (SID), geodesic distance distribution (SNU), spectral geometry (SG) and Fisher vector encoding framework-heat kernel signature (FVF-HKS). OWKS is therefore more relevant and more discriminative.

Fig. 9

Overall average P/R curves of our method (OWKS) against other approaches evaluated under SHREC-2015 dataset

Then, the five performance criteria, i.e., NN, FT, ST, E and DCG, are employed to evaluate OWKS under SHREC-2015 dataset in global shape retrieval tasks. The results are summarized in Table 7, which shows the scores of the evaluation metrics for the proposed framework and the baseline methods. As can be seen in this table, the proposed OWKS obtains better results. For instance, in terms of the NN metric, the OWKS achieves a 96.9% score, with performance improvements of 0.9 and 3.3% over the best performing baselines FVF-HKS and SG, respectively. In addition, OWKS outperforms the SID approach by 17.4% in NN, 24.8% in FT, 19.6% in ST, 19.7% in E and 15.8% in DCG. This better performance is likewise consistent with all the retrieval evaluation metrics.

For fair comparison, we compared OWKS to baseline methods of the same category (i.e., BoF-based methods). In addition, sparse coding-based approaches generally suffer from the long running time especially for constructing the Laplacian matrix and solving eigenpairs. Although SPH-SparseCoding, HAPT and SV-LSF [22] perform slightly better than OWKS, the proposed framework consistently outperforms the baseline methods in most cases, as evidenced by our experimental results.

Table 7 Comparison of retrieval results of our method (last row) with the state-of-the-art on the SHREC-2015 dataset

5 Conclusions and future work

In this paper, we proposed an optimized descriptor method for the 3D shape matching and retrieval called OWKS. The experimental results indicate that the strengthening of WKS descriptor with optimized variance parameter using MPSO achieves better performances compared with state-of-the-art retrieval methods. The effectiveness and the usefulness of our method was demonstrated on the SHREC-2015 dataset for computing shape matching and discriminate between shapes in retrieval tasks. In our ongoing research, we would like to extend our approach to partial matching and retrieval using strongly denatured 3D objects.