1 Introduction

Medical imaging is one of the most important tools among the healthcare community, not only for the record storing and visual documentation, but also for information extraction of many diseases. We can extract great valuable information and make useful history which helps us in treatment and healing by tracking the disease progress of the patient [1]. Diabetic retinopathy, hypertension, macular degeneration, hemorrhages, neovascularization, glaucoma, and vein occlusion are among the diseases that can be discovered early by analyzing the retinal images, using one of these tools before involving in critical stages that may be lead to blindness [1, 14, 15]. Analysis of the retinal blood vessels structure in such diseases can lead us to ensure the presence of the disease or not [15]. Performing such task manually is considered as a major obstacle because it has many disadvantages such as prone to human error and wasting time due to the vast amount of images and vessel structure complication [15]. So an accurate automated retinal blood vessel segmentation technique is needed to detect the retinal blood vessels perimeter and area or determine the optic disk shape [14].

Roychowdhury et al. [15] proposed unsupervised vessel segmentation method. The negative green plane image was initially reconstructed by using top-hat reconstruction, and then global thresholding was performed to segment the vessels. The resulted image was iteratively forced in adaptive thresholding to identify new vessel pixels. The new vessels were region grown to enhance the vasculature. The power point in this method is the stopping criterion at a higher level accuracy of 94.9%. Another method for vessel segmentation was presented in [12] that was based on threshold algorithm. An important preprocessing phase that used green and red channels of the fundus images was performed to prevent uniform illumination. Then, 2D Gabor filtering was performed in four different orientations to get a normalized image. Global thresholding was performed based on the structural properties of the vessel candidates to extract the large and thin vessels correctly. This method achieved an accuracy of 94.81%. The authors of this paper presented another approach in [7]. This approach achieved an accuracy of 96.25%. Other many algorithms have been proposed for vessel segmentation. However, in many real situations, issues such as high computation of a large dataset, poor contrast, and high illumination make the vessel segmentation a difficult problem [3]. To overtake most of these challenges, a hybrid method of whale optimization algorithm (WOA) along with multilevel thresholding has been performed in this paper to segment the vessels.

The rest of this paper is organized as followed: Sect. 2 presents the problem formulation of multilevel thresholding image segmentation-based WOA. Section 3 explains the concepts of image thresholding and the whale optimization algorithm. Section 4 describes in detail the phases of our proposed multilevel retinal blood vessel segmentation approach based on WOA. Section 5 shows and discusses the applied experimental results and and compares them with the alternative approaches. Finally, Sect. 6 concludes the overview of the paper.

2 Problem formulation of multilevel thresholding image segmentation-based whale optimization algorithm

Thresholding-based segmentation method is used to extract some region from its background by selecting an intensity value \(T_\mathrm{(threshold)}\) that would be used as a constant prior. A pixel is classified as a region point or a background point based on this constant value. Each pixel in the image that has intensity value less than \(T_\mathrm{(threshold)}\) is replaced with a black pixel and vice versa, and each pixel that has intensity value greater than \(T_\mathrm{(threshold)}\) is replaced with a white pixel [8]. Thresholding techniques are categorized into two types: property-based thresholding methods [16] and optimal thresholding methods [8]. Property-based thresholding technique deals with histogram; it measures some selected property to detect the thresholds. It is the better solution for multilevel thresholding because of its speed, but it has some disadvantage of determining disability of some threshold values. On the other hand, optimal thresholding technique optimizes some objective functions [16]. From another view, there are two types of thresholding techniques which are bi-level and multilevel according to segments number of the image. Bi-level thresholding is proposed in several algorithms to binaries an image [8]. Moreover, by the presence of some certain value T, the pixels with values greater than T are classified as an object and the pixels with values lesser than T are classified as a background. Other algorithms turn bi-level thresholding to be an optimization problem to search for the threshold t that maximizes \(\sigma _B ^2\) and minimizes \(\sigma _w ^2 \) [8]. For two-level thresholding, we try to search for \(T^*\) that achieves max \( \sigma _B^2(T^*)\) where 0 \(\le T^*< L\) and L is the maximum intensity value. This problem can be modeled as n-level thresholding through satisfying max \(\sigma _B^2 (T_1^* , T_2^* ,\ldots , T_{n-1}^*)\) such that \(0 \le T_1^*< T_2^*< \cdots< T_{n-1} ^* <L\). To reach the optimal values of thresholds, an exhaustive search could be applied. The exhaustive search can be implemented basing on the Otsu criterion that is simple, but it has a disadvantage of expensive computation as shown in [8]. Based on applying the exhaustive search for \(n{-}1\) optimal thresholds, there are \(n(L{-}n+1)^{n-1}\) combination of thresholds [8]. Therefore, this method is not suitable because of its high-cost computations. However, this problem can be modeled as a multidimensional optimization problem which searches for a set of thresholds that maximize the between-class variance. Whale optimization algorithm (WOA) is used in this paper as a maximization optimization technique to find these multilevel thresholds.

3 Preliminaries: Image thresholding and the whale optimization algorithm

3.1 Multithresholding

We usually try to find more efficient ways to perform image analysis. One of these ways is multilevel thresholding segmentation technique which has a problem of selecting the optimum n-level threshold in image segmentation automatically. In this section, more accurate formulation of this problem with some basic notation is introduced. If we assume that there are L intensity levels for each (red, green, blue) RGB channels of a given fundus image and the levels are in the range of 0, 1, 2 ,..., \(L{-}\)1, then we can define the probability distribution as:

$$\begin{aligned} P^{C}_{i}= \frac{S^{C}_{i}}{N}, \sum _{i=1 ,C=\{ R,G,B \} }^{N} {P^{C}_{i}}=1 \end{aligned}$$
(1)

where the number of a specific intensity level is donated by i, that ranges from 0 to \(L{-}\)1. C is the image channel, i.e., \(C={R,G,B}\), and the total number of pixels in the fundus image is represented by N. \(S_{i}^{C}\) represents the pixels count for specific level of intensity i in the channel C. The histogram of image for each C-channel is represented by \(S_{i}^{C}\). Based on all of these assumptions, the total mean of each image channel can be formulated as following:

$$\begin{aligned} \mu _T^C= & {} \sum _{i=1 , C= \{R,G,B \}}^L {i P_i ^C} \end{aligned}$$
(2)
$$\begin{aligned} F^C (x,y)= & {} {\left\{ \begin{array}{ll} 0 &{}\quad {f^C (x,y) \le {t_1^C} } \\ \frac{1}{2} \left( t_1^C + t_2^C \right) &{}\quad t_1^C< f^C(x,y) \le { t_2^C} \\ &{} . \\ &{} . \\ \frac{1}{2} { \left( t_{n-2}^C + t_{n-1}^C \right) } &{}\quad t_{n-2}^C < f^C(x,y) \le t_{n-1}^C \\ L &{}\quad f^C(x,y) > t_{n-1}^C \end{array}\right. } \end{aligned}$$
(3)

Such \(f^C(x,y)\) is the pixel within x width and y height of the image with a width (W) and a height (H). So all pixels of a given fundus image will be portioned into a number of classes n denoted by \( B_1^C ,\ldots ,B_n^C \) which may define features for one object or different multiple objects. Obtaining the optimal threshold levels values on the fundus image can be performed by maximizing the variance between any two classes, defining by:

$$\begin{aligned} \sigma _B ^{C^2}= \sum _{j=1,C\{R,G,B\}}^n {O_j^C \left( \mu _j^C - \mu _T^C \right) } \end{aligned}$$
(4)

where j represents specific class from n classes, \( \mu _j^C\) and \(O_j^C\) are the mean and the probability of occurrences, respectively, and the probability of occurrences \(O_j^C\) of n classes \(B_1^C , B_n^C\) can be modeled as following:

$$\begin{aligned} O^C_j = {\left\{ \begin{array}{ll} \sum \nolimits _{i=1,C= \{R,G,B\} }^{t_j^C} P_i^C &{}\quad j=1 \\ \sum \nolimits _{i={t_{j-1}^C+1},C=\{R,G,B\}}^{t_j^C} P_i^C &{}\quad 1<j<n \\ \sum \nolimits _{i={t_{j-1}^C+1},C=\{R,G,B\}}^{L} P_i^C &{}\quad j=n \end{array}\right. } \end{aligned}$$
(5)

\(\mu _j^C\) (the mean for each class) can be computed as:

$$\begin{aligned} \mu _j^C = {\left\{ \begin{array}{ll} \sum \nolimits _{i=1,C= \{R,G,B\} }^{t_j^C} \frac{iP_i^C}{O_j^C} &{}\quad j=1 \\ \sum \nolimits _{i={t_{j-1}^C+1},C=\{R,G,B\}}^{t_j^C} \frac{iP_i^C}{O_j^C} &{}\quad 1<j<n \\ \sum \nolimits _{i={t_{j-1}^C+1},C=\{R,G,B\}}^{L}\frac{iP_i^C}{O_j^C} &{}\quad j=n \end{array}\right. } \end{aligned}$$
(6)

3.2 Whale optimization algorithm (WOA)

Whale optimization algorithm is one of the latest optimization techniques. It is proposed by Mirjalili and Lewis [11]. Its mechanism is to mimic the social behavior of humpback whales on their journey to hunt their prey by following its location and encircle it. In the search space, the optimal position is not known a priori, so WOA initially considers the current best candidate solution as the target prey or is near to the optimum until the optimum solution is defined. The other search space agents update their positions according to the current optimum value. The following equations show this behavior:

$$\begin{aligned}&\overrightarrow{D}=\mid \overrightarrow{C}. \overrightarrow{X}^{*}(t) - \overrightarrow{X}(t) \mid \end{aligned}$$
(7)
$$\begin{aligned}&\overrightarrow{X}(t+1) = \overrightarrow{X}^{*}(t) - \overrightarrow{A} . \overrightarrow{D} \end{aligned}$$
(8)

The current iteration is denoted as t. \(\overrightarrow{A} \) and \(\overrightarrow{C}\) are coefficient vectors. The best obtained solution position vector is denoted as \(\overrightarrow{X}^{*} \). In each iteration, \(\overrightarrow{X}^{*} \) could be updated according to the better solution results. The coefficient vectors \(\overrightarrow{A} \) and \(\overrightarrow{C}\) are calculated by the following equations:

$$\begin{aligned}&\overrightarrow{A}= 2 \overrightarrow{a}\overrightarrow{r} - \overrightarrow{a} \end{aligned}$$
(9)
$$\begin{aligned}&\overrightarrow{C}= 2\overrightarrow{r} \end{aligned}$$
(10)

To control the exploration and exploitation, \(\overrightarrow{a}\) vector is used. It is linearly decreased over the iterations from 2 to 0. \(\overrightarrow{r}\) is a random vector ranging from 0 to 1, and its task is to make each agent in the search space reaching any position and thus ensure the exploration. Therefore, Eq. (8) makes any agent in search space update its position according to the current best solution and achieve the simulation of encircling the prey.

There is another behavior of humpback whales hunting which is the bubble-net strategy. It represents the exploitation phase in the algorithm. These two following approaches can model it:

  • Shrinking encircling mechanism: This behavior is performed by decreasing the value of \(\overrightarrow{A}\) which in turn is decreased by decreasing the value of \(\overrightarrow{a}\) in Eq. (9). It can be said that \(\overrightarrow{A} \) is a random value ranging from -a to a where a has a value decreasing from 2 to 0 over the iterations. The agent in search space updates its value with a new one between the original position and the position of the current best agent.

  • Spiral updating position: This technique firstly measures the distance between the whale position (the agent position in the search space) and the prey position (the current best solution). Then a spiral equation is modeled between both the whale and the prey position to imitate the humpback whales on their helix-shaped movement. The equation is formulated as following:

    $$\begin{aligned} \overrightarrow{X}(t+1) = \overrightarrow{D'}. e^\mathrm{bl}\cdot \mathrm{cos}(2 \pi l) + \overrightarrow{ X^{*} }(t) \end{aligned}$$
    (11)

    where \(\overrightarrow{D}\) is the distance between the ith whale and the prey, b represents the shape of a spiral, and l is a random value ranging from −1 to 1.

On the “humpback whales path” to swoop the prey, they simultaneously take either a shrinking circle or a spiral-shaped path. So, to add more biomimicry to the algorithm, there is a probability of 50% to select between the shrinking encircling mechanism or the spiral model while updating the whales position. Equation (12) mathematically models this idea as following:

$$\begin{aligned} \overrightarrow{ X^{*} }(t+1)\!=\!{\left\{ \begin{array}{ll}\overrightarrow{ X^{*} }(t) \!-\! \overrightarrow{A}.\overrightarrow{D} &{} if\quad P \!<\! 0.5 \\ \overrightarrow{D'}. e^{bl}\cdot \mathrm{cos}(2 \pi l) \!+\! \overrightarrow{ X^{*} }(t)&{} if \quad P \!\ge \!0.5 \end{array}\right. }\nonumber \\ \end{aligned}$$
(12)

To guarantee exploration of algorithm, \(\overrightarrow{A} \) is used with random values that are less than −1 or greater than 1 to make search agent moving far away from the reference whale. Then the search agent position is updated according to the chosen best search agent for the current iteration. So when the value of \(\overrightarrow{A}\) is greater than 1, this means that the algorithm is still in the exploration state. Equation (13) and (14) show the mathematical model as following:

$$\begin{aligned}&\overrightarrow{D}\,=\,\mid \overrightarrow{C}.\overrightarrow{X_\mathrm{rand}} - \overrightarrow{X} \mid \end{aligned}$$
(13)
$$\begin{aligned}&\overrightarrow{X}(t+1) = \overrightarrow{X_\mathrm{rand}} - \overrightarrow{A}.\overrightarrow{D} \end{aligned}$$
(14)

where \(\overrightarrow{X_\mathrm{rand}}\) is a random whale (random position vector) that is chosen from the current population.

4 The proposed multilevel retinal blood vessel segmentation approach-based whale optimization

The proposed multilevel retinal blood vessel segmentation approach (Multi-WOA)-based whale optimization consists of two main phases: (1) Preprocessing phase The brightness of the fundus images is enhanced before the segmentation, and (2) Segmentation phase Multilevel thresholding based on WOA is applied for segmentation to determine the \(n{-}1\) optimal n-level threshold on the fundus image. These two phases are described in detail in the following subsection along with the involved steps with the characteristics for each phase. The overall architecture of the proposed system is described in Fig. 1.

Fig. 1
figure 1

Architecture of the proposed segmentation model

Full size image

4.1 Preprocessing phase

The fundus image is enhanced by correcting the brightness as a facilitating step before segmentation. So the global mean gMean is measured for the whole retinal image, and then a large size window is passed over the image to ensure that the mean brightness inside the window wMean is commensurate with gMean. Equation (15) is modeled to calculate the new brightness pixel value that is centered inside the window.

$$\begin{aligned} PB= \frac{PB}{wMean} * gMean \end{aligned}$$
(15)

where PB represents the pixel brightness. The major preprocessing steps are described in Algorithm 1.

figure a

4.2 Multilevel retinal image segmentation phase

Instead of exhaustive search, WOA is used for finding the optimal threshold levels values. So our problem can be represented as an optimization problem to find the optimum thresholds \(t_j^C \) that maximizes the following objective function:

$$\begin{aligned} \eta ^C=\mathrm{max}_{1<t_1^C< \cdots<t_{n-1}^C<L} ( \sigma _B ^{C^2}(t_j^C)). \end{aligned}$$
(16)

Algorithm 2 illustrates the proposed method that starts with a random solution set. For each iteration, search agents’ positions are updated according to either randomly selected search agent (to guarantee the exploration) or the best obtained search agent (to guarantee exploitation). The parameter a decreases from 2 to 0 for more exploitation. If \(\mid \overrightarrow{A}\mid \ge 1\) is satisfied, a random search agent would be selected from search space. In contrast, if \( \mid \overrightarrow{A}\mid <1\) is satisfied, the best solution would be selected. Depending on p, the algorithm selects between the spiral or the circular movement.

figure b

5 Experimental results and discussion

The experiments were carried out to evaluate the performance of the proposed hybrid WOA with multithresholding for vessel segmentation.

5.1 Description of experimental data

Our algorithm was tested on datasets that were constructed based on real sample images from Bostan diagnostic center in Fayoum city, Egypt. Datasets contain 250 fundus images for patients with different ages ranging from 35 to 80 years. The fundus images were taken by a Canon CR5 non-mydriatic 3CCD camera at a 45-degree field of view. The examiner observer takes the color photographs with a single flash of white light. The images were stored as colored images with Tiff extension, with a size of 1504\(\times \)3100. Each image has three channels (red, green, and blue). Each channel has intensity value for pixels ranging from 0 to 255. The dataset contains 110 images for different healthy patients (normal cases) and 140 images for different unhealthy patients with diabetic retinopathy (abnormal cases). Abnormal cases are categorized into two classes moderate nonproliferative retinopathy (Moderate NPDR) (95 cases) and severe nonproliferative retinopathy (Severe NPDR) (45 cases). The presented multi-WOA image segmentation method was implemented in MATLAB on a computer with Core 3 Duo T5800 processor (2.00GHz) and 3GB of memory.

5.2 Performance measures

The known performance measures for vessel segmentation algorithms are the true positive (TP), the false positive (FP), the accuracy (ACC), sensitivity, and specificity. Accuracy is the sum of pixels that are correctly classified as vessels and the pixels that are erroneously classified as vessels divided on the all pixels number [14]. Sensitivity (SN) measures the algorithm ability for detecting the true vessels pixels. Specificity (SP) measures the algorithm ability for detecting non-vessels pixels. Table 1 illustrates these measures by equations.

Table 1 Performance measures for retinal vessel segmentation
Full size table

5.3 Parameters setting for WOA

WOA is considered as parameterized algorithm, so the parameter values must be firstly set as shown in Table 2. The selected parameters’ values of iteration number and population size are based on the conclusion of “the larger number of search agents and maximum iterations, the better approximation of the global optimum” [11] to reach with the algorithm for faster convergence with global optimum value. Any other different values will weaken the algorithm because they will focus on either exploration or exploitation [11].

Table 2 Parameters values for WOA implementation
Full size table

5.4 Experimental results

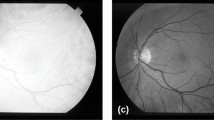
As mentioned before, the preprocessing phase has an important role in the segmentation results accuracy as it boosts the brightness homogeneous over the image while maintaining the contrast between vessels and the background. Figure 2 confirms this conclusion as it shows a sample image from the dataset in Fig. 2a with its limited segmented result in Fig. 2b, while its corresponding processed image in Fig. 2c, where brightness is corrected, enhances the structure of the segmented vessels with more important details as shown in Fig. 2d. Table 3 ensures this conclusion by illustrating the obtained accuracy for the first 20 images as a sample. When the problem dimension (the number of threshold levels) increases, WOA obtains more accurate and robust segmentation results to local solutions with little more time. The evaluation function was implemented against different threshold levels 2, 3, 4, and 5 as shown in Fig. 3. It can be noticed that by increasing the threshold level value, we get more accurate and detailed results. Table 4 also shows this conclusion; it illustrates the different accuracy values of the different threshold levels for the first seven test images, and it also shows the CPU processing time for these threshold levels. In other words, for higher threshold levels, WOA presents little higher CPU time than the previous threshold levels with more accurate results.

Fig. 2
figure 2

a Sample image from the database, b the vessel segmented image of a, c the preprocessed image and d the vessel segmented image of c

Full size image
Table 3 Accuracy, sensitivity, and specificity for the proposed retinal vessel segmentation model results
Full size table
Fig. 3
figure 3

The original image from dataset and the segmentation result with 2, 3, 4, 5 thresholds levels, respectively (from left to right)

Full size image
Table 4 The average CPU time and accuracy for different segmentation threshold levels
Full size table

5.5 Convergence analysis for the proposed hybrid WOA model against PSO

Convergence means that the algorithm has reached the optimum value (the whale caught its prey) and there are no more changes (stability state). The number of iterations has an important impact on the performance of the proposed model. In this section, the proposed model was tested with PSO instead of WOA. The iterations number effect on the best threshold level value and the convergence were tested for both WOA and PSO when the number of iterations ranged from 1 to 200. WOA has a high level of exploration [11], and this in turn allows it to roam all over the search space and prevents it from falling into local minima. However, WOA balances between the exploration and exploitation process [11], so it reached to the best value with a number of iterations less than PSO (75) as shown in Fig. 4 that illustrates the average best level thresholding value against the iterations number. On the other hand, PSO has more exploitation level that may make it falling in local minima [2], so WOA presents more power of both the exploration and exploitation speed. Depending on the number of iterations, we can judge on the convergence of our algorithm. When the number of iterations was increased, the thresholding level value became better until it reached an extent at which increasing the number of iterations has not an effect on the best threshold level value (see Fig. 4). Moreover, from this iteration number, it can be specified on the algorithm whose faster convergence. It can be noticed from Table 5 that both of WOA and PSO almost reached to the same best intensity threshold level value that is equal to 31 for our problem. However, WOA reached to stability from iteration 75, and PSO reached stability from iteration 200; so WOA has faster convergence than PSO with the same result of best threshold level value.

Fig. 4
figure 4

Convergence curve for WOA against PSO

Full size image
Table 5 Effect of the number of iterations on the performance of the proposed WOA method against PSO
Full size table

5.6 Proposed model against PSO and K-mean

In this section, a comparison was made between the proposed algorithm multi-WOA versus two previously proposed approaches [7] and [6] on the DRIVE dataset [13]. The proposed approach in [7] performed K-mean with mathematical morphology. All of its work concentrated on the preprocessing phase of mathematical morphology that targets to improve the vessels structure, but sometimes this model can not deal with the abnormal images. The second approach [6] applied PSO with multithresholding. It achieved better accuracy than the previous approach within the abnormal images as shown in Table 6, but there is a problem of locating thin vessels. The proposed approach in this paper improved the segmentation by targeting these small vessels; it achieved its robustness against changes in the input image as it was applied to different datasets with various conditions saving its accuracy regardless of whether the image of entry normal or abnormal with either exudates, hemorrhages, or micro-aneurysms. Table 6 shows that the proposed WOA system obtained the best accuracy over the other two systems.

Table 6 Proposed algorithm versus previously proposed methods on the DRIVE dataset
Full size table

5.7 Comparison with alternative methods

The performance of the proposed system multi-WOA was compared against the latest state-of-art systems on the DRIVE dataset. Table 7 shows this comparison. The proposed system performed very high accuracy comparing with other vessel segmentation methods in the literature. It saves the obtained accuracy with abnormal images and achieves accurate detailed segmentation results with tiny vessels, so it is a perfect choice for CAD systems that depends on vessel segmentation results with their estimations comparing with other alternative methods as it exceeds most of them in terms of overall accuracy.

Table 7 Proposed algorithm versus other methods on the DRIVE dataset
Full size table

6 Conclusions

In this paper, a hybrid vessel segmentation model multi-WOA in fundus images has been proposed. It is a combination of WOA with multithresholding. The obtained results have shown high accuracy when compared with the current state-of-the-art methods; they are identical comparing with the ground truth. The algorithm proves robust against the brightness problems, noise, and diseases symptoms such as hemorrhages, exudates, and micro-aneurysms. It was compared with other state-of- the-art confirming its efficiency.