1 Introduction

Image segmentation is an important step in many computer vision applications including image classification [1], visual tracking [2,3,4], gesture recognition [5], action recognition [6] and medical image analysis [7]. In the past few years, it has been attracting increasing attention and many new methods have been proposed in the literature [7,8,9,10], especially in the research of the algorithm of threshold segmentation. Such as, an image segmentation method based on fast automatic threshold selection is proposed by Singla in the literature [11]. The meaning of this algorithm is faster context–sensitive threshold selection. The advantage of this method is that it not only contains the image context information, but also does not lose the benefits of the histogram. The key of threshold image segmentation is the selection of a threshold value, which is the selection of the optimal threshold. Swarm intelligence algorithm has a great advantage in finding the optimal value. One kind of the representative swarm intelligent algorithms is artificial bee colony (ABC), which was first proposed by Turkey scholar Karaboga in 2005. It is a novel algorithm based on the swarm intelligence, optimization algorithm after the particle swarm algorithm, ant colony algorithm and artificial fish swarm algorithm, etc. The ABC algorithm was used to optimize multivariate function by Karaboga in 2007 [12]. The experimental results demonstrate that its performance is the best in comparison with genetic algorithm (GA) [13], particle swarm optimization (PSO) [14] and particle swarm evolutionary algorithm (PEA) [15].

With the development of quantum theory, quantum computation is introduced into the swarm intelligence algorithm which is more and more popular in recent years. Research of quantum computation is divided into two aspects. One is the design of new quantum algorithm, and the other is combination of quantum computation with the traditional calculation method. The idea of quantum computation introduced to the traditional intelligent algorithms is used to improve the performance of the traditional intelligent algorithms, for example improved quantum particle swarm optimization (IQPSO) [16], quantum ant colony algorithm (QACA) [17], quantum artificial fish swarm algorithm (QAFSA) and so on. At the same time, some scholars have also proposed quantum artificial bee colony (QABC). In order to improve the performance of the artificial bee colony optimization and to integrate the quantum computing model into the swarm optimization, a novel algorithm based on the quantum swarm optimization algorithm is proposed by Li et al. [18]. Compared with the basic algorithm, this one has a better optimization effect, but still cannot achieve satisfactory results.

Bloch sphere is geometry method for the binary system of pure state space representation to express more information with qubits. The performance of the algorithm is greatly improved by using the coding method based on the Bloch spherical surface to improve the artificial bee colony algorithm. The quantum bee colony optimization algorithm has been proposed by Yi et al. [19] using Bloch coordinates of quantum bit bee colony algorithm for food source. It expands the quantity of the global optimal solution and improves the bee colony algorithm to obtain the global optimal solution with probability. In this algorithm, the quantum rotation gate is used to realize the food source updating in the searching process of the bee colony algorithm. But the algorithm has some disadvantage which is the optimal path between two points of the minor in the spheres move and the optimal path is long enough to waste more time.

Above all, the improved method of applying quantum and space coordinates to the artificial bee colony algorithm is fewer in recent years. So an improved artificial bee colony algorithm is proposed in this paper, which combines the ability of “exploration” and “exploitation,” fastens convergence speed with strong searching ability. The algorithm encodes the initial nectar source using qubits space coordinates. And a novel method of updating and adjusting strategy of global optimal guidance is used in it. The improved algorithm is applied to the threshold segmentation of the standard images and the network image. The experimental results show that the improved algorithm can find the best segmentation threshold of the images, which can reflect the better threshold segmentation ability.

The rest of this paper is organized as follows. Section 2 summarizes the quantum artificial bee colony algorithm and the BQABC is proposed. BQABC is applied to image threshold segmentation in Sect. 3. Section 4 discusses the experimental results and analysis. Finally, the conclusion and prospect are drawn in Sect. 5.

2 Improved QABC algorithm based on Bloch sphere

2.1 The QABC algorithm

Quantum computation is a new calculation based on quantum theory [20]. In conventional computation, the basic unit of information is the bit, each of which is either “1” or “0,” while the smallest unit of information stores on a quantum computation is called a quantum bit (qubit). A qubit state is a two-dimensional complex space vector, it can be in the “1” state (denoted as \(|1{>}\), “0” state for the \(|0{>}\)), or in the intermediate state that constitutes a linear combination of the state \(|0{>}\) and \(|1{>}\)

$$\begin{aligned} |\phi \rangle =\alpha |0\rangle +\beta |1\rangle \end{aligned}$$
(1)

where \(\alpha \) and \(\beta \) are arbitrary complex numbers and meet the normalization requirements of the \(|\alpha |^2+|\beta |^2=1\), where the \(|\alpha |^2\)and the \(|\beta |^2\) give the probability of this in the superposition state of the quantum bits shown as “0” and “1.” Inspired by quantum computing, some scholars put forward the QABC algorithm. However, the quantum states in QABC are described in the plane of the unit circle in the Hilbert space of real numbers, only one variable, and the quantum properties are not fully utilized.

2.2 The improved QABC algorithm

Based on the shortcomings of the QABC algorithm which have been mentioned in the previous section, an improved QABC algorithm is proposed in this paper.

Step 1 The encoding scheme of the nectar based on Bloch coordinates The quantum bit (qubit) represents the minimum information unit in quantum computation. The state of a qubit can also be expressed as a formula (2)

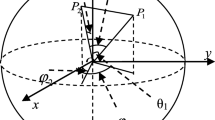
$$\begin{aligned} |\phi \rangle =\cos (2/\theta )|0\rangle +\hbox {e}^{i\varphi }\sin (2/\theta )|1\rangle . \end{aligned}$$
(2)

Each pair of parameters \(\theta \) and \(\varphi \) defines the unique point P on the Bloch sphere. (As shown in Fig. 1) From Fig. 1, we can see that every qubit is one-to-one correspondence with the point and thus the qubit coordinates are \([\cos \varphi \sin \theta ,\sin \varphi \sin \theta ,\cos \theta ]^{\mathrm{T}}\) in Bloch sphere.

Fig. 1
figure 1

Quantum bit Bloch sphere

Full size image

In the BQABC algorithm, the initial sources directly use Bloch coordinate to encode the qubits and the i-th individual \(R_{i}\) code is as follows:

$$\begin{aligned}&\begin{aligned} R_{i}=&\left[ \begin{array}{c} \cos \varphi _{i1}\sin \theta _{i1} \\ \sin \varphi _{i1}\sin \theta _{i1} \\ \cos \theta _{i1} \end{array} \right] \cdots \left[ \begin{array}{c} \cos \varphi _{ij}\sin \theta _{ij} \\ \sin \varphi _{ij}\sin \theta _{ij} \\ \cos \theta _{ij} \end{array}\right] \\&\cdots \left[ \begin{array}{c} \cos \varphi _{in}\sin \theta _{in} \\ \sin \varphi _{in}\sin \theta _{in} \\ \cos \theta _{in} \end{array}\right] \end{aligned} \end{aligned}$$
(3)
$$\begin{aligned}&\left\{ \begin{array}{c} \varphi _{ij}=2\pi \times \hbox {rand}(0,1) \\ \theta _{ij}=2\pi \times \hbox {rand}(0,1) \end{array} \right. \end{aligned}$$
(4)

where \(1 \le i \le m,1 \le j \le n\), m is the population size, n is the dimension of space and that is the number of quantum bits. There are n qubits in \(R_{i}\) and each qubit can be expressed by\([\cos \varphi \sin \theta ,\sin \varphi \sin \theta ,\cos \theta ]^{\mathrm{T}}\). So \(R_{i}\) can obviously be expressed as (5)

$$\begin{aligned} \begin{aligned} R_{i}&=\left[ \begin{array}{c} R_{ix} \\ R_{iy} \\ R_{iz} \end{array} \right] \\&=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \cos \varphi _{i1}\sin \theta _{i1}, &{} \cdots ,&{} \cos \varphi _{ij}\sin \theta _{ij}, &{} \cdots ,\\ \sin \varphi _{i1}\sin \theta _{i1}, &{} \cdots ,&{} \sin \varphi _{ij}\sin \theta _{ij}, &{} \cdots ,\\ \cos \theta _{i1}, &{} \cdots ,&{} \cos \theta _{ij}, &{} \cdots ,\\ \end{array}\right. \\&\quad \left. \begin{array}{c} \cos \varphi _{in}\sin \theta _{in} \\ \sin \varphi _{in}\sin \theta _{in} \\ \cos \theta _{in} \end{array}\right] . \end{aligned} \end{aligned}$$
(5)

From formula (5), we can see that each food source \(R_{i}\) consists of three chains of \(R_{ix}\), \(R_{iy}\) and \(R_{iz}\). Every chain is a feasible solution in the solution space. Therefore, they are denoted as \(x_{ix}\), \(x_{iy}\) and \(x_{iz}\), respectively, corresponding to three feasible solutions. Then,

$$\begin{aligned} \left\{ \begin{array}{c} x_{ix}=\left( x_{i1}^{(1)},x_{i2}^{(1)},\ldots ,x_{in}^{(1)}\right) \\ x_{iy}=\left( x_{i1}^{(2)},x_{i2}^{(2)},\ldots ,x_{in}^{(2)}\right) \\ x_{iz}=\left( x_{i1}^{(3)},x_{i2}^{(3)},\ldots ,x_{in}^{(3)}\right) \end{array} \right. \end{aligned}$$
(6)

Step 2 Food source update In the artificial bee colony algorithm, the update formula for nectar is as follows

$$\begin{aligned} V_{ij}=X_{ij}+\phi _{ij}\left( X_{ij}-X_{kj}\right) . \end{aligned}$$
(7)

In formula (7), \(X_{ij}\) is j-th dimensional position of i-th nectar source, \(X_{kj}, \) is j-th dimensional random selection location k of the other nectar. \(\phi _{ij}\) is a random number in [\({-}\)1, 1]. \(V_{ij}\) is the new source position. Because both \(X_{kj} \) and \(X_{ij}\) have a certain randomness, the update formula leads to the unspecific direction. That is, the direction of the update is also random. In BQABC algorithm, nectar update essentially is changed with every \(\varphi _{ij}\) and \(\theta _{ij}\) in Bloch coordinates. Based on the analysis of the defects and improvements in the artificial bee colony algorithm, there are the following improvements.

  1. 1.

    The update formula’s “exploration” performance has the ability to move to the optimal solution gradually with the current global optimum.

  2. 2.

    The ability of “exploitation” mainly has random factors besides moving to the current global optimum, that is to say the independent expansion ability in random number \(\phi _{ij}\) is kept. From Fig. 1, we can show that the location of a point not only connects with the angle \(\theta \) and \(\varphi \) angle, but also reflects the characteristics of random number \(\varphi _{ij} \epsilon \) [\({-}\)1, 1]. So the cosine value of the difference between \(\theta \) ( \(\theta \) current global optimal solution) and \(\theta _{\mathrm{best}}\) is used to adjust the changes in \(\varphi \), the cosine value of the difference between \(\varphi \) ( \(\varphi \) current global optimal solution) and \(\varphi _{\mathrm{best}}\) is used to adjust the changes in \(\theta \). All these take the above characteristics into account. Based on the above analysis, the formula (8) as shown in the update formula is adjusted as follows:

    $$\begin{aligned} \left\{ \begin{array}{c} \varphi _{ij}=\varphi _{ij}+\cos \left( \theta _{ij}-\theta _{\mathrm{best}}\right) \times \left( \varphi _{ij}-\varphi _{\mathrm{best}}\right) \\ \theta _{ij}= \theta _{ij}+\cos \left( \varphi _{ij}-\varphi _{\mathrm{best}}\right) \times \left( \theta _{ij}-\theta _{\mathrm{best}}\right) \end{array} \right. \end{aligned}$$
    (8)

In formula (8), \(\varphi _{ij}\) and \(\theta _{ij}\) are i-th food source \(R_{i}\) and j-th qubit phase in Bloch coordinates, respectively. \(\varphi _{\mathrm{best}}\) and \(\theta _{\mathrm{best}}\) are globally optimal Bloch coordinate phase in each generation. As can be seen from the formula (8), \(\varphi _{\mathrm{best}}\) and \(\theta _{\mathrm{best}}\) are used as the global optimum in the form of cosine function to update the formula. The range of the cosine function in trigonometric function is [\({-}\)1, 1], which is consistent with the ABC algorithm nectar update formula in the range of random numbers. Cosine function has the characteristics of periodicity and it is an even function, which can ensure that the good update direction can be repeated circularly. From the cosine function curve, it has a more smoothed trend compared with the linear straight line, it cannot be mutated and has the random in update formula. When \(\varphi _{ij} \) equals to \(\varphi _{\mathrm{best}}\), \(\varphi _{ij} \) will remain unchanged, \(\theta _{ij}\) will be adjusted with \(\theta _{ij}\) and \(\theta _{\mathrm{best}}\) only, vice versa. When \(\varphi _{ij} \) equals to \(\varphi _{\mathrm{best}}\) and \(\theta _{ij}\) equals to \(\theta _{\mathrm{best}}\), honey resource will remain unchanged, this means that the global optimal solution is found. From above, the update strategy applies the phase angle of current global optimum in every step. So it can achieve the effect that even a phase is invariant and another phase is still able to adjust the algorithm with the coefficient of \(\cos (\varphi _{ij}-\varphi _{\mathrm{best}})\) and \(\cos (\theta _{ij}-\theta _{\mathrm{best}})\). It can significantly improve the algorithm’s ability to jump out of local optimum and enhance the searching efficiency in the whole bee colony.

Step 3 Solution space transformation The search spaces range for each dimension of BQABC algorithm is [\({-}\)1, 1]. In order to calculate the fitness value of the artificial bee, it is necessary to carry out the transformation of the solution space. The coordinates on the Bloch sphere of j-th qubits in i-th food source is recorded as \([\cos \varphi _{ij}\sin \theta _{ij},\sin \varphi _{ij}\sin \theta _{ij},\cos \theta _{ij}]^{\mathrm{T}}\). Then, the solution space is transformed into the following formula

$$\begin{aligned} \left\{ \begin{array}{c} \begin{aligned} x_{ij}^{(1)}&{}=\frac{1}{2} \left[ b_{j} \left( 1+\cos \varphi _{ij}\sin \theta _{ij}\right) +a_{j}\left( 1-\cos \varphi _{ij}\sin \theta _{ij}\right) \right] \\ x_{ij}^{(2)}&{}=\frac{1}{2}\left[ b_{j} \left( 1+\cos \varphi _{ij}\sin \theta _{ij}\right) +a_{j}\left( 1-\cos \varphi _{ij}\sin \theta _{ij}\right) \right] \\ x_{ij}^{(3)}&{}=\frac{1}{2} \left[ b_{j}\left( 1+\cos \theta _{ij}\right) +a_{j}(1-\cos \theta _{ij}\right] \end{aligned} \end{array} \right. \end{aligned}$$
(9)

where \(1 \le i \le m,1 \le j \le n\). Three feasible solutions of the corresponding formula (6) in food source \(R_{i}\) can be obtained by linear transformation in the formula (9). The algorithm is summarized in Algorithm 1.

Algorithm 1. BQABC algorithm

01: Create an initial population of artificial bees by using

(3) and (4),transform the solution space by (9)

02: Evaluate the fitness of the population. Set \(\hbox {cycle}=1\)

03: While (stopping criterion is not met, the namely

\(\hbox {cycle} <\hbox {maxcycle}\) maximum \(\hbox {cycle}\) number)

04: Generate new solutions \(\varphi _{ij}\) and \(\theta _{ij}\) ; for the employed

bees by using (9) transform the solution space and

evaluate them

05: Calculate the probability values P; for the solutions

\(\varphi _{ij}\) and \(\theta _{ij}\)

06: Generate the new solutions \(\varphi _{ij}\) and \(\theta _{ij}\); for the

onlookers by using (8)from the solutions selected

depending on P; and evaluate them

07: Determine the new solutions for onlookers by

the greedy selection

08: If there exists an abandoned solution for the scout

(optimal number of Solutions \({>}\hbox {limit}\)) then

Use formula (3) and (4) to update the individuals

End if

09: Memorize the best solutions (\(\varphi _{\mathrm{gbest}},\theta _{\mathrm{gbest}}\))

achieved so far

\(\hbox {cycle}=\hbox {cycle}+1\)

10: End while (\(\hbox {cycle}=\hbox {maxcycle}\) maximum

\(\hbox {cycle}\) number)

11:Output the best solutions (\(\varphi _{\mathrm{gbest}},\theta _{\mathrm{gbest}}\))

3 Image threshold segmentation based on BQABC algorithm

3.1 The selection of fitness function

In the image segmentation using swarm intelligence algorithm, the reasonable selection of fitness function is a key problem in the effective implementation of threshold segmentation. The selections of fitness function take the statistical characteristics and visual characteristics of the image into account as well as combine with image denoising process. Thus, two-dimensional linear cross-entropy of the image is chosen to construct the algorithm’s fitness function.

Assumed f(x, y) is the gray level in \(M \times N\) image pixels (x, y), where f(x, y) is \(0, 1,\ldots , L-1, g (x, y)\) is the average gray level in \(K\times K\) neighborhood (\(K=2n+1\), n is positive integer). The gray value is same in \(0, 1, \ldots , L-1\). If \(f(x,y)=i, g(x,y)=j\), the probability of (i, j) is in the original graph and the smoothed image is shown as follows

$$\begin{aligned} \left\{ \begin{array}{l} p_{ij}=\frac{c_{ij}}{M\times N} \\ \sum \limits _{i=0}^{L-1} \sum \limits _{j=0}^{L-1}p_{ij}=1. \end{array} \right. \end{aligned}$$
(10)

In formula (10), \(i, j=0, 1,\ldots , L-1, c_{ij}\) is the frequency of the emergence of (i, j). Obviously, \(0\le p_{ij}\le 1\).

In [21], two-dimensional region in \((L-1)\times (L-1)\) is divided into two parts \(C_{0}(T)\) and \(C_{1}(T)\) with a vertical line\((i+j=T)\) to the main diagonal line, as shown in Fig. 2.

Fig. 2
figure 2

Division of two-dimensional linear-type region

Full size image

Among them, \(C_{0}(T)\) is the target and \(C_{1}(T)\) is the background. The probability of the target and the background is, respectively, as follows

$$\begin{aligned} P_{0}(T)= & {} \sum \limits _{(i,j)\epsilon C_{0}}p_{ij}\end{aligned}$$
(11)
$$\begin{aligned} P_{1}(T)= & {} \sum \limits _{(i,j)\epsilon C_{1}}p_{ij}. \end{aligned}$$
(12)

Meanwhile, \(P_{0}(T)\) and \(P_{1}(T)\) meet the \(P_{0}(T)+P_{1}(T)=1\).

The mean vectors of the target and the background are, respectively, as follows

$$\begin{aligned} \mu _{0}(T)= & {} \left[ \mu _{00}(T),\mu _{01}(T)\right] ^\prime \nonumber \\= & {} \left[ \frac{\sum \limits _{(i,j)\epsilon C_{0}}ip_{ij}}{P_{0}(T)},\frac{\sum \limits _{(i,j)\epsilon C_{0}}jp_{ij}}{P_{0}(T)}\right] \end{aligned}$$
(13)
$$\begin{aligned} \mu _{1}(T)= & {} \left[ \mu _{10}(T),\mu _{11}(T)\right] ^\prime \nonumber \\= & {} \left[ \frac{\sum \limits _{(i,j)\epsilon C_{1}}ip_{ij}}{P_{1}(T)},\frac{\sum \limits _{(i,j)\epsilon C_{1}}jp_{ij}}{P_{1}(T)}\right] . \end{aligned}$$
(14)

We can use f(x, y) and g(x, y) to define the generalized linear cross-entropy

$$\begin{aligned} \begin{aligned} I(T)&=\sum \limits _{(x,y)\epsilon C_{0}}f(x,y)\log _{2}\frac{f(x,y)}{\mu _{00}(T)}\\&\quad +\sum \limits _{(x,y)\epsilon C_{1}}f(x,y)\log _{2}\frac{f(x,y)}{\mu _{10}(T)}\\&\quad +\sum \limits _{(x,y)\epsilon C_{0}}f(x,y)\log _{2}\frac{f(x,y)}{\mu _{01}(T)}\\&\quad +\sum \limits _{(x,y)\epsilon C_{1}}f(x,y)\log _{2}\frac{f(x,y)}{\mu _{11}(T)}. \end{aligned} \end{aligned}$$
(15)

The minimization formula (15) is equivalent to the maximum formula (16)

$$\begin{aligned} \begin{aligned} I(T)&=P_{0}(T) \left[ \mu _{00}(T)\log _{2}\mu _{00}(T) +\mu _{01}(T)\log _{2}\mu _{01}(T)\right] \\&\quad +P_{1}(T)\left[ \mu _{10}(T)\log _{2}\mu _{10}(T) +\mu _{11}(T)\log _{2}\mu _{11}(T)\right] . \end{aligned} \end{aligned}$$
(16)

Thus, the BQABC algorithm for image segmentation is to obtain the optimal threshold \(T^*\) so that \(I(T^*)\) can get the maximal value, which is consistent with the maximal entropy threshold segmentation.

3.2 BQABC algorithm image segmentation process

From Fig. 2, we can see that the segmentation threshold \(T=i+j\), the gray level of the gray image is generally \(2^8=256\). So the range of T is \([0,2*(L-1)]=[0, 510]\) and meet formula (17)

$$\begin{aligned} T^*=\arg \max \limits _{(0\le T\le 510)}(I(T)). \end{aligned}$$
(17)

We can assume that the segmented image is \(f^\prime (x, y)\) and use the following formula (16) as the fitness function to obtain the segmentation threshold \(T^*\) on the image segmentation. After the \(f^\prime (x, y)\) is segmented to two values, the image is described as follows

$$\begin{aligned} f^\prime (x, y)=\left\{ \begin{array}{c@{\quad }c} 0 &{} f(x, y)+g(x, y)\le T^*\\ 255 &{} f(x, y)+g(x, y)> T^* \end{array} \right. . \end{aligned}$$
(18)

To sum up, the BQABC algorithm proposed in this paper will use 2-dimensional linear cross-entropy to construct the fitness function for image segmentation. The algorithm is summarized in Algorithm 2.

Algorithm 2. Image segmentation by BQABC

01: Create an initial population of artificial bees by using

(3) and (4),use 2-D linear-type cross-entropy to be

fitness function

02: Achieve the best solutions (\(\varphi _{\mathrm{gbest}},\theta _{\mathrm{gbest}}\)) with

Algorithm 1

03: Transform the solution space

04: Segment the image by using (18)

Fig. 3
figure 3

a Segmentation result, b, c response curves of lena.jpg

Full size image
Fig. 4
figure 4

a Segmentation result, b, c response curves of rice.png

Full size image
Fig. 5
figure 5

a Segmentation result, b, c response curves of coins.png

Full size image
Fig. 6
figure 6

a Segmentation result, b, c response curves of pears.png

Full size image
Fig. 7
figure 7

a Segmentation result, b, c response curves of swans.jpg

Full size image
Table 1 Performance comparison of OTSU, ME, MEM, ABC and BQABC
Full size table

4 Experimental results and analysis

4.1 Comparison of different image segmentation effects by BQABC algorithm

To verify the validity of BQABC algorithm, we select four standard images gallery images (lena.jpg, rice.png, coins.png, pears.png) and a network image with light cloud in the background and many swans in objects(swa ns.jpg) for image segmenting test (Figs. 3, 4, 5, 6, 7). The initial parameters of the BQABC algorithm are population size \(N=20\), \(\hbox {cycle}\) times (maximum number of limitations) \(\hbox {limit}=10\) and maximum iteration number \(\hbox {maxCycle}=40\), respectively. Every image runs 20 times with the same parameters.

From Figs. 3, 4, 5, 6 and 7, five images have different characteristics. These two-dimensional histograms, which are composed of the original and the smoothed image of the gray, can express much more information. Figure 3a shows that the segmented image can retain the image information and acquire accurately facial expressions and details of the characteristics. From the rice image segmentation effect Fig. 4a, we can see that the segmentation effect is ideal. Meanwhile, grain size, shape and the corresponding location can well show that figure 5a is the coins image after segmentation, and we can find that the outer contour of the coin can be very good to achieve and the coin pattern information in the upper left side is also more obvious from the resultant image. Figure 6a is the pears image segmentation results, pear shape, surface spots, even fruit stalk and other details of the characteristics are well presented. As shown in Fig. 7a, the head posture, body shape and feather details of swans show more clearly. It can be seen from the response curve that the speed of searching for the optimal threshold is fast. To sum up, the BQABC algorithm proposed in this paper has a good threshold segmentation effect with typical characteristics of the image.

4.2 Comparison of different algorithms for image segmentation

In order to compare BQABC algorithm proposed in this paper with the traditional Otsu method, ME, MEM and basic artificial bee colony (ABC) algorithm in image threshold segmentation, we use the same programming environment and parameter setting (population size \(N=20\), limiting the number of times \(\hbox {limit}=10\), the maximum number of iterations \(\hbox {maxCycle}=40\)) and run 20 times to compare the results of the segmentation. Performance comparison results are shown in Table 1. From Table 1, we can reach the following conclusion. The convergence times, BQABC algorithm converges all the time, Otsu method, ME, MEM and ABC fail to converge at least 2–5 times. The average value of steps and the time, BQABC algorithm’s convergence step is fewer and time is shorter than the others. The best results and the average results, five algorithms can get the best results, but the BQABC algorithm is more stable. So BQABC algorithm is better than OTSU algorithm, ME, MEM and ABC algorithm. Meanwhile, it has a better threshold segmentation effect.

5 Conclusions

Because the global detection ability of artificial bee colony algorithm is insufficient, the BQABC algorithm is proposed. The proposed algorithm uses Bloch spherical coordinates to code the initial nectar source, which expands the quantity of the global optimal solution and introduces global optimum information into the update strategy with a cosine function in every iteration.

The fitness function is the two-dimensional linear cross-entropy that is constructed by using the two-dimensional gray histogram of the original gray level and the neighborhood average gray level of the image. We use the OTSU algorithm, ME method, MEM, ABC algorithm and BQABC algorithm to do the simulation experiment with the standard images and a network image. By comparing the response curve, performance index and the experimental data of the five algorithms, the validity and practicability of the BQABC algorithm in image threshold segmentation are verified.

In this paper, we improve the artificial bee colony algorithm with qubit Bloch spherical coordinate, and the improved one is applied to image threshold segmentation and it can achieve good results. With the improvement in the research on the quantum swarm algorithm, there are some improved research directions, which mainly include three following aspects.

  1. 1.

    Encode to the food source with qubit for more uniform traversal in the whole solution space, which can improve the searching efficiency of the algorithm.

  2. 2.

    Continue to improve the artificial bee colony nectar update formula, which can improve the ability to jump out of the local optimization of the algorithm.

  3. 3.

    Combine QABC with other swarm intelligence algorithms, which can fasten the speed to the global optimal solution.