1 Introduction

Studying the signal’s structure simultaneously in both time and frequency domains can be done by projecting the signal onto the time–frequency plane. The possibility of tracking the mutation of the signal’s spectral content in time, which is typically represented by amplitude and frequency variations in the signal components, is provided by such projections that are called time– frequency representations (TFRs) [3]. There exist two main TFR classes: linear and quadratic. Linear TFRs are easy to compute but suffers from low resolution. A thorough review of liner TFRs such as the windowed Fourier transform (WFT), wavelet transform (WT) and their synchrosqueezed versions (SWFT, SWT) is presented in [3]. The quadratic class offers higher resolution. The core representative of the quadratic class of TFRs is the Wigner–Ville distribution (WVD). The WVD is obtained by taking the Fourier transform (FT) of an instantaneous autocorrelation function expressed as [2]:

$$\begin{aligned} {W_z}(t,f) = \int \limits _R {z\left( t + \frac{\tau }{2}\right) {z^*}\left( t - \frac{\tau }{2}\right) {\mathrm{e}^{ - 2j\pi f\tau }}\mathrm{d}\tau } \end{aligned}$$
(1)

where z(t) is the analytic associate of a real signal s(t) obtained by the use of the Hilbert transform. The WVD defined in Eq. 1 gives perfect localization for mono-component signal of linear frequency modulation (LFM), but it produces undesired cross-terms for nonlinear frequency-modulated (FM) or multi-component signals due to too many correlations. Filtering of the WVD removes cross-terms according to a kernel design, thus resulting in the quadratic time–frequency distributions (TFDs) [2].

$$\begin{aligned} \rho (t,f) = \gamma (t,f)\mathop *\limits _t \mathop *\limits _f {W_z}(t,f) \end{aligned}$$
(2)

where \(\gamma (t,f)\) is the 2D (t, f) smoothing kernel. Previous studies have shown that in case of quadratic class, separable kernel TFDs such as the extended modified B distribution (EMBD) and compact kernel distribution (CKD) can produce high-resolution TFDs [2, 10]. The parameter of such TFDs is usually optimized manually, but there are many automatic methods such as the one presented in [7]. Separable kernel methods do not have any parameter to adapt the direction of their smoothing kernels. Hence, the limitation of such separable kernel TFDs is their inability in concentrating energy for the signals with a certain direction of energy in the (t, f) plane [2]. This problem can be solved to certain extent by using time–frequency representations that take into account directions, e.g., multi-directional TFDs [2]. These methods fail to achieve optimum energy concentration when auto-terms of signal components overlap with cross-terms in ambiguity domain.

In order to prevail the problems affiliated with designing a single kernel for all points in the (t, f) plane, adaptive kernel TFDs have been developed including the adaptive optimal kernel TFD (AOK-TFD) and adaptive fractional spectrogram (AFS) [1, 4, 5, 11]. The time-invariant adaptive kernel TFDs are suitable for signals with a fixed (t, f) direction of energy distribution, while the time-varying ones, i.e., the AOK distribution [4, 6] provides higher (t, f) concentration for signals with time-varying (t, f) direction. Both of the AOK and AFS methods are limited in concentrating energy in case signal components have significant variation in their relative amplitudes [6]. The ADTFD is recent method that optimizes direction of the smoothing kernel locally [6]. The limitation of this technique is its manual tuning of filter parameters which cannot be adapted locally. This work defines an automatic method for locally adapting the filter parameters in ADTFD, thus resulting in a new variant of the ADTFD which is named as highly adaptive directional TFD (HADTFD). The rest of the paper is organized as follows. The HADTFD is defined in Sect. 2. Results are presented in Sect. 3. Section 4 concludes the paper.

2 Highly adaptive directional TFD

2.1 Adaptive directional TFD

In ADTFD, the angle of the smoothing kernel is adapted locally by exploiting the direction of the signal energy in (t, f) plane. The ADTFD is defined as [6]:

$$\begin{aligned} {\rho _\mathrm{(adapt)}}(t,f) = \rho (t,f)\mathop {\mathop *\limits _t \mathop *\limits _f }\limits _{}^{} {\gamma _\theta }(t,f) \end{aligned}$$
(3)

where \(\gamma _\theta (t,f)\) is the adaptive directional kernel. Its shape is determined by \(\theta \). The parameter \(\theta \) is adapted in a (t, f) plane, at each point. The direction of a smoothing kernel for any given (t, f) point is estimated by maximizing the correlation of the directional kernel with the modulus of a quadratic TFD [6].

$$\begin{aligned} \theta (t,f) = \arg \mathop {\max }\limits _\theta \left| {|\rho (t,f)\mathop {|\mathop *\limits _t \mathop *\limits _f }\limits _{}^{} {\gamma _\theta }(t,f)} \right| \end{aligned}$$
(4)

The smoothing kernel in this method is the double-derivative directional Gaussian lter (DGF).

$$\begin{aligned} {\gamma _\theta }(t,f) = \frac{{ab}}{{2\pi }}\frac{{{d^2}}}{{\mathrm{d}f_\theta ^2}}{\mathrm{e}^{ - {a^2}t_\theta ^2 - {b^2}f_\theta ^2}} \end{aligned}$$
(5)

where the rotation angle with respect to the time axis is \({\theta }, {t_\theta } = t\cos (\theta ) + f\sin (\theta )\), \({f_\theta } = - t\sin (\theta ) + f\cos (\theta )\). The DGF spread along time or frequency axis is controlled by parameters a and b [6].

2.2 The proposed method

In ADTFD algorithm, selection of different parameters of a, b and window length affect the presence of the cross-term and (t, f) resolution. In order to achieve optimum performance, both shape and direction of the smoothing kernel should be adapted locally at each point in the time–frequency plane. This leads to the definition of the fully adaptive method:

$$\begin{aligned} {\rho _\mathrm{FADTF}}(t,f) = \rho (t,f)\mathop *\limits _t \mathop *\limits _f {\gamma _{a,b,\theta }}(t,f) \end{aligned}$$
(6)

where \({\gamma _{a,b,\theta }}(t,f)\) is the same directional DGF defined in Eq. 5, but now it is optimized both for all three parameters that are a, b and \(\theta \). The optimization criterion for angle is already defined in Eq. 4. For the optimization of the shape parameters, we exploit the fact that for less extensive smoothing auto-terms have little change in the amplitude. However, as smoothing becomes more extensive the amplitudes of auto-terms decrease and the amplitudes of the cross-terms rapidly lead to zero [8]. Based on this observation, the following procedure is adopted to optimize the shape parameters of the fully adaptive method:

  • Analyze the given signal using a number of adaptive directional kernels.

    $$\begin{aligned} {\rho _i}(t,f) = \rho (t,f)\mathop *\limits _t \mathop *\limits _f {\gamma _{{a_i},{b_i},\theta }}(t,f) \end{aligned}$$
    (7)

    where \(i=1\) to L. The parameters of the directional kernels are adapted such that smoothing becomes more intense as for increasing values of i.

  • For each (t, f) point, compute the difference between two consecutive ADTFDs.

    $$\begin{aligned} \Delta {\rho _i}(t,f) = {\rho _{i + 1}}(t,f) - {\rho _i}(t,f) \end{aligned}$$
    (8)

  • The parameters that lead to the minimum difference between two ADTFDs are selected as the desired shape parameters for that (t, f) point.

    $$\begin{aligned} (a,b) = \mathop {\arg \min }\limits _{({a_i},{b_i})} \left| {\Delta {\rho _i}(t,f)} \right| \end{aligned}$$
    (9)

  • The desired value for a given (t, f) point is then obtained by taking average of two ADTFDs that lead to the minimum difference.

The aforementioned steps are also illustrated in Fig. 1. Note that the aforementioned optimization for the shape of the smoothing kernel is done locally for each (t, f) point. In order to reduce time complexity of the algorithm, and based on the mentioned principle, a is selected in the range of 2–4 and b is selected in the range of 8–30. For producing each ADTFD, the EMBD is used as the underlying distribution based on the previous work [4].

Fig. 1
figure 1

Algorithm for implementing highly adaptive directional time–frequency distribution

Full size image

3 Results and discussion

In order to demonstrate the efficacy of the proposed method, we consider two synthetic signals and two real-life EEG signals.

3.1 Synthetic signals

In this section, we demonstrate the efficacy of the proposed method through simulations both on the basis of visual and quantitative analysis. Specifically, we consider the scenario where we have both close signal components and short-duration transients.

Fig. 2
figure 2

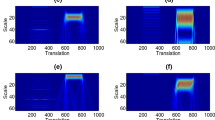
The TFDs of a multi-component signal composed of both short-duration transients and nonlinearly frequency-modulated components. a The AFS ; b the AOK-TFD; c the S-method- based TFD; d the ADTFD (\(a=2\), \(b=20\), \(\hbox {WL}=64\)); e the ADTFD (\(a=3\), \(b=8\), \(\hbox {WL}=3s2\)); and f the FAADTFD

Full size image

3.1.1 First example

Let us consider a multi-component signal which consists of four nonlinear FM signals and a Gaussian atom. The amplitudes of the chirps are selected in such a way to ensure the presence of both strong and weak components. The signal can be expressed as:

$$\begin{aligned} s(t) =\left\{ \begin{array}{ll} {s_1}(t) + {s_2}(t) + 0.5{s_3}(t) + 0.5{s_4}(t)\\ +\,{s_5}(t) + {s_6}(t) &{} 0 \le t \le 255 \\ 0 &{} \text {otherwise} \end{array}\right. \end{aligned}$$
(10)

where

$$\begin{aligned} \left\{ \begin{array}{l} {s_1}(t) = \cos (0.1\pi t + 0.000002\pi {t^3})\\ {s_2}(t) = \cos (0.15\pi t + 0.000002\pi {t^3})\\ {s_3}(t) = \cos (0.9\pi t - 0.000001\pi {t^3})\\ {s_4}(t) = \cos (0.95\pi t - 0.000001\pi {t^3})\\ {s_5}(t) = 2{\mathrm{e}^{ - 0.0015{{(t - 94)}^2}}}\cos (0.6t) \end{array}\right. \end{aligned}$$
(11)

We compare the QTFD obtained from the proposed method with AFS, AOK-TFD [4], adaptive directional TFD and S-method [8], as shown in Fig. 2. The parameters of other TFDs have been optimized based on visual inspection to maximize their energy concentration and resolution properties. Figure 2 shows that the S-method has failed to distinguish close signal components. The quadratic chirps are resolved by AFS, but the energy leakage between the close component peaks is observable. The AFS has failed in concentrating signal energy for the Gaussian atom. The AOK-TFD gives good resolution for the strong components, but it fails in concentrating energy for the components with low amplitude and the signal energy for the Gaussian atom is strewed. In case of the ADTFD, there is a compromise to either resolve the close components or maintain the time and frequency support of Gaussian atoms. Closely spaced components in the ADTFD with parameters (\(a=2\), \(b=30\)) are resolved, but the signal energy is scattered in the case of the Gaussian atoms. The ADTFD with parameters (\(a=3\), \(b=8\)) maintains the energy concentration of the Gaussian atom, but fails to resolve the nearly spaced components. It can be seen that HADTFD is very efficient in resolving both the strong and the weak signal components without degrading the energy concentration of the Gaussian atom. In general good time–frequency resolution without the presence of the cross-terms is achieved by using the HADTFD.

In order to test the robustness of the HADTFD to noise, let us now repeat the same experiment by adding additive white Gaussian noise with signal-to-noise ratio (SNR) equal to 10 dB to the signal given in Eq. 11. From Fig. 3, it can be observed that HADTFD can suppress the noise and resolves close components without degrading the energy concentration of the Gaussian atom.

Fig. 3
figure 3

The TFDs of a multi-component signal with additive white Gaussian noise, composed of both short-duration transients and nonlinearly frequency-modulated components. a The AFS ; b the AOK-TFD; c the S-method-based TFD; d the ADTFD (\(a=2\), \(b=20\), \(\hbox {WL}=64\)); e the ADTFD (\(a=3\), \(b=8\), \(\hbox {WL}=3s2\)); and f the HADTFD

Full size image

3.1.2 Second example

Let us now consider another signal composed of two quadratic chirps and three Gaussian atoms, which is expressed as:

$$\begin{aligned} q(t) =\left\{ \begin{array}{ll} {q_1}(t) + {q_2}(t) + 0.5{q_3}(t) + 0.5{q_4}(t)\\ + \,{q_5}(t) &{} 0 \le t \le 255 \\ 0 &{} \text {otherwise} \end{array}\right. \end{aligned}$$
(12)

where

$$\begin{aligned} \left\{ \begin{array}{l} {q_1}(t) = 2\cos (2\pi (0.075t + 0.0000015{t^3}))\\ {q_2}(t) = 2\cos (2\pi (0.05t + 0.0000015{t^3}))\\ {q_3}(t) = 4{\mathrm{e}^{ - 0.001{{(t - 192)}^2}}}\cos (2\pi *0.45t)\\ {q_4}(t) = 4{\mathrm{e}^{ - 0.001{{(t - 64)}^2}}}\cos (2\pi *0.45t)\\ {q_5}(t) = 4{\mathrm{e}^{ - 0.001{{(t - 192)}^2}}}\cos (2\pi *0.07t) \end{array}\right. \end{aligned}$$
(13)

This nonlinear FM signal is analyzed using the AFS, AOK-TFD, S-method, ADTFD (\(a=2\), \(b=30\)), ADTFD (\(a=3\), \(b=8\)) and the proposed HADTFD. From Fig. 4, it can be seen that the AFS maintains the time support of Gaussian atom but has failed to resolve the close component peaks. Figure 4 shows that the AOK-TFD strews the signal energy for the Gaussian atoms. The S-method has failed in resolving close signal components. The ADTFD with parameters (\(a=2\), \(b=30\)) is efficient in resolving the nearly spaced components of the signal, but it distributes signal energy for the Gaussian atoms. The ADTFD with parameters (\(a=3, b=8\)) maintains the energy concentration of the Gaussian atoms but fails in resolving the components with close frequency spectrum. The HADTFD has resolved the close parts of the reference signal without suffering from the problem of cross-terms and maintains the energy concentration of the Gaussian atoms.

Fig. 4
figure 4

The TFDs of a multi-component signal composed of both short-duration transients and nonlinearly frequency-modulated overlapped components. a The AFS; b the AOK-TFD; c the S-method-based TFD; d the ADTFD (\(a=2\), \(b=20\), \(\hbox {WL}=64\)); e the ADTFD (\(a=3\), \(b=8\), \(\hbox {WL}=32\)); and f the HADTFD

Full size image

Figure 5 shows the selected TFDs for the same signal with the presence of additive white Gaussian noise with signal-to-noise ratio (SNR) equal to 10 dB. From Fig. 5, it can be seen that HADTFD suppresses the noise completely and resolves close components without degrading the energy concentration of the Gaussian atoms.

Fig. 5
figure 5

The TFDs of a multi-component signal with additive white Gaussian noise, composed of both short-duration transients and nonlinearly frequency-modulated overlapped components. a The AFS ; b the AOK-TFD; c the S-method-based TFD; d the ADTFD (\(a=2\), \(b=20\), \(\hbox {WL}=64\)); e the ADTFD (\(a=3\), \(b=8\), WL \(=\) 32); and f the HADTFD

Full size image

3.2 Quantitative comparison

In order to quantitatively compare the performance of HADTFD method with other mentioned TFDs for the above experiments, a measure of TF energy concentration is used. The discrete form of the concentration measure for a normalized TFD (i.e., \(\sum \nolimits _{n = 1}^N {\sum \nolimits _{k = 1}^N {\rho (n,k)} } = 1\) ) is shown as [9]:

(14)

with \(p>1\). In case of high energy concentration TFD, the aforementioned energy concentration measure has a lower value and it has a higher value for a TFD with poor energy concentration. The performance of all the selected TFDs for signals s(t) and q(t) is given in Tables 1 and 2. The HADTFD has the lowest value, thus implying highest energy concentration, which is also confirmed by the visual inspection.

Table 1 Performance comparison of selected TFDs for multi-component signal s(t)
Full size table
Table 2 Performance comparison of selected TFDs for multi-component signal q(t)
Full size table
Fig. 6
figure 6

Two single-channel EEG signal. a The normal EEG signal; b the seizure EEG signal

Full size image
Fig. 7
figure 7

The TFDs of a seizure epoch. a The AFS ; b the AOK-TFD; c the S-method-based TFD; d the ADTFD (\(a=2\), \(b=20\), \(\hbox {WL}=64\)); e the ADTFD (\(a=3\), \(b=8\), \(\hbox {WL}=3s2\)); and f the HADTFD

Full size image
Fig. 8
figure 8

The TFDs of a normal epoch. a The AFS; b the AOK-TFD; c the S-method-based TFD; d the ADTFD (\(a=2\), \(b=20\), \(\hbox {WL}=64\)); e the ADTFD (\(a=3\), \(b=8\), WL \(=\) 32); and f the HADTFD

Full size image

3.3 Performance comparison using real-life EEG signal

Two types of EEG signal are illustrated using the selected TFDs. The signal is recorded from patients suffering from epilepsy. The recording includes both seizure and nonseizure segments. Two segments of EEG signal with duration of 8 s are sampled at 64 Hz. The first one is a nonseizure segment which is recorded during the normal condition of the patient (Fig. 6a). The other one is a seizure segment which is recorded during seizure event from the same patient (Fig. 6b). These segments are analyzed using the AFS, AOK-TFD, S-method, ADTFD (\(a=2, b=30\)), ADTFD (\(a=3, b=8\)) and the proposed HADTFD. Figure 7 shows the TFDs for the normal signal, and Fig. 8 shows the TFDs for the seizure signal. Both figures confirm that the HADTFD gives the best performance in terms of suppressing cross-terms while maintaining the quality of auto-terms.

3.4 Interpretation of results and computational cost analysis

The HADTFD gives the best performance but at the expense of extra computational burden. The computation of the HADTFD involves optimization of both angle and shape parameters, which is done by computing L number of ADTFDs. So the computational cost of the proposed approach is L times the computational cost of the ADTFD. For a TFD of dimensions \(N \times M\), the computational cost of the ADTFD as given in [2] is \(O(NM{\log }M+KNM)\), where K is number of quantization levels used for angle optimization. So the computational cost of fully adaptive method becomes \(O(LNM{\log }M+LKNM)\).

4 Conclusion

In this research, a generalization of adaptive directional TFD has been presented by automatically adjusting the shape parameters of adaptive directional TFD locally at each point int the (t, f) plane. The new method is named highly adaptive TFD (HADTFD). It has been shown that by locally adapting the size of the DGF, HADTFD overcomes the limitation of adaptive directional TFD in analyzing signals that have both short-duration and close components. Moreover, it provides an optimization method for ADTFD, requiring no additional inputs from the analyst except the analyzed signal. Performance of the HADTFD depends on the underlying distribution. Experimental results show that the HADTFD gives high energy concentration without suffering from cross-term interference problem. The limitation of the proposed approach is its high computational cost as compared to existing methods. This problem can be mitigated to certain extent by parallel computation of TFDs.