1 Introduction

Magnetic resonance imaging (MRI) is potentially a powerful and effective diagnostic tool. MR images can be degraded during any of the acquisition, preprocessing, compression, transmission, storage and/or reproduction phases of processing [12]. MRI signals are normally faced with several intricacies such as very low signal-to-noise ratio (SNR) and different transverse relaxation time values in overlapping resonances [1]. During the acquisition process because of the low SNR one of the dreadful conditions is thermal noise which fluctuates the signal randomly and degrades the quantitative measurements for further clinical analysis [11, 23, 36]. Averaging of MR signals can be used to increase the SNR and reduce the thermal noise, but this process in not a common practice in clinic, because this increase the acquisition time of MRI which limits their utilization in many situations where long replications are not viable, such as for unstable biological compounds [1, 24]. There is an intrinsic compromise between high SNR and visual quality (resolution) of MR images, obtaining a higher resolution image with a desired SNR increases the acquisition time of MRI [11, 28]. Therefore, after acquisition, post-processing denoising and enhancement techniques are suitable alternatives to remove the noise and increase the accuracy of clinical diagnostic system.

In MR data, noise can be Gaussian or Rician distributed depending upon the type of an image (complex or magnitude data). In this manuscript, the magnitude MR data has been analyzed. Noise estimation is usually done over magnitude MR images because this is usual output of the scanning process [3], and magnitude and phase data are more directly related to the anatomical and physiological information of interest [35]. The raw data of an MR image are complex valued k-space data, corrupted by white additive Gaussian noise having equal variances in real and imaginary parts. In order to transform the MR data from complex to magnitude, the Gaussian distribution of the noise is transformed into a Rician distribution [7, 8, 13]. Rician noise in magnitude MRI is categorized as the signal-dependent noise model [28] that may affect the performance of post-processing techniques, such as registration, segmentation, parametric image synthesis, or tensor estimation in diffusion tensor MRI [2]. Moreover, noise removal in MR images is a critical challenging task because MR signal has low SNR while containing more structural features.

A great amount of Rician noise removal techniques have been reported in the literature. One of the first attempts has been proposed by Henkelman [15], for the estimation of magnitude MR image from a noisy data degraded with Rician noise, and scrutinized the effect of noise on magnitude MR images. Many filtering methods are based on the signal averaging principle by using the natural spatial pattern redundancy in the images. In this sense, Gaussian filter is a common and simple approach, used in some denoising applications [4], but this filter blurs the edges and effects the high-frequency regions of the image. This problem has been mitigated by edge preserving filters such as anisotropic diffusion filters (ADFs) [10, 19, 30]. Several other approaches have been proposed for MRI denoising such as, conventional approach [26], wavelet-based approaches [31, 37], principal component analysis-based technique [27], discrete cosine transformation-based filter [39], maximum likelihood approach [35, 36], and machine learning-based approaches [5, 14, 16, 17, 33, 34]. The denoising performance of most of these filter depend on the optimal parameters setting and transform-threshold-inverse transform principle.

Local transform approaches provide better results than transform domain approaches [24] such as median filter (MF) and non-local means (NLM) filter. MF provides comparatively good results for smooth regions and highly corrupted images, while its performance decreases for high-intensity regions and low noise variance, in MR signal. In order to handle the problem of low noise variance in MR signal, multiple variants of NLM filter are used in the literature. NLM filter, for the first time, proposed to remove Gaussian noise form natural images [7], using pixel- based comparison for the similarity computation. NLM filters (simple NLM, unbiased NLM, adaptive NLM), based on block-wise comparison for similarity computation, proposed for Rician noise removal [23, 24]. The NLM filters provide better results if the noise can be modeled with additive Gaussian probability density function. Similarly, block-matching and 3D filtering (BM3D) denoising filter employs a non-local modeling of images by collecting similar image patches in 3D arrays [9] that gives better performance in case of additive Gaussian noise. The Rician PDF deviates from the Gaussian PDF, especially at low SNR, Rician PDF tends to Raleigh PDF which gives rise to biased results. In case of Rician noise removal, the above methods remove high-frequency signal components, results in blurring the edges, and introducing some extra bias in the quantification process. Therefore, advanced image restoration methods are required to mitigate these drawbacks.

Based on problems mentioned above, a new fuzzy logic-based hybrid filter has been proposed which combines the noise removal and detail preservation capability of local and non-local statistical filters for better restoration results. Proposed technique adaptively construct a robust fuzzy membership function by using local and global statistical parameters.

Rest of the manuscript is organized as follows: Sect. 2 presents the noise distribution in MR data, and the proposed technique is elaborated in Sect. 3. Experiment’s setup and performance measures are described in Sect. 4, followed by simulation results and discussions in Sect. 5. Finally, conclusion along with some future directions is made in Sect. 6.

2 Noise in MR images

In MR imaging, the complex valued MR raw data received from an MRI device represent the frequency domain k-space and normally corrupted by Additive White Gaussian Noise. After applying an inverse discrete Fourier transform (IDFT), the data remain complex and Gaussian distributed, because of the linearity and orthogonality of the Fourier transformation [11, 35, 36], the complex spatial MR data can be expressed as

$$\begin{aligned} C(x) = A(x) + \eta (x) \end{aligned}$$
(1)

where \(C(x)\) is the complex spatial MR signal, \(A(x)\) is the original noise-free MR signal, and \(\eta (x) \backsim \mathcal {N}(0,\sigma ^{2})\) is the complex uncorrelated Gaussian noise with zero mean and variance \(\sigma ^{2}\).

$$\begin{aligned} A(x)&= A_{R}(x) + i A_{I}(x)\nonumber \\ \eta (x)&= \eta _{R}(x) + i \eta _{I}(x) \end{aligned}$$
(2)

In the literature, the noise-free MR data from the complex valued MR data \(C(x)\) can be estimated directly from the real and imaginary components, or one can first transform the complex valued data in to magnitude data. It is common to transform the complex data in to magnitude data, since the magnitude data can better show the anatomical and physiological quantities in the MR data [11, 35]. The magnitude MR data are real valued and can be visualized easily or used for automated computer analysis [28]. Such transformation of MR data (complex to magnitude) changes the distribution of the data from Gaussian to Rician, because of the nonlinear operation performed during transformation [22]. The magnitude of \(C(x)\) is denoted by

$$\begin{aligned} M = \left| C \right| = \left[ (A_{R} + \eta _{R})^{2} + (A_{I} + \eta _{I})^{2} \right] ^ {1/2} \end{aligned}$$
(3)

The probability distribution function (PDF) of magnitude data \(M\) is represented as

$$\begin{aligned} p ( M | A, \sigma ) \!=\! \frac{M}{\sigma ^{2}} \, \hbox {exp} \left( \!- \frac{M^{2}+A^{2}}{2 \sigma ^{2}} \right) I_{o} \left( \frac{AM}{\sigma ^{2}} \right) u (M) \end{aligned}$$
(4)

where \(A\) denotes noise-free signal amplitude, \(\sigma ^{2}\) is the variance of the white Gaussian noise, \(I_{o}(.)\) denotes the \(0^{\hbox {th}}\) order modified Bessel function of the first kin, \(u(.)\) is the unit step Heaviside function, and \(M\) is the magnitude MR signal. The unit step Heaviside function \(u(.)\) indicates that the PDF of \(M\) is only valid for nonnegative values of \(M\) [36]. The Rician noise is a signal-dependent noise and depends on the local intensity of the image. In the dark region, where the SNR tends to zero, the Rician PDF approaches to Rayleigh distribution and in the signal region, where the SNR is high, it tends to Gaussian distribution [11, 24, 28]. The Rician PDF simplifies to the Rayleigh PDF, for SNR tends to zero, is defined as

$$\begin{aligned} p ( M | \sigma ) = \frac{M}{\sigma ^{2}} \, \hbox {exp} \left( - \frac{M^{2}}{2 \sigma ^{2}} \right) \, u (M) \end{aligned}$$
(5)

In MRI, noise variance estimation can play a key role in denoising and enhancement of these images. The noise can be estimated from either complex or magnitude MR images. In the literature, the estimation of noise variance is usually done in magnitude MR image by using the background region [3]. A detail survey of noise variance estimation methods is given in [2, 13].

3 Proposed technique

The aim of the proposed approach is to develop an efficient denoising filter for magnitude MR data, degraded with low or high level of Rician noise. The proposed approach is based on fuzzy logic that combines non-local fuzzy weighted and local-order statistical filters to suppress Rician noise while retaining edges and structural detail information. There are two main reasons to non- local and local filters:

  1. 1.

    Non-local statistical filters performs better, for non-smooth regions and when the MR image is corrupted with low level of Rician noise (\(\le \)15 %).

  2. 2.

    Local-order statistical filters on another hand performs better, for smooth regions and when the MR image is degraded with high level of Rician noise (\(\ge \)15 %).

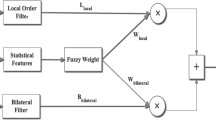
Based on above analysis, the proposed scheme constructs fuzzy membership function adaptively based on statistical features for the near optimal combination of the local and non-local fuzzy weighted filters. The proposed fuzzy-based hybrid filter is divided into four modules titled: statistical features computation, non-local fuzzy weighted statistical filter, local-order statistical filter, and fuzzy-based hybrid restoration mechanism. The first three modules are independent of each others can be executed in parallel to improve the running time of the algorithm; however, the last module is dependent upon the first three modules. The schematic block diagram of the proposed scheme is shown in Fig. 1.

Fig. 1
figure 1

The block diagram of the proposed scheme

Full size image

3.1 Statistical features

In this module of the proposed scheme, some of the statistical features are computed such as noise variance estimation and mean values of the noisy image and overlapping local neighborhoods, for the construction of fuzzy set adaptively. In order to differentiate between smooth and textural regions as well as background and foreground regions in the image, local mean \(\mu _{i}\) of a local neighborhood (centered around a pixel \(i\)) with the radius \(R_{i}\) and global mean \(\mu _{g}\) of the complete noisy image, are used in the proposed method for fuzzy membership construction.

In magnitude MR data the standard deviation \(\sigma _{g}\) of the Rician noise is estimated from the background of the squared magnitude MR image [28], as follows:

$$\begin{aligned} \sigma _{g} = \sqrt{ \frac{\mu _{b}}{2} } \end{aligned}$$
(6)

where \(\mu _{b}\) is mean value of the background region of the squared magnitude MR image. In proposed scheme, the background is selected using a threshold method proposed by Otsu [29].

3.2 Non-local fuzzy weighted statistical filter

The non-local fuzzy weighted statistical filter averages similar pixels in an image, according to their intensity distance and Gaussian fuzzy membership-based weights. The similarity between two pixels is based on patch comparison and pattern redundancy in non local region, where the pixels are not penalized due to its distance from the pixel being filtered. The non-local fuzzy weighted statistical filter can be denoted as

$$\begin{aligned} \hat{g}_{\mathrm{nonlocal}} = \sum _{\forall i \in g} \hbox {NonLocalFilter}(g(i)) \end{aligned}$$
(7)

where \(\hat{g}_{\mathrm{nonlocal}}\) is an output denoised image, \(g\) is a given noisy image corrupted with Rician noise, and \(i\) denotes a pixel in the image. The filtered value at the pixel \(i\) is calculated as a weighted average of all the pixels in the image, as defined by this formula:

$$\begin{aligned}&\hbox {NonLocalFilter}(g(i)) = \sum _{\forall j \in g } \left[ w(i,j) \times g(j) \right] \nonumber \\&0 \le w(i,j)\le 1 ,\,\,\,\,\, \sum _{\forall j \in g } \left[ w(i,j) \right] = 1 \end{aligned}$$
(8)

where \(i\) is the pixel being filtered and \(j\) stands for each one of the pixels in the image \(g\). The weights \(w(i,j)\) are computed, based on the similarity between the square neighborhoods \(M_{i}\) and \(M_{j}\), with a same radius \(R_\mathrm{sim}\), which are centered around pixels \(i\) and \(j\), respectively. The similarity \(w(i,j)\) between pixels \(i\) and \(j\) is calculated as

$$\begin{aligned}&w(i,j) = \frac{1}{C(i)} e^{ - \frac{d(i,j)}{h^{2}} } \nonumber \\&C(i) = \sum _{\forall j} e^{ - \frac{d(i,j)}{h^{2}} } \nonumber \\&d(i,j) = G_{\rho }\left\| g(M_{i}) - g(M_{j}) \right\| ^{2}_{R_{\mathrm{sim}}} \end{aligned}$$
(9)

where \(C(i)\) is the normalizing factor, \(h\) is an exponential decay control parameter, \(d\) is a Gaussian weighted euclidean distance, and \(G_{\rho }\) is a Gaussian kernel of with zero mean and \(\rho \) standard deviation. In order to avoid over-weighting effects, the value of a center pixel of the Gaussian kernel \(G_{\rho }\) is set to the same value that the pixels at a distance 1, and self-similarity \(w(i,i) = \hbox {max} \left( w(i,j) \forall j \ne i \right) \). For each pixel \(i\), it is very inefficient to calculate the similarity of all the pixels \(j\) in the image; therefore, the similarity of all the pixels in a search window \(M_{\mathrm{search}}\) with a radius \(R_{\mathrm{search}}\) has been used that can be written as

$$\begin{aligned}&\hbox {NonLocalFilter}\left( g(i), R_{\mathrm{search}}, R_{\mathrm{sim}}\right) \nonumber \\&\quad = \sum _{\forall j \in M_{\mathrm{search}}} \left[ w(i,j) \times g(j) \right] \end{aligned}$$
(10)

3.3 Local-order statistical filter

The local-order statistical filter is a nonlinear digital filtering method, one of the efficient, simple and widely used state-of-the-art technique. In case of Rician noise removal, under certain conditions (high-corrupted pixels and smooth regions), it removes noise quite efficiently with more accuracy. In local-order statistical filter, a square neighborhood \(M_{\mathrm{local}}\) with the radius \(R_{\mathrm{local}}\) convolved over the complete image and produces the median value for each pixel in the image that can be denoted as

$$\begin{aligned} \hat{g}_{\mathrm{local}} = LocalFilter(g, R_{\mathrm{local}}) \end{aligned}$$
(11)

3.4 Fuzzy-based hybrid restoration

In this section, fuzzy logic-based hybrid restoration module has been presented. In order to consider the pros and cons of the non-local fuzzy weighted and local-order statistical filters at low and high noise rates while operating on smooth and detailed regions simultaneously, fuzzy weighted hybrid filter has been employed. Proposed filter adaptively computes the weights based on local and non-local statistical features using the concept of fuzzy membership function. Fuzzy membership function has been constructed adaptively by analyzing statistical features so that better noise removal and detail preservation capability can be achieved. For this purpose, trapezoidal-shaped fuzzy membership function is constructed and contributions of non-local fuzzy weighted and local-order statistical filters are obtained. Trapezoidal-shaped fuzzy membership function can be denoted as

$$\begin{aligned} f(x;a,b,c,d) = \left\{ \begin{array}{ll} 0, &{}\quad \text {if}\; x \le a \\ \displaystyle \frac{x-a}{b-a}, &{}\quad \text {if}\; a \le x \le b \\ 1, &{}\quad \text {if}\; b \le x \le c \\ \displaystyle \frac{d-x}{d-c}, &{}\quad \text {if}\; c \le x \le d \\ 0, &{}\quad \text {if}\; d \le x \end{array} \right. \end{aligned}$$
(12)

where \(x\) is an input vector for the trapezoidal function, \(a\), \(b\), \(c\), and \(d\) are the scalar parameters, \(a\) and \(d\) locate the feet of the trapezoidal, and \(b\) and \(c\) locate the shoulders. The expressions for computing the parameters (a, b, c, and d) are given below

$$\begin{aligned} a&= k_{1}\times \hbox {min}\left\{ \mu _{i}, \mu _{g} \right\} \nonumber \\ b&= k_{2}\times \hbox {max}\left\{ \mu _{i}, \mu _{g} \right\} \nonumber \\ c&= k_{3}\times b \nonumber \\ d&= k_{4}\times c \end{aligned}$$
(13)

where \(k_{1}\), \(k_{2}\), \(k_{3}\), and \(k_{4}\) are adjusting parameters which depend upon the estimated noise level \(\sigma _{g}\) and constant values, \(\mu _{i}\) is the mean of a local neighborhood centered around a pixel \(i\) with the radius \(R_{i}\), and \(\mu _{g}\) is the mean of a complete noisy image \(g(x,y)\).

After fuzzy set construction, the fuzzy membership (weight) of non- local and local estimators are computed, using NLM \(\mu _{i}\) of the local patch, such as

$$\begin{aligned} w_{\mathrm{nonlocal}}&= f(\mu _{i} ; a, b, c, d) \nonumber \\ w_{\mathrm{local}}&= 1 - w_{\mathrm{nonlocal}} \end{aligned}$$
(14)

where \(w_{\mathrm{nonlocal}}\) and \(w_{\mathrm{local}}\) represent the near optimal contributions of the non-local and local filters, respectively. Finally, the required restored image \(\hat{f}\)(\(x,y\)) is obtained by using the mathematical model:

$$\begin{aligned} {\hat{f}}\left( x,y \right) = w_{\mathrm{nonlocal}} \times \hat{g}_{\mathrm{nonlocal}} + w_{\mathrm{local}} \times \hat{g}_{\mathrm{local}} \end{aligned}$$
(15)

In order to justify the expressions used by the proposed method for fuzzy set parameters (\(a\), \(b\), \(c\), and \(d\)) shown in the Eq. 13, remarks are given in the following:

Remark 1

Estimated noise level \(\sigma _{g}\) has been used for computing the fuzzy parameters adaptively. The non local statistic does not give good results at high noise rates for low intensity regions, so parameter \(a\) will fall near the origin of the MR signal at low noise rate. However, as the noise rate increases, distance between the origin and the parameter \(a\) increases, and hence, low weight \(w_{\mathrm{nonlocal}}\) will be assigned to non-local statistic at low-intensity regions.

Remark 2

Local and global mean statistics (\(\mu _{i}\) and \(\mu _{g}\)) control the shoulders of the trapezoidal-shaped fuzzy membership function. Close values of \(\mu _{i}\) and \(\mu _{g}\) suggest short shoulders, whereas large values indicate the wider shoulders because as the noise rate increases, \(\mu _{i}\) and \(\mu _{g}\) come closer to each other. Therefore, low noise rate suggests higher weight \(w_{\mathrm{nonlocal}}\) to the non-local statistic and vice versa.

Remark 3

Constant gains (\(k_{1}\), \(k_{2}\), \(k_{3}\), and \(k_{4}\)) used in the Eq. 13 are set experimentally to get accurate restoration results.

4 Experiment’s setup

In order to compare the effectiveness of the proposed technique, simulated (synthetic) and real (clinical) data sets of normal brain MR images have been used which are obtained from BrainWeb database [6] and Internet Brain Segmentation Repository (ISBR) [18], respectively. The data comprise of three modalities, namely T1-weighted, T2-weighted, and PD-weighted.

All of the experiments are carried out using MATLAB 7.9.0 [25]. MR images are artificially degraded with Rician noise, and the performance of restoration results are analyzed. The proposed scheme has been compared with familiar existing techniques such as ADF [10, 30, 32], BM3D denoising filter [9], MF [20], adaptive Wiener filter (AWF) [21], and non-local means (NLM) filter [23]. All the free parameters of these methods are set to the best setup as proposed by authors. The relevant values of the parameters to obtain the best results are given below:

  • ADF: number of iterations \(=\) 15, integration constant \(=\) 1/7, the actual noise variance to compute the noise level, and wide regions have privilege over smaller regions.

  • BM3D: actual noise variance is taken for computing the noise level. The values of other parameters are adjusted as described by the authors in the article [9].

  • MF: convolution window of size \(3 \times 3\).

  • AWF: convolution window using a \(5 \times 5\) neighborhood. In order to achieve the best performance of the filter, the noise variance is manually set to the actual value.

  • NLM filter: radius of the searching area \(=\) 5, radius of the local area \(=\) 2, the correction constant \(=\) 1.2, and the noise level is computed by using the actual noise variance.

In experiments, the setup of all the parameters using in the proposed scheme is shown in Table 1 and these parameters are adjusted empirically for denoising MR images.

Table 1 Parameters setup of the proposed scheme for denoising MR images
Full size table

Root mean squared error (RMSE), peak signal to noise ratio (PSNR), and structural similarity index measure (SSIM) are used for quantitative comparison, which are more extensively used in literature.

5 Comparative analysis

In this section, the performance of the proposed approach is compared with several denoising methods on simulated and real MR data sets. In order to evaluate the quantitative metrics, the ground truth MR data are artificially contaminated with a noise variance having the range 5–30 %. Average restoration results over 100 iterations of all these denoising methods are computed, based on RMSE, PSNR, and SSIM. The quantitative results (RMSE and PSNR) for different levels of Rician noise on simulated and real MR data sets are tabulated in Tables 2, 3, respectively. In case of Rician noise, a denoising method can efficiently remove noise from a noisy image either corrupted with low or high level of noise, because Rician probability distribution approaches to Raleigh PDF at low SNR and it tends to Gaussian distribution at high SNR.

Table 2 Quantitative comparison on Simulated MR data (BrainWeb) using PSNR (RMSE)
Full size table
Table 3 Quantitative comparison on Real MR data (IBSR dataset 657) using PSNR (RMSE)
Full size table

Table 2, clearly shows that the proposed hybrid technique has much better restoration results than existing methods at low as well as at high rates of Rician noise. Proposed technique exploits the fact that non-local filter gives good result at low-noise-corrupted detailed regions and local filter performs better at smooth regions degraded with high noise. Therefore, hybrid filter based on region characteristic and its noise contamination, adaptively assign appropriate fuzzy logic-based weights to local and non-local filters for better restoration of degraded image. Furthermore, at low noise rate (5 %), the proposed technique has improvement of 0.3 db for T1, 0.4 db for T2, and 0.3 db for PD as compare to the best performing NLM filter. As the noise rate increases, the performance of the hybrid filter also increases as we can see in Table 2. This is due to fact that even at high noise rates, the proposed technique accurately differentiates the low and high noise regions, and hence, better estimate of noisy pixel is obtained. Similarly, Table 3 shows that in case of real MR data sets, the proposed scheme out perform than existing techniques by same margin as discussed for Table 2.

During noise smoothing process, retaining the important structural information, such as texture and edges, is considered as an important task in image restoration. PSNR and RMSE are global quantitative measures and do not quantify that how well the detailed information, present in the image, are preserved. In order to measure the detail preservation performance of the proposed filter, a well-known quantitative measure SSIM is used. SSIM is based on the hypothesis that human visual system is highly adopted for extracting structural information. The comparison of the proposed hybrid filter using SSIM is shown in Fig. 2 using both simulated and real data sets. Figure 2 clearly indicates that the proposed technique is superior in terms of retaining structural information at all noise levels.

Fig. 2
figure 2

SSIM-based comparison of the proposed scheme with other techniques. a T1-weighted simulated (slice 70) b T1-weighted real (slice 10) c T2-weighted simulated (slice 70) d T2-weighted real (slice 10) e PD-weighted simulated (slice 50) f PD-weighted real (slice 10)

Full size image

In order to compare the visual performance, detailed results are obtained with the close up view of the restored images for better inspection in Figs. 3 and 4. Each figure incorporates, original image, noisy image, and the restored images by using existing and proposed approaches. Figure 3 shows the visual results for simulated MR slice corrupted with 10 % level of Rician noise. It can be observed from the figure that ADF and AWF are unable to smooth out noise completely. Furthermore, MF is good at preserving some details at the cost of some noisy spots, whereas NLM filter removes the noise completely but most of the image structural information has been lost. Visual results on real image data set, corrupted with 20 % level of Rician noise, are shown in Fig. 4. It can be seen in the figure that by increasing the power of noise, the NLM filter has been produced some extra blur and smoothness in the restored images. The proposed approach produces better results to overcome these limitations in the restored data by using the intelligent combination of local (such as median) and non local (such as non local means) filters.

Fig. 3
figure 3

Visual comparison for Simulated T1-Weighted MR image with 10 % Rician noise. a Original image, b noisy image c ADF d BM3D e MF f AWF g NLM h proposed

Full size image
Fig. 4
figure 4

a Original image b noisy image c ADF d BM3D e MF f AWF g NLM h proposed

Full size image

Finally, we can conclude, based on quantitative and visual results, that in all levels of Rician noise, the proposed approach has produced more pleasant results such as more noise cleaning ability, and retention of edges and structural information.

6 Conclusion and future work

In this article fuzzy logic based hybrid image restoration technique has been proposed, which combines the advantages of local and non local estimators based on noise level and region intensities. In proposed scheme trapezoidal shaped fuzzy membership function gives us a suitable degree degree of membership to local and non local statistics. It has been observed that appropriate construction of fuzzy membership parameters combines the advantages of local and non-local estimates in an innovative manner. The results show that the proposed scheme gives better performance than existing techniques based on well-known quantitative measures over simulated and real MR brain images. Furthermore, visual results confirm the achievements made through quantitative measures and clearly indicate that the proposed technique has capability of better noise removal and detail preservation. In future, unbiased estimate for the proposed technique can be computed for more accurate results.