A novel adaptive Gaussian restoration filter for reducing periodic noises in digital image

Abstract

Digital images can suffer from periodic noise, resulting in the appearance of repetitive patterns on the image data and quality degradation. In order to effectively reduce the periodic noise effects, a novel adaptive Gaussian notch filter is proposed in this paper. In the presented method, the frequency regions that correspond to noise are determined by applying a segmentation algorithm on the spectral band of the noisy image using an adaptive threshold. Then, a region growing algorithm tries to determine the bandwidth of each periodic noise component separately. Subsequently, proper Gaussian notch filters are used to decrease the periodic noises only at the contaminated noise frequencies. The proposed filter and some other well-known filters including the frequency domain mean and median filters and also the traditional Gaussian notch filter are compared to evaluate the effectiveness of the approach. The results in different conditions show that the proposed filter gains higher performance both visually and quantitatively with lower computational cost. Furthermore, compared with the other methods, the proposed filter does not need any tuning and parameter adjustments.

1 Introduction

Image noise as a random variation of intensity or color in digital images is created by means of imaging sensors, scanner circuits or digital cameras. The performance of imaging sensors is affected by a variety of factors such as environmental conditions during image acquisition and the quality of sensor elements. For example, in an imaging system with CCD cameras, light levels and sensor temperature are the main factors creating noise in the digital image. Currently, noise reduction algorithms have received a lot of interest since the image noise can significantly degrade the image quality [1].

Periodic noise, as one type of image noise, is an undesired signal that creates repetitive and intermittent patterns in the digital images. It often contaminates the whole image as impulse-like bursts while it is not simply separable or detectable from its background in the spatial domain. In frequency domain, the periodic noise appears in the frequencies corresponding to the periodic noise with high amplitudes. Different sources can generate the periodic noise including the electrical and electromechanical interference during image acquisition, the thermal instability of optical elements, electronic circuit’s gain in optical sensors and the scanning process in electro-optical scanners [2].

For example, periodic noises contaminate the output of imager system mounted on vibrated holder (e.g., in a non-stabilized helicopter) or the output of TV receiver when the receiving signal is weak, or the output of an imaging system suffers from electrical inference between receiving signal and another periodic signal, like inter-harmonics of power supply frequency.

The periodic noise is usually classified into three different categories: global periodic noises, local periodic noises and stripping patterns [3, 4]. The global periodic noise is the repetitive and undesired patterns with fixed parameters in the whole image. The interference of independent periodic signals is one of the main sources of this noise. Adjacent digital clock signals can be a source of this noise in image sensor devices. The interference of periodic digital signals with analog TV sets is another example where global periodic noise is produced. In the local periodic noise, some noise parameters including the frequency, the amplitude and the phase of the periodic noise may depend on the image relative coordinates. Unequal sensitivity of detectors and corresponding electronic circuits in multi-sensor imaging systems can cause the third type of noise known as stripping. The period of stripes is usually determined by the number of available detectors in the imaging device. Another source of striping noise can be found in the interference of florescent lamp 50 (60 Hz) light intensity fluctuations with the rolling shutter mechanism of an image sensor. Figure 1 shows three types of periodic noise.

Fig. 1

X-ray imaging from human skeleton, contaminated by, a Stripping, b local, c global periodic noise

According to the imager location in a multi-sensor system, the position of stripping noise bands is predetermined, and it is possible to reduce the noise effectively using some spatial methods such as equalization of average and variance of the gray level distribution in different bands [4]. Apart from stripping noise, simple spatial methods cannot be used to reduce global and local periodic noise.

The local and global periodic noises in spatial domain can be modeled as the sum of sinusoidal functions, given by Eq. (1), where the noisy image appears like stars with high amplitude in the frequency domain [5].

$$\begin{aligned} n(x,y)\!=\!A\sin [2\pi u_0 (x\!+\!B_x )/M \!+\!2\pi v_0 (y+B_y )/N]\qquad \end{aligned}$$

(1)

In Eq. (1), $A$ is the noise amplitude; $u_{0}$ and $v_{0}$ determine the sinusoidal frequencies with respect to the $x$ and $y$ axes, respectively, and $B_{x}$ and $B_{y}$ are phase displacements with respect to the origin.

Since the periodic noise is spread throughout the whole image, it cannot be detected directly in the spatial domain and the frequency domain is preferred for its identification and reduction.

In this paper, a novel adaptive Gaussian notch filter, which is based on an automatic analysis of image spectrum contaminated by periodic noise, is proposed in the frequency domain to effectively reduce the effect of the periodic noise. Against the other existing methods, the proposed filter does not need any tuning and parameter adjustments. First, the proposed method tries to detect the frequency regions that correspond to periodic noise by applying a segmentation and region growing algorithm on the spectral band of the noisy image using an adaptive threshold. Then, proper Gaussian notch filters in which parameters are adaptively determined are used to decrease the periodic noises only at the contaminated noise frequencies.

Comparison results show that the proposed approach needs lower computational complexity. Moreover, it also restores the image with a good quality both visually and statistically.

In the next section, a review on some conventional periodic noise reduction algorithms is presented. The proposed adaptive Gaussian notch filter is described in the Sect. 3. Comparison results between the proposed algorithm and some conventional methods are given and discussed in the Sect. 4. Finally, some concluding remarks are presented in the last section.

2 A review on the existing algorithms

In this section, some existing algorithms for periodic noise reduction in the frequency domain including mean, median and Gaussian notch filters are reviewed and discussed. These filters are constructed from two main steps, namely the periodic noise identification phase and the frequency cancelation filter phase. The identification step checks to see whether the image frequency component corresponds to the unwanted periodic noise or the image data itself. The cancelation step attempts to filter out the noise frequency. Different identification and cancelation approaches are used in each method. Furthermore, a constant threshold is used in most of the methods to distinguish the image and noise components.

2.1 Median filter in frequency domain

This filter can operate in both frequency and spatial domains [6]. The frequency domain type is implemented on the image spectrum amplitude, and it is necessary to initially identify whether the spectrum component corresponds to periodic noise or not. A moving median window of $n \times n$ dimensions is used to filter the spectrum amplitude. The median value itself is used to check the amplitude of every spectral coefficient and accordingly identify whether the coefficient is significantly higher than the median of local components. If so, the coefficient is considered due to a periodic noise source and the median filtering is applied at that location.

The identification and filtering steps can be represented by the following equation:

$$\begin{aligned} Y_{i,j} \!=\!\left\{ \begin{array}{l@{\quad }l} \hbox {median}(X_{i,j} ) &{} {\hbox {if } \frac{X_{i,j}}{\hbox {median}(X_{i,j})}\ge \theta \,\hbox {and}\, (i,j)\ne (0,0)} \\ {X_{i,j}} &{} \hbox {otherwise} \\ \end{array}\right. ,\nonumber \\ \end{aligned}$$

(2)

where $X_{i,j}$ is the spectrum amplitude of the input image at the frequency of $(i, \,j), Y$ is the spectrum amplitude of the filtered image, $\hbox {median}(X_{i,j})$ is the median in the local $n \times n$ window around the spectrum coefficient being filtered, and $\theta$ is a predefined threshold. Conventionally, the window size in the frequency median filter is chosen equal to or larger than $5 \times 5$. Based on Eq. (2), the filter is not applied to center spectral coefficient ($X_{0,0}$), because it represents only the mean brightness of the image.

2.2 Mean filter in frequency domain

The idea of mean filtering in the frequency domain is to analyze the image spectrum amplitude using a sweeping local mean calculation mask of size $n \times n$, where $n$ is an odd number [7]. The coefficients of the mask are all 1, except the center which is 0. The local mean mask averages all local spectrum amplitudes except the central element since it may be the one which corresponds to the periodic noise frequency. Based on the ratio of the image input spectrum amplitude to the mask local mean value at the corresponding location, it is decided whether the frequency should be filtered or not.

The mean filter and identification in the frequency domain can be represented by the following relation:

$$\begin{aligned} Y_{i,j} =\left\{ \begin{array}{l@{\quad }l} {\frac{X_{i,j}}{\delta }} &{} {\hbox {if } \frac{X_{i,j}}{S(X_{i,j} )}\ge \theta \,\hbox {and}\, (i,j)\ne (0,0)} \\ {X_{i,j}} &{} \hbox {otherwise} \\ \end{array}\right. , \end{aligned}$$

(3)

where $X_{i,j}$ is the spectrum amplitude of the input image at the frequency of ($i, \,j), Y$ is the spectrum amplitude of the filtered image, $S(X_{i,j})$ is the mean value based on the $n \times n$ binary mask around the spectrum coefficient to be filtered, $\theta$ is the predefined threshold, and $\delta$ is a normalizing divider to reduce the amplitude of the periodic noise frequency.

2.3 Gaussian notch filter

In this filter, which operates on the image spectrum, the median value of the local window is used to check the amplitude of every spectral coefficient and select the noisy frequency according to the peak detector and identifier [8]. The frequency ($i,\,j$) in the spectrum is contaminated by periodic noise if the following condition meets:

$$\begin{aligned} \frac{X_{i,j}}{\hbox {median}(X_{i,j} )}\ge \theta , \end{aligned}$$

(4)

where median($X_{i,j}$) is the median value in the local $n \times n$ window around the spectrum coefficient ($i,\,j$) and $\theta$ is the predefined threshold.

After detecting the frequency of the periodic noise, the corresponding $X_{i,j}$ together with its neighborhood $m \times n$ window which is called ${\hat{X}}_{i,j}^{m,n}$ is corrected by the windowed Gaussian notch filter $G^{m,n}$ as follows:

$$\begin{aligned} \hat{{Y}}_{i,j}^{m,n} =\hat{{X}}_{i,j}^{m,n} \circ G^{m,n}, \end{aligned}$$

(5)

where $Y$ is the spectrum of the filtered image, ${\hat{Y}}_{i,j}^{m,n}$ is the $m \times n$ area around $Y_{i,j}$, “$\bullet$” denotes the element-wise matrix multiplication, and $G^{m,n}$ is an $m \times n$ matrix and its ($x, \,y$) element is defined as:

$$\begin{aligned} G^{m,n}&= 1-Ae^{-B(x^{2}+y^{2})} \nonumber \\ x&= -\left[ \frac{n}{2}\right] ,\ldots ,\left[ \frac{n}{2}\right] y=-\left[ \frac{m}{2}\right] ,\ldots ,\left[ \frac{m}{2}\right] , \end{aligned}$$

(6)

where [] denotes the integer part of a real number, $0<A<1$ is the magnitude of the generated peak, and $B>0$ is a scaling coefficient along the $x$ and $y$ axes. Therefore, for the output spectrum $Y$, the relation of the Gaussian notch filter can be defined as:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \hat{{Y}}_{i,j}^{m,n} \!=\!\hat{{X}}_{i,j}^{m,n} \circ G^{m,n} &{} {\hbox {if}\, \frac{X_{i,j}}{\hbox {median}(X_{i,j})}\ge \theta \, \hbox {and}\, (i,j)\ne (0,0)} \\ {Y_{i,j} =X_{i,j}} &{} \hbox {otherwise} \end{array} \right. \nonumber \\ \end{aligned}$$

(7)

Equation (6) defines a Gaussian-like surface. This equation has a single peak in the center of the surface and the surface is of the same size as the filtering window used in Eq. (5). Equation (7) is applied locally, so only coefficients within the filtering window are affected, which makes it more beneficial. Also, Eq. (6) is possible to define the width of the generated peak (controlled by $B$), its magnitude (controlled by $A$) and the corrected area ($m$ and $n$) independently, allowing a wide peak in a narrow window to attenuate strong spectral distortions.

2.4 Comparison of existing methods

Detection and identification of the frequencies that are contaminated by periodic noises is an important challenge in the periodic noise restoration procedure, where in some cases it can be solved by median and mean filtering in the frequency domain. However, one of the disadvantages of median filter is choosing an initial threshold value and filtering window size. Furthermore, since the median value should be calculated for all frequencies of the image, the computational complexity for realization of this filter is also high and exponentially increases with the median window dimension such that despite its effectiveness, it is not suitable for time critical applications. The mean filter in the frequency domain has less computational cost compared with the median filter in the frequency domain. Experimental results show that it removes sharp periodic noise in the frequency domain properly, but when the bandwidth of the periodic noise increases, the impact of this filter degrades and so some parts of noise will remain.

In terms of visual and statistical quality, the Gaussian notch filters result in better performance compared with the other methods. However, since the detection of noise frequency is similar to the median filter in the frequency domain, it inherits the same problems from the median filtering. Thus, in images contaminated by multiple frequencies, this filter shows poor performance. Also, increasing the noise power tends to decrease noise removal quality. In this paper, in order to improve these disadvantages, a novel adaptive Gaussian notch filter is proposed.

3 Proposed method: adaptive Gaussian notch filter

The proposed method is based on the Gaussian notch filter while it is accompanied by an adaptive image noise spectrum analyzing block to detect the noise frequencies and bandwidths. The proposed algorithm includes two basic steps: detection of the noise frequencies and applying a tuned Gaussian notch filter, for each noise component.

3.1 Detection of noise frequencies

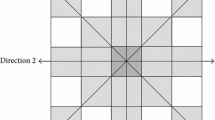
This step tries to detect the center frequency of each noise component using segmentation of noisy image spectrum and comparison with an adaptive threshold. When the image is contaminated by a periodic noise, the amplitude of the noise frequencies is generally higher than the corresponding frequencies of the original image; therefore, the noise frequencies can be separated by thresholding. On the other hand, the amplitude of spectrum frequencies near the origin (which is due to smooth part of the original image) tends to be relatively high and should not be confused with periodic noise. Therefore, before segmentation, it is necessary to separate this low frequencies region (LFR) whose radius is assumed $R_\mathrm{LFR}$, from the image spectrum. In order to determine the parameter $R_\mathrm{LFR}$, in the first step, the image spectrum is segmented into arc-shaped portions using concentric rings of 5 pixels width as shown in Fig. 2. Each ring is divided into $n$ slices, and the average value of each part is calculated. Subsequently, among the $n$ slices of each ring, the maximum average is chosen and the average intensity value of the selected slices can be plotted as a function of distance from the diagram origin. In order to choose the best $n$, we have tested different slices including 6, 12 and 16 for several images with different complexities. Averagely, for most of the images, 12 slices resulted in the best performance in terms of establishing a tradeoff between complexity and accuracy (Fig. 2).

Fig. 2

Example of image spectrum segmentation

As an example, Fig. 3 shows a noisy image, corresponding image spectrum, a mask made up of the parts featured with the maximum average, and multiplication of the mask and image spectrum. As it can be seen from the result, the noise frequencies are separated effectively by the corresponding mask.

Fig. 3

a Sample $256 \times 256$ Lena image contaminated with periodic noise. b Corresponding image spectrum. c Mask showing rings that have maximum mean and d multiplication of mask with image spectrum. The plot of slice averages that have maximum mean amplitude in their corresponding rings can be used to determine $R_\mathrm{LFR}$

Figure 4 illustrates the maximum average plot versus distance from origin for the case shown in Fig. 3d. When there are no periodic noises, the plot is almost a decreasing function of $R$, but in the existence of periodic noise, there are some peaks after the initial descending part of the plot. $R_\mathrm{LFR}$ is considered as the $R$ value of the first local minimum of the plot.

Fig. 4

Plot of mean amplitude of slices in Fig. 3c versus distance from origin (R)

Figure 5b shows the image spectrum of Fig. 3a, after resetting all amplitude of corresponding frequencies inside $R_\mathrm{LFR}$ to zero. Actually, Fig. 5b is similar to a thermal image when there are some warm target points (Figs. 4, 5).

Fig. 5

a Image spectrum of Fig. 3a, b image spectrum after resetting the region inside $R_\mathrm{LFR}$ to zero and c detection of the noise center frequencies, like warm target points in thermal images

In an infrared image, when the temperature of a point target is higher than the background, it will appear as bright spots. This condition is also observed in the image spectrum contaminated by periodic noise since the noise frequencies are higher than the other components. Therefore, the segmentation algorithm for warm point targets in the infrared images [9] can be used for the identification of the noise targets. To determine the center of noise frequencies, a proper threshold value ($A_\mathrm{th}$) is required for the image spectrum thresholding algorithm. The threshold value ($A_\mathrm{th}$) can be determined by Eq. (11) as follows:

$$\begin{aligned} A_\mathrm{th} = \frac{(A_\mathrm{max} + A_\mathrm{mean})}{2}, \end{aligned}$$

(8)

where $A_\mathrm{max}$ and $A_\mathrm{mean}$ are the maximum value and mean value of image spectrum amplitude after eliminating the LRF region, respectively. To avoid the effect of noisy frequency components in extraction of $A_\mathrm{mean}$, the corners of the image spectrum are used for this purpose. As shown in Fig. 6, the four arc regions that reside outside of the circle with radius $R$ are considered as the noise free area. The radius $R$ can be calculated by the following equation:

$$\begin{aligned} R\!=\!\hbox {maximum} \left\{ {\sqrt{\left( \frac{M}{2}\right) ^{2}\!+\! \left( \frac{N}{4}\right) ^{2}}}, \sqrt{\left( \frac{M}{4}\right) ^{2} \!+\!\left( \frac{N}{2}\right) ^{2}} \right\} ,\nonumber \\ \end{aligned}$$

(9)

where $M$ and $N$ are the image dimensions.

Fig. 6

Four arc corners used to calculate $A_\mathrm{mean}$

After computing the threshold value ($A_\mathrm{th}$) based on Eq. (8), thresholding is applied to the whole image spectrum, except the LFR region, and the center frequency of periodic noise components is extracted.

In this work, the actual noise reduction block is a Gaussian notch filter, therefore, in order to tune the parameters $m$ and $n$ in Eq. (7), besides the noise center frequency; its expansion about the center is also required. To extract the amount of noise spreading in the frequency domain, a region growing algorithm is incorporated. The proposed algorithm is similar to the method presented in Szeliski [10] and is based on selecting the noise center frequencies as the initial seeds and extending the region till a certain criteria is met. For this purpose, initially a $3 \times 3$ window is placed around the noise center frequencies that were detected by the previous adaptive thresholding step. Then, a larger $5 \times 5$ window is used for neighbor cell comparison. Figure 7 shows all pair pixels that should be used for comparison. As shown in this figure, every three corners in the larger window are compared with a single corresponding cell in the smaller window.

Fig. 7

Two $3 \times 3$ and $5 \times 5$ windows, used in the proposed region growing algorithm

Generally, when a frequency is contaminated by periodic noise, its corresponding amplitude in the larger window should be lower than its comparison pair in the smaller window. This means that when the amplitude of a frequency component in the $5 \times 5$ window is lower than its corresponding comparison cell in the $3 \times 3$ window, this frequency should be also be considered as noise frequency. If more than half of the frequencies in the $5 \times 5$ window are contaminated by periodic noise, the growing algorithm is repeated with the $5 \times 5$ window, as the initial frame, and the surrounding $7 \times 7$ window, as the comparison neighbor cells. After termination of this process, the dimensions of the surrounding window of noise frequencies are used to tune the parameters $m$ and $n$ in Eq. (5). For a sample detected noise, center frequency in Fig. 8a,b shows all frequencies contaminated by periodic noise. The surrounding window for tuning the parameters $m$ and $n$ in Gaussian notch filter is shown in Fig. 8c by the white window.

Fig. 8

a Close-up of a sample noise frequency, b all noise frequencies detected by the proposed region growing algorithm which is shown by black and c the surrounding window for tuning the Gaussian notch filter

3.2 Applying the Gaussian notch filter

After detecting all noise frequency components and corresponding dimensions of the surrounding window, the Gaussian notch filter is used to compensate these components. It means that each detected noise frequencies has its own $m$ and $n$ in Eq. (6). Since the detection of all noise frequencies and corresponding parameters is adaptively done, the proposed method is relatively robust to changes in the image and periodic noise conditions.

4 Results and comparison

The proposed adaptive Gaussian notch filter algorithm has been implemented in MATLAB environment and compared with the frequency domain mean, median and Gaussian notch filters, qualitatively and quantitatively. Moreover, execution times of compared algorithms are presented as a criterion for complexity comparison. In order to quantitatively compare the results, the mean absolute error (MAE) between the original and filtered images and its standard deviation (STD) are presented. The MAE and STD are expressed with Eq. (10a) and (10b), respectively.

$$\begin{aligned} \hbox {MAE}&= \frac{1}{N.M}\sum _{i=0}^{N-1} \sum _{j=0}^{M-1} \left[ \big | x(i,j)-y(i,j) \big | \right] \end{aligned}$$

(10a)

$$\begin{aligned} \hbox {STD}\!&= \!\left[ \frac{1}{N.M}\sum _{i=0}^{N-1} \sum _{j=0}^{M-1} \left[ \big | x(i,j)\!-\!y(i,j) \big |\!-\!\hbox {MAE} \right] ^{2} \right] ^{\frac{1}{2}}\nonumber \\ \end{aligned}$$

(10b)

In Eq. (11), $M$ and $N$ are the image dimensions; $x$ is the original noiseless image, while $y$ is the restored image after applying the restoration algorithm. Lower MAE means the restoration algorithm shows higher performance. Lower STD shows that the variation between the noiseless and restored images is lower.

MAE and STD are appealing because they are simple to calculate, have clear physical meanings and are mathematically convenient in the context of optimization. But they are not very well matched to perceived visual image quality. The measure of structural similarity (SSIM) can be used to compare the visual quality of original and distorted images [11]:

$$\begin{aligned} \hbox {SSIM} (x,y)=\frac{(2\mu _x \mu _y +C_1 )(2\sigma _{xy} +C_2)}{(\mu _x ^{2}+\mu _y^{2}+C_1 )(\sigma _x^{2}+\sigma _y^{2}+C_2 )} \end{aligned}$$

(11)

In Eq. (11), SSIM (x,y) is equal to unity if and only if x=y. $\mu _x$ is the mean intensity and $\sigma _x$ is the STD (the square root of variance) of pixels and can be calculated by Eqs. (12) and (13) as follows:

$$\begin{aligned} \mu _x&= \frac{1}{N.M}\sum _{i=0}^{N-1} {\sum _{j=0}^{M-1} {\left[ {x(i,j)} \right] }}\end{aligned}$$

(12a)

$$\begin{aligned} \mu _y&= \frac{1}{N.M}\sum _{i=0}^{N-1} {\sum _{j=0}^{M-1} {\left[ {y(i,j)} \right] }} \end{aligned}$$

(12b)

$$\begin{aligned} \sigma _x&= \left[ {\frac{1}{N.M-1}\sum _{i=0}^{N-1} {\sum _{j=0}^{M-1} {\left[ {x(i,j)-\mu _x} \right] ^{2}}}} \right] ^{\frac{1}{2}}\end{aligned}$$

(13a)

$$\begin{aligned} \sigma _y&= \left[ {\frac{1}{N.M-1}\sum _{i=0}^{N-1} {\sum _{j=0}^{M-1} {\left[ {y(i,j)-\mu _y} \right] ^{2}}}} \right] ^{\frac{1}{2}}\end{aligned}$$

(13b)

$$\begin{aligned} \sigma _{xy}&= \left[ {\frac{1}{N.M-1}\sum _{i=0}^{N-1} {\sum _{j=0}^{M-1} {\left[ {(x(i,j)-\mu _x )(y(i,j)-\mu _y )} \right] }}}\right] ^{\frac{1}{2}}\nonumber \\ \end{aligned}$$

(13c)

In Eq. (11), $C_{1}$ and $C_{2}$ are added to avoid instability when $\mu _{x}^{2}+\mu _{y}^{2}$ or $\sigma _{x}^{2}+\sigma _{y}^{2}$ are very close to zero. They can be adjusted by $C_{1}=(K_{1}L)^{2}$ and $C_{2}=(K_{2}L)^{2}$, where $K_{1} \ll 1$ and $K_{2} \ll 1$ are small constants and $L$ is the dynamic range of the pixel values (255 for 8-bit gray level images). In this work, both $K_{1}$ and $K_{2}$ are set to 0.05.

4.1 Results for simulated periodic noises

Generally, when an image is corrupted by a single frequency periodic noise, all compared restoration algorithms work well, but multi-frequency periodic noise is a challenging problem. Therefore, in the first simulation, the multi-frequency periodic signal $n(x,y)$, given by Eq. (14), was chosen as the noise source:

$$\begin{aligned} n(x,y)&= A\times [\sin (8y)+\sin (8x)\nonumber \\&+ \sin (5.25x + 5.25y) + \sin (x + 5.25y)] \end{aligned}$$

(14)

In the compared methods, including frequency domain median, mean and Gaussian notch filters, in order to obtain suitable results, some parameters should be initially tuned. The simulation results show the window dimension $11 \times 11$ is the best choice for parameter $n$ in Eqs. (2), (3) and (4). Similarly, the threshold value $\theta$ for median, mean and Gaussian notch filters was considered 6, 5 and 4.5, respectively. The normalizing divider in Eq. (3) was set to 100, and coefficients $A$ and $B$ in the Gaussian notch filter are set to 1.0 and 0.01, respectively, while $m$ and $n$ are both set at 7, in Eq. (5) [8]. In contrast, the proposed adaptive Gaussian notch filter method requires no parameter adjustments, which is a major advantage of the technique.

In the first simulation, the amplitude of periodic noise in Eq. 14 is set to 0.05. Figure 9 shows the result of the different algorithms for image restoration.

Fig. 9

a Sample noisy image with $A=0.05$ in Eq. (14), restored image with b mean, c median, d Gaussian notch filters and e the proposed adaptive Gaussian notch filter method

The quantitative results including MAE and STD as well as execution times of the compared algorithms are presented in Table 1. An Intel Core 2 Duo CPU T9550, 2.66 GHz with 4.096 GB DRAM was chosen as the processor.

Table 1 Comparison results of adaptive Gaussian notch (AGNF), Gaussian notch (GNF), median and mean filters

In order to evaluate the results in different noise amplitudes, in the second simulation, the amplitude $A$ in Eq. (14) is varied between 0.1 and 0.9. The MAE, STD and SSIM values are plotted versus $A$, in Figs. 10, 11 and 12, respectively. When the noise amplitude increases, MAE and STD also increase but SSIM decreases.

Fig. 10

Plot of MAE versus noise amplitude ($A$) for the compared algorithms

Fig. 11

Plot of STD versus noise amplitude ($A$) for the compared algorithms

Fig. 12

Plot of SSIM versus noise amplitude ($A$) for the compared algorithms

In terms of MAE and SSIM, the proposed algorithm, AGNF, shows the best results. Moreover, if the noise amplitude ($A$) increases, difference between AGNF and GNF as nearest competitor in terms of MAE and SSIM increases. It means that AGNF could adaptively work and it also does not need any parameter tuning. However, in terms of STD, at some amplitude, GNF shows better results than AGNF. Considering all the criteria, we conclude that AGNF is the best algorithm.

In the next simulation, four noise signals with arbitrary frequencies and amplitudes are added to 5 different input images and then restored using the median, mean, GNF and AGNF filters. The parameter SSIM is calculated for each case and reported in Tables 2, 3, 4 and 5. The noise signals $N_{1}$ through $N_{4}$ are given by Eqs. (15)–(18).

$$\begin{aligned} N_1 (x,y)&= 0.2\times [\sin (1.8x+1.8y)+\sin (x+y)\nonumber \\&\quad +\sin (2.2x+2.2y)+\sin (1.8x-1.8y) \nonumber \\&\quad +\sin (x-y)+\sin (2.2x-2.2y)]\end{aligned}$$

(15)

$$\begin{aligned} N_2 (x,y)&= 0.15\times [\sin (0.5x-0.5y) \nonumber \\&\quad + \sin (1.5x\!-\!1.5y)\!+\!\sin (2.5x\!-\!2.5y)]\qquad \end{aligned}$$

(16)

$$\begin{aligned} N_3 (x,y)&= 0.1\times [\sin (2x+2y) \nonumber \\&\quad +\sin (0.5x\!+\!y0.5)\!+\!\sin (3x)\!+\!\sin (4y)]\qquad \end{aligned}$$

(17)

$$\begin{aligned} N_4 (x,y)&= 0.05\times [\sin (1.1x+1.1y)+\sin (1.5x) \nonumber \\&\quad +\sin (1.5y)+\sin (1.1x-1.1y)] \end{aligned}$$

(18)

Figure 13 shows the result of reconstructing images corrupted with the periodic noise $N_{1}$ for qualitative comparison. The contaminated images are shown in the first row. In the second, third, fourth and fifth row, the results of applying median, mean, Gaussian notch and the proposed adaptive Gaussian notch method to the noise input images are represented, respectively.

Fig. 13

a Contaminated images with noise $N_{1}$, restored image with b median, c mean, d Gaussian notch filters and e the proposed adaptive Gaussian notch filter

Table 2 Comparison results for adaptive Gaussian notch (AGNF), Gaussian notch (GNF), median and mean filters applied on images degraded by periodic noise $N_{1}$

Table 3 Comparison results for adaptive Gaussian notch (AGNF), Gaussian notch (GNF), median and mean filters applied on images degraded by periodic noise $N_{2}$

Table 4 Comparison results for adaptive Gaussian notch (AGNF), Gaussian notch (GNF), median and mean filters applied on images degraded by periodic noise $N_{3}$

Table 5 Comparison results for adaptive Gaussian notch (AGNF), Gaussian notch (GNF), median and mean filters applied on images degraded by periodic noise $N_{4}$

The AGNF algorithm has also been applied to an image with periodic stripes, and the result is shown the Fig. 14.

Fig. 14

a Image with periodic stripes, b image spectrum, c restored image with the proposed method, adaptive Gaussian notch filter and d spectrum of restored image

4.2 Results for real periodic noise

In order to evaluate the performance of the compared algorithm in real situation, a real television image that has been interfered with a periodic electrical signal is tested as benchmark. Unfortunately, the MAE value of the compared algorithm cannot be computed, because the original image is not accessible. Figure 15 shows the restored images using different approaches. In this example, qualitatively, the AGNF and median filter show the best results, while AGNF complexity is lower and it does not need any parameter adjustment steps.

Fig. 15

a Real television image corrupted by a complex periodic noise, b the image spectrum, the restored image by c median filter, d mean filter, e Gaussian notch filter and finally, f adaptive Gaussian notch filter

5 Conclusions

In order to reduce the effect of periodic image noise, in this paper, an adaptive Gaussian notch filter was presented. The proposed algorithm consists of two main stages. In the first stage, the main noisy frequencies are detected by the proposed thresholding in the image spectrum space, with an adaptive threshold value. Then, for each main noise component, the proposed region growing algorithm is used to determine all corrupted frequencies. In the second stage, a tuned Gaussian notch filter is applied on the noisy image to reduce the effects of the periodic noise.

The proposed algorithm was compared with the frequency domain mean, median and Gaussian notch filters for restoring the images corrupted by simulated and real periodic noise sources. Experimental results showed that the proposed algorithm not only does not need any initial parameters setting, but also provides higher performances, quantitatively and qualitatively. Moreover, the complexity of the proposed algorithm was shown to be lower than the previously reported algorithms.

For multi-dimensional images like color images, where the noise property is equal for all dimensions, the proposed method can be used for periodic noise reduction in which computational complexity increases linearly relative to the number of dimensions.