A stochastic periodic review inventory model with back-order discounts and ordering cost dependent on lead time for the mixtures of distributions

Abstract

A mixture inventory system analyzed in this paper explores the problem that the lead time and ordering cost reductions are inter-dependent in a periodic review inventory model with back-order price discounts for protection interval demand with the mixture of normal distributions. The objectives of this paper are twofold. First, we want to correct and improve the recently studied model by optimizing the review period, back-order price discount, target level and lead time simultaneously to achieve significant savings in the total related cost and higher service level. Second, we consider that the demands of the different customers are not identical in the protection interval to accommodate more practical features of the real inventory systems. For the proposed model, a computational algorithm with the help of the software Mathematica 7 is furnished to derive the optimal solution. Finally, we provide numerical examples to illustrate the results.

1 Introduction

In most of the literature dealing with inventory problems, lead time is generally viewed as a prescribed parameter, no matter whether it is deterministic or probabilistic, and consequently cannot be controlled (see, e.g., Naddor 1966; Silver and Peterson 1985; Paknejad et al. 1995; Bartoszewicz and Lesniewski 2014). In more recent years, the issue of lead time reduction has received a lot of interest. In fact, lead time can usually be decomposed into several components (Tersine 1982) and in many practical situations, it can be reduced at an extra-added crashing cost; in other words, it is controllable. As a result by shortening the lead time, we can lower the safety stock, reduce the loss caused by stock-out and improve the service level to the customers so as to improve the competitive edge. There has been some inventory model literature in the field considering lead time reduction (see, among others, Liao and Shyu 1991; Ben-Daya and Raouf 1994; Ouyang et al. 1996; Moon and Choi 1998; Hariga 1999; Hariga and Ben-Daya 1999; Wu and Tsai 2001; Ouyang et al. 2002; Hoque and Goyal 2004; Hayya et al. 2011; Lin 2012; Jaggi et al. 2014). In addition, Pan and Hsiao (2001) studied the continuous review inventory model with back-order discounts and variable lead time. They observed that a supplier can always offer a price discount on the stock-out item to compensate the buyers to secure more back-orders when shortages occur. Thus, back ordering, as well as the lead time, appears to be negotiable and can be controlled to some extent by offering a price discount from a supplier. So, if the reduced amount does not exceed the gross marginal profit of the sale or is less significant than the loss of the goodwill of the supplier, then both parties may benefit from such a stock-out discount offer; moreover, the larger the back-order discount, the larger the back-order rate. Thus, the back-order rate is dependent on the back-order price discounts which are offered by the supplier. Chen et al. (2001) proposed a continuous review inventory model with ordering cost dependent on lead time. In a recent paper, Lin (2008) analyzed the inventory model in which the lead time and ordering cost reductions are inter-dependent in the continuous review inventory model with back-order price discount. In contrast to the continuous review inventory models, the applications of the periodic review inventory models can often be found in managing inventory cases such as smaller retail stores, drugstores and grocery stores [see the discussion in Taylor (1999)]. Ouyang et al. (2007) proposed a periodic review inventory model with the controllable back-order price discount and observed that lead time and ordering cost reductions are dependent and their functional relationship may be as linear, logarithmic, exponential and the like. But, they assumed that the protection interval demand is normally distributed and considered a restriction that the target level must satisfy the following equation $P(X>R)=q$ which implies a service level constraint. They made a mistake by including both the service level constraint and the shortage cost into the model in which both are being used redundantly to determine the appropriate level of safety stocks. Besides, in the protection interval, the demands of the different customers are not identical and the demand of distribution for each customer can be adequately approximated by a distribution. The overall demand of distribution is then a mixture (see, among others, Lee et al. 2004, 2006, 2007; Lee 2005; Wu et al. 2007, 2009; Lin 2013; we note that these papers focus on the continuous review inventory model). Thus, we cannot use only a single distribution [such as Ouyang et al. (2007)] to describe the demand of the protection interval. The periodic review inventory model involving protection interval demand with the mixtures of distributions has rarely been discussed in the existing literature. Following the above motivation, in this study, we extend and correct the Ouyang et al. (2007) model by considering the mixture of normal distributions and allowing the target level as a decision variable; it is obvious that we can obtain a better solution by allowing the target level as a decision variable. A significant amount of savings over their model can be achieved. Furthermore, a computational algorithm with the help of the software Mathematica 7 is furnished to find the optimal values of the decision-making variables. Some numerical examples are given to illustrate our model.

The rest of this paper is organized as follows. In Sect. 2, the notation and assumptions are presented. In Sect. 3, we formulate a periodic review inventory model with back-order price discounts and ordering cost dependent on lead time for protection interval demand with the mixture of normal distributions. We solve the cases of the linear and logarithmic relationships between lead time and ordering cost reduction and then develop a computational algorithm to find the optimal solution. Section 4 provides numerical examples to demonstrate the results. Finally, Sect. 5 concludes the paper.

2 Notation and assumptions

The following notation and assumptions are used throughout the paper to develop the proposed models.

Notation

$A_0$ :

Original ordering cost (before any investment is made)

$A(L)$ :

Ordering cost per order, $0<A(L)\le A_0$

$D$ :

Expected demand per year

$h$ :

Holding cost per unit per year

$L$ :

Length of lead time (decision variable)

$p$ :

The weight of the component distributions, $0\le p\le 1$

$R$ :

Target level (decision variable)

$T$ :

Length of a review period (decision variable)

$\beta$ :

Fraction of the shortage during the stock-out period that will be backordered, i.e., back-order ratio, $\beta \in [0,1)$ (decision variable)

$\beta _0$ :

Upper bound of the back-order ratio

$\pi _x$ :

Back-order price discount offered by the supplier per unit (decision variable)

$\pi _0$ :

Marginal profit (i.e., cost of lost demand) per unit

$X$ :

The protection interval demand has the mixtures of cumulative distribution function (c.d.f.) $F_*=pF_1 +(1-p)F_2 ,$ where $F_1$ has finite mean $\mu _1 (T+L)$ and standard deviation $\sigma \sqrt{T+L}$ and $F_2$ has finite mean $\mu _2 (T+L)$ and standard deviation $\sigma \sqrt{T+L} ,$ $\mu _1 -\mu _2 ={\eta \sigma } / {\sqrt{T+L} },$ $\eta >0,$ a random variable

$E {[\cdot ]}$ :

Mathematical expectation

$x^+$ :

Maximum value of $x$ and 0, i.e., $x^+=\max \{x,0\}$

Assumptions

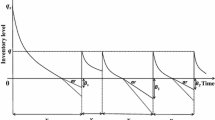
• 1. The inventory level is reviewed every $T$ units of time. A sufficient quantity is ordered up to the target level, $R,$ and the ordering quantity is received after $L$ units of time.

• 2. The length of the lead time $L$ does not exceed an inventory cycle time $T$, so that there is never more than a single order outstanding in any cycle, i.e., $L\le T.$

• 3. The target level, R = expected demand during the protection interval + safety stock (SS), and $SS=k\, \times \,$(standard deviation of protection interval demand), i.e., $R=\mu _*(T+L)+k\sigma _*\sqrt{T+L} ,$ where $\mu _*=p\mu _1 +(1-p)\mu _2 ,$ $\sigma _*=\sqrt{1+p(1-p)\eta ^2} \sigma ,$ $\mu _1 ={\mu _*+(1-p)\eta \sigma } /{\sqrt{T+L} },$ $\mu _2 ={\mu _*-p\eta \sigma } /{\sqrt{T+L} },$ and $k$ is known as the safety factor.

• 4. The lead time $L$ consists of $m$ mutually independent components. The $l$th component has a minimum duration $a_l$ and normal duration $b_l ,$ and the crashing cost per unit time, $c_l .$ Furthermore, these $c_l$ are assumed to be arranged such that $c_1 \le c_2 \le \cdots \le c_m .$

• 5. The components of lead time are crashed one at a time starting with the component of least $c_l ,$ and so on.

• 6. If we let $L_0 =\sum \nolimits _{j=1}^m {b_j }$ and $L_i$ be the length of lead time with components $1, 2,\;\ldots ,$ $i$ crashed to their minimum duration, then $L_i$ can be expressed as $L_i =\sum \nolimits _{j=1}^m {b_j } -\sum \nolimits _{j=1}^i {(b_j -a_j )} ,$ $i=1,$ $2, \ldots ,\;m$ and the lead time crashing cost per cycle, $C(L),$ for a given $L\in (L_i ,L_{i-1} ]$ is given by $C(L)=c_i (L_{i-1} -L)+\sum \nolimits _{j=1}^{i-1} {c_j (b_j -a_j )}$.

• 7. The reduction of lead time $L$ accompanies a decrease of ordering cost, $A(L),$ and $A(L)$ is a strictly concave function of $L$, i.e., ${A}'(L)>0$ and ${A}''(L)<0.$

• 8. During the stock-out period, the back-order ratio, $\beta ,$ is variable and is in proportion to the back-order price discount offered by the supplier per unit, $\pi _x$. Thus, $\beta ={\beta _0 \pi _x } /{\pi _0 },$ where $0\le \beta <1$ and $0\le \pi _x \le \pi _0$ (Pan and Hsiao 2001).

3 Model formulation

In this section, we consider the protection interval demand, $X,$ has a mixture of normal distributions $F_*=pF_1 +(1-p)F_2 ,$ where $F_1$ has a normal distribution with finite mean $\mu _1 (T+L)$ and standard deviation $\sigma \sqrt{T+L}$ and $F_2$ has a normal distribution with finite mean $\mu _2 (T+L)$ and standard deviation $\sigma \sqrt{T+L}$, $\mu _1 -\mu _2 ={\eta \sigma } /{\sqrt{T+L} },$ $\eta >0.$ Thus, the mixture of probability density function of $X$ is

$$\begin{aligned} f_{X} (x)=p\frac{1}{\sqrt{2\pi } \sigma \sqrt{T+L} } \mathrm{e}^{{-\frac{1}{2}\left( {\frac{x-\mu _1 (T+L)}{\sigma \sqrt{T+L} }}\right) }^2} +(1-p)\frac{1}{\sqrt{2\pi } \sigma \sqrt{T+L}} \mathrm{e}^{{-\frac{1}{2}\left( {\frac{x-\mu _2 (T+L)}{\sigma \sqrt{T+L} }}\right) }^2}, \end{aligned}$$

(1)

where $\mu _1 -\mu _2 ={\eta \sigma } / {\sqrt{T+L} }$, $\eta >0$, $x\in \mathrm{R}$, $0\le p\le 1$, $\sigma >0$. Moreover, the mixture of normal distribution is a unimodal distribution for all $p$ if $(\mu _1 -\mu _2 )^2<{27\sigma ^2} / {8(T+L)}$ (or $0<\eta <\sqrt{{27}/8} )$ (Everitt and Hand 1981) and the target level $R=\mu _*(T+L)+k\sigma _*\sqrt{T+L}$, where $k$, $\mu _*$ and $\sigma _*$ are defined as above. Using the same approach as in Montgomery et al. (1973) for the periodic review case, the expected net inventory level at the beginning of the period is $R-DL+(1-\beta )E(X-R)^+$, and the expected net inventory level at the end of the period is $R-DL-DT+(1-\beta )E(X-R)^+$. Thus, the expected annual holding cost is approximately $h\left[ {R-DL-\frac{DT}{2}+(1-\beta )E(X-R)^+} \right]$, and the expected annual stock-out cost is ${\left[ {\pi _x \beta +\pi _0 (1-\beta )} \right] E(X-R)^+} / T$, where $E(X-R)^+=\int _R^{\;\infty } {(x-R)dF_*(x)}$ is the expected demand shortage at the end of the cycle.

$$\begin{aligned} E(X-R)^+=\int _R^{\;\infty } {(x-R)f_X (x)dx=\sigma \sqrt{T+L} \Psi (R_1 ,R_2 ,p)} , \end{aligned}$$

(2)

where

$$\begin{aligned} \Psi (R_1 ,R_2 ,p)=p\left\{ {\phi (R_1 )\,{-}\,R_1 \left[ {1\,{-}\,\Phi (R_1 )} \right] } \right\} +(1\,{-}\,p)\left\{ {\phi (R_2 )\,{-}\,R_2 \left[ {1\,{-}\,\Phi (R_2 )} \right] } \right\} , \end{aligned}$$

$$\begin{aligned} R_1 =\frac{R-\mu _1 (T+L)}{\sigma \sqrt{T+L} }=k\sqrt{1+p(1-p)\eta ^2} -(1-p)\eta , \end{aligned}$$

and $R_2 =\frac{R-\mu _2 (T+L)}{\sigma \sqrt{T+L} }=k\sqrt{1+p(1-p)\eta ^2} +p\eta$; $\phi$ and $\Phi$ denote the standard normal p.d.f. and cumulative distribution function (c.d.f.), respectively. This is done by direct calculation. Due to $R=\mu _*(T+L)+k\sigma _*\sqrt{T+L}$ (by assumption 3), we can treat the safety factor, $k$, as a decision variable instead of target level, $R$, and moreover, due to $\beta ={\beta _0 \pi _x } / {\pi _0 }$ (by assumption 8), the back-order price discount offered by a supplier per unit, $\pi _x$, can be viewed as a decision variable instead of the back-order ratio, $\beta$. The objective of the problem is to minimize the total expected annual cost which is the sum of the ordering cost, inventory holding cost, stock-out cost and lead time crashing cost. Symbolically, our problem is

$$\begin{aligned} \mathop {\text{ Min }}\limits _{(T,\pi _x ,k,L)} \;{\text{ EAC }}(T,\pi _x ,k,L)&= \frac{A(L)+C(L)}{T}\nonumber \\&+h\left[ {\frac{DT}{2}+k\sigma \sqrt{\left[ {1+p(1-p)\eta ^2} \right] (T+L)} } \right] \nonumber \\&+\left[ {h( {1\!-\!\frac{\beta _0 \pi _x }{\pi _0 }})+\frac{G(\pi _x )}{T}} \right] \sigma \sqrt{T+L} \Psi (R_1 ,R_2 ,p),\nonumber \\ \end{aligned}$$

(3)

where $\mathrm{EAC}(\cdot )$ denotes the total expected annual cost and $G(\pi _x )=\pi _0 -\beta _0 \pi _x +\frac{\beta _0 \pi _x ^2}{\pi _0 }>0.$ To solve this nonlinear programming problem, we take the first-order partial derivatives of $\mathrm{EAC}(T,\pi _x ,k,L)$ with respect to $T,$ $\pi _x ,$ $k$ and $L\in (L_i ,L_{i-1} ).$ We obtain

$$\begin{aligned}&\frac{\partial \mathrm{EAC}(T,\pi _x ,k,L)}{\partial T}\nonumber \\&\quad =- \frac{A(L)+C(L)}{T^2}+h\left[ {\frac{D}{2}+\frac{k\sigma \sqrt{1+p(1-p)\eta ^2} }{2\sqrt{T+L} }} \right] \nonumber \\&\qquad -\frac{G(\pi _x )\sigma \sqrt{T\!+\!L} \Psi (R_1 ,R_2 ,p)}{T^2} \!+\!\frac{\left[ {h( {1\!-\!\frac{\beta _0 \pi _x }{\pi _0 }}) \!+\!\frac{G(\pi _x )}{T}} \right] \sigma \Psi (R_1 ,R_2 ,p)}{2\sqrt{T\!+\!L} },\quad \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\partial \mathrm{EAC}(T,\pi _x ,k,L)}{\partial \pi _x }=\left[ {\frac{2\beta _0 \pi _x }{\pi _0 T}-\frac{\beta _0 }{T}-\frac{h\beta _0 }{\pi _0 }} \right] \sigma \sqrt{T+L} \Psi (R_1 ,R_2 ,p),\end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial \mathrm{EAC}(T,\pi _x ,k,L)}{\partial k}=h\sigma \sqrt{\left[ {1+p(1-p)\eta ^2} \right] (T+L)} +\sqrt{\left[ {1+p(1-p)\eta ^2} \right] } \nonumber \\&\qquad \times \left[ {h( {1-\frac{\beta _0 \pi _x }{\pi _0 }})+\frac{G(\pi _x )}{T}} \right] \sigma \sqrt{T+L} \left[ {F_*(R)-1} \right] , \end{aligned}$$

(6)

and

$$\begin{aligned} \frac{\partial \mathrm{EAC}(T,\pi _x ,k,L)}{\partial L}&= \frac{{A}'(L)-c_i }{T}+\frac{hk\sigma \sqrt{1+p(1-p)\eta ^2} }{2\sqrt{T+L} } \nonumber \\&+\frac{\left[ {h( {1-\frac{\beta _0 \pi _x }{\pi _0 }})+\frac{G(\pi _x )}{T}} \right] \sigma \Psi (R_1 ,R_2 ,p)}{2\sqrt{T+L} }. \end{aligned}$$

(7)

Where $F_*(R)=p\Phi (R_1 )+(1-p)\Phi (R_2 )$.

By examining the second-order sufficient conditions, it can be shown that $\mathrm{EAC}(T,\pi _x ,k,L)$ is not a convex function of $(T,\pi _x ,k,L)$. However, for fixed $( \hbox {T},\pi _x ,k),$ $\mathrm{EAC}(T,\pi _x ,k,L)$ is concave in $L\in [L_i ,L_{i-1} ],$ since

$$\begin{aligned} \frac{\partial ^2\mathrm{EAC}(T,\pi _x ,k,L)}{\partial L^2}&= \frac{{A}''(L)}{T}-\frac{hk\sigma \sqrt{1+p(1-p)\eta ^2} }{4(T+L)^{3/2}}\nonumber \\&-\frac{\left[ {h( {1-\frac{\beta _0 \pi _x }{\pi _0 }})+\frac{G(\pi _x )}{T}} \right] \sigma \Psi (R_1 ,R_2 ,p)}{4(T+L)^{3 / 2}}<0. \end{aligned}$$

(8)

Thus, for fixed $T,$ $\pi _x$ and $k,$ the minimum total expected annual cost will occur at the end points of the interval $[L_i ,L_{i-1} ].$ However, it is difficult to solve the problem by deriving an explicit equation of the solution from the following equations: ${\partial \mathrm{EAC}(T,\pi _x ,k,L)} /{\partial T=0},$ ${\partial \mathrm{EAC}(T,\pi _x ,k,L)} /{\partial \pi _x =0}$ and ${\partial \mathrm{EAC}(T,\pi _x ,k,L)} / {\partial k=0}.$ It is also hard to verify that the sufficient conditions of optimality of the solutions are satisfied. Solving these equations for $T,$ $\pi _x$ and $k,$ we obtain

$$\begin{aligned}&\frac{A(L)+C(L)}{T^2}+\frac{G(\pi _x )\sigma \sqrt{T+L} \Psi (R_1 ,R_2 ,p)}{T^2}\nonumber \\&\quad =\frac{hD}{2}+\frac{h\sigma }{2\sqrt{T+L} }\left[ {k\sqrt{1+p(1-p)\eta ^2} +\left( {1-\frac{\beta _0 \pi _x }{\pi _0 }}\right) \Psi (R_1 ,R_2 ,p)} \right] \nonumber \\&\qquad +\frac{G(\pi _x )\sigma \Psi (R_1 ,R_2 ,p)}{2T\sqrt{T+L} },\end{aligned}$$

(9)

$$\begin{aligned}&\pi _x =\frac{\pi _0 +Th}{2}, \end{aligned}$$

(10)

and

$$\begin{aligned} 1-F_*(R)=\frac{h}{h( {1-\frac{\beta _0 \pi _x }{\pi _0 }})+\frac{G(\pi _x )}{T}}. \end{aligned}$$

(11)

However, the total expected annual cost function is convex in $T$ because

$$\begin{aligned}&\frac{\partial ^2\mathrm{EAC}(T,\pi _x ,k,L)}{\partial T^2} \nonumber \\&\quad =\frac{2\left[ {A(L)+C(L)} \right] }{T^3}-\frac{h\sigma }{4(T+L)^{3 /2}}\left[ k\sqrt{1+p(1-p)\eta ^2}\right. \end{aligned}$$

(12)

$$\begin{aligned}&\qquad \left. +\left( {1-\frac{\beta _0 \pi _x }{\pi _0 }}\right) \Psi (R_1 ,R_2 ,p) \right] +G(\pi _x )\sigma \Psi (R_1 ,R_2 ,p)\nonumber \\&\qquad \times \left[ {-\frac{1}{T^2\sqrt{T+L} }+\frac{2\sqrt{T+L} }{T^3}-\frac{1}{4T(T+L)^{3 /2}}} \right] \nonumber \\&\quad =\frac{2\left[ {A(L)+C(L)} \right] }{T^3}-\frac{A(L)+C(L)}{2T^2(T+L)}+\frac{hD}{4(T+L)}+G(\pi _x )\sigma \Psi (R_1 ,R_2 ,p)\nonumber \\&\qquad \times \left[ \frac{1}{4T(T+L)^{3 /2}}-\frac{\sqrt{T+L} }{2T^2(T+L)}-\frac{1}{T^2\sqrt{T+L} }\right. \nonumber \\&\qquad \quad \left. +\frac{2\sqrt{T+L} }{T^3}-\frac{1}{4T(T+L)^{3 / 2}} \right] [\hbox {by Eq. (9)}] \end{aligned}$$

(13)

$$\begin{aligned}&\quad =\frac{\left[ {A(L)\!+\!C(L)} \right] ( {3T\!+\!4L})}{2T^3(T\!+\!L)}\!+\!\frac{hD}{4(T\!+\!L)}\!+\!G(\pi _x )\sigma \Psi (R_1 ,R_2 ,p)\frac{( {T\!+\!4L})}{2T^3\sqrt{T\!+\!L} }\!>\!0,\nonumber \\ \end{aligned}$$

(14)

and it also has local minimum in $k$ and $\pi _x$, respectively, because

$$\begin{aligned}&\frac{\partial ^2\mathrm{EAC}(T,\pi _x ,k,L)}{\partial \pi _x ^2}=\frac{2\beta _0 \sigma \sqrt{T+L} \Psi (R_1 ,R_2 ,p)}{\pi _0 T}>0.\end{aligned}$$

(15)

$$\begin{aligned}&\frac{\partial ^2\mathrm{EAC}(T,\pi _x ,k,L)}{\partial k^2}\nonumber \\&\quad =\sigma \sqrt{T+L} \left[ {1+p(1-p)\eta ^2} \right] \left[ {p\phi (R_1 )+(1-p)\phi (R_2 )} \right] \nonumber \\&\qquad \times \left[ {h\left( {1-\frac{\beta _0 \pi _x }{\pi _0 }}\right) +\frac{G(\pi _x )}{T}} \right] >0. \end{aligned}$$

(16)

Therefore, we develop the following algorithmic procedure to find the optimal solutions. Based on the proposal, the optimal $T,$ $\pi _x ,$ $k$ and $L$ can be found by the following algorithmic procedure.

Algorithm

Step 1. Input the values of $D$, $A_0$, $h,$ $\pi _0 ,$ $\sigma ,$ $\beta _0 ,$ $\eta ,$ $p,$ $\lambda ,$ $\tau ,$ $a_l ,$ $b_l ,$ $c_l$ and $l=1,2,3,\ldots , m.$

Step 2. Use the $a_l$, $b_l$ and $c_l$, $l=1,2,3,\ldots , m$, to compute $L_i$, $i=0,1,2,\ldots , m.$

Step 3. For each $L_i$, $i=0,1,2,\ldots , m$, compute the values of $T_i$, $\pi _{x_i }$ and $k_i$ by iteratively solving the simultaneous Eqs. (9)–(11). Denote the solution by $( {\dot{T}_i ,\dot{\pi }_{x_i } ,\dot{k}_i })$.

Step 4. Compare $\dot{T}_i$ with $L_i$ and $\dot{\pi }_{x_i }$ with $\pi _0 ,$ respectively.

• (i) If $\dot{T}_i >L_i$ and $\dot{\pi }_{x_i } <\pi _0 ,$ then the solution found in Step 3 is optimal for the given $L_i$. We denote the optimal solution by $( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i }),$ i.e., if $( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i })=( {\dot{T}_i ,\dot{\pi }_{x_i } ,\dot{k}_i }),$ go to Step 6.

• (ii) If $\dot{T}_i \le L_i$ and $\dot{\pi }_{x_i } <\pi _0 ,$ then for this given $L_i ,$ set $\dot{T}_i =L_i$ and utilize Eqs. (10) and (11) (replace $T_i$ by $L_i )$ to determine the new $( {\dot{T}_i ,\dot{\pi }_{x_i } ,\dot{k}_i })$; the result is denoted by $( {\bar{T}_i ,\bar{\pi }_{x_i } ,\bar{k}_i })$. If $\bar{\pi }_{x_i } <\pi _0$, then the optimal solution is obtained, i.e., $( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i })=( {L_i ,\bar{\pi }_{x_i } ,\bar{k}_i })$, go to Step 6; otherwise, go to Step 5.

• (iii) If $\dot{T}_i >L_i$ and $\dot{\pi }_{x_i } \ge \pi _0 ,$ then for this given $L_i ,$ set $\hat{\pi }_{x_i } =\pi _0$ and utilize Eqs. (9) and (11) (replace $\pi _{x_i }$ by $\pi _0 )$ to determine the new $( {\dot{T}_i ,\dot{\pi }_{x_i } ,\dot{k}_i });$ the result is denoted by $( {\bar{T}_i ,\bar{\pi }_{x_i } ,\bar{k}_i }).$ If $\bar{T}_i >L_i ,$ then the optimal solution is obtained, i.e., $( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i })=( {\bar{T}_i ,\pi _0 ,\bar{k}_i }),$ go to Step 6; otherwise, go to Step 5.

• (iv) If $\dot{T}_i \le L_i$ and $\dot{\pi }_{x_i } \ge \pi _0 ,$ go to Step 5.

Step 5. For the given $L_i$, set $\dot{T}_i =L_i$ and $\hat{\pi }_{x_i } =\pi _0 ,$ and utilize Eq. (11) to determine the corresponding optimal solution $\hat{k}_i$.

Step 6. For each $( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i ,L_i })$, $i=0,1,2,\ldots , m$, calculate the corresponding total expected annual cost $\mathrm{EAC}( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i ,L_i }),$ utilizing Eq. (3).

Step 7. Find $\min _{i=0,1,\ldots ,m} \mathrm{EAC}( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i ,L_i }).$

If $\mathrm{EAC}( {T^*,\pi _x^*,k^*,L^*})\!=\!\min _{i=0,1,\ldots ,m} \mathrm{EAC}( {\hat{T}_i ,\hat{\pi }_{x_i } ,\hat{k}_i ,L_i }),$ then $( {T^*,\pi _x^*,k^*,L^*})$ is the optimal solution

Step 8. Stop.

Note that, once $( {T^*,\pi _x^*,k^*,L^*})$ is obtained, the optimal ordering cost $A^*=A(L^*),$ the optimal target level $R^*=\mu _*(T^*+L^*)+k\sigma _*\sqrt{T^*+L^*}$ and the optimal back-order rate $\beta ^*={\beta _0 \pi _x^*}/ {\pi _0 }$ follow.

4 Numerical examples

The numerical examples given below illustrate the above solution procedure. We consider an inventory system with the following data: $D = 600$ units/year, $A_0 =\$ 200$/order, $h=\$ 20$/unit/year, $\pi _0 =\$ 50$/unit, $\sigma =7$ units/week, and the lead time has three components with data shown in Table 1.

Table 1 Lead time data

Example 1

We assume that the lead time and ordering cost reductions act dependently with the following relationship (Chiu 1998): ${(A_0 -A(L))} / {A_0 }=(1 /\lambda )(L_0 -L)/L_0 ,$ which implies $A(L)=a+bL,$ where $\lambda >0$ is a constant scaling parameter to describe the linear relationship between percentages of reductions in lead time and ordering cost, $a=( {1-1 / \lambda })A_0$ and $b={A_0 } /{( {\lambda L_0 })}.$ We want to solve the cases when $\eta =0.7$, $p=0(0.2)1$, the upper bound of the back-order ratio $\beta _0 =0.8$, and the scaling parameter $\lambda =0.75$, $1.00$, $1.25$, $2.50$, $5.00$. Applying the algorithm, we obtain the optimal solutions which are summarized in Table 2. Further, to see the effect of lead time reduction with interaction of ordering cost, we list the results of fixed ordering cost model, i.e., $\lambda =\infty ,$ in the same table.

Table 2 Summary of the optimal solutions of Example 1 ($T^*,$ $L^*$ in weeks and $\eta =0.7)$

Using the computer software, Mathematica 7, a three-dimensional graph of $\mathrm{EAC}$ is depicted in Fig. 1. The shape of the determinant function of the Hessian matrix of $\mathrm{EAC}$ is depicted in Fig. 2, which shows that the value is positive. From Figs. 1 and 2 and Eqs. (14) and (15), the function of $\mathrm{EAC}$ is a convex function for fixed $k$ and $L$, and a corresponding optimal solution $(T^*,\pi _x^*)$ existed, which minimized the total expected annual cost.

Example 2

We use the same data as given in numerical Example 1, except that the lead time and ordering cost reductions act dependently with the following relationship (Ouyang et al. 2007): ${(A_0 -A(L))} /{A_0 }=\tau \ln ( {L /{L_0 }})$, which implies $A(L)=f+g\ln L$, where $\tau (<0)$ is a constant scaling parameter to describe the logarithmic relationship between percentages of reductions in lead time and ordering cost, $f=A_0 ( {1+\tau \ln L_0 })$ and $g=-\tau A_0 >0.$ We attempt to solve the cases when $\eta =0.7$, $p=0(0.2)1$, the upper bound of the back-order ratio $\beta _0 =0.8$, and the scaling parameter $\tau =0.0$, $-0.2$, $-0.5$, $-0.8$, $-1.0$. Applying the similar procedure as proposed in algorithm, we obtain the optimal solutions which are summarized in Table 3. Moreover, to see the effect of lead time reduction with interaction of ordering cost, we list the results of fixed ordering cost model, i.e., $\tau =0,$ in the same table.

Note that, Ouyang et al. (2007) set the service level to 70 $\%$ and consequently, the target level has been predetermined. The comparison of computational results is summarized in Table 4a, b. The savings range from $9.12$ to 20.85 $\%$ for the lead time and ordering cost reductions with the linear relationship and from $12.32$ to 26.15 $\%$ for the lead time and ordering cost reductions with the logarithmic relationship which show significant savings can be achieved by simultaneously optimizing over the review period, back-order price discount, target level and lead time. It is interesting to observe that our procedure results in a higher service level for each case by spending less money.

Fig. 1

Shape of the total expected annual cost function on $(0,20] \times [0,30]$ for $p = 0.20$, $\lambda = 1.25$, $k = 1.482$ and $L=4$

Fig. 2

Shape of Hessian matrix function of the total expected annual cost function on $(0,20] \times [0,30]$ for $p = 0.20$, $\lambda = 1.25$, $k = 1.482$ and $L=4$

On the basis of the results of Tables 2 and 3, the following observations can be made:

Table 3 Summary of the optimal solutions of Example 2 ($T^*$, $L^*$ in weeks and $\eta =0.7)$

Table 4 Comparison of the two procedures ($T$ and $L$ in weeks)

• (1) The review period $T^*$, the back-order price discount $\pi _x ^*$, the target level $R^*$, the ordering cost $A(L^*)$ and the minimum total expected annual cost $\mathrm{EAC}(T^*,\pi _x ^*,R^*,L^*)$ increase (decrease) as $\lambda$ increases ($\tau$ decreases) for the fixed $p$.

• (2) When the value of $\lambda$ is fixed, the ordering cost $A(L^*)$ is the same for various $p$. In addition, as can be seen, no matter what values of $p$ are adopted, the ordering cost $A(L^*)$ is approached to the same value for the fixed $\tau$ except $\tau =-0.5$.

• (3) As the value of $\lambda$ and the value of $\tau$ decrease, respectively, the larger savings of total expected annual cost are obtained (comparing the result with fixed ordering cost model) for the fixed $p$.

• (4) No matter what values of $p$ are adopted, the optimal lead time $L^*$ is equal to a certain value (3 weeks) for $\lambda =0.75$ ($\tau =-0.8,\;-1.0)$; however, the optimal lead time $L^*$ is equal to a certain value (4 weeks) for $\lambda =1.00$, $1.25$, $2.50$, $5.00$ ($\tau =-0.2)$ and $L^*$ is equal to a certain value (6 weeks) for $\lambda =\infty$ ($\tau =0)$.

• (5) The review period $T^*$ and the back-order price discount $\pi _x ^*$ decrease and then increase as $p$ increases for the fixed $\lambda$ while the target level $R^*$ and the minimum total expected annual cost $\mathrm{EAC}(T^*,\pi _x ^*,R^*,L^*)$ increase and then decrease as $p$ increases for the fixed $\lambda$. Thus, for the fixed $\lambda$, when $p=0$ or $1$, the model considers only one kind of customers’ demand; when $0<p<1$, the model considers two kinds of customers’ demand. It implies that $\mathrm{EAC}(T^*,\pi _x ^*,R^*,L^*)$ of two kinds of customers’ demand is larger than $\mathrm{EAC}(T^*,\pi _x ^*,R^*,L^*)$ of one kind of customers’ demand. Thus, $\mathrm{EAC}(T^*,\pi _x ^*,R^*,L^*)$ increases as the distance between $p$ and $0$ (or $1)$ increases for the fixed $\lambda$. On the other hand, as can be seen, we have the same consequence for the fixed $\tau$. Thus, if the true distribution of the protection interval demand is the mixture of normal distributions, we use a single distribution [such as (Ouyang et al. 2007) using a normal distribution] to substitute the true distribution of the protection interval demand then the minimum expected total annual cost will be underestimated.

5 Concluding remarks

In this paper, we deal with the problem that the lead time and ordering cost reductions are inter-dependent in a periodic review inventory model with back-order price discounts for protection interval demand with the mixture of normal distributions. The objectives of this paper are twofold. First, we correct and improve the Ouyang et al. (2007) model by optimizing the review period, the back-order price discount, target level and lead time simultaneously to achieve significant savings in the total related cost and higher service level. Second, we consider that the demands of the different customers are not identical in the protection interval to accommodate more practical features of the tangible inventory systems. For the proposed model, we solve the cases of the linear and logarithmic relationships between lead time and ordering cost reduction. By analyzing the total expected annual cost function, a computational algorithm with the help of the software Mathematica 7 is furnished to determine the optimal solution so that the total expected annual cost incurred has the minimum value. In addition, numerical examples are provided to demonstrate the results. For future research, it would be interesting to study other types of functional relationships of lead time and ordering cost reductions. Another possible direction may be conducted by considering stochastic inventory models with a service level constraint or incorporating the defective items in the future extension of the present article.