A new optimal electricity market bid model solved through perspective cuts

Abstract

On current electricity markets the electrical utilities are faced with very sophisticated decision making problems under uncertainty. Moreover, when focusing in the short-term management, generation companies must include some medium-term products that directly influence their short-term strategies. In this work, the bilateral and physical futures contracts are included into the day-ahead market bid following MIBEL rules and a stochastic quadratic mixed-integer programming model is presented. The complexity of this stochastic programming problem makes unpractical the resolution of large-scale instances with general-purpose optimization codes. Therefore, in order to gain efficiency, a polyhedral outer approximation of the quadratic objective function obtained by means of perspective cuts (PC) is proposed. A set of instances of the problem has been defined with real data and solved with the PC methodology. The numerical results obtained show the efficiency of this methodology compared with standard mixed quadratic optimization solvers.

1 Introduction

In current electricity markets, the generation companies (GenCo) have to lead with different situations coming from the various available short- and medium-term market mechanisms. One of the main changes produced by the liberalization of the electricity markets it that the price of electricity has become a significant risk factor because it is unknown in the moment when the GenCo has to take the operational decisions. Some medium-term products are used for hedging against this market-price risk, as, for instance, the futures or the bilateral contracts.

This work is applied to the Iberian Electricity Market (MIBEL), which includes the Spanish and Portuguese electricity systems. This market has been recently improved with the creation of the Derivatives Market and the introduction of new kind of bilateral contracts beside the classical ones. Nowadays, the MIBEL includes in the short term: the day-ahead market (DAM) and a set of balancing, reserve and adjustment markets (intraday markets); these markets are complemented with the medium- and long-term mechanisms: a derivatives market and different kinds of bilateral contracts (see Fig. 1). This structure is similar to other European electricity markets. Generation companies can no longer optimize their short-term generation planning decisions, i.e. their bidding strategies, without considering the relationship between the short-term bid and the medium-term physical products. The MIBEL’s rules explain how to include some of this medium-term mechanisms into the DAM bid. In this work, the medium-term mechanisms included are the national bilateral contracts (BC) and the futures physical contracts (FC) matched at the derivatives market.

Fig. 1

MIBEL’s market mechanisms

An FC is an exchange-traded derivative that represents agreements to buy/sell some underlying asset in the future at a specified price (Hull 2002). The main characteristics of an FC are the asset, the contract size, the delivery arrangements and period, and the characteristics of the price. As it has been mentioned, MIBEL’s rules (BOE 2006b) force the GenCo to include into the DAM bid process the settlement of the energy from the derivative market products. The DAM’s operator demands every GenCo to commit the quantity designed to each FC through the DAM bidding of a given set of generation units. This commitment is done through the so-called price acceptant offer, that is, a sale offer with a bid price of 0 €/MWh. Due to the algorithm, the market operator uses to clear the DAM, all instrumental price offers will be matched (i.e. accepted) in the clearing process, that is, this energy shall be produced and will be remunerated at the DAM spot price. BC, as defined in the MIBEL, are agreements between a generation company and a qualified consumer to provide a given amount of electrical energy at a stipulated price along a delivering period. The characteristics of the bilateral contracts (energy, price, delivering period) are negotiated before the DAM and the energy that is destined to the BC cannot be included in the DAM bid. Moreover, the MIBEL rules (BOE 2006a) force the DAM bid of each unit to include the whole available energy not allocated to the BC contracts. Thus, the GenCo has to take into account all these FC and BC obligations when finding the optimal unit commitment and DAM bid.

In order to participate in the DAM, the GenCo must build an hourly bid composed by pairs of energy and price. One of the main objectives of this work is to find an analytical expression for this bid. There are some previous works that deal with this problem. For instance, Conejo et al. (2002) propose an optimal stepwise bidding strategy for a price-taker GenCo based on the units characteristics, the expected spot price, and the optimal generation. Furthermore, Gountis and Bakirtzis (2004) consider the approximation of stepwise bid curves by linear bid functions based on the marginal costs and the optimal generation quantity. Also, Ni et al. (2004) use the concept of price-power function, which is similar to the matched energy function used in our work, to derive the optimal bid curves of a hydrothermal system. Nowak et al. (2005) and Fleten and Kristoffersen (2007) also distinguish between the variables representing the bid energy and those corresponding to the matched energy in the case of a price-taker GenCo. Moreover, general considerations about optimal bidding construction in electricity markets can be obtained in Anderson and Philpott (2002) and Anderson and Xu (2002).

The second important objective is to include in the DAM bidding strategy the futures physical and the bilateral contracts. Some different approaches to the inclusion of FC in the management of a GenCo can be found in the electricity market literature. Most of the works described forward contracts as the contracts with physical settlement and futures contracts as the contracts with financial settlement. In the case of BC, it is a classic topic that has been tackled from very different points of view and there are numerous works that analyze their characteristics, their definition and the behavior that a GenCo must have in front of them. For example, Dahlgren et al. (2003) provide a state of the art on the analysis of different risk-hedging mechanisms, among them BCs. Bjorgan et al. (1999) describe in a theoretical framework the integration of physical futures contracts into the risk management of a GenCo. Also, Chen et al. (2004) analyze specifically the impact of physical and financial contracts on the bidding strategies of a GenCo. They demonstrate that the GenCo optimal bidding strategy will be affected differently, depending on which medium-term product is considered. The relation between the optimal day-ahead bid and the bilateral contracts was explicitly modeled by Heredia et al. (2010, 2011) through a set of additional variables and linear constraints. Furthermore, Conejo et al. (2008) optimize the forward physical contracts portfolio up to one year, taking into account the day-ahead bidding. Moreover, on a medium-term horizon, Guan et al. (2008) optimize the generation asset allocation between different derivatives products and the spot market, taking into account short-term operating constraints. Finally, Corchero and Heredia (2011) present a model for the inclusion of the MIBEL futures physical contract in the DAM bid which is solved with commercial MIQP solvers.

As stated above, we are dealing with a new situation, due to the MIBEL rules for the inclusion of physical futures and bilateral contracts. Thus the main difference from the previous commented works is the definition of the optimal bid function together with the coordination between day-ahead bidding strategies and physical futures and bilateral contracts settlement. The optimization model presented in this work improves the one presented by Corchero and Heredia (2011) in two ways. First, the modelization of the electricity market are extended, with the consideration of the bilateral contracts, both into the stochastic programming model and in the analytical expression of the optimal bid. Second, contrary to the work of Corchero and Heredia (2011) where commercial solvers were used, the optimization problems arising from the new electricity market model are solved here with specialized algorithms.

The utility would need to predict the unknown price in order to design its bidding strategies and to maximize its profits. Therefore, as the market price is a random variable whose realization is only known once the market has been cleared, the programs presented are based on stochastic techniques and the unknown market-price is modeled by means of a scenario set of forecasted prices. The set of scenarios is used to feed a two-stage stochastic optimization model that finds the optimal day-ahead bid of a price-taker GenCo (an electrical utility without influence over the market prices) operating in the MIBEL and holding bilateral and physical futures contracts.

On the other hand, the deterministic equivalent of this stochastic optimization problem will be a mixed-integer quadratic programming problem (MIQP), which is difficult to solve efficiently, particularly for large-scale instances. Hence, in order to improve the efficiency in the solution of this kind of problems, the quadratic objective function of this problem will be approximated by a polyhedral outer approximation by means of perspective cuts (PC) as was suggested by Frangioni and Gentile (2006), so that we can exploit the efficiency of general-purpose solvers for mixed-integer linear problems (MILP); in this case we use CPLEX 12.1. An alternative to the perspective cuts methodology is the Second-Order Cone Program reformulation (SOCP; Tawarmalani and Sahinidis 2001), but for quadratic problems the perspective cuts reformulation was reported to be more efficient (Frangioni and Gentile 2009). Finally, Branch-and-Fix Coordination (BFC) methods has also been used successfully to solve two-stage stochastic mixed-integer linear problems (Escudero et al. 2009). However, the BFC methods, together with their extension to quadratic problems, require a more complex implementation compared with the PC formulation, as this last can be easily integrated within the CPLEX 12.1 branch and cut framework with the help of the cutcallback procedure.

The main contributions of this paper are as follows:

• A new quadratic mixed-integer stochastic programming model for the inclusion of the bilateral and physical futures contracts into the day-ahead bid that maximizes the generation companies benefits.

• The derivation of the analytical expression of the optimal bid function that ensures the maximization of the expected benefits of the GenCo considering both the BC and FC obligations.

• A efficient numerical solution for this kind of electricity market problems applying perspective cuts.

From the point of view of the GenCo, the business benefits of the proposed methodology are twofold: first, the stochastic programming model and the derived optimal bid function provide the GenCos with a tool to maximize their long-run expected profits; second, the perspective cuts methodology reduces the running time in such a way that real-life instances of the problem can be solved several times within a working day, which is crucial for the applicability of the method.

The remainder of the paper is organized as follows. Section 2 presents the mathematical formulation of our day-ahead bid model. Section 3 includes the definition of the optimal bid function for a price-taker GenCo with bilateral and physical futures contracts obligations. Section 4 puts forward the perspective cut methodology and how it is applied to our model in order to be solved as a MILP. Finally, Sect. 5 shows the numerical results when solving the proposed models and Sect. 6 offers the conclusions.

2 Day-ahead electricity market bid with futures and bilateral contracts model (DAMB-FBC)

In this section the model (DAMB-FBC) is presented. It is a two-stage stochastic programming problem that allows a price-taker generation company to optimally decide the unit commitment of its thermal units, the economic dispatch of the bilateral and futures contracts between the thermal units, and the optimal generation bid of the committed units to the MIBEL’s day-ahead market.

The objective function of the model represents the expected profits of the GenCo obtained with the participation in the day-ahead market. The constraints assure that the MIBEL’s rules for the included market mechanisms are defined and that all the operational restrictions of the units are respected. The main decision variables are the ones that model the start-up and shut-down of the units, the quantity that will be bid at instrumental price and the scheduled energy committed to the bilateral and the futures contracts settlement.

2.1 Parameters

The (DAMB-FBC) model is built for a price-taker GenCo owning a set of thermal generation units that bid to the hourly auctions of the DAM.

The parameters for the ith thermal unit are:

• $c^{b}_{i}$, $c^{l}_{i}$ and $c^{q}_{i}$, generation costs with constant, linear and quadratic coefficients (€, €/MWh and €/MWh², respectively);

• ${\overline{P}}_{i}$ and ${\underline{P}}_{i}$, upper and lower bounds on the hourly generation (MWh);

• $c^{\mathrm{on}}_{i}$ and $c^{\mathrm{off}}_{i}$, start-up and shut-down costs (€);

• $t^{\mathrm{on}}_{i}$ and $t^{\mathrm{off}}_{i}$, minimum operation and minimum idle time (h).

A base load physical futures contract is defined by:

• , the set of generation units allowed to cover the FC j;

• $L^{F}_{j}$, the amount of energy (MWh) to be procured each interval of the delivery period by the set of generation units to cover contract j;

• $\lambda^{F}_{j}$, the price of contract j (€/MWh).

A base load bilateral contract is defined by:

• $L^{B}_{k}$, the amount of energy (MWh) to be procured at each interval of the delivery period by the set of available generation units to cover the BCs;

• $\lambda^{B}_{k}$, the price of the contract k (€/MWh).

The random variable $\lambda^{D}_{t}$, the clearing price of the tth hourly auction of the DAM, is represented in the two-stage stochastic model by a set of scenarios , each one with its associated clearing price for each DAM auction :

• $\lambda^{D,s}_{t}$ clearing price for auction t at scenario s (€/MWh);

• P ^s probability of scenario s.

2.2 Variables

Those decision variables that do not depend on the scenarios are called first-stage (or here-and-now) variables and in our formulation are, for each and :

• u _ti , the unit commitment (binary);

• $c^{u}_{ti},\ c^{d}_{ti}$, the start-up/shut-down costs variables;

• q _ti , the instrumental price offer bid;

• f _tij , the scheduled energy for FC ;

• b _ti , the scheduled energy for the pool of BCs.

Decision variables that can adopt different values depending on the scenario are called second-stage variables and in our formulation are, for each , and scenario :

• $g_{ti}^{s}$, the total generation;

• $p_{ti}^{s}$, the matched energy in the day-ahead market.

2.3 Constraints

2.3.1 Bilateral and futures contracts constraints

The coverage of both the physical futures contracts and the bilateral contracts must be guaranteed. The constraints for each futures contract are:

(1)

(2)

and the bilateral contract constraints are:

(3)

(4)

where $L_{k}^{B}$ is the energy that has to be settled for contract .

2.3.2 Day-ahead market and total generation constraints

As we have introduced, we will use the value of the matched energy in our formulation. The matched energy is the accepted energy in the clearing process, that is, the energy generated that will be rewarded at the clearing price. This matched energy is uniquely determined by the sale bid and the clearing price and it will play a central role in the presented model. See Sect. 3 for a formal definition of the bid function and the matched energy function.

The MIBEL’s rules affecting the day-ahead market establish the relation between the variables representing the matched energy $p^{s}_{\mathit{ti}}$, the energy of the bilateral contracts b _ti , the energy of the futures contracts f _tij , the instrumental price offer bid q _ti , and the commitment binary variables u _ti . The energies $L^{F}_{j}$ and $L^{B}_{k}$ must be integrated in the MIBEL’s DAM bid observing the two following rules:

• 1. If generator i contributes with f _tij MWh at period t to the coverage of the FC j, then the energy f _tij must be offered to the pool for free (instrumental price bid).

• 2. If generator i contributes with b _ti MWh at period t to the coverage of any of the BCs, then the remaining production capacity $\overline{P}_{i}-b_{\mathit{ti}}$ must be bid to the DAM.

These rules can be included in the model by means of the following set of constraints:

(5)

(6)

(7)

(8)

where:

• (5) and (6) ensure respectively that the matched energy $p^{s}_{\mathit{ti}}$ will be greater than the instrumental price bid q _ti and less than the total available energy not allocated to BC.

• (7) and (8) guarantee respectively that the instrumental price bid will be greater than the minimum generation output of the unit and greater than the contribution of the unit to the FC coverage.

Please note that (2) together with (8) assures that q _ti will be always non-negative. The total generation level of a given unit i, $g^{s}_{\mathit{ti}}$, is defined as the addition of the allocated energy to the BC plus the matched energy of the DAM:

(9)

Contraints (1)–(9) assure that $g^{s}_{\mathit{ti}}$ will be always either zero or $g^{s}_{\mathit{ti}}\in [\underline{P}_{i},\overline{P}_{i}]$, i.e.:

(10)

2.3.3 Unit commitment constraints

This section includes the formulation for the unit commitment of the thermal units (Carrión and Arroyo 2006). The first two sets of constraints model the start-up and shut-down costs and the next ones control minimum operation and idle time for each unit. First, the start-up and shut-down costs are modeled:

(11)

(12)

(13)

(14)

The initial state of each thermal unit i can be taken into account through the parameters G _i and H _i that represent, respectively, the number of the initial time periods along which the thermal unit must remain on (G _i ) or off (H _i ). These conditions are imposed by the following set of constraints:

(15)

(16)

Finally, the minimum up and down time, $t^{\mathrm{on}}_{i}$ and $t^{\mathrm{off}}_{i}$, are imposed, up to the periods and , through the following set of constraints:

(17)

(18)

and for the last $t^{\mathrm{on}}_{i}-1$ and $t^{\mathrm{off}}_{i}-1$ time periods:

(19)

(20)

2.4 Objective function

The quadratic function associated to the expected profits of the GenCo after the participation in the DAM is:

(21a)

(21b)

where

• (21a) is the on/off fixed cost of the unit commitment of the thermal units, deterministic and independent of the realization of the random variable $\lambda^{D,s}_{t}$, and

• (21b) represents the expected value of the benefits from the DAM. The term between parentheses corresponds to the expression of the quadratic generation costs associated with the total generation of the unit $g^{s}_{\mathit{ti}}$ while the last term, $\lambda^{D,s}_{t} p^{s}_{\mathit{ti}}$, computes the incomes from the DAM due to a value $p^{s}_{\mathit{ti}}$ of the matched energy.

Please note that the constant incomes from the BC and FC,

and

have been dropped from the objective function.

2.5 Model (DAMB-FBC)

The model defined so far can be represented as:

$$\hbox{(DAMB-FBC)}\left\{\begin{array}{l}\min \ {\mathrm{E}}_{\lambda^D}[C(u,c^u,c^d,g,p;\lambda^D)] \\\hbox{s.t.}\\\quad \mbox{Equations\ (1)--(4)} \quad \mbox{BC and FC constraints}\\\quad \mbox{Equations\ (5)--(9)}\quad \hbox{DAM and total gen. constraints}\\\quad \mbox{Equations\ (11)--(20)}\quad \hbox{Unit commitment constraints}\\\end{array} \right.$$

Model (DAMB-FBC) is the optimization problem associated with the two-stage stochastic programming problem with a set of scenarios for the spot price $\lambda^{D}_{t}$, where . This optimization problem is a convex MIQP with a well defined global optimal solution.

3 Optimal bid

The (DAMB-FBC) model developed so far does not include an explicit representation of the bid function to be submitted to the day-ahead market. Instead of this, the expression of the optimal bid function, that is, the bid function that must be submitted by the GenCo in order to ensure the long-run optimal expected profits found by the (DAMB-FBC) model, can be derived from the optimality conditions of this problem. With this objective in mind, let us first introduce the formal definition of three basic concepts: the bid function, the matched energy function and the optimal bid function.

Definition 1

(Bid function)

A bid function for the thermal unit i is a non-decreasing function defined over the interval $[0,\overline{P}_{i}]$ that gives, for any feasible value of the bid energy $p^{b}_{\mathit{ti}}$, the asked price per MWh from the day-ahead market:

$$\begin{array}{l@{\quad }l}\lambda^{b}_{\mathit{ti}}{\colon}& [0,\overline{P}_i] \longrightarrow \Re^+\cup{0}\\[2pt]& p^b_{\mathit{ti}} \longmapsto \lambda^b_{\mathit{ti}}(p^b_{\mathit{ti}})\end{array}$$

Subsequently, for a given bid function $\lambda^{b}_{\mathit{ti}}$, the matched energy associated with the clearing price $\lambda^{D}_{t}$, $p^{m}_{\mathit{ti}}$ is defined through the matched energy function:

Definition 2

(Matched energy function)

The matched energy associated with the bid function $\lambda^{b}_{\mathit{ti}}$ is defined as the maximum bid energy with an asked price not greater than the clearing price $\lambda^{D}_{t}$, and is represented by the function:

$$ p^M_{\mathit{ti}} \bigl(\lambda^D_t\bigr)= \max \bigl\{ p^b_{\mathit{ti}}\in[0,\overline{P}_i]\>|\> \lambda^{b}_{\mathit{ti}} \bigl(p^b_{\mathit{ti}}\bigr) \le \lambda^D_t\bigr\}$$

(22)

Definition 3

(Bid function’s optimality conditions)

Let x ^∗ be an optimal solution of the (DAMB-FBC) problem. The bid function $\lambda^{b*}_{\mathit{ti}}$ of a thermal unit i committed at period t (i.e. u _ti =1) is said to be optimal if

(23)

that is, if the matched energy function (22), associated with every scenario’s clearing price $\lambda^{D,s}_{t}$, coincides with $p^{s*}_{\mathit{ti}}$, the optimal value of the matched energy in the solution of model (DAMB-FBC).

It is straightforward to note that if a GenCo submits a bid function satisfying (23) systematically to the DAM, in the long run, the expected profit of the GenCo will be maximized according to the (DAMB-FBC) problem. The objective of this section is to prove the existence of such an optimal bid function $\lambda^{b*}_{\mathit{ti}}$ and to obtain its analytical expression. In order to do so, the properties of the optimal solutions of the problem (DAMB-FBC) will be studied in the next section and used to derive the expression of the optimal matched energy $p^{s*}_{\mathit{ti}}$ in terms of the optimal values of the instrumental energy bid $q^{*}_{\mathit{ti}}$ and the committed energy $b_{\mathit{ti}}^{*}$ of the bilateral contracts.

3.1 Optimal matched energy

Let x ^∗′=[u ^∗,c ^u∗,c ^d∗,g ^∗,p ^∗,q ^∗,f ^∗,b ^∗]′ represent the optimal solution of the (DAMB-FBC) problem. Fixing the unit commitment variables u ^∗,c ^u∗ and c ^d∗ to its optimal value in the formulation of the (DAMB-FBC) problem, we get the following continuous convex quadratic problem:

with , i.e., the set of thermal units committed at time t. Of course, the optimal solution of this continuous problem coincides with the optimal value of the continuous variables of the original (DAMB-FBC) problem, g ^∗, p ^∗, q ^∗, b ^∗ and f ^∗. The (DAMB-FBC^∗) problem is separable by intervals, being the problem associated with the tth time interval, in standard form (Luenberger 2004):

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

where π ¹, π ², μ ¹, π ³, μ ², μ ³, μ ⁴, μ ⁵, μ ⁶, μ ⁷ and μ ⁸ are the Lagrange multipliers associated with each constraint. The Karush–Kuhn–Tucker (KKT) conditions of the ($\mbox{DAMB-FBC}^{*}_{t}$) problem can be expressed as:

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

(50)

The next proposition comes directly from the KKT conditions and the convexity of problem (DAMB-FBC).

Proposition 1

Let x ^∗′=[u ^∗,c ^u∗,c ^d∗,g ^∗,p ^∗,q ^∗,f ^∗,b ^∗]′ be an optimal solution of the (DAMB-FBC) problem. Then, for any x ^∗ there exist Lagrange multipliers π ¹, π ², π ³, μ ¹, μ ², μ ³, μ ⁴, μ ⁵, μ ⁶, μ ⁷ and μ ⁸ such that the values of variables g ^∗, p ^∗, q ^∗, f ^∗ and b ^∗ satisfy the KKT system (35)–(50). Conversely, for any solution g ^∗, p ^∗, q ^∗, f ^∗ and b ^∗ of the KKT system (35)–(50) associated with $I^{*}_{\mathit{on}_{t}}$, the correspondent solution x ^∗ is optimal for the (DAMB-FBC) problem.

The fact that any solution of the (DAMB-FBC) problem must satisfy the system (35)–(50) will be exploited to derive the expressions of the optimal matched energy in next lemma.

Lemma 1

(Optimal matched energy, quadratic costs)

Let x ^∗ be an optimal solution of the (DAMB-FBC) problem. Then, for any unit i with quadratic convex generation costs (i.e. $c_{i}^{q}>0$) committed at period t (i.e. $i\in I^{*}_{\mathit{on}_{t}}$), the optimal value of the matched energy $p^{s*}_{\mathit{ti}}$ can be expressed as:

$$ p^{s*}_{\mathit{ti}}=\max \bigl\{ q^*_{\mathit{ti}}, \rho^s_{\mathit{ti}}\bigr\}$$

(51)

where $\rho^{s}_{\mathit{ti}}$ is defined as:

$$ \rho^s_{\mathit{ti}} =\begin{cases}[\underline{P}_i-b^*_{\mathit{ti}}]^+ & \hbox{if\ }\theta^s_{\mathit{ti}}\leq [\underline{P}_i-b^*_{\mathit{ti}}]^+\\[3pt]\theta^s_{\mathit{ti}} &\hbox{if\ }[\underline{P}_i-b^*_{\mathit{ti}}]^+<\theta^s_{\mathit{ti}} < (\overline{P}_i-b^*_{\mathit{ti}})\\[3pt](\overline{P}_i-b^*_{\mathit{ti}}) & \hbox{if\ } \theta^s_{\mathit{ti}}\geq (\overline{P}_i-b^*_{\mathit{ti}})\\\end{cases}$$

(52)

with

$$ \theta^s_{\mathit{ti}}=\frac{(\lambda^{D,s}_t-c^l_i)}{2c^q_i}-b^*_{\mathit{ti}}$$

(53)

and

$$\bigl[\underline{P}_i-b^*_{\mathit{ti}}\bigr]^+=\max \bigl\{0,\underline{P}_i-b^*_{\mathit{ti}}\bigr\}$$

Proof

As Proposition 1 establishes, any optimal solution of the (DAMB-FBC) problem must satisfy the KKT system (35)–(50). Additionally, (27)–(29) establish that any optimal solution x ^∗ of the (DAMB-FBC) problem must satisfy:

$$ \underline{P}_i-b_{\mathit{ti}} \le q^*_{\mathit{ti}} \le p^{s*}_{\mathit{ti}}\le \overline{P}_i-b_{\mathit{ti}}$$

(54)

As we want to see that the optimal value of the matched energy $p^{s*}_{\mathit{ti}}$ is equivalent to expression (51), we need to distinguish whether $[\underline{P}_{i}-b_{\mathit{ti}}]^{+}$ is equal to $(\underline{P}_{i}-b_{\mathit{ti}})$ or 0, i.e., whether $b_{\mathit{ti}} <\underline{P}_{i}$ or not. Thus, to derive the relationship (51), the solution of the KKT system will be analyzed in these two situations. For each one, we will analyze five cases among which any optimal solution of the (DAMB-FBC) problem could be classified according to (54):

• (a) $b_{\mathit{ti}}< \underline{P}_{i} \Rightarrow [\underline{P}_{i}-b_{\mathit{ti}}]^{+} = (\underline{P}_{i}-b_{\mathit{ti}})$

  • (a.1) $(\underline{P}_{i}-b_{\mathit{ti}})< q^{*}_{\mathit{ti}} = p^{s*}_{\mathit{ti}} = (\overline{P}_{i} - b_{\mathit{ti}})$: This is a trivial case, because, by definition (52), $\rho^{s}_{\mathit{ti}}\le(\overline{P}_{i}-b_{it})$ and $p^{s*}_{\mathit{ti}}=\max \{ q^{*}_{\mathit{ti}}=(\overline{P}_{i}-b_{\mathit{ti}}),\rho^{s}_{\mathit{ti}}\le(\overline{P}_{i}-b_{\mathit{ti}})\}=(\overline{P}_{i}-b_{\mathit{ti}})$.

  • (a.2) $(\underline{P}_{i}-b_{\mathit{ti}}) \leq q^{*}_{\mathit{ti}} < p^{s*}_{\mathit{ti}} = (\overline{P}_{i} - b_{\mathit{ti}})$: Condition (42) gives $\mu^{3,s}_{\mathit{ti}}=0$ that, together with (37) and the non-negativity of the lagrange multipliers μ, gives $\mu^{1}_{\mathit{ti}}=\mu^{4}_{\mathit{ti}}=\mu^{5}_{\mathit{ti}}=0$ and then (36) gives $\pi^{2,s}_{\mathit{ti}}=\mu_{\mathit{ti}}^{2,s}-P^{s}\lambda^{D,s}_{t}$. This result, combined with the definition $g^{s*}_{\mathit{ti}}=p^{s*}_{\mathit{ti}}+b_{\mathit{ti}}^{*}$ and together with (35), gives:

    $$p^{s*}_{\mathit{ti}}=\biggl[\frac{\lambda^{D,s}_t-c_i^l}{2c^q_i}-b^*_{\mathit{ti}}\biggr]-\frac{\mu^{2,s}_{\mathit{ti}}}{2c_i^qP^s}\leq \theta^{s}_{\mathit{ti}}.$$

    Then, as it is assumed that $p^{s*}_{\mathit{ti}} =(\overline{P}_{i} - b_{\mathit{ti}})$ and we have concluded that $\theta^{s}_{\mathit{ti}}\geq p^{s*}_{\mathit{ti}}$, by definition (52), $\rho^{s}_{\mathit{ti}}=(\overline{P}_{i}-b_{\mathit{ti}})$. So, $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}^{*}<(\overline{P}_{i}-b_{\mathit{ti}}),\rho^{s}_{\mathit{ti}}=(\overline{P}_{i}-b_{\mathit{ti}})\}=(\overline{P}_{i}-b_{\mathit{ti}})$.

  • (a.3) $(\underline{P}_{i}-b_{\mathit{ti}})\le q^{*}_{\mathit{ti}} < p^{s*}_{\mathit{ti}}< (\overline{P}_{i}-b_{\mathit{ti}})$: On the one hand, conditions (37), (42) and the non-negativity of the lagrange multipliers give $\mu^{3,s}_{\mathit{ti}}=\mu^{1}_{\mathit{ti}}=\mu^{4}_{\mathit{ti}}=\mu^{5}_{\mathit{ti}}=0$. On the other hand, it is assumed that $p^{s*}_{\mathit{ti}} <(\underline{P}_{i}-b_{\mathit{ti}})$ and thus condition (41) gives $\mu_{\mathit{ti}}^{2,s}=0$. These two results, combined with condition (36), give $\pi^{2,s}_{\mathit{ti}}=-P^{s}\lambda^{D,s}_{t}$, which together with (35) and (27) give:

    $$p^{s*}_{\mathit{ti}}=\biggl[\frac{\lambda^{D,s}_t-c_i^l}{2c^q_i}-b^*_{\mathit{ti}}\biggr]= \theta^{s}_{\mathit{ti}}.$$

    Then, as it is assumed that $(\underline{P}_{i}-b_{\mathit{ti}})<p^{s*}_{\mathit{ti}} < (\overline{P}_{i} - b_{\mathit{ti}})$, so is $\theta^{s}_{\mathit{ti}}$ and, by definition (52), $\rho^{s}_{\mathit{ti}} = \theta^{s}_{\mathit{ti}}$. Therefore $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}^{*}<\theta^{s}_{\mathit{ti}},\rho^{s}_{\mathit{ti}}=\theta^{s}_{\mathit{ti}}\}=\theta^{s}_{\mathit{ti}}$.

  • (a.4) $(\underline{P}_{i}-b_{\mathit{ti}}) < q^{*}_{\mathit{ti}} =p^{s*}_{\mathit{ti}} <(\overline{P}_{i}-b_{\mathit{ti}})$: In this case the assumptions, together with (36), (41) and (43), force $\mu^{2,s}_{\mathit{ti}}= \mu^{4}_{\mathit{ti}}=0$ and $\pi^{2,s}_{\mathit{ti}}=-P^{s}\lambda^{D,s}_{t}$. Analogously to case (a.3), $p^{s*}_{\mathit{ti}} = \theta^{s}_{\mathit{ti}} =\rho^{s}_{\mathit{ti}}$ and, as it is assumed that $q^{*}_{\mathit{ti}} =p^{s*}_{\mathit{ti}}$, then $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}^{*}=\theta^{s}_{\mathit{ti}},\rho^{s}_{\mathit{ti}}=\theta^{s}_{\mathit{ti}}\}=\theta^{s}_{\mathit{ti}}$.

  • (a.5) $(\underline{P}_{i}-b_{\mathit{ti}}) = q^{*}_{\mathit{ti}} = p^{s*}_{\mathit{ti}}< (\overline{P}_{i}-b_{\mathit{ti}})$: Condition (41) sets $\mu^{2,s}_{\mathit{ti}}=0$ which, by taking into account condition (36), provides $\pi^{2,s}_{\mathit{ti}}=-\mu^{4,s}_{\mathit{ti}}-P^{s}\lambda^{D,s}_{t}$. This result, combined with the definition $g^{s*}_{\mathit{ti}}=p^{s*}_{\mathit{ti}}+b_{\mathit{ti}}^{*}$, and together with (35), gives:

    $$p^{s*}_{\mathit{ti}}=\biggl[\biggl(\frac{\lambda^{D,s}_t-c_i^l}{2c^q_i}-b^*_{\mathit{ti}}\biggr)+\frac{\mu^{4,s}_{\mathit{ti}}}{2c_i^qP^s}\biggr]\geq \theta^{s}_{\mathit{ti}}.$$

    Then, as it is assumed that $p^{s*}_{\mathit{ti}} =(\underline{P}_{i} - b_{\mathit{ti}})$ and then $\theta^{s}_{\mathit{ti}}\leq (\underline{P}_{i}-b_{\mathit{ti}})$, by definition (52), $\rho^{s}_{\mathit{ti}}=(\underline{P}_{i}-b_{\mathit{ti}})$. So, $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}^{*}=(\underline{P}_{i}-b_{\mathit{ti}}),\rho^{s}_{\mathit{ti}}=(\underline{P}_{i}-b_{\mathit{ti}})\}=(\underline{P}_{i}-b_{\mathit{ti}})$.

• (b) $b_{\mathit{ti}} \geq \underline{P}_{i} \Rightarrow [\underline{P}_{i}-b_{\mathit{ti}}]^{+} = 0$

  • (b.1) $0 < q^{*}_{\mathit{ti}} = p^{s*}_{\mathit{ti}} = (\overline{P}_{i} - b_{\mathit{ti}})$: In this case, assumptions q _ti >0 and $q_{\mathit{ti}}>(\overline{P}_{i} - b_{\mathit{ti}})$, together with conditions (43) and (44), force $\mu^{4}_{\mathit{ti}}=\mu^{5}_{\mathit{ti}}=0$. Then, (36) gives $\pi^{2,s}_{\mathit{ti}}=\mu_{\mathit{ti}}^{2,s}-P^{s}\lambda^{D,s}_{t}$ that, analogously to case (a.2), gives $\theta^{s}_{\mathit{ti}}\geq p^{s*}$, and then $\theta^{s}_{\mathit{ti}}\geq (\overline{P}_{i}- b_{\mathit{ti}})$. Therefore, by definition (52), $\rho^{s}_{\mathit{ti}}=(\overline{P}_{i} - b_{\mathit{ti}})$ and $p^{s*}=\max\{q^{*}_{\mathit{ti}}=(\overline{P}_{i} - b_{\mathit{ti}}),\rho^{s}_{\mathit{ti}} = (\overline{P}_{i} -b_{\mathit{ti}})\}=(\overline{P}_{i} - b_{\mathit{ti}})$.

  • (b.2) $0 \leq q^{*}_{\mathit{ti}} < p^{s*}_{\mathit{ti}} = (\overline{P}_{i} - b_{\mathit{ti}})$: This case is equivalent to (a.2) because the key is the assumption $q^{*}_{\mathit{ti}} < p^{s*}_{\mathit{ti}} =(\overline{P}_{i} - b_{\mathit{ti}})$. Consequently, $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}^{*}<(\overline{P}_{i}-b_{\mathit{ti}}),\rho^{s}_{\mathit{ti}}=(\overline{P}_{i}-b_{\mathit{ti}})\}=(\overline{P}_{i}-b_{\mathit{ti}})$.

  • (b.3) $0 \le q^{*}_{\mathit{ti}} < p^{s*}_{\mathit{ti}} < (\overline{P}_{i}-b_{\mathit{ti}})$: The reasoning for this case is equivalent to (a.3) until the result $p^{s*}_{\mathit{ti}} = \theta^{s}_{\mathit{ti}}$. Then as it is assumed that $0 < p^{s*}_{\mathit{ti}} <(\overline{P}_{i}-b_{\mathit{ti}})$, so is $0<\theta^{s}_{\mathit{ti}}<(\overline{P}_{i}-b_{\mathit{ti}})$ and then, by definition (52), $\rho^{s}_{\mathit{ti}}=\theta^{s}_{\mathit{ti}}$. Therefore, $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}^{*}<\theta^{s}_{\mathit{ti}},\rho^{s}_{\mathit{ti}}=\theta^{s}_{\mathit{ti}}\}=\theta^{s}_{\mathit{ti}}$.

  • (b.4) $0 < q^{*}_{\mathit{ti}} = p^{s*}_{\mathit{ti}} <(\overline{P}_{i}-b_{\mathit{ti}})$: Analogously to (a.4), it is concluded that $p^{s*}_{\mathit{ti}}= \theta^{s}_{\mathit{ti}}$ and, as it is assumed that $0 <p^{s*}_{\mathit{ti}} < (\overline{P}_{i}-b_{\mathit{ti}})$, the situation is analogous to case (b.3) and therefore $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}^{*}<\theta^{s}_{\mathit{ti}},\rho^{s}_{\mathit{ti}}=\theta^{s}_{\mathit{ti}}\}=\theta^{s}_{\mathit{ti}}$.

  • (b.5) $0 = q^{*}_{\mathit{ti}} = p^{s*}_{\mathit{ti}} < (\overline{P}_{i}-b_{\mathit{ti}})$: In this case, the assumption $p^{s*}_{\mathit{ti}}<(\overline{P}_{i}-b_{\mathit{ti}})$, together with condition (41), gives that $\mu^{2,s}_{\mathit{ti}}=0$ and then condition (36) gives $\pi^{2,s}_{\mathit{ti}}=-\mu_{\mathit{ti}}^{4,s}-P^{s}\lambda_{t}^{D,s}$. Following the same reasoning as in (a.5), this result, combined with the definition $g^{s*}_{\mathit{ti}}=p^{s*}_{\mathit{ti}}+b_{\mathit{ti}}^{*}$ and expression (35), gives that $p^{s*}_{\mathit{ti}}\geq \theta_{\mathit{ti}}^{s}$. Then $\theta^{s}_{\mathit{ti}}\leq 0$ and, by definition (52), $\rho^{s}_{\mathit{ti}}=0$. Therefore, $p^{s*}_{\mathit{ti}}=\max\{q_{\mathit{ti}}=0,\rho^{s}_{\mathit{ti}}=0\}=0$.

 □

Lemma 2

(Optimal matched energy, linear costs)

Let x ^∗ be an optimal solution of the (DAMB-FBC) problem. Then, for any unit i with linear generation costs (i.e. $c_{i}^{q}=0$) committed at period t (i.e. $i\in I^{*}_{\mathit{on}_{t}}$), the optimal value of the matched energy $p^{s*}_{\mathit{ti}}$ can be expressed as:

$$ p^{s*}_{\mathit{ti}} =\begin{cases}q^*_{\mathit{ti}} & \mbox{if }\lambda^{D,s}_t \le c^l_i\\\overline{P}_i-b^*_{\mathit{ti}} & \mbox{if }\lambda^{D,s}_t > c^l_i\end{cases}$$

(55)

As in Lemma 1, the proof of Lemma 2 is based on the fact that any optimal solution of the (DAMB-FBC) problem must satisfy the KKT system (35)–(50).

3.2 Optimal bid function

The next theorem develops the expression of the optimal bid function associated with the (DAMB-FBC) problem, that is, the bid function satisfying the optimality condition (23).

Theorem 1

(Optimal bid function)

Let x ^∗′=[u ^∗,c ^u∗,c ^d∗,g ^∗,p ^∗,q ^∗,f ^∗,b ^∗]′ be an optimal solution of the (DAMB-FBC) problem and i be any thermal unit committed in period t of the optimal solution (i.e. $i\in I^{*}_{\mathit{on}_{t}}$). Then, for a unit i with quadratic convex generation costs, the bid function:

$$ \lambda^{b*}_{\mathit{ti}}\bigl(p^{b}_{\mathit{ti}}\bigr) =\begin{cases}0 & \mbox{if\ } p^{b}_{\mathit{ti}} \leq q^*_{\mathit{ti}}\\[2pt]2c^q_i(p^{b}_{\mathit{ti}}+b^*_{\mathit{ti}})+ c^l_i& \mbox{if\ } q^*_{\mathit{ti}} < p^{b}_{\mathit{ti}} \leq (\overline{P}_i-b^*_{\mathit{ti}})\end{cases}$$

(56)

is optimal, i.e., it satisfies $p^{s *}_{\mathit{ti}} =p^{M}_{\mathit{ti}}(\lambda^{D,s}_{t})$, .

Proof

First, we consider the case where $c^{q}_{i}>0$. To illustrate this proof, the expression (56) has been represented graphically in Fig. 2 for two cases: the first one, when $b^{*}_{\mathit{ti}}<\underline{P}_{i}$ (Fig. 2(a)) and therefore $q^{*}_{\mathit{ti}}\geq\underline{P}_{i}-b^{*}_{\mathit{ti}}$; and the second one, when $b^{*}_{\mathit{ti}}>\underline{P}_{i}$ (Fig. 2(b)) and therefore $q^{*}_{\mathit{ti}}\geq 0$. It is easy to see that the matched energy function associated with the bid function $\lambda^{b*}_{\mathit{ti}}$ at scenario s (i.e. $\lambda_{t}^{D}=\lambda_{t}^{D,s}$) is for both cases (Fig. 3):

$$ p^{M*}_{\mathit{ti}} \bigl(\lambda^{D,s}_t\bigr)=\begin{cases}q^*_{\mathit{ti}} & \mbox{if}\ \lambda^{D,s}_t \le \underline{\lambda}_{\mathit{ti}}\\[2pt]\theta^{s}_{\mathit{ti}} &\mbox{if}\ \underline{\lambda}_{\mathit{ti}} < \lambda^{D,s}_t \le \overline{\lambda}_{\mathit{ti}}\\[2pt]\overline{P}_i-b^*_{\mathit{ti}} & \mbox{if}\ \lambda^{D,s}_t > \overline{\lambda}_{\mathit{ti}}\\[2pt]\end{cases}$$

(57)

where the threshold prices $\underline{\lambda}_{\mathit{ti}}$ and $\overline{\lambda}_{\mathit{ti}}$ are defined as:

$$ \underline{\lambda}_{\mathit{ti}}=2c^q_i \bigl(q^*_{\mathit{ti}}+b_{\mathit{ti}}^*\bigr) + c^l_i;\qquad \overline{\lambda}_{\mathit{ti}}=2c^q_i\overline{P}_i+ c^l_i$$

(58)

and $\theta^{s}_{\mathit{ti}}$ is the parameter defined in (53). Thus, to demonstrate the optimality of bid function (57), it is sufficient to prove that $p^{M*}_{\mathit{ti}}(\lambda^{D,s}_{t}) = p^{s*}_{\mathit{ti}} =\max\{q^{*}_{\mathit{ti}},\rho^{s}_{\mathit{ti}}\}$. We verify this equivalence for the three cases of expression (57) (Fig. 3):

• (a) If, for some , $\lambda^{D,k}_{t} \le \underline{\lambda}_{\mathit{ti}}$ then $\theta^{k}_{\mathit{ti}}\le q^{*}_{\mathit{ti}} \le \overline{P}_{i}-b_{\mathit{ti}}$ and, by definition (52), $\rho^{k}_{\mathit{ti}}=\max\{\theta^{k}_{\mathit{ti}},[\underline{P}_{i}-b^{*}_{\mathit{ti}}]^{+}\}$, which will always be less than or equal to $q^{*}_{\mathit{ti}}$. Then, we can write that $p^{k*}_{\mathit{ti}}=\max\{q^{*}_{\mathit{ti}},\rho^{k}_{\mathit{ti}}\}=q^{*}_{\mathit{ti}}$ and, as expression (57) gives $p^{M*}_{\mathit{ti}}=q^{*}_{\mathit{ti}}$, we can conclude that $p^{M*}_{\mathit{ti}}(\lambda^{D,k}_{t}) =p^{k*}_{\mathit{ti}}$.

• (b) If, for some , $\underline{\lambda}_{\mathit{ti}} < \lambda^{D,l}_{t} \le \overline{\lambda}_{\mathit{ti}}$ then $[\overline{P}_{i}-b_{\mathit{ti}}]^{+}\leq q^{*}_{\mathit{ti}}<\theta^{l}_{\mathit{ti}}\le (\overline{P}_{i}-b^{*}_{\mathit{ti}})$ and, by definition (52) $\rho^{l}_{\mathit{ti}}=\theta^{l}_{\mathit{ti}}$. Then, $p^{l*}_{\mathit{ti}}=\max\{q^{*}_{\mathit{ti}},\rho^{b,l}_{\mathit{ti}}=\theta^{l}_{\mathit{ti}}\geq q^{*}_{\mathit{ti}}\}=\theta^{l}_{\mathit{ti}}$. As expression (57) gives $p^{M*}_{\mathit{ti}}(\lambda^{D,l}_{t})=\theta^{l}_{\mathit{ti}}$, we can conclude that $p^{M*}_{\mathit{ti}}(\lambda^{D,l}_{t})=p^{l*}_{\mathit{ti}}$.

• (c) If, for some , $\lambda^{D,r}_{t} > \overline{\lambda}_{\mathit{ti}}$ then $\theta^{r}_{\mathit{ti}} > (\overline{P}_{i}-b^{*}_{\mathit{ti}})$ which, together with definition (52), sets $\rho^{r}_{\mathit{ti}}=(\overline{P}_{i}-b^{*}_{\mathit{ti}})$ and thus $p^{r*}_{\mathit{ti}}=\max\{q^{*}_{\mathit{ti}},\rho^{r}_{\mathit{ti}}=(\overline{P}_{i}-b^{*}_{\mathit{ti}})>q^{*}_{\mathit{ti}}\}=(\overline{P}_{i}-b^{*}_{\mathit{ti}})$. As expression (57) gives $p^{M*}_{\mathit{ti}}(\lambda^{D,r}_{t})=(\overline{P}_{i}-b^{*}_{\mathit{ti}})$, we can conclude that $p^{M*}_{\mathit{ti}}(\lambda^{D,r}_{t})=p^{r*}_{\mathit{ti}}$.

Note that if $c_{i}^{q}=0$ (i.e., a thermal unit with linear generations costs), the bid function (56) reduces to:

$$\lambda^{b*}_{\mathit{ti}} \bigl(p^{b}_{\mathit{ti}}\bigr) =\begin{cases}0 & \mbox{if\ } p^{b}_{\mathit{ti}} \leq q^*_{\mathit{ti}}\\c^l_i & \mbox{if\ } q^*_{\mathit{ti}} < p^{b}_{\mathit{ti}} \leq (\overline{P}_i-b^*_{\mathit{ti}})\end{cases}$$

and the optimal matched energy function associated with this optimal bid function is:

$$ p^{M*}_{\mathit{ti}} \bigl(\lambda^{D}_t\bigr)=\begin{cases}q^*_{\mathit{ti}} & \mbox{if}\ \lambda^{D}_t \le c_i^l\\[3pt]\overline{P}_i-b^*_{\mathit{ti}} & \mbox{if}\ \lambda^{D}_t > \overline{c}_i^l\\\end{cases}$$

(59)

It is straightforward to see that this expression (59) is equivalent to expression (55) and then in this case $p^{M*}_{\mathit{ti}}(\lambda^{D,s}_{t})\equiv p^{s*}_{\mathit{ti}}$ also applies.

Fig. 2

Optimal bid function $\lambda^{b*}_{\mathit{ti}}(p^{b}_{\mathit{ti}})$ when (a) $b^{*}_{\mathit{ti}}<P_{i}$, (b) $b^{*}_{\mathit{ti}}>P_{i}$

Fig. 3

Associated matched energy function $p^{M,s*}_{\mathit{ti}}$

 □

4 Efficient solution of the (DAMB-FBC) problem: the perspective cuts formulation

As stated in Sect. 2, problem (DAMB-FBC) is a mixed-integer quadratic programming problem. These kinds of optimization problems can be solved with the help of commercial optimization software (i.e. CPLEX 2009) through the use of nonlinear branch and cut algorithms, at the expense of high computational execution times. The perspective cut formulation is an alternative to the nonlinear branch and cut that was successfully applied in the past (Frangioni and Gentile 2006) to solve some unit commitment problems. Perspective cuts, a method specially conceived to deal with quadratic objective function over semi-continuous domains, is a sort of outer approximation to the quadratic objective function built through special supporting hyperplanes related with the perspective function, the so-called perspective cuts. To see how this outer approximation is developed, let us consider the objective function (21a)–(21b) that, taken into account that the sum of the probabilities P ^s is one, can be expressed in the following way:

(60)

with:

$$f\bigl(g^s_{\mathit{ti}}, u_{\mathit{ti}}\bigr)=c^q_i\bigl(g^s_{\mathit{ti}}\bigr)^2+c^l_i g^s_{\mathit{ti}}+c^b_{i}u_{\mathit{ti}},$$

In the rest of the section we drop the indices for notational simplicity. An approach to properly linearize the quadratic function

$$f(g,u)=c^qg^2+c^lg+c^bu $$

(61)

is to use the outer approximation based on ideas developed by Frangioni and Gentile (2006). Note that the domain of the function (61), defined by (10) and the binary nature of variable u, can be expressed as , and that, consequently, function f(g,u) can be rewritten as (see Fig. 4):

$$f(g,u)=\begin{cases}0, & \hbox{if}\ u=0\cr f(g)=c^qg^2+c^lg+c^b, & \hbox{if}\ u=1.\end{cases}$$

Fig. 4

Graphic of the function h(g,u), together with the perspective cut over $(\widehat {g}, 1)$

Moreover, when we use the branch and cut methods in order to find lower bounds for the optimal value, we solve continuous relaxations of the mixed-integer linear problem, i.e. with u∈[0,1]. Therefore, a natural question is whether we can obtain a convex function with a tighter epigraph for f(g,u), which can be used to calculate those lower bounds. This leads us to take into account the convex envelope of f(g,u) over the disconnected domain . This is the convex function with an epigraph equal to the convex envelope of the epigraph of f(g,u), which corresponds to the cone generated by epi(f(g,1)) and (0,0,0)) (see Fig. 4). As is shown in Frangioni and Gentile (2006), this convex envelope is:

$$h(g,u)=\left\{\begin{array}{l@{\quad }l}0, & \hbox{if}\ (g,u)=(0,0) \\[3pt]\displaystyle\frac{c^qg^2}{u}+c^lg+c^bu, & \displaystyle{\left\{\hbox{if} ~u\underline{P}\le g\le u\overline{P}, \atop \hbox{for}~u\in(0,1]\right\}}\\[3pt]+\infty, & \hbox{otherwise}.\end{array}\right. $$

(62)

This function is the perspective-function $\breve{f}(g,u)=uf(g/u)$ of f(g), for u limited to be in (0,1], which is convex if f(g) is convex, see Hiriart-Urruty and Lemaréchal (1993). In addition, to show that h is a tighter objective function than f for the continuous relaxation, it is enough to compare (61) and (62) for 0<u≤1. Note that the definition of h(0,0) is redundant, as if is the domain of h, i.e. the pyramid having a base $[\underline{P},\overline{P}]\times \{1\}$ and vertex [0,0], then for all sequences that converge to [0,0], we have

$$0\le u_kf\biggl(\frac{g_k}{u_k}\biggr)\le u_k\biggl(c^b+c^q \biggl(\frac{g_k}{u_k}\biggr)^2+c^l\biggl(\frac{g_k}{u_k}\biggr)\biggr)\le u_k\Bigl(\sup_{g\in [\underline{P},\overline{P}]} f(g)\Bigr)$$

and, therefore, lim _k→∞ u _k f(g _k /u _k )=0, as f is convex and finite on the compact $[\underline{P},\overline{P}]$.

Also, for $g\in [\underline{P},\overline{P}]$ and u∈[0,1] it can be shown that the maximum value of h(g,u)−f(g,u) over the domain of both functions is $c^{q}\overline{P}^{2}/4$, attained at $(\overline{P}/2,1/2)$, i.e. h penalizes the highest non-integrality in the domain. Nevertheless, due to the strong nonlinearity and the non-differentiability of h(g,u) at (0,0), it is not practical to use it as the objective function instead of f(g,u). A way of overcoming this difficulty is to replace h(g,u) with the pointwise supremum of affine functions, which is possible because of the convexity of h.

The subgradient inequality for h over $(\widehat {g},\widehat {u})$ is given by

$$h(g,u)\ge h(\widehat{g},\widehat{u})+ (s_1,s_2)\bigl((g,u)-(\widehat{g},\widehat{u})\bigr), $$

(63)

where $(s_{1},s_{2})\in \partial h(\widehat {g},\widehat {u})$. Then, all (v,g,u) in the epigraph of h must verify this inequality for all . In order to characterize the epigraph of h, we notice, first, that every element (g,u) in belongs to the line $g=\widehat {g}u$ for a given $\widehat{g} \in [\underline{P},\overline{P}]$ and, second, that the subgradient (s ₁,s ₂) is constant along this line, and equal to $(s_{1},s_{2})= (2c^{q}\widehat {g}+c^{l} ,c^{b}-c^{q}{\widehat{g}}^{2})$, making only necessary to consider the subgradient inequality (63) over the points $(\widehat {g},1)$. Therefore, the epigraph of h is defined by the subset of:

$$\bigl\{(v,g,u) \mid u\underline{P}\le g\le u\overline{P} ~\hbox{and} ~0\le u\le 1\bigr\}$$

that is the solution of the infinite linear-inequality system:

$$v\ge \bigl(2c^q\widehat{g}+c^l\bigr)g+ \bigl(c^b-c^q\widehat{g}^2\bigr)u, \quad \hbox{taking}\ \widehat {g}\in [\underline{P},\overline{P}] $$

(64)

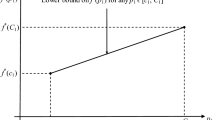
For each $\widehat {g}\in [\underline{P},\overline{P}]$ we have an inequality so-called a perspective cut (PC), which is the unique supporting hyperplane to the epigraph of the function passing by (0,0) and $(\widehat {g},1)$ (see Fig. 2).

4.1 PCF formulation of problem (DAMB-FBC)

PC formulation (PCF) consists of using the perspective cuts (64) to construct an objective function that is the pointwise maximum of the linear functions of these hyperplanes, i.e. it is a polyhedral outer approximation of the function h over the domain . A more detailed explanation can be found in Frangioni and Gentile (2006). In this section we will outline how this PCF is used to solve efficiently problem (DAMB-FBC). In the PCF of problem (DAMB-FBC) the quadratic function $f(g^{s}_{\mathit{ti}},u_{\mathit{ti}})$ in (60) is replaced by its perspective cut approximation $v^{s}_{\mathit{ti}}$:

(65)

where, for each t, i, and s, $v^{s}_{\mathit{ti}}$ must satisfy a finite subset of the inequality (64) defined over the elements of a given finite discrete domain , that is:

(66)

As a result of this formulation, the problem to be solved in the PCF of model (DAMB-FBC) is:

$$\hbox{(DAMB-FBC-PCF)}\left\{\begin{array}{l}\min {\mathrm{E}}_{\lambda^D}[\widehat{C}(u,c^u,c^d,g,p,v;\lambda^D)] \\\hbox{s.t.}\\\quad \mbox{Equations (1)--(4)}\quad \mbox{BC and FC constraints}\\\quad \mbox{Equations (5)--(9)}\quad \mbox{DAM and total gen. constraints}\\\quad \mbox{Equations (11)--(20)}\quad \mbox{Unit commitment constraints}\\\quad \mbox{Equation (66)}\quad \mbox{Perspective cuts}\end{array} \right.$$

which is a MILP that can be solved with a branch and cut algorithm. The set of constraints (66) (or, equivalently, the elements in ) are defined dynamically as the branch and cut algorithm proceeds, in the following manner. At the first iteration of the algorithm, the constraints (66) include, for each s, i and t, just the two inequalities defined over the extreme values of the interval $[\underline{P}_{i},\overline{P}_{i}]$, that is . At every subsequent iteration k, once a solution (v ^∗,g ^∗,u ^∗) to the relaxed subproblem is found, if $u^{*}_{\mathit{ti}}>0$ then new inequalities (64) are generated over $\widehat{g}=g^{s,*}_{\mathit{ti}}/u^{*}_{\mathit{ti}}$ and, if violated by the current solution $(v^{s,*}_{\mathit{ti}},g^{s,*}_{\mathit{ti}},u^{*}_{\mathit{ti}})$, they are added to the set of constraints (66), i.e. .

5 Numerical tests

In this section we present some results of the numerical tests done in order to evaluate the computational advantages of these optimization techniques for the presented model. Table 1 shows the main characteristics of the set of instances of the (DAMB-FBC) problem used to evaluate the performance of the perspective cuts method. These instances are defined based on real data of a GenCo operating in the MIBEL. These instances have a pool of bilateral contracts with 300 MWh committed for each interval, a set of 3 futures contracts with 700 MWh committed, 9 thermal units (see Table 2 for the units’ operational characteristics) and 24 hourly intervals. The difference between the set of problems presented is the scenario prices and probabilities used: they are generated with different statistical methods. In Table 1, , , and are the cardinality of the corresponding sets. means the number of bilateral contracts, # var is the number of variables in problem (DAMB-FBC), # var _PCF is the number of variables in problem (DAMB-FBC) for the PC formulation, # bin is the number of binary variables and # constr represents the number of constraints in problem (DAMB-FBC). Note that, if we use the PC formulation, the number of variables increases in , due to the addition of variables v. Moreover, the number of constraints also increases due to the presence of the perspective cuts (66): initially there are 2⋅m extra constraints and, at the termination of the branch and cut algorithm, there is a variable number of perspective cuts dynamically added, which is stated in column # PC.

Table 1 Test problems, CPU times and number of PC

Table 2 Operational characteristics of the thermal units used in the study

In our numerical tests we have used CPLEX 12.1, which allows to input directly the (DAMB-FBC) problem as a mixed-integer linearly constrained quadratic program and solve it. Moreover, for PCF the dynamic generation of PCs can be easily implemented by means of the cutcallback procedure. Thus, apart from the basic formulation, the same sophisticated tools (valid inequalities, branching rules, etc.) are used for both formulations: MIQP and PCF. In both cases we have set the default gap (0.01%) and have used only one CPU thread.

A few differences remain: e.g. the need for invoking the callback functions disables the more efficient dynamic search of CPLEX 12.1 for adding cuts, whereas this skill is used when the (DAMB-FBC) problem is solved by CPLEX as a MIQP. Apart from these, the same tools are used with both formulations, allowing a fair comparison.

The tests have been performed on HP with Intel(R) Core(TM)2 Quad CPU Q8300 2.50 GHz 4 CPU under SUSE Linux Enterprise Desktop 11 (x86_64).

In Table 1, t _MIQP points out the CPU-times (in seconds) used by CPLEX to solve these problems by MIQP techniques; under t _PCF we have the time used by CPLEX with PC formulation and MILP techniques; effi=t _MIQP/t _PCF gives us the PCF efficiency with regard to MIQP. As can be observed, in the solution of these (DAMB-FBC) problems CPLEX with PCF has been significantly more efficient than without it, as is suggested in Frangioni and Gentile (2006), in fact the average of the efficiency without the extreme values is 9.91 and the maximum efficiency, 44.81, is obtained for the problem “B10”. Moreover, PCF not only converges faster than the MIQP counterpart, but also gives the optimal solution to the original quadratic problem (DAMB-FBC): the relative discrepancy between the actual quadratic objective function (60) computed over the PCF-MILP and the MIQP solutions is around 10⁻⁸ in all the cases shown in Table 1, which is absolutely negligible. In summary, the PCF formulation has been able to find the optimal solution of all the (DAMB-FBC) instances in 1/10 of the execution times of the MIQP formulation, on the average. This reduction of the execution time which, for the largest case C125 means the change from more than 3 hours to less than 1 hour on a standard personal computer, is of special value for the electrical utilities because this problem usually has to be solved several times within the same working day.

Let us now illustrate different situations concerning the bid strategy. We use the problem C75 and we represent some optimal bid curves (Fig. 5). In Fig. 5(a), the optimal bid curve is shown for thermal unit 1 at interval 23. It can be seen that, in this case, $b^{*}_{23,1}=80$ is lower than the minimum capacity. Thus, the instrumental price bid must be at least the minimum capacity minus this quantity that is committed to BCs. In this case, the instrumental price bid quantity $q^{*}_{23,1}=179$. In the other case, Fig. 5(b), the optimal bid curve of unit 6 at interval 18 is represented. Contrary to the previous case, the quantity committed to bilateral contracts is greater than the minimum capacity ($b^{*}_{18,6}=86$); therefore, the instrumental price bid quantity is forced, by the coverage of the FCs, to be greater than 0.

Fig. 5

Bidding curve for (a) unit 1 at interval 23 and (b) unit 6 at interval 18

6 Conclusion

In this work we have presented a mixed-integer quadratic stochastic programming model for the integration of the physical futures and classical bilateral contracts into the day-ahead bidding problem of a GenCo operating in the MIBEL. The rules for the integration of the BCs and FCs in the DAM process have been described and the analytical expression of the optimal bid function that maximizes the expected long-run benefits of the GenCo was obtained. The optimal solution of our model determines not only the optimal bid to the DAM but also the optimal operation of the units (unit commitment), and the optimal way to procure both the futures and bilateral contracts.

There also has been studied and presented an implementation of the perspective cut methodology in the solution of decision problems under uncertainty. We have applied this methodology to the model for day-ahead market bid with bilateral and futures contracts. The computational experience shows that if we use a commercial software as CPLEX together with these techniques to solve (DAMB-FBC) problems, an average speed-up factor of ten is obtained with respect to the running time of standard MIQP branch and cut methods. Therefore, these results show that appropriate formulations of (DAMB-FBC) problems can be used to find good-quality solutions in relatively short time by using general-purpose optimization software. The computational tests were performed using real data on the thermal units of a price-taker producer operating in the MIBEL.