1 Introduction

Micro forming is an appropriate technology to manufacture very small parts, especially for bulk production, as they are required in many industrial products resulting from microtechnology. In case of downscaling the size of the work piece to the dimensions of micro forming, not all parameters can be changed according to the rule of similarity, e.g. the surface roughness and grain size [1, 2]. This causes the so called size effects, i.e. the occurrence of unexpected results concerning the forming force or the forming limit [3].

Since deep drawing is essentially affected by the friction between the work piece and tools [4, 5], which is also affected by the size effects [6–8], the trilobogical size effects in sheet metal forming were investigated in our previous work [1–3]. The size dependent friction functions were acquired from scaled strip drawing test. A size dependent FEM-simulation for deep drawing was realized applying the acquired friction functions. However the simulated punch force vs. punch travel curve did not agree with the experimental one perfectly. A difference of about 11% at maximum force in micro strip drawing test was detected. Thus the analytical model is further developed in this paper.

2 Investigation

2.1 Method

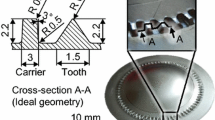
Compared to usual deep drawing there is no tangential force F t at flange area in strip drawing, see Fig. 1. This difference makes it easier to find the relation between the punch force and the friction coefficient.

Fig. 1
figure 1

a Strip drawing, b deep drawing

Full size image

Strip drawing experiments with six different punch diameters (1, 5, 10, 20, 50 and 100 mm) were carried out. All geometrical parameters of tools and work pieces are scaled by the same scaling factor and all process parameters are constant for all experiments according to the law of similarity. For example the drawing radius has a constant ratio to the punch diameter in all experiments. A drawing ratio of 1.8 and the blank holder forces with an initial pressure of 1 N/mm2 at the flange was applied. The ratio of work piece thickness to punch diameter, the work piece materials, the material and surface quality of the tools are all the same.

Al99.5 is used as work piece material in every process dimension. Regarding that, the properties of the material are also affected by size effects [8, 9]. For the determination of the bending force in this investigation the flow stress is required. Thus, the tensile tests were carried out to acquire the flow curves of Al99.5 in each thickness and taken into account. The flow curves of Al99.5 in different thicknesses show clearly difference from each other, see Fig. 2.

Fig. 2
figure 2

Flow curves of Al99.5 in different thicknesses

Full size image

Besides the tools for macro strip drawing, a test setup is especially installed for micro strip drawing including a force measurement system with an accuracy of 0.01 N and a position measurement system with an accuracy of 0.003 mm. We thus get the punch force versus punch travel curves, which can be used for the calculation for friction functions in strip drawing processes.

2.2 Size-dependent friction functions

Applying the calculation model described in [1] a friction function is determined from the punch force measured in strip drawing tests for each punch diameter. A graphic display of these friction functions is shown in Fig. 3. A difference with a factor of about 2 between the friction functions with punch diameter of 1 and 100 mm is described, which illustrates a tribological size effect within this investigation. The curves can be described through some mathematic functions. An exponential function in the following form is used in this work:

Fig. 3
figure 3

Friction functions for different punch diameters

Full size image
$$ \mu = C_{1} + C_{2} \cdot \exp ( - P \cdot C_{4} ) + C_{3} \cdot \exp ( - P \cdot C_{5} ) $$
(1)

where μ = friction coefficient, P = contact pressure, C 1 –C 5  = coefficients (They are listed in Table 1).

Table 1 Coefficients of friction function
Full size table

2.3 Size-dependent FEM-simulation

In this work the software ABAQUS 6.6.3 was used to simulate this forming process. A 2-dimensional model was created for the strip drawing test, in which the tools were defined as analytical rigid line and the blank was defined as deformable object. The 4-node bilinear plane stress element CPS4R was used to mesh the blank. Within the thickness of the blank there are four elements. For simulation of the experiments with blanks in different thicknesses, the flow stress curves of Al99.5 in different thicknesses were applied respectively in the simulation model. Using the normalization described in [3] the simulated punch force vs. travel curves for strip drawing with punch diameters of 1 and 100 mm shown in Fig. 4 were obtained.

Fig. 4
figure 4

Comparison of simulated and experimental punch force versus punch travel curves

Full size image

For punch diameter of 1 mm, the maximum point of the simulated curve FEM-1 is about 11% lower than that of the experimental curve EXP-1. While the maximum point of the curve FEM-100 is about 8% lower than that of EXP-100 for punch diameter of 100 mm. The reason for this might be the assumption in the calculation model that the normal pressure at the radius is uniform [1]. But the simulation shows local contact zones, where the normal contact pressure is much higher than that on other surfaces, see Fig. 5. In this investigation these local contact zones are called high impact contact. Compared to this, other contact surfaces are called low impact contact, where the normal pressure is very small and thus can be neglected.

Fig. 5
figure 5

Distribution of contact pressure at drawing radius

Full size image

The position of high impact contact changes with the punch travel, see Fig. 6.

Fig. 6
figure 6

High impact contact at drawing radius vs. punch travel

Full size image

The diagram above shows the changes of the local contact zones between the blank and the die within strip drawing with punch diameter of 1 mm. At the beginning there is only one high impact contact at the entrance from flange to the drawing radius. As the punch goes deeper into the die, the length of the high impact contact Lc increases from about 0.01 mm to about 0.02 mm at the punch travel of about 0.05 mm. Then this high impact contact divides into two high impact contacts. One keeps at the entrance from the flange to the die, while the other one moves into the die as the punch goes deeper into the die. Each of them has a length of about 0.01 mm.

Furthermore the distribution of pressure at the flange area is also not uniform according to the FEM-simulation. The local contact zone between the blank and the blank holder for strip drawing with punch diameter of 1 mm is shown in Fig. 7. The length of the high impact contact as well as the value of the normal pressure changes a little within the whole process.

Fig. 7
figure 7

High impact contact at flange versus punch travel

Full size image

2.4 New analytical model

The analytical model described in [1] is improved, taking into account the non-uniform distribution of pressure shown above. The forces involved in strip drawing process are shown in Fig. 8.

Fig. 8
figure 8

Analysis of forces in strip drawing

Full size image

Five assumptions are applied:

  • The Coulomb’s Law is valid in consideration of μ = f(P), whereby P is normal contact pressure.

  • The contact zone between the blank and the die at drawing radius divides into two zones, if the length of the contact zone is bigger than the thickness of the blank. After partition the two contact zones have the same length, i.e. half of the blank thickness.

  • The length of local contact zone between the blank and the blank holder is half of the blank thickness.

  • The normal contact pressure within the high impact contact zone has a constant value, see Fig. 5 (the curve: analytical assumption).

  • Under the same forming condition (same materials, same amount of lubricant the same roughness of surface) and same normal pressure the friction coefficient on plane surface is equal to that on round surface.

According to the Coulomb’s Law the friction force between the blank and the blank holder, which results from the blank holder force, follows as:

$$ F_{fN} = F_{N} \cdot \mu_{1} (P_{1} ) $$
(2)

whereby μ 1  = f(P 1) means that μ 1 is dependent on the normal pressure P 1. Within strip drawing the blank is bended at the drawing radius (r M) and at the radius of the punch (r P). The bending moment of the blank follows [10, 11] as:

$$ M_{B} = \frac{{b_{0} k_{f} s_{0}^{2} }}{4} $$
(3)

whereby:

M B :

bending moment

b 0 :

original width of blank

s 0 :

original thickness of blank

k f :

flow stress of work piece material

Then bending force at point A is:

$$ F_{BA} = \frac{{M_{B} }}{{L_{1} }} $$
(4)

whereby, L 1 is the bending arm from the punch to the point A.

Similarly, the bending force at the radius of the punch is:

$$ F_{BP} = \frac{{M_{B} }}{{L_{2} }} $$
(5)

whereby, L 2 is the bending arm from the die to the radius of the punch.

Regarding that the blank is back bended at point B at the drawing radius by the longitudinal force [12], thus the back bending force at point B is:

$$ F_{BB} = \frac{{M_{B} }}{{\left( {r_{M} + \frac{{s_{0} }}{2}} \right)}} $$
(6)

whereby, r M is the drawing radius.

Since both F N and F BA result in a reacting force at point A with the same value respectively, the friction force between the blank and the die at point A follows as:

$$ F_{fA} = (F_{N} + F_{BA} ) \cdot \mu_{2A} (P_{2A} ) $$
(7)

According to the second assumption, the whole strip drawing process is considered as two phases:

Phase 1

There is only one high impact contact between the blank and the die at drawing radius, and

$$ L_{C} \le s_{0} $$
(8)

whereby, L C is the length of the high impact contact between the blank and the die and follows:

$$ L_{C} = r_{M} \cdot \alpha $$
(9)

whereby

α: the bending angle of the blank around the die.

Considering that the reacting force of F BP results in also friction force (F fBP ) at the drawing radius, thus:

$$ F_{fBP} = F_{BP} \cdot \mu_{2A} (P_{2A} ) $$
(10)

According to the calculation of rope friction [13] the drawing force at point A is:

$$ F_{LA} = (F_{fN} + F_{fA} + F_{fBP} ) \cdot \exp (\alpha \cdot \mu_{2A} (P_{2A} )) $$
(11)

According to the relation between the punch force and F L as well as F C shown in Fig. 8, the horizontal component of F T can be compensated by the same force on the other side. Therefore the punch force follows as:

$$ F_{P} = 2\left( {F_{L} \sin \alpha + F_{C} \cos \alpha + F_{BA} } \right) $$
(12)

The total longitudinal force F L is the sum of F BB and F LA . The transverse force F C is equal to F BP . Thus the punch force can be written as:

$$ F_{P} = 2\left( {(F_{BB} + F_{LA} ) \cdot \sin \alpha + F_{BP} \cos \alpha + F_{BA} } \right) $$
(13)

The normal contact pressure at drawing radius can be determined by:

$$ P_{2A} = \frac{{F_{N} + F_{BA} + F_{BP} + 2F_{LA} \cdot \sin (0.5\alpha )}}{{b_{0} \cdot L_{C} }} $$
(14)

Phase 2

There are two high impact contacts (L CA and L CB ) between the blank and the die at drawing radius, and

$$ L_{CA} = L_{CB} = 0.5 \cdot s_{0} $$
(15)

Similar to the calculation in phase 1, the longitudinal drawing force at point A is:

$$ F_{LA} = (F_{fN} + F_{fA} + F_{BA} ) \cdot \exp (\alpha_{s} \cdot \mu_{2A} (P_{2A} )) $$
(16)

whereby, α s is the open angle for the high impact contact with a length of 0.5 s 0.

$$ \alpha_{S} = \frac{{0.5 \cdot s_{0} }}{{r_{M} }} $$
(17)

Then the longitudinal drawing force at point B is:

$$ F_{LB} = (F_{LA} + F_{fBP} ) \cdot {\rm exp}(\alpha_{s} \cdot \mu_{2B} (P_{2B} )) $$
(18)

Thus the punch force follows as:

$$ F_{P} = 2\left( {(F_{BB} + F_{LB} ) \cdot \sin \alpha + F_{BP} \cos \alpha + F_{BA} } \right) $$
(19)

The normal contact pressure at point A and point B at drawing radius are determined by:

$$ P_{2A} = \frac{{F_{N} + F_{BA} + 2F_{LA} \cdot \sin (0.5\alpha_{s} )}}{{b_{0} \cdot L_{CA} }} $$
(20)
$$ P_{2B} = \frac{{F_{BP} + (F_{LB} + F_{BB} + F_{LA} ) \cdot \sin (\alpha - \alpha_{s} )}}{{b_{0} \cdot L_{CB} }} $$
(21)

2.5 Friction functions according to the new analytical model

According to the new analytical model, new friction functions were acquired from the same experimental punch force versus punch travel curves. The friction function curves for all punch diameters are shown in Fig. 9.

Fig. 9
figure 9

New friction functions

Full size image

Similar to the Fig. 3, a factor of about 2 was observed between the curves for the punch diameters of 1 and 100 mm. The form of Eq. 1 was also used for a mathematical description of these functions. The corresponding function coefficients are listed in Table 2.

Table 2 Coefficients of new friction function
Full size table

2.6 FEM-simulation with new friction functions

Applying the friction functions above into the FEM-simulation model described in Sect. 2.3, the simulated punch force versus punch travel curves were acquired. Using the normalization in [3] the curves are shown in Fig. 10.

Fig. 10
figure 10

Comparison of experimental and simulated punch force versus punch travel curves using new friction functions

Full size image

Compared with Fig 4, Fig. 10 shows clearly a better agreement between the simulated and the experimental punch force versus punch travel curves for both punch diameters of 1 and 100 mm.

3 Conclusion

An analytical model was developed in BIAS, with which the friction functions can be acquired from the experimentally measured punch force vs. punch travel data. The friction functions can be applied in FEM-simulation using the program ABAQUS to realize size-dependent FEM-simulation for sheet metal forming.

The analytical model for calculation of friction function from punch force versus punch travel measured in strip drawing test was improved, whereby the non-uniform distribution of contact pressure were taken into account. New friction functions were acquired using this new analytical model.

Applying the new friction functions in FEM-simulation using the program ABAQUS, the simulated punch force vs. punch travel curves showed a better agreement with the experimental curves.