Particle swarm variants: standardized convergence analysis

Abstract

This paper presents an objective function specially designed for the convergence analysis of a number of particle swarm optimization (PSO) variants. It was found that using a specially designed objective function for convergence analysis is both a simple and valid method for performing assumption free convergence analysis. It was also found that the canonical particle swarm’s topology did not have an impact on the parameter region needed to ensure convergence. The parameter region needed to ensure convergent particle behavior was empirically obtained for the fully informed PSO, the bare bones PSO, and the standard PSO 2011 algorithm. In the case of the bare bones PSO and the standard PSO 2011, the region needed to ensure convergent particle behavior differs from previous theoretical work. The difference in the obtained regions in the bare bones PSO is a direct result of the previous theoretical work relying on simplifying assumptions, specifically the stagnation assumption. A number of possible causes for the discrepancy in the obtained convergent region for the standard PSO 2011 are given.

1 Introduction

Particle swarm optimization (PSO) is a stochastic population-based search algorithm that has been effectively utilized to solve numerous real-world optimization problems (Poli 2008). PSO and its variants have also undergone numerous theoretical investigations (Ozcan and Mohan 1998, 1999; Clerc and Kennedy 2002; Zheng et al. 2003; Van den Bergh and Engelbrecht 2006; Trelea 2003; Cleghorn and Engelbrecht 2014a; Kadirkamanathan et al. 2006; Gazi 2012; Poli 2009; Campana et al. 2010; Bonyadi and Michalewicz 2014; Blackwell 2012; Montes de Oca and Stützle 2008; Liu 2014). Despite the numerous theoretical investigations, there still exist important aspects of PSO’s behavior that are not completely understood. For example, the conditions necessary for PSO to enter a state of stagnation are still unknown.

As with most theoretical studies, where the problem being analyzed is intractable, a number of simplifying assumptions are needed in order to be able to reasonably derive a result. The last assumption that remains in all theoretical work on all stochastic PSO variants is the stagnation assumption. The stagnation assumption in its strongest form assumes that the personal and neighborhood best positions remain constant for each particle. The weakest stagnation assumption used in a recent study done by Liu (2014) assumed that only the particle with the best objective function evaluation is constant. With the presence of the stagnation assumption in theoretical investigations, it is not clear that the derived criteria for convergent particles will ensure convergent particle behavior in practice. While the stagnation assumption appears reasonable, particularly the weak variant (Liu 2014), there is no guarantee that PSO will in fact ever enter a state of stagnation, it is for this reason that theoretical analysis performed under any form of stagnation should be verified empirically in an assumption free context.

In the paper, we define convergence to be order-2 stability, as defined by Poli (2009). Specifically, a sequence of random variables $z_n$ is order-2 stable if

$$\begin{aligned} \lim _{n\rightarrow \infty }E[z_n]=\mu \text { and } \lim _{n\rightarrow \infty }StdDev[z_n]=\sigma \end{aligned}$$

(1)

This definition of stability, as apposed to one where the standard deviation approaches zero, is based on the derivation by Poli (2009) for the canonical PSO, that shows that the standard deviation only approaches 0 if the personal best and the neighborhood best positions become equal. However, in practice, there is no guarantee of this equality occurring for multiple particles, let alone the swarm as a whole.

There are two primary aims in this study. The first aim is to empirically verify the use of a specially designed objective function for particle swarm optimization (PSO) convergence analysis. The second aim is to analyze the parameter region needed to ensure convergent particle behavior of PSO variants utilizing the specially designed objective function. The empirical analysis presented in this paper imposes no simplifying assumption on the analyzed PSO variants, resulting in a true reflection of the PSO variants’ convergence behavior.

A brief description of the PSO algorithm is given in Sect. 2. A description of the fully informed PSO (FIPS), bare bones PSO (BPSO), and the standard PSO 2011 (SPSO2011) is given in Sect. 3. A summary of the theoretical convergence results obtained for PSO and PSO’s variants is presented in Sect. 4. The experimental setup and results for each experiment are presented in Sect. 5. Section 6 presents a summary of the findings of this paper, as well as a discussion of topics for future research.

2 Particle swarm optimization

Particle swarm optimization (PSO) was originally developed by Kennedy and Eberhart (1995) to simulate the complex movement of birds in a flock. The standard variant of PSO this section focuses on includes the inertia coefficient proposed by Shi and Eberhart (1998).

The PSO algorithm is defined as follows: Let $f:{\mathbb {R}}^k\rightarrow {\mathbb {R}}$ be the objective function that the PSO algorithm aims to find an optimum for, where k is the dimensionality of the objective function. For the sake of simplicity, a minimization problem is assumed from this point onwards. Specifically, an optimum ${\varvec{o}}\in {\mathbb {R}}^k$ is defined such that, for all ${\varvec{x}}\in {\mathbb {R}}^k$, $f({\varvec{o}})\le f({\varvec{x}})$. In this paper, the analysis focus is on objective functions where the optima exist. Let $\varOmega \left( t\right)$ be a set of N particles in ${\mathbb {R}}^k$ at a discrete time step t. Then $\varOmega \left( t\right)$ is said to be the particle swarm at time t. The position ${\mathbf{x}}_{i}$ of particle i is updated using

$$\begin{aligned} {\varvec{x}}_{i}\left( t+1\right) = {\varvec{x}}_{i}\left( t\right) +{\varvec{v}}_{i}\left( t+1\right) , \end{aligned}$$

(2)

where the velocity update, ${\varvec{v}}_{i}\left( t+1\right)$, is defined as

$$\begin{aligned} {\varvec{v}}_{i}\left( t+1\right)= & {} w{\varvec{v}}_{i} \left( t\right) + c_{1}{\varvec{r}}_{1}(t) \otimes ({\varvec{y}}_{i}(t)-{\varvec{x}}_{i}\left( t\right) )+ c_{2}{\varvec{r}}_{2}(t) \otimes ({\hat{\varvec{y}}}_{i}(t) - {\varvec{x}}_{i}\left( t\right) ), \end{aligned}$$

(3)

where ${r}_{1,j}(t),{r}_{2,j}(t)\sim \ U\left( 0,1\right)$ for all t and $1\le j \le k$. The operator $\otimes$ is used to indicate component-wise multiplication of two vectors. The position ${\varvec{y}}_{i}(t)$ represents the “best” position that particle i has visited, where “best” means the location where the particle had obtained the lowest objective function evaluation. The position ${\hat{\varvec{y}}}_{i}(t)$ represents the “best” position that the particles in the neighborhood of the i-th particle have visited. The coefficients $c_1$, $c_2$, and w are the cognitive, social, and inertia weights, respectively.

A primary feature of the PSO algorithm is social interaction, specifically the way in which knowledge about the search space is shared amongst the particles in the swarm. In general, the social topology of a swarm can be viewed as a graph, where nodes represent particles, and the edges are the allowable direct communication routes. The social topology chosen has a direct impact on the behavior of the swarm as a whole (Kennedy 1999; Kennedy and Mendes 2002; Engelbrecht 2013a). Some of the most frequently used social topologies are discussed below:

• Star The star topology is one where all the particles in the swarm are interconnected as illustrated in Fig. 1a. The original implementation of the PSO algorithm utilized the star topology (Kennedy and Eberhart 1995). A PSO utilizing the star topology is commonly referred to as the Gbest PSO.

• Ring The ring topology is one where each particle is in a neighborhood with only two other particles, with the resulting structure forming a ring as illustrated in Fig. 1b. The ring topology can be generalized to a network structure where larger neighborhoods are used. The resulting algorithm is referred to as the Lbest PSO.

• Von Neumann The Von Neumann topology is one where the particles are arranged in a grid-like structure. The 2-D variant is illustrated in Fig. 1c, and the 3-D variant is illustrated in Fig. 1d.

The PSO algorithm is summarized in algorithm 1. The PSO, as defined in this section, is referred to as canonical PSO (CPSO) within the remainder of this paper.

Fig. 1

Common social topologies. a Star topology. b Ring topology. c 2-D Von Neumann topology. d 3-D Von Neumann topology

3 Particle swarm optimization variants

There exists a large number of PSO variants (Engelbrecht 2007). The simplest variants alter one or more of the PSO velocity update equation’s coefficients to be a function of time, in an attempt to control the exploration–exploitation behavior of the swarm over the course of the search. There are also more sophisticated PSO variants that substantially alter the PSO’s behavior. This section focuses on three of these variants that are commonly used: the fully informed PSO (FIPS), bare bones PSO (BPSO), and the standard PSO 2011 (SPSO2011).

3.1 Fully informed PSO

The FIPS algorithm was inspired by the observation made by Kennedy and Mendes (2003) that human individuals are not influenced by only a single individual, but rather by a statistical summary of the state of their neighborhood. Based on this observation, the velocity equation is altered such that each particle is influenced by the successes of all its neighbors, and not by the performance of only one other individual in the neighborhood.

The velocity update equation of FIPS is defined as follows:

$$\begin{aligned} {\varvec{v}}_{i}\left( t+1\right)= & {} w{\varvec{v}}_{i}\left( t\right) + \sum _{m=1}^{|{\mathcal {N}}_i|} \varvec{\gamma }_m(t)\otimes \frac{({\varvec{y}}_{m}(t) - {\varvec{x}}_{i}\left( t\right) )}{|{\mathcal {N}}_i|}, \end{aligned}$$

(4)

where ${\mathcal {N}}_i$ is set of particles in particle i’s neighborhood, $|{\mathcal {N}}_i|$ is the cardinality of ${\mathcal {N}}_i$, and ${\gamma }_{m,j}(t)\sim U\left( 0,c_1+c_2\right)$ for $1\le j \le k$.

The FIPS algorithm was originally proposed using constriction. For a detailed explanation of constriction, the reader is refereed to Clerc and Kennedy (2002). However, the velocity update equation (4) can be rewritten to utilize constriction instead of an inertia weight by setting the constriction factor ${\mathcal {X}}$ equal to w, and $\left( c_1+c_2\right) /{\mathcal {X}} = {\hat{c}}_1 + {\hat{c}}_2$, where ${\hat{c}}_1$ and ${\hat{c}}_2$ are coefficients chosen for a PSO using constriction. From a theoretical perspective, the models are equivalent.

3.2 Bare bones PSO

Kennedy (2003) proposed the BPSO algorithm based on the empirical observation that the distribution of particle positions are centered around the weighted average between the personal best and neighborhood best positions, specifically

$$\begin{aligned} {\varvec{\zeta }}_i = \frac{c_1{\varvec{y}}_{i}(t) + c_2{\hat{\varvec{y}}}_{i}(t)}{c_1+c_2}. \end{aligned}$$

(5)

This observation was later supported by the theoretical work of Van den Bergh and Engelbrecht (2006) and Trelea (2003), where it was shown for the deterministic PSO model under the stagnation assumption that each particle converges to the point defined in Eq. (5) (assuming a star neighborhood topology).

For BPSO, the velocity update equation changes to

$$\begin{aligned} v_{i,j}\left( t+1\right)\in & {} N\left( \zeta _{i,j},\phi _{i,j}\left( t\right) \right) , \end{aligned}$$

(6)

where $\phi _{i,j}\left( t\right) = |y_{i,j}(t)-{\hat{y}}_{i,j}(t)|$. The position update equation is changed to

$$\begin{aligned} {\varvec{x}}_{i}\left( t+1\right)= & {} {\varvec{v}}_{i}\left( t+1\right) . \end{aligned}$$

(7)

In the standard implementation of BPSO (Kennedy 2003), $c_1$ and $c_2$ are assumed to be equal resulting in the point of convergence being

$$\begin{aligned} \frac{{\varvec{y}}_{i}(t)+{\hat{\varvec{y}}}_{i}(t)}{2}. \end{aligned}$$

(8)

For the purposes of this paper, the case where $c_1$ and $c_2$ are equal is treated as a special case of the BPSO in the convergence analysis.

3.3 Standard PSO 2011

Clerc (2011) developed SPSO2011 in an attempt to define a new baseline for future PSO improvements. The two primary benefits of the SPSO2011 are stated to be rotational invariance and an adaptive topology. The first published work on SPSO2011 was by Zambrano-Bigiarini and Clerc (2013). The particle velocity update equation is defined as follows:

$$\begin{aligned} {\varvec{v}}_{i}\left( t+1\right)= & {} w{\varvec{v}}_{i}\left( t\right) + {\mathcal {H}}_{i}\left( {\varvec{g}}_{i} \left( t\right) ,|| {\varvec{g}}_{i}-{\varvec{x}}_{i}||_2\right) - {\varvec{x}}_{i}\left( t\right) , \end{aligned}$$

(9)

where ${\varvec{g}}_{i}$ is defined as

$$\begin{aligned} {\varvec{g}}_{i}\left( t\right)= & {} \frac{ {\varvec{x}}_{i}\left( t\right) +{\varvec{\alpha }}_{i}\left( t\right) +{\varvec{\beta }}_{i}\left( t\right) }{3}, \end{aligned}$$

(10)

where ${\varvec{\alpha }}_{i}\left( t\right)$ and ${\varvec{\beta }}_{i}\left( t\right)$ are defined as

$$\begin{aligned} {\varvec{\alpha }}_{i}\left( t\right)= & {} {\varvec{x}}_{i}\left( t\right) + c_1{\varvec{r}}_{1}\otimes \left( {\varvec{y}}_{i}(t) - {\varvec{x}}_{i}\left( t\right) \right) , \end{aligned}$$

(11)

$$\begin{aligned} {\varvec{\beta }}_{i}\left( t\right)= & {} {\varvec{x}}_{i} \left( t\right) + c_2{\varvec{r}}_{2}\otimes \left( {\hat{\varvec{y}}}_{i}(t)-{\varvec{x}}_{i} \left( t\right) \right) . \end{aligned}$$

(12)

The function ${\mathcal {H}}_{i}\left( {\varvec{g}}_{i}\left( t\right) , ||{\varvec{g}}_{i}-{\varvec{x}}_{i}||_2\right)$ returns a uniformly sampled random position from a hypersphere centered at ${\varvec{g}}_{i}\left( t\right)$ with a radius of $||{\varvec{g}}_{i}-{\varvec{x}}_{i}||_2$.

The samples from ${\mathcal {H}}_{i}$ are obtained using the following approach: Construct a random k dimensional vector, ${\varvec{rv}}$, whose scalar components are sampled from the normal distribution $N\left( 0,1\right)$. The random vector must then be normalized and multiplied by a random scalar sampled uniformly from 0 to the hypersphere’s radius. The random vector ${\varvec{rv}}$ must then be translated to the specified center point.

In the work of Zambrano-Bigiarini and Clerc (2013), no special consideration was made for the case where ${\varvec{y}}_{i}(t)={\hat{\varvec{y}}}_{i}(t)$; however, in the original work, Clerc (2011) replaced equation (10) with

$$\begin{aligned} {\varvec{g}}_{i}\left( t\right)= & {} \frac{ {\varvec{x}}_{i}\left( t\right) +\left( {\varvec{x}}_{i} \left( t\right) + c\left( {\varvec{y}}_{i}(t)-{\varvec{x}}_{i}\left( t\right) \right) \right) }{2}. \end{aligned}$$

(13)

This paper uses the following equation for the center of gravity, which applies the same principle used by Zambrano-Bigiarini and Clerc (2013) for the case where ${\varvec{y}}_{i}(t)\ne {\hat{\varvec{y}}}_{i}(t)$:

$$\begin{aligned} {\varvec{g}}_{i}\left( t\right)= & {} \frac{ {\varvec{x}}_{i}\left( t\right) + {\varvec{\alpha }}_{i}\left( t\right) }{2}. \end{aligned}$$

(14)

The topology used by SPSO2011 is a particular case of the stochastic star topology proposed by Mirinda et al. (2008). On initialization, each particle’s neighborhood is constructed by selecting three particles randomly from the swarm and the particle itself (the same particle is allowed to be chosen several times). If an unsuccessful iteration occurs, the neighborhoods are reconstructed. An unsuccessful iteration is defined as an iteration where no new position was found that improved the previous best objective evaluation obtained by the whole swarm.

In the work of Zambrano-Bigiarini and Clerc (2013), the SPSO2011 algorithm prevents particles from leaving the search space by setting the component of the particle that breached the search space boundary to the boundary value and the particle’s whole velocity to zero. This addition is not present in the original work of Clerc (2011).

4 Theoretical particle swarm optimization background

This section briefly presents the relevant theoretical findings for the CPSO, FIPS, BPSO, and the SPSO2011 algorithms in Sects. 4.1, 4.2, 4.3, and 4.4, respectively. Each subsection focuses specifically on the theoretical convergence results of each PSO variant.

The primary assumptions that occur in the theoretical PSO research are as follows:

Deterministic assumption It is assumed that ${\varvec{\theta }}_{1}={\varvec{\theta }}_{1}(t) = c_{1} {\varvec{r}}_{1}(t)$, and ${\varvec{\theta }}_{2}={\varvec{\theta }}_{2}(t)=c_{2}{\varvec{r}}_{2}(t)$, for all t.

Stagnation assumption It is assumed that ${\varvec{y}}_{i}(t)={\varvec{y}}_{i}$, and ${\hat{\varvec{y}}}_{i}(t)={\hat{\varvec{y}}}_{i}$, for all t sufficiently large.

Weak chaotic assumption It is assumed that both ${\varvec{y}}_{i}\left( t\right)$ and ${\hat{\varvec{y}}}_{i}\left( t\right)$ will occupy an arbitrarily large finite number of unique positions (distinct positions), $\psi _{i}$ and ${\hat{\psi }}_{i}$, respectively.

Weak stagnation assumption It is assumed that ${\varvec{y}}_{{\hat{i}}}\left( t\right) ={\varvec{y}}_{{\hat{i}}}$, for all t sufficiently large, where ${\hat{i}}$ is the index of the particle that has obtained the best objective function elevation.

For a more detailed discussion of when and why each assumption was made in the theoretical literature, the reader is referred to the article by Cleghorn and Engelbrecht (2014a).

4.1 Theoretical results for canonical PSO

This subsection presents each theoretically derived region that is sufficient for particle convergence in the CPSO algorithm, along with the corresponding assumptions utilized in the region’s derivation.

Under the deterministic and weak chaotic assumptions, Cleghorn and Engelbrecht (2014a) derived the following region for particle convergence:

$$\begin{aligned} c_1+c_2<2\left( 1+w\right) , \quad c_1>0, \quad c_2>0, \quad -1<w<1, \end{aligned}$$

(15)

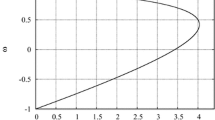
which generalized the work of Van den Bergh and Engelbrecht (2006); Van den Bergh (2002), and that of Trelea (2003). Equation (15) is illustrated in Fig. 2, as the triangle AFB.

Fig. 2

Theoretically derived regions sufficient for particle convergence

Under the stagnation assumption only, Kadirkamanathan et al. (2006) derived the following region for particle convergence:

$$\begin{aligned} {\left\{ \begin{array}{ll} c_1+c_2<2\left( 1+w\right) &{}\quad \text {for } w\in \left( -1,0\right] \\ c_1+c_2<\frac{2\left( 1-w\right) ^2}{1+w} &{}\quad \text {for } w\in \left( 0,1\right) . \end{array}\right. } \end{aligned}$$

(16)

Still under the stagnation assumption, Gazi (2012) expanded the derived region of Eq. (16), resulting in the region

$$\begin{aligned} {\left\{ \begin{array}{ll} c_1+c_2<\frac{24\left( 1+w\right) }{7} &{}\quad \text {for } w\in \left( -1,0\right] \\ c_1+c_2<\frac{24\left( 1-w\right) ^2}{7\left( 1+w\right) } &{}\quad \text {for } w\in \left( 0,1\right) . \end{array}\right. } \end{aligned}$$

(17)

The regions corresponding to Eqs. (16) and (17) are illustrated in Fig. 2 as triangle like regions ADB and AEB, respectively. Unfortunately, both Eqs. (16) and (17) are very conservative regions, as they were derived utilizing the Lyapunov condition (Kisacanin and Agarwal (2001)).

Lastly, without the use of the Lyapunov condition, Poli (2009) and Poli and Broomhead (2007) derived under stagnation the following region:

$$\begin{aligned} c_1+c_2<\frac{24\left( 1-w^2\right) }{7-5w}\quad \text {for } w\in \left[ -1,1\right] . \end{aligned}$$

(18)

The region defined by Eq. (18) is illustrated in Fig. 2 as the curved line segment AB. The region defined by Eq. (18) was also independently derived by Jiang et al. (2007) under the stagnation assumption. More recently, Liu (2014) was able to obtain the region defined by Eq. (18) using only the weak stagnation assumption. The work of Liu (2014) also implies that the convergence region of Eq. (18) is the same irrespective of the social network topology utilized by CPSO.

The choice of which region to use in practice is difficult, as each region’s derivation relies on at least one simplifying assumption. As a result, a study was done by Cleghorn and Engelbrecht (2014b), which showed with the support of empirical evidence that the region of Eq. (18) derived by Poli matched almost perfectly with the convergence behavior of a non-simplified Gbest CPSO, making the region defined by Eq. (18) the best choice in practice when utilizing the star topology.

It should be made clear that selecting parameters from a convergent parameter region does not necessarily guarantee higher-quality solutions. That said, it is unlikely to experience fruitful searches with divergent parameters, as the rate of particle velocity increases under a divergent parameter configuration is near exponential, with particles traveling at each iteration distances orders of magnitude greater than the initial search space (Cleghorn and Engelbrecht 2014b). Even if a technique is utilized to prevent particles from leaving a predetermined search space, particles will forever be colliding with the search space boundaries instead of exploring the search space.

4.2 Theoretical results for fully informed PSO

The FIPS algorithm has undergone far less theoretical investigation than CPSO. The two primary contributions with regard to convergence analysis are discussed in this subsection.

Poli (2007) was the first to analyze the FIPS algorithm from a theoretical perspective. The analyses were performed under the stagnation assumption and focused on the case where the neighborhood size was three (i.e., FIPS3). The analysis compared the order 1, 2, 3, and 4 (mean, deviation, skewness, kurtosis) stability of the social-only and canonical PSO with that of FIPS3. It was found that FIPS3 was surprisingly the most stable of the three, despite the FIPS3 algorithm containing more sources of randomness. No general region of convergence was provided for an arbitrary choice of neighborhood size.

In the study performed by Montes de Oca and Stützle (2008), it was shown that particles are attracted to the centroid of its neighborhood best found positions, given that coefficients where selected that satisfy the constriction conditions as defined in (Clerc and Kennedy 2002). The centroid is defined as the average over all the neighborhood best positions. The study was performed under the stagnation and deterministic assumptions, where $\gamma _m$ in Eq. (4) was replaced with the expected value $\left( c_1+c_2\right) /2$. A general region for particle convergence was not presented. The study did, however, empirically determine that a more connected swarm topology resulted in a smaller region of the search space being explored. It was also found that the FIPS algorithm has a very strong bias to the centroid of each particle’s previously found neighborhood best positions.

4.3 Theoretical results for bare bones PSO

Despite the BPSO algorithm being well supported by theoretical convergence results of CPSO, the algorithm itself has not undergone much theoretical study. The primary contribution is that of Blackwell (2012). The study focused on a generalized class of PSO update equations. The class of PSOs considered were those with update equations that could be applied component wise and that can be rearranged to the form

$$\begin{aligned} {x}_{ij}(t+1)+a(t){x}_{ij}(t) + b(t){x}_{ij}(t-1)=c(t,{\mathcal {N}}_i), \end{aligned}$$

(19)

where a(t) and b(t) are random variables, and $c(t,{\mathcal {N}}_i)$ is a random variable that also depends on constant neighborhood positions. Blackwell (2012) was able to show that under the stagnation assumption, the sequence of particle positions is weakly stationary for BPSO. If a series is weakly stationary, it is by implication order-2 stable as shown by Kendall and Ord (1990). Alterations of the BPSO algorithm with theoretically derived non-collapse conditions were also presented.

Blackwell (2012) used the same approach to derive the convergence criteria for CPSO, which matched the earlier derived convergence criteria of Poli (2009). However, the technique used by Blackwell (2012) is computationally simpler than that used by Poli.

4.4 Theoretical results for standard PSO2011

The only theoretical work to date on SPSO2011 is by Bonyadi and Michalewicz (2014). The analysis was completed under the stagnation assumption and without the special treatment of ${\varvec{g}}_{i}\left( t\right)$ when ${\varvec{y}}_{i}(t)={\hat{\varvec{y}}}_{i}(t)$ as defined by Eq. (14). It was shown that SPSO2011 was not locally convergent to an optimum. However, SPSO2011 was shown to be rotationally invariant. The convergent (stable) region of SPSO2011 was plotted using an empirical technique under forced stagnation, with each particle’s personal best and neighborhood best positions set to be equal. Forced stagnation is a situation when either the personal and neighborhood best positions are not allowed to update or the objective function is a constant. The former was used in the study by Bonyadi and Michalewicz (2014). It was shown that the size of the convergent region appeared to decrease as the dimensionality of the problem increased. However, no explicit conditions for convergence were presented.

5 Experiments

This section provides an empirical analysis of the proposed objective function for use in empirical convergence analysis, in addition to the empirical analysis of PSO variants.

The first experiment, presented in Sect. 5.1, aims to empirically justify the effectiveness of the proposed objective function (for use in empirical convergence analysis). The second experiment (Sect. 5.2) analyzes the impact that the social topology has on the convergence criteria of CPSO. The three remaining experiments focus on empirically analyzing the criteria necessary for particle convergence in PSO variants using the objective function defined in Sect. 5.1. The FIPS, BPSO, and SPSO2011 algorithms are analyzed in Sects. 5.3, 5.4, and 5.5, respectively. It should be noted that for all the PSO variants considered, no boundary checking or particle correction is performed, so as to prevent adding unnecessary noise to the behavior of the algorithms.

5.1 Objective function proposed for convergence analysis

There is an inherent difficulty in empirically analyzing the convergence behavior of PSO particles, specifically with regards to understanding the influence of the underlying objective function’s landscape on the PSO algorithm. It is proposed that the following objective function can be used as the reference function for convergent region analysis:

$$\begin{aligned} \hbox {CF}({\varvec{x}})\sim U\left( -1000,1000\right) , \end{aligned}$$

(20)

as originally presented in (Cleghorn and Engelbrecht 2014a).

The value of $\hbox {CF}$, for each ${\varvec{x}}$ in the domain of $\hbox {CF}$, is calculated and stored the first time it is required in the execution of the PSO algorithm. The calculated value for each ${\varvec{x}}$ in the domain of $\hbox {CF}$ remains static after its initial computation. Objective function values are generated anew for each independent run of the PSO algorithm. In other words, for each evaluated ${\varvec{x}}$ in the domain of $\hbox {CF}$ a unique random value from the uniform distribution $U\left( -1000,1000\right)$ is assigned. What the objective function in Eq. (20) provides is an environment that is rife with discontinuities and completely unstructured, resulting in a search space in which the PSO algorithm will be highly unlikely to enter a state of full stagnation.

The aim of most theoretical convergence research performed on PSO and PSO variants (Blackwell 2012; Poli and Broomhead 2007; Poli 2009; Jiang et al. 2007) is to prove a simplified version of the following theorem for a specific set of parameter configurations, with the hope that the derived results are applicable to the unsimplified version:

Theorem 5.1

There exists a set C of PSO parameter values such that if parameters are selected from C then for all objective functions $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ there exists an iteration T such that for all iterations $t>T$ each particle’s position is order-2 stable.

The objective function in Eq. (20) is designed to be an ideal counter example to Theorem 5.1. The premise is that if a PSO variant can converge for a given parameter configuration using Eq. (20) as an objective function, then the parameter configuration is very likely to be a truly convergent parameter configuration for all objective functions.

The experiment conducted in this subsection aims to justify the use of a specifically designed objective function for the convergent parameter region analysis. The experimental setup and results are presented in Sects. 5.1.1 and 5.1.2, respectively.

5.1.1 Experimental setup

The measure of convergence used in this paper is:

$$\begin{aligned} \Delta \left( t+1\right) =\frac{1}{N}\sum _{i=1}^{N} \Vert {\varvec{x}}_{i}\left( t+1 \right) -{\varvec{x}}_{i}\left( t \right) \Vert _{2}. \end{aligned}$$

(21)

Equation (21) is chosen as the measure of convergence because if any particle is divergent, the convergence measure value will reflect this divergence within the swarm. A swarm can only be classified as convergent if every particle in the swarm exhibits convergent behavior.

The experiment utilizes the following static parameters: Swarm size of 64 particles, 5000 iterations, and a 50-dimensional search space. A swarm size of 64 particles is utilized to allow for all the social topologies tested to be complete structures. Particle positions are initialized within $(-100,100)^k$, and velocities are initialized to ${\varvec{0}}$.

The experiment is conducted over the following parameter region:

$$\begin{aligned} w\in \left[ -1.1,1.1\right] \text { and } c_1+c_2\in \left( 0,4.3\right] , \end{aligned}$$

(22)

where $c_1=c_2$, with a sample point every 0.1 along w and $c_1+c_2$. The experiment is performed for each of the following neighborhood topologies: star, ring, 2-D, and 3-D von Neumann. The experiment is conducted using CF and 11 base objective functions from the CEC 2014 problem set (Liang et al. 2013). The functions are as follows: Ackley, High Conditioned Elliptic, Bent Cigar, Discus, Rosenbrock, Griewank, Rastrigin, HappyCat, HGBat, Katsuura, and Expanded Griewank plus Rosenbrock. The region of Eq. (22) contains exactly 504 points that satisfy equation (18). A total of 989 sample points from the region defined in Eq. (22) are used per objective function and topology pair. The results reported in Sect. 5.1.2 are the averages over 35 independent runs for each sample point. It should be noted that, for all PSO variants used in this paper, no form of search space bounding is performed. Any attempt to force particles to remain within a given bounded area would seriously hinder the ability to perform an empirical analysis, and implicitly impose a form of order-2 stability on the swarm.

In order to allow for a sensible comparison of convergence properties, the convergence measure values are bounded as follows: If $[l,u]^k$ is the initial domain of the objective function, then

$$\begin{aligned} \Delta _{\max } = \sqrt{k\left( l -u\right) ^2}, \end{aligned}$$

(23)

where l and u are the lower and upper bound of the domain per dimension, respectively. $\Delta _{\max }$ is the maximum distance of two points in the initialized search space. For this subsection, $\Delta _{\max }=1414.214$. Utilizing $\Delta _{\max }$ to bound the presented results is reasonable as any swarm that has the average particle movement exceeding the maximum initial distance possible between two particles in the search space after 5000 iterations cannot be thought of as convergent in a practical context. The convergence measure values are bounded instead of log scaled as multiple parameter configurations resulted in particle movement so extreme that a 64-bit floating point number was experiencing overflow. The value of $\Delta _{\max }$ also has a secondary purpose as the classification boundary between convergent and divergent particle movement. While $\Delta _{\max }$ appears to be a large allowance for convergence, it will aid in the correct classification of particles that are converging at a very slow rate. Utilizing $\Delta _{\max }$ will in addition still correctly classify particles that are slowly diverging, as it is easy for particles to exceed $\Delta _{\max }$ after swarm initialization, due to the well-known phenomenon of particle velocity explosion (Engelbrecht 2013b).

5.1.2 Experimental results and discussion

This subsection presents a table per PSO social topology containing the following measurements per objective function:

• Measurement A The number of CPSO parameter configurations that resulted in a final convergence measure value less than or equal to the final convergence measure obtained if the CF objective function was used instead.

• Measurement B The number of CPSO parameter configurations that resulted in a final convergence measure value greater than the final convergence measure obtained if the CF objective function was used instead.

• Measurement C The number of CPSO parameter configurations that resulted in a final convergence measure greater than or equal to $\Delta _{\max }$.

• Measurement D The number of CPSO parameter configurations that resulted in a final convergence measure less than $\Delta _{\max }$.

• Measurement E The number of CPSO parameter configurations that satisfied equation (18) and resulted in a final convergence measure less than $\Delta _{\max }$.

• Measurement F The number of CPSO parameter configurations that satisfied equation (18) and did not result in a final convergence measure less than $\Delta _{\max }$.

• Measurement G The average convergence measure value across all parameter configurations, with all elements bounded at $\Delta _{\max }$. It should be noted that reported averages for this measurement are calculated after bounding of the convergence measure has occurred, so as to prevent divergent configurations from radically affecting the results.

Measurements A and B provide a concise way of seeing, per objective function, how much better or worse the CF objective function performs as a reference convergence analysis function. An ideal convergence analysis function is one that, in general, will yield the highest resulting convergence measure for all possible parameter configurations. The higher the resulting convergence measure value is, the harder it was for the PSO to have converged under a given objective function. Measurements C and D give a clear picture of how effectively the underlying objective function highlights possible divergent particle behavior. Given the tested region of Eq. (22), there are a total of 504 parameter configurations that satisfy equation (18), leaving 485 parameter configurations that should produce divergent behavior. Ideally, an objective function utilized for convergence analysis should result in a value for measurement C as close as possible to 485, and a value for measurement D as close as possible to 504. Measurements E and F are an extension of measurements C and D, in that an objective function should have at most 504 parameter configurations that both satisfy equation (18) and have a convergence measure value not exceeding $\Delta _{\max }$. An objective function with a measurement E value smaller than 504 is more conservative in assigning the label of a convergent particle. A slightly conservative assignment is a positive feature of an objective function being used for convergence analysis, as falsely classifying a parameter configuration as convergent could lead to a PSO user obtaining radically unexpected results when utilizing the parameter configuration in practice. Measurement G provides an overall view of how difficult the used objective function has made it for the CPSO algorithm to converge.

A snapshot of the convergence measure values is presented for three cases:

• Case A For each parameter configuration, the maximum convergence measure value across all 11 objective functions and topologies is reported.

• Case B For each parameter configuration, the maximum convergence measure value across all topologies using only the CF objective function is reported.

In order to deduce the convergence region from the empirical data of all 11 base functions and all topologies, the largest recorded convergence measure value of each parameter configuration is reported in case A. Case B is presented to illustrate the similarity between the mapped out convergence region of the CPSO algorithm using the CF objective function to the mapped out convergence region of the CPSO algorithm in case A, which is constructed using the complete pool of gathered data of the 11 objective functions.

• Cases C and D For each parameter configuration, the maximum convergence measure value across all topologies using the two objective functions which have the most similar resulting measurements to case B is reported.

Cases C and D are presented to illustrate that the mapped out convergence region of cases A and B is not identical to the convergence regions of any arbitrary objective function. In particular, cases A and B should result in a subset of the region produced by an arbitrary objective function.

Measurements A and B in Table 1 show that the Gbest CPSO applied to the CF objective function resulted in a higher convergence measure evaluation than 9 of the 11 other objective functions for nearly all parameter configurations. For the two remaining objective functions, Katsuura is the only objective function close to the CF objective function in terms of measurement A. However, Katsuura has an average convergence measure of 49.672 less than CF has, making CF the better objective function for convergence analysis. The CF objective function also obtained the largest number of parameter configurations that resulted in a convergence measure that exceeded the bound of $\Delta _{\max }$ and the highest average convergence measure evaluations. These measurements indicate the effectiveness of CF as an objective function for convergence analysis. The CF objective function under the star topology provides an environment that is much harder for CPSO particles to converge in than using any of the other objective functions.

Table 1 Convergence properties per objective function under the Star topology

Measurements A and B in Table 2 show that the Lbest CPSO applied to the CF objective function resulted in a higher convergence measure evaluation than 9 of the 11 other objective functions for nearly all parameter configurations. Once again, Katsuura provided the second lowest value for measurement A, while CF provided the best results for all other measurements, applying the same analysis logic used for the star topology. Though inferior, Ackley resulted in values for C, D and G very close to that obtained by the CF objective function. However, CF provided far better results in terms of measurement A, making CF the best choice as an objective function for convergence analysis.

Table 2 Convergence properties per objective function under the Ring topology

Measurements A through G in Tables 3 and 4 show for both the 2-D and 3-D von Neumann topologies that the results remain almost identical to those of the ring and star topologies. This provides evidence that the topology has a negligible impact on the effectiveness of CF as an objective function for convergence analysis.

Table 3 Convergence properties per objective function under the 2-D von Neumann topology

Table 4 Convergence properties per objective function under the 3-D von Neumann topology

For case A, the convergent region as illustrated in Fig. 3a matches the derived region of Eq. (18) almost perfectly, as does the region seen in Fig. 3b for case B. While there exists a slight difference between Fig. 3a and b in terms of convergence measure values, the overall convergent regions are nearly identical. The similarity observed between Fig. 3a and b indicate that the utilization of the CF function is sufficient for the purpose of empirical convergence analysis. The similarity between Fig. 3a and b is not observed for the other objective functions. For example, in case C, the Katsuura function, when used with CPSO, resulted in properties similar to the CPSO using CF in Tables 1, 2, 3 and 4. However, Katsuura has a substantially different convergent region to both Fig. 3a and b, with an apex extending past $c_{1}+c_{2}=4.5$, as illustrated in Fig. 3c. For Case D, the convergent region obtained when using the Ackley objective function is illustrated in Fig. 3d. The obtained convergent region is substantially closer to the convergent region obtained in case A and B; however, that apex of the convergent region obtained when using the Ackley objective function is quite jagged in comparison with case A and B.

Fig. 3

Convergence measure values at the 5000th iteration. a Case A: Optimal region. b Case B: CF region. c Case C: Katsuura region. d Case D: Ackley region

A very promising feature of the convergence analysis approach presented in this paper is the high level of accuracy that can be obtained when using CF as an objective function and $\Delta _{\max }$ as a classification boundary. Specifically, with the CPSO algorithm, if every parameter configuration with a convergence measure value below $\Delta _{\max }$ is classified as convergent and every parameter configuration with a convergence measure value above or equal to $\Delta _{\max }$ is classified as divergent, a total accuracy of 98.79 % is obtained when compared to the region derived by Poli (2009), with only 12 of the 989 parameter settings misclassified (10 falsely classified as divergent and two falsely classified as convergent).

5.2 Canonical PSO, convergence analysis of topological influence

This subsection aims to verify that the theoretically derived region of Poli (2009) remains valid under multiple social topologies. Considering the results of Sect. 5.1, it is clear that the topology does not have a very meaningful impact on the convergence results. This is seen in the similarity between Tables 1, 2, 3 and 4 where, under all measurements, there is minimal to no change, implying that the topology has no real influence on the parameter region needed for particle convergence.

A snapshot of all parameter configurations’ resulting convergence measure values is presented for the following situation:

• Topology influence The optimal convergence region is constructed for each investigated topology, using the same method as explained in case A of Sect. 5.1. The resulting optimal region that has the greatest distance in terms of convergence measure values from case A is reported.

The snapshot is presented to illustrate the maximum deviation between the convergent parameter region under multiple topologies. If the convergent parameter regions between the presented snapshot and that of case A from Sect. 5.1 are identical, then the topological choice has no influence on the convergent parameter regions.

For the case investigating the topological influence, the ring topology had the greatest Euclidean distance from the optimal region of case A from Sect. 5.1. The convergent region is illustrated in Fig. 4. Despite the ring topology having the greatest Euclidean distance from the optimal region of case A, Fig. 4 appears identical to the region of Fig. 3a, as the difference in convergence measure values is very small. The close similarity between Figs. 3a and 4 is a clear indication that the topology used within the CPSO algorithm has no meaningful impact on the convergent region of a CPSO. The conclusion that CPSO’s convergent region is independent of the social topology used is supported by the analysis done by Liu (2014).

Fig. 4

Topology influence: ring topology region. Convergence measure values at the 5000th iteration

5.3 Fully informed PSO convergence analysis

This subsection aims to empirically obtain the convergence criteria for FIPS utilizing the proposed objective function of Sect. 5.1.

The FIPS algorithm is implemented using the CPSO description in algorithm 1 with the velocity update equation 3 replaced with Eq. 4. The experimental setup and results are presented in Sects. 5.3.1 and 5.3.2, respectively.

5.3.1 Experimental setup

Upon inspection of the FIPS update equation defined in Eq. (4), it is clear that the neighborhood size might be a contributing factor in the convergence criteria of FIPS. As a result, the convergence criteria are investigated for neighborhood sizes 2, 4, 8, 16, 32, and 64.

The experiment utilizes the same static parameters as Sect. 5.1, except that the LBest topology is used. The analysis is done in one dimension as the update equations operate on the particles position and velocity components independently, resulting in $\Delta _{\max }=200$ for this subsection. The experiment of this subsection utilizes the convergence measure of Eq. (21) and the objective function defined in Eq. (20). The use of only the objective of Eq. (20) is validated by the experimental results of Sect. 5.1, which proved the effectiveness of the objective function for convergence analysis.

The experiment is conducted over the following parameter region:

$$\begin{aligned} w\in \left[ -1.1,1.1\right] \text { and } c_1+c_2\in \left( 0,7\right] , \end{aligned}$$

(24)

where $c_1=c_2$, with a sample point every 0.1 along w and $c_1+c_2$. The parameter region was empirically determined by increasing the values of $c_1+c_2$ and w until the complete convergent subregion was contained. A total of 1610 sample points from the region defined in Eq. (24) are used. The results reported in Sect. 5.3.2 are the averages over 35 independent runs for each sample point.

5.3.2 Experimental results and discussion

A snapshot of the resulting convergence measure values across the region defined in Eq. (24) under varying neighborhood sizes is presented in Fig. 5, for 2, 4, 8, 16, 32, and 64 dimensions.

Fig. 5

Fully Informed PSO convergence results. a FIPS with neighborhood of size 2. b FIPS with neighborhood of size 4. c FIPS with neighborhood of size 8. d FIPS with neighborhood of size 16. e FIPS with neighborhood of size 32. f FIPS with neighborhood of size 64

The convergence region obtained in Fig. 5a is very similar to the convergent region found for the CPSO algorithm in Sect. 5.1.

The similarity of the convergent regions is to be expected given that if the neighborhood size of 2 is used and $c_1=c_2$, FIPS can be shown to be the CPSO algorithm assuming that each particle is within its own neighborhood.

The convergent region found for FIPS with a neighborhood size of 4, as seen in Fig. 5b, is larger than that of FIPS with a neighborhood size of 2. The general form of the convergent region is close to that of FIPS with a neighborhood size of 2.

Upon inspection of FIPS with the neighborhood sizes of 8 and 16 in Fig. 5c, d, it is clear that the neighborhood size has a meaningful effect on the convergent region. The convergent region continues to allow for greater values of $c_1+c_2$ as the neighborhood size increases. There is also a clear favoring of positive inertia coefficients the larger $c_1+c_2$ gets.

The increase in the size of the convergent region continues with neighborhood sizes 32 and 64, as is seen in Fig. 5e, f. The convergent region’s shape is substantially different from the convergent region obtained when a small neighborhood size is utilized. The convergent region in Fig. 5f is almost triangular in shape.

It is clear that the larger the neighborhood size, the larger the convergent region becomes. The region also appears to extend indefinitely while simultaneously becoming more triangular in shape. This finding is inline with the observation made by Poli (2007) that the FIPS algorithm appears to be more stable with the larger neighborhood size of 3 than if a neighborhood size of 2 was used. The idea of increased stability of FIPS is empirically supported in this subsection for larger neighborhood sizes.

From a practical perspective, it is informative to note that the convergent region for FIPS with neighborhood size n is a subset of the convergent region for FIPS with neighborhood size $n+1$. Given this knowledge, if the neighborhood size changes over time, convergent parameters should be selected from the region matching the lowest possible neighborhood size, if the PSO user wished to guarantee convergent particle behavior.

5.4 Bare bones PSO convergence analysis

This subsection focuses on the convergence criteria for the BPSO algorithm. The experimental setup and results are presented in Sects. 5.4.1 and 5.4.2, respectively.

5.4.1 Experimental setup

The experiment utilizes the same static parameters as Sect. 5.3, except that the star topology is utilized.

The experiment is conducted over the following parameter region:

$$\begin{aligned} c_1\in \left( 0,7\right] \text { and } c_2\in \left( 0,7\right] , \end{aligned}$$

(25)

with a sample point every 0.1 along $c_1$ and $c_2$. The parameter region was selected as it allows for values of $c_1$ and $c_2$ twice as large as the region needed to contain all of FIPS’s convergent regions, as determined in Sect. 5.3. The theoretical work of Blackwell (2012) predicts that at least the line where $c_1=c_2$ should exhibit convergent particle behavior. A meaningful segment of this line is therefore included in the investigated parameter region. A total of 4900 sample points from the region defined in Eq. (25) are used.

The results reported in Sect. 5.4.2 are obtained from averaging over either 35, 70, or 1000 independent runs for each sample point. A differing number of independent runs are used to illustrate the amount of noise present in the BPSO experimentation.

5.4.2 Experimental results and discussion

A snapshot of the resulting convergence measure values across the region defined in Eq. (25) using a convergence measure bound of $\Delta _{\max }$ and $5*\Delta _{\max }$ , and varying sample runs, are presented in Figs. 6, 7, and 8, respectively, for 35, 70 and 1000 sample runs.

Fig. 6

BPSO convergence results for 35 samples. a BPSO: 35 samples, bounded at 200. b BPSO: 35 samples, bounded at 1000

Fig. 7

BPSO convergence results for 70 samples. a BPSO: 70 samples, bounded at 200. b BPSO: 70 samples, bounded at 1000

Fig. 8

BPSO convergence results for 1000 samples. a BPSO: 1000 samples, bounded at 200. b BPSO: 1000 samples, bounded at 1000

Figure 6a reports the convergence measure values bounded at $\Delta _{\max }$ based on 35 independent runs. The convergence results of BPSO are somewhat surprising, as there are very few parameter choices that potentially indicate some level of convergent behavior. Furthermore, there are no parameter configurations that are clearly convergent, with the smallest reported convergence measure being 52.32. BPSO is actually divergent regardless of parameter choice. If one considers parameter settings where $c_1$ is larger than $c_2$, then more divergent behavior is indicated. When the bound on the reported convergence measure is increased to $5*\Delta _{\max }$ (see Fig. 6b), it is more clearly seen that greater divergence occurs when $c_1$ is larger than $c_2$. The results of both Fig. 6a, b have a large degree of noise present despite being the result of 35 independent runs on each sample point.

In an attempt to reduce the level of noise, the same experiment was run 70 independent times as illustrated in Fig. 7a, b. In Fig. 7a, the number of parameter choices that do not result in the bound of $\Delta _{\max }$ to be exceeded has been reduced slightly. Despite the increased number of independent runs, the results clearly still contain a large amount of noise, indicating a large level of unpredictability in BPSO’s behavior between runs. This unpredictability is attributed to the heavy reliance of BPSO on the normal distribution as defined in Sect. 3.2.

The results presented in Fig. 8a, b are the result of 1000 independent runs. In Fig. 8a, there are only three parameter settings that did not exceed the convergence measure bound, $\Delta _{\max }$. There is substantially less noise present in Fig. 8b, making the early mentioned trend that the divergent behavior is more severe if $c_1$ is greater than $c_2$ clearer. It is also seen in Fig. 8b that, while the divergent behavior is more severe if $c_1$ is greater then $c_2$, the amount by which this affects the divergent behavior decreases as $c_1$ and $c_2$ increase.

The convergence measure values are also not remaining constant over the latter part of the search. In fact, the convergence measure values increase with respect to the increase in t, as illustrated in Fig. 9 where the convergence measure is reported over the course of 5000 iterations of a BPSO algorithm with $c_1=c_2$.

Fig. 9

BPSO average change in particle position (1000 samples)

From the presented results, it is clear that BPSO is in fact not guaranteed to converge. Even for the standard BPSO model, where it is assumed that $c_1$ and $c_2$ are equal, convergence does not occur. If convergence were to occur when $c_1$ is equal to $c_2$, a straight line ($c_1=c_2$) of low convergence measures values would have been present in Fig. 8b. It is also worth noting that BPSO’s particle movement is fairly unpredictable given how much noise is present in the results even with 1000 independent runs, which implies a large amount of unpredictability in the behavior of BPSO.

The theoretical finding of Blackwell (2012) that BPSO is order-2 stable is clearly not an accurate representation of the algorithm as the increase in the convergence measure over time in Fig. 9 implies that convergence in standard deviation to a fixed value is not occurring in practice. The nature of the normal distribution may well imply that very high, though statistically unlikely, particle movement will be seen periodically. However, if this was the sole reason for high convergence measure values, the continued increase in the convergence measure as seen in Fig. 9 would not have occurred. Even if particles’ personal and neighborhood positions stagnated at a great distance form each other, the convergence measure would only be high and not increasing.

Given the simple structure of the BPSO’s update equation (6), it is easy to see that at least one of the following two particle interactions occurs if the convergence measure is increasing:

• The midpoint between the personal best and the neighborhood best positions is moving through the search space at an increasing velocity. This implies that at least one of the personal best or the neighborhood best is moving at an increasing velocity.

• The component-wise distance between the personal best and the neighborhood best positions is increasing. This implies that at least one of the personal best or the neighborhood best is moving.

From this analysis, it is clear that the swarm is not entering a state of stagnation.

The only possible justification for the discrepancy between the theoretical findings and the empirical results of this subsection is due to the theoretical work being performed under the stagnation assumption. In order to verify that the discrepancy is in fact caused by the stagnation assumption, the BPSO was rerun, but with stagnation forced from iteration 20 onwards, by not updating any personal or neighborhood best positions. The results are illustrated in Fig. 10. When stagnation is forced, the results match the theoretical derivations of Kennedy (2003) perfectly. The difference between Figs. 9 and 10 shows that the stagnation assumption resulted in an inaccurate theoretical model for the BPSO algorithm. The reason why stagnation is not occurring is not immediately apparent and warrants further investigation.

Fig. 10

BPSO average change in particle position (1000 samples) with forced stagnation from iteration 20

5.5 Standard PSO 2011 convergence analysis

This subsection focuses on the convergence criteria for the SPSO2011 algorithm. The experimental setup and results are presented in Sects. 5.5.1 and 5.5.2, respectively.

5.5.1 Experimental setup

The SPSO2011 algorithm’s velocity update equation (9) cannot be analyzed in one dimension and then generalized to an arbitrary dimension as in the CPSO, FIPS, and BPSO algorithms, since the function that generates a random point in a hypersphere cannot be investigated component wise (Bonyadi and Michalewicz 2014). As a result, the convergence criteria are investigated for dimension sizes 1, 10, 20, and 50.

The experiment utilizes the same static parameters as in Sect. 5.3 except that the SPSO2011 topology, as defined in Sect. 3.3, is utilized. The SPSO2011 algorithm is analyzed with and without the special treatment of the center of gravity calculation.

• Case 1 uses only the center of gravity equation (10), as suggested by Zambrano-Bigiarini and Clerc (2013).

• Case 2 uses the center of gravity equation (10) if the particle’s personal best and neighborhood best positions are different. If the particle’s personal best and neighborhood best positions are the same, the center of gravity equation (14) is used.

The experiment is conducted over the following parameter region:

$$\begin{aligned} w\in \left[ -1.1,1.1\right] \text { and } c_1+c_2\in \left( 0,13\right] , \end{aligned}$$

(26)

where $c_1=c_2$, with a sample point every 0.1 along w and $c_1+c_2$. The parameter region of Eq. (26) was selected as it contains the convergent parameter regions reported by Bonyadi and Michalewicz (2014). A total of 1610 sample points from the region defined in Eq. (26) are used. The results reported in Sect. 5.5.2 are the averages over 35 independent runs for each sample point. Analysis is done with convergence measure bounded at the corresponding $\Delta _{\max }$ values, namely 200, 632.456, 894.427, and 1414.214, respectively.

5.5.2 Experimental results and discussion

Snapshots of the resulting convergence measure values across the region defined in Eq. (26) for SPSO2011 are presented under varying dimensionality for cases 1 and 2 in Figs. 11, 12, 13, and 14, respectively, for 1, 10, 20, and 50 dimensions.

Fig. 11

SPSO2011 convergence results for 1 dimension. a SPSO2011: 1 dimension, case 1. b SPSO2011: 1 dimension, case 2

Fig. 12

SPSO2011 convergence results for 10 dimensions. a SPSO2011: 10 dimensions, case 1. b SPSO2011: 10 dimensions, case 2

Fig. 13

SPSO2011 convergence results for 20 dimensions. a SPSO2011: 20 dimensions, case 1. b SPSO2011: 20 dimensions, case 2

Fig. 14

SPSO2011 convergence results for 50 dimensions. a SPSO2011: 50 dimensions, case 1. b SPSO2011: 50 dimensions, case 2

The convergent region for SPSO2011 in 1 dimension is presented in Fig. 11a, b. SPSO2011 has a clear boundary between convergent parameter settings and divergent parameter settings, unlike BPSO. In Fig. 11a, the convergent region is symmetrical around $w=0$, which is substantially different from the convergent regions of FIPS and CPSO where there is a preference toward a positive inertia weight selection for particle convergence. The convergent regions for both cases 1 and 2, as seen in Fig. 11a, b, are very similar. However, the convergent region for case 2 is slightly larger. Note that, with or without the special treatment of the center of gravity calculation, there is no substantial change in the convergent region. The found convergent regions in both Fig. 11a, b are substantially different in size from the found region of Bonyadi and Michalewicz (2014). The convergence region found by Bonyadi and Michalewicz (2014) has its apex at $c_1+c_2=12$ as opposed to the apex in Fig. 11a at around 8.5. At present, it is not completely clear what the exact source of the discrepancy is. However, possible sources present in the work of Bonyadi and Michalewicz (2014) are as follows:

• the study is performed under the presence of forced stagnation;

• the particles’ personal and neighborhood best positions are set to be equal;

• there is a linear increase in the number of iterations used based on the dimensionality of the search space; however, the maximum distance between two points in a search space only increases sublinearly; and

• it is not stated how the spherical distribution, ${\mathcal {H}}$, is calculated.

The analysis done in this paper made use of neither of the two mentioned simplifications. As a result, the regions presented in Fig. 11a, b should be a more accurate representation of SPSO2011’s convergent behavior.

The convergent regions for SPSO2011 in 10 and 20 dimensions are presented in Figs. 12a, b and 13a, b. In both 10 and 20 dimensions, the difference in the convergent regions for case 1 and case 2 is relatively minor. However, the convergent regions for case 2 are slightly larger than those of case 1. The convergent regions appear to be stable under an increase in dimension, as the regions plotted for 1, 10, and 20 dimensions appear unchanged for both cases 1 and 2.

The finding that the convergent region of SPSO2011 does not depend upon the dimensionality of the search space is in opposition to the results of Bonyadi and Michalewicz (2014). Even in 50 dimensions, as seen in Fig. 14a, b, the convergent region does not appear to change. In the work of Bonyadi and Michalewicz (2014), the apex of the found convergent region decreases by 33.3 % with the increase from a 1-dimensional search space to a 50-dimensional search space. This trend is clearly not present in the results of this subsection.

6 Conclusion

This study had two primary aims: The first was to show that the objective function, $\hbox {CF}({\varvec{x}})\sim U\left( -1000,1000\right)$, is an effective objective function to utilize for convergent region analysis. The second was to analyze the parameter region needed to ensure convergent particle behavior of particle swarm variants utilizing the proposed objective function, CF.

It was found that the CF objective function was able to capture the convergent behavior of the CPSO, as the found convergent regions matched both the theoretically derived region of Poli (2009) and the “optimal” region, where the “optimal” region was constructed using the maximum convergence measure value across all topologies and objective functions used (excluding CF). It was also found that the social topology used by CPSO had no meaningful impact on the convergent region.

Using the CF objective function, the convergent region was empirically obtained for FIPS, BPSO, and SPSO2011. It was observed that FIPS’s convergent region grows with an increase in neighborhood size. It was shown that BPSO does not converge for any choice of $c_1$ and $c_2$. More specifically, in practice, it was shown that BPSO is not order-2 stable, despite theoretical findings (Blackwell 2012). The discrepancy is linked to the theoretical work being performed under the stagnation assumption. For SPSO2011, it was found that the convergent region does not depend on the dimensionality of the problem, as previously observed by Bonyadi and Michalewicz (2014). The region needed to ensure convergent particle behavior in SPSO2011 is also different from those obtained by Bonyadi and Michalewicz (2014). The discrepancies are attributed to the simplifications used by Bonyadi and Michalewicz (2014).

Potential future work will include utilizing the empirical techniques of this paper to obtain the convergence regions for other PSO variants. Another direction for future work is the automation of an approach to extract from empirical analysis the equations that describe the approximate convergent regions.