Comparing Covariance Matrices by Relative Eigenanalysis, with Applications to Organismal Biology

Abstract

Most biologists are familiar with principal component analysis as an ordination tool for questions about within-group or between-group variation in systems of quantitative traits, and with multivariate analysis of variance as a tool for one useful description of the latter in the context of the former. Less familiar is the mathematical approach of relative eigenanalysis of which both of these are special cases: computing linear combinations for which two variance–covariance patterns have maximal ratios of variance. After reviewing this common algebraic–geometric core, we demonstrate the effectiveness of this exploratory approach in studies of developmental canalization and the identification of divergent and stabilizing selection. We further outline a strategy for statistical classification when group differences in variance dominate over differences in group averages.

Introduction

Most biologists are familiar with the multivariate ordination techniques that seek particularly interesting directions (linear combinations) along which to sort a sample of organisms in a high-dimensional data space. Principal components analysis (PCA) finds the directions that have greatest variance when the coefficients are scaled to have unit sum of squares; canonical variate analysis (CVA) and multivariate analysis of variance (MANOVA) find the directions that have greatest between-group variance in proportion to the pooled within-group variance of the same linear combination. Even though these directions and the corresponding scores are not presumed a priori to convey any biological meaning, together they often enable a useful exploration of patterns and differences.

These methods are mainly aimed at identifying differences among group averages, but differences in variance among groups may be at least as important as differences among their averages. Variance differences may indicate genetic or environmental perturbations, breakdown of regulatory processes during development, or multiple kinds of selection and other population processes (see, among others, Tanner 1963; Lande 1979; Philipps and Arnold 1989; Gibson and Wagner 2000; Debat and David 2001; Hallgrimsson et al. 2002; Badyaev and Foresman 2004; Hallgrimsson and Hall 2005; Mitteroecker 2009; Mitteroecker et al. 2012). In evolutionary theory, genetic and phenotypic variation are the key determinants of a population’s response to selection, and, still in theory, this determination is often expressed well in terms of variances and covariances (e.g., Lande 1979; Falconer and Mackay 1996).

In contrast to the well-known statistical hypothesis tests for homogeneity or proportionality of variance–covariance matrices (e.g., Mardia et al. 1979; Manly and Rayner 1987; Martin et al. 2008), it is less common to encounter explorations of differences in variance and covariance across a multivariate data set—to be shown how two variance–covariance matrices differ and to see these differences described in biologically interpretable ways.

How does one compare variances across groups for a single variable? For quantities whose values have to be positive, like measured weights or concentrations, one conceptually accessible way to report comparisons is as ratios: the average in group 2 is double the average in group 1, or half. The construction of ratio scales for temperature and for energy were two of the triumphs of nineteenth-century physics, for instance. Variances are positive numbers, and ratios of variances make intuitive sense. For example, they do not depend on linear transformations of the variables such as changes of the unit of measurement.

Now extend the topic from single measurements to multiple measurements. For p variables, we have p variances and p(p − 1)/2 covariances, usually arranged in a symmetric p × p covariance matrix. The matrix analogue to a division is multiplying one covariance matrix by the inverse of the other covariance matrix. The resulting matrix product specifies how to transform one covariance matrix into the other. When representing this matrix as an ellipse (in two dimensions) or an ellipsoid (in three or more dimensions), the length of the axes of this ellipse equal the ratio of variances of the two groups in that direction. This matrix product hence is a useful way to report the differences between two variance–covariance structures, comprising the ratios of variances for the original variables along with all their linear combinations.

Principal component analysis seeks the direction along which one group has maximum variance for fixed sum of squares of coefficients—the first eigenvector of the corresponding covariance matrix. In a different exploratory strategy, one might seek the direction along which the ratio of variances between two groups is a maximum. This direction is the first eigenvector of the matrix product described above—the first relative eigenvector of the first covariance matrix with respect to the second. As for PCA, we can also find a direction with the minimum ratio of variances and other directions with an intermediate ratio. We refer to this exploratory style of analysis as relative eigenanalysis or relative principal component analysis, because it is an eigenvector decomposition of one covariance matrix relative to another one. Biological inferences can be based on the actual ratios of variances (relative eigenvalues), the loadings of the vectors (relative eigenvectors), and on the individual scores along these vectors (relative principal component scores).

But, in fact, ordinary PCA can be considered as a special case of relative eigenanalysis: a relative eigenanalysis with respect to a covariance matrix that is an exact multiple of the identity matrix (the matrix with 1’s down the diagonal and 0’s everywhere else). In other words, ordinary principal components are just relative eigenvectors with respect to a hypothetical comparison population in which all of the original variables have variance 1 and correlations 0 (which is of course no useful biological hypothesis).

The properties of relative eigenvalues and eigenvectors for the comparison of two covariance matrices were already described explicitly by Flury (1983, 1985), and their roles in several likelihood ratio tests and other statistics are well documented (e.g., Anderson 1958; Mardia et al. 1979; Manly and Rayner 1987; see also below). However, relative eigenanalysis has rarely been used as an exploratory tool in biometrics.

In this paper, we present the algebraic and geometric properties of this technique in a contemporary biometric context and outline its relation to various existing statistical methods. We demonstrate how relative eigenanalysis can be used as an effective exploratory technique to study selective forces underlying geographic variation of taxa and the emergence or canalization of phenotypic variance during ontogeny. We further outline a strategy for statistical classification when group differences in variance dominate over differences in group averages. Even though our examples are limited to phenotypic covariance matrices, relative eigenanalysis can also be applied to genetic covariance matrices.

Algebraic and Geometric Properties

Consider two groups of individuals A, B and for each specimen a set of p quantitative measurements $x_1, x_2, \ldots, x_p$, collectively denoted as a column vector x. Assume, as morphometricians always assume, that every linear combination $a_1 x_1+a_2 x_2+\ldots + a_p x_p={\bf a'x}$ of the measured variables can in principle be interpreted as a new variable within the given scientific context. Then we can compute the variance of the same linear combination in both groups: $\hbox{Var}(\mathbf{a'x}_A)$ and $\hbox{Var}(\mathbf{a'x}_B).$ For some linear combinations, that is for some vectors a, group A might have more variance than group B, suggesting perhaps that the conditions in which the two groups differ may have inflated the variance in one group relative to the other. For other linear combinations, the two variances might be approximately equal because these measured properties are not affected by the assessed conditions, and for still other linear combinations group A might have less variance than group B. We seek a general exploratory multivariate method that will allow us to uncover and speculate on all of these possibilities at the same time for a given vector of measures x whose covariance matrix is observed twice under substantially different conditions. For this purpose we modify the familiar rationale of principal component analysis, that of finding linear combinations with maximal, minimal, or intermediate variance. In this case we seek linear combinations that maximize or minimize ratios of variances between two groups.

In the easiest version of the question, we have two variables x ₁ and x ₂ each of variance 1 in each of two groups. What linear combination has the highest ratio of variances between the groups? It must be either x ₁ + x ₂ or x ₁ − x ₂ (a linear combination with weights either 1,1 or 1, −1) depending on which group has the higher correlation between x ₁ and x ₂. The ratio of var(x ₁ ± x ₂) between the groups is (1 ± r ₁)/(1 ± r ₂), where r is the correlation coefficient between the two variables, no further algebra required (Fig. 1a, b).

Fig. 1

Equal frequency ellipses representing the variance–covariance structures of two groups A and B. In a both groups have unit variance for both variables x ₁, x ₂. Group A has a correlation of 0.8 between the two variables; group B, −0.5. The major axis of the equal frequency ellipse of A is aligned with the minor axis of B. In this direction, A has the largest variance relative to B. The coefficients of this vector, which are (1,1), are the weights for the linear combination we seek, and the resulting maximal ratio of variances is (1 + 0.8)/(1 − 0.5) = 3.6. Notice that this quantity is equal to the ratio of the squared maximum diameter of the ellipse of A to the minimum squared diameter of B. In part b of this figure, the correlation for group B is 0.5 instead of −0.5, and all variances are still 1. The major and minor axes are the same for both groups and the direction we seek is the common major axis of the two ellipses. The associated ratio of variances is (1 + 0.8)/(1 + 0.5) = 1.2, which is equal to the ratio of squared maximum diameters. In c group B has unit variance in every direction (hence zero correlation) so that the direction of the ratio of maximal variance is simply the maximum diameter or the first principal component of A

Consider another special case: two groups of individuals for any number of variables, where the covariance matrix of group B is equal to the identity matrix (that is, this group has an isotropic distribution: every linear combination of variables with coefficients whose squares sum to 1 has the same variance). Figure 1c is a two-dimensional example of such a case. What direction maximizes the variance in group A relative to that of group B? Since the variance of B is 1 in all directions, this problem reduces to finding the direction that maximizes the variance in group A. But of course this direction is just the first eigenvector of the corresponding covariance matrix: the first principal component in this group, the major axis of the corresponding equal frequency ellipse. The actual maximal ratio of variances is equal to the first eigenvalue, the squared maximum diameter of the ellipse.

One way of arriving at the general case is by giving up the constraint of isotropy in either group. That is, for two groups with arbitrary covariance matrices (as in Fig. 2a), how to find a linear combination that maximizes the ratio of variances between the two groups? A ratio of variances is invariant (unchanged) under all possible linear transformations (e.g., Huttegger and Mitteroecker 2011). Hence we are free to linearly transform the variables so that one equal frequency ellipse becomes a circle (one distribution becomes isotropic). For these transformed variables, the problem reduces to the simpler problem above: the direction we seek is the first principal component of the transformed second group (Fig. 2b).

Fig. 2

a Equal frequency ellipses representing the variance–covariance structures $\varvec{\Upsigma}_A, \varvec{\Upsigma}_B$ of two groups A and B. b For the variables y ₁, y ₂, which are linear combinations of the original variables x ₁, x ₂, group B has a circular equal frequency ellipse. The red line is the major axis of the resulting distribution of A. This is the direction along which A has the greatest variance relative to B. The actual ratio of variances is equal to the ratio of squared diameters of A and B in this direction. c For the variables z ₁, z ₂, which are another pair of linear combinations of x ₁, x ₂, the distribution of group A is circular, and so the minor axis of the resulting group B is the direction along which A has the greatest variance relative to B. The ratio of variances is the same as in (b) (Color figure online)

Let $\varvec{\Upsigma}_A$ be the p × p covariance matrix of group A and $\varvec{\Upsigma}_B$ that of group B, and assume both matrices are invertible. To transform the variables so that group B has a circular distribution, multiply the variables x by the inverse square root matrix $\varvec{\Upsigma}_B^{-1/2}$. The transformed covariance matrix of group A is the matrix product $\varvec{\Upsigma}_B^{-1/2} \varvec{\Upsigma}_A \varvec{\Upsigma}_B^{-1/2}$. The maximal ratio of variances is given by the first eigenvalue of $\varvec{\Upsigma}_B^{-1/2} \varvec{\Upsigma}_A \varvec{\Upsigma}_B^{-1/2}$, and you get to the actual linear combination carrying this ratio by multiplying the transformed variables $\mathbf{x'} \varvec{\Upsigma}_B^{-1/2}$ by the first eigenvector of this matrix.

The same scores, up to linear scaling, can also be computed by multiplying the original variables x by the first eigenvector of $\varvec{\Upsigma}_B^{-1} \varvec{\Upsigma}_A$. To show this, consider the vector a that maximizes the ratio $\mathbf{a}' \varvec{\Upsigma}_A \mathbf{a} / \mathbf{a}' \varvec{\Upsigma}_B \mathbf{a}$ and re-express this as the maximization of $\mathbf{a}' \varvec{\Upsigma}_A \mathbf{a}$ given $\mathbf{a}' \varvec{\Upsigma}_B \mathbf{a}=1$. Let $\mathbf{b}=\varvec{\Upsigma}_B^{1/2}\mathbf{a}$. Then the maximum of $\mathbf{a}'\varvec{\Upsigma}_A \mathbf{a}$, subject to the above constraint, can be written as

$$ \max_{{\mathbf{b}}} {\mathbf{b}}' \varvec{\Upsigma}_B ^{-1/2} \varvec{\Upsigma}_A \varvec{\Upsigma}_B^{-1/2}{\mathbf{b}} \;\;\;\; \hbox{for} \;\;\;\; {\mathbf{b}}'{\mathbf{b}}={\mathbf{a}}' \varvec{\Upsigma}_B {\mathbf{a}}={\bf 1}. $$

The solution to this classical “relative eigenvalue problem” is the first eigenvector $\varvec\gamma_{\rm 1}$ of $\varvec{\Upsigma}_B ^{-1/2} \varvec{\Upsigma}_A^{} \varvec{\Upsigma}_B^{-1/2},$ and $\mathbf{a}=\varvec{\Upsigma}_B^{-1/2}\varvec\gamma_{\rm 1}$ is the scaled first eigenvector of $\varvec{\Upsigma}_B ^{-1} \varvec{\Upsigma}_A^{}$ (see also Mardia et al. 1979, A.9.2; Flury 1983; Mitteroecker and Bookstein 2011).

Both approaches yield the same scores and also the same eigenvalues. But the actual eigenvectors for the two matrix products are different. Biological interpretations of the vector loadings, or visualizations in a geometric morphometric context, need to refer to the original variables; these must be the eigenvectors of $\varvec{\Upsigma}_B^{-1} \varvec{\Upsigma}_A$ (see also Mitteroecker and Bookstein 2011).

The eigenvalues of either $\varvec{\Upsigma}_B^{-1} \varvec{\Upsigma}_A$ or $\varvec{\Upsigma}_B ^{-1/2} \varvec{\Upsigma}_A \varvec{\Upsigma}_B^{-1/2}$ are called the relative eigenvalues of $\varvec{\Upsigma}_A$ with respect to $\varvec{\Upsigma}_B$. We have seen that the first relative eigenvalue λ₁ is equal to the maximal ratio of variances:

$$ \lambda_1=\max_{\mathbf{a}} \frac{{\hbox{Var}}({\mathbf{a'x}}_A)}{{\hbox{Var}}({\mathbf{a'x}}_B)}= \frac{{\hbox{Var}}({\mathbf{e}}_1'{\mathbf{x}}_A)}{{\hbox{Var}}({\mathbf{e}}_1'{\mathbf{x}}_B)}. $$

It is also equal to the last eigenvalue of $\varvec{\Upsigma}_A^{-1} \varvec{\Upsigma}_B^{},$ the minimum of $\mathbf{a}' \varvec{\Upsigma}_B \mathbf{a} / \mathbf{a}' \varvec{\Upsigma}_A \mathbf{a}:$

$$ \begin{aligned} \lambda_p=& \min_{\mathbf{a}} \frac{{\hbox{Var}}({\mathbf{a}}'{\mathbf{x}}_A)}{{\hbox{Var}}({\mathbf{a}}'{\mathbf{x}}_B)}=\frac{{\hbox{Var}}({\mathbf{e}}_p'{\mathbf{x}}_A)}{{\hbox{Var}}({\mathbf{e}}_p'{\mathbf{x}}_B)} \\ =&\left ( \max_{\mathbf{a}} \frac{{\hbox{Var}}({\mathbf{a}}'{\mathbf{x}}_B)}{{\hbox{Var}}({\mathbf{a}}'{\mathbf{x}}_A)} \right )^{-1}, \end{aligned} $$

where $\mathbf{e}_1$ and $\mathbf{e}_p$ are the first and last eigenvectors of $\varvec{\Upsigma}_B^{-1} \varvec{\Upsigma}_A$.

Besides the eigenvector of largest eigenvalue, which is the linear combination of greatest inflation of variance of ${\varvec\Upsigma}_A$ with respect to ${\varvec\Upsigma}_B$, and the eigenvector of smallest eigenvalue, which is the linear combination of the least variance inflation or greatest variance deflation, there are p − 2 other directions having “stationary variance ratios.” Variance ratios in these directions behave like the diameter of an ellipsoid in the direction of its intermediate axis, the axis that is neither the longest nor the shortest. The derivative of the ratio in every direction around this variable is zero, but the second derivative is positive in some directions and negative in others. So the sphere on this diameter falls inside the ellipsoid in one plane, the plane that includes the long axis, and falls outside the ellipsoid in another plane, the plane that includes the short axis. Like the corresponding second, third, … principal components in a principal component analysis, these second, third, … relative eigenvectors have no biological meaning by themselves. But each one, taken in combination with all those of higher order, specifies a plane or hyperplane over which values of the corresponding linear combinations a′x can be scattered for cases from both of the groups under analysis. The patterns in these scatterplots are often very interesting, and likewise the import of the pattern vectors a that represent their relation to the covariance geometry of their measurement space.

The relative eigenvectors of two arbitrary covariance matrices usually are not orthogonal (at right angles) because the product $\varvec{\Upsigma}_B^{-1}\varvec{\Upsigma}_A$ is usually not a symmetric matrix (Fig. 3a). Only after standardizing one covariance matrix are the relative eigenvectors orthogonal (both $\varvec{\Upsigma}_B^{-1/2}\varvec{\Upsigma}_A\varvec{\Upsigma}_B^{-1/2}$ and $\varvec{\Upsigma}_A^{-1/2}\varvec{\Upsigma}_B\varvec{\Upsigma}_A^{-1/2}$ are symmetric matrices; Fig. 2b, c). Furthermore, whereas in ordinary PCA all principal components are mutually uncorrelated as pooled over all groups, the scores along the relative eigenvectors are uncorrelated within each group: $\mathbf{e}'_i \varvec{\Upsigma}_A \mathbf{e}_j=\mathbf{e}'_i \varvec{\Upsigma}_B \mathbf{e}_j=0$ for any i ≠ j. This is illustrated by Fig. 3b, in which the two covariance matrices are expressed on the basis of the relative eigenvectors: both ellipses are separately aligned along their axes (this is called the property of being conjugate directions).

Fig. 3

a The two relative eigenvectors of the two groups A and B, which are the eigenvectors of $\varvec{\Upsigma}_B^{-1}\varvec{\Upsigma}_A$, are shown as solid red line and dashed black line. These eigenvectors are not orthogonal. The scores along these vectors have the maximal and minimal ratio of variances, respectively. The maximal ratio is equal to the ratio of squared distances between the filled dots and the open dots, which are the projections of the two ellipses on the first relative eigenvector. b Equal frequency ellipses of the relative principal components (scores along the relative eigenvectors) for the two groups A, B. These scores are uncorrelated within each group (Color figure online)

Affine Invariance

The relative eigenvalues of two covariance matrices are invariant to all linear transformations of the variables. This is an important property of a statistical method whenever the scales of the variables are incommensurate (Mitteroecker and Huttegger 2009; Huttegger and Mitteroecker 2011), which is often the case in conventional morphometrics although rarely a concern in geometric morphometrics. Variables may further be geometrically dependent (e.g., due to common size correction, common superimposition of landmarks, distance measurements with common start or end points) and subject to spatial autocorrelation. Changes of interdependencies can be approximated by a shear of the data space. Relative eigenvalues are invariant to these linear transformations and hence do not depend on any (usually unrealistic) assumption of geometric and spatial independence among the measured variables, which is an important part of any guarantee that the relative eigenvectors should sustain a biological interpretation.

Modern morphometrics and imaging techniques typically produce a very large number of closely spaced measurements, allowing for the identification of small spatial signals. Many of these measurements—those closely adjacent—are to a large part redundant, which is not per se a problem but leads to a “weighting” of anatomical structures by the number of variables covering the structure. Many statistics (such as distances and angles in the data space, PCA and related techniques) hence are influenced by the numerosity and spatial distribution of measurements (see also Mitteroecker et al. 2012). Huttegger and Mitteroecker (2011) demonstrated that changes in the number of redundant measurements leads to an approximately linear transformation within the space of the first few principal components. Relative eigenvalues based on a small number of principal components thus are also largely invariant to changes in the redundancy of measurements.

Other Statistical Contexts for Relative Eigenvalues

The relative eigenvalues and corresponding eigenvectors of two covariance matrices appear in several multivariate statistical contexts, but they are rarely used in the exploratory style outlined in this paper. Perhaps the reader may know them from the context of CVA, the generalization of linear discriminant analysis via relative eigenanalysis of the between-group covariance matrix $\mathbf{B}$ with respect to the within-group covariance matrix $\mathbf{W}$. The usual canonical variates are the eigenvectors of $\mathbf{W}^{-1}\mathbf{B}$. Often, both the loadings of the eigenvectors and the scores along them are plotted and interpreted. Whereas relative eigenanalysis is applied to investigate differences in covariance matrices between groups, CVA assumes homogeneous covariances across all groups. Likewise, squared Mahalanobis distance, the squared distance between two individuals or between two group means relative to some variance–covariance structure, can be regarded as a simple form of relative eigenanalysis in which the squared Mahalanobis distance is the first relative eigenvalue of $\mathbf{B}$ and $\mathbf{W}$.

Wilks’ Lambda, a commonly used multivariate test statistic, is $\prod{(1+\lambda_i})^{-1}$ where the λ’s are the relative eigenvalues of two covariance matrices $\mathbf{S}_1$ and $\mathbf{S}_2.$ In some likelihood ratio test contexts, for instance, multivariate analysis of variance, $\mathbf{S}_1$ is the error variance and $\mathbf{S}_2$ the variance explained by the model. The same list of all the relative eigenvalues is central to likelihood ratio tests of proportionality of covariance matrices (e.g., Mardia et al. 1979; Manly and Rayner 1987; Martin et al. 2008), including proportionality to the identity. For instance, under the hypothesis of proportional covariance matrices $\mathbf{S}_2=k \mathbf{S}_1$, the maximum-likelihood estimate of the scaling factor is

$$ k= \hbox{tr}({\mathbf{S}}_1^{-1}{\mathbf{S}}_2)/p, $$

(1)

which is the average of the relative eigenvalues (Mardia et al. 1979).

One standard quantification of the overall amount of variation in a multivariate data set is the “generalized variance”, usually computed as the determinant of the corresponding sample covariance matrix (the product of its ordinary eigenvalues). Correspondingly, the ratio of the generalized variances of two groups is equal to the product of their relative eigenvalues λ _i :

$$ \hbox{det}({\mathbf{S}}_1)/\mathrm{det}({\mathbf{S}}_2)=\prod \lambda_i. $$

This ratio is unchanged under linear change of basis, whereas the ordinary single-group generalized variance is not.

Mitteroecker and Bookstein (2009) suggested a metric distance function for full rank covariance matrices given by the two-norm of the log-transformed relative eigenvalues λ _i :

$$ d_{cov}({{\mathbf{S}}_1,{\mathbf{S}}_2})=\sqrt{\sum_{i=1}^{p}({\rm{log}} \;\lambda_i)^2}. $$

(2)

This function is symmetric, i.e., $d_{cov}({\mathbf{S}_1,\mathbf{S}_2})=d_{cov}({\mathbf{S}_2,\mathbf{S}_1}),$ because (log λ _i )² = (log 1/λ _i )². It is actually the appropriate affine-invariant geodesic distance on this space of covariance matrices when treated as a Riemannian manifold (Förstner and Moonen 1999; Smith 2005).

Tyler et al. (2009) used relative eigenanalysis under the term “Invariant Coordinate Selection” (ICS) to compare two scatter matrices for the same group of individuals in order to identify deviations from an elliptical symmetric distribution. They claim that eigenanalysis of the usual variance–covariance matrix relative to a more robust scatter matrix (e.g., based on ranks), or relative to a scatter matrix based on higher moments, often leads to a useful ordination for identifying outliers, clusters of individuals, and other deviations from multivariate normality.

In evolutionary quantitative genetics, the heritability h ² of a trait is the ratio of (additive) genetic variance to total phenotypic variance of this trait. In theory, heritability determines the trait’s response to selection. A multivariate generalization of heritability is the matrix product $\mathbf{GP}^{-1}$, where $\mathbf{G}$ is the additive genetic variance–covariance matrix and $\mathbf{P}$ the phenotypic variance–covariance matrix (e.g., Roff 2000; Klingenberg et al. 2010). The first eigenvector of this matrix product corresponds to the linear combination with maximum heritability (namely, the first relative eigenvalue). For example, Houle and Fierst (2013) used sets of relative eigenvectors to construct subspaces having different heritabilities.

To this point we have set a relative eigenanalysis in the context of comparing two covariance structures on the same measurement vector. The multivariate version of Felsenstein’s (1985, 1988) popular method of “phylogenetic contrasts” can be considered as another kind of relative eigenanalysis, in which only one of the matrices is an observed covariance, whereas the other consists of an explicit list of vectors that should be considered as orthogonal and of equal variance. In this setting each of the linear combinations of interest is some specific contrast of one clade against an individual specimen or against the complementary clade. The contrasts are listed carefully so as to involve independent combinations of increments on the presumed phylogenetic model, and then each one is normalized to the same unit of effective time on a powerful Brownian hypothesis of pure genetic drift. Note that the contrasts do not include any actual biometric data; they encode only the given phylogeny (including its clock if available). Once these contrast vectors have been set up, the investigator computes the corresponding linear combinations of the actual specimen-by-specimen data, and takes the principal components of these linear combinations. Those PC’s are the same as the relative eigenvectors one would get from the measurement vectors in the basis for which the phylogenetically derived contrasts are in fact orthonormal. In other words, the PCs of the contrasts are the same as the relative eigenvectors from a two-matrix analysis whose second matrix comes from the phylogeny, not the measurement data, but does not ever need to be explicitly displayed.

Applications

This section illustrates applications of relative eigenanalysis to evolutionary and developmental biology by three examples. One concerns emergence and canalization of phenotypic variance during development, the second outlines an approach for identifying divergent and stabilizing selection, and the third shows how relative eigenanalysis clarifies an important context of classification.

Neurocranial Growth in Rats

Our first example investigates postnatal changes of the phenotypic variance–covariance pattern in the rat neurocranium. The analysis is based on eight landmarks digitized by Melvin Moss from a longitudinal roentgenographic study by Henning Vilmann of 21 genetically homogeneous male laboratory rats (Fig. 4a). The data, collected at eight ages (7, 14, 21, 30, 40, 60, 90, and 150 days), were published in full as Appendix A.4.5 of Bookstein (1991). In Mitteroecker and Bookstein (2009) we studied the eight age-specific covariance matrices of the Procrustes shape coordinates of these landmarks by an ordination analysis using the summed squared log relative eigenvalues as a metric (Eq. 2 above). We showed that the covariance matrix is continually changing during the investigated time period and that the “ontogenetic trajectory” of the covariance matrix alters its direction between the ages of about 21 and 40 days (Fig. 4b). In fact, the direction of the trajectory (the pattern of covariance changes) almost perfectly reverses between the range of 7–21 days and the range of 40–90 days of age. To show how the covariance matrices actually differ, we carry out two relative eigenanalyses: covariance at 21 days versus covariance at 7 days, and covariance at 90 days vs. covariance at 40 days. Both analyses use the first five principal components of all the Procrustes shape coordinates pooled.

Fig. 4

a Midsagittal section of a rat cranium with eight neurocranial landmarks. For more details see Bookstein (1991). b Scatter plot of the first two principal coordinates (PCoord) of the eight age-specific covariance matrices (Mitteroecker and Bookstein 2009). c Relative eigenvalues for the 21-day covariances versus the 7-day covariances, plotted on a logarithmic scale. d Relative eigenvalues for the 90-day covariances versus the 40-day covariances

Figure 4c gives the eigenvalues for the 21- versus 7-day analysis. It is useful to plot them on a logarithmic scale because we want an eigenvalue λ to be just as far away from 1 (indicating equal variance) as the eigenvalue 1/λ. (Note that also the metric used in the ordination analysis is based on the sum of squares of these log relative eigenvalues.) Figure 4c shows that, except for the first dimension, all relative eigenvalues are smaller than 1, indicating that variance is decreasing in most directions of phenotype space. For the 90- versus 40-day analysis, by contrast, the first two relative eigenvalues are clearly larger than 1, indicating an increase in variance, and only the last eigenvalue indicates a strong reduction of variance for this direction (Fig. 4d).

Because the analysis is based on Procrustes shape coordinates, the relative eigenvectors can be visualized as deformation grids (Bookstein 1991; see also Mitteroecker and Bookstein 2011). Figure 5 shows the visualizations of the first and the last relative eigenvectors for the two analyses. From 7 to 21 days of age, variance in the relative size of the foramen magnum and the parietal bone is slightly increasing (first relative eigenvector), whereas variance in the overall length of the neurocranium relative to its height, associated with a reorientation of the foramen magnum, is sharply decreasing (last relative eigenvector). From 40 to 90 days of age, by contrast, the pattern is reversed. Variance in relative length of the neurocranium and in the angulation of the foramen magnum is increasing (first relative eigenvector), while variance in relative size of the foramen magnum and the parietal is decreasing (last relative eigenvector). These findings confirm the observation of ontogenetic trajectories of the covariance matrix in opposite directions (Fig. 4b).

Fig. 5

Visualization of the two relative eigenanalyses in Fig. 4 as deformation grids. The shape pattern depicted by each relative eigenvector is visualized by deformations of the mean shape along the positive and the negative direction of the corresponding vector

Reduction of variance during development, usually referred to as canalization or targeted growth, is a well-known phenomenon in animal development, even though the underlying mechanisms are still not well understood (e.g., Tanner 1963; Gibson and Wagner 2000; Debat and David 2001; Hallgrimsson et al. 2002, 2006). In rats and mice, ontogenetic changes of covariance patterns, particularly reduction of certain variances during early postnatal development, have been documented in several studies (e.g., Atchley and Rutledge 1980; Nonaka and Nakata 1984; Zelditch et al. 1992, 2004, 2006). These authors typically compared age-specific variances for single variables or single principal components, or they summed the variances over all variables. Relative eigenanalysis is a more effective tool for this purpose, allowing a more complex and finer-grained comparison of variance–covariance patterns.

Stabilizing Versus Divergent Selection of Human Craniofacial Shape

Our second example uses relative eigenanalysis as an exploratory tool to study differences in craniofacial shape among human ethnicities. There is a long-standing tradition in quantitative genetics of inferring past selective regimes from heritable phenotypic (co)variance within and between populations or species. Under a list of idealized assumptions, the amount of evolutionary divergence in a set of phenotypic traits due only to genetic drift is proportional to the amount of additive genetic variance for these traits within the ancestral population (e.g., Lande 1979; Felsenstein 1988; Falconer and Mackay 1996). For multiple traits, many empirical studies thus interpreted deviations from proportionality of the between-population covariance matrix B and the average within-population genetic covariance matrix G (estimating the ancestral covariance matrix) as results of past divergent or stabilizing selection. Because genetic covariance matrices are difficult to estimate, many authors have used the average phenotypic within-population covariance matrix P instead of G (see, e.g., Cheverud 1988; Roff 1995; Koots and Gibson 1996).

Most empirical studies of this kind were limited to statistical tests of the proportionality of B and G. But in any comprehensive list of measurements of a complex anatomical structure, such as the vertebrate skull, it is likely that some traits or combination of traits are under divergent selection while, simultaneously, other traits are under stabilizing selection, and some are more or less selectively neutral. Hence, we apply relative eigenanalysis to identify linear combinations of traits with the largest (or smallest) excess of between-group variance over within-group variance. If there was any divergent or stabilizing selection, these are the directions that must have borne it, and in any interpretation these traits are candidates for functional models. (In other words, we are using relative eigenanalysis to generate hypotheses about possible selection regimes, not to test anything.)

We illustrate this exploratory approach using W. W. Howells’ celebrated data set of 1996, comprising 57 classical craniometric measurements on a total of 2504 skulls from 28 different human populations. Based on sample size, homogeneity of the data, and reproducibility of the measurements, we selected 23 populations and 10 measurements representing the height and width of the major cranial elements (Fig. 6). The sample size of these populations ranges from 69 to 111, giving a total sample size of 2238. For our present purpose, we removed the effects of sexual dimorphism for each population by subtracting the sex-specific mean from the corresponding individuals. We computed the 23 population covariance matrices, the between-population covariance matrix $\mathbf{B}$ (i.e., the covariance matrix of the population means) and the pooled phenotypic within-population covariance matrix $\mathbf{P}$ (a weighted average of the population covariance matrices). We scaled $\mathbf{B}$ to $\mathbf{P}$ using the average relative eigenvalue as a scaling factor (see formula 1 above).

Fig. 6

Ten cranial measurements from Howells’ (1996) data set, representing the height and width of the orbits (OBH, OBB), the nasal aperture (NLH, NLB), and the upper jaw (NPH, MAB), as well as interorbital breadth (DKB), bimaxillary breadth (ZMB), and height and width of the braincase (basion-bregma height BBH, biauricular breadth AUB)

A maximum likelihood test (Mardia et al. 1979; Martin et al. 2008) informs us that the two matrices $\mathbf{P}$ and $\mathbf{B}$ deviate significantly from proportionality (p < 0.01). We wish to ask further how much and in which way they differ. To this end we computed an ordination of the 23 population covariance matrices together with the matrices $\mathbf{P}$ and $\mathbf{B}$. (Note that both the maximum likelihood test and the metric for covariance matrices used in this ordination are based on relative eigenvalues.) In this ordination (Fig. 7), the population covariance matrices constitute a relatively homogeneous cluster around their weighted average $\mathbf{P}$, whereas $\mathbf{B}$ falls far outside of this cluster: $\mathbf{P}$ and $\mathbf{B}$ differ beyond any doubt. So we proceed with a relative eigenanalysis to explore the pattern in which $\mathbf{B}$ differs from $\mathbf{P}$.

Fig. 7

Principal coordinate ordination of the 23 population covariance matrices together with the pooled within-population covariance matrix $\mathbf{P}$ and the between-group covariance matrix $\mathbf{B}$

Figure 8a presents the relative eigenvalues and Table 1 shows the loadings of the first and the last relative eigenvectors. The first relative eigenvector has negative loadings for the measurements of upper facial breadth, positive loadings for measurements of upper facial height, and a positive loading for neurocranial breadth (biauricular breadth). Measurements of the upper jaw have loadings close to zero (Fig. 8b). Specimens with high scores for this component thus have a narrow and tall upper face and a wide neurocranium. The last relative eigenvector has negative loadings for all measurements of facial breadth except for nasal breadth, which is highly positively loaded, and positive loadings for measurements of facial height, again to the exception of nasal height, which is negatively loaded (Fig. 8c). This component thus represents the size of the nasal cavity relative to overall facial size.

Fig. 8

a Relative eigenvalues of the matrices B and P plotted on a logarithmic scale. b Visualization of the loadings of the first relative eigenvector. Positive loadings are shown in blue and negative ones in red. Loadings close to zero are gray. c Visualization of the last relative eigenvector

Table 1 Loadings of the ten measurements on the first and the last relative eigenvector (rel evec). They are visualized in Fig. 8b, c

These results suggest that if there has been divergent selection for craniofacial shape it pertained to facial height relative to neurocranial breadth. By contrast, the relative size of the nasal cavity is the feature with minimal between-population variance relative to the within-population variance and thus might be likeliest to have been under stabilizing selection if any trait was. Overall proportions of the upper face relative to the neurocranium vary considerably among human populations, but no direct functional relevance is known; note, too, that the size of the jaw does not load on this relative eigenvector. Nasal size, by contrast, is closely associated with the size of the airways and hence of apparent physiological relevance; stabilizing selection for this trait in modern humans seems to be likely.

Classification of Prenatal Alcohol Exposure Based on Infant Brain Shape

Classification—the assignment of individuals to one of two or more groups based on a set of measurements—is a classic statistical domain for which the groups’ variance–covariance structures are of central importance. The likelihood ratio for assigning an individual to one group or the other depends on the averages and the variances in both groups. In the unusual situation that the groups have equal variance–covariance matrices, the ratio of likelihoods can be computed from a single linear dimension because the structure separating the two classification regions (the “separatrix” along which the likelihoods are identical) is linear (a line in two dimensions, a plane or hyperplane in more dimensions); hence this approach is referred to as linear discrimination. For heterogenous covariance matrices, the separatrix is a conic section or quadric surface, and the maximum likelihood classification is based on a quadratic function (quadratic classification; see, e.g., Rao 1948; Mitteroecker and Bookstein 2011). When, for every variable, group A has more variance than group B, the separatrix is an ellipse or ellipsoid, assigning group label A to points that fall outside the curve and group label B to those that fall inside. In other circumstances we can dissect the morphospace into two subspaces, one in which group A has more variance than group B in all directions, and the other in which group B has more variance than group A. These subspaces are spanned by the relative eigenvectors with relative eigenvalues larger than 1 and smaller than 1, respectively. Except when 1 or more relative eigenvalues are exactly 1, a quadratic maximum likelihood classification can be derived from the two subspaces, in each of which, separately, the separatrix is an ellipse or ellipsoid. Whereas biological interpretation of linear discriminant functions usually is difficult (Mitteroecker and Bookstein 2011), distances in the two subspaces may sometimes reflect actual biological properties or processes, especially if the two groups are known to differ in their extent of canalization.

We illustrate this approach by a reanalysis of the data used in Bookstein et al. (2007), 44 configurations of four landmarks representing the midline corpus callosum shape of human infants aged four months or less (Fig. 9a). Twenty-three of these infants were exposed in utero to high levels of alcohol, and 21 infants were unexposed.

Fig. 9

a An average of multiple unwarped freezeframes of a transfontanelle ultrasound video of the midsagittal plane, along with the four landmarks used for analysis. Points 1 and 2 are reliable Type 2 landmarks, the “corner” of genu and the tip of splenium. Landmarks 3 and 4 are semilandmarks, the point of the upper arch margin just over the middle of the segment connecting genu and splenium, and the point on the upper margin where the medial axis segment running up the middle of the splenium, if extrapolated, would hit this margin. b Scatterplots of the Procrustes shape coordinates landmark by landmark. Open circles are unexposed individuals, filled circles exposed individuals

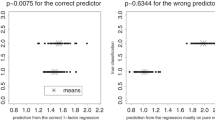
The landmark-by-landmark displays suggest numerous group differences in variances and covariances but only a moderate group mean shape difference (Fig. 9b). The Procrustes shape space here is of four dimensions; hence there are four conventional principal components. The heteroscedasticity is concentrated along PC 1 (Fig. 10a). A quadratic discriminant analysis based on all 4 PCs classifies infants to the appropriate exposure group with log likelihood ratios (LLR) from −1.78 to 6.83. The average log-odds in the “correct” direction is 1.45, corresponding to 81 % odds of a correct classification. We see that the 12 most extreme scores on PC1 all arise in the exposed group of children, leading to the startlingly effective classifier unearthed intuitively for the original publication. Note that in contrast to linear discrimination, in a quadratic discrimination the likelihood ratios comparing the actual strengths by which an observation can support one specific classification or the other may differ between the two groups in regard to mean or range. In the example here, many of the exposed individuals can be classified as ‘exposed’ with greater certainty than most of the unexposed individuals can be classified as ‘unexposed.’ This difference is not intrinsic to the quadratic method, but is a function of the actual data distributions involved.

Fig. 10

a Scatterplot of the first two principal components (PCs) together with contours of equal log-likelihood for the hypothesis of exposure versus that for nonexposure. The title line sets out the average log likelihood ratio in the direction of the correct hypothesis, and then the exponentiation of that log-likelihood, which approximates the odds of a correct classification in a new specimen. b Scatterplot of the first two relative eigenanalysis scores (relative principal components, RPCs) together with contours of equal log-likelihood for the hypothesis of exposure versus that for nonexposure. Open circles are unexposed individuals, filled circles exposed individuals

The PC plot in Fig. 10a also shows contours of equal log-likelihood for the hypothesis of exposure versus that for nonexposure. The likelihood ratios of analyses like this one are invariant against changes of basis for the descriptor space, and so a shear to the basis of relative eigenvectors for the two covariance structures per se, exposed divided by unexposed, will not change the LLR for any infant here. It will, however, alter the axes in Fig. 10a to the more effective set shown in Fig. 10b. The four relative eigenvalues are 1.565, 1.389, 0.894, and 0.734, highlighting the two dimensions showing substantially greater variance for the exposed children than for the unexposed. In that plane, the discriminant function should look like a set of concentric rings out of a center within the unexposed group (the ellipses are almost circular because the first two relative eigenvalues are nearly the same). And that is exactly what we see in Fig. 10b, with a mean odds ratio of 3.08, larger than we had for the more nearly linear discriminator within the first two ordinary PCs. In other words, by paying more attention to the differences in covariance structure, we arrive at a better, simpler predictor that may yield a more useful biological reification of the classification rule than standard classification approaches do.

The classification of these baby brain features as unexposed or exposed is, to a first approximation, not a linear score at all, but instead a thresholding of their distance from a standard form. This interpretation conforms to the traditional understanding of the effect of prenatal alcohol exposure on the developing brain as a dysregulation that produces hypervariation in most shape measurements at the same time (Bookstein et al. 2002). This is a distinctly different interpretation from “a mean shift of the angle at splenium” (the description of the discrimination in the original publication).

Discussion

Whether in systematics, evolutionary biology, or anywhere else in organismal biology, the empirical study of high-dimensional phenotypic variance–covariance patterns is made more challenging by the application of inappropriate statistical tools. In particular, attempts to summarize covariance matrices or differences between covariance matrices by one or a few single quantities are difficult to interpret biologically, unless they have been explicitly derived from some formal biological theory that is argued as credible on other grounds (see, e.g., Hansen and Houle 2008). This paper advocates the use of relative eigenanalysis to decompose the differences between two covariance matrices into a series of linear combinations with extremal ratios of variance between the groups. The phenotypic patterns described by the relative eigenvectors and relative eigenvalues (those variance ratios) may afford a possibility of strong biological inferences. The convenient geometric properties of this relatively simple and intentionally “theory-free” technique allows for an effective exploratory study of high-dimensional variance–covariance patterns.

Relative eigenanalysis was already described at length by Flury (1983, 1985), but not in any specific biometric context (the data example, in fact, dealt with Swiss paper money). Flury noted that despite frequent applications of significance tests for homogeneity of covariance matrices to test for the assumptions underlying parametric multivariate methods such as MANOVA, “methods for comparing two or more covariance matrices have been given little attention in applied statistical analysis” (1983:98). Little has changed in this regard over the past 30 years (even though the importance of parametric tests requiring homogeneous covariance matrices has reduced since we can compute exact significance levels by randomization tests). Our paper is an attempt to provide a new description of relative eigenanalysis in contemporary biological and morphometric contexts that emphasizes its exploratory use when theory is absent or quite distant from actual data. We demonstrated, for instance, how this tool can be used to study the developmental patterning of phenotypic variance within a population and also the evolutionary patterning of variance between populations. Thereby we showed that the variance of different shape features can have very different developmental or evolutionary dynamics, which might be hidden when pooling variance of all variables or when analyzing other linear combinations such as ordinary principal components. Such findings do not report experimental results, but certainly can suggest them.

Principal component analyses change, often radically, under linear transformations of the variables; indeed, that is one of its better-known drawbacks for a biological interpretation. They can be considered as eigenanalyses of a covariance matrix relative to the identity matrix, which is in general without biological meaning and which in any event does not transform with the data. Relative eigenanalysis is a principal component analysis of one group relative to another group, and the resulting ratios of variance (the relative eigenvalues) are unchanged under linear transformation of the variables, including changes of linear dependence. The relative eigenanalysis also appropriately localizes the consequences of variational change in a single factor, e.g., size allometry, to one single component. In ordinary PCA, by contrast, this change would likely be distributed over multiple components.

Relative eigenanalysis supports an interpretation of the differences between two covariance matrices in terms of increased or decreased variance for certain principal linear combinations that may or may not correspond to real biological factors. But in many biological data sets, differences between covariance matrices can also result from the rotation of the direction of a factor rather than from increase or decrease of its variance. For example, ontogenetic or static allometry, which typically is the dominant factor of shape or form variation within a group, may differ in direction between two groups, thereby leading to different covariance structures. In these situations the most useful interpretation is that of an altered average pattern of growth, not of increased or decreased individual variance for certain traits. It is thus advisable to model dominant factors of form or shape variation, such as growth and allometry, directly on their own, narrated in different terms from “differences in variance.” Relative eigenanalysis should then be applied to the residual data after these factors have been removed from the data set.

In order to compute a relative eigenanalysis, at least one covariance matrix must be invertible. But in modern morphometrics, covariance matrices typically are non-invertible, as usually the count of shape variables exceeds the count of cases. Here the number of variables needs to be reduced by methods such as principal component analysis or partial least squares analysis prior to a relative eigenanalysis.

As a general rule we do not recommend statistical test procedures of any kind in connection with exploratory data analyses like these. It is particularly inappropriate to use such tests when groups have already been identified in advance. If groups differ in mean shape, then surely they ought to be expected to differ in variance as well; the usual “null hypothesis” of no difference is particularly obtuse when applied in domains such as organismal biology. If thresholds there must be, the Appendix explains how to investigate whether two relative eigenvalues are different enough to warrant separate interpretation, or, put another way, whether the samples at hand are large enough for the explanatory work they are being asked to support.

Appendix

Corresponding to the maneuvers here is a null model that is often helpful in deciding whether a relative eigenanalysis reveals anything worth thinking about. We’re not testing the ratio, only asking that it be at least as large as the value expected on the absence of any signal. The approach parallels the analogous decision regarding eigenvectors arising from successive eigenvalues of one single matrix (Coquerelle et al. 2011; Bookstein 2014). That approach, in turn, is a modification of the stepdown test for sphericity that is already in the advanced textbooks (cf. Morrison 1976, pp. 336–337). As this argument has not apparently been published before, we sketch it here for any interested reader. Our notation is borrowed from Anderson (1963), where several of the corresponding asymptotic likelihood ratio tests were published.

Suppose we are observing a covariance matrix on a sample of size N for a list of p variables that are all actually independent Gaussians of mean 0 and variance 1. Let the matrix $\mathbf{U}$ be $\sqrt{N}$ times the deviation of the empirically observed covariance matrix from the correct answer, which is the identity matrix of rank p. As samples grow large, $\mathbf{U}$ becomes Gaussian with mean zero for every element and variance 2 along its diagonal, 1 elsewhere.

That theorem corresponds to a $\mathbf{U}$ that was generated to describe some multivariate Gaussian distribution’s ordinary eigenvalues. The relative eigenvalues, which we have been depicting here as the eigenvalues of $\mathbf{T}^{-1/2}\mathbf{S}\mathbf{T}^{-1/2}$, are also the eigenvalues of $\mathbf{S}\mathbf{T}^{-1}$. For large samples, the distribution of the deviation of $\mathbf{T}^{-1}$ from the identity is the same as the distribution of the deviation of $\mathbf{T}$. The effect of this additional factor of $\mathbf{T}^{-1}$ on what was already the deviation of the sample described by $\mathbf{S}$ is to alter $\mathbf{U}$ by another term, additive in this metric, of exactly the same distribution. Their sum, scaled by $\sqrt{N}$, thus is in the limit a set of Gaussians with terms of mean zero and variances 4 down the diagonal, 2 elsewhere.

At equation 3.9, pages 132–133 of this same paper, Anderson shows, by expressing the eigenvalues themselves in terms of the elements of $\mathbf{U}$, that for the ordinary eigenproblem the log likelihood ratio for the null hypothesis of sphericity for any q consecutive eigenvalues (not necessarily the full set of all p corresponding to the p original variables) is the quantity log a/g, where a is the arithmetic mean of the eigenvalues and g is their geometric mean. Using the theorem about $\mathbf{U}$ for ordinary eigenvalues, he shows that in the limit of large samples this log likelihood ratio is distributed approximately as 1/Nq times a χ² on (q − 1)(q + 2)/2 degrees of freedom, where q is the number of eigenvalues being compared (in our applications, usually, q = 2). It follows, then, that in the relative eigenanalysis application the same quantity log a/g is distributed as 2/Nq times the same χ² (Fig. 11).

Fig. 11

From the expected value of the corresponding χ² distributions comes a permissive criterion for narrative validity of relative eigenvectors: restrict the text only to those for which the relative eigenvalue λ _i has a ratio to its successor λ _i+1 as least as large as the value given in this diagram. Solid line curve for ordinary eigenvalues. Dotted line curve for relative eigenvalues