Introduction

Many researchers have investigated the effects of environment, geometry of the specimen, frequency, etc. on fatigue life or crack growth characteristics of several material [1–3]. Kondo et al. [4] studied the effects of water environment on fatigue life of A-302 B steel. It is reported that fatigue life in water environment is shorter than that in air environment. Amzallag et al. [2] found no effect of environment for austenitic and ferritic stainless steel tested in both air and in 3.5% NaCl solution at about 20 Hz. Conclusions of Vosikovsky [3] are also similar to Amzallag et al. [2]. Scott et al. [5] studied the effect of notch on fatigue crack initiation and propagation in structural steel exposed to sea water and air. These investigations indicate that fatigue life is influenced by salt solution, notch, or surface condition of the specimen.

It is well known that when the identical specimens or parts are subjected to same fluctuating stress or load levels, they usually fail at different cycles because of non-homogeneity in material properties, variations in the surface condition, etc. Hence, fatigue life or strength of a material usually shows large variations even when tested under same loading conditions. Also, the amount of fatigue life scatter associated is affected by several other parameters like environment, specimen geometry, stress level, frequency, etc. The author [6, 7] has developed methods for estimating error or scatter factor associated with fatigue life prediction at different probabilities and confidence levels using log normal and Weibull distribution. The safe life can be determined by fatigue scatter factor and full scale fatigue test. The fatigue scatter factor plays a vital role in life prediction of aircraft structures. However, in the past, the fatigue scatter factor was general, and the differences of different stages were not considered.

Recently, the economic life prediction and reliability assessment of aircraft structures on the basis of scatter factor have been presented by Chuliang and Kege [8]. Many other studies related to fatigue life scatter and probability distribution functions are available in the literature [9–12].

In this article, critical examination of the sample size selection for estimation of fatigue life under different environmental conditions has been presented. Effect of the presence of notch on the sample size selection has been studied. Effects of geometry and environment on scatter factor have also been investigated. On the basis of the present investigations, minimum number of specimens required for fatigue testing has been put forward.

Experiment

Material and Specimen

The materials used for the experiments described here are made of commercial structural carbon steel. The chemical compositions are 0.26 C, 0.26 Si, 0.44 Mn, 0.02 Ni, 0.02 Cr, and 0.01 P. The yield and ultimate strengths are 330 and 470 MPa, respectively. Smooth (unnotched) and 1 mm circumferential V-notched specimens were machined to the dimensions and shapes, as shown in Fig. 1, from 20 mm × 20 mm bar. The bar was normalized at 450 °C for 2 h before the preparation of specimen.

Fig. 1
figure 1

Specimen geometry and dimensions in mm

Full size image

Experimental Method

The fatigue testing was conducted on rotating fatigue-testing machine at room temperature. The tests were performed in air, 3.5% KCl, and 5.5% KCl salt solutions at 270 and 260 MPa stress amplitudes both for smooth and 1-mm circumferential V notched specimens. Specimens were exposed to salt solution at room temperature. An extra attachment was designed to test the specimens in salt solution. Provision was made to have constant flow rate of 217 cc/h of continuous flow of KCl salt solution from a plastic reservoir on to the specimen. 25 specimens were tested at each stated condition. The results are presented in Table 1. In this analysis some results are also taken from the author’s previous studies [6, 7] which are not included in Table 1.

Table 1 Fatigue life data of 0.26 C carbon steel at different test conditions
Full size table

Theory

Estimation of error involved in the fatigue experiments has been carried out using the equations previously developed by the author [6]. Only brief review of the equations developed is presented here.

Weibull Distribution Model

The percent of error involved in the fatigue experiment is defined as the error made when the sample life is accepted to be the population life, then the percent of error involved in the prediction of fatigue life from the sample data is the difference between the two expectations, \( E\left( {\mu_{x} } \right) \) and \( \mu_{x} \) expressed as percentage. Thus, the percentage of error can be expressed as

$$ {\text{Error}} = \frac{{E\left( {\mu_{x} } \right) - \mu_{x} }}{{\mu_{x} }} \times 100 $$

If the fatigue life, Nf, follows Weibull distribution, then the percentage of error involved in estimating the fatigue life from sample size, n, is given by

$$ Rw = \left\{ {\frac{{\bar{\delta }}}{{\mu_{x} + \left( {d + \lambda } \right)\bar{\delta }}}} \right\}\frac{t}{{\sqrt {n - 1} }}\sqrt {\frac{{\chi^{2} V_{\text{o}} Cn}}{{\chi_{{\left[ {C(n - 1)} \right]}}^{2} }}} $$
(1)

where \( \mu_{x} = \bar{x} + \left( {d + \lambda } \right)\bar{\delta } \); \( \bar{\delta } = 1/\bar{\beta } \), \( \bar{\beta } \) is Weibull slope; \( \lambda = \log \left( { - \log \left[ {1 - \alpha } \right]} \right) \), α is the percent probability of failure; \( \bar{x} = \bar{\xi } + \lambda \bar{\delta } \); and \( \bar{\xi } = \ln \left( {\bar{\theta }} \right), \) where \( \theta \) is characteristic fatigue life of the two-parameter Weibull distribution model. \( \left( {\overline{ \ldots } } \right) \) indicates that the parameter is estimated from the sample data. χ 2 and t are obtained from the χ 2 distribution function and t distribution function for the given probability, confidence level, and sample size.

$$ d = \left\{ {\frac{{ - a_{12} u^{2} - n\lambda + u\varepsilon }}{{n - a_{22} u^{2} }}} \right\} $$

where n is the sample size; \( \varepsilon = \left[ {\left( {a_{12}^{2} - a_{11} a_{12} } \right)u^{2} + na_{11} + 2na_{12} \lambda + na_{22} \lambda } \right]^{0.5} \); u is the normal deviate corresponding to α percent of probability of failure; \( a_{11} = 1.10876,a_{22} = 0.6079,a_{12} = - 0.25702, \) and C = 0.822; \( V_{\text{o}} = v_{22} + (2\lambda + d)^{2} v_{11} + 2(2\lambda + d)cv_{12} \); \( v_{11} = \text{var} \left( {\frac{{\overline{\delta } }}{\delta }} \right),v_{22} = \text{var} \left( {\frac{{\overline{\zeta } }}{\zeta }} \right), \) and \( cv_{12} = co.\text{var} \left( {\frac{{\overline{\delta } }}{\delta },\frac{{\overline{\zeta } }}{\zeta }} \right) . \)

The scatter factor indicates the variation of a parameter from its mean value. In term of statistical parameter, the fatigue scatter factor is defined as the ratio of the standard deviation to mean life for a specified probability of failure and confidence level. Thus, the scatter factor shows the variability in the fatigue life data of a material under given test conditions. On the basis of probability distributional parameters, the scatter factor for Weibull distribution model is defined as

$$ \phi_{\text{W}} = \frac{{\overline{\delta } }}{{\left( {\mu_{x} + \left\{ {d + \lambda } \right\}\overline{\delta } } \right)}}, $$

which measures the scatter of the fatigue life data.

Log Normal Model

If the fatigue life Nf follows normal distribution, then x = log (Nf) will follow log normal distribution. Then, the percentage of error can be estimated from the relation;

$$ Rn = \frac{{t \cdot s\sqrt {\left( {\frac{1}{n} + u^{2} \left\{ {\psi^{2} - 1} \right\}} \right)} }}{{\bar{x} + u \cdot \psi \cdot s}} $$
(2)

where, s standard deviation of log fatigue life; \( \overline{x}\) = sample mean of log fatigue life; and t student “t” value.

In statistical analysis unbiased estimation of a standard deviation is required. Hence, a factor which corrects the bias in the estimation of the sample standard deviation is known as correction factor for sample standard deviation. This factor depends on statistical distribution of the random variable. When the random variable is normally distributed, the correction factor given by ψ eliminates the bias. The factor ψ is obtained as

$$ \psi = \sqrt {\frac{n - 1}{2}} \frac{{\Upgamma \left( {\frac{n - 1}{2}} \right)}}{{\Upgamma \left( \frac{n}{2} \right)}} $$

is the correction factor for the sample standard deviation. \( \Upgamma \left( n \right) \) is the gamma function.

In this article, the scatter factor for log normal distribution is defined as

$$ \phi_{\text{N}} = \frac{s}{{\bar{x} + u \cdot \psi \cdot s}} $$

At 50% probability, u = 0, and the above equation degenerates to the well-known relation of coefficient of variation. Hence, the scatter factor defined here is also known as the coefficient of variation.

Equation 1 and 2 are solved for different probabilities, confidence levels, and test conditions. The results are presented in Figs. 2, 3, 4, 5, 6, 7, and 8. The variation of the error or gradient of error (GR) shown in different figures obtained from sample fatigue life for a given stress level and probability condition varies with sample size.

Fig. 2
figure 2

Variation of scatter factor at 260 and 270 MPa, 50% probability, and 5.5% KCl salt solution for notched geometry

Full size image
Fig. 3
figure 3

Effect of probability level on scatter factor for 270 MPa, 3.5% KCl, and smooth geometry

Full size image
Fig. 4
figure 4

Effect of environment on error for 270 MPa, 90% probability, and 95% confidence level (log normal distribution)

Full size image
Fig. 5
figure 5

Effect of probability distribution function on error at 50% probability and 95% confidence level, 5.5% KCl, and smooth geometry

Full size image
Fig. 6
figure 6

Effect of probability distribution function on sample size at 50% probability, 95% confidence level, 5.5% KCl and smooth geometry

Full size image
Fig. 7
figure 7

Effect of notch on error at 260 MPa, 95% probability and confidence level, and 5.5% KCl salt solution

Full size image
Fig. 8
figure 8

Effect of salt concentration on error at 90% probability and 90% confidence level

Full size image

Results and Discussion

Fatigue Life Scatter and Sample Size

The sample standard deviation or Weibull slope is the measure of the scatter of the fatigue life data. Hence, the fatigue life scatter factor expressed as the coefficient of variation or distribution parameters influences sample size selected for fatigue life estimation. The variation of scatter factor with sample size is shown in Fig. 2 both for log normal and Weibull distributions for 260 MPa, notched specimen, and 5.5% KCl salt solution. It is seen that the scatter factor is higher for Weibull distribution than that for log normal distribution. Figure 3 shows the influence of probability on scatter factor. From Figs. 2 and 3, it can be inferred that the scatter factor is higher for lower stress amplitude than for higher stress amplitude. It is found that for all level of probabilities and confidence levels, the scatter factor varies from 0.017 to 0.055 for log normal distribution and from 0.015 to 0.057 for Weibull distribution at 270 MPa stress amplitude; however, it varies from 0.019 to 0.0671 for log normal distribution and from 0.0162 to 0.069 for Weibull distribution model at 260 MPa for notched and smooth specimen, when tested under different environmental conditions. The scatter factor is found to be higher for notched specimen than that for smooth specimen at 5.5% KCl salt solution and 260 MPa stress amplitude. This shows that the presence of crack or crack like defects in metal or structure has influence on the fatigue life scatter. Hence, sample size selection should be made more carefully while predicting fatigue life for notched specimen than that for smooth specimen.

Effect of Salt Solution on Sample Size Selection

Salt solution significantly reduces the fatigue life of specimen. In the present investigation, it has been observed that scatter factor is also influenced by the salt solutions. The scatter factor is found to be higher in 5.5% KCl salt solution than that in 3.5% KCl salt solution for all levels of test conditions described in the article. These results reveal that scatter in fatigue life data is more in the case of higher percentage of salt solutions (higher concentration), higher level of probability, higher confidence level, and lower stress amplitude. Figure 4 shows that error in estimating fatigue life is highly influenced by environmental conditions. Table 2 shows that about 3–5 specimens are needed in 3.5% salt solution whereas 4–6 specimens are required in 5.5% salt solution to predict the fatigue life using log normal distribution at 270 MPa stress amplitude, smooth geometry, and for all levels of probability and confidence discussed above with maximum permissible error of 5%. It is also found that number of specimens required is higher at 260 MPa and varies from 3–9 for the above stated conditions. When specimen requirement was compared with air medium, it is found to be higher [7].

Table 2 Minimum sample sizes required for estimation of fatigue life within 5% acceptable error for probability levels of 50, 90, and 95%
Full size table

Probability Distribution Function and Sample Size

The variations of error with sample size at 50% probability and 95% confidence level for both Weibull and log normal distributions are shown in Figs. 5 and 6. It is evident from the figures that error for Weibull model is higher than that for log normal distribution. It is seen from Table 2 that as high as 8–9 specimens are required for estimation of fatigue life at 50% probability using Weibull distribution model, whereas a maximum number of six specimens are sufficient to predict the fatigue life within 5% of permissible error at 260 MPa stress amplitude using log normal distribution model. The K–S statistics for goodness of fit tests in Table 3 show the relative goodness-of-fit of fatigue life data for log normal and Weibull distribution. It is clear from the Table 3 that fatigue life distribution at 270 and 260 MPa stress amplitude under smooth and notched conditions tested at different environmental conditions, fits well with Weibull distribution. Though log normal distribution is slightly better for the distribution of fatigue life than Weibull distribution at 270 MPa, 5.5% KCl salt solution and for notched specimen geometry, the error is found to be higher for Weibull distribution model than that for log normal distribution model. It can be concluded from the present discussion that sample size requirement to estimate fatigue life using Weibull distribution model within same percentage of permissible error is higher than that for log normal distribution irrespective of distribution function assumed to model the fatigue life data.

Table 3 K.S. statistics
Full size table

Effect of Notch on Sample Size

Presumption of the presence of small defect or some initial flaws in the structural components is undoubtedly beneficial in the fatigue analysis and reliable estimation of the fatigue life or strength. This has a great importance because a small change in the S–N design curves at high cycle lives can have a large influence in the predicted value. Hence, the study of the effect of notch on uncertainty of the fatigue life and the selection of sample size under such conditions carry a great importance.

Figure 7 gives the effect of the presence of notch on error estimation from a specified sample size. It is seen that the error is higher for the notched specimen than for the smooth specimen. Figure 8 shows the effect of notch on error for different stress amplitudes and salt solutions at 90% probability and confidence level. It is seen that 5.5% KCl salt solution with the presence of notch at lower stress amplitude has higher error than at higher stress level. Table 2 shows that about 8–9 specimens are required to estimate the fatigue life from notched data at 260 MPa stress amplitude with 5% acceptable error using Weibull distribution, whereas 6–7 specimens are needed for smooth specimen at 95% probability and confidence level. Table 2 shows that higher number of sample size is required in the case of notched data than that required for smooth data for the prediction of fatigue life within 5% of threshold error.

Effect of Stress Amplitude on Error and Sample Size

Figure 9 shows that estimation of error is higher for lower stress amplitude than that for higher stress amplitude for a given probability, confidence level, and specified sample size. It is also seen that the difference in error estimated for different stress amplitude is negligible beyond certain sample size. Hence, higher number of specimens should be taken for lower stress amplitude to predict the fatigue life.

Fig. 9
figure 9

Effect of stress amplitude on error at 50% probability, 90% confidence level, and 5.5% KCl salt solution

Full size image

Analysis of Variance (ANOVA)

On the basis of ANOVA procedure [13], the results and conclusions made from Figs. 2, 3, 4, 5, 6, 7, and 8 are backed by the statistical test of significance. The ANOVA results are presented in Table 4. In this case, the probability of making wrong conclusions is 1% or less.

Table 4 ANOVA results
Full size table

Parametric Representation of Error and Sample Size

The variations of error with sample size as shown in Figs. 2, 3, 4, 5, 6, 7, and 8 show that there exists a threshold error, irrespective of sample size which mainly depends on confidence level, probability, distribution function, and the coefficient of variation of the fatigue life data or scatter factor. A mathematical expression for the error data has been proposed. The presented mathematical form for the error data could be useful especially in determination of sample size for reliable estimation of fatigue life for engineering purposes.

The proposed equation for error data may be expressed as

$$ n\left( {R - R_{\text{o}} } \right)^{m} = C $$
(3)

where R is the error value, n is the sample size, and m, C, and R o are constants required to be optimized.

Fitting of the Eq 3 to experimental data has been done by correlation coefficient method at each test condition. In this method, value of Ro is optimized by a computer-aided trial-and-error method corresponding to maximum correlation coefficient of the points. The estimated parameters are presented in Tables 5 and 6.

Table 5 Regression parameters of Eq 3 at 3.5% KCl salt solution and notched geometry
Full size table
Table 6 Regression coefficients of Eq 3 for smooth geometry at 3.5% KCl salt solution
Full size table

Prediction of S–N Curve or Fatigue Life

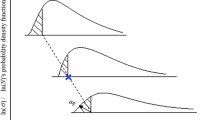
It is seen that the variation of error or GR has high magnitude up to certain sample size, and beyond certain sample size, it is negligible for all the combinations of probabilities, confidence levels, etc. Figure 10 shows that the curve is very steep up to certain sample size, and GR is negligible when it exceeds the value of −1.0. In other words, beyond certain sample size, the variation in the GR is very small and remains constant even if more number of data are added in the analysis. On the basis of these observations, a novel method for optimization of sample size and estimation of fatigue life or S–N curve is presented in Fig. 11. This method is the most suitable for reliable estimation of fatigue life at any level of probability and confidence. Hence, its applicability in the field of fatigue life estimation and reliability assessment of a component is very wide. The model is of significant scientific value for products to provide longer economic life, higher reliability, and lower cost.

Fig. 10
figure 10

Variation of GR with sample size at 270 MPa

Full size image
Fig. 11
figure 11

Procedure for determination of minimum sample size and estimation of fatigue life or S–N curve

Full size image

The method presented here is based on the selection of the minimum number of sample size. The minimum sample size required in predicting the fatigue life is the sample size when the GR approaches a critical value, GRCRI. This critical value, GRCRI, may be taken between 0 to −1.0 as seen in the experimental results. The detailed procedure for the determination of sample size and S–N curve is shown in Fig. 11. The proposed method has been verified by considering the fatigue life data of 0.26 C steel. The results are presented in Table 7.

Table 7 Minimum sample size determination and S–N curve prediction (Data 0.26 C steel)
Full size table

Validation

In order to verify the proposed method, standardized method for judging the equalities of two or more S–N curves has been applied [14, 15]. This method is based on the statistical test of significance between the regression equations fitted to each set of S–N data. Four conditions are required for the same as follows:

Condition 1 :

Test of linearity of data

Condition 2 :

Test of equality of residual squares between regression equation and data.

Condition 3 :

Test of equality of slope of the regression equations.

Condition 4 :

Test of equality of intercepts of the regression equations.

Details of the mathematical derivations are available in the literature [14, 15].

Three independently fitted regression equations, one with minimum number of sample size, \( n_{0} \) (Eq 1—in the present case, the minimum sample size determined using proposed method is 4, 5, and 7 for stress amplitude 300, 290, and 270 MPa, respectively); population sample size, \( n_{p} \) (Eq 2—in the present case, it is 30 per stress level); and the sample size of \( \left( {n_{0} - j} \right) \) (Eq 3—where j is the number of stress amplitude considered for describing the S–N curve) have been obtained. The regression equations thus determined are used for significance test. The summary of the results of the analysis is presented in Table 8. It is seen that conditions 1–4 are satisfied when Eq 1 is compared with Eq 2, and all hypotheses are accepted at 95% significance level. When Eq 3 is compared with Eq 2, it is rejected because the condition 3 is not satisfied at 95% significance level. This proves the validity of the proposed model.

Table 8 Summary of judgment results
Full size table

The method discussed above can be used for failure analysis and prediction of fatigue life or fatigue strength. The fatigue failure is a significant problem because it can occur because of repeated loads below the static yield strength of the material. It is a progressive localized damage due to fluctuating stresses and strains on the material. This can result in an unexpected and catastrophic failure in use. The main problem areas in preventing fatigue failure are prediction of stress levels that causes failure or estimation of scatter in fatigue life. The present method which focused on the prediction of amount of scatter in stresses or fatigue life is an effective technique that can be used for reliability-based design or prevention of fatigue failure.

Conclusions

  1. 1.

    For a given material and test conditions, higher sample size is required for estimation of fatigue life by Weibull distribution than log normal distribution.

  2. 2.

    Fatigue life scatter or scatter factor depends on environmental conditions, specimen geometry, probability, confidence level, and stress amplitude. The lower the stress amplitude the higher the scatter factor.

  3. 3.

    Higher sample size is required to estimate the fatigue life at lower stress amplitude than that at higher stress amplitude at specified probability and confidence level, or under notched geometry than smooth geometry.

  4. 4.

    There exists a threshold error, which is independent of sample size but depends on probability, confidence level, and test conditions.

  5. 5.

    Salt environment has prominent effect on sample size selection.

  6. 6.

    The method presented for sample size estimation and S–N curve or fatigue life estimation can be used for any loading condition, and it is a suitable, economical method of reliability assessment of a component.