Introduction

Instrumented indentation is a widely used technique for measuring the mechanical properties of materials such as elastic modulus and hardness. It is also increasingly used to probe time-dependent material behavior for thin films and bulk materials. However, assessing creep behavior through instrumented indentation is not as straightforward as the standard uniaxial creep test. Accordingly, research aimed to gain insight on the relationship between indentation creep and uniaxial creep is of great interest.

Metallic materials display time-dependent plastic deformation (creep) at high homologous temperatures. Conventionally, a creep test involves applying a constant uniaxial stress to a bulk specimen. After a transient duration, a steady state is reached where the strain increases nearly linearly with time, i.e., the creep strain rate remains constant. The relationship between steady-state strain rate \(\dot{\upvarepsilon }_{\text{s}}\), applied stress σ, and temperature is often found to be (Ref 1-3)

$$\dot{\upvarepsilon }_{\text{s}} = A^{{\prime }} \left[ {\exp \left( { - \frac{Q}{RT}} \right)} \right]\upsigma^{n} ,$$
(1)

where A′ is a constant, Q is the activation energy, R is the universal gas constant, T is the temperature (in K), and n is the stress exponent for creep. At a constant temperature, the expression becomes

$$\dot{\upvarepsilon }_{\text{s}} = A\upsigma^{n} ,$$
(2)

where the creep coefficient A has incorporated the temperature effect. The constants A and n uniquely characterize this power-law creep response. With a series of uniaxial tests, the constants A and n can be determined by plotting the measured strain rates against the applied stresses, both in logarithmic scales.

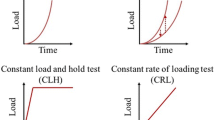
A representative early development of indentation-based creep measurement is the impression creep method (Ref 4-6), which involves pressing a flat-end cylinder onto the test material under a constant load and observing the increase in depth. The creep stress exponent and/or activation energy obtained by this technique have been found to be consistent with those measured by conventional uniaxial creep tests (Ref 5-7). As for the commonly used sharp indenter geometries (pyramidal and conical), the most widely employed technique is the constant-load creep, where the indentation is held at a fixed peak load over a duration of time, while the penetration depth continues to increase (Ref 8-17). The hardness H is defined as

$$H = \frac{P}{{A_{\text{c}} }},$$
(3)

where P is the load and A c is the instantaneous projected contact area. The indentation strain rate is defined as (Ref 8)

$$\dot{\upvarepsilon }_{\text{I}} = \frac{1}{h}\left( {\frac{dh}{dt}} \right),$$
(4)

where h is the instantaneous indentation displacement (depth) and t is time. During the hold period hardness continues to decrease as the projected contact area increases, and the indentation strain rate also decreases with time. Note that the creep stress is proportional to H and the indentation strain rate \(\dot{\upvarepsilon }_{\text{I}}\) is assumed to be proportional to the uniaxial strain rate \(\dot{\upvarepsilon }_{\text{s}}\) in a conventional creep test. By monitoring the changes in hardness and indentation strain rate during the constant-load hold, the stress exponent n can be determined by means of Eq 2. Reasonable agreement of n values with those measured by conventional uniaxial creep tests has been reported (Ref 8-13). However, uncertainty also exists, especially due to deviation from the steady-state creep condition during the constant-load indentation (Ref 14-16).

During the constant-load hold indentation creep, both the hardness and strain rate are simultaneously changing. If the indentation strain rate can be held constant during the indentation loading process, a steady-state creep may be more easily attained. In other words, if a prescribed constant \(\dot{\upvarepsilon }_{\text{I}}\) gives rise to a stable value of H (over a range of independent depth), then the power-law creep relation, Eq 2, can be readily assessed. The constant indentation strain rate test may be easily achieved in a displacement-controlled machine (Ref 18). For geometrically self-similar indentation, a constant indentation strain rate, \(\frac{1}{h}\left( {\frac{dh}{dt}} \right)\), can be obtained by imposing a constant normalized load rate, \(\frac{1}{P}\left( {\frac{dP}{dt}} \right)\), under the condition of a steady-state value of hardness (Ref 19, 20). Applying this approach to indium (In), Lucas and Oliver (Ref 19) showed good agreement with the literature data for both the stress exponent n and activation energy Q. Further studies of creep mechanisms in aluminum (Al), tin (Sn), and bismuth (Bi), employing this constant strain rate technique, have also been reported (Ref 15, 21, 22).

Numerous studies have shown good correlation between the stress exponents n determined by indentation and by conventional uniaxial creep tests, as described above. However, the viability of using instrumented indentation to characterize the uniaxial creep response will also rely on a quantifiable relation between \(\dot{\upvarepsilon }_{\text{I}}\) and \(\dot{\upvarepsilon }_{\text{s}}\) (Ref 23). Equivalently, the question is how and if the coefficient A in Eq 2, at a fixed temperature, can be determined by indentation. Poisl et al. (Ref 24) studied indentation and uniaxial creep of amorphous selenium (Se), which displays a Newtonian viscous behavior (with the stress exponent of unity) at above its glass transition temperature. The ratio \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) was found to be approximately 0.09. Takagi et al. (Ref 25) examined an aluminum (Al)-magnesium (Mg) solid solution alloy with a stress exponent of 3.2, and obtained the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio as 0.28. In our previous numerical finite element study subjecting Sn-based model materials to the constant indentation-strain-rate method, the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio was found to be 0.33 (Ref 26). It is unclear if these values are representative of other materials showing general power-law creep behavior.

The present study aims to correlate the indentation strain rate \(\dot{\upvarepsilon }_{\text{I}}\) and uniaxial strain rate \(\dot{\upvarepsilon }_{\text{s}}\) from a numerical modeling standpoint, to cover a very wide range of power-law creep parameters. In the first part of the study, we apply both the constant-load hold method and constant indentation-strain-rate method to Sn-based materials, to extract hardness (and thus stress, σ) values at different indentation strain rates (\(\dot{\upvarepsilon }_{\text{I}}\)). The \(\dot{\upvarepsilon }_{\text{I}} - \upsigma\) relationships obtained from the two methods are compared with the uniaxial creep response (which serves as the input for the finite element model). In doing so, we will illustrate that the constant indentation-strain-rate method yields a more consistent result than the constant-load hold method. The second part of the study is then devoted to the constant indentation-strain-rate method, with the constants A and n systematically varied. The objective is to examine how the indentation-derived creep response may be influenced by the actual uniaxial creep parameters (used, again, as the model input). We will develop a “map” showing the variation of indentation-derived stress exponent and \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio with the uniaxial creep constants A and n. The result will thus provide practical quantitative guidance on how to extract the uniaxial creep parameters from the constant indentation-strain-rate creep test.

Model Description

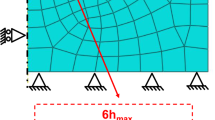
Figure 1 shows the model geometry. The model is axisymmetric, with the left boundary being the symmetry axis. The specimen has a lateral span (radius) of 200 µm and a height of 200 µm. The indenter is a diamond cone with a semi-angle of 70.3°, which results in the same nominal projected contact area, for a given depth, as that of a Berkovich indenter. Use of the conical indenter is a practical way to model the indentation process in a two-dimensional setting (Ref 27). During indentation, the left boundary is allowed to displace only in the 2-direction. The bottom boundary is allowed to move only in the 1-direction. The right edge is not constrained. The top surface of the specimen, when not in contact with the indenter, is also free to move. The coefficient of friction between the indenter and the top surface is taken as 0.1, which is a typical value for the diamond/metal contact pair (Ref 28, 29). A total of 61,608 continuum 4-node quadrilateral elements are included in the model, with a finer element size near the upper left corner of the test material. Mesh convergence was checked through the modeled indentation hardness values resulting from a total of three meshes with different extents of refinement (Ref 30). The finite element program ABAQUS (Version 6.12, Dassault Systemes Simulia Corp., Providence, RI) was used to carry out all the simulations.

Fig. 1
figure 1

Schematic showing the indenter and test material, along with the boundary conditions and local mesh used in the axisymmetric model. The left boundary is the symmetry axis. The entire specimen is 200 μm in lateral span (radius) and 200 μm in height

Full size image

In the case of constant-load hold test, the indentation process is load-controlled with two peak loads considered: 50 and 100 μN. A duration of 10 s is used to bring the load to the target value. The load is then held for 30 h during which the variation of indentation depth with time is monitored. Contact geometry during this period is also monitored for extracting the instantaneous contact radius. When determining the contact radius from the simulation, the last nodal point on the top surface in contact with the indenter is identified in the deformed mesh. Therefore, the effect of possible “pile-up” or “sink-in” of material at the indentation edge is automatically taken into account. The evolution of hardness and indentation strain rate are then determined from Eq 3 and 4. Choosing several points during the hold time history will then provide a \(\dot{\upvarepsilon }_{\text{I}} - H\) relationship for a given material.

In the case of constant indentation-strain-rate test, displacement (h) is applied on the top face of the indenter such that the indentation strain rate, \(\dot{\upvarepsilon }_{\text{I}}\) (defined in Eq 4), maintains a prescribed value. This was implemented in a piecewise manner, through successive intervals with an increasing displacement rate up to a maximum indentation depth of 4 μm. The range of \(\dot{\upvarepsilon }_{\text{I}}\) considered in this study is from 10−7 to 10−4 s−1. Under a constant applied indentation strain rate, if the hardness (calculated by the evolutions of load and contact radius) remains constant, then a steady state is reached. Several simulation runs with different prescribed indentation strain rates will then be sufficient to establish a \(\dot{\upvarepsilon }_{\text{I}} - H\) relationship for a given material.

In order to obtain the correspondence between indentation creep and uniaxial creep, the relationship between hardness and creep stress is needed. Here the creep stress σ is taken as (Ref 24, 25, 31-35)

$$\upsigma = \frac{H}{3}.$$
(5)

The \(\dot{\upvarepsilon }_{\text{I}} - \upsigma\) relation thus obtained, from both the constant-load hold method and constant indentation-strain-rate method, for any given material will be contrasted against its uniaxial counterparts (\(\dot{\upvarepsilon }_{\text{s}} - \upsigma\) relation), and the difference can then be quantified.

In the numerical model, the Young’s modulus and Poisson’s ratio of the elastic diamond indenter are 1141 GPa and 0.07, respectively. The test materials are taken to be elastic-creep solids with a true time scale. For the comparison study of the constant-load hold and constant indentation-strain-rate methods, four different material models are considered: pure Sn at 25 °C, pure Sn at 120 °C, Sn-3.9Ag-0.7Cu alloy at 25 °C, and Sn-3.9Ag-0.7Cu alloy at 120 °C, all in their bulk form. Their experimentally measured uniaxial steady-state power-law creep response (Ref 36, 37), following Eq 2 and reproduced in Fig. 2, is used as the model input. In the multiaxial stress state, stress σ in Eq 2 is the von Mises effective stress and strain rate \(\dot{\upvarepsilon }_{\text{s}}\) is the equivalent creep strain rate, defined by

$$\dot{\upvarepsilon }^{\text{cr}} = \frac{\sqrt 2 }{3}\left[ {\left( {\dot{\upvarepsilon }_{1} - \dot{\upvarepsilon }_{2} } \right)^{2} + \left( {\dot{\upvarepsilon }_{2} - \dot{\upvarepsilon }_{3} } \right)^{2} + \left( {\dot{\upvarepsilon }_{3} - \dot{\upvarepsilon }_{1} } \right)^{2} } \right]^{1/2} ,$$
(6)

where \(\dot{\upvarepsilon }_{1}\), \(\dot{\upvarepsilon }_{2}\) , and \(\dot{\upvarepsilon }_{3}\) are the principal components of creep strain rate. The constitutive formulation is very similar to standard metal plasticity (Ref 38). Table 1 lists the elastic and creep parameters of the four models. Note that temperature does not explicitly exist in the simulations; its effect on material behavior is manifested by the different creep parameters.

Fig. 2
figure 2

Experimentally measured steady-state creep response for the four materials considered (re-created from the linear fit in Ref 36)

Full size image
Table 1 Material properties used in the finite element model (E: Young’s modulus, ν: Poisson’s ratio, Α: power-law creep coefficient, n: stress exponent), for the comparison study between the constant-load hold and constant indentation-strain-rate methods
Full size table

As described in introduction, a parametric analysis of indentation creep is also conducted for the constant indentation-strain-rate method. Here the stress exponent n from 1 through 10 and the constant A spanning many orders of magnitude are considered.

Results and Discussion

The Constant-Load Hold Analysis

Two separate runs were performed for each of the four Sn-based material models, one with a peak load of 50 μN and the other 100 μN. Consider pure Sn at 120 °C as an example. Figure 3 shows the simulated indentation load-displacement response for the two peak loads. It is evident that, during the constant-load stage, a significant increase in indentation depth is achieved and the higher peak load results in a deeper penetration over the 30-hour hold period. Figure 4(a) and (b) shows the contour plots of equivalent creep strain, defined as \(\mathop \smallint \nolimits \dot{\upvarepsilon }^{\text{cr}} dt\), in pure Sn at 120 °C, at the beginning and end of the hold period under 100 μN, respectively. Only the region close to the indentation site is included in the presentation. During initial loading, creep deformation has occurred (Fig. 4a), with the largest creep strain at the tip of the indentation. As the indenter sinks further during the 30 h hold, significant expansion of local creep field also takes place (Fig. 4b). The same observation holds true for the other material models.

Fig. 3
figure 3

Simulated indentation load-displacement curves for pure Sn at 120 °C under two different peak loads. The hold period is 30 h

Full size image
Fig. 4
figure 4

Contour plots of equivalent creep strain in the indented pure Sn at 120 °C, at the (a) beginning and (b) end of the constant 100 μN load hold period

Full size image

The constant-load hold method focuses exclusively on the creep behavior during the holding stage of indentation. The indentation depth (h)-time (t) response is directly taken from the indentation modeling data. An example is shown in Fig. 5, with pure Sn at 120 °C under both the 50 and 100 μN peak loads. The other three material models showed identical qualitative behavior, and thus are not shown here. For each curve, five points (times) were arbitrarily selected: 25, 350, 1.08 × 104, 6.02 × 104, and 1.08 × 105 s. The depth rates, \(\frac{dh}{dt}\), are then evaluated at these five points to obtain the indentation strain rates \(\dot{\upvarepsilon }_{\text{I}}\). The projected contact areas are evaluated by locating the corresponding contact edges from the deformed model configurations, so hardness H and thus stress σ can be calculated. Sufficient data are therefore in place to construct the \(\dot{\upvarepsilon }_{\text{I}} - \upsigma\) relationship for each material under a given peak load.

Fig. 5
figure 5

Simulated depth (h)-time (t) response for pure Sn at 120 °C under two different peak loads

Full size image

Figure 6 shows the simulated relationship between indentation strain rate (\(\dot{\upvarepsilon }_{\text{I}}\)) and creep stress (σ) for all four material models. The dashed lines and symbols represent the indentation peak loads at 50 and 100 μN, respectively. Also included in the figure (solid lines) are the uniaxial power-law creep relations based on experimental measurements (Ref 36, 37) and used as model input. Note that some of the input power-law lines in Fig. 6 are direct extensions of the experimental result shown in Fig. 2, for easier comparison with the indentation modeling result. The material models and simulation conditions considered in this study yield strain rates spanning from below 1 × 10−6 to above 1 × 10−3 s−1, and stresses from about 2 to 65 MPa. It is evident that the two different peak loads result in essentially the same linear appearance in all cases. The indentation-derived curves are also nearly parallel to the uniaxial creep response, which suggests nearly identical stress exponents (n) between indentation creep and uniaxial creep for the respective materials. The indentation-derived stress exponents are listed in Table 2. Comparing the n values in Tables 1 and 2, it is confirmed that the stress exponent may be accurately obtained through the constant-load hold indentation test.

Fig. 6
figure 6

Relationship between indentation strain rate (\(\dot{\upvarepsilon }_{\text{I}}\)) and creep stress (σ), obtained from the indentation modeling using the constant-load hold method. (The dashed lines and symbols represent peak loads at 50 and 100 μN, respectively.). The solid lines represent the uniaxial power-law creep relations, based on experiments and used as model input

Full size image
Table 2 Stress exponent n and the ratio \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\), obtained from indentation modeling using the constant-load hold method
Full size table

The satisfactory correlation of stress exponents shown above is widely known. However, as described in introduction, the relationship of creep coefficients A resulting from indentation and uniaxial tests is much less reported in the literature. In the present context, such a relation may be expressed as the ratio of uniaxial strain rate and indentation strain rate, \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\), which quantifies the extent of translating the indentation-measured curve to match the uniaxial curve as shown in Fig. 6. The calculated strain rate ratios are given in Table 2. It is observed that, for a given material under the two different peak loads, the ratio \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) exhibits reasonable consistency, with the largest discrepancy of 6% occurring in the case of SnAgCu at 120 °C. When comparing all four Sn-based material models, the values of \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) span from about 0.31 for pure Sn at 120 °C (the weakest material among the four) to 0.42 for SnAgCu at 25 °C (the strongest among the four). In fact, there is a clear trend of increasing \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) as the creep resistance of the material increases.

The Constant Indentation-Strain-Rate Analysis

Attention is now turned to extracting the power-law creep parameters using the constant indentation-strain-rate method. Again, the same four Sn-based material models are used. Figure 7 shows the simulated load-displacement curves for SnAgCu at 25 °C, at four different indentation strain rates from 1 × 10−7 to 1 × 10−4 s−1. A significant rate effect is revealed—a higher indentation strain rate results in a harder response. The other three materials showed the same load-displacement trend and are not presented here.

Fig. 7
figure 7

Simulated load-displacement response of SnAgCu at 25 °C, under the four indicated indentation strain rates (\(\dot{\upvarepsilon }_{\text{I}}\))

Full size image

Representative contour plots in the deformed configuration are presented in Fig. 8 and 9. Figure 8(a) and (b) shows the equivalent creep strain fields in SnAgCu at 25 °C, with the prescribed indentation strain rates of 1 × 10−4 and 1 × 10−7 s−1, respectively, when the indentation displacement is at 4 μm. It can be seen that the creep strain fields are virtually indistinguishable for the two cases, irrespective of the widely different strain rates. This is to be expected, since the two cases are in the same overall deformation state (same indentation depth). As the indentation depth increases, the creep zone also increases. But when the two cases with different strain rates reach the same depth, the inelastic deformation fields are identical. The rate effect is better manifested by the von Mises effective stress field, as shown in Fig. 9. Here the same material, strain rates, and indentation depth as shown in Fig. 8 are considered. It is clear that, with a greater applied indentation strain rate, the material volume directly underneath the indenter experiences higher stresses, thus giving rise to a harder response. It can also be seen that a harder material response results in a higher stress state in the elastic indenter.

Fig. 8
figure 8

Contour plots of equivalent creep strain for the model SnAgCu at 25 °C under the indentation strain rates of (a) 1 × 10−4 s−1 and (b) 1 × 10−7 s−1, when the indentation displacement is at 4 μm

Full size image
Fig. 9
figure 9

Contour plots of von Mises effective stress (in MPa) for the model SnAgCu at 25 °C under the indentation strain rates of (a) 1 × 10−4 s−1 and (b) 1 × 10−7 s−1, when the indentation displacement is at 4 μm

Full size image

The indentation hardness, calculated based on Eq 3, as a function of indentation depth is shown in Fig. 10 for SnAgCu at 25 °C under the four different indentation strain rates. It can be seen that hardness increases as the strain rate increases, and the hardness value stays nearly constant at any given strain rate. This observation illustrates that a steady state is established using the constant indentation-strain-rate approach—a feat that the constant-load hold was unable to accomplish due to the continuous change in hardness and strain rate (Ref 14). These observations hold true for the other three Sn-based material models.

Fig. 10
figure 10

Simulated hardness as a function of indentation depth for SnAgCu at 25 °C. Results from the four different indentation strain rates are included

Full size image

The simulated relationship between indentation strain rate and creep stress is plotted in Fig. 11 (dashed lines with symbols). Also included in the figure (solid lines) are the uniaxial power-law creep relations for the four materials based on experimental measurements (Ref 36, 37) and used as model input. Within the range of strain rates considered, the creep stress values of the four materials cover a range from 1.5 to over 50 MPa. As in the constant-load hold method, the constant indentation-strain-rate curves are all generally linear, and are nearly parallel to the corresponding uniaxial creep response. The slopes of the four dashed lines, listed in Table 3, are the indentation-derived stress exponent n. Comparing the n values in Tables 1 and 3, it is clear that the stress exponent for a given material under uniaxial creep is essentially the same as that obtained from the constant indentation-strain-rate test.

Fig. 11
figure 11

Relationship between indentation strain rate and creep stress, obtained from the constant indentation-strain-rate modeling (dashed lines with symbols). The solid lines represent the uniaxial power-law creep relations, based on experiments and used as model input

Full size image
Table 3 Stress exponent n and the ratio \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\), obtained from indentation modeling using the constant indentation-strain-rate method
Full size table

As before, the parallel nature of the indentation and uniaxial creep behaviors observed in Fig. 11 makes possible a meaningful determination of the quantitative difference between the indentation strain rate (\(\dot{\upvarepsilon }_{\text{I}}\)) and uniaxial strain rate (\(\dot{\upvarepsilon }_{\text{s}}\)). The calculated strain rate ratios \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) are also listed in Table 3. A remarkably consistent value of 0.33 is found in all four cases. The finding implies that, when the indentation strain rate versus creep stress is plotted after indentation creep testing, one may vertically translate the curve to 33% of its strain rate position to yield the “uniaxial” creep response of the material.

Of the four Sn-based material models investigated thus far, the constant indentation-strain-rate method results in a more uniform response than the constant-load hold method. In Table 3, the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratios stay essentially constant but in Table 2 there is a trend of increasing \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) with the increase in creep resistance. It remains to be seen if the consistent \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio of 0.33 with the constant indentation-strain-rate method still holds true, for materials displaying different power-law creep properties (i.e., different combinations of A and n in Eq 2). An expanded parametric modeling analysis is therefore carried out, as presented in the section below.

Parametric Analysis Using the Constant Indentation-Strain-Rate Method

The same constant indentation-strain-rate approach employed in the previous section is used, with the only varying input being the power-law creep parameters. Aside from the four Sn-based systems considered above, the material models being investigated were artificially chosen with values of A and n spanning virtually the entire possible range for typical metallic materials. A total of 60 simulations were conducted, yielding 15 \(\dot{\upvarepsilon }_{\text{I}} - \upsigma\) relations each with four strain rate conditions. These \(\dot{\upvarepsilon }_{\text{I}} - \upsigma\) relations were then used to calculate both the indentation-derived stress exponent and the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio as was done previously. The results are organized into a “map” form, where the abscissa and ordinate are parameters n and A, respectively, used as model input.

Figure 12 shows the simulated 15 sets of n (indentation-derived) and R (the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio) values distributed in the domain of input parameter n (uniaxial) and A (uniaxial). It can be seen that the strain rate ratio R tends to increase from the lower left region to the upper right region of the map. The entire domain is roughly divided into five zones, for ease of discussion, based on the R value. Note that Zone V (the lower left region) is virtually unattainable by creep-deforming materials under reasonable loading conditions, since the steady-state creep would be extremely slow. For example, the upper left and lower right open circles in this zone, when loaded by 100 MPa of uniaxial stress, will possess a steady-state creep rate of about 1 × 10−10 and 1 × 10−14 s−1, respectively. The materials thus behave elastically unless the applied stress becomes exceedingly large. The indentation-derived stress exponents n for these open circles are also drastically different from the corresponding uniaxial values. As one moves away from Zone V, the indentation method is seen to produce accurate n values.

Fig. 12
figure 12

Indentation-derived stress exponent n and strain rate ratio R (\(= \dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\)), obtained from the constant indentation-strain-rate simulations, plotted within the domain defined by the uniaxial power-law creep parameters n and A used as model input. The map is divided into five zones based on the R value. Zone V is virtually unattainable by actual materials under realistic loading conditions

Full size image

Figure 12 reveals that in Zones I, II, and III, the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratios are all between about 0.27 and 0.35. The four Sn-based material models considered in section 3.2 all fall within Zone II (with R being approximately 0.33). It is worth identifying the positions for actual materials from the limited experimental characterizations mentioned in introduction, and comparing them with the present numerical result. The position of amorphous selenium (Se) at above its glass transition temperature studied by Poisl et al. (Ref 24) has a uniaxial n of unity, and is located approximately at the same far-upper-left point within Zone IV in Fig. 12. The measured R was 0.09, which is somewhat below the simulated value of 0.159. However, it is noted that both the measured and simulated R ratios showed relatively low values, and the material is located near the less well-defined region on the chart. Next, the Al-Mg solid solution alloy studied by Takagi et al. (Ref 25) has a uniaxial n of 3.2, and its uniaxial creep response at between 636 and 773 K is located near the upper region of Zone III close to the boundary with Zone IV. The measured R value was 0.28, which is in good agreement with the modeling result.

Figure 12 illustrates that the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio is not a “universal” constant, so the vertical distance between the indentation-measured and uniaxial strain rate-stress lines (as shown in Fig. 11) is not fixed and will depend on the material. Nevertheless, Fig. 12 shows that this distance (expressed as R, the \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio) is around 0.3 for a vast range of A and n, which can serve as a quick estimate of power-law creep response from the indentation creep measurement. Since indentation creep generally returns an accurate stress exponent n, an “unknown” material can thus be tested with its horizontal position in Fig. 12 (with the obtained n) established. This will help limit the numerical range of R, which in turn can provide a more accurate determination of the uniaxial power-law creep behavior based on the measured indentation strain rate-stress response.

Conclusions

Numerical finite element modeling was carried out to examine the correlation between indentation creep and conventional uniaxial creep, for metals following the steady-state power-law creep behavior. The constant-load hold indentation method and the constant indentation-strain-rate methods were assessed, using pure Sn and a SnAgCu alloy at two different temperatures as the model system. Both methods were able to yield an accurate stress exponent n. The constant indentation-strain-rate method was able to generate more uniform creep coefficients A than the constant-load hold method, thus rendering more consistent ratios of uniaxial strain rate and indentation strain rate (\(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\)). Steady-state creep can also be established with the constant indentation-strain-rate method. A parametric analysis taking into account a wide span of uniaxial A and n values was performed using the constant indentation-strain-rate method. It was found that, except for the combinations of A and n that lead to essentially a non-creeping response, the indentation measurement gives rise to accurate stress exponents throughout the entire range. The \(\dot{\upvarepsilon }_{\text{s}} /\dot{\upvarepsilon }_{\text{I}}\) ratio displays an increasing trend toward greater values of A and n, but is generally between 0.27 and 0.35 for most of the materials. The graphical presentation of the parametric analysis offers practical guidance in determining the uniaxial power-law creep response from the indentation technique.