Introduction

Magnesium-based alloys containing rare earth metals (Mg-RE alloys) are important structural materials, as they combine low density with high-strength properties. This makes them particularly attractive for industry, especially in cases where the low weight of constructions is critical, as in aircraft and space apparatus construction (Ref 1, 2). One of the remarkable features of alloys is the significant difference made by individual rare earth metals when they are added to magnesium. Besides the classical WE54 and WE43 alloys, the most successful Mg-RE alloy developed to date being the novel alloy systems (e.g., Mg-Gd-Y, Mg-Gd-Nd and Mg-Dy-Nd) also gained much attention from the researchers (Ref 3-5). Zhang et al. (Ref 6) studied the microstructure and mechanical property of Mg-13Gd-5Er-1Zn-0.3Zr alloy, and their research showed that, after hot extrusion and aging treatment, the Vickers hardness, ultimate tensile strength, and yield strength increase to 125.6, 410.9 MPa, and 338.8 MPa at ambient temperature. Peng et al. (Ref 7) studied the Mg-12Gd-4Y-2Nd-0.3Zn-0.6Zr alloys and made a conclusion that the best mechanical properties are observed after the T6 heat treatment. Of all the Mg-RE alloys, the most prominent alloys are Mg-Gd-Y-Zr series (Ref 8). The addition of Zn to the Mg-Gd-Y-Zr alloys can significantly enhance age hardening of the alloy, and different types of long periodic stacking ordered (LPSO) structures including 18R, 24R, 10H, 14H et al. can easily form during solidification or by heat treatment in many Mg-RE-Zn series (Ref 9-12). Yamasaki et al. (Ref 13) have developed a hot-extruded Mg-2.3Zn-14Gd (wt.%) alloy which displays a highest tensile proof strength (345 MPa) and better elongation (6.3%) due to precipitation of a coherent 14H LPSO structure from the supersaturated α-Mg matrix. In addition, Nie et al. (Ref 14) reported that addition of Zn to Mg-6Gd-0.6Zr alloy could improve the mechanical and creep properties, contrasting with Zn-free alloys. The notable improvement of mechanical properties is attributed to a dense and uniform distribution of Mg5Gd phase.

The microstructures and mechanical properties of the Mg-Gd-Y-Zn-Zr alloy have been investigated by the previous research (Ref 15-17). However, only little data about hot deformation parameters of the homogenized as-cast Mg-Gd-Y-Zn-Zr alloy can be obtained and thus limits their applications. Therefore, the present paper has been initialized to study the plastic flow behaviors of the homogenized as-cast Mg-Gd-Y-Zn-Zr alloy by constitutive models and processing maps.

Constitutive models and processing maps are useful methods to study the flow behaviors and workability of alloys. By these two methods, various magnesium alloys, such as Mg-3Al, Mg-Zn-Y-Zr, Mg-3Sn-1Ca, and ZE41A have been studied. In former papers, constitutive models usually predicted the peak stress only. But in this paper, the constitutive model with a softening factor can predict the stress at any strain. Besides, Prasad criterion was chosen to build processing maps because it is accurate and easy to calculate, which makes it widespread in application.

Materials and Experimental Procedure

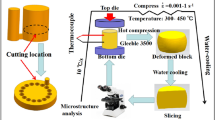
Actual composition of the studied alloy was Mg-13Gd-4Y-2Zn-0.6Zr (wt.%). It was prepared by using semi-continuous casting. In order to offset the as-cast segregation, the as-cast ingot was homogenized at 520 °C for 12 h. The cylindrical samples with a diameter of 8 mm and a length of 12 mm were machined out from as-cast ingot. The cylindrical surface of samples was polished before compression testing. Prior to be compressed, a sample was conductively heated to the designed temperature at a heating rate of 5 °C/s and held at the temperature for 180 s to ensure that the temperature was homogeneous throughout the samples. Uniaxial compression tests were conducted on a Gleeble-3500 simulator at constant true strain rates in the range of 0.001-0.5 s−1 and temperature range of 300-480 °C. In order to reduce the deformation friction, a graphite lubricant was used between the sample and the crosshead. The samples were deformed up to 50% height reduction. After deformation, all samples were quenched in water immediately to maintain deformed microstructures.

The samples for microstructure analysis were sectioned in the center parallelling to the compression axis. Photomicrographs were taken with ZEISS metallographic microscope. The observation specimens were cut out from the middle part of the deformed samples. The etching solution was the solution of 4 vol.% HNO3 with ethanol.

Results and Discussion

Flow Stress Behavior

Flow stress-strain curves for the magnesium alloy at different deformation temperatures and strain rates are shown in Fig. 1. The flow stress as well as the shape of the flow curves is sensitively dependent on temperature and strain rate. The general characteristics of the flow curves are similar at all deformation conditions, i.e., the flow stress increases to a peak (corresponding to σp) and then decreases to a steady state, suggesting a typical dynamic recrystallization (DRX) accompanied plastic flow process (Ref 18). Especially, this trend is more noticeable in low temperature region (350 °C) and high strain rates (0.1-0.5 s−1). At any strain rates, the peak stress and peak strain increase along with the decrease of temperature, suggesting that the working hardening effect is more significant at low temperatures. At a given temperature, the peak stress increases along with the increase of strain rate, indicating that the release of work hardening factors like dislocation accumulation is more effective during slower deformation processes (Ref 19). On the other hand, the steady stress is reached at a certain strain that decreases with the increase of temperature and decrease of strain rate. This suggests that DRX proceeds more rapidly at higher temperatures and more extensively at slower strain rate. At strain rate of 0.5 s−1, some serrations in stress-strain curve were obtained because of discontinuous dynamic recrystallization (DDRX) mechanism (Ref 20). However, the optimum parameters for forging process cannot be obtained only relying on the stress-strain curves, and constitutive model is also important for the numerical simulation of the alloy.

Fig. 1
figure 1

True stress-true strain curves of as-cast Mg-Gd-Y-Zn-Zr alloy under different strain rates with temperatures: (a) 300 °C; (b) 350 °C; (c) 400 °C; (d) 450 °C; (e) 480 °C

Full size image

Deformation Constitutive Equation

Based on the characteristics of the flow curves shown in Fig. 1, it has been clarified that the deformation behavior of Mg-13Gd-4Y-2Zn-0.6Zr alloy is typically accompanied by DRX. Therefore, the peak stress on the flow curve should be used in the hyperbolic sinus law (Eq 1, (Ref 21)) to study the mechanical behaviors of the alloy during the thermomechanical processes in this study (Ref 22).

$$Z = \dot{\upvarepsilon }\exp \left( {{Q \mathord{\left/ {\vphantom {Q {(RT)}}} \right. \kern-0pt} {(RT)}}} \right) = A\left( {\sinh \left( {\upalpha \upsigma } \right)} \right)^{n} ,$$
(1)

where A is a material constant, α a material constant, n the stress exponent, \(\dot{\upvarepsilon }\) the strain rate, σ the flow stress, Q the thermal activate energy, 8.314 J/mol K, R the gas constant, T the absolute temperature, and Z is the Zener-Hollomon parameter.

Firstly, the relationship among peak stress, peak strain, and Z can be found.The researchers (Ref 23) expressed Eq 1 as follows for the low stress level (ασ < 0.8):

$$Z = \dot{\upvarepsilon }\exp \left( {{Q \mathord{\left/ {\vphantom {Q {(RT)}}} \right. \kern-0pt} {(RT)}}} \right) = A\left[ {\sinh \left( {\upalpha \upsigma } \right)} \right]^{n} \approx A_{1} \upsigma^{{n_{1} }} .$$
(2)

The researchers (Ref 23) expressed Eq 1 as follows for the high stress level (ασ > 0.8):

$$Z = \dot{\upvarepsilon }\exp \left( {{Q \mathord{\left/ {\vphantom {Q {(RT}}} \right. \kern-0pt} {(RT}})} \right) = A\left[ {\sinh \left( {\upalpha \upsigma } \right)} \right]^{n} \approx A_{ 2} { \exp }\left( {\upbeta \upsigma } \right),$$
(3)

where A 1 and A 2 are material constants. The approximate α is:

$$\upalpha = \upbeta /n_{1} .$$
(4)

To simplify the equations, natural logarithms were applied to both sides of Eq 2 and 3, and Eq 2 and 3 can be expressed as following, respectively:

$$\ln \,\upsigma = \frac{{\ln \,\dot{\upvarepsilon }}}{{n_{1} }} - \frac{{\ln \,A_{1} }}{{n_{1} }} + \frac{Q}{{RTn_{1} }},$$
(5)
$$\upsigma = \frac{{\ln \,\dot{\upvarepsilon }}}{\upbeta } - \frac{{\ln \,A_{2} }}{\upbeta } + \frac{Q}{RT\upbeta }.$$
(6)

From the study of McQueen (Ref 24), it is feasible to regard the peak stress σp as σ for calculations of Eq 5 and 6. Utilizing the experimental data, the plots that describe the relationship between peak stress and strain rate according to the power law and exponential law are given in Fig. 2(a) and (b), respectively. Based on the best-fitting lines in the plots, the values of β and n 1 are deduced to be 0.07364 and 6.81966, respectively.

Fig. 2
figure 2

Relationship between peak stress and strain rate according to the (a) power law and (b) exponential law, respectively

Full size image

In this situation, the mean value of α was obtained as 0.009205 MPa−1 according to Eq 4.

Taking the logarithm for both sides of the above Eq 1, we have

$$\ln \,\,\dot{\upvarepsilon } = \,\ln \,A - {Q \mathord{\left/ {\vphantom {Q {(RT)}}} \right. \kern-0pt} {(RT)}} + n\,\,\ln \,\left( {\sinh \left( {\upalpha \upsigma_{p} } \right)} \right).$$
(7)

From Eq 7, for a particular strain rate, the Q value could be obtained as follows:

$$Q = R\left[ {\frac{{\partial \left( {\ln \,\left( {\sinh \left( {\upalpha \upsigma_{p} } \right)} \right)} \right)}}{{\partial \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 T}}\right.\kern-0pt} \!\lower0.7ex\hbox{$T$}}} \right)}}} \right]_{\upvarepsilon } \cdot \left[ {\frac{{\partial \,\ln \,\dot{\upvarepsilon }}}{{\partial \left( {\ln \,\left( {\sinh \left( {\upalpha \upsigma_{p} } \right)} \right)} \right)}}} \right]_{T} .$$
(8)

According to Eq 8, the relationship between \(\ln (\dot{\upvarepsilon })\) and ln (sinh (ασ)) at different temperatures, and that between ln (sinh (ασ)) and 1000/T at different strain rates are illustrated in Fig. 3(a) and (b), respectively. The average Q value of homogenized as-cast Mg-13Gd-4Y-2Zn-0.6Zr alloy is 273.42 kJ/mol, which is higher than many other Mg alloys, such as AZ80 and ZK60, whose Q values are 165 kJ/mol and 158 kJ/mol, respectively. Then, a conclusion could be received, addition of rare earth elements would increase the value of Q. Substituting the obtained values of α and Q into Eq 1, the relationship between ln Z and ln (sinh (ασ)) is plotted in Fig. 4. From the slope of the fitting line, the exponential coefficient n is to be 6.81966. Meanwhile, the intercept of fitted curves in Fig. 4 is accepted as the value of ln A = 42.561345, of which A value is obtained as 3.049 × 1018 s−1.

Fig. 3
figure 3

Standard analysis of the constitutive equation. (a) \(\ln (\dot{\upvarepsilon })\)-ln (sinh (ασ)); (b) ln (sinh (ασ))-ln (sinh (ασ))

Full size image
Fig. 4
figure 4

The relationship between ln (sinh (ασ)) and ln Z

Full size image

Substituting the measured values of A, a, n, and Q into Eq 1 the constitutive model for the hot compression of test alloy is extracted as follows:

$$\dot{\upvarepsilon } = 3.049 \times 10^{18} \left( {\sinh \left( {0.009205\upsigma } \right)} \right)^{6.81966} \exp \left( {{{ - 32887} \mathord{\left/ {\vphantom {{ - 32887} T}} \right. \kern-0pt} T}} \right).$$
(9)

However, there is a lack of strain item in Eq 9 that could not express the softening degree caused by DRX during hot compression. It is valuable that a constitutive model can express the dependence of the flow stress not only on strain rate and temperature but also on the strain.

According to Liu et al. (Ref 25), the peak stress is taken as the function of the temperature and the strain rate according to the creep equation. Since the DRX is a thermally activated process, the recrystallized volume fraction can be regarded as the function of strain through Avrami equation. The descending of flow stress is mainly dominated by the recrystallized volume fraction. So, the flow stress at different strain is regarded as the function of the peak stress and the strain. They proposed a new model to describe the dependence of the flow stress on various temperatures, strain rates and strains, and the new model is expressed as,

$$\upsigma = \exp \left[ {\uplambda (\upvarepsilon - \upvarepsilon_{p} )^{2} \ln \upzeta \upvarepsilon + \ln \upsigma_{p} } \right].$$
(10)

The peak stress σp can be written as a function of Zener-Hollomon parameter, considering the definition of the hyperbolic law:

$$\upsigma_{P} = \frac{1}{\upalpha } \cdot \,\ln \,\left( {\left( \frac{Z}{A} \right)^{\frac{1}{n}} + \left( {\left( \frac{Z}{A} \right)^{\frac{2}{n}} + 1} \right)^{\frac{1}{2}} } \right).$$
(11)

The relationship of the peak strain ɛP (corresponds to σp in the flow stress-strain curves) and Z is illustrated in Fig. 5. We can find that it is suitable to regard the peak strain ɛP and Z as follows:

$$\ln \upvarepsilon_{P} = {{\left( {\ln Z - C_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {\ln Z - C_{1} } \right)} {C_{2} }}} \right. \kern-0pt} {C_{2} }},$$
(12)

where C 1 is 0.17048; C 2 is −7.22652.

Fig. 5
figure 5

The relationship between ɛp and Z

Full size image

In Eq 10 there contains only two parameters ζ, λ. ζ is taken as an adjustment parameter by which the regular law can be obtained at various deformation temperatures. λ depends on deformation temperature and strain rate. In order to analyze the softening caused by DRX, the relationships between the strain and the difference of stress and stress peak are plotted in Fig. 6(a) and (b).

Fig. 6
figure 6

The relationships among (ln σ − ln σp)/ ln ζɛ, ∂ [(ln σ − ln σp)/ ln ζɛ]/ ∂ ɛ and ɛ at the strain rate of 0.5 s−1: (a) (ln σ − ln σp)/ ln ζɛ − ɛ; (b) ∂ [(ln σ − ln σp)/ ln ζɛ]/ ∂ ɛ − ɛ

Full size image

In order to facilitate the following derivation, a ‘softening-factor’ was introduced, which was defined as (Ref 25):

$$\upeta^{ * } = \frac{{\ln \upsigma - \ln \upsigma_{p} }}{{\ln \left( {\upzeta \upvarepsilon } \right)}}.$$
(13)

After analysis, it can be found that, when ζ is less than or equal to 0.7, η* and ɛ meet the relationship as follows:

$$\frac{{\ln \upsigma - \ln \upsigma_{\text{p}} }}{{\ln \left( {\upzeta \upvarepsilon } \right)}} = \omega \left( {\frac{{\upvarepsilon - \upvarepsilon_{\text{p}} }}{{\upvarepsilon_{\text{p}} }}} \right)^{2} ,$$
(14)

where ∂ η*/ ∂ ɛ = aɛ − b (see Fig. 6b), ω = b 2/2a, λ = a/2

Apparently, Eq 14 can be rewritten as Eq 10. Theoretically, the equation with two unknowns can be solved just needing two equations. There are so many data obtained from hot compression tests that ζ and λ could be obtained by the least squares regression method as 0.6815 and 1.5980, respectively. Comparisons between the model prediction results and experimental results are shown in Fig. 7, which indicates that the proposed model of flow stress is in good agreement with the experimental tests data.

Fig. 7
figure 7

Comparison of modeling calculated results with experimental result for flow stress at strain rate of 0.5 s−1

Full size image

Processing Map

Processing map has been proven to be a useful tool for the optimization of hot working processes for a wide range of metals and their alloys, like titanium alloy, aluminum alloy (Ref 26, 27), which are constructed using the principles of dynamic material model. In this model, the workpiece under hot working conditions is considered to be a dissipater of power, whose dissipative process is irreversible. Efficiency of power dissipation of a nonlinear dissipater can be expressed as a dimensional parameter η, which is the main factor affecting the evolution of the microstructure:

$$\upeta = \frac{J}{J_{\max}} = \frac{2m}{m + 1},$$
(15)

where the J co-content represents the power dissipation through microstructure transition, such as dynamic recovery, DRX, superplastic flow, phase transformations, as well as damage of material. J max is the maximum dissipation and strain rate sensitivity of flow stress m is given by:

$$m = \frac{\partial J}{\partial G} = \frac{\partial \,\ln \upsigma }{{\partial \,\ln \dot{\upvarepsilon }}},$$
(16)

where σ is the flow stress and\(\dot{\upvarepsilon }\) is the strain rate. G content represents the power dissipation due to plastic deformation, most of which transforms into viscoplastic temperature rise.

The variation of the efficiency with temperature and strain rate constitutes a power dissipation map, which exhibits different domains that may be correlated with specific microstructure processes, such as DRX and dynamic recovery, but the workability cannot be described completely. An instability criterion applied to continuum mechanics of large plastic flow is obtained by utilizing the principle of maximum rate of entropy production and given by (Ref 28):

$$\upxi (\dot{\upvarepsilon }) = \frac{{\partial \,\ln ({m \mathord{\left/ {\vphantom {m {(m + 1)}}} \right. \kern-0pt} {(m + 1)}})}}{{\partial \,\ln \dot{\upvarepsilon }}} + m < 0,$$
(17)

where ξ is the instability parameter, which varies with the deformation temperature and strain rate. The instability map can be obtained by plotting ξ at different temperatures and at different strain rates where ξ is negative. The flow instabilities are mainly in the form of adiabatic shear bands or flow localizations in the microstructure.

Then, the processing map can be obtained by combining the power dissipation map and instability map. The processing map is obtained at different strains on the basis of the flow stress data at different temperatures and strain rates. Firstly, according to Eq 16, strain rate sensitivity at different temperatures and strain rates and constant strain can be obtained by functional relation between ln σ and \(\ln \dot{\upvarepsilon }\) matching by cubic spline function. Then, power dissipation map can be plotted by efficiency of power dissipation that can be calculated by Eq 15. In a similar way, instability map can be plotted by the continuum criterion given by Eq 17. The processing maps are obtained by a superimposition of the instability maps over the power dissipation maps.

The processing maps of the test alloy obtained at a strain of 0.3, 0.5, and 0.7 are shown in Fig. 8. The magnitudes in the processing maps represent η and the gray regions represent the instable domain.

Fig. 8
figure 8

The processing map at different strains: (a) ε = 0.3; (b) ε = 0.5; (c) ε = 0.7

Full size image

According to the processing maps, following rules can be obtained: η increases with the decrease of strain and the increase of temperature. The maximum is from 0.45 to 0.49 at strain of 0.3 to 0.5, and then they stay constant approximately, until strain becomes 0.7. At strain of 0.3, the maximum η occurs in two domains in Fig. 8(a): domain I at 450 °C, 0.001 s−1, domain II at 480 °C, 0.01 s−1. As the strain increases, domain I and domain II move to the lower temperature regions.

In the present work, the optimum parameters were investigated based on processing map at strain of 0.7. According to the previous study (Ref 29), for the metals with low stacking fault energy, such as magnesium alloy, the main deformation mechanism would be dynamic recover at η of about 0.2~0.3, and then DRX would take place with η higher than 0.3.

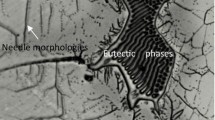
The microstructure at different η is shown in Fig. 9, and the η of which is 0.3, 0.45 (domain I), and 0.48 (domain II), respectively. In Fig. 9(a), some twinning exits in the grains, and there are few fine grains. In Fig. 9(b), a small amount of fine grains could be seen easily at grain boundary and twining grain boundary. Figure 9(c) shows no twining grain but obvious and abundant fine grains, whose average diameter is 40 μm. Therefore, a conclusion could be received that the higher η, the more obvious recrystallization, and the better grain refinement. Combining a microstructure analysis and process maps, we can get the conclusion that the optimum temperature and strain rate for hot working of the homogenized as-cast alloy were 480 °C and 0.01 s−1, respectively.

Fig. 9
figure 9

The microstructure at different conditions with true strain of 0.7: (a) T = 350 °C, \(\dot{\upvarepsilon }\) = 0.001 s−1; (b) T = 400 °C, \(\dot{\upvarepsilon }\) = 0.001 s−1; (c) T = 480 °C, \(\dot{\upvarepsilon }\) = 0.01 s−1

Full size image

Figure 8(c) shows that instable region consists of domain III and domain IV. The condition of domain III is 350-400 °C/0.1-0.01 s−1, and condition of domain IV is 450-480 °C/0.1 s−1. The microstructure of instable region could be seen in Fig. 10. Generally, instable phenomenon results from adiabatic shear band, flow localization, wedge cracking, and interspace between particles and matrix. At low temperature and high strain rate conditions, the energy of plastic deformation could not been effectively transmitted to other regions, which leads to higher temperature and lower flow stress at some points. Then deformation concentrate at these points and flow localization occur accompanied by microcracks. With continuous deformation, the microcracks propagation causes sample fracturing. The angle between the crack direction and compressive axis is about 45°, in Fig. 10(a). At high temperatures, the grain boundary and phase boundary could slip easily, leading to stress concentration and interface cracking (Ref 30, 31), in Fig. 10(b). If strain rate increases, making the slip rate of α-Mg matrix greater than interface, the influence of interface slip decreases and even no cracking would take place. If strain rate becomes lower, leaving enough time to release the concentrated stress formed by dislocation pile-up, the cracking also would not occur.

Fig. 10
figure 10

The microstructure of two instability regions with true strain of 0.7: (a) T = 350 °C, \(\dot{\upvarepsilon }\) = 0.1 s−1; (b) T = 450 °C, \(\dot{\upvarepsilon }\) = 0.1 s−1

Full size image

Verification of Processing Parameters

Isothermal Precision Formation of Components

Based on the analysis of the hot deformation behavior and the processing map, the homogenized as-cast alloy was used to forge a component. The conical cup components (32 mm in wall thickness, 315 mm in outer diameter, and 307 mm in height) were forged by the isothermal formation, which keeps the temperature steady to improve the plasticity of magnesium alloy. Based on the microstructure analysis and process maps above, the isothermal forging temperature is determined to be 480 °C, and the rate of upper die is 3 mm/s. Figure 11 shows a photograph of four successful Mg-13Gd-4Y-2Zn-0.6Zr alloy components produced by isothermal die forging formation. It is evident that the components had a very good surface finish and no problem was experienced in filling. This also suggests that the hot deformation parameter for the as-extruded Mg-13Gd-4Y-2Zn-0.6Zr alloy is reasonable.

Fig. 11
figure 11

Four successful Mg-13Gd-4Y-2Zn-0.6Zr alloy components

Full size image

Microstructure and Mechanical Property of the Component

Tensile bars were cut from homogenized Mg-13Gd-4Y-2Zn-0.6Zr alloy and formed a workpiece along the height direction. The bars’ diameter, gage length, and parallel length were 10, 50, and 60 mm, respectively. Tensile tests were conducted at a quasi-static strain rate of 10−3/s on a hydraulic MTS load frame. The homogenized bars’ ultimate tensile strength, yield strength, and elongation were 326 MPa, 295 MPa, and 5.9%, respectively, and the formed component’s ultimate tensile strength, yield strength, and elongation were 386 MPa, 331 MPa, and 6.3%, respectively. These data showed better mechanical properties of formed workpiece and verified the accuracy of hot deformation parameter (Fig. 12, 13)

Fig. 12
figure 12

The microstructure of billet after 520 °C/12 h homogenization

Full size image
Fig. 13
figure 13

The microstructure of the formed component along the height direction

Full size image

Conclusions

In the present work, several modeling approaches, including flow stress-strain curves, a constitutive model, and processing map were used to characterize the hot deformation behavior of the homogenized as-cast Mg-13Gd-4Y-2Zn-0.6Zr alloy in the temperature range of 300-480 °C and the strain rate range of 0.001-0.5 s−1.From the constitutive analysis, processing map, and the verification of processing parameter, the following conclusions have been drawn from this investigation:

  1. (1)

    The constitutive equation of the test alloy for hot deformation is

$$\dot{\upvarepsilon } = \,Z\,\exp \left( {{{ - Q} \mathord{\left/ {\vphantom {{ - Q} {(RT)}}} \right. \kern-0pt} {(RT)}}} \right) = A\left( {\sinh \left( {\upalpha \upsigma } \right)} \right)^{n} \exp \left( {{{ - Q} \mathord{\left/ {\vphantom {{ - Q} {(RT)}}} \right. \kern-0pt} {(RT)}}} \right)\, {\text{or }}\upsigma = { \exp }\left[ {\uplambda \left( {\upvarepsilon - \upvarepsilon_{p} } \right)^{ 2} \,{ \ln }\,\upzeta \upvarepsilon + \,{ \ln }\,\upsigma_{p} } \right],$$

where A = 3.049 × 1018  s−1, α = 0.009205 MPa−1, n = 6.81966, Q = 273420 J/mol, R = 8.314 J/mol K, ζ = 0.6815, λ = 1.5980, ɛP = exp ((ln Z − C 1)/(ln Z − C 1)C 2.C 2), C 1 = 0.17048, C 2 = −7.22652,

$$\upsigma_{P} = \frac{1}{\upalpha } \cdot \,\ln \left( {\left( \frac{Z}{A} \right)^{\frac{1}{n}} + \left( {\left( \frac{Z}{A} \right)^{\frac{2}{n}} + 1} \right)^{\frac{1}{2}} } \right)$$

(2)The optimum temperature and strain rate for hot working of the test alloy were 480 °C and 0.01 s−1, respectively. Furthermore, the flow instability occurred in the two areas where the temperature ranged from 350 to 480 °C at the strain rate of 0.01-0.1 s−1, and the temperature ranged from 450 to 480 °C with a strain rate of 0.1 s−1.(3)According to the determined hot deformation parameters, four components were successfully prepared, and the components possessed excellent surface quality, and the ultimate tensile strength, yield strength, and elongation of the component were 386 MPa, 331 MPa, and 6.3%, respectively.