Introduction

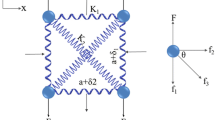
In recent years, lightweight metallic foams have been greatly used in high-performance load bearing applications. But irregular and inhomogeneous cell architecture of such materials leads to overly conservative design criteria, which makes them unsuitable to be used in several applications such as aerospace structures (Ref 1, 2). It is shown that it is possible to design cellular lattice structures which offer greater strength- and stiffness-to-weight ratios than those of traditional foam materials (Ref 3). Since the microstructure of such materials is regular, their mechanical properties can be adjusted to what is needed too. Until now, several architectures have been studied for cellular materials including octet truss (Ref 4), pyramidal (Ref 5), triangulated planar truss faces (Ref 5), BCC (Ref 6), BCC-Z (Ref 6), and F2FCC (Ref 6). It is demonstrated that ‘angle-ply’ lattices, whose struts are oriented in 45°, offer nearly optimized configurations under bending, compression, and shear loadings. Accordingly, BCC and BCC-Z microstructures have attracted a great interest. The repeating unit cells of these two architectures are shown in Fig. 1.

Fig. 1
figure 1

The repeating unit cell architecture of (a) BCC and (b) BCC-Z lattices

Full size image

Several attempts have been made to fabricate and to characterize the mechanical behavior of cellular lattice structures in the literature (Ref 1, 7-12). Since fabrication and characterization of cellular lattices are time consuming and expensive, predicting the mechanical properties of lattices before fabrication is of great importance. To this end, several models were developed using beam theory (Ref 4, 13), continuum element-based finite element method (Ref 14), and beam element-based finite element method (Ref 5, 13-16).

One of the most important difficulties for modeling the mechanical behavior of these lattices is existence of imperfections and defects in lattices’ struts. Micro-computed tomography images from the micro struts of cellular lattices show that the struts’ diameters are not uniform along their length. Also, some micro (nano) pores and un-melted or semi-melted powders may exist in struts. These imperfections and defects can severely affect the mechanical properties of lattices. Another important difficulty which may arise in modeling is to find suitable material parameters to be attributed to the bulk material. The mechanical properties of the lattices’ struts are influenced by the processing parameters in fabrication process (for example, laser parameters of the selective laser melting machine (Ref 17)). Accordingly, these properties can be sharply different from those of the raw powder used for fabrication (Ref 18).

Several attempts have been made to compel the above-mentioned difficulties. Tsopanos et al (Ref 17) fabricated some 316L stainless steel micro-lattice structures using selective laser melting method. To find suitable stress-strain response of the bulk material, they also fabricated some microstruts using the same processing parameters as those used for fabrication of the lattices and tested them in compression. The obtained elastic modulus of the strut was just about 3% of the bulk value which was far from the real elastic modulus of the strut. They corrected the obtained stress-strain curve of the strut by adjusting the elastic modulus of the lattice in a finite element analysis. This method was previously suggested by Mines (Ref 8). They then used this corrected stress-strain curve as the bulk material for modeling the mechanical behavior of the lattices. As the stress-strain response of the strut was obtained in tension, it did not include buckling of the strut. Labeas and Sunaric (Ref 6) modified the corrected stress-strain curve of the lattices’ struts presented in (Ref 8, 17) to include the effects of possible buckling in vertical struts. They used this modified stress-strain curve to predict the mechanical behavior of the lattice structures with three different cell topologies. Gumruk and Mines (Ref 19) realized that the difference between the measured elastic modulus and the real value reported in (Ref 8, 17) is due to slip between the strut and the grippers of a testing machine. To overcome this problem, they designed new grippers with the ability of eliminating the slip. They used a rapid araldite adhesive to glue a clip gage to the strut to measure the exact displacement of the strut between the clip gages. Using this method, they obtained the stress-strain curve of the struts and used them to simulate the mechanical compression of two lattices utilizing both theoretical and finite element analyses. Smith et al (Ref 20) used the same stress-strain response to predict the mechanical behavior of BCC and BCC-Z lattices using beam and solid finite element models. In the above-mentioned modeling approaches, no geometrical irregularities are needed to be included in the model because the measured stress-strain curve of the strut already represents the effects of imperfections within the microstruts (Ref 19). To consider variations in the struts’ diameter along their length, Campoli et al (Ref 21) developed some beam finite element models to study the elastic behavior of cellular lattices fabricated by selective laser melting and electron beam melting. Using statistical models, they implemented irregularities caused by the manufacturing process including structural variations of the architecture. Karamooz Ravari et al (Ref 22) proposed beam and solid finite element models to predict the mechanical stress-strain curve of polylactic Acid BCC-Z cellular lattice structures fabricated by fused deposition modeling. Their model was capable of considering the effects of variations in the struts’ diameter along their length.

To the authors’ information, there is no modeling approach in which the base material of the lattice’s struts and the imperfections are directly taken into account. In this paper, a new method is developed to obtain the stress-strain curve of a lattice structure using just the stress-strain response of the simple tension sample fabricated by the same processing parameters as those used for the lattice. To this end, first, a single strut of the lattice is modeled with its imperfections using the stress-strain curve of the base material in simple tension to obtain stress-strain response of that single strut. Then, this stress-strain response is attributed to the bulk material of the lattice in a unit cell model without any kind of imperfections and defects. To account for the material concentration in the vicinity of vertices, a higher elastic modulus is used in regions near the vertices. The obtained stress-strain curve of the lattice is shown to be in a good agreement with the experimental one. The elastic modulus of the lattice is obtained to be about 14.31 MPa, which is 90.87% of the experimental one, and the collapse strength is obtained to be nearly 0.446 MPa, which is about 17.14% higher than the experimentally measured value. At the end, the effects of single strut’s length and its micropores on the mechanical properties of the lattice are assessed. The results show that the strut’s length does not significantly affect the mechanical properties while the effects of micropores are crucial. Based on the obtained results, this paper presents a computationally efficient method for simulating mechanical properties of cellular lattice structures using just the stress-strain curve of simple tension samples.

Modeling Procedure

There might be several kinds of defects in lattices’ struts such as variable cross-sectional area along their length, wavy struts, and micro (nano) pores. These defects severely affect the mechanical properties of a lattice structure. Li et al (Ref 23) studied the effects of cell shape and variations in strut’s cross-sectional area on the elastic properties of three-dimensional open-cell foams. They showed that these imperfections have a significant influence on the mechanical properties of foams. Jang et al (Ref 24) found out that it is necessary to consider material distribution in the ligaments for obtaining nearly accurate results.

Figure 2 shows deformed configuration of a lattice structure fabricated by selective laser melting from 316L stainless steel. In this figure, two kinds of defects i.e., wavy struts and variable struts’ diameter can be easily observed. Although it is vital to consider geometrical details in modeling process, it can considerably increase the computational time.

Fig. 2
figure 2

Deformed configuration of a 316L cellular lattice structure fabricated by selective laser melting technique (Reprinted from Ref 19, with permission from Elsevier)

Full size image

Gumruk and Mines (Ref 19) showed that, to consider the effects of the struts’ imperfections, one can just assign the stress- strain response of single struts to the bulk material. Although this method provides good results, fabricating single struts can be time consuming and expensive. Moreover, a designer must be able to predict the mechanical properties of the lattice before fabricating any samples. It can help to choose an appropriate machine and processing parameters. The following subsections are proposed to achieve such a modeling scheme.

Strut Model

To model the struts’ geometry, it is supposed that each strut can be constructed by putting some spheres on each other. This method for building the struts’ geometry can be concluded from Fig. 2. Figure 3 shows a schematic two-dimensional view of the modeling process. As is seen, the axis of the strut is first determined. Some spheres with random diameters are then generated along the axis until the strut’s length (L s) is satisfied, and the over-plus regions are finally removed. Each sphere is supposed to intersect with its adjacent ones by a random penetration value (L p). To account for wavy strut’s defects, the center of each sphere is shifted to a random position in the plane whose normal vector is the strut’s axis.

Fig. 3
figure 3

Two-dimensional schematic of the strut’s modeling process

Full size image

The distance between the center’s position and strut’s axis is called “deviation from strut’s axis” throughout this manuscript and is indicated by A d. Equations 1 to 3 are used for calculating the spheres’ diameter, deviation from strut’s axis, and the spheres’ penetration value, respectively.

$$D = D_{\hbox{min} } + r(D_{\hbox{max} } - D_{\hbox{min} } )$$
(1)
$$A_{\text{d}} = r \cdot A_{{{\text{d}}\hbox{max} }}$$
(2)
$$L_{\text{p}} = \hbox{min} (R_{1} ,R_{2} ),$$
(3)

where D min and D max are the minimum and maximum values of the struts’ diameter, respectively, and are determined according to the SEM images. r is a random number between 0 and 1 from a Gaussian distribution, A dmax is the maximum value of the deviation from strut’s axis, and R 1 and R 2 are the radii of two spheres which should be penetrated to each other.

In this paper, the microstructural observations reported in (Ref 17) are used for constructing the geometry of the struts. It is reported that the struts’ diameter is in the range of D = 207 ± 10 µm for single struts. The A dmax is supposed to be 20 µm based on SEM images. Figure 4 shows a random model of the strut.

Fig. 4
figure 4

A random model of the lattice’s strut

Full size image

The next step for simulation of the strut’s mechanical behavior is to assign material parameters to the strut’s bulk material. In the present work, the stress-strain curve of a vertically generated tensile specimen fabricated by SLM (Ref 25) is used. The processing parameters of the sample are the laser power of 90 W and the layer thickness of 50 µm. The obtained samples are almost 99% dense, so their stress-strain response can be assigned to the bulk material. It should be noted that these material processing parameters are similar to those utilized for the fabrication of the desired lattice structure. Figure 5 shows the stress-strain curve of the sample after removing its initial non-linear part called the toe region. In this paper, isotropic, elastic-plastic, strain-rate independent material behavior together with J2 plasticity and isotropic hardening material model is applied. Table 1 shows all the utilized model parameters of the struts.

Fig. 5
figure 5

Stress-Strain curve used to define the bulk material of the single struts (Ref 25)

Full size image
Table 1 The utilized parameters for strut’s model
Full size table

As the strut should be tested in simple tension, one end of the strut is fixed in all directions while the other end is stretched to about 18% of its initial length (L s). The stress and strain of the strut are calculated using the following equations, respectively:

$$\sigma = \frac{4F}{{\pi D_{\text{av}}^{2} }}$$
(4)
$$\varepsilon = \frac{\delta }{{L_{\text{s}} }}$$
(5)

in which F is the reaction force, D av is the average diameter of the strut, and δ is displacement of the moving end of the strut.

Unit Cell Model

The mechanical properties of a cellular lattice structure with body-centered cubic microstructure are chosen for verifying the presented method. This lattice was fabricated by Gumruk and Mines (Ref 19). Figure 6 shows the unit cell used for modeling the cellular lattice structure. The cell size of the lattice is 2.5 mm, and the average diameter of the struts is about 218 µm. Smith et al (Ref 20) showed that the stress-strain curve of a BCC lattice can be predicted by just one unit cell. Thus, in this paper, only one unit cell is considered for modeling the mechanical properties of the lattice.

Fig. 6
figure 6

The unit cell details for modeling the mechanical properties of the BCC cellular lattice structure

Full size image

Since the struts of the unit cell are modeled using beam elements, an adaption of the stiffness in the vicinity of the vertices is needed. As shown in Fig. 7(a), each strut of the unit cell is partitioned into three regions. As proposed by Luxner et al (Ref 14), an elastic modulus of 1000 times greater than that of the bulk material is assumed for the regions in the vicinity of the vertices. These regions are called “vertex regions” in the rest of the paper. The length of each vertex region is found using SEM images such as the one depicted in Fig. 7(b). To this end, a circle is drawn, which covers all the material in the vertices. The diameter of the circle is measured to be about 2.4 × D av. Accordingly, the size of the vertex regions is supposed to be 1.2 × D av at each end of the struts.

Fig. 7
figure 7

(a) Partitioning the struts into three regions (2) Details on how to find the size of the vertex regions (Reprinted from Ref 11, with permission from Elsevier)

Full size image

As a unit cell is used for modeling the mechanical behavior of the lattice, periodic boundary conditions should be applied. For a beam finite element model, the periodic boundary conditions are as follows (Ref 26): let the three pairs of opposite bounding faces of the cell be (∂R i1, ∂R i2), i = 1, 3. Displacements and rotations of points on these faces are, respectively, denoted by (u i1, u i2) and (θ i1, θ i2), i = 1, 3. The following relationships for the degrees of freedom are prescribed for points on each pair of the faces:

$$u_{i1} - u_{i2} = u_{i1}^{\text{ref}} - u_{i2}^{\text{ref}}$$
(6)
$$\theta_{i1} - \theta_{i2} = 0,$$
(7)

where u ref i1 and u ref i2 are displacements of two reference points on the opposite bounding faces.

Results

All the following simulations are performed on 2 Intel Xeon X5670 (12 core), 2.93 GHz processors with 24 cores and 24 GB RAM.

Strut model

A script is developed through ABAQUS/ STANDARD 6.11-1 which is able to model the strut and its imperfections. Since the lattice’s cell size is L = 2.5 mm, the single strut’s length is set to be \(L_{s} = 2.5\sqrt 3 /2\) mm. The strut is meshed using 10-node modified tetrahedron elements with hourglass control. At first, a mesh-sensitivity study is performed. The size of the elements is reduced until change in the stress-strain curve is very negligible (the results are not presented here), and the appropriate mesh size is obtained to be about 1.2 × (D max − D min). Fig. 8 shows one-fourth of the meshed strut.

Fig. 8
figure 8

One-fourth of the meshed strut

Full size image

To reduce the effects of the strut’s random microstructure on its stress-strain response, 20 different models are generated and solved, and the average curve is reported as the stress-strain curve of the single strut of the lattice. Shown in Fig. 9 are the stress-strain responses of the strut and its base material. The elastic modulus of the strut is about 83.32% of the bulk material. Tsopanos et al (Ref 17) showed that the elastic modulus of the struts is about 75% of that of the bulk material using experimental calibrations, but Gurmuk and Mines (Ref 19) reported that the strut’s elastic modulus was 30% lower than what was reported by Tsopanos et al (Ref 17).

Fig. 9
figure 9

The stress-strain curve of the single strut and bulk material

Full size image

Unit Cell Model for the Lattice

After finding the strut’s stress-strain response, this curve is attributed to the base material of the lattice struts. To do so, a MATLAB code is developed to separate elastic and plastic data points which are in the format of ABAQUS material module. As the effects of defects are included in the stress-strain curve of the strut, no defects should be taken into account in the unit cell model of the lattice.

A script is prepared in ABAQUS/EXPLICIT 6.11-1 which generates the unit cell model and its boundary conditions. The struts are modeled as 3-node quadratic beams based on Timoshenko beam formulation accounting for shear strains. By mesh-sensitivity study of the model, each strut is meshed using 1 element in the vertex regions and 4 elements in the middle region.

In this paper, the experimental result of a cellular lattice reported by Gumruk and Mines (Ref 19) is used for validating the numerical predictions. This experimental measurement was performed on lattice blocks whose side is approximately 20-21 mm in length. The tests were carried out at a crosshead speed of 0.25 mm/min. Figure 10 shows the stress-strain curves of the lattice obtained from the model and experimental measurements. As it can be seen, a good agreement exists between experimental and finite element modeling results. The elastic modulus of the lattice is found to be about 14.31 MPa, which is about 90.87% of the experimentally measured one. The collapse strength of the lattice is nearly 0.446 MPa, which is 17.14% higher than the experimental one.

Fig. 10
figure 10

Stress-strain curve of the lattice structure: experimental and modeling

Full size image

Discussion

In this section, the effects of the single strut’s length and the porosity of the strut are investigated.

Effects of Strut’s Length on the Mechanical Properties

Since the length of a single strut can increase the computational time, it would be of interest to examine the effects of the strut’s length. As mentioned earlier, the size of the single strut is supposed to be equal to the size of the lattice’s struts as \(L_{\text{s}} = 2.5\sqrt 3 /2\) mm. To assess the effects of the single strut’s length, \(L_{\text{s}} = 2.5\sqrt 3 /2^{n + 1}\) is supposed where n varies between 0 and 4. Figure 11 shows the stress-strain curve of single struts with different lengths. As shown in this figure, the single strut’s length does not have a very significant influence on the elastic modulus. However, the collapse strength increases by reducing the strut’s length. It might be due to the number of defects in the strut. As the length of the strut increases, the number of defects increases leading to the reduction of the collapse strength. The collapse strength of the shortest strut is about 534.6 MPa, which is just 10.89% greater than that of the longest one. Accordingly, the single strut’s length can be decreased for computational efficiency.

Fig. 11
figure 11

Stress-strain curve of single struts with different lengths

Full size image

Effects of the Strut’s Porosity on the Mechanical Behavior

As mentioned before, the mechanical properties of fabricated parts by selective laser melting technique can be severely affected by the processing parameters of the method. One of the most important defects affecting the mechanical properties is the existence of pores or un-melted powders within the lattice’s struts. Meier and Haberland (Ref 25) showed that a higher scanning speed as well as a lower laser power can increase the micropores in the specimens. Similar observations are reported in (Ref 27). To assess the effects of the existence of the micropores in the struts, a model of strut with some pores is developed. To do so, some spherical voids with random diameters are added to the struts in random positions while the desired value of porosity is satisfied according to Eq 8. The diameters of the pores are supposed to be between 30 and 40 µm, which are obtained based on the scanning electron micrograph of some sections of lattices’ struts (Ref 10, 17).

$$P = \frac{{V_{\text{voids}} }}{{V_{\text{s}} }} \times 100$$
(8)

In relation above, Vvoids and Vs are the volumes of voids and strut without any voids, respectively. Figure 12 shows a view cut of a strut with about 5% porosity. As is seen, the pores can penetrate to each other in consistence with the reality.

Fig. 12
figure 12

The view cut of a porous strut with 5% porosity

Full size image

To reduce the effects of randomness, 20 models are generated for each value of porosity, and the average stress-strain curve is reported. Shown in Fig. 13(a) is the stress-strain curve of single struts with different values of porosity. It is obvious that the existence of pores in struts can significantly affect the mechanical properties of the lattice’s struts. All the simulations are performed for a strut with a length of \(L_{\text{s}} = 2.5\sqrt 3 /32\) mm. Figure 13(b) shows variations of the elastic modulus and collapse strength with porosity of the single strut. As it can be seen, elastic modulus and collapse strength are changed almost linearly with the porosity.

Fig. 13
figure 13

(a) Stress-strain curve of porous struts with different values of porosity. (b) Variations of the elastic modulus and collapse strength with porosity

Full size image

Conclusion

The focus of this paper is on the basics of modeling the mechanical properties of cellular lattice structures in connection with the bulk material and strut’s imperfections. The modeling process is started by simulating the mechanical properties of a single strut with geometrical imperfections and defects. The material parameters of the strut are then as attributed to the bulk material of the lattice’s struts without any imperfections, and the stress-strain curve is obtained. The result shows that the obtained stress-strain response is in a good agreement with the experimental one. Using this method, the lattice’s elastic modulus is obtained about 14.31 MPa, which is 90.87% of the experimental one, and the collapse strength is obtained about 0.446 MPa, which is about 17.14% higher than the experimentally measured value. The effects of the single strut’s length and its micropores are also assessed on the mechanical properties. The results indicate that the single strut’s length does not significantly affect its stress-strain curve while the effects of the micro pores are not negligible. It is shown that the elastic modulus and collapse strength of a single strut decrease almost linearly as the porosity increases. According to the obtained results, this paper presents a computationally efficient method with a reasonable accuracy for simulating the mechanical properties of cellular lattice structures.