Introduction

As the main solidification structure of continuously cast strand, the dendrite contributes much to the formation of solidification defects such as inclusions, cracks, and segregation, which are unfavorable to the yield and the performance of steel products.[1,2,3] Compared with the columnar structure, the equiaxed dendrite is more favored for a majority of steel grades, because it avoids the preferential push of the enriched solute to the strand center leading to a more homogenous distribution of the solute. The equiaxed dendrite prefers to grow in the undercooled melt and can move with the melt, which changes the solute distribution at the macroscopic scale. At the microscopic scale, the release of the latent heat and the solute at the solidification interface alters the undercooling and solute distributions around the equiaxed dendrite. So, the equiaxed dendritic solidification has drawn much interest of metallurgists from the microscopic to the macroscopic scale.

At first, researchers focused on the macroscopic transport phenomena and coupled them with the microscopic nucleation and growth kinetics to investigate variations of the temperature and the solute concentration during the equiaxed dendritic solidification. Generally, the equiaxed dendrite was simplified into a sphere and grew according to the analytical kinetics to avoid the direct tracking to the equiaxed dendritic morphology. Thévoz et al.[4] took the release of the latent heat as the link to couple the macroscopic heat transfer and the microscopic dendritic solidification, accordingly predicted the cooling curves during the equiaxed dendritic solidification of Al-7Si alloy in weight percentage. Wang and Beckermann[4] considered the influences of the melt convection and the movement of equiaxed dendrites and developed a two-phase solidification model based on the volume average method. In the model, the dendrite phase included the solid phase and the inter-dendritic liquid phase so that the micro-segregation around the solid dendrite was taken into account. They calculated the transport equations in these phases separately and connected them through the interfacial transfers, as a result successfully predicted the temperature and the solute distributions together for Al-4Cu alloy.[5,6] Wu and Ludwig[7] introduced the columnar solidification and developed a columnar-equiaxed mixed solidification model to predict the solidification structure and the macro-segregation of Fe-0.34C alloy.

Although these methods can simulate the equiaxed dendritic solidification process, even the segregation evolution at the macroscopic scale, they provide little information on the dendritic morphology. The key point of the numerical description of the dendritic morphology is to track directly or indirectly the evolution of the solidification interface in two- and three-dimensional (2D and 3D) spaces. It comes true with the springing up of numerical methods such as phase field (PF) and cellular automaton (CA).[8,9] Firstly, the case with a single equiaxed dendrite growing in the undercooled melt has been usually concerned. In this case, the steady tip growth velocity and radius were measured to compare with the analytical results to validate the dendritic growth models.[10,11] Secondly, metallurgists have paid much attention to the influence of the melt flow on the equiaxed dendritic morphology. They described the upstream development of primary and secondary dendritic arms in detail and attributed it to the movement of enriched solute from the upstream side to the downstream side.[12,13,14,15] Also, they compared the growth difference between 2D and 3D cases and found that the equiaxed dendrite become more asymmetrical in 2D cases due the lack of one dimension for momentum and solute transports.[16,17] Thirdly, some researchers[18,19,20] have focused on the recalescence and segregation phenomena during the evolution of the multi-equiaxed-dendrite growth. CA method depends on the configuration and capture rules of neighboring cells to track the evolution of the solidification interface. Since equiaxed dendrites are with random orientations, it is necessary to reduce or eliminate the mesh anisotropy for CA method. Beltran-Sanchez and Stefanescu[18] virtually determined the location of the solidification interface according to the interface norm and the solid fraction and changed the interior liquid cells located into interface cells, which was defined as VFT method. Accordingly, they predicted the cooling curve during the multi-equiaxed-dendrite solidification of Al-4Cu alloy. Based on VFT method, Zhu et al.[19] determined the interface growth kinetics according to the difference between the equilibrium and actual solute concentration in the liquid phase at the interface rather than the solute balance. Subsequently, they predicted the segregation evolution among the equiaxed dendrites of Al-2Cu alloy and made a comparison with Scheil model. Luo and Zhu[20] employed the decentered square (DCS) algorithm to simulate the multi-equiaxed-dendrite solidification of Fe-0.6C alloy. Different from the VFT method, DCS algorithm introduced a series of squares with diagonals parallel to the dendritic orientations to aid the propagation of the solidification interface. The main virtue of DCS algorithm is that it can be implemented on a relatively coarser mesh compared with the VFT method. Additionally, there are other useful methods such as Zigzag,[21] Multi-layer-mesh,[22] and Father-son.[23] The authors of this manuscript developed a serials of dendritic growth models for Fe-0.82C alloy with CA approach and reduced the computational cost and the mesh anisotropy with the parallel computation and the DCS algorithm, respectively.[24,25] Moreover, the authors successfully simulated the dendritic evolution of Fe-0.82C alloy billet in 2D space during the continuous casting and analyzed the influences of the processing parameters on the dendritic structure.[26,27]

The previous works mentioned above focused more on the morphology of equiaxed dendrites than the temperature and solute variations. So, taking Fe-0.82C alloy as an example, the present work investigates the recalescence and segregation behaviors during the multi-equiaxed-dendrite solidification of alloy and reveals their dependence on the cooling conditions. In Section II, models for heat transfer, solute diffusion, and dendritic growth kinetics will be briefly introduced as well as their solution methods. In Section III, the capability of the present model will be evaluated through comparing the dendritic growth kinetics with LGK analytical model.[28] Moreover, the influences of the released latent heat on the growth of the single equiaxed dendrite will be discussed in detail. In section IV, the recalescence and segregation behaviors during the multi-equiaxed-dendrite solidification of Fe-0.82C alloy under different cooling conditions will be described. An in-depth explanation to the recalescence phenomenon will be also given on the basis of the difference between the released latent heat and the heat dissipation by convention around the domain boundaries. In addition, the reason for the variation of the segregation ratio will be analyzed.

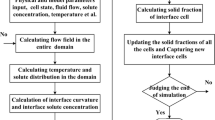
Model Description

Heat Transfer

The heat transfer in the 2D space is governed by[26]

$$ \rho c\frac{\partial T}{\partial t} = \lambda \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \rho L\frac{{\partial f_{\text{s}} }}{\partial t}, $$
(1)

where T is the temperature, t is the solidification time, x and y are coordinates of wide direction and thick direction, respectively, ρ is the steel density, λ is the thermal conductivity of steel, c is the specific heat capacity of steel, L is the solidification latent heat of steel, and fs is the solid fraction.

Solute Diffusion

The solute diffusions in liquid and solid phases are calculated separately, according to Eqs. [2] and [3]:

$$ \frac{{\partial C_{\text{l}} }}{\partial t} = D\left( {\frac{{\partial^{2} C_{\text{l}} }}{{\partial x^{2} }} + \frac{{\partial^{2} C_{\text{l}} }}{{\partial y^{2} }}} \right) + C_{\text{l}} \left( {1 - k_{0} } \right)\frac{{\partial f_{\text{s}} }}{\partial t} $$
(2)
$$ \frac{{\partial C_{\text{s}} }}{\partial t} = D\left( {\frac{{\partial^{2} C_{\text{s}} }}{{\partial x^{2} }} + \frac{{\partial^{2} C_{\text{s}} }}{{\partial y^{2} }}} \right), $$
(3)

where Cl and Cs are the solute concentration in the liquid and solid phase, Ds and Dl are the solute diffusion coefficient in the liquid and solid phase, and D is the weighted solute diffusion coefficient according to the solid fraction fs.

The segregation ratio in the modeling domain SR is defined as

$$ SR = \frac{{\sum\limits_{i,j} {C_{i,j}^{\text{l}} \left( {1 - f_{i,j}^{\text{s}} } \right)} }}{{\sum\limits_{i,j} {C_{0} \left( {1 - f_{i,j}^{\text{s}} } \right)} }}, \, \left( {i,j} \right) \in \left\{ {\left( {i,j} \right)\left| {S_{i,j} < = 0} \right.} \right\}, $$
(4)

where Si,j represents the state of cell (i,j). SR is the ratio between the average concentration in the liquid phase and the initial carbon content.

Growth Kinetics

The interface growth kinetics is determined according to the local solute balance:

$$ \varvec{V}_{\varvec{n}} C_{\text{l}}^{ *} \left( {1 - k_{0} } \right) = D_{\text{s}} \left. {\frac{{\partial C_{\text{s}} }}{{\partial \varvec{n}}}} \right|^{*} - D_{\text{l}} \left. {\frac{{\partial C_{\text{l}} }}{{\partial \varvec{n}}}} \right|^{*} $$
(5)
$$ C_{\text{s}}^{*} = k_{0} C_{\text{l}}^{*}, $$
(6)

where \( \varvec{V}_{\varvec{n}} \) is the normal growth velocity of the solidification interface, k0 is the equilibrium partition coefficient of the solute, and \( C_{\text{l}}^{*} \) and \( C_{\text{s}}^{*} \) are equilibrium solute concentrations of solid and liquid phases at the solidification interface, respectively. \( C_{\text{l}}^{*} \) is calculated according to by the local temperature and curvature at the solidification interface:

$$ C_{\text{l}}^{*} = C_{0} + \frac{1}{{m_{\text{l}} }}\left( {T^{*} - T_{\text{l}}^{{}} + \Gamma \cdot \kappa \cdot f\left( {\varphi ,\theta } \right)} \right) $$
(7)
$$ f\left( {\varphi ,\theta } \right) = 1 - 15\varepsilon_{\text{A}} { \cos }\left( {4\left( {\varphi - \theta } \right)} \right), $$
(8)

where C0 is the initial content of the solute, Γ is the Gibbs–Thomson coefficient of the alloy, εA is the anisotropy parameter, φ is the angle between the interface norm and the x axis, and θ is the preferential growth orientation. As the interface curvature, κ is determined according to the first and second derivatives of fs.[27]

The increment of the solid fraction ∆fs is determined according to the interface movement and the cover length of the interface cell along the interface norm:

$$ \Delta f_{\text{s}} = GF\frac{{\left| {\varvec{V}_{\varvec{n}} } \right|\Delta t}}{{L_{n} }}, $$
(9)

where ∆t is the time step, \( \left| {\varvec{V}_{\varvec{n}} } \right| \) is the normal growth velocity \( \varvec{V}_{\varvec{n}} \), GF is a correction coefficient in consideration of states of neighboring cells, Ln is the maximum projection of the interface cell diagonal on the interface norm. The calculation details of \( \left| {\varvec{V}_{\varvec{n}} } \right| \), GF, and Ln were described in detail in Reference 27. The related physical property parameters of Fe-0.82C alloy are listed in Table I.[26,27]

Table I Physical Property Parameters for Thermal and Solute Diffusion of Fe-0.82C Alloy[26,27]
Full size table

Solution Strategy

According to the thermal and solutal properties of Fe-0.82C alloy listed in Table I,[26,27] the thermal diffusivity is about 1000 times higher than the solute diffusivity. In the present work, thermal and solute diffusion equations are discretized on the same mesh. Therefore, the implicit discrete method is used to ensure the solution stability for the heat transfer process. The heat transport is successive in the entire domain regardless of the CA cell state. However, the solute diffusion is not successive from the liquid phase to the solid phase because of the solute redistribution at the interface. The governing equation for the solute diffusion in the liquid phase is also implicitly discretized, while that for the solute diffusion in the solid phase explicitly solved. Moreover, the solidification interface is explicitly tracked indicating the time step is also controlled by interface evolution. So, the time step is governed by the following equation.

$$ \Delta t \le {\text{Min}}\left[ {\frac{\Delta x}{{V_{n,\hbox{max} } }},\frac{{\left( {\Delta x} \right)^{2} }}{4D}} \right], $$
(10)

where Vn,max is the maximum growth velocity of solidification interface at time t.

Discrete equations are solved with TDMA (tri-diagonal matrix algorithm). The convergence of solute diffusion and heat transport equations should satisfy Eqs. [11] and [12]:

$$ {\text{Max}}\left[ {\left| {T_{i,j}^{n + 1} - T_{i,j}^{n} } \right|} \right] < \chi $$
(11)
$$ {\text{Max}}\left[ {\frac{{\left| {C_{i,j}^{n + 1} - C_{i,j}^{n} } \right|}}{{C_{0} }}} \right] < \chi, $$
(12)

where n is iteration steps, χ is a number far less than unity, and (i, j) represents the serial number of the CA cell. The magnitude of χ is set to be 0.0001 in the present work.

Case Design

A 301 μm × 301 μm domain is designed and meshed into 1 μm × 1 μm cells. One nucleus with the orientation parallel with the mesh is placed in the domain center. The present layout can make sure the same growth of four primary arms of the equiaxed dendrite. The domain temperature is determined according to the liquidus temperature Tl of Fe-0.82C alloy and the given melt undercooling ∆T, that is Tl−∆T. This case is noted as case I where the dendritic growth is purely controlled by the solute diffusion. In order to illustrate the influence of the released latent heat, the heat transfer is introduced in case II. At the domain boundaries, the temperature is constant at Tl−∆T during the single-equiaxed-dendrite solidification.

For the recalescence and segregation phenomena, a 300 μm × 300 μm domain is designed and meshed into 1 μm × 1 μm cells. 16 nuclei with different orientations are randomly placed in the domain. The domain is initially full of Fe-0.82C alloy melt at the liquidus temperature and cooled down by the convection heat transfer at the surround boundaries. In addition, the temperature of the cooling medium is 298.15 K. This case is noted as case III to investigate the influences of the convection coefficients on the recalescence and segregation behavior of Fe-0.82C alloy during the multi-equiaxed-dendrite solidification.

In addition, a 500 μm × 500 μm domain is designed and meshed into 1 μm × 1 μm cells. 21 nuclei with different orientations are randomly placed in the domain. The domain is initially full of Fe-0.82C alloy melt at the liquidus temperature and cooled down according to the given cooling rate. This case is noted as case IV to illustrate the influence of the cooling rate on the segregation phenomenon among the equiaxed dendrites.

Although the domain size is different in these cases, the mesh size is the same. For all cases, the solute flux at domain boundaries is 0.

Model Evaluation

Firstly, the growth behavior of a single equiaxed purely controlled by the solute diffusion (case I) is presented. Figure 1 shows the predicted equiaxed dendritic morphology of Fe-0.82C alloy at the melt undercooling and the solidification time of 10 K and 0.3 second, as the preset orientation θ varies from 0 to 45 deg. As the preset orientations are 0 and 45 deg, the arms of the equiaxed dendrite are symmetrical along the domain centerline and diagonal, respectively. Meanwhile, their growth orientations are consistent with the preset values. At θ = 0 deg, the solid cells pile up so compactly that secondary arms form difficultly. As θ deviates from the mesh, the solute distribution and the mesh configuration influence more on the capture and growth of the interface cells, promoting the formation of secondary arms. As the preset orientations are 10 and 15 deg, secondary arms at both sides of the primary arm present a good symmetry. However, as the preset orientations are 20 and 30 deg, secondary arms become weak again. As the preset orientations are 35 and 40 deg, secondary arms at the downside of the primary arm are more developed, which is contrary to the case at θ = 5 deg. So, the mesh configuration influences much on the capture of decentered squares.

Fig. 1
figure 1

Equiaxed dendritic morphology of Fe-0.82C alloy at ∆T=10 K and t=0.3 s (case I) as preferential growth orientation varies from 0 to 45 deg

Full size image

Figure 2(a) shows comparison between the predicted orientation and the preset values. Except some deviation observed at θ = 25 and 30 deg, the predicted orientations agree with the preset conditions. Generally, the correlation coefficient is 0.998. Figure 2(b) shows relative deviations of the arm length and the solid fraction of equiaxed dendrites with different orientations as the melt undercooling is 10 K. At θ = 0 deg, the primary arm length is 78.6 μm, and the solidification is 4.60 pct. It can be seen that the relative deviations of the primary arm length and the solid fraction are − 7.58 to 4.33 and − 4.58 to 2.95 pct, respectively, as θ varies from 5 to 45 deg. So, the present model can not only ensure the dendritic growth orientation well, but also keep the dendritic growth consistency to some extent.

Fig. 2
figure 2

Growth characteristics of a single equiaxed dendrite of Fe-0.82C alloy in the undercooled melt (case I): (a) preferential growth orientation and (b) solid fraction

Full size image

Secondly, the release of the latent heat during the growth of equiaxed dendrite is taken into consideration in case II. Figure 3 shows the solute and undercooling distributions around the equiaxed dendrite Fe-0.82C alloy at ∆T=10 K as the solidification time is 0.3 second. Meanwhile, primary arm lengths and solid fraction are measured and listed in Table II, as well as their comparisons with those in case I. With the proceeding of the equiaxed-dendrite solidification, solidification latent heat is gradually released. So, the temperature around the solid dendrite increases reducing the melt undercooling there and causing negative thermal gradients in front of the dendritic tip. As the preferential growth orientations are 0, 10, 20, 30, and 40 deg, the minimum undercoolings in the domain are 9.78 K, 9.77 K, 9.80 K, 9.66 K, and 9.80 K, respectively. Meanwhile, the undercooling distribution has much to do with the preferential growth orientation, as shown in Figure 3(b). Compared with case I, secondary arms are less developed at θ = 10 and 40 deg in case II, as shown in Figures 1 and 3(a). Moreover, at θ = 10 deg, the mesh anisotropy becomes significant with the introduction of the solidification latent heat. Besides, the released latent heat does a pronounced effect on the dendritic growth kinetics. As the preferential growth velocity varies from 0 to 40 deg, the primary arm length falls into the range of 70.02 to 75.02 μm, and the solid fraction locates in the range 3.98 to 4.23 pct. At θ = 10 deg, both the primary arm length and the solid fraction are in maximum. Meanwhile, they are in minimum at θ = 30 deg. Compared with the pure solute diffusion case, the arm length and solid fraction decrease by 4.56 to 10.22 and 6.20 to 12.43 pct, as shown in Table II. The reduction of the arm length and solid fraction at θ = 30 deg are 10.19 and 12.43 pct which are relatively greater than other preferential growth orientations mentioned. The reduction of the arm length and solid fraction at θ = 10 and 40 deg are relatively lower than other cases. Obviously, these phenomena correspond to the undercooling recoveries.

Fig. 3
figure 3

Influence of latent heat on equiaxed dendritic morphology of Fe-0.82C alloy at ∆T=10 K and t=0.3 s (case II): (a) solute distribution and (b) undercooling distribution

Full size image
Table II Comparison Between Growth Characteristics of Equiaxed Dendrite in Cases I and II
Full size table

The tip growth velocity is defined as the ratio between the size of the tip cell and its duration at interface state. According to the dendritic growth theory,[29] the necessary length for an equiaxed dendrite to reach the steady state is on the orders of \( 5D_{\text{l}} k_{0}^{ - 1} \bar{V}_{n}^{ - 1} \). For example, the transient length is 1.2 mm as ∆T is 7 K, according to the steady tip growth velocity (61.7 μm s−1) predicted by LGK model in case I. Therefore, the dendritic growth at ∆T = 7 K will be influenced by boundary conditions before the steady state is reached. An alternative method proposed by Beltran-Sanchez and Stefanescu[18] is used rather than adjusting the domain size at different unerdercoolings. The steady tip growth velocity is determined as the solute concentration at the boundary towards the tip reaches 1.01C0.[18] In LGK analytical model,[28] the stability parameter is determined as 0.1785 according to the linearized solvability theory.[30]

Figure 4 shows the comparison between the predicted steady tip growth velocity and the analytical result at θ = 0. With the introduction of the solidification latent heat, the steady tip growth velocity reduces, which becomes more significant with the improvement of the melt undercooling. According to LGK analytical model, the steady tip growth velocity decreases from 16.1 and 254.7 to 14.7 and 233.3 μm s−1 as the melt undercooling increases from 5 K to 10 K. As predicted by present CA model, the steady tip growth velocity decreases by 4.6 and 11.3 μm s−1 at ∆T = 5 K and 10 K. The predicted steady tip growth velocities agree with the analytical results at ∆T = 9 K. The predicted steady tip growth velocities are higher than the analytical results as ∆T < 9 K. It is mainly attributed to the limitation induced by the domain size as mentioned above. As ∆T > 9 K, the predicted steady tip growth velocities are lower than the analytical results. In the present work, the mesh size is constant at 1 μm, so the mesh anisotropy increases the tip radius causing the decrease of steady tip growth velocity. This phenomenon becomes more pronounced at higher melt undercoolings.

Fig. 4
figure 4

Comparison between the predicted steady tip growth velocities and LGK analytical results

Full size image

Results and Discussion

Recalescence Behavior

Case III is employed to illustrate the recalescence phenomena during the multi-equiaxed-dendrite solidification of Fe-0.82C alloy. Figure 5 shows the equiaxed dendritic morphology and the temperature distribution at fs = 0.5 as the convection heat transfer coefficient hw is 2000 W m−2 K−1. Under the intensive cooling condition, the nuclei develop quickly into equiaxed dendrites, which reduces the solidification time and the thickness of the enriched solute layer around the solid dendrite. Meanwhile, the temperature decreases from the inner domain to the outer domain. So, compared with the inner domain, the outer domain is more compact and is with more developed secondary arms.

Fig. 5
figure 5

Solute distribution (a) and temperature distribution (b) at fs=0.5 during equiaxed dendritic growth of Fe-0.82C alloy as the cooling condition is 2000 W m−2 K−1

Full size image

Figure 6 shows the records of the center temperature and solid fraction as the convection heat transfer coefficients are 200 and 2000 W m−2 K−1. At the initial solidification stage, the solid fraction increases slowly since the undercooling is low. At the intermediate solidification stage, the solid fraction increases faster and linearly. At the end of the solidification, the increase of the solid fraction becomes gentler, because of the solute enrichment among equiaxed dendrites. However, the center cooling curve presents two different tendencies under these cooling conditions. At hw = 2000 W m−2 K−1, with the solidification proceeding, the center temperature decreases sharply to a valley value Tva at first, then recovers to a peak value Tpe, and finally decreases with the continuously improving rate. The temperature recovery from Tva to Tpe is defined as the recalescence process. The difference between Tpe and Tva is noted as the temperature recalescence ∆Tre. Tva and Tpe correspond to the start and end points of the fast growth stage, indicating the temperature recalescence is located in the intermediate solidification stage. Under this cooling condition, Tva and Tpe are 1706.04 K and 1710.31 K, and the corresponding solid fractions are 9.46 and 26.1 pct, respectively. Obviously, the variation tendency of the center temperature depends on the solid fraction and the release of the solidification latent heat. At the fast growth stage, the released latent heat is greater than the heat carried away by the cooling, so the temperature recovery occurs. However, at hw = 200 W m−2 K−1, the released latent heat during the fast growth cannot resist the temperature drop induced by the cooling. So, the decrease of the center temperature just gets gentle as shown in Figure 6(a).

Fig. 6
figure 6

Variations of solid fraction and temperature of domain center as cooling conditions are (a) 200 W m−2 K−1 and (b) 2000 W m−2 K−1

Full size image

In order to explain the temperature curves in Figure 6, the released latent heat and its alleviation to the heat dissipation in the whole domain are extracted. Figures 7 and 8 show the released latent heat and difference between heat dissipation and released latent heat during the multi-equiaxed-dendrite solidification of Fe-0.82C alloy at hw = 200 and 2000 W m−2 K−1, respectively. At the initial solidification stage, the latent heat is released weakly, and the heat dissipation is efficient. With the extraction of the heat, the undercooling becomes deeper, so the solidification becomes faster causing the released latent heat become significant. The released latent heats reach maximums around 290 and 3240 W m−1 as the convection coefficients are 200 and 2000 W m−2 K−1, respectively. Obviously, the faster solidification at 2000 W m−2 K−1 brings out a larger released latent heat. At these points, differences between heat dissipation and released latent heat are around 51 and 134 W m−1 at hw = 200 and 2000 W m−2 K−1, respectively. And their minimums are − 88.33 and − 286.79 W m−1, respectively. So, the higher convection coefficient is, the more pronounced temperature recalescence will be. Afterwards, the amount of the released latent heat generally reduces with some occasional explosions. So, the recalescence may occur at other places except the domain center at hw = 200 W m−2 K−1, as predicted from Figure 7. In a addition, compared with the heat variation in the whole domain, the response of the center temperature delays, as shown in Figures 6 through 8.

Fig. 7
figure 7

Heat variation during multi-equiaxed-dendrite solidification at 200 W m−2 K−1: (a) released latent heat and (b) difference between heat dissipation and released latent heat

Full size image
Fig. 8
figure 8

Heat variation during multi-equiaxed-dendrite solidification at 2000 W m−2 K−1: (a) released latent heat and (b) difference between heat dissipation and released latent heat

Full size image

Figure 9 shows changes of Tva, Tpe, and ∆Tre in the domain center and solid fractions corresponding to Tva and Tpe with the cooling conditions. With the improvement of the cooling intensity, both Tva and Tpe decrease gradually; however, the former tendency is more significant. ∆Tre is linearly extended, and its slope is 2.59 × 10−3 K2 m2 W−1. Meanwhile, solid fractions corresponding to Tva and Tpe generally increase. Tva, Tpe, and ∆Tre are 1718.53 K, 1720.08 K, and 1.56 K at hw = 1000 W m−2 K−1, and become 1700.55 K, 1706.03 K, and 5.48 K at hw = 2500 W m−2 K−1, respectively. Under intensive cooling conditions, it needs more latent heat to neutralize the quick temperature drop, so Tva moves to the deeper undercooling and the corresponding solid fraction increase linearly. Simultaneously, the dendritic growth gets faster and faster, causing ∆Tre extends linearly and the solid fraction corresponding to Tpe increases exponentially, as shown in Figure 9(b).

Fig. 9
figure 9

Influences of cooling intensity on the recalescence process: (a) Tva, Tpe, and ∆Tre and (b) solid fractions corresponding to Tva and Tpe

Full size image

Segregation Phenomenon

Firstly, the influence mechanism of the cooling rate on the solute segregation is introduced based on case IV. Figure 10 shows the solute distribution and the equiaxed morphology at fs = 0.5 as the cooling rates (CR) are 20, 50, and 100 K s−1. With the improvement of the cooling rate, the growth velocity of the equiaxed dendrite increases, and equiaxed dendrites are with thinner primary arms and more developed secondary arms. Moreover, the solute concentration in some region gets lower as shown in Figure 10(a).

Fig. 10
figure 10

Equiaxed dendritic morphology of Fe-0.82C alloy at fs=0.5 as cooling rates (CR) are (a) 20 K s−1, (b) 50 K s−1, and (c) 100 K s−1

Full size image

Figure 11 shows the segregation evolutions as the cooling rate varies from 0.5 to 100 K s−1. Although equiaxed dendrites grow fast under intensive cooling condition, the solute distributes more non-uniform, promoting the development of secondary arms. So, it is unfavorable to the further improvement of the solid fraction, causing the solute segregation is more pronounced than the weak cooling condition. As CR= 100 K s−1, equiaxed dendrites grow faster, further reducing the solidification time and extending the low concentration region. So, the segregation ratio is reduced. At fs = 0.8, the segregation ratios are 1.83, 2.10, 2.52, and 2.46 as the cooling rates are 0.5, 2.5, 50, and 100 K s−1, respectively.

Fig. 11
figure 11

Influence of cooling rate on segregation of carbon in the domain

Full size image

Secondly, influence mechanism of the convection coefficient on the solute segregation is investigated based on case III. Figure 12 shows the solute distribution and the equiaxed morphology at fs = 0.5 as the convection coefficients are 200, 500, and 1000 W m−2 K−1. Figure 13 shows the evolution of the segregation ratio as the convection coefficient varies from 200 to 2000 K s−1. Similar to case III, the improvement of the convection coefficient promotes the development of secondary arms of equiaxed dendrites and causes thinner solute envelopes around them. So, the solute segregation gets less pronounced. As the convection coefficient increases from 200 to 2000 W m−2 K−1, the segregation ratio at fs = 0.8 declines from 2.07 to 1.75, as shown in Figure 13.

Fig. 12
figure 12

Equiaxed dendritic morphology of Fe-0.82C alloy at fs=0.5 as convection coefficients (hw) are (a) 200 W m−2 K−1, (b) 500 W m−2 K−1, and (c) 1000 W m−2 K−1

Full size image
Fig. 13
figure 13

Influence of convection coefficient on segregation of carbon in the domain

Full size image

Conclusion

A CA model was developed to investigate the recalescence and segregation behaviors during the multi-equiaxed dendritic solidification of Fe-0.82C alloy. The main conclusions are summarized as follows:

  1. (1)

    Compared with the purely solute diffusion controlled case, the growth velocity of the equiaxed dendrite gets lower as the release of solidification latent heat is taken into consideration. In both two cases, the predicted steady tip growth velocities are consistent with the analytical results at the undercooling of 9 K. In addition, the CA model can well maintain the growth consistency of equiaxed dendrites with different orientations.

  2. (2)

    The recalescence phenomenon becomes more significant with the improvement of the applied convection coefficients. The temperature recalescence of the domain center increases linearly with the increases of the convection coefficient, whose slope is 2.59 × 10−3 K2 m2 W−1. Meanwhile, the corresponding solid fractions move to higher values so that the heat dissipation can be compensated for.

  3. (3)

    With strengthening the cooling rate, equiaxed dendrites become more developed, and the solute segregation becomes more pronounced. However, the segregation ratio decreases at the extreme cooling rate. With the improvement of the convection coefficient, secondary arms are also promoted, and the solute segregation gets less significant.