Introduction

During liquid steel solidification, the solute element is rejected from the solid dendrite and enriches in the interdendritic melt. With the effect of fluid flow, the rejected solute element is carried away and transported a long distance, leading to the macrosegregation formation.[1] In the past few decades, many different theories have been provided to explain the reasons for center segregation in the continuously casting strand, such as the thermosolutal convection,[2,3,4] the grain sedimentation,[4] the shell bulging,[5,6,7] the grain bridging and solidification shrinkage,[8,9] and the thermal shrinkage.[10,11]

Due to the density difference caused by thermal and solute gradients, the liquid steel is forced to move, leading to thermosolutal convection. In this aspect, Aboutalebi et al.[2] applied the continuum model to investigate solute transport in the billet continuous casting and found the solute concentration increasing continuously to the strand center. Sun and Zhang[3] also studied the thermosolutal convection and observed an irregular positive segregation near the bloom center, while the negative segregation in the periphery zone was not obtained. Jiang and Zhu[4] developed a multiphase solidification model to simulate solute transport and solidification structure in the billet continuous casting process. It was found that the negative segregation around positive segregation was created by grain sedimentation and thermosolutal flow, while the calculated data in the periphery zone were clearly larger than the measured data. For the shell bulging, Miyazawa and Schwerdtfeger[5] investigated the fluid flow with solid deformation and observed that center segregation increased obviously as the slab passed the supporting roller. Subsequently, Kajitani et al.[6] simulated the solid deformation and interdendritic flow between several supporting rollers. It was demonstrated that the shell bulging-compression sequence contributed to center segregation. Mayer et al.[7] studied the liquid flow induced by shell bulging and solidification shrinkage. They also found that the center segregation was dominated by shell bulging. However, Murao et al.[8] did not think the shell bulging was a necessary condition for center segregation and held the grain bridging and solidification shrinkage were the main reasons. As the grains bridging formed in the strand, the concentrated liquid was sucked to the center by solidification shrinkage, resulting in the positive segregation. Based on plant trails, Suzuki[9] observed the positive segregation was beneath the grains bridging in the etched strand sample. Except the viewpoint discussed previously, Janssen et al.[10] also did not believe the center segregation was caused by shell bulging and proposed the thermal shrinkage theory. With a freely deformed tubular region assumed in the strand center, the solid phase contracted with the decreasing temperature and the center segregation was created. Lesoult and Sella[11] also considered the spongy behavior of the mushy zone and found that the center segregation was closely related to solid deformation, which could be caused by thermal shrinkage. However, the relative movement between the solid and liquid was not provided.

At present, the solidified shell bulging is commonly supposed to be the main reason for slab center segregation formation.[12,13] However, the influence of thermal shrinkage on liquid flow and solute transport in the continuous casting process is rarely reported, although some numerical models were built.[10,11] In this article, a thermal shrinkage model is developed to consider solid phase contraction with the decreasing temperature. Moreover, it is coupled with a two-dimensional (2-D) multiphase solidification model to simulate solute redistribution and solidification structure evolution in slab continuous casting. The multiple effects on fluid flow and solute transport are investigated, including the solidification shrinkage, the thermal shrinkage, the grain sedimentation, and the thermal flow.

Mathematical Model

In the continuous casting process, the liquid steel transports to the mold zone from the submerged entry nozzle (SEN) and the solid shell begins to form with heat extracted from the slab surface. Then, the slab with liquid core is drawn to the secondary cooling zone and solidifies in the later stage, as shown in Figure 1. In order to describe the transport phenomenon, some assumptions are made to simplify the numerical model.

Fig. 1
figure 1

Schematic diagram of slab casting and treatment of gravity direction

Full size image
  1. (1)

    The curved slab is simplified to be straight and the gravity direction (g) is adjusted to consider the caster curve. The gravity acceleration in the casting direction is obtained by g y  = −g·cos(α) and that in the transverse direction is calculated by g x  = −g·sin(α), where α is the angle between the horizontal line and the casting position (0 ≤ α ≤ 90 deg).

  2. (2)

    The transport behaviors in the continuous casting process are assumed to be steady. The effects of SEN and electromagnetic stirring are not considered, and the fluid flow is assumed to be laminar. The slab surface assumes to be the fixed side, and columnar or equiaxed grains contract directionally toward the slab surface.

  3. (3)

    In the solidification process, not all of the solute rejected from the solid dendrite can transport into the extradendritic melt and some still remains in the interdendritic melt,[14] so a grain envelope enclosing the primary and secondary dendrite tips is used to separate the interdendritic melt from the extradendritic, as shown in Figure 2. Besides, columnar and equiaxed grain envelopes are simplified as sphere and cylinder, respectively.

    Fig. 2
    figure 2

    Schematic diagram of (a) columnar and (b) equiaxed phases

    Full size image
  4. (4)

    The columnar dendrite and interdendritic melt are regarded as the columnar phase and move with casting speed u c,y . They are quantified with volume fractions (f cs , f cd , f c) and characterized by solute concentrations (c cs , c cd , c e); hence, f c = f cs  + f cd and f c c c = f cs c cs  + f cd c cd . Similarly, the equiaxed dendrite and interdendritic melt form the equiaxed phase and move with the same velocity u e . They are also quantified with volume fractions (f es , f ed , f e) and characterized by solute concentrations (c es , c ed , c e); hence, f e = f es  + f ed and f e c e = f es c es  + f ed c ed . The densities of interdendritic melt and solid dendrite are assumed to be the same ρ s. The extradendritic melt forms the liquid phase, and the corresponding volume fraction, solute concentration, and density are f l, c l, and ρ l, respectively.

  5. (5)

    As the partition coefficients of solute elements are almost less than one and the distributions of C, Si, Mn, P, and S are similar, only the carbon element transport during the solidification is calculated. Besides, the peritectic reaction during steel solidification is also neglected.

The Mass-Transfer Model

The mass conservation equations for different phases are solved simultaneously and expressed as follows:[14]

$$ \begin{aligned} \frac{\partial }{\partial t}(f_{\text{l}} \rho_{\text{l}} ) + \nabla (f_{\text{l}} \rho_{\text{l}} \varvec{u}_{\text{l}} ) = - M_{\text{le}} - M_{\text{lc}} \hfill \\ \frac{\partial }{\partial t}(f_{\text{c}} \rho_{\text{s}} ) + \nabla (f_{\text{c}} \rho_{\text{s}} \varvec{u}_{\text{c}} ) = M_{\text{lc}} \hfill \\ \frac{\partial }{\partial t}(f_{\text{s}}^{\text{c}} \rho_{\text{s}} ) + \nabla (f_{\text{s}}^{\text{c}} \rho_{\text{s}} \varvec{u}_{\text{c}} ) = M_{\text{ds}}^{\text{c}} \hfill \\ \frac{\partial }{\partial t}(f_{\text{e}} \rho_{\text{s}} ) + \nabla (f_{\text{e}} \rho_{\text{s}} \varvec{u}_{\text{e}} ) = M_{\text{le}} \hfill \\ \frac{\partial }{\partial t}(f_{\text{s}}^{\text{e}} \rho_{\text{s}} ) + \nabla (f_{\text{s}}^{\text{e}} \rho_{\text{s}} \varvec{u}_{\text{e}} ) = M_{\text{ds}}^{\text{e}} \hfill \\ \end{aligned} $$
(1)

The source terms represent the mass-transfer rates, where M lc and M le are from the liquid phase to columnar and equiaxed phase, respectively, and M eds or M cds is from interdendritic melt to columnar or equiaxed dendrite. The columnar grain grows perpendicularly from the strand surface, as shown in Figure 2(a). The state indexes (i c) of columnar front and columnar trunk regions are updated by the columnar front tracking model, which was described in a previous article.[4] In the columnar trunk region (i c = 2), grains grow in the radical direction, so the parameter γ is equal to zero in Eq. [2]. In the columnar front region (i c = 1), the average mass-transfer rate contains the growth in radical and tip directions, so the parameter γ is equal to one. The average mass-transfer rate from liquid to columnar phase is defined as

$$ M_{\text{lc}} = v_{\text{env}}^{\text{c}} S_{\text{env}}^{\text{c}} \rho_{\text{s}} + \gamma M_{\text{tip}} = (\phi_{\text{env}}^{\text{c}} v_{\text{tip'}}^{\text{c}} )(2\pi r_{\text{c}} f_{\text{l}} /\lambda_{ 1}^{2} )\rho_{\text{s}} + \gamma v_{\text{tip}}^{\text{c}} n_{\text{c}} \pi r_{\text{tip}}^{ 2} \rho_{\text{s}} f_{\text{l}} $$
(2)

where \( v_{\text{env}}^{\text{c}} \) is the grain growth velocity in the radical direction; \( S_{\text{env}}^{\text{c}} \) is the area concentration of the columnar trunk envelope; M tip is the mass-transfer rate in the columnar front region; \( \phi_{\text{env}}^{\text{c}} \) is a shape factor (0.798); and \( v_{{{\text{tip}}\prime }}^{\text{c}} \) is the secondary dendrite tip velocity and is determined by the LGK model, according to Wu et al.[14] r c is the average columnar trunk radius; λ 1 is the primary arm spacing; n c is the columnar tip density and n c = f c/(πr 2c l y); l y is the columnar length in the columnar front region; r tip is the columnar tip radius; and \( v_{\text{tip}}^{\text{c}} \)is the primary dendrite tip velocity and is calculated by the KGT model, which could be obtained in Hou et al.’s work.[15] The mass-transfer rate from interdendritic melt to columnar solid dendrite can be expressed as

$$ M_{\text{ds}}^{\text{c}} = v_{\text{sd}}^{\text{c}} S_{\text{s}}^{\text{c}} \rho_{\text{s}} + \gamma M_{\text{tip}} = \frac{{2D_{\text{l}} (c_{\text{l}}^{*} - c_{\text{d}}^{\text{c}} )}}{{\beta \lambda_{2} f_{\text{d}}^{\text{c}} (c_{\text{l}}^{*} - c_{\text{s}}^{*} )}} \cdot \frac{{2f_{\text{d}}^{\text{c}} f_{\text{c}} }}{{\lambda_{2} }}\rho_{\text{s}} + \gamma v_{\text{tip}}^{\text{c}} n_{\text{c}} \pi r_{\text{tip}}^{2} \rho_{\text{s}} f_{\text{l}} $$
(3)

where \( v_{sd}^{c} \) is the growth velocity of the solid-interdendritic interface; \( S_{s}^{c} \) is the columnar interfacial surface concentration; D l is the liquid diffusion coefficient; β is a constant and equals 0.8; and λ 2 is the secondary arm spacing, as shown in Figure 3. The zero point represents the slab center, and the positive and negative directions are inner and external arc sides, respectively. c l* and c s* are the equilibrium liquid and solid concentrations, respectively, c s* = k e c l* and c l* = (T l − T f)/m, where k e is the solute partition coefficient, T f is the melting point of pure iron, T l is the liquid phase temperature, and m is the liquidus slope.

Fig. 3
figure 3

Measured primary and secondary arm spacings

Full size image

For equiaxed phase solidification, the equiaxed grain envelope is simplified as sphere and the average mass-transfer rate from liquid to equiaxed phase is given as

$$ M_{\text{le}} = v_{\text{env}}^{\text{e}} S_{\text{env}}^{\text{e}} \rho_{\text{s}} = (\phi_{\text{env}}^{\text{e}} v_{\text{tip}}^{\text{e}} )\,(4n_{\text{e}} \pi r_{\text{e}}^{2} f_{\text{l}} )\rho_{\text{s}} $$
(4)

where \( v_{\text{env}}^{\text{e}} \) is the growth velocity of equiaxed grain; \( S_{\text{env}}^{\text{e}} \) is the area concentration of equiaxed grain; \( \phi_{\text{env}}^{\text{e}} \) is the shape factor (0.683); \( v_{\text{tip}}^{\text{e}} \) is the equiaxed dendrite tip velocity and is determined by the LGK model; n e is the grain density; r e is the radius of equiaxed grain, which is calculated by f e = n e(4π/3)r 3e . n e is grain density and can be obtained by Eq. [5]:

$$ \frac{{\partial (n_{\text{e}} )}}{\partial t} + \nabla \cdot (\varvec{u}_{e} n_{e} ) = (m\varvec{G}_{\text{c,l}} \cdot \varvec{u}_{\text{l}} - \varvec{G}_{{T,{\text{l}}}} \cdot \varvec{u}_{\text{l}} ) \cdot \frac{{n_{\hbox{max} } }}{{\sqrt {2\pi } \cdot \Delta T_{\sigma } }} \cdot e^{{ - \frac{1}{2}(\frac{{\Delta T - \Delta T_{\text{N}} }}{{\Delta T_{\sigma } }})^{2} }} $$
(5)

where G c,l and G T,l are the gradients of liquid solute concentration and temperature, and n max, ΔT N, and ΔT σ are the maximum density of nuclei, average nucleation undercooling, and standard deviation, respectively.[16] The undercooling ΔT is calculated by ΔT = T f + mc l − T l. The mass-transfer rate from interdendritic melt to equiaxed dendrite can be expressed as

$$ M_{\text{ds}}^{\text{e}} = v_{\text{sd}}^{\text{e}} S_{\text{s}}^{\text{e}} \rho_{\text{s}} = \frac{{2D_{\text{l}} (c_{\text{l}}^{*} - c_{\text{d}}^{\text{e}} )}}{{\beta \lambda_{2} f_{\text{d}}^{\text{e}} (c_{\text{l}}^{*} - c_{\text{s}}^{*} )}} \cdot \frac{{2f_{\text{d}}^{\text{e}} f_{\text{e}} }}{{\lambda_{2} }}\rho_{\text{s}} $$
(6)

where \( v_{\text{sd}}^{\text{e}} \) is the growth velocity of the equiaxed solid-interdendritic interface and \( S_{\text{s}}^{\text{e}} \) is the equiaxed interfacial surface concentration.

The Fluid Flow Model

As the columnar phase grows from the slab surface and moves with the solidified shell, the columnar phase velocity is set to be casting speed u c,y and lateral contracting velocity u c,x , which will be discussed in Section II–E. The velocity of the liquid phase and the movement of the equiaxed grains are obtained by solving the Navier–Stokes equations:[17]

$$ \frac{\partial }{\partial t}(f_{\text{l}} \rho_{\text{l}} \varvec{u}_{\text{l}} ) + \nabla \cdot (f_{\text{l}} \rho_{\text{l}} \varvec{u}_{\text{l}} \varvec{u}_{\text{l}} ) = - f_{\text{l}} \nabla P + \nabla \cdot [f_{\text{l}} \mu_{\text{l}} (\nabla \varvec{u}_{\text{l}} + (\nabla \varvec{u}_{\text{l}} )^{T} )]\,\text{ + }f_{\text{l}} \rho_{\text{l}} \beta_{\text{l}} (T_{\text{l}} - T_{\text{ref}} )\varvec{g} + \varvec{U}_{\text{cl}} + \varvec{U}_{\text{el}} $$
(7)
$$ \frac{\partial }{\partial t}(f_{\text{e}} \rho_{\text{s}} \varvec{u}_{\text{e}} ) + \nabla \cdot (f_{\text{e}} \rho_{\text{s}} \varvec{u}_{\text{e}} \varvec{u}_{\text{e}} ) = - f_{\text{e}} \nabla P + \nabla \cdot \left[ {f_{\text{e}} \mu_{\text{e}} (\nabla \varvec{u}_{\text{e}} + (\nabla \varvec{u}_{\text{e}} )^{T} )} \right]\, + f_{\text{s}}^{\text{e}} \Delta \rho \varvec{g} + F_{\text{u}} (\varvec{u}_{\text{e}} - \varvec{u}_{\text{c}} ) + \varvec{U}_{\text{le}} + \varvec{U}_{\text{ce}} $$
(8)

where P is the pressure, T ref is the reference temperature and is defined as liquidus temperature (1793.89 K) according to the initial content of solute, β l is the liquid thermal expansion coefficient, Δρ is the density difference between the liquid and equiaxed dendrite, g is the gravitational acceleration, μ l is the liquid viscosity, and μ e is the viscosity of equiaxed phase and is calculated by Eq. [9].[18] f coh is the equiaxed coherent fraction, assumed to be 0.3, and F u is a switch function, which will transfer from zero to a large number with equiaxed fraction above coherent fraction:

$$ \mu_{\text{e}} = \mu_{\text{l}} [(1 - f_{\text{e}} /f_{\text{coh}} )^{{ - 2.5f_{\text{coh}} }} - (1 - f_{\text{e}} )]/f_{\text{e}} $$
(9)

where U lc, U le, and U ce are the momentum exchange terms due to drag force. The columnar phase moves with the casting velocity and is treated as porosity media. The permeability is calculated through the Kozen–Carmon method,[19] and the momentum exchange term is calculated by Eq. [10]:

$$ \varvec{U}_{\text{lc}} = K_{\text{lc}} (\varvec{u}_{\text{l}} - \varvec{u}_{\text{c}} ) = {f_{\text{l}}^{2}}\frac{{180(1 - f_{\text{l}} )^{2}\mu_{\text{l}}}}{{f_{\text{l}}^{3} \lambda_{2}^{2} }}(\varvec{u}_{\text{l}} - \varvec{u}_{\text{c}} ) $$
(10)

For the equiaxed zone, the initial equiaxed grain is surrounded by liquid steel and moves freely with fluid flow. So, the mushy zone is treated as slurry and the momentum exchange term is calculated according to Wen and Yu’s model.[20] As the equiaxed fraction exceeds the coherent fraction (f coh), the equiaxed grains impinge with each other and move with the solid shell. The mushy zone should be treated as porosity media, and the momentum exchange term is calculated by Eq. [11]:

$$ \varvec{U}_{\text{le}} = K_{\text{le}} (\varvec{u}_{\text{l}} - \varvec{u}_{\text{e}} ) $$
(11)
$$ K_{{{\text{le}}}} = \left\{ {\begin{array}{*{20}l} {\frac{{\beta ^{2} \mu _{{\text{l}}} }}{{r_{{\text{e}}}^{2} }}f_{{\text{l}}}^{2} } \hfill & {f_{{\text{e}}} \le f_{{{\text{coh}}}} } \hfill \\ {\frac{{180(f_{{\text{s}}}^{{\text{e}}} )^{2} \mu _{{\text{l}}} }}{{(1 - f_{{\text{s}}}^{{\text{e}}} )\lambda _{2}^{2} }}} \hfill & {f_{{\text{e}}} \,{>}\, f_{{{\text{coh}}}} } \hfill \\ \end{array} } \right.$$
(12)
$$ \beta = \left[ {\frac{9}{2}(1 - f_{\text{l}} )\frac{{2 + 1.333\,(1 - f_{\text{l}} )^{5/3} }}{{2 - 3\,(1 - f_{\text{l}} ) + 3\,(1 - f_{\text{l}} )^{5/3} - 2(1 - f_{\text{l}} )^{2} }}\frac{1}{{C_{\text{p}} \,(\phi_{\text{e}} )}}} \right]^{1/2} $$
(13)

where C p (ϕ e) is the correction coefficient related to the shape of the dendrite envelope.[21] For the momentum exchange between the columnar and equiaxed phases, an infinite drag force coefficient (K ce) for U ce = K ce ( u c − u e ) is introduced as the equiaxed grain is captured.

Heat-Transfer Model

The enthalpy conservation equations for each phase are solved and can be rewritten as follows:

$$ \begin{aligned} \frac{\partial }{\partial t}(f_{\text{l}} \rho_{\text{l}} h_{\text{l}} ) + \nabla \cdot (f_{\text{l}} \rho_{\text{l}} \varvec{u}_{\text{l}} h_{\text{l}} ) = \nabla \cdot (f_{\text{l}} k\nabla T_{\text{l}} ) - (M_{\text{lc}} + M_{\text{le}} )h^{*} + H^{*} (T_{\text{c}} - T_{\text{l}} ) + H^{*} (T_{\text{e}} - T_{\text{l}} ) \hfill \\ \frac{\partial }{\partial t}(f_{\text{c}} \rho_{\text{s}} h_{\text{c}} ) + \nabla \cdot (f_{\text{c}} \rho_{\text{s}} \varvec{u}_{\text{c}} h_{\text{c}} ) = \nabla \cdot (f_{\text{c}} k\nabla T_{\text{c}} ) + M_{\text{lc}} h^{*} + H^{*} (T_{\text{l}} - T_{\text{c}} ) \hfill \\ \frac{\partial }{\partial t}(f_{\text{e}} \rho_{\text{s}} h_{\text{e}} ) + \nabla \cdot (f_{\text{e}} \rho_{\text{s}} \varvec{u}_{\text{e}} h_{\text{e}} ) = \nabla \cdot (f_{\text{e}} k\nabla T_{\text{e}} ) + M_{\text{le}} h^{*} + H^{*} (T_{\text{l}} - T_{\text{e}} ) \hfill \\ \end{aligned} $$
(14)

where T l, T c, and T e are the temperatures of liquid, columnar, and equiaxed phases, respectively, and h l, h c, and h e are the enthalpies of different phases.[17] As the local thermal equilibrium is assumed, a large heat exchange coefficient (H *) is used to eliminate the temperature difference between phases.[18] h* is the phase exchanging enthapy, which depends on solidification or remelting, as shown Eq. [11]. During the simulation process, the heat-transfer coefficient is applied to the slab surface, as shown in Figure 4:

Fig. 4
figure 4

Heat-transfer coefficient at the slab surface

Full size image
$$ h^{*} = \left\{ {\begin{array}{*{20}l} {h_{{\text{l}}} } \hfill & {({\text{solidification}},{\text{ }}M_{{{\text{lc}}}} {\text{ (or }}M_{{{\text{le}}}} ){\text{ > 0}})} \hfill \\ {h_{{\text{c}}} {\text{(or }}h_{{\text{e}}} {\text{)}}} \hfill & {({\text{remelting}},{\text{ }}M_{{{\text{lc}}}} {\text{ (or }}M_{{{\text{le}}}} ){\text{ < 0}})} \hfill \\ \end{array} } \right. $$
(15)

Solute Transport Model

The solute concentrations of each phase are obtained by solving solute transport equations, which can be expressed as follows:[14]

$$ \begin{aligned} \frac{\partial }{\partial t}(f_{\text{l}} \rho_{\text{l}} c_{\text{l}} ) + \nabla \cdot (f_{\text{l}} \rho_{\text{l}} \varvec{u}_{\text{l}} c_{\text{l}} ) = - C_{\text{lc}} - C_{\text{le}} \hfill \\ \frac{\partial }{\partial t}(f_{\text{c}} \rho_{\text{s}} c_{\text{c}} ) + \nabla \cdot (f_{\text{c}} \rho_{\text{s}} \varvec{u}_{\text{c}} c_{\text{c}} ) = C_{\text{lc}} \hfill \\ \frac{\partial }{\partial t}(f_{\text{s}}^{\text{c}} \rho_{\text{s}} c_{\text{s}}^{\text{c}} ) + \nabla \cdot (f_{\text{s}}^{\text{c}} \rho_{\text{s}} \varvec{u}_{\text{c}} c_{\text{s}}^{\text{c}} ) = M_{\text{ds}}^{\text{c}} c_{\text{s}}^{*} \hfill \\ \frac{\partial }{\partial t}(f_{\text{e}} \rho_{\text{s}} c_{\text{e}} ) + \nabla \cdot (f_{\text{e}} \rho_{\text{s}} \varvec{u}_{\text{e}} c_{\text{e}} ) = C_{\text{le}} \hfill \\ \frac{\partial }{\partial t}(f_{\text{s}}^{\text{e}} \rho_{\text{s}} c_{\text{s}}^{\text{e}} ) + \nabla \cdot (f_{\text{s}}^{\text{e}} \rho_{\text{s}} \varvec{u}_{\text{e}} c_{\text{s}}^{\text{e}} ) = M_{\text{ds}}^{\text{e}} c_{\text{s}}^{*} \hfill \\ \end{aligned} $$
(16)

where C lc and C le are the solute transfers from the liquid to columnar and equiaxed phases, as shown:

$$ C_{\text{lc}} = (v_{\text{env}}^{\text{c}} S_{\text{env}}^{\text{c}} \rho_{\text{s}} c_{\text{env}}^{\text{c}} + \gamma M_{\text{tip}}^{\text{c}} c_{\text{s}}^{*} ) - \rho_{\text{s}} S_{\text{env}}^{\text{c}} \frac{{D_{l} (c_{\text{env}}^{\text{c}} - c_{\text{l}} )}}{{l_{\text{l}}^{\text{c}} }}Sh $$
(17)
$$ C_{\text{le}} = v_{\text{env}}^{\text{e}} S_{\text{env}}^{\text{e}} \rho_{\text{s}} c_{\text{env}}^{\text{e}} - \rho_{\text{s}} S_{\text{env}}^{\text{e}} \frac{{D_{\text{l}} (c_{\text{env}}^{\text{e}} - c_{\text{l}} )}}{{l_{\text{l}}^{\text{e}} }}Sh $$
(18)

where \( c_{\text{env}}^{\text{c}} \) and \( c_{\text{env}}^{\text{e}} \) are the solute concentrations at the columnar and equiaxed envelopes; they can be calculated by \( c_{\text{env}}^{\text{c}} = \, \left( {l_{\text{d}} c_{\text{l}} + l_{\text{l}}^{\text{c}} c_{\text{d}}^{\text{c}} } \right)/\left( {l_{\text{d}} + l_{\text{l}}^{\text{c}} } \right) \) and \( c_{\text{env}}^{\text{e}} = \, \left( {l_{\text{d}} c_{\text{l}} + l_{\text{l}}^{\text{e}} c_{\text{d}}^{\text{e}} } \right)/\left( {l_{\text{d}} + l_{\text{l}}^{\text{e}} } \right). \) l d is the solute diffusion length of the interdendritic melt and is calculated by l d = (βλ 2 f ed )/(2f e); l cl and l el are the diffusion lengths in columnar and equiaxed extradendritic melts and can be assumed as l cl  = D l/\( v_{\text{env}}^{\text{c}} \) and l el  = D l/\( v_{\text{env}}^{\text{e}} \), respectively. Sh, the Sherwood number, is expressed as Sh = 2 + 0.95Re n Sc 0.33, where Re and Sc are the Reynolds and Schmidt numbers, respectively, and n is a constant and is assumed to be 2 in this article. The mixed solute concentration (c mix) and solute segregation (c mix/c 0) are used to analyze strand macrosegregation:

$$ {\text{c}}_{\text{mix}} = \frac{{f_{\text{l}} \rho_{\text{l}} c_{\text{l}} + f_{\text{c}} \rho_{\text{s}} c_{\text{c}} + f_{\text{e}} \rho_{\text{s}} c_{\text{e}} }}{{f_{\text{l}} \rho_{\text{l}} + f_{\text{c}} \rho_{\text{s}} + f_{\text{e}} \rho_{\text{s}} }}. $$
(19)

Thermal Shrinkage Model

In the solidification process, the columnar and equiaxed phases contract with the decreasing temperature. The solid density is assumed to be ρ s = ρ s,0 (1 + β s (T s − T ref)), and T s is the temperature of the columnar or equiaxed phase. The volume shrinkage is obtained by the following equation:

$$ \varepsilon_{\text{v}} = \frac{{\rho_{{{\text{s}},T_{\text{s}} }} - \rho_{{{\text{s}},T_{\text{s}} + \Delta T_{\text{s}} }} }}{{\rho_{{{\text{s}},T_{\text{s}} }} }} = \frac{{ - \beta_{\text{s}} \Delta T_{\text{s}} }}{{(1 + \beta_{\text{s}} (T_{\text{s}} - T_{\text{ref}} ))}} $$
(20)

where ΔT s is the solid temperature variation in a time interval Δt and β s is the solid thermal expansion coefficient. It is commonly known that volume shrinkage is one-third of linear shrinkage ε l = 1/3ε v,[22] which means the solid phase contracted from a single direction will only compensate for a part of volume shrinkage. The linear shrinkage could be expressed by

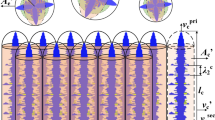
$$ \varepsilon_{\text{l}} = \frac{{ - \beta_{\text{s}} \Delta T_{\text{s}} }}{{3(1 + \beta_{\text{s}} (T_{\text{s}} - T_{\text{ref}} ))}} $$
(21)

During the molten steel solidification, the columnar and equiaxed grains show different characteristics in the cooling process. For the columnar phase, the columnar root welds together and is assumed to be fixed side, as shown in Figure 5. With the decreasing temperature, the columnar tip contracts toward the strand surface and the contracting velocity should be integrated:

Fig. 5
figure 5

Schematic diagram of columnar and equiaxed phase shrinkage

Full size image
$$ u_{c,x} = \text{ }\frac{\Delta x}{\Delta t} = \int\limits_{0}^{X} {\frac{{ - \beta_{\text{s}} }}{{3(1 + \beta_{\text{s}} (T_{\text{s}} - T_{ref} ))}}\frac{{\Delta T_{\text{s}} }}{\Delta t}\,} {\text{d}}x\text{ (0} \le X \le l_{\text{c}} \text{)} $$
(22)

For the equiaxed zone, the initial equiaxed grains move freely with the liquid phase and the thermal shrinkage could be supplied by the surrounding liquid steel. As the equiaxed phase exceeds the coherent point, the equiaxed grains impinge with each other and will contract directionally in the later solidification. Due to the existence of liquid film, the equiaxed grains will slide with each other, which is different from the columnar phase. It should be noted that the movement of equiaxed grains is also affected by the deformation of the columnar phase near the strand surface, so Eq. [23] is used to calculate the contracting velocity of the equiaxed phase:

$$ u_{c,x} = \int\limits_{0}^{{l_{\text{c}} }} {\frac{{ - \beta_{\text{s}} }}{{3(1 + \beta_{\text{s}} (T_{\text{s}} - T_{\text{ref}} ))}}\frac{{\Delta T_{\text{s}} }}{\Delta t}\,} {\text{d}}x + \left( {\frac{{f_{\text{s}} - f_{\text{scr}} }}{{1 - f_{\text{scr}} }}} \right)^{2} \int\limits_{{l_{c} }}^{X} {\frac{{ - \beta_{\text{s}} }}{{3(1 + \beta_{\text{s}} (T_{\text{s}} - T_{\text{ref}} ))}}\frac{{\Delta T_{\text{s}} }}{\Delta t}\,} {\text{d}}x\text{ (}l_{\text{c}} < X\text{)} $$
(23)

For the thermal shrinkage, the columnar or equiaxed phase movement is closely related to the variation of solid density. In the present work, the whole strand is divided into the liquid zone (I), mushy zone (II), solidified shell above the solidification end (III), and final solidified strand (IV), as shown in Figure 6. For the liquid zone (I), there is no solid phase. In the mushy zone (II), the columnar or equiaxed phase contracts toward the slab surface with the decreasing temperature. As the liner shrinkage in the lateral direction could only compensate for one-third of the volume shrinkage, the existing liquid phase will transport to feed the volume shrinkage. However, for the solid shell region (III), there is no liquid steel. In order to keep the calculation convergence, the solid density is modified as ρ s = ρ s,ref1(1 + (1/3)·β s(T s − T ref1)) and the lateral linear shrinkage can fully compensate for the volume shrinkage. Meanwhile, the solid reference density ρ s,ref1 and temperature T ref1 are updated. With the center liquid steel finally solidified (zone IV), the columnar or equiaxed phase contraction will not affect solute distribution. So, the reference density ρ s,ref2 is redefined and the solid density does not change any more in the later stage. It should be noted that the reference data (ρ ref1, ρ ref2, T ref1) is dependent on the solidification behavior and should be transferred from the previous grid to the next one with casting speed. During the numerical simulation, the physical properties and process parameters are shown in Table I.

Fig. 6
figure 6

Schematic diagram of the different zones in the strand

Full size image
Table I Physical Properties and Process Parameters for Simulation
Full size table

In this article, a 2-D model from the meniscus to the solidification end is built to study the fluid flow and solute transport during the slab continuous casting process. In the model, the rectangular finite volume mesh is used. The grid size in the transverse direction is 2 mm and that in the casting direction is from 4 to 12 mm. During the solution procedure, the conservation equations for momentum, enthalpy, species, and grain growth are solved by control-volume-based FLUENT software. The liquid, columnar, and equiaxed phases share a single pressure field, which is solved by a phase coupled SIMPLE algorithm. In the iteration, the physical properties and intermediate quantities are updated first. Then, the exchange terms \( \left( {M_{\text{le}} ,M_{\text{lc}} ,M_{\text{ds}}^{\text{e}} ,M_{\text{ds}}^{\text{c}} ,U_{\text{le}} ,U_{\text{lc}} ,C_{\text{lc}} ,C_{\text{le}} } \right) \) and thermal contracting velocity (u c,x ) are calculated based on the data of the last time-step. Finally, the conservation equations are solved simultaneously, which means that they are coupled by the phase exchange terms and source terms. In the model, the calculated enthapy residual should be less than 10−6 and the convergence limit of other items is 10−4.

Results and Discussion

In order to understand the solidification structure and solute segregation behavior, a slice sample is cut from Q345 steel slab with the transverse section of 250 mm × 1800 mm, and then is etched by hot acid, as shown in Figure 7(a). The columnar length at the inner arc side is 107 mm, while that at the external arc side is 78 mm. As the solute segregation cannot be seen from the etched macrograph, the steel filings are obtained by boring along the transverse direction with a diameter of 5-mm drill and analyzed with the carbon-sulfur analyzer, as shown in Figure 7(b). With the distance from the slab surface, solute segregation undergoes ups and downs. It is observed that the positive segregation forms in the center accompanied by negative segregation in the periphery zone. In order to explore the main reason for center segregation formation, the solidification shrinkage, thermal shrinkage, grain sedimentation, and thermal flow will be investigated individually in the following part.

Fig. 7
figure 7

(a) Slab-etched macrograph and (b) measured solute segregation along the transverse direction

Full size image

The Effect of Solidification Shrinkage

In this section, the liquid steel solidifies with the columnar phase and the densities of liquid and solid phases are assumed to be constant; hence, ρ l = 7000 kg/m3 and ρ s = 7220 kg/m3. Only the solidification shrinkage on the fluid flow and solute transport is investigated in this section.

With heat extracted from the slab surface, the solid shell thickness gradually increases with the distance from the meniscus. Near the solidification end, some liquid steel still remains in the center part, as shown in Figure 8(a). Figure 8(b) illustrates the liquid velocity along the transverse direction at 18.1 m from the meniscus. The longitudinal velocity is more negative in the slab center, which means that the liquid steel moves faster to compensate for solidification shrinkage. The lateral velocity is positive at the inner arc side, while it is negative at the external arc side; this indicates that liquid steel moves from the center part to the columnar root near the solidification end, as shown in Figure 8(c). It should be noted that liquid solute concentration is obviously larger than that of the columnar phase and is not evenly distributed in the liquid pool, as shown in Figure 8(d). As liquid steel moves to the columnar root, the solute element will also transport from the slab center to the periphery zone.

Fig. 8
figure 8

(a) Liquid fraction in the longitudinal section, (b) liquid velocities along the transverse direction, (c) schematic diagram of fluid flow, and (d) solute concentration of different phases at 18.1 m from the meniscus

Full size image

Figures 9(a) and (b) show the carbon segregation in the longitudinal section and along the transverse direction with the solidification shrinkage considered. The solute segregation is slightly positive in the middle part, and it decreases obviously near the slab center. That is because the density of the columnar phase is larger than that of the liquid phase and enriched liquid steel is sucked to the columnar root to compensate for the solidification shrinkage. As the solute element transports with the fluid flow, the negative segregation forms in the slab center. Therefore, the solidification shrinkage is not the main reason for the center positive segregation formation.

Fig. 9
figure 9

Carbon segregation (a) in the longitudinal section and (b) along the transverse direction

Full size image

The Effect of Thermal Shrinkage

The solidification shrinkage is caused by the density difference between the liquid and solid, while the thermal shrinkage is due to the decreasing temperature. With the solid density assumed to be a function of temperature ρ s = 7000·(1 + β s(T s − T ref)), the columnar phase contracting behavior can be obtained by the thermal shrinkage model. Accordingly, the effect of the thermal contraction on the fluid flow and solute transport is discussed in this section.

Figure 10 shows the contracting velocity and the temperature at the columnar front along the casting direction. Due to a large amount of heat extracted from the slab surface, the columnar phase contracts intensely in the mold zone. As the cooling rate gradually decreases in the secondary cooling zone, the contracting velocity decreases and drops between each conjunction. Because less latent heat needs to dissipate near the solidification end, the temperature decreases quickly, causing the columnar front to contract intensively. In order to deeply understand the fluid flow and solute transport with thermal shrinkage, three positions (A, B, and C) with 17, 17.7, and 18 m from the meniscus are monitored.

Fig. 10
figure 10

Contracting velocity and temperature at the columnar front along the casting direction

Full size image

Figure 11(a) shows the lateral velocities of the columnar and liquid phases along the transverse direction in position A. It can be seen that the lateral velocity of the columnar phase is negative at the external arc side and positive at the inner arc side, which means the columnar dendrite contracts from the columnar front to the slab surface with the decreasing temperature. Because the thermal contraction is not enough to compensate for volume shrinkage, the liquid velocity is larger than that of the columnar phase. With the proceeding of the solidification, the fluid flow pattern near the columnar root is changed, as shown in Figure 11(b). The liquid phase moves contrarily to the contraction of the columnar phase, which means the liquid phase is squeezed out. However, near the columnar front region, the liquid phase still moves in the same direction with the columnar phase to compensate for volume shrinkage. Figure 11(c) shows that the fluid flow pattern in position C is totally different and the liquid steel moves opposite to the slab center, compared with that in Figure 11(a). That is because the center temperature decreases quickly near the solidification end and the cooling rate near the slab center increases obviously, as shown in Figure 11(d), leading to the sharp increase of the contracting velocity. As the columnar phase contracts toward the slab surface, the solute-enriched liquid is squeezed out and transports toward the slab center.

Fig. 11
figure 11

Lateral velocities of columnar and liquid phases along the transverse direction in positions (a) A, (b) B, and (c) C, and (d) the cooling rate along the transverse direction

Full size image

Figure 12(a) shows the carbon segregation and liquid fraction along the casting direction. It is observed that the solute segregation decreases first before arriving at position B and then turns to rise significantly with a further increase in the distance from the meniscus. That is because the liquid phase first transports toward the columnar root to compensate for thermal shrinkage and then is squeezed out with the columnar phase contracting intensively. As the solute element transports with fluid flow, the center positive segregation and the negative segregation in the periphery part come into being, as shown in Figure 12(b). So, it is demonstrated that the center positive segregation accompanied by the negative segregation in the periphery zone is mainly caused by thermal shrinkage near the solidification end.

Fig. 12
figure 12

(a) Center carbon segregation and liquid fraction along the casting direction and (b) carbon segregation along the transverse direction

Full size image

The Effect of Grain Sedimentation and Thermal Flow

In this section, the equiaxed grain growth is taken into account and the Boussinesq method[14] is used to consider grain sedimentation and thermal flow. In order to avoid the volume shrinkage during solidification, the liquid and solid densities are assumed to be equal.

Figure 13(a) shows the equiaxed fraction at the external arc side exceeds the critical fraction (f scr = 0.49), while that at the inner arc side is still not enough. That is because the initial equiaxed grains near the culumnar front are free to move and sink with gravity force, as shown in Figure 13(b). The lateral velocity of the equiaxed phase is negative, which means the equiaxed grains transport from the inner arc side to the external arc side. The longitudinal velocity of the equiaxed phase is more negative than the casting speed, so equiaxed grains sedimentate along the columnar front. As equiaxed grains are solute depleted, the grain sedimentation will also affect solute transport.

Fig. 13
figure 13

(a) Equiaxed phase distribution in the longitudinal section and (b) equiaxed velocity along the transverse direction

Full size image

Figure 14(a) shows the distribution of different phases along the transverse direction at 15.3 m from the meniscus. It can be seen that the columnar front stops advancing and the columnar-to-equiaxed transition (CET) has already completed. The columnar length at the external arc side is 80 mm and that at the inner arc side is 105 mm, which shows good agreement with the measured data from the etched macrograph, as shown in Figure 7(a). Because the equiaxed fraction exceeds the coherent fraction and the volume shrinkage is not considered in this section, the liquid steel will not move around in the later solidification and the solute segregation pattern does not change any more, as shown in Figure 14(b). It is found that the carbon segregation is asymmetrical with grain sedimentation, and solute concentration in the equiaxed zone at the external arc side (zone A1) is negative. With the solute element enriching at the inner arc side, the positive segregation near the CET (position B1) forms. Therefore, the grain sedimentation and thermal flow mainly affect the positive segregation near the CET position at the inner arc side (position B1) and the negative segregation at the external arc side (zone A1).

Fig. 14
figure 14

(a) Phase fraction and (b) carbon segregation along the transverse direction at 15.3 m from the meniscus

Full size image

Multiple Effects on Macrosegregation Formation

In the continuous casting process, the solute distribution is affected by solidification shrinkage, thermal shrinkage, grain sedimentation, and thermal flow simultaneously, so the multiple effects mentioned previously will be taken into account. The liquid and solid densities are assumed to be functions of temperature, namely, ρ s = 7220·(1 + β s(T − T ref)) and ρ l = 7000·(1 + β l(T − T ref)).

Figure 15(a) shows the liquid fraction and longitudinal velocity along the transverse direction at 15.9 m from the meniscus. It is illustrated that some liquid phase remains in the liquid pool and the equiaxed fraction has already exceeded the coherent fraction. With the thermal and solidification shrinkage considered, the liquid phase moves faster to compensate for volume shrinkage. Figure 15(b) illustrates the distribution of solute segregation along the transverse direction. It is observed that a positive segregation forms near the CET at the inner arc side (position B1), but it is clearly weak compared with that in Figure 14(b), which is due to the fluid flow caused by volume shrinkage. It is also found that the positive segregation in the slab center is not formed, so the solute distribution will still be affected by thermal and solidification shrinkage in the later stage.

Fig. 15
figure 15

(a) Liquid fraction and longitudinal velocity and (b) carbon segregation along the transverse direction at 15.9 m from the meniscus

Full size image

Figure 16 illustrates the calculated and measured carbon segregation along the transverse direction. The center positive segregation and the negative segregation in the periphery zone are formed in the solidified slab, which is mainly caused by the thermal shrinkage in the later solidification. Since the equiaxed grains sink to the external arc side, the carbon segregation shows slightly negative in zone A1. With solute element enriching at the inner arc side, the positive segregation near position B1 comes into being. As the fluid flow caused by SEN and secondary electromagnetic stirring is not considered, there are some deviations between the measured and calculated data near the slab surface and in the middle part.

Fig. 16
figure 16

Measured and calculated carbon segregation along the transverse direction

Full size image

In this article, the slab surface is assumed to be the fixed side and the solid phase contracts directionally, which is not very reasonable in the mold zone. As the initial solidified shell is thin, it also deviates from the copper mold with thermal shrinkage. Therefore, the advanced model considering solid thermal/mechanical behavior and fluid flow should be developed to describe the solute redistribution in the continuous casting process.

Conclusions

Based on the cooling rate and density variation, a thermal shrinkage model is built to obtain the contracting behavior of solid phase. Moreover, the thermal shrinkage model is coupled with the multiphase solidification model to investigate multiple effects on the fluid flow and solute transport during the slab continuous casting process. The results demonstrated that the center positive segregation and the negative segregation in the periphery zone are mainly caused by thermal shrinkage. The following conclusions can be drawn.

  1. 1.

    With the solidification shrinkage being taken into account, the liquid steel moves from the center part to the columnar root region, leading to the negative segregation in the slab center.

  2. 2.

    Because the center temperature decreases sharply near the solidification end and the columnar phase contracts intensively with thermal shrinkage, the solute-enriched liquid phase is squeezed out to the slab center, resulting in the center positive segregation accompanied by the negative segregation in the periphery zone.

  3. 3.

    With the effects of grain sedimentation and thermal flow, the initial equiaxed grains sink with the gravity force, so the negative segregation at the external arc side (zone A1) and positive segregation near the CET at the inner arc side (position B1) come into being.

  4. 4.

    In the continuous casting process, the grain sedimentation and thermal flow only influence solute transport before equiaxed grains impinge with each other, while the solidification and thermal shrinkages still affect solute redistribution in the later solidification.