Introduction

The argon–oxygen decarburization (AOD) process is the most common process for the refining of stainless steel.[1] Owing to violent agitation caused by the high blowing rates, the AOD vessel has very good mixing characteristics.[2,3,4,5] Nowadays, top-blowing is employed in conjunction with side-blowing in the early part of the decarburization stage in order to maximize oxygen delivery into the melt.[6] As illustrated in Figure 1, two main reaction areas can be identified during combined blowing: (1) inside the gas plume, and (2) on the surface of the bath, including metal droplets.[7,8]

Fig. 1
figure 1

Schematic illustration of combined blowing in an AOD vessel

Full size image

Numerous reaction models have been proposed for the decarburization[8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] and nitrification[7,38,39,40] of steel in an AOD vessel. The majority of the models applicable for side-blowing decarburization have been reviewed elsewhere.[21,41] Despite the vast number of reaction models available, there are only a few models that explicitly address the reactions during top-blowing in the AOD process. Arguably the most relevant examples found in the literature are those proposed by Watanabe and Tohge,[9] Tohge et al.,[17] Kikuchi et al.,[23,42] and Wei et al.[8,21,22,26,28] Some similarities in the modeling setting can be found in the reaction models proposed for the VOD process.[41,43] To summarize, it can be stated that the top-blowing models proposed so far are capable of predicting the decarburization with a reasonable degree of accuracy and have laid the basic foundations for further investigations. However, more research is required along these lines in order to obtain information on the related reaction interfaces and chemical reaction rate phenomena.

In our previous work,[29,30] a fundamental model was proposed and validated for the reactions inside the bath during side-blowing in the AOD process. Consequently, the aim of this work was to extend the original model by developing a mathematical model for reactions during top-blowing. In order to provide more information on the controlling mechanisms and dynamics of decarburization during top-blowing, the model combines the transient solution of multicomponent equilibria with a description of the constraining mass transfer. This paper presents the description of the model, while validation and preliminary results are presented in the second part of this work.[44]

Derivation of the Model

The model was programmed using C++, and the main assumptions can be summarized as follows:

  1. 1.

    The top-blown oxygen may react with iron and the species dissolved in iron, dissolve in the metal bath, or escape through the gas exit.

  2. 2.

    Reactions between gas, metal, and slag species take place simultaneously at the surface of the cavity as well as at surface of the metal droplets generated due to top-blowing.

  3. 3.

    Owing to the high temperature, the reaction rates are assumed to be limited by mass transfer onto and from the reaction interfaces, and hence the reaction interfaces are able to reach their constrained thermodynamic equilibrium at any given moment.

  4. 4.

    Conservation of mass and heat is solved successively.

The liquid metal phase is assumed to consist of Fe as the solvent and Cr, Mn, Si, C, O, N, Ni, Al, and S as solutes. The gas phase consists of O2, CO, CO2, N2, and Ar. The slag phase consists of FeO, Cr2O3, MnO, SiO2, CaO, MgO, Al2O3, CaF2, and MeO x , which is a generic oxide and depicts the residual species. The reaction system considered is defined by the following reactions:

$$ \{ {\text{O}}_{2} \} \rightleftharpoons 2[{\text{O}}], $$
(1)
$$ [{\text{C}}] + \frac{1}{2}\{ {\text{O}}_{2} \} \rightleftharpoons \{ {\text{CO}}\} , $$
(2)
$$ [{\text{C}}] + \{ {\text{O}}_{2} \} \rightleftharpoons \{ {\text{CO}}_{2} \} , $$
(3)
$$ {\text{Fe}}_{{({\text{l}})}} + \frac{1}{2}\{ {\text{O}}_{2} \} \rightleftharpoons ({\text{FeO}}), $$
(4)
$$ 2[{\text{Cr}}] + \frac{3}{2}\{ {\text{O}}_{2} \} \rightleftharpoons ({\text{Cr}}_{2} {\text{O}}_{3} ), $$
(5)
$$ [{\text{Mn}}] + \frac{1}{2}\{ {\text{O}}_{2} \} \rightleftharpoons ({\text{MnO}}), $$
(6)
$$ [{\text{Si}}] + \{ {\text{O}}_{2} \} \rightleftharpoons ({\text{SiO}}_{2} ). $$
(7)

The rate expressions were formulated as reversible according to a modified Law of Mass Action, a method that has been discussed more comprehensively in our earlier work.[45,46] More specifically, the rate expressions are defined such that concentrations are replaced with activities and partial pressures, as illustrated below for the oxidation of the dissolved carbon to carbon monoxide:

$$ R^{\prime\prime} = k_{\text{f}} \left( {a_{{[{\text{C}}]}} p_{{{\text{O}}_{2} }}^{1/2} - \frac{{p_{\text{CO}} }}{K}} \right), $$
(8)

where k f is the forward reaction rate coefficient, a [C] is the activity of dissolved carbon, \( p_{{{\text{O}}_{2} }} \) is the partial pressure of gaseous oxygen, and K is the equilibrium constant.

Conservation of Mass

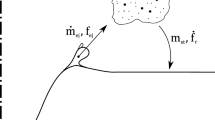
The observed system consists of gas input, gas exit, two reaction interfaces, and three bulk volumes, as shown in Figure 2. It should be noted that the reaction interfaces have neither thickness nor mass.

Fig. 2
figure 2

Schematic illustration of the interaction of the reaction interfaces

Full size image

It has been proposed that during simple side-blowing, post-combustion takes place in the off-gas flue, but not in the AOD vessel itself.[47] However, during combined top- and side-blowing, a part of the top-blown oxygen may be consumed in the post-combustion of CO to CO2 before the gas jet impacts the bath surface.[8] In order to simplify the modeling setting, the model proposed in this paper considers post-combustion only at the reaction interfaces. Because the entrainment of cold air from the atmosphere outside the vessel can be neglected under normal operating conditions,[48] the top-lance and the tuyères can be taken as the only gas inputs of the system. More specifically, it was assumed that the side-blown gas exits the metal bath through the plume eye and comes into contact with the top-blown gas. The mass flow of gaseous species through the top lance into the observed system is given by

$$ \dot{m}_{{{\text{G}},{\text{in}},{\text{lance}}}} = \dot{V}_{{{\text{G}},{\text{lance}}}} \rho_{{{\text{G}},{\text{STP}}}} , $$
(9)

where \( \dot{V}_{{{\text{G}},{\text{lance}}}} \) is the volumetric gas flow rate through top lance (in Nm3/s) and \( \rho_{{{\text{G}},\,{\text{STP}}}} \) is the density of the gas mixture under standard temperature and pressure according to the DIN 1343 standard[49]: 273.15 K (0 °C) and 101325 Pa. The model is coupled with the earlier-proposed model for side-blowing decarburization,[29] which calculates the mass flow of gaseous species from the plume eye (into the observed system). In the case of inert gases, the mass flow rate of gas from the plume eye is equal to the mass flow rate of gas from the tuyères. Preventing the suction of atmospheric gas, the mass flux of gas exiting the system is obtained from

$$ \dot{m}_{{{\text{G,out}}}} = \hbox{max} \left( {\underbrace {{\dot{m}_{{{\text{G}}, \; {\text{in,lance}}}} + \dot{m}_{{{\text{G}}, \; {\text{in,plume}}}} }}_{{{\text{gas}}\;{\text{injection}}}} - \underbrace {{\dot{m}_{{{\text{G}}, \; {\text{cav}}}} - \dot{m}_{{{\text{G,md}}}} }}_{{{\text{gas} \;{\text{consumption}}}\;}},0} \right), $$
(10)

where \( \dot{m}_{{{\text{G,in}},{\text{plume}}}} \) is the mass flow of gas from the plume eye, \( \dot{m}_{{{\text{G,cav}},}}\) is the mass flow of gas from the cavity interface, and \( \dot{m}_{{{\text{G}},{\text{md}}}} \) is the mass flow of gas from the metal droplet interface. In order to avoid the mathematical complexity of the Maxwell–Stefan equations and the generalized Fick’s law, an effective diffusion model was employed.[50] The conservation of species at the two reaction interfaces is defined by the reaction rates and mass-transfer rates onto and from the reaction surfaces. Employing a first-order upwind scheme for the Stefan flow, the conservation of species i in phase ψ at reaction interface ω is given by

$$ \underbrace {{\beta_{i,\psi ,\omega } \rho_{\psi ,\omega } (y_{{i,{\rm B}}} - y_{i,\omega }^{*} )}}_{{{\text{mass}}\,{\text{transport}}}} + \underbrace {{\hbox{max} (m_{\psi ,\omega }^{\prime\prime} ,0)y_{i,B} - \hbox{max} ( - m_{\psi ,\omega }^{\prime\prime} ,0)y_{i,\omega }^{*} }}_{{{\text{Stefan}}\;{\text{flow}}}} + \underbrace {{\mathop \sum \limits_{k = 1}^{r} R_{k,\omega }^{\prime\prime} \bar{\nu }_{i,k} }}_{{{\text{chemical}}\;{\text{reactions}}}} = 0, $$
(11)

where β is the mass-transfer coefficient, ρ is the density, \( y_{{i,\,{\text{B}}}} \) is the mass fraction of species i in the bulk phase (i.e., metal bath, gas jet, or top slag), y * i,ω is the interfacial mass fraction of species i, m″ is the total mass flux, R″ is the reaction rate, and \( \bar{\nu } \) is the mass-based stoichiometric coefficient. It should be noted that all properties are specific to the reaction interface in question. In order to account for conservation of mass within the metal droplets, the following expression is employed for species in the metal phase at the metal droplet interface:

$$ \underbrace {{\left( {\frac{{m_{\text{md}} }}{{A_{\text{md}} \bar{t}_{\text{md}} }} - m_{{{\text{L}},{\text{md}}}}^{\prime\prime} } \right)\bar{\eta }_{{i,{\text{M}},{\text{md}}}} \left( {y_{{i,{\text{bath}}}} - y_{{i,{\text{md}}}}^{*} } \right)}}_{{{\text{mass}}\;{\text{transport}}}} + \underbrace {{m_{{{\text{L}},{\text{md}}}}^{\prime\prime} y_{{i,{\text{bath}}}} }}_{{{\text{Stefan}}\;{\text{flow}}}} + \underbrace {{\mathop \sum \limits_{k = 1}^{r} R_{{k,{\text{md}}}}^{\prime\prime} \bar{\nu }_{i,k} }}_{{{\text{chemical}}\;{\text{reactions}}}} = 0, $$
(12)

where m md, A md, and \( \bar{t}_{\text{md}} \) are the mass, surface area, and average residence time of the metal droplets, respectively, and \( \bar{\eta }_{{i,{\text{M}},{\text{md}}}} \) is the average microkinetic efficiency for mass transfer of species i in the metal droplets. The total mass flux of the metal phase is subject to the constraint \( m_{{{\text{L}},{\text{md}}}}^{\prime\prime} \le \frac{{m_{\text{md}} }}{{A_{\text{md}} \bar{t}_{\text{md}} }}. \) The average microkinetic efficiency was calculated based on the average residence time of the metal droplets:

$$ \bar{\eta }_{{i,{\text{M}},{\text{md}}}} = \frac{{y_{{i,{\text{bath}}}} - y_{{i,{\text{md}}}} }}{{y_{{i,{\text{bath}}}} - y_{{i,{\text{md}}}}^{*} }} = 1 - \exp \left( { - \beta_{{i,{\text{L}},{\text{md}}}} \frac{{A_{\text{md}} }}{{V_{\text{md}} }}\bar{t}_{\text{md}} } \right), $$
(13)

where y i,md is the composition of species i in the metal droplets. The mass-based stoichiometric coefficients \( \bar{\nu }_{i,k} \) are defined in relation to key components:

$$ \bar{\nu }_{i,k} = \nu_{i,k} \frac{{M_{i} }}{{M_{K,k} }}, $$
(14)

where ν i,k is the stoichiometric coefficient of species i in reaction k, \( M_{K,k} \) is the molar mass of the key component of reaction k, and M i is the molar mass of species i. The key components of the reactions shown in Eqs. [1] through [7] are O2, C, C, Fe, Cr, Mn, and Si, respectively. The total mass flux of phase ψ at reaction interface ω is given by

$$ m_{\psi ,\omega }^{\prime\prime} = - \sum\limits_{i = 1}^{n} {\sum\limits_{k = 1}^{r} {\varGamma_{i,\psi } R_{k,\omega }^{\prime\prime} \bar{\nu }_{i,k} } } , $$
(15)

where \( \varGamma_{i,\psi } \) is a binary operator, which is defined as 1 if species i is in phase ψ and 0 otherwise. The total mass flows \( \dot{m}_{\psi ,\omega } \) are obtained by multiplying the mass flux \( m_{\psi ,\omega }^{\prime\prime} \) m ψ,ω ″ by the corresponding interfacial area A ω . Employing the implicit Euler method for time integration, the conservation of species i in the metal bath, top-blown gas, and top slag is defined by Eqs. [16] through [18], respectively.

$$ - \beta_{{i,{\text{L}},{\text{cav}}}} \rho_{{{\text{L}},{\text{cav}}}} A_{\text{cav}} \left( {y_{{i,{\text{bath}}}} - y_{{i,{\text{cav}}}}^{*} } \right) - \hbox{max} \left( {m_{{{\text{L}},{\text{cav}}}}^{\prime\prime} ,0} \right)A_{\text{cav}} y_{{i,{\text{bath}}}} + \hbox{max} \left( { - m_{{{\text{L}},{\text{cav}}}}^{\prime\prime} ,0} \right)A_{\text{cav}} y_{{i,{\text{cav}}}}^{*} - \left( {\frac{{m_{\text{md}} }}{{\bar{t}_{\text{md}} }} - m_{{{\text{L}},{\text{md}}}}^{\prime\prime} A_{\text{md}} } \right)\bar{\eta }_{{i,{\text{M}},{\text{md}}}} \left( {y_{{i,{\text{bath}}}} - y_{{i,{\text{md}}}}^{*} } \right) - m_{{{\text{L}},{\text{md}}}}^{\prime\prime} A_{\text{md}} y_{{i,{\text{bath}}}} - \frac{{m_{\text{bath}} y_{{i,{\text{bath}}}} - m_{\text{bath}}^{{{\text{t}} - \Delta{t}}} y_{{i,{\text{bath}}}}^{{{\text{t}} - \Delta{t}}} }}{\Delta{ t}} = 0 $$
(16)
$$ \mathop \sum \limits_{\omega } \left[ { - \beta_{{i,{\text{G}},\omega }} \rho_{{{\text{G}},\omega }} A_{\omega } \left( {y_{{i,{\text{jet}}}} - y_{i,\omega }^{*} } \right) - \hbox{max} \left( {m_{{{\text{G}},\omega }}^{\prime\prime} ,0} \right)A_{\omega } y_{{i,{\text{jet}}}} + \hbox{max} \left( { - m_{{{\text{G}},\omega }}^{\prime\prime} ,0} \right)A_{\omega } y_{i,\omega }^{*} } \right] + \dot{m}_{{{\text{G}},{\text{in}},{\text{lance}}}} y_{{i,{\text{in}},{\text{lance}}}} + \dot{m}_{{{\text{G}},{\text{in,plume}}}} {\text{y}}_{{i,{\text{in}},{\text{plume}}}} - \dot{m}_{{{\text{G,out}}}} y_{{i,{\text{jet}}}} - \frac{{m_{\text{jet}} y_{{i,{\text{jet}}}} - m_{\text{jet}}^{t - \Delta t} y_{{i,{\text{jet}}}}^{t - \Delta t} }}{\Delta t} = 0, $$
(17)
$$ \mathop \sum \limits_{\omega } \left[ { - \beta_{{i,{\text{S}},\omega }} \rho_{{{\text{S}},\omega }} A_{\omega } \left( {y_{{i,{\text{slag}}}} - y_{i,\omega }^{*} } \right) - \hbox{max} \left( {m_{{{\text{S}},\omega }}^{\prime\prime} ,0} \right)A_{\omega } y_{{i,{\text{slag}}}} + \hbox{max} \left( { - m_{{{\text{S}},\omega }}^{\prime\prime} ,0} \right)A_{\omega } y_{i,\omega }^{*} } \right] - \frac{{m_{\text{slag}} y_{{i,{\text{slag}}}} - m_{\text{slag}}^{{t - {\Delta }t}} y_{{i,{\text{slag}}}}^{{t - {\Delta }t}} }}{\Delta t} = 0, $$
(18)

where m bath, m jet, and m slag are the masses of the metal bath, gas jet, and top slag, respectively; and Δt is the time step. The conservation equations for the total mass of the bulk phases (for the metal bath, gas jet, and top slag) are defined correspondingly by summation of the mass transport terms and fluxes of species that are relevant to the bulk phase in question. Metal losses to dust were not accounted for as their effect on the composition of the metal bath is negligible.

Conservation of Heat

Temperature increase is defined by the difference in heat generation and heat losses. While heat is generated by exothermic reactions, it is consumed by endothermic reactions as well as heat losses through the refractory lining, and top slag, and exiting gas. The conservation of heat at the cavity interface is defined according to

$$ \underbrace {{\alpha_{{{\text{L}},{\text{cav}}}} (T_{\text{bath}} - T_{\text{cav}}^{*} ) + \alpha_{{{\text{G}},{\text{cav}}}} (T_{\text{jet}} - T_{\text{cav}}^{*} ) + \alpha_{{{\text{S}},{\text{cav}}}} (T_{\text{slag}} - T_{\text{cav}}^{*} )}}_{{{\text{heat}}\;{\text{transport}}}} - \underbrace {{\mathop \sum \limits_{k = 1}^{r} R_{{k,{\text{cav}}}}^{\prime\prime} \Delta h_{k} }}_{{{\text{chemical}}\,{\text{reactions}}}} = 0 $$
(19)

where α is the heat-transfer coefficient, T bath is the temperature of the metal bath, T *cav is the temperature of the cavity reaction interface, T jet is the temperature of the gas jet, and Δh k is the specific reaction enthalpy of reaction k. The conservation of heat at the metal droplet interface was defined according to

$$ \underbrace {{\frac{{m_{\text{md}} }}{{A_{\text{md}} \bar{t}_{\text{md}} }}c_{{{\text{p}},{\text{L}}}} \bar{\eta }_{{{\text{H}},{\text{md}}}} (T_{\text{bath}} - T_{\text{md}}^{*} ) + \alpha_{{{\text{G}},{\text{md}}}} (T_{\text{jet}} - T_{\text{md}}^{*} ) + \alpha_{{{\text{S}},{\text{md}}}} (T_{\text{slag}} - T_{\text{md}}^{*} )}}_{{{\text{heat}}\;{\text{transport}}}} - \underbrace {{\mathop \sum \limits_{k = 1}^{r} R_{{k,{\text{md}}}}^{\prime\prime} \Delta h_{k} }}_{{{\text{chemical}}\;{\text{reactions}}}} = 0 $$
(20)

where T *md is the interfacial temperature of the metal droplets, and \( \bar{\eta }_{{{\text{H}},{\text{md}}}} \) is the average microkinetic efficiency of heat transfer in the metal droplets:

$$ \bar{\eta }_{{{\text{H}},{\text{md}}}} = \frac{{T_{\text{bath}} - T_{\text{md}} }}{{T_{\text{bath}} - T_{\text{md}}^{*} }} = 1 - \exp \left( { - \alpha_{{{\text{L}},{\text{md}}}} \frac{{A_{\text{md}} }}{{m_{\text{md}} c_{{{\text{p}},{\text{L}}}} }}\bar{t}_{\text{md}} } \right), $$
(21)

where T md is the temperature of the metal droplets. Employing the implicit Euler method for time integration, the conservations of heat in the metal bath, in the top-blown gas, and in the top slag can be expressed according to Eqs. [22] through [24], respectively.

$$ - \alpha_{{{\text{L}},{\text{cav}}}} A_{\text{cav}} (T_{\text{bath}} - T_{\text{cav}}^{*} ) - \frac{{m_{\text{md}} }}{{\bar{t}_{\text{md}} }}c_{{{\text{p}},{\text{L}}}} \bar{\eta }_{{{\text{H}},{\text{md}}}} (T_{\text{bath}} - T_{\text{md}}^{*} ) - \mathop \sum \limits_{\omega } \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{k = 1}^{r} \varGamma_{i,L} R_{k,\omega }^{\prime\prime} \bar{\nu }_{i,k} A_{\omega } c_{{\text{p}},i} (T_{\text{bath}} - T_{\omega }^{*} ) - q_{\text{lining}} A_{\text{lining}} - m_{\text{bath}} c_{{{\text{p}},{\text{bath}}}} \frac{{T_{\text{bath}} - T_{\text{bath}}^{t - \Delta t} }}{\Delta t} = 0, $$
(22)
$$ \mathop \sum \limits_{\omega } \left[ { - \alpha_{{{\text{G}},\omega }} A_{\omega } \left( {T_{\text{jet}} - T_{\omega }^{*} } \right) - \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{k = 1}^{r} \varGamma_{{i,{\text{G}}}} R_{k,\omega }^{\prime\prime} \bar{\nu }_{i,k} A_{\omega } c_{{{\text{p}},i}} \left( {T_{\text{jet}} - T_{\omega }^{*} } \right)} \right] - \dot{m}_{{{\text{G}},{\text{in}},{\text{lance}}}} \mathop \smallint \limits_{{T_{{\text{in}},{\text{lance}}} }}^{{T_{\text{jet}} }} c_{{{\text{p}},{\text{lance}}}} {\text{d}}T - \dot{m}_{{{\text{G}},{\text{in}},{\text{plume}}}} \mathop \smallint \limits_{{T_{\text{plume}} }}^{{T_{\text{jet}} }} c_{{{\text{p}},{\text{plume}}}} {\text{d}}T - m_{\text{jet}} c_{{{\text{p}},{\text{jet}}}} \frac{{T_{\text{jet}} - T_{\text{jet}}^{{{\text{t}} - {\Delta t}}} }}{\Delta t} = 0, $$
(23)
$$ \mathop \sum \limits_{\omega } \left[ { - \alpha_{{{\text{S}},\omega }} A_{\omega } \left( {T_{\text{slag}} - T_{\omega }^{*} } \right) - \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{k = 1}^{r} \varGamma_{{i,{\text{S}}}} R_{k,\omega }^{\prime\prime} \bar{\nu }_{i,k} A_{\omega } c_{{{\text{p}},i}} \left( {T_{\text{slag}} - T_{\omega }^{*} } \right)} \right] - q_{\text{slag}} A_{\text{slag}} - m_{\text{slag}} c_{{{\text{p}},{\text{slag}}}} \frac{{T_{\text{slag}} - T_{\text{slag}}^{{{\text{t}} - {\Delta t}}} }}{\Delta t} = 0, $$
(24)

where q lining is the heat flux through the refractory lining, A lining is the surface area of the refractory lining, q slag is the heat flux through the slag, and A slag is the cross-sectional surface area of the top slag. The values of A lining and A slag are calculated based on the geometry of the simulated converter. The heat flux through the refractory lining was set to q lining = 12,500 W/m2 as in our previous work.[29] The heat losses through the slag were determined on the basis of radiative heat transfer through the mouth of the vessel. Neglecting back-radiation, the radiative heat flux can be calculated as follows[51]:

$$ q_{\text{slag}} = \frac{{\sigma T_{\text{slag}}^{4} }}{{\left[ {\frac{{A_{\text{slag}} + A_{\text{mouth}} - 2A_{\text{slag}} F}}{{A_{\text{mouth}} - A_{\text{slag}} F^{2} }} + \left( {\frac{1}{{\varepsilon_{\text{S}} }} - 1} \right)} \right]}}, $$
(25)

where σ is the Stefan–Boltzmann constant; F is the view factor between the top slag and the converter mouth; A mouth is the cross-sectional area of the vessel mouth; and ɛ S is the emissivity of the slag phase, which was assumed to be ɛ S = 0.95. The view factor for the top slag in relation to the vessel mouth is determined by[51]

$$ F = \frac{1}{{2r_{\text{slag}}^{2} }}\left[ {z^{2} + r_{\text{slag}}^{2} + r_{\text{mouth}}^{2} - \left\{ {\left( {z^{2} + r_{\text{slag}}^{2} + r_{\text{mouth}}^{2} } \right)^{2} - 4r_{\text{slag}}^{2} r_{\text{mouth}}^{2} } \right\}^{1/2} } \right], $$
(26)

where z is the distance between the top slag and the vessel mouth, r slag is the radius of the top slag, and r mouth is the radius of the vessel mouth. The cooling effect of the side-blown gas on the metal bath temperature is calculated separately by the earlier-proposed model for side-blowing decarburization[29] and is not repeated here.

Geometry of the Cavity

The gas jet exits the lance nozzle at a supersonic velocity, but starts to spread and lose its velocity after the supersonic core. The entrainment of gases from the ambient atmosphere affects the gas jet not only by decreasing its velocity, but also by increasing its mass flow, and—if the ambient temperature is higher than that of the gas jet—by increasing its temperature.[52] Considering that the length of the supersonic region is typically 20 to 30 times the nozzle exit diameter at steelmaking temperatures,[53] it is apparent that the gas jet impacts the surface of the metal bath at subsonic velocity. Upon impact, the momentum of the gas jet forms a cavity on the bath surface,[53] while the liquid metal outside the cavity is pushed toward the refractory walls of the vessel in the radial direction.[5]

Molloy[54] distinguished three cavity modes, namely, dimpling, splashing, and penetrating. Dimpling refers to mere depression of the surface without droplet formation, while outwardly directed splashes start to form the edges of the depression when the mode changes to splashing. In the penetrating mode, the penetration depth is deeper, and outwardly directed splashes are reduced. The different modes can also be distinguished based on the frequency and amplitude of the cavity oscillation.[55] Figure 3 presents a schematic illustration of the gas jet impact area with a one-hole lance in the splashing mode.

Fig. 3
figure 3

Schematic illustration of the gas jet impact area with a one-hole lance

Full size image

In this work, the modeling setting was simplified by defining the reaction area between the gas jet and the metal bath as the surface area of the cavity. Because the surface of the cavity is in oscillating motion, the analysis must be based on quasi-steady-state flow conditions.[53,56] It has been suggested that chemical reactions[57,58] and the interference of top slag[57] do not affect the geometry of the cavity to a significant extent and on this account their effect was excluded in this work. In accordance with Cheslak et al.,[59] it was assumed that the geometry of the cavity follows the form of a paraboloid of revolution with an impact radius of r cav and an impinging depth of h cav (see Figure 3). The surface area of the paraboloid of revolution, excluding its base, can be calculated as follows[60]:

$$ A_{{{\text{cav}},1}} = \frac{\pi }{6}\frac{{r_{\text{cav}} }}{{h_{\text{cav}}^{2} }}\left[ {\left( {r_{\text{cav}}^{2} + 4h_{\text{cav}}^{2} } \right)^{3/2} - r_{\text{cav}}^{3} } \right]. $$
(27)

For a three-hole lance, the geometry is slightly more complicated. Depending on the inclination angle of the gas jets, the gas jets may either coalesce and form only one large cavity, or penetrate the bath surface as three separate jets, whereupon each gas jet will form its own cavity.[61,62] Even if the gas jets do not coalesce, the cavities may still coalesce provided that they are sufficiently close to each other[63] as shown in Figure 4. Observations with high-speed cameras[64] suggest that the cavities remain noncoalescing when the inclination angle is greater than 10 deg. In this work, it is assumed that the gas jets do not coalesce and that the number of cavities is equal to the number of the gas jets (see Figure 4(a)). Therefore, the total surface area of the cavities caused by a multihole lance can be calculated simply by multiplying the surface area of a single cavity with the number of exit ports in the top lance[52,65]:

$$ A_{\text{cav}} = n_{\text{lance}} \times A_{{{\text{cav}},1}} . $$
(28)

The effects of various operating parameters on the depth and form of the cavity have been studied extensively. In this work, the correlations for the geometry of the cavity were taken from Koria and Lange.[63] The equations required for calculating the depth and radius of the cavity are given in Table I. These are based on a dimensional analysis of experimental data on the penetration of oxygen jets in molten pig iron and pure iron-carbon alloys with both single- and multihole lances.[63] It should be noted that Eq. [35] is applicable only for diatomic ideal gases (e.g., O2 or N2) and their mixtures. For other gas mixtures, a more general expression for \( \dot{m}_{\text{t}} \) can be derived based on the equations presented by Koria.[66]

Fig. 4
figure 4

Schematic illustration of the gas jet impact area with a 3-hole lance with noncoalescing (a) and coalescing (b) cavities

Full size image
Table I Equations for Calculating the Geometry of the Cavity[63]
Full size table

Droplet Generation

The generation of metal droplets during top-blowing is important for steelmaking processes, because it brings about a considerable increase in the interfacial area available to chemical reactions.[67] The contribution of metal droplets to the decarburization rate during top-blowing in the AOD process has been acknowledged likewise.[7,8,23,42,68,69,70] However, foaming of the AOD slag does take place under typical operating conditions. Considering the high blowing rates and high viscosity of the slag, the behavior of slag should be somewhere between a void-free and an expanded slag. In such cases, the gas void fraction would depend on the gas velocity.[71]

Different mechanisms contribute to generation of metal droplets. If the momentum flux of the top-blown gas jet is sufficiently high, the liquid surface becomes unstable and the splashing of metal droplets occurs.[72] Standish and He[73] identified two regions of droplet generation: dropping and swarming. In the dropping region, single droplets are gradually formed and ejected. This is the mechanism of droplet generation when the gas flow rate is relatively low. When the gas flow rate is increased past a certain limit, the system reaches the swarming region and the mechanism of droplet generation changes so that not only single droplets but also large tears of liquid phase are ejected from the bath. Generation of metal droplets is also caused by side-blowing through a mechanism referred to as bubble bursting.[74,75,76,77] This phenomenon occurs when a rising gas bubble reaches the surface of the metal bath and bursts creating very small metal droplets from the thin film of metal around the bubble.[74,75,76,77] A related mechanism is the entrainment of large droplets due to jet formation, which is caused by the collapsing of the cavity after the rupture of the iron film.[76]

The secondary break-up of the metal droplets can occur due to various reasons, e.g., due to the aerodynamic forces of the gas jet,[78] impact on the slag layer[79] or bursting resulting from spontaneous CO nucleation within the droplet.[80] In the absence of suitable quantitative descriptions for the break-up mechanisms and due to uncertainties related to the trajectories of the droplets, the effect of the various break-up mechanisms on the droplet size distribution was not accounted for.

Based on the available knowledge, the lifespan of the metal droplets was assumed to consist of three successive steps. At first, the metal droplets are generated at the vicinity of the cavity, from which they are ejected onto a gas–metal–slag emulsion. This also includes metal droplets, which have been ejected into the atmosphere and land on the emulsion. Thereafter, the metal droplets pass though the emulsion layer, reacting simultaneously with gas and slag species. Finally, the metal droplets return to the metal bath, where they mix with the metal bath immediately. Based on experimental findings[81] it was assumed that the initial composition of the metal droplets corresponds to the bulk composition. Furthermore, the metal droplets were assumed to be spherical in geometry. This assumption should hold well for small droplets,[82] which are expected to form the majority of the surface area. Considering the distribution of emulsified metal droplets residing in the emulsion, their mass and surface area are obtained from the following equations:

$$ m_{\text{md}} = \mathop \sum \limits_{i} m_{{{\text{md}},i}} , $$
(36)
$$ A_{\text{md}} = \mathop \sum \limits_{i} \frac{{6m_{{{\text{md}},i}} }}{{d_{{{\text{md}},i}} \rho_{\text{L}} }}, $$
(37)

where m md,i and d md,i are the mass and diameter of the droplet size class i, respectively. As a matter of practice, the droplet distribution was calculated from a diameter of 0.1 mm up to the diameter corresponding to the largest 99.9 pct by weight using a step size of 0.1 mm. The mass of droplets in the size class i residing in the emulsion can be solved from

$$ m_{{{\text{md}},i}} = f_{{{\text{md}},i}} \dot{m}_{\text{md}} \hbox{min} \left( {t_{{{\text{md}},i}} ,t} \right), $$
(38)

where f md,i , \( \dot{m}_{\text{md}} \) and t md,i are the mass fraction of size class i at place of birth, the metal droplet generation rate and the residence time of size class i, respectively, and t is the time. The Sauter mean diameter of the metal droplets residing in the emulsion at a given moment is obtained from

$$ d_{{32,{\text{md}}}} = \frac{{6m_{\text{md}} }}{{\rho_{\text{L}} A_{\text{md}} }}. $$
(39)

Droplet generation rate

The blowing number, which relates the intensity of the jet momentum to the properties of the liquid metal, is defined by the following expression[67]:

$$ {\text{N}}_{\text{B}} = \frac{{\rho_{\text{G}} u_{\text{G}}^{2} }}{{2\sqrt {\sigma_{\text{L}} g\rho_{\text{L}} } }} = \frac{{\eta^{2} p_{\text{d}} }}{{\sqrt {\sigma_{\text{L}} g\rho_{\text{L}} } }}\quad {\text{where}}\quad \eta = \frac{{u_{\text{G}} }}{{u_{\text{j}} }}, $$
(40)

where u G denotes the critical gas velocity, σ L is the surface tension of the liquid steel, η is a constant, p d is the dynamic pressure of the gas jet, and u j is the axial velocity of the gas jet. The criterion for the Kelvin–Helmholtz instability, and thus the onset of droplet formation, is represented with a value of NB = 1.[67] The experimental results of other studies suggest that η is not independent of the lance height[83,84,85] or the gas jet angle.[86] Here, the variation of η as a function of the gas jet angle was treated in a similar fashion as by Alam et al.[86] Making use of the concept of blowing number, Subagyo et al.[67] proposed an empirical expression for droplet generation rate \( (\dot{m}_{\text{md}} ) \) in the splashing cavity mode:

$$ \frac{{\dot{m}_{\text{md}} }}{{\dot{V}_{{{\text{G}},\;{\text{lance}}}} }} = \frac{{({\text{N}}_{\text{B}} )^{3.2} }}{{\left[ {2.6 \times 10^{6} + 2.0 \times 10^{ - 4} ({\text{N}}_{\text{B}} )^{12} } \right]^{0.2} }}\quad R^{2} = 0.97, $$
(41)

where \( \dot{V}_{{{\text{G}},{\text{lance}}}} \) is the volumetric gas flow rate through the top lance (Nm3/s). As noted by Sarkar et al.[87] and Rout et al.,[88] Eq. [41] yields droplet generation rates which are considerably below the values estimated from plant data. According to Rout et al.,[88] one reason for the discrepancy is the fact that Eq. [41] has been derived for conditions corresponding to room temperature. Similar to Rout et al.,[88] Eq. [41] was modified such that the blowing number \( {\text{N}}_{\text{B}} \) and the volumetric gas flow rate \( \dot{V}_{{{\text{G}},{\text{lance}}}} \) are temperature corrected for the conditions at the point of impact:

$$ \frac{{\dot{m}_{\text{md}} }}{{\dot{V}_{{{\text{G}},{\text{lance}}}}^{\prime} }} = \frac{{({\text{N}}_{\text{B}}^{\prime} )^{3.2} }}{{\left[ {2.6 \times 10^{6} + 2.0 \times 10^{ - 4} ({\text{N}}_{\text{B}}^{\prime} )^{12} } \right]^{0.2} }}, $$
(42)

where NB′ is the modified blowing number and \( \dot{V}_{{{\text{G}},{\text{lance}}}}^{\prime} \) is the modified volumetric gas flow rate. The modified blowing number NB′ is obtained from Eq. [40] by employing the dynamic pressure at the point of impact. In this work, the dynamic pressure at the point of impact was calculated according to an experimental relationship proposed by Deo and Boom[52]:

$$ p_{\text{d}} = 230p_{0} \left( {\frac{{h_{\text{lance}} }}{{d_{\text{t}} }}} \right). $$
(43)

The modified gas flow rate is calculated as follows[88]:

$$ \dot{V}_{{{\text{G}},\,{\text{lance}}}}^{\prime} = \frac{{p_{{{\text{G}},{\text{STP}}}} }}{{p_{\text{G}} }}\frac{{T_{\text{G}} }}{{T_{{{\text{G}},{\text{STP}}}} }}\dot{V}_{{{\text{G}},\,{\text{lance}}}}, $$
(44)

where p G,STP is the standard pressure, p G is the total pressure of the gas at the impact point, T G is the temperature of the gas at the impact point and T G,STP is the standard temperature. Rout et al.[88] suggested also that due to low lance height, the experiments conducted by Subagyo et al.[67] did not actually correspond to splashing mode, but rather the penetrating mode of jet interaction, which is characterized by a lower droplet generation rate than in the splashing mode. For this reason, a dimensionless parameter J eff was introduced similar to Sarkar et al.[87] in order to calculate the effective droplet generation rate:

$$ \dot{m}_{{{\text{md}},{\text{eff}}}} = J_{\text{eff}} \times \dot{m}_{\text{md}}. $$
(45)

It should be noted that J eff is essentially a fitting parameter, which is evaluated based on plant data.

Droplet size distribution

The size distribution of the metal droplets at their place of birth was determined according to Koria and Lange,[89] who proposed a formulation based on the Rosin–Rammler–Sperling (RRS) function:

$$ RF = (0.001)^{{\left( {\frac{{d_{{{\text{md}},i}} }}{{d_{\text{limit}} }}} \right)^{n} }} , $$
(46)

where RF is the cumulative weight-fraction, d limit is the limiting droplet diameter (which corresponds to RF = 0.001) and n is the distribution exponent. Experimental studies indicate that the parameter n is independent from the limiting diameter,[89] maximum impact pressure of the gas jet[89] and the blowing number.[67] The reported values for the parameter n vary in a relatively wide range from 1.0 to 1.828.[89,90] In this work, a value of n = 1.26 was taken from Koria and Lange,[89] because it represents an arithmetic mean for a relatively large amount of data. For noncoalescing jets, the limiting diameter (in m) can be obtained from Koria and Lange[91]:

$$ d_{\text{limit}} = 5.513 \times 10^{ - 6} \times \left[ {10\left( {\frac{{d_{\text{t}}^{2} }}{{h_{\text{lance}}^{2} }}} \right)p_{\text{amb}} \left( {1.27\frac{{p_{0} }}{{p_{\text{amb}} }} - 1} \right)\cos \theta } \right]^{1.206} , $$
(47)

where p 0 and p amb are the lance supply pressure (in Pa) and the ambient pressure (in Pa), respectively. This expression suggests that droplet sizes increase with increasing lance supply pressure and decreasing lance height, and thus it appears to be in accordance with other studies.[67,90,92] Modifying the expression presented by Deo et al.[93] to a more general form, the mass fraction of size class i at place of birth can be obtained from

$$ f_{{{\text{md}},i}} = - \ln \left( {0.001} \right)n\,RF\frac{{d_{{{\text{md}},i}}^{n - 1} }}{{d_{\text{limit}}^{n} }}. $$
(48)

Residence time

The average residence time of the metal droplets is obtained from

$$ \bar{t}_{\text{md}} = \frac{{m_{\text{md}} }}{{\dot{m}_{\text{md}} }}. $$
(49)

According to the results available in the literature, the average residence time of the droplets increases with an increasing top gas flow rate[94] and decreasing droplet size.[94,95] As shown by Urquhart and Davenport,[96] the size distribution of the metal droplets in the emulsion is shifted toward smaller droplets than the distribution of the generated droplets. The residence time of an individual droplet in the emulsion can be defined as the ratio of the trajectory length to the average velocity.[67] However, for the simplified setting considered in this work, it is more convenient to define the residence time of size class i through a constant κ as follows[67]:

$$ t_{{{\text{md}},i}} = \kappa \frac{{h_{\text{em}} }}{{u_{{{\text{md}},i}} }}, $$
(50)

where h em is the height of the emulsion layer and u md,i is the terminal velocity of size class i. Because the residence time approaches infinity as the droplet diameter approaches zero, the residence time was limited to t md,i  ≤ 60 seconds in order to avoid computational problems. The terminal velocity of the metal droplets in the emulsion was defined in three Reynolds ranges according to the equations proposed by Subagyo and Brooks.[97] In the absence of suitable values, κ was taken here as unity. Moreover, it was assumed that all droplets of the same size class have the same residence time. The average thickness of the emulsion layer can be approximated from:

$$ h_{\text{em}} = \frac{{m_{\text{em}} }}{{A_{\text{slag}} \rho_{\text{em}} }} = \frac{{m_{\text{em}} }}{{(A_{\text{bath}} - n_{\text{lance}} \times \pi r_{\text{cav}}^{2} )\rho_{\text{em}} }}, $$
(51)

where m em is the mass of the emulsion, A slag is the surface area of the top slag layer residing around the cavities, ρ em is the density of the emulsion and A bath is the cross-sectional area of the metal bath. The density of the slag-metal-slag emulsion is calculated according to Subagyo and Brooks[97]:

$$ \rho_{\text{em}} = \rho_{\text{L}} \phi_{\text{L}} + \rho_{\text{S}} (1 - \phi_{\text{L}} ), $$
(52)

where ϕ L denotes the volume fraction of metal droplets in emulsion, and is obtained from

$$ \phi_{\text{L}} = \frac{{V_{\text{L}} }}{{V_{\text{L}} + V_{\text{G}} + V_{\text{S}} }}\quad{\text{where}}\quad V_{\text{G}} = \frac{{\phi_{\text{G}} }}{{1 - \phi_{\text{G}} }}\left( {V_{\text{L}} + V_{\text{S}} } \right), $$
(53)

where V L, V G, and V S denote the volumes of metal, gas, and slag phases in emulsion, respectively. The volume-fraction of gas in the emulsion was solved numerically from the correlation proposed by Gou et al.[98]:

$$ \frac{{\phi_{\text{G}}^{2} }}{{1 - \phi_{\text{G}} }} = 0.91u_{\text{s}}^{0.57} , $$
(54)

where u s is the superficial velocity. The superficial velocity was defined as the ratio of gas flow rate from the plume and cross-sectional area of the slag layer, i.e., \( u_{\text{s}} = \dot{V}_{{{\text{G}},{\text{plume}}}} /A_{\text{slag}} \).

Mass- and Heat-Transfer Coefficients

The mass and heat-transfer coefficients were defined according to Eqs. [55] and [56], respectively.

$$ \beta = {\text{Sh}}\frac{D}{L}, $$
(55)
$$ \alpha = {\text{Nu}}\frac{\lambda }{L}, $$
(56)

where Sh is the Sherwood number, D is the mass diffusivity, L is the characteristic length, Nu is the Nusselt number, and λ is the heat conductivity. A detailed treatment of these parameters is provided in the following subsections.

Cavity interface

At the cavity interface, the cavity radius (r cav) was employed as the characteristic length. The mass-transfer correlations employed for the gas jet were taken from Oeters.[99] These correlations are based on the experimental data published by Lohe[100] and can be represented as follows:

$$ {\text{Sh}} = \left\{ {\begin{array}{lll} {1.41 {\text{Re}}^{0.51} {\text{Sc}}^{0.33} } & {{\text{when}}\quad 2 \times 10^{3} \le {\text{Re}} \le 3 \times 10^{4} } \\ {0.41{\text{Re}}^{0.75} {\text{Sc}}^{0.33} } & {{\text{when}}\quad 3 \times 10^{4} \le {{\text{Re}}} \le 2 \times 10^{5} } \\ \end{array} } \right., $$
(57)

where Re is the Reynolds number and Sc is the Schmidt number. Similarly to Dogan et al.,[101] the values of Re and Sc were defined in relation to the properties of the gas film at the impact surface:

$$ {\text{Re}} = \frac{{u_{\text{G}} r_{\text{cav}} \rho_{\text{G}} }}{{\mu_{\text{G}} }}, $$
(58)
$$ {\text{Sc}} = \frac{{\mu_{\text{G}} }}{{\rho_{\text{G}} D_{\text{G}} }}, $$
(59)

where u G is the critical gas velocity, μ G is the dynamic viscosity of the gas film, and ρ G is the density of the gas film. The critical gas velocity (u G) is calculated from the free axial velocity of the gas jet (u j). For the metal phase in contact with gas jet, the turbulent diffusion boundary layer thickness and the corresponding Sherwood number were defined according to Eqs. [60] and [61], respectively.[99]

$$ \delta_{\text{N}} = \sqrt {\frac{{D_{\text{L}} \sigma_{\text{equiv}} }}{{0.41\rho_{\text{L}} u_{\tau }^{3} }}}, $$
(60)
$$ {\text{Sh}} = \frac{{r_{\text{cav}} }}{{2\delta_{\text{N}} }}, $$
(61)

where u τ is the turbulent shear stress velocity, and σ equiv is the equivalent surface tension. The thickness of the thermal boundary layer (δ Pr ) can be obtained from Eq. [60] by replacing the mass diffusivity D L with the ratio μ L/ρ L, i.e., kinematic viscosity. As a first approximation, the mass-transfer coefficients of the slag species were similarly calculated as was done for the metal species, but making use of the properties of the slag species. Similar to Memoli et al.,[102] the turbulent shear stress velocity was calculated on the basis of momentum transfer between the gas jet and the metal bath. Assuming that the axial velocity of the gas jet is zero at the bottom of the cavity, the turbulent shear stress velocity can be calculated as follows:

$$ u_{\tau } = \sqrt {\frac{{\rho_{\text{G}} }}{{\rho_{\text{L}} }}} u_{\text{j}}. $$
(62)

The heat-transfer coefficients for gas, metal, and slag phases were derived from the mass-transfer correlations according to the analogs of heat and mass transfers by replacing the Sherwood number (Sh) and the Schmidt number (Sc) with the Nusselt number (Nu) and the Prandtl number (Pr), respectively.

Metal droplet interface

At the metal droplet interface, the mass- and heat-transfer coefficients were calculated by employing the Sauter mean diameter of the metal droplets (d 32,md) as the characteristic length. The mass-transfer coefficient mass of the gas phase in contact with the metal droplets can be calculated from the Steinberger and Treybal[103] correlation, which accounts for the effects of both natural and forced convections:

$$ {\text{Sh}} = {\text{Sh}}_{0} + 0.347({\text{ReSc}}^{1/2} )^{0.62}, $$
(63)
$$ {\text{Sh}}_{0} = \left\{ {\begin{array}{*{20}c} {2 + 0.569(\overline{{\text{Gr}}} {\text{Sc}})^{1/4} } & {{\text{for}}\quad\overline{{\text{Gr}}} {\text{Sc}} < 10^{8} } \\ {2 + 0.0254(\overline{{\text{Gr}}} {\text{Sc}})^{1/2} {\text{Sc}}^{0.244} } & {{\text{for}}\quad\overline{{\text{Gr}}} {\text{Sc}} > 10^{8} } \\ \end{array} ,} \right. $$
(64)

where \( \overline{{\text{Gr}}} \) is the mean Grashof number. The mean Grashof number (\( \overline{{\text{Gr}}} \)), the Reynolds number (Re), and the Schmidt number (Sc) were defined as follows:

$$ \overline{{\text{Gr}}} = {\text{Gr}}_{\text{M}} + {\text{Gr}}_{\text{H}} \left( {\frac{{\text{Sc}}}{{\text{Pr}} }} \right)^{1/2} , $$
(65)
$$ {\text{Re}} = \frac{{u_{\text{G}} d_{{32,{\text{md}}}} \rho_{\text{G}} }}{{\mu_{\text{G}} }}, $$
(66)
$$ {\text{Sc}} = \frac{{\mu_{\text{G}} }}{{\rho_{\text{G}} D_{\text{G}} }}, $$
(67)

where GrM is the Grashof number for mass transfer, GrH is the Grashof number for heat transfer, and Pr is the Prandtl number. Here, GrM, GrH, and Pr were defined according to Eqs. [68] through [70], respectively. It should be noted that the value of GrM depends on the species in question.

$$ {\text{Gr}}_{{{\text{M}},i}} = \frac{{g\rho_{\text{G}} d_{{32,{\text{md}}}}^{3} \left( {y_{{i,{\text{md}}}}^{ *} \rho_{{{\text{G}},{\text{md}}}} - {\text{y}}_{{i,{\text{jet}}}} \rho_{{{\text{G}},{\text{jet}}}} } \right)}}{{\mu_{\text{G}}^{2} }}, $$
(68)
$$ {\text{Gr}}_{\text{H}} = \frac{{g\rho_{\text{G}}^{2} d_{{32,{\text{md}}}}^{3} \left( {T_{\text{md}}^{ *} - T_{\text{jet}} } \right)}}{{T_{\text{G}} \mu_{\text{G}}^{2} }}, $$
(69)
$$ {\text{Pr}} = \frac{{c_{{{\text{p}},{\text{G}}}} \mu_{\text{G}} }}{{\lambda_{\text{G}} }}, $$
(70)

where c p,G is the specific heat capacity of the gas phase, and λ G is the heat conductivity of the gas phase. The heat-transfer coefficient was calculated by means of Eqs. [63] and [64] by replacing Sh, \( \overline{{\text{Gr}}}, \) and Sc with Nu, GrH, and Pr, respectively. It is known that mass transfer within small metal droplets takes place almost entirely by diffusion, while larger droplets may exhibit uninhibited circulatory flow.[99,104] In this work, it was assumed that only creeping laminar circulation takes place within the metal droplets. Therefore, the mass-transfer coefficient can be calculated according to the Kronig and Brink[105] solution, which can be expressed in terms of the Sherwood number as follows[106]:

$$ {\text{Sh}} = \frac{32}{3}\frac{{\mathop \sum \nolimits_{i = 1}^{\infty } A_{i}^{2} \lambda_{i} \exp \left( { - 16\lambda_{i} {\text{Fo}}_{\text{M}} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{\infty } A_{i}^{2} \exp \left( { - 16\lambda_{i} {\text{Fo}}_{\text{M}} } \right)}}, $$
(71)

where FoM is the Fourier number for mass transfer. The first seven values for the parameters A i and \( \lambda_{i} \) were taken from the literature[107] and provide a sufficient convergence. Despite its limited range of theoretical applicability, experimental studies have shown that the Kronig and Brink solution gives a reasonably good prediction of the mass-transfer coefficient even at Reynolds numbers well above those corresponding to creeping flow.[108] Employing the average residence time of the metal droplets (\( \bar{t}_{\text{md}} \)) as the characteristic time, the Fourier number for mass transfer can be defined according to

$$ {{\text{Fo}}}_{\text{M}} = \frac{{4D_{\text{L}} \bar{t}_{\text{md}} }}{{d_{{32,{\text{md}}}}^{2} }}. $$
(72)

The corresponding Fourier number for heat transfer (FoH) is obtained from Eq. [72] by replacing mass diffusivity with thermal diffusivity. Thus, the heat-transfer coefficient for the metal droplets is obtained by replacing Sh and FoM with Nu and FoH, respectively. The mass transfer in the slag phase surrounding the metal droplets was calculated according to Eq. [73], which is valid for fluid spheres in creeping flow.[109]

$$ {\text{Sh}} = 0.65\left( {\frac{{\mu_{\text{S}} }}{{\mu_{\text{S}} + \mu_{\text{L}} }}} \right)^{1/2} {{\text{Re}}}^{1/2} {\text{Sc}}^{1/2} = 0.65\left( {\frac{{\mu_{\text{S}} }}{{\mu_{\text{S}} + \mu_{\text{L}} }}} \right)^{1/2} \left( {\frac{{\rho_{\text{S}} \bar{u}_{\text{md}} d_{{32,{\text{md}}}} }}{{\mu_{\text{S}} }}} \right)^{1/2} \left( {\frac{{\mu_{\text{S}} }}{{\rho_{\text{S}} D_{\text{S}} }}} \right)^{1/2} , $$
(73)

where \( \bar{u}_{\text{md}} \) is the average terminal velocity of the metal droplets in the emulsion. The heat-transfer coefficient for the slag phase in contact with the metal droplets was obtained using the analogs of heat and mass transfers by replacing Sh and Sc with Nu and Pr, respectively.

Thermodynamic Properties

All the thermodynamic properties were defined at the composition and temperature of the reaction interface in question. The equilibrium constants are defined by

$$ K = \exp \left( { - \frac{{\Delta {G^{\circ}}}}{{RT^{*} }}} \right)\quad{\text{where}}\quad\Delta G^\circ = \Delta H^\circ - T^{*} \Delta S^\circ, $$
(74)

where R is the gas constant; T* is the temperature of the reaction interface; and ΔG°, ΔH°, and ΔS° are the changes in Gibbs free energy, enthalpy, and entropy of reaction, respectively. The reaction enthalpy and reaction entropy were calculated according to Eqs. 75 and 76, respectively.

$$ \Delta H^{\circ} = \mathop \sum \limits_{i = 1}^{n} \nu_{i} H_{i}^{\circ } , $$
(75)
$$ \Delta S^{\circ} = \mathop \sum \limits_{i = 1}^{n} \nu_{i} S_{i}^{\circ} , $$
(76)

where ν i , \( H_{i}^{\circ } \) and \( S_{i}^{\circ } \) are the stoichiometric coefficient, enthalpy and entropy of species i. The values of \( H_{i}^{\circ } \) and \( S_{i}^{\circ } \) at temperature T were calculated as follows:

$$ H^{\circ} (T) = H_{298.15}^{\circ } + \int\limits_{298.15}^{T} {C_{\text{p}} {\text{d}}T + H_{{{\text{tr}},T}}^{\circ } + H_{\text{dis}}^{\circ } } , $$
(77)
$$ S^\circ (T) = S_{298.15}^{\circ } + \int\limits_{298.15}^{T} {\frac{{C_{\text{p}} }}{T}{\text{d}}T + S_{{{\text{tr}},T}}^{\circ } + S_{\text{dis}}^{\circ } } , $$
(78)

where \( H_{298.15}^{\circ } \) is the enthalpy at 298.15 K (25 °C), C p is the molar heat capacity, \( H_{\text{tr}}^{\circ } \) is the total enthalpy of phase transformations from 298.15 K (25 °C) to T, \( H_{\text{dis}}^{\circ } \) is the enthalpy of dissolution, \( S_{298.15}^{\circ } \) is the entropy at 298.15 K (25 °C), \( S_{\text{tr}}^{\circ } \) is the total entropy of phase transformations from 298.15 K (25 °C) to T, and \( S_{\text{dis}}^{\circ } \) is the entropy of dissolution. The enthalpies H° and entropies S° correspond to the following standard states: the Henrian standard state for the species dissolved in the metal bath, and the Raoultian standard states for the gas and slag species. For the dissolved species, the relevant values of \( H_{\text{dis}}^{\circ } \) and \( S_{\text{dis}}^{\circ } \) were obtained from Sigworth and Elliott,[110] while for the gas and slag species, \( H_{\text{dis}}^{\circ } \) and \( S_{\text{dis}}^{\circ } \) were set to zero. The molar heat capacity at temperature T is solved from the Shomate equation[111]:

$$ C_{\text{p}} = A + B \cdot 10^{ - 3} T + C \cdot 10^{5} T^{ - 2} + D \cdot 10^{ - 6} T^{2} , $$
(79)

where A, B, C, and D are fitting parameters applicable to a certain temperature interval. A comprehensive database of the Shomate equation parameters was taken from HSC Chemistry.[111] The partial pressures of the gaseous species can be calculated from the ideal gas law based on the total gas pressure at the reaction interface. The Henrian activity coefficients of the species in the liquid metal phase were calculated by means of the Unified Interaction Parameter (UIP) formalism[112]:

$$ \ln \gamma_{i}^{\text{H}} = \ln \frac{{\gamma_{i}^{\text{R}} }}{{\gamma_{i}^{\circ } }} = - 0.5\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\varepsilon_{j}^{k} x_{j}^{*} x_{k}^{*} + \sum\limits_{j = 1}^{n} {\varepsilon_{i}^{j} x_{j}^{*} } } } , $$
(80)

where γ H i is the Henrian activity coefficient of species i, γ R i is the Raoultian activity coefficient of species i, γ ° i is the activity coefficient of species i at infinite dilution, ɛ is the first-order molar interaction parameter, and x* is the molar fraction at the reaction interface. The employed first-order molar interaction parameters are given in Table II.

Table II Employed First-Order Molar Interaction Parameters in Liquid Iron at 1873 K (1600 °C)
Full size table

The activity coefficients of the slag species were calculated according to the model employed by Wei and Zhu.[21] The Raoultian activity coefficients of FeO, Cr2O3, MnO, and SiO2 are given by Eqs. [81] through [84], respectively.

$$ \log_{10} \gamma_{\text{FeO}}^{\text{R}} = \frac{{\varepsilon_{1} }}{{T^{*} }}\left( {x_{\text{CaO}}^{*} + x_{\text{MgO}}^{*} } \right)\left( {x_{{{\text{SiO}}_{2} }}^{*} + 0.25x_{{{\text{AlO}}1.5}}^{*} } \right) + \frac{{\varepsilon_{2} }}{{T^{*} }}x_{\text{MnO}}^{*} \left( {x_{{{\text{SiO}}_{2} }}^{*} + 0.45x_{{{\text{CrO}}1.5}}^{*} } \right) + \frac{{\varepsilon_{3} }}{{T^{*} }}x_{{{\text{AlO}}1.5}}^{*} x_{{{\text{SiO}}_{2} }}^{*} + \frac{{\varepsilon_{4} }}{{T^{*} }}x_{\text{MnO}}^{*} x_{{{\text{AlO}}1.5}}^{*} + \frac{{\varepsilon_{5} }}{{T^{*} }}x_{{{\text{CrO}}1.5}}^{*} x_{{{\text{SiO}}_{2} }}^{*}, $$
(81)
$$ \log_{10} \gamma_{{{\text{Cr}}_{2} {\text{O}}_{3} }}^{\text{R}} = \log_{10} \gamma_{\text{FeO}}^{\text{R}} - \frac{{\varepsilon_{6} }}{{T^{*} }}\left( {x_{\text{CaO}}^{*} + x_{\text{MgO}}^{*} } \right) - \frac{{\varepsilon_{7} }}{{T^{*} }}x_{\text{MnO}}^{*} - \frac{{\varepsilon_{5} }}{{T^{*} }}x_{{{\text{SiO}}_{2} }}^{*}, $$
(82)
$$ \log_{10} \gamma_{\text{MnO}}^{\text{R}} = \log_{10} \gamma_{\text{FeO}}^{\text{R}} - \frac{{\varepsilon_{2} }}{{T^{*} }}\left( {x_{{{\text{SiO}}_{2} }}^{*} + 0.45x_{{{\text{CrO}}1.5}}^{*} } \right) - \frac{{\varepsilon_{4} }}{{T^{*} }}x_{{{\text{AlO}}1.5}}^{*}, $$
(83)
$$ \log_{10} \gamma_{{{\text{SiO}}_{2} }}^{\text{R}} = \log_{10} \gamma_{\text{FeO}}^{\text{R}} - \frac{{\varepsilon_{1} }}{{T^{*} }}\left( {x_{\text{CaO}}^{*} + x_{\text{MgO}}^{*} } \right) - \frac{{\varepsilon_{2} }}{{T^{*} }}x_{\text{MnO}}^{*} - \frac{{\varepsilon_{3} }}{{T^{*} }}x_{{{\text{AlO}}1.5}}^{*} - \frac{{\varepsilon_{5} }}{{T^{*} }}x_{{{\text{CrO}}1.5}}^{*}, $$
(84)

where ɛ 1, …, ɛ 7 are the interaction coefficients of the model. Table III shows the interaction coefficients reported by Wei and Zhu[21] for early and later periods of refining. In this work, the coefficients applicable for the early period of refining were employed. Similar to Wei and Zhu,[21] it was assumed that \( a_{{{\text{Cr}}_{2} {\text{O}}_{3} }}^{\text{R}} = 1 \) if the interfacial Cr2O3 content is greater than the maximum solubility of Cr2O3 in the slag.

Table III Interaction Coefficients of the Slag Model[21]
Full size table

Physical Properties

The physical properties of the metal and slag phases were estimated at the temperature of the reaction interface, while the properties of the gas phase were defined at gas film temperature, which was approximated as[117]

$$ T_{\text{G}} = 0.5 \times \left( {T^{*} + T_{\text{jet}} } \right), $$
(85)

where T* is the temperature of reaction interface, and T jet is the temperature of the gas jet. The effective mass diffusivity was defined for each species in the metal phase as the interdiffusivity in liquid iron, while only one effective diffusivity value was assigned for the gas and slag phases. Where possible, the temperature dependency of the mass diffusivity of solutes in liquid iron was described by an Arrhenius type relationship.[118] In order to account for the effects of pressure and temperature, the mass diffusivity of the gaseous species was treated similar to Järvinen et al.[29]:

$$ D_{\text{G}} = D_{{{\text{G}},{\text{eff}}}} \times \left( {\frac{{T_{\text{G}} }}{{T_{\text{ref}} }}} \right)^{1.5} \left( {\frac{{p_{\text{ref}} }}{{p_{\text{G}} }}} \right), $$
(86)

where D G,eff is the effective mass diffusivity at T ref and p ref, T ref. is the reference temperature, p ref. is the reference pressure, and p G is the total gas pressure. The pressure changes in the gas jet are small enough to be neglected,[72] and hence the total gas pressure was taken as equal to the atmospheric pressure at both reaction interfaces. The treatment of other physical properties is summarized in Table IV along with their corresponding references.

Table IV Employed Models and Parameters for Physical Properties
Full size table

During decarburization, the top slag consists of a molten slag phase saturated with chromium oxide and a solid chromium oxide phase.[130] For this reason, it is necessary to consider the effect of solid particles on the viscosity of the top slag. The viscosity of the liquid part (μ S(l)) was calculated using the viscosity model proposed by Forsbacka et al.,[125] which is an extension of the modified Urbain model[131] for the Al2O3-CaO-CrO-Cr2O3-‘FeO’-MgO-SiO2 system. The effective viscosity of the top slag was determined as relative to the viscosity of the liquid slag phase:

$$ \mu_{\text{S}} = \mu_{{{\text{S}}({\text{l}})}} \mu_{{{\text{S}},{\text{rel}}}}. $$
(87)

The relative viscosity μ S,rel was calculated according to the equation proposed by Thomas.[126] Figure 5 provides a comparison of the Thomas[126] equation with other relative viscosity equations available in the literature.[132–138] With the exception of the Einstein equation,[132] the equations produce similar results up to a solid volume fraction of 0.3, but begin to diverge as the solid volume fraction approaches unity. The solid volume fraction was calculated as a function of Cr2O3 content as shown in the second part of this work.[44]

Fig. 5
figure 5

Calculated relative viscosity as a function of the volume fraction of solids[126,132–138]

Full size image

Numerical Solution

The objective of the numerical solution routine is to minimize the error in free variables, while minimizing the error in thermodynamic equilibrium at the reaction interfaces. The thermodynamic equilibrium equations at the reaction interface and the mass transfer onto and from the interface are solved simultaneously. However, conservations of mass and heat are solved successively. Using small time steps, this does not cause significant inaccuracy, but greatly improves the numerical stability. The flowchart of the model is shown in Figure 6.

Fig. 6
figure 6

Flowchart of the reaction model

Full size image

The numerical solutions of both iteration loops are obtained by Newton’s method, which approximates the solution by its tangent line.[139] For a set of nonlinear equations, the Newton’s method can be expressed as follows[50]:

$$ {\mathbf{J}} {\mathbf{\Delta x}} = - {\mathbf{f}}, $$
(88)

where J is the Jacobian matrix of the system with respect to all free variables, \( {\mathbf{\Delta x}} \) is the correction vector, and f is the residual vector, which approaches zero asymptotically during the iteration. The system of linear equations defined by Eq. [88] is solved by Gauss–Jordan elimination method. During iteration, the vector of free variables is updated similar to the relaxed Newton’s method. The calculation procedure is repeated until the numerical error is sufficiently small or the maximum number of iterations is exceeded. The error in the residual vector f is measured using the l 2-norm, which is the Euclidian length of the correction vector:

$$ ||{\mathbf{\Delta x}}||_{2} = \sqrt {\mathop \sum \limits_{i} {\Delta }x_{i}^{2} }. $$
(89)

As stated earlier, one of the main assumptions of the model is that the reaction interfaces reach their mass-transfer constrained equilibrium composition at every instant. During the numerical solution, the interfacial composition asymptotically approaches the composition dictated by the equilibrium constants, provided that the forward reaction rate coefficients (k f) are sufficiently large. In order to assess the fulfillment of the equilibrium assumption, the concept of equilibrium number is introduced:

$$ {\text{E}} = \left| {1 - \frac{Q}{K}} \right|, $$
(90)

where Q and K denote the reaction quotient and the equilibrium constant, respectively. The reaction quotient is defined as follows:

$$ Q = \frac{{\mathop \sum \nolimits_{p} a_{p}^{{\nu_{p} }} }}{{\mathop \sum \nolimits_{r} a_{r}^{{\nu_{r} }} }}, $$
(91)

where p and r denote reaction products and reactants, respectively. By definition, Q = K at equilibrium. Because Q → K as k f  → ∞, it follows that E → 0 as k f → ∞. Owing to these properties, the equilibrium number provides a practical measure of the relative fulfillment of the equilibrium assumption. As a preliminary setting, the maximum allowed error was set to E = 0.1 pct for all the studied reactions. During numerical solution, the forward reaction rate coefficients are increased periodically until the equilibrium numbers of all the reactions are below the maximum allowed error. A typical calculation time per time step is in the order of few seconds using a desktop PC (3.4 GHz).

Conclusions

The objective of this work was to develop a fast numerical model for the reactions that occur during top-blowing in the AOD process. More specifically, the aim was to create a model that considers reactions both between the top-blown gas and the metal bath and between metal droplets and top slag. Employing the categorization proposed by Ding et al.,[41] the model derived in this work can be classified as a complex process mechanism model, because it emphasizes the local thermodynamic equilibrium and local heat and mass-transfer characteristics. In the second part of this work,[44] the model is validated with heats from a full size AOD vessel. In the future, the combined top- and side-blowing stage of the AOD process can be simulated as a combination of the top-blowing model derived in this work and the side-blowing model proposed earlier by Järvinen et al.[29]