Introduction

Recent progress made in the computational modeling of cooling of cast iron is credited to its ability to predict microstructural characteristics and, along with them, the service properties of a cast component, allowing the substitution of expensive experimental tests by virtual tests performed in a computer. At present, the computational models used to predict the resulting microstructure obtained at the end of the cooling (or heat treatment) of a cast part solve the problem at two different but closely related scales. At the macroscale, the physical laws of mass conservation, energy, momentum, and species, allow the evaluation of temperature, cooling rate, pressure, and composition fields. The microscale models, on the other hand, allow determining phase fractions, spacing between the primary and secondary dendrites, grain size, and interlamellar spacing, among others, which cannot be obtained with models posed solely on a macroscale.

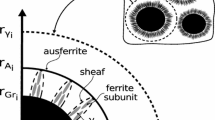
A typical microstructure of nodular cast iron at the end of a casting process can be observed in Figure 1, where the graphite nodules are surrounded by ferrite, leading to the characteristic “bull’s eye” of these ternary Fe-C-Si alloys, while the remaining of the matrix is formed by the microconstituent known as pearlite.

Fig. 1
figure 1

Micrograph corresponding to semipearlitic/ferritic nodular cast iron (100 times magnification and 2 pct Nital etching)

Full size image

A thermo-metallurgical model for the analysis of cooling process and phase changes (including liquid–solid and solid–solid) of a nodular cast iron of eutectic composition is proposed in this study. The main original contribution of this study is the consideration of such phenomena in a unified plurinodular-based context. The importance of a comprehensive understanding of the cooling of cast iron is that the development of the stable and metastable eutectoid phase changes depends on the characteristics of the microstructure at the end of the solidification process. For example, a large number of graphite nodules favor the transformation of austenite according to the stable system of Fe-C, while the small grains of austenite and the micro-segregations of alloyed elements such as Cu, Mn, Sb, or Sn foster the transformation of austenite according to the metastable system of Fe-C. The numerical model predicts evolutions of temperature, phase fractions, and graphite nodules size, and distribution. A literature review is presented in Section II, while the main features of the thermo-metallurgical formulation used for the analysis of the problem at macro and microscales are presented in Section III. Section IV describes the proposed metallurgical models. Sections V and VI, respectively, present the main aspects of the experimental and numerical procedures developed in this context. Section VII reports the analysis and comparisons between the numerical and experimental results. Finally, conclusions are drawn in Section VIII.

Literature Review

To the best of our knowledge, most of the research related to the modeling of phase transformations of nodular cast iron deals with the study of the solidification and its thermal treatments, whereas few models attempt to follow the cooling process from the pouring temperature to room temperature.

Of all the theories that attempt to explain the solidification process of the nodular cast iron, the most successful ones have been the uninodular and plurinodular theories.[1–3] The uninodular theory claims that the graphite nodules nucleate in the liquid, and then the austenite wraps the graphite nodules and grows forming a layer around the graphite spheres. The plurinodular theory establishes that both phases, graphite and austenite, nucleate independent of the other in the liquid, and that during the period of its dendritic growth, the austenite reaches and encapsulates the graphite nodules forming the characteristic eutectic grain. Most of the computational research on the solidification of nodular cast iron adopts simplified models based on the uninodular theory.[4–12] On the other hand, the present authors have contributed to develop numerical models of the solidification of nodular cast iron of eutectic composition based on the premises of the plurinodular theory.[13,14] In this context, the proposed modeling accounts for the independent nucleation of the austenite grains and graphite nodules in the liquid, the independent equiaxial dendritic growth of the austenite, and the spherical growth of the graphite nodules in the interdendritic and intergranular liquid zones. The main features of this solidification model are that it allows knowing the evolution in time of the liquid fractions of graphite and austenite, the amount of silicon in the liquid, the size of the austenite grain, and the size and distribution of the graphite nodules. It is well known that the final microstructure is important to the cast industry because it has a marked influence on the mechanical properties of an alloy. The first steps toward the experimental validation of the numerical results obtained with this model have been reported in a recent article.[15]

Among the main modeling studies addressing phase transformations in solid state in nodular cast irons, Venugopalan[16] studied the transformation of austenite according to a stable Fe-C system for a series of isothermal processes assuming equilibrium at the graphite/ferrite and ferrite/austenite interfaces, and modeling the nucleation of ferrite as a phenomenon that occurs instantly in the graphite/austenite interface, some time after the incubation period associated with limitations in the kinetics of the nucleation. At the moment of nucleation, the graphite nodules are enclosed by a ferrite layer having a thickness equivalent to 1 pct of the volume fraction of the Representative Volume Element (RVE). For the ferrite and graphite growths, he considered the carbon diffusion from the ferrite/austenite interface toward both the graphite nodules and the austenite far from this interface. Chang, Shangguan, and Stefanescu[17] modeled the complete cooling of hypereutectic nodular cast iron, and determined microstructural characteristics such as phase fractions, pearlite interlamellar spacing, and grain sizes. The solidification was represented by a uninodular theory. The eutectoid phase changes considered instantaneous nucleation laws. The growth rate of ferrite was assumed as a function of the carbon diffusion from the austenite to the graphite nodules. To calculate the fraction of pearlite, the additive rule for non-isothermal processes was applied by means of the Johnson–Mehl–Avrami equation. Out of all references considered in this article, the study of Chang, Shangguan, and Stefanescu[17] is the only one that makes a computational and experimental study of the complete cooling of nodular cast iron of hypereutectic composition, from pouring temperature to room temperature. Aspects not considered in this valuable study are the desaturation in carbon of the austenite between the eutectic and the stable eutectoid temperature, and that the metastable eutectoid transformation is modeled according to a macroscopic law, which only allows knowing the fraction of transformed pearlite but not its microstructural characteristics. Wessén and Svensson[12] simulated the stable eutectoid transformation of eutectic nodular cast iron considering that the ferrite grains nucleation and growth process occurs in three sequential steps. In the first step, the ferrite nucleates 20 degrees below the stable eutectoid temperature. The thickness of the ferrite grains remains constant until the nodules have been completely enveloped. In the second step, it is assumed that the growth of the ferrite grains is regulated by an interfacial reaction that takes place in the graphite/ferrite interface, so that the growth rate varies inversely to the radius of the graphite nodule. Finally, in the third step, the growth of the ferrite layer is modeled as a process controlled by the carbon diffusion from the austenite to the graphite nodules through the ferrite shell. Lacaze and Gerval[18] studied the stable and metastable eutectoid transformations of the nodular cast iron of eutectic composition considering that stable and metastable phase changes are competitive processes. Because the eutectic phase change was not modeled, the size of the graphite nodules at the beginning of the eutectoid transformation is determined by means of experimental measurements and empirical law to estimate the density of the graphite nodules and the size of the RVE. Equilibrium is assumed in the ferrite/austenite interface, while a reaction that modifies the equilibrium carbon concentration is considered in the graphite/ferrite interface. The growth rates of the graphite nodules and ferrite envelope are calculated according to the carbon diffusion from the austenite to the graphite nodules. The nucleation of pearlite colonies is modeled as a continuous process that is proportional to the undercooling, to the cooling rate, and to the density of the graphite nodules, and it is assumed to finish when the density of the pearlite colonies reaches the density of the graphite nodules. For temperatures 100 degrees below the stable eutectoid temperature, the growth rate of the pearlite colonies is calculated as being proportional to the cube of the undercooling and to a coefficient that depends on the thermodynamic parameters of the alloy.

Chang et al.[10] investigated the stable eutectoid phase change in nodular cast iron during the isothermal process. They considered the ferrite nucleation as an instantaneous phenomenon taking place at an experimentally determined temperature. For the graphite growth, they used an approximate formula of mass balance in the graphite/ferrite interface.

Thermo-Metallurgical Formulation

The cooling problem of a nodular cast iron can be considered as the result of the coupling between two different but closely related problems: the energy transfer and the phase transformations. Therefore, an adequate modeling of cooling in the alloy should consider both phenomena and their coupling.

Thermal Problem

The heat transfer in a nodular cast iron part can be modeled, at a macroscopic scale, through the energy balance equation in the system under consideration. For the most general case, the rate of energy change in the system would be equal to the sum of the rate of the energy exchange due to conduction, convection, and radiation processes the mechanical work resulting from the changes in volume per unit time, the fluid movement, and the heat generated or absorbed by chemical reactions.

The hypotheses posed for the macroscopic formulation of the problem in this study are (i) both part and mold are considered as isotropic media, (ii) the energy generated or absorbed due to the mechanical work and the fluid movement is negligible, (iii) the effects of the separation between the mold and the metal during the cooling stage are considered through appropriate heat transfer coefficients in the mold/metal interface, and (iv) the generation of energy is due to the phase changes that occur during the cooling stage.

Taking such hypotheses into account, the energy equation results in the form:

$$ \rho c {\dot{T}} = \nabla \cdot \left( {k\nabla T} \right) + \dot{Q}$$
(1)

where ρ is the density, c is the specific heat, T is the temperature, k is the thermal conductivity, and Q is the heat generated due to phase changes. A dot on top of a variable indicates a time derivative.

Boundary conditions

The boundary conditions imposed at the casting/mold, casting/air and mold/air interfaces respond to a Newton-type law expressed as

$$ q = h(T_{1} - T_{2} ) $$
(2)

where q is the normal heat flux, h is the heat transfer coefficient at those interfaces, and T 1–2 are the temperatures at both sides of the interface.

Initial conditions

The contact of the alloy with the walls of a cold mold induces thermal gradients. The relevance of these thermal gradients and their convective effect vary depending on the size and complexity of the geometry, which are important in metal components of large size and complex geometries, and may be neglected in small parts and simple geometries. Thus, the initial conditions vary according to the case of study. In the current analysis, uniform initial temperature distributions are considered for both the casting part and the mold.

Heat generation due to phase changes

Several methods may be employed to account for the generation of latent heat due to phase changes in the energy equation (see Eq. [1]), including the method of temperature recovery, the method of specific heat, the enthalpy method, the micro-enthalpy method, and the method of latent heat.[19] The first three do not allow representing the characteristics of the phase transformations such as recalescence. Owing to this, the method of latent heat has been implemented in this study, according to which the rate of heat generation due to phase changes is

$$ \dot{Q} = L\rho {\dot{f}}$$
(3)

where L is the specific latent heat associated to each phase change and f is the solid volumetric fraction generated during the process, which is given by the metallurgical models detailed in Section IV.

Metallurgical Problem

The model of phase changes implemented here is based on multiscale homogenization theories applied to continuous and heterogeneous media. In these models, the field of interest in a macroscopic domain can be considered as the value of the same field calculated in microscopic scale on the RVE, which is the smallest sample of material which exhibits an invariant macroscopic response. Clearly, this condition is fulfilled when the sample is large enough to contain a large number of heterogeneities and to possess small boundary field fluctuations relative to its size.[20] In the current study, the microstructural evolution is treated by phenomenological laws which allow knowing the values of different microstructural variables (such as phase volumetric fractions and nodule size) but not their position and distribution within the RVE. Details of the microstructural models are given below.

Thermo-Metallurgical Coupling

Figure 2 shows the scales of analysis of the thermal and metallurgical problems. In the same scheme a RVE associated to each Gauss integration point of the finite element mesh can be observed, in which the phase fraction and other microstructural variables are averaged. The RVE technique is advantageous in terms of computational time and memory requirements, even though loss of information could occur when averaging the model variables at a microscopic scale.[21,22] The effect of the volumetric phase fraction evolution computed in Section IV is considered in the thermal balance via Eq. [3].

Fig. 2
figure 2

Relation between thermal and microstructural fields in a phase change problem solved using finite elements

Full size image

Metallurgical Models

The rate of heat generation assumed in this article depends on the kinetics of the liquid/solid (eutectic) and the solid/solid (stable and metastable eutectoid) phase changes. The solid volumetric fraction f in Eq. [3] is given by

$$ f = f_{\gamma } + f_{\text{gr}} $$
(4)
$$ f = f_{\text{gr}} + f_{\alpha } + f_{\text{P}} $$
(5)

Equation [4] is considered from the beginning of solidification up to the initiation of the stable eutectoid transformation while Eq. [5] accounts for the eutectoid transformation (stable and metastable). The volumetric fractions involved in these equations are related to austenite f γ, graphite f gr, ferrite (stable) f α and pearlite (metastable) f P. The evolutions of the variables included in Eqs. [4] and [5] are discussed in the next sections.

Equilibrium Parameters

During the solidification process, the equilibrium carbon concentrations at their different interfaces are calculated using the expressions[13]:

$$ C^{{\rm l}/\gamma} = \frac{1}{97.3}(1,569 - T - 24.32{\text{Si}}) $$
(6)
$$ C^{{\rm l}/gr} = \frac{1}{389.1}(T - 129.7{\text{Si}} + 503.2) $$
(7)
$$ C^{\gamma/{\rm l}} = \frac{1}{177.9}(1528.4 - T - 32{\text{Si}}) $$
(8)
$$ C^{\gamma/gr}= \frac{{(T - 1154.6 - 6.5{\text{Si}})(1.5 - 0.216{\text{Si}})}}{{(354.6 + 6.5{\text{Si}})}} + 2.1 - 0.216{\text{Si}} $$
(9)

where \( C^{{{\rm l}/\gamma}} \) and \( C^{{\rm l}/\text{gr}}\) are the carbon concentrations at equilibrium of the liquid at the liquid/austenite and liquid/graphite interfaces, respectively; \( C^{{\gamma/{\rm l}}} \) and \( C^{{\gamma /{\text{gr}}}} \)are the carbon concentrations at equilibrium of the austenite at the austenite/liquid and austenite/graphite interfaces, respectively. Finally, Si the silicon concentration of the liquid evolution of which is computed using Scheil’s equation (which assumes no diffusion in the solid and complete mixing in the liquid):

$$ {\text{Si}} = {\text{Si}}_{0} (1 - f)^{{k_{\text{Si}} - 1}} $$
(10)

Si0 is the silicon initial content; k Si = 1.09[1] is the silicon partition coefficient; and the value of the solid fraction f is calculated during solidification according to Eq. [4].

The solubility of carbon in austenite at the eutectic temperature (see Figure 3(a)) is given by[13]

Fig. 3
figure 3

(a) Schematic representation of the stable Fe-C phase diagram showing the compositions of interest for a temperature T α < T* < T E. (b) Profile of carbon concentration. (c) Representative volume element (RVE) corresponding to graphite growth between the eutectic and stable eutectoid temperatures

Full size image
$$ C_{\text{E}} = 2.1 - 0.216{\text{Si}} $$
(11)

The eutectic temperature is obtained as[23]

$$ T_{\text{E}} = 1154.6 + 6.5{\text{Si}} $$
(12)

The values of Si in Eqs. [11] and [12] are obtained from Eq. [10].

Equilibrium concentrations of carbon in ferrite in contact with austenite and graphite, and of austenite in contact with ferrite (see Figure 4(a)) are calculated as

Fig. 4
figure 4

(a) Schematic representation of the stable Fe-C phase diagram showing the compositions of interest for a temperature T* < T α. (b) Profile of carbon concentration. (c) Representative volume element (RVE) corresponding to the stable eutectoid phase change

Full size image
$$ C^{\alpha /\gamma } = 0.02\frac{{\left( {T - 910} \right)}}{{\left( {T_{\alpha } - 910} \right)}} $$
(13)
$$ C^{\alpha /gr} = 0.02 + (0.02 - 0.006)\frac{{\left( {T - T_{\alpha } } \right)}}{{T_{\alpha } }} $$
(14)
$$ C^{\gamma /\alpha } = 0.8\frac{{\left( {T - 910} \right)}}{{\left( {T_{\alpha } - 910} \right)}} $$
(15)

where T α is the stable eutectoid temperature, as indicated in Figure 4(a). Equations [13] through [15] were obtained in this study by linear interpolation of the characteristic temperature and carbon concentrations of the Fe-C phase diagram.

Moreover, the expressions used to calculate the coefficients of carbon diffusion in austenite[24] and ferrite are[25]

$$ D_{\text{C}}^{\gamma } = 2.343 \times 10^{ - 5} \exp \left( { - \frac{17.767}{T}} \right) $$
(16)
$$ D_{\text{C}}^{\alpha } = 2.0 \times 10^{ - 6} \exp \left( { - \frac{10.115}{T}} \right)\exp \left\{ {0.5898\left[ {1 + \frac{2}{\pi }\tan^{ - 1} \left( {\frac{15.629}{{T_{\text{C}} }} - \frac{15.309}{T}} \right)} \right]} \right\} $$
(17)

where T C is the Curie temperature calculated as[18]

$$ T_{\text{C}} = 1,043 - 1 {\text{Si}} $$
(18)

Finally, the values of the stable and metastable eutectoid temperatures indicated in Table I were obtained by analyzing the first derivative of experimental cooling curve according to the standard characterization procedure.[26]

Table I Thermophysical and Metallurgical Properties of Nodular Cast Iron
Full size table

Liquid/Solid Phase Change

The solidification model implemented in this study, based on the plurinodular theory, has been previously described by Dardati, Godoy, and Celentano[14]; therefore, only the main aspects are described below.

Nucleation laws

The proposed model assumes that the graphite nodules and austenite grains nucleate in the liquid independent of each other. The graphite nucleation is assumed to be continuous, starting at the time when the temperature of the alloy is less than the eutectic temperature. The nucleation stops if recalescence is produced, and restarts if the temperature takes a value lower than the lowest temperature reached since the beginning of the process, provided that the solidification has not yet finished. The austenite nucleation is instantaneous and occurs when the temperature reaches the eutectic value; the final size of de austenite grains is determined by the number of grains that nucleate. The nucleation laws of graphite nodules[1] and austenite grain[13] are written as

$$ {\dot{N}}_{\text{gr}} = b\Updelta T\exp \left( { - \frac{c}{\Updelta T}} \right)\left( {1 - f} \right) $$
(19)
$$ N_{\gamma } = A {\dot{T}}$$
(20)

where the coefficients b and c in Eq. [19] are fixed for a given composition and liquid treatment; N gr represents the numbers of graphite nodules per unit of volume; and ΔT is the undercooling of liquid with respect to the eutectic temperature. In Eq. [20], N γ is the density of austenite grains; the value of coefficient A depends on the liquid treatment and \({\dot{T}}\) is the cooling rate, which is calculated in the step before the austenite nucleation starts. As shown in Figure 5, the model considers two different nucleation zones for the graphite: the interdendritic and the intergranular liquids, denoted as z2 and z3 in Figure 5(a), respectively.

Fig. 5
figure 5

(a) Simplified scheme of the RVE of the dendritic equiaxial solidification for a eutectic nodular cast iron; (b) profile of carbon concentration

Full size image

The values of coefficients b and c are evaluated from Reference 1 and the value of coefficient A is computed by assuming that the size of the austenite grain should be approximately 2 mm.[3]

Determination of RVE size

Because an equiaxed solidification is simulated, the final shape of the austenite grain is considered to be spherical with radius R T for simplicity (see Figure 5(b)). Based on the austenite density grain obtained from Eq. [20], the radius of each RVE corresponding to a material point in the macroscopic domain is obtained as[13]

$$ R_{\text{T}} = \sqrt {\frac{3}{{4\pi N_{\gamma } }}} $$
(21)

Growth of the austenite grain

The volume of zone 1 (z1 in Figure 5(a)) is equal to the sum of the volume of the austenite plus the graphite nodules that have been already surrounded by austenite. The growth rate of the tip radius of the main dendrites of the equiaxial austenite grain R γ ,[27] and that of the radius of the spherical zone 1,[13] are, respectively, given by

$${\dot{R}}_{\gamma } = \frac{{k_{\rm C} {\kern 1pt} D_{\rm c}^{\rm l} \,m\,C_{0} }}{{2{\kern 1pt} \,\pi^{2} \Upgamma \,\left( {k_{\rm C} - 1} \right)}}\left( {\frac{{C^{{\rm l}/\gamma } - C_{\infty \;g} }}{{C_{0} }}} \right)^{2} $$
(22)
$$ R_{n} = \sqrt {\frac{{3D_{\rm c}^{\rm l} \left. {R_{\gamma }^{2} \frac{\partial C}{\partial r}} \right|_{{R_{\gamma } }} \Updelta t + C^{{\rm l}/\gamma } \left( {1 - k_{\rm C} } \right)R_{n}^{3} + R_{\gamma }^{3} \left( {C^{{l/\gamma^{\prime } }} - C^{{\rm l}/\gamma } } \right)}}{{C^{{\rm l}/\gamma } \left( {1 - k_{\rm C} } \right) + \left( {C^{{l/\gamma^{\prime } }} - C^{{\rm l}/\gamma } } \right)}}} $$
(23)

In Eq. [22], m is the slope of the austenite liquidus line in the corresponding Fe-C stable phase diagram, Γ is the Gibbs–Thompson coefficient, C 0 is the initial carbon concentration, \( k_{\rm C} \) is the partition carbon coefficient, \(C_{{\infty_{g} }}\) is the carbon concentration in the intergranular liquid out of the spherical zone delimited by the tips of austenite dendrites (considering its boundary layer), and \( D_{\rm C}^{\rm l} \) is the diffusion coefficient of carbon in the liquid. In Eq. [23], \( \Updelta t \) is the time step used in integration; \( C^{{l/{\gamma^{\prime} }}} \) and \( C^{{\rm l}/\gamma } \) are the carbon concentrations at equilibrium of the liquid at the liquid/austenite interface at two successive time steps. Finally, \( \left. {\partial C/\partial r} \right|_{{r = R_{\gamma } }} \) is the carbon gradient at radius\( R_{\gamma } \) computed as[28]

$$ \left. {\frac{\partial C}{\partial r}} \right|_{{r = R_{\gamma } }} = \frac{{C^{{\rm l}/\gamma } - C_{{\infty_{g} }} }}{\delta /2} $$
(24)

where the boundary layer thickness δ corresponds to a transformation planar front as shown in Figure 5(a), and is given by[28]

$$ \delta = \frac{{2D_{\rm C}^{\rm l} }}{{{\dot{R}}_{\gamma } }} $$
(25)

Once the austenite has grown, the carbon concentrations in the interdendritic and intergranular liquids change. The value of \( C^{{l/\gamma^{\prime} }} \)present in Eqs. [22] through [24] is obtained through carbon mass conservation in the RVE according to the next expression[13]:

$$ C^{{{\text{l}}/\gamma}} = \frac{{C^{{{\text{l}}/\gamma}} \left({1 - U_{\text{gr}}^{{z_{2} }} } \right)\rho_{\gamma} +C_{\text{gr}} \left( {U_{\text{gr}}^{{z_{2} }} -U_{\text{gr}}^{{z_{2}^{\prime}}} } \right)\rho_{\text{gr}}}}{{\left( {1 - U_{\text{gr}}^{{z_{2}^{\prime } }}}\right)\rho_{\gamma } }} $$
(26)

where ργ and ρgr are the austenite and graphite densities, respectively, C gr is the carbon concentration in graphite; and \( U_{\text{gr}}^{{z_{2} }} \) is the carbon content in z2. A dash on a variable indicates that its value is computed after the growth of austenite.

A detailed explanation of the derivation of Eq. [22] may be found in Reference 28, whereas the derivations of Eqs. [23] and [26] and the evaluation of \( C_{{\infty_{\gamma } }} \)and \( U_{\text{gr}}^{{z_{2} }} \) may be found in Reference 13.

Growth of graphite nodules

As shown in Figure 5(a), the model considers that the volume of the austenite grain is divided in three zones. It is assumed that the nodules enclosed by austenite, zone 1, do not grow, while the radius growth rate of the graphite nodules existing in zones 2 and 3 are, respectively, given by[13]

$$ {\dot{R}}_{\text{gr}} = \frac{{D_{\text{C}}^{\text{l}} \left( {C^{{{\text{l}}/\gamma }} - C^{{{\text{l}}/{\text{gr}}}} } \right)\rho_{\text{l}} }}{{R_{\text{gr}} \left( {C_{\text{gr}} \rho_{\text{gr}} - C^{{{\text{l}}/{\text{gr}}}} \rho_{\text{l}} } \right)}} $$
(27)
$$ {\dot{R}}_{\text{gr}} = \frac{{D_{\text{C}}^{\text{l}} \left( {C_{\text{pro}} - C^{{{\text{l}}/{\text{gr}}}} } \right)\rho_{\text{l}} }}{{R_{\text{gr}} \left( {C_{\text{gr}} \rho_{\text{gr}} - C^{{{\text{l}}/{\text{gr}}}} \rho_{\text{l}} } \right)}} $$
(28)

where ρl is the liquid density, and C pro is the carbon concentration in the intergranular liquid out of the zone delimited by the tips of austenite dendrites (without considering the boundary layer and assuming a uniform carbon concentration in zone 3). As in the case of austenite, once the graphite nodules have grown, the carbon concentration in the interdendritic and intergranular liquids changes. The value of \( C^{{\rm l}/\gamma } \), present in Eq. [27], is obtained from Eq. [26]; and the value of C pro, present in Eq. [28], is obtained through carbon mass conservation in the RVE according to the next expression[13]:

$$ C_{\text{pro}} = \frac{{C_{\text{pro}} \left( {R_{\text{T}}^{3} - R_{n}^{3} } \right) + 3D_{\text{C}}^{\text{l}} \rho_{\gamma } R_{\gamma }^{2} \left. {\frac{\partial C}{\partial r}} \right|_{{r = R_{\gamma } }} }}{{\left( {R_{\text{T}}^{3} - R_{\gamma }^{3} } \right)}} - C^{{{\text{l}}/\gamma }} $$
(29)

A detailed explanation of the derivation of Eq. [29] may be found in Reference 13.

The only difference between Eqs. [27] and [28] is the concentration of carbon of liquid that surrounds the graphite nodules, as it is interdendritic liquid of concentration \( C^{{\rm l}/\gamma } \) in which the value is calculated from Eq. [26] for the graphite nodules of the zone 2, and the intergranular liquid of C pro in which the value is obtained from Eq. [29] evaluation of which may be found in Reference 13.

Determination of Graphite and Austenite Fractions

Once the graphite nodules have grown, and the radii of the zones 1, 2, and 3 have changed, the volume fractions corresponding to graphite and austenite must be recalculated.

The fractions of graphite per unit of total volume corresponding to the three zones indicated in Figure 5(b) are obtained from the following expressions:

$$ f_{\text{gr}}^{{{\text{z}}_{ 1} }} = \frac{4}{3}\pi \sum\limits_{j = 1}^{K} {N_{{{\text{gr}}\,j}}^{{{\text{z}}_{ 1} }} } \;R_{{{\text{gr}}\,j}}^{{{\text{z}}_{1\,\;3} }} \quad f_{\text{gr}}^{{{\text{z}}_{ 2} }} = \frac{4}{3}\pi \sum\limits_{j = 1}^{K} {N_{{{\text{gr}}\,j}}^{{{\text{z}}_{ 2} }} } \;R_{{{\text{gr}}\,j}}^{3} \quad f_{\text{gr}}^{{{\text{z}}_{ 3} }} = \frac{4}{3}\pi \sum\limits_{j = 1}^{K} {N_{{{\text{gr}}\,j}}^{{{\text{z}}_{ 3} }} } \;R_{{{\text{gr}}\,j}}^{3} $$

where \( N_{{{\text{gr}}\,j}}^{{{\text{z}}_{ 1} }} \,N_{{{\text{gr}}\,j}}^{{{\text{z}}_{ 2} }} \,{\text{and}}\,N_{{{\text{gr}}\,j}}^{{{\text{z}}_{ 3} }} \) are the number of nodules nucleated and belonging to a family j in zones 1 to 3 per unit of total grain volume, respectively; \( R_{{{\text{gr}}\,j}}^{{{\text{z}}_{ 1} }} \,{\text{and}}\,R_{{{\text{gr}}\,j}} \) are the radius of graphite nodules belonging to a family j in zones 1, 2, and 3, respectively; the index K corresponds to the number of families of graphite nodules nucleated during the solidification process.

Finally, the volume fractions of graphite and austenite per unit of total volume grain present in Eq. [4] are calculated from

$$ f_{\text{gr}} = f_{\text{gr}}^{{{\text{z}}_{1} }} + f_{\text{gr}}^{{{\text{z}}_{2} }} + f_{\text{gr}}^{{{\text{z}}_{3} }} \quad f_{\gamma } = 1 - f_{\text{gr}} $$

Growth of the Graphite Nodules Between the End of Solidification and Beginning of Stable Eutectoid Transformation

The stable Fe-C phase diagram plotted an intermediate temperature T* between the eutectic and stable eutectoid temperatures is shown (Figure 3(a)) together with the carbon concentration profile (Figure 3(b)) and the RVE corresponding to the mentioned temperature interval (Figure 3(c)). Once the solidification process has ended, and as the alloy temperature decreases, the solubility of carbon in austenite decreases according to line ES in Figure 3. The carbon rejected from the austenite spreads toward the existing graphite nodules, which increase in size due to this effect. Assuming that the carbon concentration in austenite in contact with graphite is that of equilibrium, the difference between this concentration and that of the austenite far from the graphite/austenite interface represents the driving force so that the carbon diffuses toward the graphite nodules.

The growth rate of the graphite nodules is assumed as a function of the carbon flux toward the graphite nodules through the austenite phase; thus, the equilibrium of carbon at the graphite/austenite interface is

$$ \rho_{\text{gr}} (C_{\text{gr}} - C^{{\gamma /{\text{gr}}}} ){\dot{R}}_{\text{gr}} = \rho_{\gamma } D_{\text{C}}^{\gamma } \left. {\frac{{\partial C^{\gamma } }}{\partial r}} \right|_{{r = R_{\text{gr}} }} $$
(30)

where \( \left. {\partial C^{\gamma } /\partial r} \right|_{{r = R_{\text{gr}} }} \) is the carbon gradient in austenite at radius R gr (see Figure 3(b)). Next, the carbon through the austenite is considered as a stationary process, and the carbon profile is

$$ C_{(r)} = - \frac{a}{r} + b $$
(31)

where the values of a and b are calculated from the boundary conditions at the graphite/austenite interface. According to Figure 3(b)

$$ \left\{ \begin{array}{l} r = R_{\text{gr}} \to C_{{r = R_{\text{gr}} }} = C^{{\gamma /{\text{gr}}}} \hfill \\ r = R_{\text{T}} \to C_{{r = R_{\text{T}} }} = C_{\gamma } \hfill \\ \end{array} \right. $$
(32)

where C γ is the carbon content in austenite far from graphite/austenite interface (see Figures 3(b) and (c)), in which the value is calculated as (see Appendix)

$$ C_{\gamma } = \frac{{C_{\gamma } \left( {1 - U_{\text{gr}} } \right)\rho_{\gamma } + C_{\text{gr}} \left( {U_{\text{gr}} - U_{\text{gr}}^{\prime } } \right)\rho_{\text{gr}} }}{{\left( {1 - U_{\text{gr}}^{\prime } } \right)\rho_{\gamma } }} $$
(33)

where U gr is the amount of carbon corresponding to graphite nodules. A dash on a variable indicates that the value is computed at the following time step.

Replacing the values from Eq. [32] into Eq. [31], the resulting value for a (present in Eq. [31]) is

$$ a = R_{\text{T}} R_{\text{gr}} \left( {\frac{{C^{{\gamma /{\text{gr}}}} - C_{\gamma } }}{{R_{\text{T}} - R_{\text{gr}} }}} \right) $$
(34)

Thus, the concentration gradient of carbon in austenite at the interface with graphite is obtained by deriving Eq. [31] and replacing Eq. [34] into it, resulting in

$$ \left. {\frac{{\partial C^{\gamma } }}{\partial r}} \right|_{{r = R_{\text{gr}} }} = \frac{{R_{\text{T}} }}{{R_{\text{gr}} }}\left( {\frac{{C^{{\gamma /{\text{gr}}}} - C_{\gamma } }}{{R_{\text{T}} - R_{\text{gr}} }}} \right) $$
(35)

Finally, the growth rate of the graphite nodules is obtained by replacing Eq. [35] into Eq. [30], leading to

$$ {\dot{R}}_{\text{gr}} = D_{\text{C}}^{\gamma } \frac{{R_{\text{T}} }}{{R_{\text{gr}} (R_{\text{T}} - R_{\text{gr}} )}}\frac{{\rho_{\gamma } }}{{\rho {}_{\text{gr}}}}\frac{{(C_{\gamma } - C^{{\gamma /{\text{gr}}}} )}}{{(C_{\text{gr}} \rho_{\text{gr}} /\rho_{\gamma } - C^{{\gamma /{\text{gr}}}} )}} $$
(36)

The values of \( C^{{\gamma /{\text{gr}}}} \) and \( D_{\text{C}}^{\gamma } \) are calculated from Eqs. [9] and [16], respectively.

Eutectoid Phase Change

The eutectoid model implemented in this study considering the stable and metastable eutectoid transformations assumes that both phase changes are two competitive processes. They are separately described below.

Stable eutectoid phase change

At temperatures below the stable eutectoid temperature (T α in Figure 4(a)), which is the temperature value at which austenite transforms into ferrite and graphite, austenite is transformed according to the Fe-C stable system sketched in Figure 4, in ferrite and graphite. Ferrite, which is the stable phase of iron at these temperatures, nucleates over the graphite nodules due to the micro-segregation and deposition of silicon on the graphite surface raising the stable eutectoid temperature. The ferrite growth rate is a function of carbon diffusion from austenite, both to the graphite nodules through the ferrite envelopes, and to the volume of austenite far from the ferrite/austenite interface. The gradients of carbon concentration that assist its diffusion during the ferrite growth correspond to the difference between the carbon concentrations in ferrite at the graphite/ferrite and ferrite/austenite interfaces and, in addition, to the difference between the equilibrium carbon concentrations at the austenite/ferrite interface and the austenite volume away from that same interface.

In this study, it is assumed that when nodular cast iron reaches the stable eutectoid temperature, each graphite nodule is enclosed by a ferrite layer with a radius that is 1 pct larger than that of the corresponding graphite nodule. The growth rate of the layers of ferrite is due to the impoverishment in the austenite caused by carbon diffusion toward the graphite nodules, and far from the austenite/ferrite interface. The carbon mass balance at the ferrite/austenite interface is

$$ \rho_{\alpha } (C^{\gamma /\alpha } - C^{\alpha /\gamma } ){\dot{R}}_{\alpha } = \rho_{\alpha } D_{\rm C}^{\alpha } \left. {\frac{{\partial C^{\alpha } }}{\partial r}} \right|_{{r = R_{\alpha } }} - \rho_{\gamma } D_{\text{C}}^{\gamma } \left. {\frac{{\partial C^{\gamma } }}{\partial r}} \right|_{{r = R_{\alpha } }} $$
(37)

where \( \rho_{\alpha } \) is ferrite density, \( D_{\text{C}}^{\alpha } \) is the diffusion coefficient of carbon in ferrite, R α is the radius of the ferrite layer enveloping the graphite nodule (see Figure 4(c)), and \( \left. {\partial C^{\alpha } /\partial r} \right|_{{r = R_{\alpha } }} \,{\text{and}}\,\left. {\partial C^{\gamma } /\partial r} \right|_{{r = R_{\alpha } }} \) are the carbon gradients in ferrite and austenite at radius R α, respectively (see Figure 4(b)).

Moreover, the growth of the graphite nodules is a function of the carbon flux that diffuses from the ferrite/austenite interface toward the graphite nodules through the ferrite layers. The carbon mass balance at the ferrite/graphite interface results in

$$ \rho_{\text{gr}} (C_{\text{gr}} - C^{{\alpha /{\text{gr}}}} ){\dot{R}}_{\text{gr}} = \rho_{\alpha } D_{\text{C}}^{\alpha } \left. {\frac{{\partial C^{\alpha } }}{\partial r}} \right|_{{r = R_{gr} }} $$
(38)

where \( \left. {\partial C^{\alpha } /\partial r} \right|_{{r = R_{\text{gr}} }} \) is the carbon gradient in ferrite at radius R gr (see Figure 4(b)).

The growth rate of the ferrite spherical layers and the graphite nodules can be obtained by integrating Eqs. [37] and [38]. Setting a small time step in the integration of these equations, one can consider that the profile of carbon concentration through the ferrite layer responds to the same type of law proposed in Eq. [31].

Following the same procedure of Section IV–D, the gradients of carbon in ferrite at the graphite/ferrite and ferrite/austenite interfaces are, respectively, given by

$$ \left. {\frac{{\partial C^{\alpha } }}{\partial r}} \right|_{{r = R_{\alpha } }} = \frac{{\left( {C^{\alpha /\gamma } - C^{\alpha /gr} } \right)\;R_{\text{gr}} }}{{R_{\alpha } (R_{\alpha } - R_{\text{gr}} )}} $$
(39)
$$ \left. {\frac{{\partial C^{\alpha } }}{\partial r}} \right|_{{r = R_{\text{gr}} }} = \frac{{\left( {C^{\alpha /\gamma } - C^{{\alpha /{\text{gr}}}} } \right)\;R_{\alpha } }}{{R_{\text{gr}} (R_{\alpha } - R_{\text{gr}} )}} $$
(40)

Furthermore, following the same reasoning given by Zener,[29] the carbon gradient in the austenite at the austenite/ferrite interface can be approximated as

$$ \left. {\frac{{\partial C^{\gamma } }}{\partial r}} \right|_{{r = R_{\alpha } }} = \frac{{\left( {C_{\text{S}} - C^{\gamma /\alpha } } \right)}}{{R_{\alpha }^{\prime } }} $$
(41)

where the carbon concentration in austenite C S is assumed constant during the whole process and is obtained by substituting the value of T α available in Table I into Eqs. [14] or [15] (see point S in Figure 4(a), which is obtained from the intersection of the line corresponding to \( C^{\gamma /\alpha } \), given by Eq. [14], and the line corresponding to T α in the same figure). The gradient computed via Eq. [41] presents a maximum at the beginning of the eutectoid transformation and decreases as the transformation progress because of the radius growth of the ferrite envelope.

Finally, Eqs. [37] through [41] give

$$ {\dot{R}}_{\alpha } = \left( {D_{\text{C}}^{\alpha } \frac{{(C^{\alpha /\gamma } - C^{{\alpha /{\text{gr}}}} )}}{{(C^{\gamma /\alpha } - C^{\alpha /\gamma } )}}\frac{{R_{\text{gr}} (R_{\alpha } - R_{\text{gr}} )}}{{R_{\alpha } }} - \frac{{\rho_{\gamma } }}{{\rho_{\alpha } }}D_{\text{C}}^{\gamma } \frac{1}{{R_{\alpha }^{\prime } }}\frac{{(C_{\text{S}} - C^{\gamma /\alpha } )}}{{(C^{\gamma /\alpha } - C^{\alpha /\gamma } )}}} \right)F_{{{\text{T}}_{\gamma } }} $$
(42)
$$ {\dot{R}}_{\text{gr}} = D_{\text{C}}^{\alpha } \frac{{\rho_{\alpha } }}{{\rho_{\text{gr}} }}\frac{{(C^{\alpha /\gamma } - C^{{\alpha /{\text{gr}}}} )}}{{(C_{\text{gr}} - C^{{\alpha /{\text{gr}}}} )}}\frac{{R_{\alpha } }}{{R_{\text{gr}} (R_{\alpha } - R_{\text{gr}} )}} $$
(43)

where \( F_{{{\text{T}}_{\gamma } }} \) is the ratio between the current austenite fractions with respect to that existing one at the end of the solidification (ranging from 1 to 0), and it is included in this expression to take the impingement into account. The values of the carbon concentrations at interfaces and carbon diffusion coefficients present in Eqs. [42] and [43] are obtained from Eqs. [13] through [17].

Eutectoid metastable phase change

When the temperature reaches the eutectoid metastable point, which is the temperature value at which austenite transforms to pearlite (ferrite and cementite), if the austenite has not been totally transformed into graphite and ferrite, then the pearlite colonies nucleate and start growing. In this study, a spherical shape is assumed for the pearlite colonies that nucleate in the remaining austenite volume.

The nucleation of pearlite colonies is considered as a continuous process that starts when the alloy reaches the metastable eutectoid temperature modeled according to the following expression[18]:

$$ {\dot{N}}_{\text{P}} = A_{\text{P}} \left( {N_{\max } - N_{\text{P}} } \right)F_{{{\text{T}}_{\gamma } }} \left( {\Updelta T_{\text{P}} } \right)^{m} {\dot{T}} $$
(44)

where N P is the density of pearlite colonies; N max is the maximum density of pearlite colonies (value of which is determined from an instantaneous nucleation law such that the maximum size of a colony as a result of the simulation is not greater than 20 μm); A P is the pearlite nucleation coefficient with its value being given in Reference 18 and depends on the cooling rate and chemical composition of the alloy; ΔT P is the undercooling with respect to the metastable eutectoid temperature; and the value of m is usually set to 2.[18] The nucleation of pearlite colonies stops when N P is equal to N max or when recalescence occurs.

The equations used to calculate the growth rate of the pearlite colonies are based on the theory of Zener–Hillert.[30,31] Using this theory and considering that the diffusion of carbon occurs in the volume of austenite, the rate of growth of the pearlite colonies is given by[32]

$$ {\dot{R}}_{\text{P}} = c_{\text{P}} \exp ( - Q_{\text{V}} /RT)F_{{{\text{T}}_{\gamma } }} (\Updelta T_{\text{P}} )^{n} $$
(45)

where R P is the radius of pearlite colonies; c P is a coefficient that depends on the composition of the alloy as given by Varma et al.,[32] exp −Q v/RT is a factor that considers the mobility of carbon at the pearlite/austenite interface; Q v is the activation energy for the carbon diffusion at austenite/pearlite interface; R is the universal constant of gas; and the exponent n distinguishes the type of growth of the pearlite colonies (which could be considered to be controlled by either diffusion in the austenite volume or by diffusion in the boundaries of grain). In this study, we assume that the pearlite growth is controlled by austenite volume diffusion of carbon (i.e., n = 2).

Determination of Graphite, Ferrite and Pearlite Fractions

Once the growth computation of graphite nodules, ferrite envelopes, and pearlite colonies is performed, the related volume fractions as well as the remaining austenite fraction must be recalculated.

The fractions of graphite, ferrite, and pearlite per unit of volume of the total grain are calculated from the following expressions:

$$ f_{\text{gr}} = \frac{4}{3}\pi \sum\limits_{j = 1}^{K} {N_{{{\text{gr}}\;j}} \,} R_{{{\text{gr}}\;j}}^{3} \quad f_{\alpha } = \frac{4}{3}\pi \sum\limits_{j = 1}^{K} {N_{{{\text{gr}}\;j}} } \left( {R_{\alpha \;j}^{3} - R_{{{\text{gr}}\;j}}^{3} } \right)\,f_{\text{P}} = \frac{4}{3}\pi \sum\limits_{j = 1}^{L} {N_{{{\text{P}}\;j}} \,} R_{{{\text{P}}\;j}}^{3} $$

where \( N_{{{\text{gr}}\;j}} \) and \( N_{{{\text{P}}\;j}} \) are the graphite nodules and pearlite colonies per unit of total volume grain belonging to a j family; \( R_{{{\text{gr}}\,j}} \) and \( R_{\alpha \;j} \) are the radii of graphite nodules and ferrite envelope on graphite nodules belonging every to a family j; \( R_{{{\text{P}}\,j}} \) is the radius of pearlite colonies belonging to a family j; and indexes K and L correspond to the total number of graphite nodules and pearlite colonies nucleated during solidification and metastable eutectoid phase change, respectively.

The values of \( R_{{{\text{gr}}\,j}} \), \( R_{\alpha \;j} \) and \( R_{{{\text{P}}\,j}} \) are obtained from Eqs. [36], [42], [43] and [45].

Description of the Experimental Procedure

To validate the present numerical model, the computational results have been compared with experimental measurements performed by Chiarella.[33] In the experimental study, a nodular cast iron of slight hypereutectic composition was poured on a standardized Quick-Cup. As shown in Figure 6, the square section coupons are instrumented with a K-type thermocouple covered with quartz at the center of the cavity.

Fig. 6
figure 6

QuicK-Cup sample containing K-type thermocouple. Cup dimensions are height = 58 mm, thickness = 7 mm for lateral and bottom walls

Full size image

The alloy used was molten in an induction furnace, and the charge consisted of 28 pct steel scrap of commercial quality, 70 pct recycled cast iron, 0.5 pct graphite, and 2.5 pct Fe-Si 75 pct. All the percentages are with reference to the total weight of the absolute load of the furnace. The inoculation and nodularization were made by the Sandwich Method, which consists of pouring the liquid metal in the first ladle where the inoculant and the nodularizing catalyst were previously covered with discarded iron and steel material. Afterward, the liquid metal was poured in the second ladle. The liquid treatment was carried out with 1.0 pct of Fe-Mg and inoculant 0.3 pct of Fe-Si 75 pct.

Ten coupons with two different cast compositions were employed, five from each cast. The experimental procedure encompassed the analysis of samples 1, 4, and 5. Since very similar microstructural results were obtained in these three samples, only the experimental measurements of sample 4 corresponding to the four points indicated in Figure 7 are considered in the results presented in Section VII.

Fig. 7
figure 7

Sample dimensions (in mm), thermocouple location (point 2) and points for microstructural analysis via metallography

Full size image

The chemical composition of the alloy used can be seen in Table II. The thermo-metallurgical study consisted of two parts. First, the cooling curves were recorded from the pouring temperature up to room temperature. Then, the final microstructure of the coupons was analyzed. Once the part had cooled down, eight samples were prepared (corresponding to eight different locations in the part) and micrographs were obtained for them to quantify the phases and to characterize the graphite nodules according to their size and quantity. The samples for metallography were prepared according to standard metallographic techniques (i.e., polished and etched in 2 pct Nital). The microstructure constituents (graphite, ferrite, and pearlite) were quantified using an automatic image analysis system (Image-Pro Plus).

Table II Average Chemical Composition (Main Elements) of Samples, wt pct
Full size table

It was observed in the experimental measurements that the smallest graphite nodule corresponds to a diameter of 10.1 μm and the largest one had a diameter of 62.1 μm. Taking these values of graphite nodule diameters as lower and upper bounds, the graphite nodules were grouped according to their size in 11 “families” to facilitate the interpretation and comparison of the experimental with the computed results. Table III shows the radius ranges assigned to the graphite nodules that delimit each family and the family numbers assigned. After processing the results of thermal evolution, the phase fractions and the quantity and distribution of the graphite nodules, the fourth coupon of the first cast was selected, according to the reasons given by Dardati et al.,[15] as that exhibiting the most representative results for the sake of comparison with the numerical predictions. Micrographs corresponding to different locations of this sample are shown in Figure 8.

Table III Radius Range of Each Family
Full size table
Fig. 8
figure 8

Micrographs corresponding to different zones of sample #4 (100 times magnification and 2 pct Nital etching)

Full size image

Main Aspects of the Computational Procedure

The simulation of the nodular cast iron cooling studied in this study was carried out using the finite element method, via the thermo-metallurgical formulation described in Sections III and IV. Owing to the symmetry of the problem, one fourth of the casting/mold ensemble was discretized using hexahedric elements of 8 nodes: 1500 elements for the mold and 1000 elements for the part. Further, gap elements were used to represent the heat flux between the casting and the mold and boundary elements to represent the heat exchange by means of convection at the external surfaces of the mold and casting that are in contact with the environment. Figure 9 depicts a schematic representation of the casting system. Table I summarize the values of the coefficients and thermo-physical properties of the casting, and Tables IV, V, and VI, respectively, summarize the values of the thermal properties of the casting/environment and mold/environment interfaces, thermal properties of the casting/mold interface, and thermo-physical properties of the mold considered for the numerical simulation. The casting initial temperature of the process was assumed to be equal to the pouring temperature, namely 1499 K (1226 °C). For the mold, an initial temperature of 288 K (15 °C) was adopted in the computations.

Fig. 9
figure 9

Schematic representation of a quarter of the casting and mold

Full size image
Table IV Thermal Properties of the Casting/Environment and Mold/Environment Interfaces[15]
Full size table
Table V Thermal Properties of the Casting/Mold Interface[15]
Full size table
Table VI Thermo-Physical Properties of the Mold[15]
Full size table

Results and Discussion

Figures 10 and 11, respectively, plot the simulated cooling and cooling rate curves for points 1, 2, 3 and 4 (see Figure 7). From Figure 10, it can be seen that the differences between the cooling curves associated with the four points listed are relatively small. However, Figure 11 clearly shows that the cooling rates at these locations differ during both phase changes. At the beginning of solidification, the points that are closer to the mold walls (points 3 and 4), cool at a faster rate. As the mold increases its temperature the cooling curves cross each other. Point 1 is the first to start the stable and metastable eutectoid phase change. This is because when the mold increases its temperature, the heat flux tends to be a maximum at the points in locations near to the top and those close to external boundaries.

Fig. 10
figure 10

Simulated cooling curves at points 1 to 4

Full size image
Fig. 11
figure 11

Simulated cooling rate curves at points 1 to 4

Full size image

The simulated and experimental cooling and cooling rate curves at point 2 are shown in Figures 12 and 13, respectively. A good overall agreement can be appreciated. Figure 12 shows that the plateau corresponding to solidification in the simulated curve has a slightly bigger extension than that recorded during the test. This fact can also be observed in Figure 13 (the computed solidification time is 232 seconds). Once the solidification comes to an end and before the stable eutectoid transformation begins, the numerical and experimental cooling rates are very similar. Finally, the stable and metastable eutectoid phase changes span for a shorter time in the simulation than in the experiment. All these numerical-experimental discrepancies can be mainly attributable to the values of the thermo-physical coefficients of the alloy or the mold used in the computer simulations. Even considering such differences and the separation among the cooling curves during the eutectoid phase change, a reasonable agreement reached in terms of time and plateau of the given phase change is achieved.

Fig. 12
figure 12

Experimental and simulated cooling curves at point 2

Full size image
Fig. 13
figure 13

Experimental and simulated cooling rate curves at point 2

Full size image

Figure 14 plots the computed evolution of temperature and phase fractions at points 1, 2, 3 and 4. The order in which the points solidify (starting by point 3, followed by 4, 1 and 2) is seen to be related to the extension of the plateau during the solidification process. The predicted phase fractions are related to the cooling rate of these four points: larger graphite and ferrite fractions are obtained at points with less cooling rate (i.e., points 1 and 2 in Figure 11), while locations with larger cooling rates at the beginning of the stable eutectoid transformation (i.e., points 3 and 4 in Figure 11) are those that present a greater amount of pearlite. It may be seen that the simulated phase fractions are very similar in all four points. These results are acceptable for a nodular cast iron and a small cast part, for which a rather uniform cooling rate at the points located in the central area of the part is developed.

Fig. 14
figure 14

Simulated cooling curves and volumetric phase fractions evolutions at points 1 to 4

Full size image

The final fractions of graphite, ferrite, and pearlite resulting from the simulation and the laboratory tests for points 1, 3 and 4 are plotted in Figure 15. Even considering the graphite growth during the entire cooling process, the simulated amounts of this phase were lower than the experimental values at these three points. The same trend occurs with the amount of ferrite, with the exception of point 4, where a good agreement is reached. The obtainment of fewer quantities of ferrite and graphite in the simulation could be due to the greater cooling rate recorded in the simulation of the test during the eutectoid phase change (see Figure 13), which favors the transformation of carbon to iron carbide instead of graphite, or to inadequate values of the coefficients A P and/or c P for the specific chemical composition of the alloy used in this study. This results in greater computed amounts of pearlite than those observed in the test at all points. Figure 16 shows experimental and computed values for the density of graphite nodules at points 1, 2, 3, and 4 evaluated at the end of the eutectoid phase change. They were classified according to the nodule families indicated in Table III. These results show that the computed density of graphite nodules corresponding to family 0 is null in points 3 and 4 and negligible at points 1 and 2. The most notorious difference between the amount of simulated and experimental density of graphite nodules corresponds to family 1 at points with larger cooling rate and lower solidification plateau extension, i.e., points 3 and 4 (see Figures 10 and 11). Considering the relation between the phase quantities (Figure 15) and the distribution of graphite nodules (Figure 16), one could observe that the point with greater number of graphite nodules belonging to family 1 (point 2) presents the largest amounts of graphite and ferrite, followed by points 1, 4, and 3 with the same order of trend. In contrast, there is no similarity in the relation between the phase quantities determined from the experiments. Also, it seems that there is a correlation between the distribution of graphite nodules and the extension of the plateau of solidification, the cooling rate, and the solidification time (Figures 11 and 14) with the larger number of graphite nodules belonging to family 0, 1 and 2 at points 1 and 2 that cool down at a slower pace.

Fig. 15
figure 15

Experimental and simulated final volumetric fractions of graphite, ferrite, and pearlite at points 1, 3, and 4

Full size image
Fig. 16
figure 16

Experimental and simulated final graphite density at points 1 to 4

Full size image

The computed results of the solidification process of this alloy reported by Dardati et al.,[15] indicate a high number of graphite nodules that belong to family 0 than that shown in Figure 16. However, when considering the growth of graphite nodules during the entire cooling process, as in the present study, these nodules now become part of families 1 and 2. It should be noted that this is consistent with the experimental measurements.

From the present results, it is seen that the differences between simulated and experimental phase fractions at points 1, 3, and 4 could be due to a higher computed cooling rate throughout the eutectoid transformation than that observed in the experiments (see Figure 13). The phase fractions resulting from the simulation are very similar in the four points, which shows the consistency of the numerical model with respect to the conducted experiments. The phase volume fractions obtained via computations and experiments at four points provide a ferritic/pearlitic matrix in all cases (see Figure 15), which is an acceptable result for a non-alloy cast and in which the points considered have approximate cooling velocities (see Figure 11).

The computational model establishes a tendency for obtaining a ferritic matrix in the locations where the cooling velocity is lower (point 2), and a pearlitic matrix at points close to the mold in which the cooling rate is higher (points 1, 3, and 4). Moreover, there is a significant relation between the distribution of graphite nodules, the cooling rate, the extension in the solidification plateau, and the graphite and ferrite fractions obtained. This trend was not observed in the experimental phase fractions.

Conclusions

A new formulation to simulate the thermo-metallurgical phenomena that take place during the complete cooling process (from pouring temperature to room temperature) of an eutectic nodular cast iron has been presented in this study. The models defined in the microscopic scale involve the description of the solidification according to the plurinodular theory, the growth of graphite nodules between eutectic temperature and stable eutectoid temperature, and, in addition, the stable and metastable eutectoid phase changes considering both transformations as two competitive processes.

The main contributions of this model may be summarized as follows:

  1. 1.

    The present model represents an improvement with respect to previous studies in the literature because it couples the solidification based on plurinodular theory with a model of phase transformation in solid state for an eutectic nodular cast iron.

  2. 2.

    All phase changes involved in the model were represented at a microstructural level through the laws of nucleation and growth, which is a new aspect in relation to previous studies in this field.

  3. 3.

    As a new feature, the present model includes the growth of graphite nodules during the complete cooling process.

  4. 4.

    This is the first time in which simulated and experimentally measured values considering the entire cooling have been compared. Crucial aspects that were measured include the size distribution of graphite nodules, which influences the mechanical properties of a nodular cast iron.

The results show that phase fractions depend on cooling rate in such a way that there is a relationship between cooling rate and phase fractions forming metal matrix and size and size distribution of nodules. Larger cooling rates result in more and smaller graphite nodules and, hence, smaller distances to carbon to diffuse so that the graphite nodules and stable eutectoid phase change is favored.

To validate the theoretical developments, the experimental measurements resulting from the cooling process of casting of a nodular cast iron of slight hypereutectic composition in a standardized Quick-Cup were compared with those obtained from the computational model. An overall good agreement was obtained. In particular, the computational model adequately predicts the main characteristics of the nodular graphite cast iron, including the graphite size, the graphite size distribution, and the final percentages of graphite, pearlite, and ferrite, which are the principal characteristics that define the mechanical properties of a nodular cast iron part during its service life.

This study highlights the predictive role, not frequently seen in the literature, of the numerical modeling of a fully coupled thermo-metallurgical phenomena present in the cooling process of nodular cast iron. This may be seen in the prediction of the cooling curve and cooling velocity, the graphite, ferrite, and pearlite fractions, and the size of node distributions of graphite (shown in Figures 12, 13, 14, 15, and 16), which greatly influence the macroscopic properties of a nodular cast iron part.

The present contribution may also be viewed as a starting point toward modeling the influence of micro-segregations, the spacing between secondary dendrite the solid state.