1 Introduction

Quenching is one of the most important heat-treatment processes for improving the mechanical properties of steel. During quenching, various phase transformations can occur depending on the cooling rate for a given steel, generating a variety of microstructures at different locations within a quenched component.[1] Moreover, the difference in the cooling rates at the surface and the core of a quenched component induces thermal stress. Additionally, the expansion caused by phase transformations, such as martensitic transformation, will result in transformation stress. The interaction between the thermal and transformation stresses makes quenching stress rather complex. The quenching stress is also a source of cracking. The importance of the measurement of the residual stress distribution in a component lies not only in the determination of the location of the maximum tensile stress, which is often the cause of cracking,[2] but also in the data measured as a benchmark for examining the accuracy of computer simulations. As early as 1925, Scott[3] studied the cracking conditions of tool steel when quenched in water or oil. Using analytical calculations and experimental measurements of the axial stress distribution in the quenched cylinders, he concluded that the cracking was due to the tensional stress at the surface. Isomura and Sato[2] measured the residual stress of 18-mm-diameter and 100-mm-long cylinders after quenching in water or brine, respectively, and revealed that the quenching cracks were caused by the triaxial tension stress below the surface of the high carbon cylinders. Moore and Evans[4] proposed the correction formulation, which is used to precisely measure the residual stress distribution along the radius of a cylinder by X-ray diffraction (XRD). The precise measurement of the residual stress distribution is the basis of process design. However, experimental measurements have three main limitations: (1) for a large and complex component, the measurement of the internal stress as a function of depth is not only difficult but also time-consuming; (2) in most cases, cracking of a quenched component is caused by transient stress during quenching, whereas the experiment can only measure the final internal stress (residual stress), rather than the transient stress; and (3) the origin of complex quenching stresses cannot fully be understood if there is no assist of computer simulation of the stress analysis. For these reasons, finite element simulation (FES) of quenching was rapidly developed to predict the temperature, phase, and stress evolution to optimize the quenching process.[5,6,7,8] Jung et al.[1] proposed a new method for determining the variables: the starting temperature for bainitic transformation (B s) and the starting temperature for martensitic transformation (M s), and the accuracy of the simulated residual stress was improved. Ariza et al.[9] predicted the residual stresses of carbon and low-alloy steels, which agreed very well with the XRD measurements. Bok et al.[7] investigated the stress development and shape change during press hardening using different material modeling schemes and claimed that the phase-transformation-related strains in the material model are essential.

In the development of computer simulations, transformation plasticity (TP) is one of the difficult issues that need to be addressed to obtain a precise prediction of the residual stress. TP is an irreversible strain observed when metallurgical transformation occurs under a small external stress lower than the yield stress of the weaker phase.[10,11,12] The effect of TP on the simulated residual stress causes some divergences. Inoue and Wakamatsu[13] proposed a unified plastic flow theory and employed it on a quenched blank gear wheel, demonstrating that TP dramatically affected the stress distribution compared to results without the TP effect. Denis et al.[14] considered that TP must be taken into account when describing the stress and strain states at each moment during cooling. However, Wang et al.’s[15] work demonstrated that the calculated and measured residual stress distributions along the radius of 1080 steel (pearlitic steel) agreed well in the case in which TP was not included in the FES. Nagasaka et al.[16] proposed a mathematical model and applied it to the water spray quenching of 1035 carbon steel and nickel-chromium alloyed steel. The results demonstrated that there was no significant difference in the calculated stress distribution even though TP was not taken into account for the 1035 steel (pearlite matrix), implying that TP can be ignored. In contrast, in the alloyed steel bar (martensite matrix), a marked influence of TP on the residual stress distribution was predicted, meaning that TP must be included in the thermomechanical model. Taleb et al.[10] measured the variation of TP with the volume fraction of bainite, which was termed “TP kinetics,” and compared it with the prediction based on functions describing the TP kinetics proposed by Abrassart, Desalos, and Leblond. The result indicates that their functions lead to almost the same kinetics, which largely underestimates the experimental result. Recently, we proposed an exponent-modified (Ex-Modified) normalized function describing the TP strain,[17] which was used to fit the experimental result from Taleb et al.,[10] showing that the Ex-Modified normalized function better describes the TP kinetics than Abrassart’s and Desalos’s functions, and in turn the FES for the residual stress distributions in quenched AISI 4140 cylinders with two diameter sizes better agrees with XRD measurements.[17]

Although computer simulation of heat treatment has been developed rapidly in recent years, and many commercial packages, such as HEARTS,[5] DANTE,[18] COSMAP,[19] and DEFORM-HT,[20] are available on the market, any software only includes one of the TP kinetics models. Therefore, various TP kinetics models cannot be compared by the software packages except when new subroutines are written. Such a comparison has not been performed by other investigators. Quenching stress results from the interaction between the thermal and phase transformation stresses, and how they individually affect the stress distribution is still unanswered. A clear conclusion on whether TP should be considered when performing quenching simulations has not yet been reached. Therefore, the present study will focus on the three issues mentioned previously.

In this work, three typical microstructures in quenched steels were designed using three different hardenability medium carbon steel cylinders with the same diameter of 60 mm and length of 240 mm. The materials are 45 (Chinese steel mark) with a pearlite matrix, 42CrMo with a bainite matrix, and 40CrNiMo with a martensite matrix. The residual stress distributions in the three cylinders were measured using XRD. Based on the normalized function describing the TP kinetics, the thermo-elasto-plastic constitutive equation was derived. The commercial finite element software, Abaqus/Standard, was used to solve the coupled temperature, microstructure, and stress (strain) fields. Several models for the TP kinetics, including the Ex-Modified normalized function proposed by the authors, were added in the User subroutine UMAT to calculate the internal stress using the CAX4 element, and thus the effects of various models on the internal stresses were compared. In the FES, the parameters simulating the cooling curves and microstructure were determined in succession by comparisons with experiments. Based on the preceding parameters and normalized functions, the calculation for the individual influence of the thermal stress and phase transformations on the quenching stress was performed. Finally, the FES predictions of the stress distributions along the radius of three hardenable cylinders were compared with XRD measurements.

2 Experimental Procedures

The chemical composition of three commercial steels and the calculated critical temperature by JmatPro are given in Table I. The tested cylinders were 60 mm in diameter and 240 mm in length. The advantage of using a cylinder to evaluate a thermally coupled simulation program is due to its axisymmetric geometry. A surface temperature/time characteristic for a cylinder can be measured with one surface mounted thermocouple and gives a relative precise heat transfer boundary condition. Before the quenching test, all of the cylinders were annealed at 1123 K (850 °C) for 7200 seconds.

Table I Chemical Composition and Critical Temperatures of the Investigated Steels
Full size table

During the quenching process, the 45, 42CrMo, and 40CrNiMo commercial steel cylinders were first heated in a pit furnace at 1123 K (850 °C) for 4500, 5400, and 6000 seconds, respectively, to ensure that the specimens were completely austenitized. After heating, the specimens were precooled in air for 30 seconds and then immersed in water [room temperature 305 K (32 °C)] for 150 seconds. The preceding precooling is to reduce the thermal capacity and accelerate the cooling rate during the quenching stage.[21]

The quenched cylinders were cross sectioned, mechanically polished, and then etched first with 2 pct Nital (2 mL HNO3 and 98 mL ethyl alcohol) for 10 seconds and subsequently with Vilella (0.5 mL picric acid, 2.5 mL HCl, and 50 mL C2H5OH) for 5 seconds. The etched samples were used for optical microscopy (OM; Imager A1m) and field-emission–scanning electron microscopy (FE-SEM; JEOLFootnote 1 JSM7600F). The volume fractions of ferrite, bainite, and martensite were measured using image software according to the pixels a phase occupies. The residual stresses in the quenched cylinders were measured using XRD (iXRD combo, Proto Company, ON, Canada). The sin2 ψ method[22] was used in this study. If the stress state is biaxial, a straight line should be experimentally obtained. The stress in the φ direction, σ φ , is calculated from the slope of the straight line:

$$ \sigma_{\varphi } = \frac{{\left( {\frac{{\partial \varepsilon_{\varphi \psi }^{{\left\{ {hkl} \right\}}} }}{{\partial \sin^{2} \psi }}} \right)}}{{\frac{1}{2}S_{{_{2} }}^{{\left\{ {hkl} \right\}}} }} $$
(1)

where φ is the angle between a measured direction in the plane of the specimen and the projection in that plane of the normal to the diffracting lattice planes, and φ = 0 in this work for Omega geometry, ψ is the angle between the normal of the specimen and the normal of the diffracting lattice planes, \( \varepsilon_{\varphi \psi }^{{\left\{ {hkl} \right\}}} \) is the strain in the direction defined by the angles φ and ψ for the family of lattice planes {hkl}, and \( \frac{1}{2}S_{{_{2} }}^{{\left\{ {hkl} \right\}}} \) is the X-ray elasticity constants for the family of lattice planes {hkl}. Cr radiation (λ = 0.2291 nm) was employed with a spot diameter of 2 mm. The values for ψ were ±0, ±12, ±24, ±30, ±37, and ±43 deg. The reference crystallographic plane was {211} of bcc phase, and the corresponding elasticity constants \( \frac{1}{2}S_{{_{2} }}^{{\left\{ {211} \right\}}} \) were 5.06 × 10−6 MPa−1 for 45 steel and 5.92 × 10−6 MPa−1 for both the 42CrMo and 40CrNiMo steels. To measure the residual stress distribution along the radius, the removal of the outer layer was required. The cylinder was first lathed and then etched using an aqueous solution of nitric acid (150 mL HNO3, 50 mL H2O2, 20 g H2C2O4, and 300 mL H2O) to remove at least 0.5 mm. The removal of the outer layer may redistribute the stress, meaning that the measured values for the residual stress after the removal of material need to be corrected to obtain the true stress distribution existing prior to the layer removal. The correction formulations proposed by Moore and Evans[4] were used in this study:

$$ \begin{aligned} \sigma_{\text{t}} \left( r \right){ = }\sigma_{t,m} \left( r \right) - \int_{r}^{R} {\sigma_{t,m} } \left( \xi \right) \cdot \frac{{{\text{d}}\xi }}{\xi } \hfill \\ \sigma_{\text{z}} \left( r \right){ = }\sigma_{z,m} \left( r \right) - 2\int_{r}^{R} {\sigma_{z,m} } \left( \xi \right) \cdot \frac{{{\text{d}}\xi }}{\xi } \hfill \\ \end{aligned} $$
(2)

where σ t(r) and σ z(r) are tangential stress and axial stress corrected at the radius of r, respectively; σ t,m (r) and σ z,m (r) are the measured tangential stress and axial stress at the radius of r; and R is the initial radius of the specimen.

3 Simulation Details

The coupling between the temperature, phase transformations, and mechanical behavior was presented by Leblond et al.[23] Among these interactions, the influence of the mechanical behavior on temperatures via deformation energy was ignored, as this effect is small [approximately 2 K (2 °C)],[23] and the effect of the stress/strain on the phase transformations[24] was also not considered here due to a lack of experimental data and reliable models. Therefore, the entire coupling can be simplified into a sequentially coupled thermal-stress analysis.

3.1 Calculation of Temperature Distribution

By introducing the phase transformation latent heat, a governing equation for the calculation of temperature was determined and is expressed as[25]

$$ \rho C_{p} \left( {\varphi_{i} ,T} \right)\dot{T} = \nabla \left( {k\left( {\varphi_{i} ,T} \right) \cdot \nabla T} \right) + \dot{Q} $$
(3)

where ρ is the density of 7850 kg/m3; C p and k are the specific heat and thermal conductivity of the phase mixture, respectively; T is the temperature; \( \dot{T} \) is the time derivative of the temperature; ∇ denotes the gradient operator; and \( \dot{Q} \) is the transformation latent heat rate:

$$ \dot{Q} = \sum\limits_{i = 2}^{5} {\Delta H_{i} \dot{\varphi }_{i} } $$
(4)

where \( \Delta H_{i} \) represents the enthalpy of the phase transformation, \( \dot{\varphi }_{i} \) is the transformation rate for the i phase, and i represents austenite, ferrite, pearlite, bainite, and martensite for i = 1, 2, 3, 4, and 5, respectively.

The values for C p and k are functions of temperature and phase constituent, and their data are taken from Jung et al.[1] for 45 steel and Kakhki et al.[26] for both the 42CrMo and 40CrNiMo steels used in this work. The latent heats of ferrite, pearlite, bainite, and martensite are −5.95 × 108, −5.26 × 108, −5.12 × 108, and −3.14 × 108 J/m3, respectively.[9,27]

The initial temperature for the analysis was set at a uniform value of 1123 K (850 °C), which is the austenitization temperature for the 45, 42CrMo, and 40CrNiMo steels. Boundary (film) conditions were set at the surfaces of the cylinders in contact with the water:

$$ - k\left( {\varphi_{i} ,T} \right)\nabla T = h\left( T \right)\left( {T_{\text{s}} - T_{\text{w}} } \right) $$
(5)

where h(T) is the heat transfer coefficient (HTC) of the water and T s and T w are the temperatures of the cylinder’s surface and water, respectively.

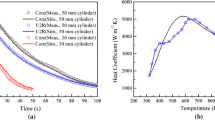
The HTC as a function of surface temperature was obtained by trial and error[17]: (1) discretize the continuous function to several temperature points, and (2) adjust the HTC at each temperature point until the calculated cooling curves at the cylinder’s center and 1/2 radius are consistent with the measured cooling curves and the HTCs corresponding to these temperature points are optimized. The commercial finite element software Abaqus/Standard was used to solve the heat transfer analysis. Phase transformation was implemented in the user subroutine UMATHT. Details on the phase transformation calculation are discussed in Section III–B. A four-node linear diffusive heat transfer element DCAX4 was used because of the axially symmetric geometry and the loads for the quenched cylinders. The 60-mm diameter was meshed into 6364 nodes and 6174 elements with refined elements near the surface.

3.2 Phase Transformation Calculation

During quenching, various phase transformations occur depending on the cooling rate and hardenability of steel, generating a variety of microstructures: ferrite, pearlite, bainite, and martensite.

The kinetics of austenite-martensite transformation in steels is dependent only on the temperature, and there are several empirical kinetic models for the athermal martensite transformation. A review of these models was presented by Lee.[28] Equation [6] describes the volume fraction of martensite, φ M, as a function of temperature[29,30]:

$$ \varphi_{M} = 1 - \exp \left[ { - \alpha_{M} \left( {M_{s} - T_{q} } \right)} \right] $$
(6)

where α M is a rate parameter and T q is the lowest temperature reached during quenching. Koistinen and Marburger[29] argued that α M = 0.011 K−1, independent of composition, whereas van Bohemen and Sietsma[30] concluded that α M is composition dependent for the low alloyed steels with carbon contents ranging between 0.3 and 1.1 wt pct. The rate parameter is described by the simple linear equation:

$$ \alpha_{\text{M}} = 0.0224 - 0.0107x_{\text{C}} - 0.0007x_{\text{Mn}} - 0.00005x_{\text{Ni}} - 0.00012x_{\text{Cr}} - 0.0001x_{\text{Mo}} $$
(7)

Equations [6] and [7] were employed in this study.

For the ferrite, pearlite, and bainite, the kinetic equation at constant temperature proposed by Austin and Rickett[31] was used and is described as

$$ \frac{{\varphi_{i} }}{{1 - \varphi_{i} }} = \left[ {\frac{t}{{\tau_{i} \left( T \right)}}} \right]^{{n_{i} \left( T \right)}} $$
(8)

where τ i (T) is a function of temperature and is the time required to transform 50 pct of the i phase, and n i (T) is a parameter weakly dependent on the temperature. These two parameters were obtained by fitting to the TTT diagrams in Reference 32. The alloy elements and grain size for the steel in Reference 32 may be different from those in this work. Therefore, the values for τ i (T) were modified based on the work performed by Kirkaldy and Venugopalan.[33] However, during continuous cooling of the quenching, the phase transformations mentioned previously occur neither at a constant temperature nor under a constant cooling rate condition, making the calculation of the phase transformations during quenching rather complex. It can be imagined that the calculated volume fraction of ferrite, pearlite, or bainite is not better than that of martensite in terms of precision. The common solution for this problem is combining the isothermal equation with Scheil’s additive rule.[34]

3.3 Stress/Displacement Analysis

During the process of quenching, the total strain increment was divided into five parts:

$$ \Delta \varepsilon_{ij} = \Delta \varepsilon_{{_{ij} }}^{\text{el}} + \Delta \varepsilon_{{_{ij} }}^{\text{pl}} + \Delta \varepsilon_{{_{ij} }}^{\text{th}} + \Delta \varepsilon_{{_{ij} }}^{\text{tr}} + \Delta \varepsilon_{{_{ij} }}^{\text{tp}} $$
(9)

where \( \Delta \varepsilon_{{_{ij} }}^{\text{el}} \), \( \Delta \varepsilon_{{_{ij} }}^{\text{pl}} \), \( \Delta \varepsilon_{{_{ij} }}^{\text{th}} \), \( \Delta \varepsilon_{{_{ij} }}^{\text{tr}} \), and \( \Delta \varepsilon_{{_{ij} }}^{\text{tp}} \) are the strain increments for the elastic, plastic, thermal, phase transformation, and TP components, respectively. Assuming that the materials are isotropic, the thermal strain and transformation strain increment are also isotropic and can be calculated by the following equations, respectively:

$$ \begin{aligned} \Delta \varepsilon_{{_{ij} }}^{\text{th}} = \delta_{ij} \sum\limits_{i = 1}^{5} {\varphi_{i} } \left[ {\varepsilon_{i} \left( {T + \Delta T} \right) - \varepsilon_{i} \left( T \right)} \right] \hfill \\ \Delta \varepsilon_{{_{ij} }}^{\text{tr}} = \delta_{ij} \sum\limits_{i = 2}^{5} {\Delta \varphi_{i} } \left[ {\varepsilon_{i} \left( {T + \Delta T} \right) - \varepsilon_{1} \left( {T + \Delta T} \right)} \right] \hfill \\ \end{aligned} $$
(10)

where ε i is the relative strain of the i phase and was calculated based on experimental thermal expansion curves.

When phase transformations occur under stress, an anomalous plastic strain, known as TP, will occur even though the equivalent stress of the external stresses is below the yield strength of austenite.[35] The increment of the TP strain is expressed as[36]

$$ \Delta \varepsilon_{{_{ij} }}^{\text{tp}} = \frac{3}{2}K\left( \sigma \right)f'\left( \varphi \right)\Delta \varphi s_{ij} $$
(11)

where K(σ) is the TP coefficient, which is a function of the equivalent stress, and was obtained by fitting to the experimental results provided by Liu et al.;[37] s ij denotes the deviatoric stress tensor; \( f'\left( \varphi \right) \) is the derivative function of the \( f\left( \varphi \right) \) normalized function; and the various expressions of \( f\left( \varphi \right) \) proposed by Abrassart, Desalos, Leblond, and the authors are shown in Table II.

Table II Various Expressions of f(φ) Functions
Full size table

The elastic prediction including TP was first derived:

$$ \begin{aligned} \Delta \sigma_{{_{ij} }}^{\text{pr}} = \Delta s_{{_{ij} }}^{\text{pr}} + \frac{1}{3}\Delta \sigma_{kk} \delta_{ij} \hfill \\ = \left[ {\frac{2G}{l}\Delta \varepsilon_{ij} + \left( {B - \frac{2G}{3l}} \right)\Delta \varepsilon_{kk}^{\text{el}} \delta_{ij} } \right] + \left[ {\frac{2\Delta G}{l}\varepsilon_{ij}^{\text{el}} + \left( {\Delta B - \frac{2\Delta G}{3l}} \right)\varepsilon_{kk}^{\text{el}} \delta_{ij} } \right] - \frac{2G}{l}\chi \left. {s_{ij} } \right|_{n} \hfill \\ \chi = \frac{3}{2}K\left( \sigma \right)f'\left( \varphi \right)\Delta \varphi \hfill \\ l = 1 + 2G\chi \hfill \\ \end{aligned} $$
(12)

where the superscript pr denotes prediction; σ ij is the Cauchy stress tensor; B and G are the bulk and shear modulus of the mixture phase, respectively, and were calculated by the linear rule of mixtures; and χ and l are variables.

The material is assumed to be rate independent. The von Mises yield surface with kinematic hardening was used to include the plasticity of the material.[38] The yield function was written as

$$ f\left( {s_{{_{ij} }}^{\text{pr}} ,\varepsilon_{eq}^{\text{pl}} } \right) = \sqrt {\frac{ 3}{ 2}\left( {s_{{_{ij} }}^{\text{pr}} - \alpha_{ij} } \right)\left( {s_{{_{ij} }}^{\text{pr}} - \alpha_{ij} } \right)} - \sigma_{\text{y}} \left( {\varepsilon_{eq}^{\text{pl}} } \right) $$
(13)

where α ij is the deviator of the backstress tensor, and σ y is the yield strength of the phase mixture, which was calculated based on a nonlinear (parabolic approximation) mixture rule[39] since a relatively large overestimation of the stress is observed when using the simple linear rule.[39,40] Due to the difficulties of measuring various phases’ flow stresses and the weak effect of the difference in flow stresses on the simulated residual stress (which was verified by our FES), the mechanical properties for medium carbon steels for a variety of phases were taken from References 41 and 42. The plastic flow rule was expressed as[38,43]

$$ \begin{aligned} \Delta \varepsilon_{ij}^{\text{pl}} = \frac{3}{2}\left( {s_{ij}^{\text{pr}} - \alpha_{ij}^{0} } \right)\Delta \varepsilon_{eq}^{\text{pl}} /\sigma_{eq}^{\text{pr}} \hfill \\ \Delta \alpha_{ij} = \frac{2}{3}H\Delta \varepsilon_{ij}^{\text{pl}} \hfill \\ \end{aligned} $$
(14)

where H is the plastic hardening modulus. The value of H for the mixture of austenite, martensite, and bainite was calculated using the linear rule of mixtures. The equivalent stress was calculated based on purely elastic behavior (Eq. [12]). Plastic flow will occur if \( f\left( {s_{{_{ij} }}^{\text{pr}} ,\varepsilon_{eq}^{\text{pl}} } \right) > 0 \). The backward Euler method is used to determine the increment of plastic strain.[43]

4 Results

4.1 Temperature Evolution During Quenching

Figure 1(a) shows a comparison between the measured and calculated cooling curves for the 42CrMo cylinder at the core, 1/2 radius, and 5-mm distance from the surface. The calculated curves agree well with the measured ones, as shown in Figure 1(a). This indicates that the HTC, h(T), determined by the preceding trial/error method is reliable. The cooling curves for the three commercial steels at four different locations were further calculated, as shown in Figure 1(b). At the precooling stage in air during the initial 30 seconds, the temperature decreased slowly because of the low HTC of the air but dropped dramatically after immersion in water due to the high HTC of water. The cooling curves at the initial stage of air cooling for the three steels are similar due to the identical diameters, but during subsequent water cooling, obvious differences are seen, especially at the core and 1/2 radius of the cylinders. The calculated cooling curve at the core of the cylinder exhibited a small hump at approximately 933 K (660 °C) for 45, 753 K (480 °C) for 42CrMo, and 593 K (320 °C) for 40CrNiMo, which are attributed to the latent heat of the pearlitic, bainitic, and martensitic transformations (Figure 1(b)), respectively. In contrast, for the calculated cooling curves at the surface, the latent heat of the martensitic transformation did not significantly influence the temperature due to the fast cooling rate. The cooling rate between 873 K and 473 K (600 °C and 200 °C) for the 45 steel at the core or 1/2 radius of the cylinder was greater than those for the 42CrMo or 40CrNiMo steels due to the higher conductivity of the ferrite/pearlite microstructure than that of undercooling austenite.[1,21]

Fig. 1
figure 1

(a) Comparison of temperature history measured and calculated for 42CrMo cylinder. (b) Calculated temperature history of 45, 42CrMo, and 40CrNiMo cylinders at the core, 1/2 radius, 25-mm radius, and surface during quenching in water

Full size image

4.2 Phase Distribution

The OM photographs in Figure 2 and SEM photographs in Figure 3 show the microstructures of the 45, 42CrMo, and 40CrNiMo steels at the 1/2 radius and core of the cylinders after quenching in water, respectively. In the 45 steel, there is proeutectoid ferrite and pearlite. As the cooling rate increases from the core to the surface, the amount of pearlite gradually increases, as shown in Figures 2(a) and (b). However, a great amount of martensite and bainite, instead of pearlite, appears at the surface and subsurface, which is not shown in this article. The interlamellar spacing of the pearlite is so fine that it is not clearly discriminated by OM, necessitating SEM to observe the fine microstructure, as shown in Figures 3(a) and (b). In the 42CrMo steel, we observe the presence of bainite and martensite. The amount of martensite gradually increases from the core to the surface, but the amount of bainite is still greater than that of martensite, as shown in Figures 2(c), (d), 3(c), and (d). In the 40CrNiMo steel, we observe the presence of martensite and bainite, and the amount of martensite gradually increases from the core to the surface. Moreover, the amount of martensite is always much larger than that of bainite, as shown in Figures 2(e) and (f) and 3(e) and (f).

Fig. 2
figure 2

Optical microstructures of the quenched cylinders: (a), (c), and (e) are at the 1/2 radius of the cylinders for 45, 42CrMo, and 40CrNiMo, respectively; (b), (d), and (f) are at the core of cylinders for 45, 42CrMo, and 40CrNiMo, respectively

Full size image
Fig. 3
figure 3

Scanning electron micrograph of the quenched cylinders: (a), (c), and (e) are at the 1/2 radius of the cylinders for 45, 42CrMo, and 40CrNiMo, respectively; (b), (d), and (f) are at the core of cylinders for 45, 42CrMo, and 40CrNiMo, respectively

Full size image

Figure 4 shows a comparison of predicted and measured microstructure fractions for the three steels. The predicted volume fraction of pearlite or ferrite for the 45 cylinder is basically consistent with what is measured. At the subsurface (25-mm radius), the pearlite fraction calculated is as much as 90 pct, but rapidly drops to zero when approaching the surface, where the pearlite is replaced by bainite and martensite due to the high rate of cooling (Figure 1(b)). For the 42CrMo or 40CrNiMo steels, the calculated bainite or martensite fraction matched well with the measured result at the core, but matched relatively poorly at the 1/2 radius. These results indicate that the 45 steel has low hardenability, the 42CrMo steel has moderate hardenability, and the 40CrNiMo steel has the highest hardenability.

Fig. 4
figure 4

Comparison of the simulated and calculated microstructure distributions along the radius of (a) 45, (b) 42CrMo, and (c) 40CrNiMo

Full size image

4.3 Residual Stress Distribution

The calculated and measured axial and tangential stress distributions for the three different hardenable steels are shown in Figure 5. The calculated residual stress for the 40CrNiMo steel is most consistent with the measured results due to the best prediction of the microstructure fraction, followed by the 42CrMo steel. For the 45 carbon steel, the calculated compressive stress at the surface or subsurface of the cylinder is much larger than the measured results, which may be attributed to overestimating the volume fraction of the martensite or bainite, as they exhibit higher phase transformation expansion coefficients than pearlite. For the 42CrMo steel, there is a small calculated tensile stress at the 1/2 radius, whereas measurements show the presence of a small amount of compression. This is likely a result of underestimating the martensite fraction, as shown in Figure 4(b). The 45 and 42CrMo steels exhibit the following characteristics in terms of the residual stress distribution: (1) the maximum tensile stress is located in and around the core, (2) the maximum tensile axial stress is higher than the tangential stress, and (3) the surface or subsurface of the cylinders exhibits a high level of compressive stress. Such characteristics of stress distribution, classified as type I,[44] agree with those reported by Wang et al.[15] The residual stress of the 40CrNiMo steel exhibits the following characteristics: (1) the maximum tensile stress is located at the subsurface; (2) the maximum tangential stress is larger than the axial stress; (3) there is a compressive stress at the surface of the cylinder, for which the magnitude of the tangential stress is larger than that of the axial stress; and (4) there is a compressive stress at the core, which differs from that of the 45 or 42CrMo steel. These stress distribution characteristics are classified as type II[44] and agree with those measured by Isomura and Sato.[2] In general, the FES can predict the different residual stress distribution features for the three steels, verifying the accuracy of the FES model.

Fig. 5
figure 5

Measured and calculated residual stress distributions along the radius of the three hardenable steels after water quenching: (a) axial stress and (b) tangential stress

Full size image

5 Discussion

5.1 A Comparison of the TP Equations When Simulating the Residual Stress Distribution

For the description of the TP, the normalized function f(φ) has several types of expressions,[10] such as those proposed by Abrassart, Deslos, and Leblond, as shown in Table II. Taleb et al.[10] noted that Abrassart’s, Desalos’s, and Leblond’s functions largely underestimate the experimental results. We analyzed the curve feature of the normalized function, f(φ), measured by Taleb et al. At the initial stage of transformation, the normalized function rapidly increases, and at the ending stage of transformation, it slowly increases. As a result, we proposed an Ex-Modified normalized function linking with the TP strain:

$$ f\left( \varphi \right) = A \, \exp \left( {B\varphi^{n} } \right) $$
(15)

where A is a parameter used to adjust the normalization. Equation [15] was used to fit the experimental curve of Taleb et al., and the parameters in Eq. [15] were determined to be A = 1.105, B = −0.0994, and n = −0.91, as shown in Table II. The results indicate that the fitted curve based on the Ex-Modified normalized function is more consistent with the curve measured by Taleb et al. than the curves fitted by the normalized functions proposed by Abrassart, Desalos, and Leblond.[17] To reflect the effects of the normalized functions on the internal stress, a comparison between the measured and calculated internal stresses in the 40CrNiMo steel based on four normalized functions (Ex-Modified, Abrassart, Desalos, and Leblond) was performed, as shown in Figure 6. The FES of the distribution of the internal stresses based on the Ex-Modified normalized function, including the axial and tangential stresses, is more consistent with that measured by XRD than the FES based on the normalized functions proposed by Abrassart, Desalos, and Leblond. This is because the Ex-Modified normalized function better describes the TP. The FES coupled with an improved TP function reconfirms the importance of accurate models for better prediction of residual stress when dealing with TP kinetics.

Fig. 6
figure 6

Measured and calculated residual stress distributions based on various TP equations of 60-mm-diameter 40CrNiMo after water quenching: (a) axial stress and (b) tangential stress

Full size image

5.2 Effects of Hardenability on the Thermal and Phase Transformation Stresses

Residual stress arises from the interaction of thermal and phase transformation stresses. To understand the difference in the residual stress distributions among the three hardenable steels, the thermal and phase transformation stresses were calculated separately. Figure 7 shows the calculated thermal stress distributions for the 45, 42CrMo, and 40CrNiMo steels. The thermal stress distributions for the three different hardenable steels exhibited similar characteristics and values: (1) the maximum tensile stress is at the core of the cylinder and (2) the maximum compressive stress is at the surface. In short, the thermal stress gradually changes from a compressive stress at the surface to a tensile stress at the core. This similarity of the thermal stress distributions is the expected result, since we used the same water-quenching technique and the same diameter for the three steel cylinders. This was done specifically so that the effect of the phase transformation on the internal stress can be investigated. This feature of the thermal stress distribution was explained based on our calculations of the changes in the temperature and thermal distribution with time as follows: during initial cooling, there are tensile stresses at the surface and compressive stresses at the core. Then, at the point of maximum temperature difference between the surface and core, there is a stress conversion; the surface is in compression relative to the core until cooling is completed, which is in agreement with Reference 45.

Fig. 7
figure 7

Calculated thermal stress distributions of 45, 42CrMo, and 40CrNiMo cylinders: (a) axial stress and (b) tangential stress

Full size image

Figure 8 shows the phase transformation stress distributions calculated for the three different hardenable steels. In contrast to the thermal stresses, the transformation stresses gradually change from a tensile stress at the surface of the 42CrMo or 40CrNiMo steel cylinders to a compressive stress at the core. This feature of the phase transformation stress distribution is explained based on our calculation of the changes in the microstructures and phase transformation stress with time. As shown in Figure 1, the cooling rate increases as we move from the core to the surface, meaning that the martensite transformation occurs gradually from the surface to the core. Initially, due to the rapid cooling rate at the surface, a large compressive stress is produced due to the martensitic transformation and reaches a maximum at approximately 80 pct volume fraction of martensite. Then, the phase transformation stress gradually increases to a tensile stress with the transformation fraction increment. During this process, martensitic transformation begins at the core, accompanied by the formation of a compressive stress at this location, resulting in the compressive stress at the core and tensile stress at the surface reaching a balance after quenching is completed. It is worth noting that the transformation stress in the 45 cylinder gradually changes from a compressive stress at the core to a tensile stress near the subsurface but drops sharply from a tensile to a compressive stress at the subsurface. This abnormal phenomenon is explained as follows. At first, due to the rapid cooling rate at the surface, a large compressive stress is produced by the martensitic transformation, which reaches a maximum at approximately 70 pct volume fraction of martensite. Then, the phase transformation stress gradually increases to a tensile stress, and a large amount of pearlite forms at the subsurface (Figure 4(a)), which produces a small compressive stress, as the volume expansion of the pearlitic transformation is much less than that of the nearby martensitic or bainitic transformation.[45] This causes a sharp increase in the stress, which gradually increases from a compressive stress forward to a tensile stress. When the pearlitic transformation finally occurs at the core, a large compressive stress is produced that balances with the small tensile stress at the surface after quenching is complete.

Fig. 8
figure 8

Calculated phase transformation stress distributions of 45, 42CrMo, and 40CrNiMo cylinders: (a) axial stress and (b) tangential stress

Full size image

The residual stress distribution is the result of the thermal and phase transformation stresses overlapping. Combining Figure 7 with Figure 8, the origin of the residual stress distribution features in the three steels is analyzed as follows. The relatively higher tensile thermal stress and the lower compressive phase transformation stress at the core cause the residual stress to be a tensile stress for the 45 and 42CrMo steels, as shown in Figure 5. In contrast, the relatively higher phase transformation stress is compressive and the lower thermal stress is tensile at the core of the 40CrNiMo steel, resulting in a compressive residual stress at the core, as shown in Figure 5. The surface of the three hardenable steel cylinders contains a compressive stress predominantly from the thermal stress, which is much larger than the tensile stress arising from the phase transformation stress. The effects of hardenability on the residual stress can be more markedly demonstrated using a residual stress contour map, as shown in Figures 9 and 10, where a deep blue color denotes the maximum compressive stress and a deep red color denotes the maximum tensile stress, with the colors green through yellow describing stress states between them. For the axial stress, the area of the deep red distribution (maximum tensile stress) in the 45 cylinder is replaced by a yellow area (small tensile stress) in 42CrMo, which is replaced by a mixed area of light blue, green, and yellow (compressive stress) in 40CrNiMo, as shown in Figure 9. For the tangential stress, the areas of deep red and light red for the 45 cylinder are replaced by deep yellow (relative small tensile stress) for the 42CrMo cylinder and deep green (compressive stress) for the 40CrNiMo cylinder.

Fig. 9
figure 9

Contours of axial residual stress simulated in three steels: (a) 45, (c) 42CrMo, and (e) 40CrNiMo with TP and (b) 45, (d) 42CrMo, and (f) 40CrNiMo without TP (scale factor: 20)

Full size image
Fig. 10
figure 10

Contours of tangential residual stress simulated in three steels: (a) 45, (c) 42CrMo, and (e) 40CrNiMo with TP and (b) 45, (d) 42CrMo, and (f) 40CrNiMo without TP (scale factor: 20)

Full size image

5.3 Effect of TP on the Residual Stress

Figure 11 shows the comparison of the calculated residual stress distributions in the three different hardenable steels with TP included and excluded using FES. It can be found from Figure 11(a) that there was no significant difference in the calculated and measured stress distribution features, except for the surface, despite TP being excluded for the 45 carbon steel. In other words, TP can be ignored for steels with microstructures of pearlite and ferrite. In contrast, for the 42CrMo and 40CrNiMo alloyed steels, the inclusion of TP causes a marked difference in the residual stress distribution. Namely, the calculated stress distribution is consistent with the measured stress distribution when TP is included in the FES, whereas there is a significant deviation between the calculated and measured stress distribution when TP is not included. For the tangential stress in the 40CrNiMo example, (1) the calculated maximum tensile stress is located at the core when TP is ignored (Figure 11(c)), but the measured maximum tensile stress is located approximately 10 mm below surface; (2) the calculated value for the compressive stress at the surface is much larger than that measured when TP is not included; and (3) the stresses measured and calculated are compressive stress from the core to a location at a 12-mm radius when TP is included in the FES, but the stress calculated is a tensile stress when TP is not included in the FES, causing a stress reversal. The effects of TP on the residual stress are more evidently demonstrated in the residual stress contour maps shown in Figures 9 and 10. For example, there is no significant difference in the various color distributions for axial or tangential stress in the 45 steel when comparing Figure 9(a) with (b) or 10(a) with (b) when TP is included or excluded in the FES. However, a marked difference in the color distributions corresponding to the axial or tangential stresses in two alloyed steels is seen when comparing Figures 9 and 10. Using the tangential stress from the 40CrNiMo cylinder as an example, the neighboring area of the core exhibits a yellow color (compressive stress) when TP is included in the FES, but this is replaced by a deep red color (maximum tensile stress) when TP is excluded. Therefore, we conclude that TP must be considered in the FES for a bainite or martensite matrix containing steels. The rationality behind these conclusions is that the TP caused by the pearlitic or ferritic transformation is most relaxed at the high temperature of pearlitic transformation. Thus, TP can be ignored for pearlite matrix steels (such as the 45). In contrast, the TP caused by the bainitic or martensitic transformation is less or hardly relaxed due to the relatively low temperatures associated with bainitic or martensitic transformation. Therefore, TP must be considered in the FES for bainitic matrix steels (such as 42CrMo) and martensitic matrix steels (such as 40CrNiMo).

Fig. 11
figure 11

Comparison of the calculated residual stress distributions with and without TP considered of (a) 45, (b) 42CrMo, and (c) 40CrNiMo after water quenching

Full size image

6 Conclusions

To understand the effect that TP has on residual stress, three typical kinds of microstructures containing a pearlite matrix, a bainite matrix, and a martensite matrix in medium carbon steels were created in identical diameter cylinders exposed to identical water-quenching conditions. The stress distribution measured by XRD was compared to those calculated by FES. The main conclusions are as follows.

  1. 1.

    The FES for the stress distribution in the 45, 42CrMo, or 40CrNiMo steel based on the Ex-Modified normalized function proposed here is more consistent with XRD measurements than the FES results based on the normalized functions proposed by Abrassart, Desalos, and Leblond. This is attributed to the Ex-Modified normalized function better describing TP.

  2. 2.

    For predicting the residual stress distribution using FES, TP can be ignored for the 45 steel but must be included for the 42CrMo and 40CrNiMo alloyed steels. This is attributed to the degree of TP relaxation for the different temperatures associated with the pearlitic, bainitic, and martensitic transformations.

  3. 3.

    The interaction of the thermal and phase transformation stresses leads to a complex residual stress state. The separated calculations revealed that the three steels exhibit similar thermal stress distributions but different phase transformation stress distributions between 45 carbon steel and the 42CrMo/40CrNiMo alloyed steels, leading to differences in the axial and tangential residual stress distributions.