1 Introduction

The AISI 4140 medium carbon steel has been widely used to cylindrical components by quenching and tempering in engineering.[1] The mechanical properties of steel components can be improved markedly by the quenching and subsequently tempering process. However, there are also several problems in the quenching process, such as distortion and cracking caused by internal stress. Internal stress is caused by nonuniform cooling and phase transformation at different locations of a component. It is vital to know the internal stress distribution and transient stress histories during quenching in the design of the quenching process. The measurement of the internal stress distribution in a quenched component along depth is necessary as the base of the design of the quenching process. However, experimental measurement has two main limitations. (1) For a component with large scale and complex shape, the measurement of the internal stress along depth is not only difficult but also time-consuming. (2) In most cases, the cracking of a quenched component is caused by transient stress during quenching, while experiment can only measure the final internal stress (residual stress), rather than transient stress. For these reasons, the computer simulation of quenching was developed to predict the temperature, phase, and stress evolution so as to optimize the quenching process.[2,3] Şimşir and Gür[4] used a three-dimensional (3D) finite element method-based model to predict temperature history, evolution of microstructure, and internal stresses of eccentrically drilled C60 steel cylinders during quenching, and the comparison with experimental results indicates that the model can effectively predict the trends in the distribution of residual stresses for 3D asymmetric components. Jung et al.[5] proposed a new method for determining variables: the start temperature of bainitic transformation (B s), and the start temperature of martensitic transformation (M s), the accuracy of the simulated residual stress was improved. Lee and Lee[6] suggested a new calculation method of M s and kinetics equations of diffusive and diffusionless transformations. Ariza et al.[7] predicted the residual stresses of carbon and low-alloy steels, and the predicted results correspond well with the X-ray diffraction (XRD) measurement results.

Although computer simulation of heat treatment has been developed rapidly in recent years, and many commercial software products, such as HEARTS,[2] SYSWELD,[8] DANTE,[9] COSMAP,[10] and DEFORM-HT,[11] are available in the market, there are still some issues that need to be resolved. Among these issues, transformation plasticity is one of the difficulties that barriers the development of heat treatment simulation. Besides, any software only includes one model of transformation plasticity, and thus, various models of transformation plasticity cannot be compared using one of the software products mentioned previously, except when new subroutines are written. Transformation plasticity is the observed plastic strain caused by phase transformation. Details about transformation plasticity can be found in some articles.[12,13] Denis et al.[14] considered that transformation plasticity has to be taken into account in a description of the stress and strain states at each moment during cooling. Yao et al.[15] also emphasized the importance of transformation plasticity on the reliability of the simulation results. There are two ways to incorporate this effect into the model: one is to artificially lower the yield stress of the overall phase during phase transformation,[16,17] and the other is to add an additional plastic strain in the constitutive equation.[4] The latter was used in this article. There are several expressions proposed in describing transformation plasticity.[18,19,20] Taleb et al.[21] measured the variation of transformation plasticity with the volume fraction of bainite, and this was compared with the prediction based on functions describing the transformation plasticity kinetic proposed by Abrassart and Desalos, respectively. The result indicates that Abrassart’s and Desalos’s functions lead to almost the same kinetic, which largely underestimates the experimental result. For example, at 20 pct of formed bainite, the experiment shows that about 70 pct of the entire transformation plasticity is reached. At the same proportion of formed bainite, Desalos’s and Abrassart’s models predict, respectively, only 36 and 42 pct. However, further comparison of the residual stress predicted by using these transformation plasticity kinetic functions has not been yet made. In this work, a coupled thermometallurgical and mechanical process was implemented by using the UMATHT and UMAT subroutines of commercial software ABAQUS. An exponent-modified (Ex-Modified) normalized function describing the transformation plasticity strain was proposed and was used for fitting the experimental result of Taleb et al.,[21] from which the distributions of internal stress in quenched AISI 4140 cylinders with two sizes of diameter were predicted by finite element simulation (FES) and were compared with the XRD results to verify the validity of the Ex-Modified normalized function used in FES.

2 Experimental Procedures

The composition of the studied steel AISI4140 was chemically analyzed as Fe-0.39C-0.28Si-0.59Mn-1.01Cr-0.17Mo-0.022Ni. Two different diameter cylinders (30 and 50 mm) were used to verify the simulation model. The lengths of the cylinders were 150 mm for the 30-mm cylinder and 300 mm for the 50-mm cylinder.

Two K-type thermocouples were inserted into the holes of the 50-mm cylinder at the core and 1/2 radius (1/2R) to measure cooling curves quenched in the water. Only one thermocouple was inserted into the core of the 30-mm cylinder due to its small diameter to verify the optimized heat-transfer coefficient (HTC).

During the quenching process, the specimens were first heated in a pit-type furnace at 1123 K (850 °C); the holding times were 3000 seconds for the 30-mm cylinder and 5400 seconds for the 50-mm cylinder to ensure that the specimens were completely austenitized. After heating, the specimens were precooled in air for 25 and 40 seconds for the 30- and 50-mm cylinders, respectively, and then immersed into water at 291 K (18 °C) until the temperature of the specimens dropped below 323 K (50 °C). The preceding precooling is to reduce the thermal capacity and accelerate the cooling rate of the quenching stage.[1]

The quenched cylinders were cross sectioned, then polished, and finally etched by a step-etching procedure that was proposed by De et al.[22] first dipped in the 4 pct picral solution (4 g dry picric acid in 100 mL ethanol mixed with 1 mL concentrated hydrochloric acid) for 50 seconds, and then further dipped in freshly prepared sodium metabisulfite solution for 6 seconds. The etched samples were used for optical microscopy (OM; Imager A1m) observation. Specimens for transmission electron microscopy (TEM) were prepared by mechanically polishing and electropolishing in a twin-jet polisher using 6 pct perchloric acid and 94 pct ethanol at 253 K to 243 K (−20 °C to −30 °C). TEM was performed in a JEOLFootnote 1-2100F microscope operated at 200 kV.

The residual stress of the quenched cylinders was measured by XRD (iXRD combo, Proto Company, Ontario, Canada). The sin2 ψ method was used in this study.[23] The Cr radiation (λ = 0.2291 nm) was employed with a spot diameter of 2 mm. The values of ψ were ±0, ±11.95, ±23.9, ±31.95, and ±46.95 deg. The reference plane was {211} of the bcc phase.

In order to measure the stress profile along the depth, the outer layer of the cylinders was lathed first and then etched by 15 pct nitric acid aqueous solution for 0.5 mm. The removal of the outer layer may cause the redistribution of the stress. Equation [1] was used to correct this change:[24]

$$ \sigma_{\text{t}} \left( r \right) = \sigma_{\text{t,m}} \left( r \right) - \int_{r}^{R} {\sigma_{\text{t,m}} } \left( \xi \right) \cdot \frac{{{\text{d}}\xi }}{\xi } $$
(1)

where σ t(r) is tangential stress corrected at the radius of r, σ t,m(r) is the measured tangential stress at the radius of r, and R is the initial radius of the specimen.

3 Simulation Details

During the quenching process, temperature, phase transformation, and stress interact with each other, and such a coupling between these fields was depicted in some published articles.[4,25] Heat transfer is the driving force of phase transformation and the origin of the thermal stress; meanwhile, temperature can be disturbed by latent heat of phase transformation and deformation energy in quenching. Besides, stress is another factor that affects phase transformation, such as stress (strain)-induced martensitic transformation.[26] Because of the lack of the relative model and experimental data, this effect was not included in this work. The entire simulation was divided into two aspects: heat-transfer analysis and static stress/strain analysis.

3.1 Calculation of Temperature Distribution

During cooling of water quenching, phase transformation latent heat should be considered in order to accurately calculate the temperature field.[27] Since the effect of deformation energy on the temperature change is very small [about 2 K (2 °C)], compared to the temperature change from conduction,[25] this effect was neglected in this study. So the governing equation for the calculation of temperature can be written as[28]

$$ \rho \left( {\varphi_{k} ,T} \right)C_{\text{p}} \left( {\varphi_{k} ,T} \right)\dot{T} = \nabla \left( {k\left( {\varphi_{k} ,T} \right) \cdot \nabla T} \right) + \dot{Q} $$
(2)

where ρ is the density taken as 7850 kg/m3; C p and k are the specific heat and thermal conductivity of the phase mixture, respectively; T is the temperature; \( \dot{T} \) is the time derivative of the temperature; \( \nabla \) denotes the gradient operator; and \( \dot{Q} \) is the transformation latent heat rate:

$$ \dot{Q} = \sum\limits_{k = 2}^{3} {\Delta H_{k} \dot{\varphi }_{k} } $$
(3)

where \( \Delta H_{k} \) represents the enthalpy of the phase transformation, \( \dot{\varphi }_{k} \) is the transformation rate of k phase, and k represents bainite or martensite in this article.

The C p and k are a function of temperature, and their data from Kakhki et al.[29] for the AISI 4140 of various phases were used in this work. The latent heat of austenite transformed to bainite or martensite was set as −5.12 × 108 or −3.14 × 108 J/m3, respectively.[6,7]

The initial temperature of the analysis was set to a uniform value of 1123 K (850 °C), which is the austenitizing temperature of AISI 4140. Boundary (film) conditions were set to the surfaces of the cylinders, which contact the water:

$$ - k\left( {\varphi_{k} ,T} \right)\nabla T = h\left( T \right)\left( {T_{\text{s}} - T_{\text{w}} } \right) $$
(4)

where h(T) is the HTC of water; T s and T w are the temperature of the cylinder’s surface and the water [291 K (18 °C)], respectively.

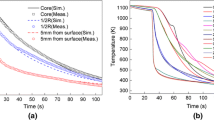
The HTC as a function of surface temperature was obtained by the following trial and error method: (1) the temperature function of the HTC was discretized into several temperature points, and the temperature between the points was interpolated linearly; (2) the initial values (which were drawn from Reference 29) of the HTC were set at every temperature point; and (3) the values of HTC were optimized using the particle swarm optimizing method in 1stOpt software, in which the object function was the minimum sum areas between the measured and calculated cooling curves at the core and 1/2R of the 50-mm cylinder (Figure 1(a)). Figure 1(b) shows the optimized HTC and the set initial value of the HTC from Reference 29. The calculated cooling curve at the core of the 30-mm cylinder using the optimized HTC of the 50-mm cylinder also shows good agreement with the measured one, as shown in Figure 1(a).

Fig. 1
figure 1

(a) Comparison between the measured and calculated cooling curves of the 50- and 30-mm cylinders and (b) optimized HTC of water

Full size image

The commercial finite element software, Abaqus/Standard, was used to solve the heat-transfer analysis. Phase transformation was implemented in a UMATHT subroutine. Details about the phase transformation calculation will be discussed in Section III–B. A four-node linear diffusive heat-transfer element DCAX4 was used because of the axial symmetry in geometry and the loads for the quenched cylinder. The 2280 nodes and 2162 elements with a gradient in mesh size were used for the 30-mm cylinder and the 6320 nodes and 6123 elements were used for the 50-mm cylinder.

3.2 Phase Transformation Calculation

Figure 2 (black lines) is the time–temperature–transformation (TTT) diagram of AISI 4140 steel (Fe-0.38C-0.64Mn-0.23Si-0.99Cr-0.16Mo-0.08Ni, pct).[30] Since the composition of the previous steel is slightly different from that of the AISI 4140 steel in this work, the M s, B s, and TTT curves were modified based on Reference 31, as shown in Figure 2 (blue lines). From Figure 1(a), we know that the slowest cooling rate at the center of the 50-mm cylinder is about 15 K/s (15 °C/s). Combined with Figure 2, we can conclude that there are no ferrite and pearlite transformation in both the 50-mm cylinder and the 30-mm one, and thus the calculation of volume fraction only refers to bainite and martensite.

Fig. 2
figure 2

TTT diagram of AISI 4140 and modified curves

Full size image

When the temperature drops below M s, martensitic transformation, which is time independent, will occur. There are several empirical kinetic models of athermal martensite transformation. The review of these models was presented by Lee.[32] Among those models, the following K–M equation, which was proposed by Koistinen and Marburger,[33] is the most widely used:

$$ \begin{aligned} \varphi_{\gamma } = \exp \left[ { - 1.10 \times 10^{ - 2} \left( {M_{\text{s}} - T_{\text{q}} } \right)} \right] \hfill \\ M_{\text{s}} > T_{\text{q}} > 193{\text{ K }}\left( { - 80 \, {}^{^\circ }{\text{C}}} \right) \hfill \\ \end{aligned} $$
(5)

where φ γ represents the volume fraction of retained austenite and T q the lowest temperature reached during quenching.

Equation [5] was derived from Fe-C alloys; there may be some inaccuracies in using this equation to model the martensitic transformation of AISI 4140 containing alloy elements. Lee and Van Tyne[34] proposed a new kinetics model that can be adjusted to account for the various effects of composition on the kinetics. The proposed model is

$$ \varphi_{\text{M}} = 1 - \exp \left[ { - K_{\text{LV}} \times \left( {M_{\text{s}} - T} \right)^{{n_{\text{LV}} }} } \right] $$
(6)

where φ M is the volume fraction of martensite; K LV and n LV are functions of the chemical composition, and these two parameters can be obtained by fitting with the experimental data of martensitic transformation, as shown in Figure 3. The fitted K LV and n LV were 0.0142 and 1.04, respectively. It is clear from Figure 3 that the volume fraction of martensitic transformation in AISI 4140 calculated by the K–M equation will lead to a large deviation from experimental data. The value of M s was determined by an empirical equation proposed by Lee and Park:[35]

$$ M_{\text{s}} \left( {{}^{^\circ }C} \right) = 475.9 {\text -} 335.1{\text{C}} {\text -} 34.5{\text{Mn}} {\text -} 1.3{\text{Si}} {\text -} 15.5{\text{Ni}} {\text -} 13.1{\text{Cr}} {\text -} 10.7{\text{Mo}} {\text -} 9.6{\text{Cu}} + 11.67\ln \left( {d_{\gamma } } \right) $$
(7)

where d γ represents the average grain diameter (micrometer) of prior austenite and was measured as about 16 μm in the 30-mm cylinder based on Figure 4(a), and the d γ of the 50-mm cylinder (Figure 4(b)) is close to that of the 30-mm cylinder, so 16 μm was set as the average grain size of prior austenite for the 50-mm cylinder.

Fig. 3
figure 3

Comparison of the predicted volume fraction of martensite using the K–M equation and the fitted equation with experimental data

Full size image
Fig. 4
figure 4

Prior austenite grain boundary of the (a) 30- and (b) 50-mm cylinders after quenching

Full size image

When the temperature drops below B s, bainitic transformation will occur. The value of B s was calculated by using the empirical equation provided by Lee:[36]

$$ B_{\text{s}} \left( {{}^{^\circ }{\text{C}}} \right){\text{ = 745{-}110C{-}59Mn{-}39Ni{-}68Cr{-}106Mo}} + \text{17MnNi + 6Cr}^{ 2} {\text{ + 29Mo}}^{ 2} $$
(8)

The bainitic transformation is controlled by diffusion. The Johnson–Mehl–Avrami–Kolmogorov (JMAK) equation[37] with Scheil’s additive rule is the most used method to calculate the diffusion-controlled transformation. However, the JMAK equation cannot capture the feature of the sluggish termination of the bainitic reaction,[31] and thus, an equation based on the work of Kirkaldy and Venugopalan[31] was presented according to the composition known of AISI 4140 steel in this work:

$$ \dot{\varphi }_{\text{B}} = \nu \left( T \right) \cdot \varphi_{\text{B}}^{{0.66\left( {1 - \varphi_{\text{B}} } \right)}} \cdot \left( {1 - \varphi_{\text{B}} } \right)^{{0.66\varphi_{\text{B}} }} \cdot \exp \left( { - c\left( T \right)\varphi_{\text{B}}^{2} } \right) $$
(9)

where ν and c are functions of temperature, and the values of ν and c were obtained by fitting with the TTT diagram of AISI 4140 (Figure 2); these two parameters were modified to consider the difference of the alloy elements between the published work[30] and this work. Table I lists the values of modified ν and c used in this work. As shown in Figure 2, the modified TTT curves shift to the right because the steel studied in this work contains more carbon and alloy elements.

Table I Variation of Modified ν and c with Temperature
Full size table

3.3 Stress/Displacement Analysis

During the process of quenching, the total strain increment was divided into five parts:

$$ \Delta \varepsilon_{ij} = \Delta \varepsilon_{{_{ij} }}^{\text{el}} + \Delta \varepsilon_{{_{ij} }}^{\text{pl}} + \Delta \varepsilon_{{_{ij} }}^{\text{th}} + \Delta \varepsilon_{{_{ij} }}^{\text{tr}} + \Delta \varepsilon_{{_{ij} }}^{\text{tp}} $$
(10)

where \( \Delta \varepsilon_{{_{ij} }}^{\text{el}} \), \( \Delta \varepsilon_{{_{ij} }}^{\text{pl}} \), \( \Delta \varepsilon_{{_{ij} }}^{\text{th}} \), \( \Delta \varepsilon_{{_{ij} }}^{\text{tr}} \), and \( \Delta \varepsilon_{{_{ij} }}^{\text{tp}} \) are the strain increments of elastic, plastic, thermal, phase transformation, and transformation plasticity, respectively.

Thermal strain and transformation strain are isotropic and calculated by the following equations,[3] respectively:

$$ \begin{aligned} \Delta \varepsilon_{{_{ij} }}^{\text{th}} = \delta_{ij} \sum\limits_{k = 1}^{3} {\varphi_{k} \alpha_{k} \Delta T} \hfill \\ \Delta \varepsilon_{{_{ij} }}^{\text{tr}} = \delta_{ij} \sum\limits_{k = 2}^{3} {\Delta \varphi_{k} \beta_{k} } \hfill \\ \end{aligned} $$
(11)

where k (=1, 2, 3) denotes austenite, bainite, and martensite, respectively; α k is the thermal expansion coefficient of the k phase; β k is the transformation expansion coefficient of the k phase; and δ ij is the Kronecker’s delta function. The values of the thermal expansion coefficient of austenite, bainite, and martensite were measured as 2.25 × 10−5, 1.30 × 10−5, and 1.15 × 10−5, respectively. The variation of transformation strain of austenite to bainite or martensite with temperature was measured as 9.0 × 10−3 to 9.5 × 10−6 T or 9.5 × 10−3 to 1.1 × 10−5 T during phase transformation.

The stress increment was calculated by the following equation:[38]

$$ \begin{aligned} \Delta \sigma_{ij} = \lambda \delta_{ij} \Delta \varepsilon_{kk}^{\text{el}} + 2\mu \Delta \varepsilon_{ij}^{\text{el}} + \Delta \lambda \delta_{ij} \varepsilon_{kk}^{\text{el}} + 2\Delta \mu \varepsilon_{ij}^{\text{el}} \hfill \\ \lambda = \frac{E}{1 - 2\nu } - \frac{E}{{3\left( {1 + \nu } \right)}} \hfill \\ \mu = \frac{E}{{2\left( {1 + \nu } \right)}} \hfill \\ \end{aligned} $$
(12)

where σ ij is the Cauchy stress tensor; E and ν are the elastic modulus and Poisson ratio of the mixture, respectively, and were calculated by the linear rule of mixtures.

The material was assumed to be rate independent in this article. The Von Mises yield surface with kinematic hardening was used to include the plasticity of the material.[38] The yield function was written as

$$ \begin{aligned} \sqrt {\frac{3}{2}\left( {s_{ij} - \alpha_{ij} } \right)\left( {s_{ij} - \alpha_{ij} } \right)} - \sigma_{y} = 0 \hfill \\ \Delta \alpha_{ij} = \frac{2}{3}H\Delta \varepsilon_{ij}^{\text{pl}} \hfill \\ \end{aligned} $$
(13)

where s ij denotes the deviatoric stress tensor, α ij is the deviator of the backstress tensor, σ y is the yield strength of the mixture, and H is the plastic hardening modulus. The value of H for the mixture of austenite, martensite, and bainite was calculated by the linear rule of mixtures. The calculation of the yield strength was described as follows based on a nonlinear mixture rule, since the relatively large overestimation of the stress is exhibited by using the simple linear mixture rule:[39,40]

$$ \sigma_{\text{y}} = g\left( {\varphi_{\text{A}} } \right)\sigma_{\text{y,A}} + \left[ {1 - g\left( {\varphi_{\text{A}} } \right)} \right]\sigma_{\text{y,BM}} $$
(14)

where σ y,A is the yield strength of austenite, and σ y,BM is the yield strength of the mixture of bainite and martensite, which was calculated by a linear rule of mixtures; g(φ A) is a normalized function of austenite. The values of the function g(φ A) used in this work are from Reference 40. The values of E, ν, and σ y of various phases and temperatures are from Reference 41; the values of H are from Reference 42.

The equivalent stress based on purely elastic behavior was first calculated. If the elastic stress predicted exceeds the yield stress of the mixture, plastic flow will occur; in this case, the backward Euler method was used to integrate Eqs. [12] and [13].[43]

When phase transformations occur under external stresses, an anomalous plastic strain, which is called transformation plasticity, will occur even though the equivalent stress of external stresses is below the yield strength of austenite.[13] The incremental transformation plasticity strain was expressed as[13,18]

$$ \Delta \varepsilon_{{_{ij} }}^{\text{tp}} = \frac{3}{2}Kf^{\prime}\left( \varphi \right)h\left( {\sigma_{\text{eq}} ,\sigma_{\text{y}} } \right)s_{ij} \Delta \varphi $$
(15)

where K is the transformation plasticity coefficient, \( f^{\prime}\left( \varphi \right) \) is the derivative function of the \( f\left( \varphi \right) \) normalized function, and h(σ eq, σ y) is the function of equivalent stress and the yield stress of the mixture. The addition of h(σ eq, σ y) was to account for the nonlinearity with respect to the stress applied. The expression of h(σ eq, σ y) given by Leblond[18] was

$$ h\left( {\sigma_{\text{eq}} ,\sigma_{\text{y}} } \right) = \left\{ \begin{aligned} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} \frac{{\sigma_{\text{eq}} }}{{\sigma_{\text{y}} }} \le \frac{1}{2}{\kern 1pt} \hfill \\ 1 + 3.5\left( {\frac{{\sigma_{\text{eq}} }}{{\sigma_{\text{y}} }} - \frac{1}{2}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} \frac{{\sigma_{\text{eq}} }}{{\sigma_{\text{y}} }} \ge \frac{1}{2} \hfill \\ \end{aligned} \right. $$
(16)

The value of the transformation plasticity coefficient K can be determined by experiment or by theoretical calculation. The function f(φ) has several types of expressions,[21] such as ones proposed by Abrassart, Deslos, and Leblond, respectively, as shown in Table II.

Table II f(φ) Functions Proposed by Abrassart, Desalos, and Leblond
Full size table

Taleb et al.[21] pointed out that Abrassart’s and Desalos’s functions largely underestimate the experimental result. As a result, we proposed an Ex-Modified normalized function linked with transformation plasticity strain as follows:

$$ f\left( \varphi \right) = A \, \exp \left( {B\varphi^{n} } \right) $$
(17)

where A is a parameter used to adjust normalization. Equation [17] was used to fit the experimental curve of Taleb et al.,[21] and the parameters in Eq. [17] were determined as A = 1.105, B = −0.0994, and n = −0.91. Figure 5 shows the comparison between the experimental result of f(φ) vs the calculated results based on the functions proposed by Abrassart, Desalos, Leblond, and the present authors, respectively.

Fig. 5
figure 5

Comparison between the experimental result of Taleb et al.[21] and the calculated results based on Desalos’s, Abrassart’s, Leblond’s, and the Ex-Modified functions

Full size image

In order to evaluate the validity of various models of the transformation plasticity in the prediction of internal stress distribution during quenching, Eq. [18] lists the transformation plasticity strain equations based on the normalized functions proposed by Desalos, Abrassart, Leblond, and the present authors. The K value of AISI 4140 was taken from the literature as 4.2 × 10−5.[12]

$$ \begin{aligned} \left( {\text{a}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varepsilon_{ij}^{\text{tp}} = 0 \hfill \\ \left( {\text{b}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varepsilon_{ij}^{\text{tp}} = \frac{3}{2}ABKn\exp \left( {B\varphi^{n} } \right)\varphi^{n - 1} \Delta \varphi s_{ij} \hfill \\ \left( {\text{c}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varepsilon_{ij}^{\text{tp}} = \frac{3}{2}ABKnh\left( {\sigma_{\text{eq}} ,\sigma_{\text{y}} } \right)\exp \left( {B\varphi^{n} } \right)\varphi^{n - 1} \Delta \varphi s_{ij} \hfill \\ \left( {\text{d}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varepsilon_{ij}^{\text{tp}} = \frac{9}{2}K\left( {1 - \varphi^{0.5} } \right)\Delta \varphi s_{ij} \hfill \\ \left( {\text{e}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varepsilon_{ij}^{\text{tp}} = 3K\left( {1 - \varphi } \right)\Delta \varphi s_{ij} \hfill \\ \left( {\text{f}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varepsilon_{ij}^{\text{tp}} = - \frac{\Delta V}{V}\frac{1}{{\sigma_{\text{y,A}} }}h\left( {\sigma_{\text{eq}} ,\sigma_{\text{y}} } \right)\left( {\ln \left( \varphi \right)} \right)\Delta \varphi s_{ij} \hfill \\ \end{aligned} $$
(18)

where (a) indicates that the phase transformation plasticity was not considered; (b) and (c) are based on the Ex-Modified normalized function, in which (c) includes h(σ eq, σ y); and (d), (e), and (f) link the phase transformation plasticity proposed by Abrassart, Desalos, and Leblond, respectively.

The commercial finite element software, Abaqus/Standard, was used to solve the stress/strain field. The models of transformation plasticity mentioned previously were added in the user subroutine UMAT to calculate the internal stress by using the element type of CAX4.

4 Results

4.1 Calculation of Cooling Curves

Figure 6 shows the calculated cooling curves of the two diameter cylinders. It can be seen from Figure 6 that the mean cooling rates from 1073 K to 773 K (800 °C to 500 °C) at the core of the 30- and 50-mm cylinders are about 40 K/s (40 °C/s) and 15 K/s (15 °C/s), respectively. The increase of the diameter will dramatically lower the cooling rate of the core.

Fig. 6
figure 6

Calculated cooling curves at the surface, 1/2R, and core of (a) 30- and (b) 50-mm-diameter cylinders

Full size image

4.2 Microstructural Characterization

Figure 7 is the XRD spectra of the AISI 4140 cylinders with 30- and 50-mm diameter at the core and 1/2R, showing that there only exists bcc phase in the cylinders. The microstructure of the quenched cylinders is shown by OM in Figure 8. From Figures 8(a) and (b), it can be seen that the main microstructure is the martensite in the 30-mm cylinder accompanied by a few bainite formed even at the 1/2R of the cylinder. A lot of bainite plates formed in the 50-mm cylinder at the locations of both the core and 1/2R because of the slower cooling rates (Figures 8(c) and (d)). The TEM observation for the specimen at the core of the cylinder further reveals that martensite is a dislocation-type one; moreover, there is filmlike retained austenite between martensite laths, as shown in Figures 9(a) and (b). The dark-field image in Figure 9(b) clearly exhibits filmlike retained austenite, and selected area electron diffraction (SAED) patterns inserted in Figure 9(b) show the \( \left( {\bar{1}\bar{1}0} \right)_{\alpha } //\left( {1\bar{1}1} \right)_{\gamma } \), \( \left[ {00\bar{1}} \right]_{\alpha } //\left[ {011} \right]_{\gamma } \) (N–W) orientation relationship between martensite and retained austenite. This is typical microstructure of low and medium carbon martensitic steels.[44,45] Since the diffraction peaks of fcc retained austenite do not appear in XRD, the volume fraction of retained austenite is less than 3 pct, which is the lowest limit of the XRD measurement in this work. The bright-field image in Figure 9(c) shows long straight martensite laths, filmlike retained austenite between martensite laths, and short flakelike lower bainite. Figure 10 is the calculated distribution of bainite and martensite in the volume fraction from the core to the surface of the 30- and 50-mm cylinders, respectively. The volume fractions of bainite at the 1/2R and core of 30-mm cylinders were measured as 6 and 9 pct, respectively, and those fractions were 57 and 61 pct, respectively, for the 50-mm cylinder based on Figure 7; they were added in Figure 9. The calculated and measured fractions match very well. Obviously, with the increase of the cylinder diameter accompanying the decrease of the cooling rate, the volume fraction of bainite increases.

Fig. 7
figure 7

XRD spectra of the AISI 4140 cylinders with 30- and 50-mm diameters at the core and 1/2R

Full size image
Fig. 8
figure 8

Microstructure of the quenched cylinders shown by OM: (a) and (b) microstructure of the 30-mm cylinder at the location of the 1/2R and core, respectively; (c) and (d) microstructure of the 50-mm cylinder at the location of the 1/2R and core, respectively

Full size image
Fig. 9
figure 9

TEM observation of microstructures at the core of the 50-mm cylinder: (a) bright-field image of martensite and retained austenite; (b) dark-field image of retained austenite and inserted SAED pattern; and (c) bright-field image of martensite, retained austenite, and lower bainite

Full size image
Fig. 10
figure 10

Calculated phase fraction distribution of the AISI 4140 cylinders with diameters of (a) 30 mm and (b) 50 mm

Full size image

4.3 Variation of Residual Stress with Diameter

Figure 11 shows the comparison of the residual stress distribution from the core to the surface of the AISI 4140 cylinders with 30- and 50-mm diameter between the calculated and experimental results, in which every experimental value (solid square in Figure 11) is the mean of two corrected values and the error bars of the measured values from the standard deviation show rather good measured precision. It can be seen from Figure 11 that the calculated stress distribution with Ex-Modified normalized function is well consistent with the measured stress distribution in both 30- and 50-mm cylinders. Besides, for the 30-mm cylinder, the maximum tensile stress locates at about the 10-mm radius and the maximum compressive stress locates at the surface; while for the 50-mm cylinder, the maximum tensile stress locates at the core of the cylinder and the maximum compressive stress locates at the surface of the cylinder, which indicates that with the decrease of diameter, the maximum tensile stress shifts from the core to the surface.

Fig. 11
figure 11

Measured and calculated residual stress distribution using various transformation plasticity equations in the cylinders with diameters of (a) 30 mm and (b) 50 mm

Full size image

5 Discussion

5.1 Effect of Temperature Distribution on the Phase Formation

As mentioned previously, the XRD spectra of the AISI 4140 cylinders only exhibit bcc phase. The OM and TEM further demonstrate that the microstructures of the AISI 4140 cylinders consist of bcc dislocation-type martensite, bcc lower bainite, and fcc retained austenite. The theoretical calculation and experimental results indicate that the volume fractions of phases are different at the various positions of two cylinders. This phenomenon can be explained as follows. It can be seen from Figure 1 that the temperature range of bainitic transformation between 873 K and 623 K (600 °C and 350 °C) (Figure 2) maintains about 20 seconds at the center of the 50-mm cylinder, which is larger than 10 seconds at the center of the 30-mm cylinder, leading to the much higher volume fraction of bainite in the 50-mm cylinder than in the 30-mm cylinder. Besides, it can be seen from Figure 1 that in the region near to the surface of cylinders, the temperature rapidly lowers to below M s, which makes martensitic transformation occur and almost avoids the formation of bainite, while in the region near the core of cylinders, the temperature lowers between 873 K and 623 K (600 °C and 350 °C) so that bainitic transformation occurs. Once martensite and bainite form, the carbon will partition from the supersaturated martensite[46] or bainite[47] to the untransformed austenite phase. With further cooling, the temperature in the interior lowers below M s accompanied by the formation of martensite; moreover, the partitioning of carbon will occur during the whole cooling course, and thus carbon-enriched retained austenite will stabilize to room temperature, as shown in Figure 9. In general, the larger temperature range of bainitic transformation leads to more bainite in the 50-mm cylinder than that in the 30-mm cylinder, and the more rapid cooling rate in the surface region of cylinders results in more martensite than that in the interior of cylinders.

5.2 Origin of Residual Stress Distribution

As demonstrated previously, the residual stress gradually changes from compressive stress to tensile stress from the surface to the core of the 50-mm cylinder, while the residual stress of the 30-mm cylinder exhibits a peak value; that is, the residual stress gradually rises from compressive stress to tensile stress and then lowers to compressive stress from the surface to the core. In order to reveal the origin of such a feature of residual stress distribution, we separately calculated the distributions of thermal stress, phase transformation stress, and the sum of them, as shown in Figure 12. It can be seen from Figure 12 that the thermal stress gradually changes from compressive stress at the surface of the cylinder to tensile stress at the core in both cylinders. With the increase of the diameter, the values of compressive stress and tensile stress increase, because the thermal stress is caused by the temperature gradients of the cylinder: the bigger the diameter is, the larger the difference of temperature between the surface and the core is, as shown in Figure 6. In contrast, the transformation stress makes the tensile stress gradually change to the compressive stress from the surface to the core of the 30- and 50-mm cylinders, in which the compressive stress at the core in the 30-mm cylinder is bigger than that in the 50-mm cylinder, which is attributed to more martensite in the core of the 30-mm cylinder (Figure 9) since the transformation strain of martensite is larger than that of bainite. The sum (interaction) of thermal stress and transformation stress leads to the compressive stress at the surface of 30- and 50-mm cylinders; meanwhile, with increasing the diameter of the cylinder, the maximum tensile stress shifts from the surface to the core of the cylinder, which is well consistent with the distribution of residual stress in the measured and calculated ones (Figures 11 and 12). It is worthy to note that the larger transformation stress and smaller thermal stress in the 30-mm cylinder than in the 50-mm cylinder leads to the appearance of the peak value of the tensile stress.

Fig. 12
figure 12

Comparison of thermal stress, phase transformation stress, and the summation of thermal and phase transformation stress of (a) 30- and (b) 50-mm-diameter cylinders

Full size image

5.3 Effect of Transformation Plasticity Function on the Residual Stress Distribution

The precision prediction of residual stress distribution by FES depends on the precision prediction of the temperature distribution and microstructure field and the correct description of the transformation plasticity. In the preceding three factors, the correct description of transformation plasticity is, so far, the most difficult. For the description of transformation plasticity, we analyzed the curve feature of the normalized function, f(φ), measured by Taleb et al.[21] that is, at the initial stage of the transformation, the normalized function rapidly increases, and at the end stage of the transformation, it slowly increases. Therefore, we proposed an exponent function to describe such a feature of the normalized function, and the result indicates that the fitting curve based on the Ex-Modified normalized function is more consistent with the curve measured by Taleb et al.[21] than the curves fitted by the normalized function proposed by Abrassart, Desalos, and Leblond, respectively, as shown in Figure 5.

In order to reflect the effects of normalized functions on internal stress, the comparison between the measured internal stress and the calculated internal stress based on four normalized functions mentioned previously (Eq. [18]) was performed; meanwhile, the internal stress without considering phase transformation plasticity also was calculated, as shown in Figure 11. It can be found that the maximum of the tensile stress and compressive stress calculated without considering transformation plasticity is much bigger than those measured, which is attributed to the loss of the stress relaxation effect from transformation plasticity.[48] Besides, the FES of the distribution of internal stress based on the Ex-Modified normalized function is more consistent with that measured by XRD than FES based on the normalized function proposed by Abrassart, Desalos, and Leblond, respectively, which stems from the Ex-Modified normalized function better describing transformation plasticity. From the better FES of internal stress based on the Ex-Modified normalized function, it reasonably included that the normalized function, f(φ), measured by Taleb et al.[21] is precise. It is worth pointing out that the addition of h(σ eq, σ y) slightly raises the accuracy of the prediction (comparing curve b with c in Figure 11). As a result, we can conclude that the normalized function describing transformation plasticity has a more significant effect on the simulation of quenching stress than does the h(σ eq, σ y) function.

6 Conclusions

In this work, the FES was employed to predict the distribution of internal stress in quenched AISI 4140 cylinders with two sizes of diameter. The commercial finite element software, Abaqus/Standard, was used to solve the coupled temperature field, microstructure field, and stress (strain) field. Several models of transformation plasticity were added in User subroutine UMAT to calculate the internal stress by using the element type CAX4; thus, the effects of various models on internal stress can be compared. In FES, the simulated parameters of cooling curves were at first determined by comparison with measured cooling curves. Then, the simulated parameters of microstructure distribution were determined by comparing the theoretical calculation with experiments. Finally, an Ex-Modified normalized function linked with transformation plasticity strain was proposed, and it better describes the experimental curve of transformation plasticity measured by Taleb et al. than the normalization functions proposed by Abrassart, Desalos, and Leblond, respectively, which leads to the fact that the internal stress distribution simulated based on the Ex-Modified normalized function is more consistent with that measured by XRD.