1 Introduction

Macrosegregation in metallic alloys is a complex casting defect that is a function of the transport phenomena during processing and is affected by material properties, cooling conditions, and system geometry. One difficulty with exploring the mechanisms underlying the formation of macrosegregation patterns is the quantification of the comparison of large compositional datasets, obtained either experimentally or computationally. Commonly, either full composition fields or specific profiles are reported (e.g., References 1 through 3). These data have been used to visualize macrosegregation and explain the physical phenomena responsible for it, but these visualizations are difficult to compare quantitatively. To aid in such a comparison, a single numerical metric that represents the composition field is frequently calculated. A reliable metric is also useful for quantifying uncertainty propagation, in which the behavior of the metric can be used to understand the probable range of the macrosegregation level as a function of the variation of the process input.[4]

One metric that is commonly used for quantifying compositional variation is the macrosegregation number,[5,6] the normalized standard deviation of a Gaussian distribution fitted to the composition field:

$$ M = \frac{1}{{C_{0} }}\left[ {\frac{1}{{V_{\text{tot}} }}\iiint_{V} {\left( {C - C_{0} } \right)^{2} {\text{d}}V}} \right]^{{\frac{1}{2}}}, $$
(1)

where C 0 is the nominal composition, V tot is the total volume of the domain, and C is the measured or predicted local composition field. The integral in Eq. [1] is approximated as the summation

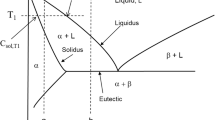
$$ M = \frac{1}{{C_{0} }}\left[ {\frac{1}{{V_{\text{tot}} }}\sum\limits_{i = 1}^{N} {\left( {C_{i} - C_{0} } \right)^{2} \Delta V_{i} } } \right]^{{\frac{1}{2}}}, $$
(2)

where ΔV i is the control volume in which C i represents the local average composition and N is the number of samples (or control volumes in numerical results). This metric assumes that the composition field is normally distributed about the mean or nominal composition. However, it is quite common for this volume-averaged composition distribution to be asymmetric about this mean, depending on the process parameters and material properties. It is also found that this distribution is skewed to lower compositions for elemental partition coefficients (k) greater than unity and to higher values for k < 1 (Figure 1).[7] As a consequence of the assumptions implicit in Eqs. [1] and [2], the commonly used macrosegregation number is only an accurate depiction of the overall compositional variation for the limiting case of a symmetric, Gaussian distribution. When fitting a Gaussian distribution to a skewed dataset, the longer tail is truncated and the shorter tail is artificially extended. Overall, the fitted distribution tends to overpredict the total amount of macrosegregation and underpredict the volume of material near the nominal composition.

Fig. 1
figure 1

Composition distributions in an ingot of Ni alloy 625 produced through electroslag remelting showing the asymmetry in (a) Nb with k < 1 and (b) Cr with k > 1 (data taken from[7])

Full size image

Fezi et al.[7] analyzed the composition fields produced by numerical simulations of the electroslag remelting process by plotting the volume-averaged composition distributions for different components in a superalloy (alloy 625) for various process conditions. The composition distributions were all found to be asymmetric, and the implications of the distribution shapes were discussed. Along with the macrosegregation number, the ingot volume fraction outside of the alloy composition specification range was used to characterize the degree of macrosegregation. This latter metric is useful to consider, especially for industrial processes and alloys, but it fails to provide information about compositional variations within the specification limits.

Voller and Vušanović[8] recently proposed that the normalized compositional survival function be used for verification, validation, and analysis of numerical macrosegregation predictions. They applied their method to experimental data given by Quillet et al.[9] for a cast Sn-10 wt pct Bi ingot and to numerical results for this system. The composition data was sorted in descending order of the ratio C/C 0, from j = 1 to j = n = 120. Each sorted composition was given a value determined by its survival plotting position, \( S = \frac{j}{n + 1} \), forming the compositional survival function, S(C/C 0) (although it is erroneously referred to as the cumulative distribution function in Reference 8). This survival function was interpreted as the ingot volume fraction corresponding to a macrosegregation level greater than or equal to the corresponding value of S. The corresponding CDF can be calculated easily from the survival function as 1 − S. They found a linear relationship between the composition and the survival function when the positive segregation was plotted on log–log axes. Also, the grid size did not affect the linear fit but did change the maximum composition in the positive segregation region. Fitting this positive portion of the survival function with a power law function yields a slope that may be used to quantify the level of macrosegregation, and the survival functions themselves may be useful for visualizing data. Such visualization was used recently to investigate the effect of permeability models[10] in segregation development. Voller and Vušanović[8] also suggested using the slope of the power law function as the shape factor for the Pareto power law distribution, but never tested the Pareto distribution for its validity. While these approaches succeed at expressing the macrosegregation in a casting with a single metric, they ignore all negative segregation and do not accurately reflect the shape of the full composition distribution. This shortcoming might be particularly severe in cases where the macrosegregation strongly tails toward the negative side of the distribution, or in alloys with elements with partition coefficients greater than unity, which tend to skew to lower compositions. The linearity of the positive region of the survival function does not extend throughout the positive segregation region which further limits this metric. Also, as Voller and Vušanović point out, this method is valid only when the composition data are on a uniform grid, because their survival function weights each composition measurement the same.

In an effort to address these issues, and to properly capture the entire skewed composition distribution, and not just the positively segregated region, this study develops and uses a three-parameter Weibull distribution to characterize macrosegregation. In particular, the advantages over the macrosegregation number are detailed and comparisons are made to the power law function and Pareto distribution methods. (These were proposed by Voller and Vušanović, although they only demonstrate the former technique.[8]) While the present analysis uses statistical functions as tools to describe composition distributions, it should not be mistaken as a rigorous statistical analysis. Statistical distributions are useful because they fit composition distributions found in solidified ingots well, but their use should not be read as a suggestion that the composition is a random variable, as the distribution of composition values is controlled by specific, non-random physical processes. The new method is first applied to experimental data given by Quillet et al.,[9] and then used to describe the influence of cooling conditions, grid size, and grid uniformity in simulations of solidification of a simple binary alloy (Al-4.5 wt pct Cu) and of a multicomponent nickel-based superalloy (Inconel 625) with a columnar, rigid dendritic structure. This method can be applied without alteration to other segregation prone alloys, solidification microstructures, and industrial solidification processes, such as direct chill casting, ingot casting of steel, and electroslag remelting.

2 Mathematical Description

The three-parameter Weibull probability distribution function (PDF) of a random variable x (in this case, the composition) is defined as

$$ {\text{PDF}}_{\text{W}} (x) = \frac{\alpha }{\beta }\left( {\frac{x - \gamma }{\beta }} \right)^{\alpha - 1} \exp \left( { - \left( {\frac{x - \gamma }{\beta }} \right)^{\alpha } } \right), $$
(3)

where α is the shape parameter, also known as the Weibull slope, β the scale parameter, and γ the threshold value. The shape and scale parameters control the asymmetry and the size or range of the distribution, respectively. The lower end of the distribution is limited by the threshold value such that all random variables x are greater than or equal to γ. The PDF is the derivative of the corresponding cumulative distribution function:

$$ {\text{CDF}}_{\text{W}} (x) = 1 - \exp \left( { - \left( {\frac{x - \gamma }{\beta }} \right)^{\alpha } } \right). $$
(4)

The variance of the Weibull distribution is

$$ \sigma_{\text{W}}^{2} = \beta^{2} \left[ {\Gamma \left( {1 + \frac{2}{\alpha }} \right) - \Gamma^{2} \left( {1 + \frac{1}{\alpha }} \right)} \right], $$
(5)

where Γ is the gamma function,

$$ \Gamma (z) = \int_{0}^{\infty } {t^{z - 1} e^{ - t} {\text{d}}t,} $$
(6)

and the deviation is defined as the square-root of the variance:

$$ \sigma_{\text{W}} = \beta \left[ {\Gamma \left( {1 + \frac{2}{\alpha }} \right) - \Gamma^{2} \left( {1 + \frac{2}{\alpha }} \right)} \right]^{{\frac{1}{2}}}. $$
(7)

The full composition field of a cast alloy is continuous but is sampled (measured or predicted) at discrete spatial locations. Each sample is assumed to be the average of a corresponding control volume. The control volumes can be uniform in size, as in the case of Voller and Vušanović,[8] or non-uniform, in which each composition measurement may characterize a different ingot volume fraction. A cumulative volume distribution function (CVDF) may be constructed which quantifies, for each unique composition in the dataset, the ingot volume fraction that has a composition less than or equal to that unique composition measurement. This cumulative volume function, using discrete composition data, has a similar meaning to that of a CDF, with a random variable x, and for simplicity is interpreted in that way for this study. To construct this plot, a dataset comprised of the composition field and corresponding control volume sizes must first be ranked by composition from lowest to greatest. This dataset is taken over the full composition range (both negative and positive segregation regions) in this study. The CVDF value for each ranked composition, C j , is calculated as shown in Eq. [8],

$$ {\text{CVDF}}(C_{j} ) = \frac{{\sum\nolimits_{i = 1}^{i = j} {V_{i} } }}{{\sum\nolimits_{i = 1}^{i = n} {V_{i} } }}, $$
(8)

in which the ingot is made up of n control volumes, each occupying a volume V i . The use of volume allows non-uniform grids to be used to calculate the CVDF. If all control volumes are equal in size, then Eq. [8] reduces to a form similar to 1 − S as used by Voller and Vušanović.[8] The result of this process is a CVDF of the composition dataset that can be fit to a continuous CDF.

It was found that the Weibull distribution fit the compositional data best if the data and Weibull PDF skewed toward higher compositions. For cases that skew toward lower compositions (i.e., \( (C_0^i - C_{\min}^i) > \;(C_{\max}^i - C_0^i) \), where \( C_{\min}^i\;{\text{and}}\;C_{\max}^i \) are minimum and maximum compositions, respectively), the data were fit to a Weibull distribution using \( (1 - C^{i} ) \) as the random variable. The compositional CVDF datasets are linearized using the following relationships, which can be found by rearranging Eq. [3]:

$$ x_{j} = \ln (C_{j} - \gamma ), $$
(9)

and

$$ y_{j} = \ln \left\{ { - \ln \left[ {1 - {\text{CVDF}}(C_{j} )} \right]} \right\}, $$
(10)

where C j is the composition of data point j and is the volume fraction of material with a composition less than or equal to C j , as defined in Eq. [8]. A least squares fit of a straight line is made to the linearized dataset, y j = f(x j ), where the slope is the shape parameter, α, and the scale parameter, β, is related to the y-intercept by:

$$ \beta = \exp \left( {\frac{{ - y_{\text{int}} }}{\alpha }} \right). $$
(11)

Selection of the threshold value, γ, must be done carefully in order to obtain the best fit. In this case, a γ value of zero was used as an initial guess and then incremented up to the minimum composition found in the domain. The best possible threshold value was determined by comparing the fitted Weibull CDF and the CVDF of the compositional data and minimizing the difference calculated using the root mean square error (RMSE):

$$ {\text{RMSE}} = \sqrt {\sum\limits_{n = 1}^{n} {\frac{{({\text{CVDF}} - {\text{CDF}}_{\text{W}} )^{2} }}{n}.} } $$

Increments in γ of 10−5 were found to be sufficiently small for the cases examined. The three-parameter Weibull distribution reduces to the two-parameter form if the best fit is found with a threshold of zero.

The shape parameter (α) controls the location of the peak value of the fitted PDFW, while the scale parameter (β) controls the range of the distribution. Both of these parameters are important in characterizing the macrosegregation and one metric that combines the effects of these two parameters is the Weibull deviation. To compare this metric directly to the macrosegregation number, the Weibull deviation is normalized by the nominal composition of a given component, shown in Eq. [12]. The raw data was converted into a volume distribution function (VDF), similar to that of a PDF, by binning the data and creating a histogram. The height of each bin corresponds to the volume fraction of ingot occupied in that composition range, divided by the bin width. This way the total area occupied by the histogram, or VDF, is equal to one.

$$ W = \frac{{\sigma_{\text{W}} }}{{C_{0} }} = \frac{\beta }{{C_{0} }}\left[ {\Gamma \left( {1 + \frac{2}{\alpha }} \right) - \Gamma^{2} \left( {1 + \frac{1}{\alpha }} \right)} \right]^{{\frac{1}{2}}}. $$
(12)

It is important to understand that by ordering the dataset from least to greatest in terms of the composition to construct the CVDF, the information about spatial distribution of the composition field is lost. Further manipulations of the data by fitting a particular distribution type and representing that distribution with a single parameter necessarily reduce the amount of information conveyed by the dataset. Therefore, while these types of metrics are useful for comparisons of otherwise unwieldy datasets, they do not contain all the necessary information to understand the mechanisms by which macrosegregation patterns develop. Instead, trends in these metrics should be used to point toward particular cases in which the spatial and temporal data may be examined more closely to gain a deeper understanding of the physics of the process.

3 Results and Discussion

Use of the three-parameter Weibull distribution and the normalized Weibull deviation is implemented in several examples presented below. First, experimental measurements of the composition profile of a Sn-10 wt pct Bi ingot[9] are used to compare the present method to the macrosegregation metrics proposed by Voller and Vušanović and the macrosegregation number. Next, numerical predictions of a static casting of Al-4.5 wt pct Cu are used to show the versatility of the Weibull distribution compared to the macrosegregation number. The normalized Weibull deviation is also used to conduct a grid dependence study for this alloy system. Finally, a multicomponent superalloy is simulated to show the relationship between the normalized Weibull deviation and the elemental partitioning.

3.1 Measured Segregation in Sn-10 wt pct Bi Ingot

The proposed characterization metric for macrosegregation was first applied to experimental data from a static casting of a Sn-10 wt pct Bi alloy (Quillet et al.[9]). The ingot was 5 × 6 × 1 cm3 and cooled from one of the 5 × 1 cm2 vertical walls while the remaining walls were insulated. Composition measurements were reported for a uniform 10 × 12 grid from the 5 × 6 cm2 midplane of the casting. Using these data, Voller and Vušanović took the survival function in Figure 2(a) and plotted the positive segregation region (C/C 0 ≥ 1) on a log–log plot and fitted it with a straight line (Figure 2(b)).

Fig. 2
figure 2

Compositional survival function with (a) linear and (b) log scales. These experimental data are from the cast Sn-10 wt pct Bi ingot reported by Quillet et al.[9]

Full size image

A least squares fit to positive portion of Figure 2(b) yielded the following equation:

$$ y = 0.3823\frac{C}{{C_{0} }}^{ - 5.059} . $$
(13)

(The exponent in Eq. [13] is not the value in,[8] where m = −4.45 was picked as an estimate to indicate the power law trend in the data.[11])

Voller and Vušanović also suggested that the negative of m may be used as the shape factor in a Pareto distribution, although they did not compare that distribution to the measurements.[8] The Pareto survival distribution for a random variable x is:

$$ S_{\text{P}} = \left( {\frac{{x_{\hbox{min} } }}{x}} \right)^{m} , $$
(14)

where x min is the minimum value allowed for x, and S P = 1 when x < x min. Since the exponent was found from a fit the positively segregated data, x min was set to the nominal composition. The Pareto PDF and CDF for x ≥ x min are defined as

$$ {\text{CDF}}_{\text{P}} = 1 - \left( {\frac{{x_{\hbox{min} } }}{x}} \right)^{m}, $$
(15)
$$ {\text{PDF}}_{\text{P}} = \frac{{mx_{\hbox{min} }^{m} }}{{x^{m + 1} }}. $$
(16)

Equations [15] and [16] are plotted against the composition dataset in Figure 3, using the exponent in Eq. [13]. The Pareto distribution follows the slope of the positively segregated region reasonably well; however, it is offset from the dataset. Clearly this distribution fails to adequately match the experimental results.

Fig. 3
figure 3

(a) VDF and PDF and (b) CVDF and CDF plots of the Sn-10 wt pct Bi compositional data reported by Quillet et al.[9] overlaid with corresponding Pareto distribution using the exponent in Eq. [13]

Full size image

To construct the Weibull distribution, each compositional measurement was assumed to be representative of its 5 × 5 × 10 mm3 volume. Figures 3(a) and (b) show the compositional probability and cumulative distributions functions. The compositional PDF is constructed by first grouping the data into 30 compositional bins, where the height of each bin (or probability density) is the volume fraction of the ingot that falls within each bin divided by the width of the bin.

The experimental data are plotted in both VDF and CVDF form in Figure 4 and overlaid with the corresponding curves for the three-parameter Weibull, normal distributions, and power law using the fitting parameter given in Eq. [13]. The power law function fits the measurement distribution well for the positive segregation. However, roughly half of the ingot is negatively segregated and that part of the distribution, including the compositions with the highest probability, is not described by this method. It is also clear that the experimental distribution is asymmetric and is skewed in the direction of positive segregation. The normal distribution assumed by the usual macrosegregation number overpredicts the tail to the left and underpredicts the likelihood of finding material near the nominal composition, while the fit to the Weibull distribution closely matches the asymmetry of the data. From these observations, it is expected that the macrosegregation number, being based on the assumption of normally distributed data, would overpredict the level of macrosegregation in the domain, as seen by comparing the macrosegregation number for this ingot (M = 0.238) to the normalized Weibull deviation (W = 0.195). To further illustrate the effectiveness of the three-parameter Weibull distribution, the RMSE of the fitted CDFW (0.024) is compared to that of the normal distribution (0.076). The fit to the Weibull distribution has roughly 1/3 the error than that of the normal distribution.

Fig. 4
figure 4

(a) CVDF and CDF and (b) VDF and PDF plots of the Sn-10 wt pct Bi compositional data reported by Quillet et al.[9] overlaid with corresponding three-parameter Weibull, normal, and power law distributions fit to the data. The power law CDF is covered by the experimental data, but is only plotted for the positively segregated region. It is clear that the Wiebull distribution more accurately represents the asymmetry of the experimental data

Full size image

3.2 Predicted Segregation in Al-4.5 wt pct Cu Ingot

One important use of the macrosegregation metrics described above is to compare the change in the composition distribution as a function of process variables or properties. Example data for this task were produced by a series of two-dimensional numerical simulations of the static casting of an Al-4.5 wt pct Cu binary alloy. The model used was a standard continuum mixture-based finite volume model for columnar solidification based on the work of Bennon and Incropera,[12] but including the temperature formulation of the energy equation,[13] using Voller and Swaminathan’s[14] linearization for the transient latent heat source term. The 10 × 10 cm2 domain was Cartesian, with an 80 × 80 uniform, structured, and staggered grid. Alloy properties were taken from Vreeman and Incropera.[15] Three of the domain walls were insulated, with a heat transfer coefficient applied to one of the side walls. This active boundary condition was varied to influence the heat transfer and fluid flow, and subsequently, the macrosegregation development within the casting.

Cases were run with heat transfer coefficients ranging from 500 to 4000 W/m2K. The normalized Weibull deviations and macrosegregation numbers for each of these cases are shown in Figure 5. The macrosegregation number decreases monotonically with heat transfer coefficient. However, the normalized Weibull deviation has a minimum value near h = 1250 W/m2K, after which this trend reverses at intermediate values until the normalized Weibull deviation is equal to the macrosegregation number, at which point, it begins decreasing again. Above h = 2000 W/m2K, W begins to decrease slightly faster than M.

Fig. 5
figure 5

Normalized Weibull deviation (W) and macrosegregation number (M) shown as functions of heat transfer coefficient for Al-4.5 wt pct Cu solidification simulations

Full size image

The cause of the normalized Weibull deviation behavior is the changing symmetry of the composition distributions, which are shown (both PDF and CDF) for the extreme cases, in Figure 6, plotted for data divided into 50 bins. For small heat transfer coefficients, the composition distribution skews strongly to higher compositions, but has almost no tail to the left. The normal distribution in this case greatly exaggerates the overall macrosegregation since it overpredicts the negative segregation, while the Weibull distribution much more accurately represents the asymmetric shape of the data. However, as the heat transfer coefficient increases, the left tail lengthens and the right tail shrinks. Eventually, the distribution is nearly symmetric (Figure 6(b)). Here, both the Weibull and normal distributions represent the shape of the data reasonably well.

Fig. 6
figure 6

Comparison of predicted composition data to fitted Weibull and normal PDFs and CDFs for Al-4.5 wt pct Cu with two different boundary conditions (a) h = 500 W/m2K and (b) h = 2000 W/m2K. There is more symmetry in the distribution with higher h

Full size image

The results in Figures 5 and 6 indicate several important characteristics of these two metrics. First, the three-parameter Wiebull distribution appears to be a more comprehensive method for describing the extent of macrosegregation than a normal distribution because it can fit both symmetric and asymmetric composition distributions accurately. This greater accuracy of the Weibull metric can also reveal trends that may not be apparent in the macrosegregation number, e.g., Figure 5. Also, because the macrosegregation number is only accurate for symmetric distributions, the difference between these two values may be taken as a measure of the asymmetry of the composition distribution. This trend is shown in Figure 7, normalized by the macrosegregation number to account for changes in the width of the distribution, along with four examples of the corresponding fitted Weibull distributions, varying from highly asymmetric (low h) to nearly symmetric (high h). As the heat transfer coefficient increases, the right tail of the distribution tends to shrink, while the left tail grows. This gradual shift in the shape of the distribution explains how the Weibull deviation first decreases with heat transfer coefficient, and then increases slightly before decreasing again, as shown in Figure 5.

Fig. 7
figure 7

The difference between the macrosegregation number (M) and the normalized Weibull deviation (W) plotted for Al-4.5 wt pct Cu simulating over a range of heat transfer coefficients (M–W) indicates the asymmetry of the Weibull PDFs, shown at right for three selected cases, where the x-axes are Cu wt. fr. and the y-axes are probability density

Full size image

While fitting the composition field to a probability distribution and calculating these simple metrics can illuminate trends in the macrosegregation development, these advantages come at the expense of spatial information about the composition field. In order to gain a deeper understanding of the development of macrosegregation, these metrics must be related to the behavior during solidification. To this end, plots of the composition fields for the three PDFs shown in Figures 7 (a) through (c) are given in Figure 8. The first solid solidified on the left wall and was Cu poor (k < 1). Thermal and solutal buoyancy drive the flow in the liquid in a counterclockwise rotating cell that slightly penetrates the mushy zone (Figure 9). This mushy zone flow moves the Cu-enriched interdendritic liquid to the bottom of the domain, where it pools until fully solidified. This enriched liquid is replaced in the mushy zone by liquid closer to the nominal composition, leaving a depleted layer at the left wall. This process continues as the solidification front progresses left to right, until the average solid composition approaches the nominal composition, and the top of the domain becomes depleted. The last liquid to freeze is at the bottom right corner of the domain, where the most enriched fluid has collected. The center of the domain, where the composition is near the nominal, corresponds to the peak of the PDF. The enriched layer at the bottom and right wall corresponds to the right tail of the PDF, while the depleted regions at the left wall and top of the domain correspond to the left tail of the PDF.

Fig. 8
figure 8

Composition fields of fully solidified Al-4.5 wt pct Cu for 3 different heat transfer coefficients. (a) h = 500 W/m2K, (b) h = 1250 W/m2K, (c) h = 2000 W/m2K

Full size image
Fig. 9
figure 9

Composition field plots at various times during the solidification of Al-4.5 wt pct Cu with h = 500 W/m2K at (a) 200 s and (b) 1400 s showing counterclockwise stream lines and the mushy zone extent. Results with h = 2000 W/m2K are shown (c) at 50 s and (d) at 200 s

Full size image

Differences in the distribution results for changes in the heat transfer coefficient are caused by coincident changes in the flow at the edge of the mush, where macrosegregation is caused by the relative motion of enriched liquid and depleted solid (k < 1). Because copper is more dense than aluminum, the combined thermosolutal driving force of the enriched liquid near the liquidus temperature is downward, tending to collect in a copper rich region at the bottom of the domain. This natural convective flow is limited by the low permeability in the mush. At the beginning of the process, the thermal buoyancy is directly related to the boundary condition. For high heat transfer coefficients, a strong thermally driven convective flow carries enriched liquid away from the first solid to form towards the bottom of the domain, to be replaced by relatively lean liquid at the top. Lower heat transfer coefficients cause weaker thermally driven flow that advect less enriched liquid from the mush. The result is a region of solid at the left wall that is more depleted with stronger flows corresponding to higher cooling rates. This initially lengthens the left tail of the composition distribution with increasing heat transfer coefficient (Figure 7). With even higher cooling rates, the amount of time available for advection of the enriched liquid become the dominant factor. Very high solidification rates freeze the liquid in place before significant macrosegregation can develop, eventually reducing the length of the left tail of the distribution as shown in Figure 7(d). This slightly increases the asymmetry of the distribution, which explain the minimum, then increase in the difference between the macrosegregation number and the normalized Weibull deviation.

Later in the process, the level of macrosegregation is controlled by the width of the mush and the time available for the advection of solute. For low cooling rates and therefore lower temperature gradients, the fractions solid gradient is also lower, and the mush is relatively wide, as shown in Figures 9(a) and (b). The wider mush allows a larger region over which the permeability is high enough that thermosolutal buoyancy of the enriched liquid drives it out of the mush to collect at the bottom of the domain. Additionally, the slower solidification rate allows more time for advection to occur. At higher cooling rates, the mush is thinner (Figures 8(c) and (d)), and other than in a very narrow region at the edge of the mush, the permeability is too low to allow significant solute transport. The distance over which solute is advected is also limited by the increased solidification rate. These factors generally result is more positive segregation at the bottom and right wall of the ingot for low cooling rates, and less for high cooling rates. Consequently, as shown in Figure 7, the right tail of the distribution shrinks with increase heat transfer coefficient.

Next, a grid refinement study was conducted to test whether the normalized Weibull deviation was sensitive to the grid spacing, and therefore may be used to determine grid convergence. A previous study[8] showed that, in many solidification processes, simulations grid convergence was generally not achieved. The composition of the last liquid to freeze is averaged over its control volume, so as the grid is refined, the maximum composition tends to increase. It should be expected, therefore, that the right tail of the composition distribution will become larger, and the corresponding value of the normalized Weibull deviation will also increase similarly with the number of cells. The grid was varied from 40 × 40 to 180 × 180 and the resulting normalized Weibull deviation, macrosegregation number, and composition PDFs are shown in Figure 10. There is a physical limitation to the grid refinement in that the permeability model for the mushy zone assumes that the control volume is much larger than the dendrite arm spacing. Darcy’s Law, used to derive the permeability terms in the momentum mixture equations, average out the details of flow through a porous medium. For fine grids, the continuum approximation breaks down and a model that predicts the alloy microstructure must be employed. As anticipated, both the macrosegregation number and normalized Weibull deviation increase with an increasing number of control volumes. This phenomenon was also reported by Voller and Vušanović, in which the composition that constituted a drop off of the survival function from the power law tail occurred at increasing values when the grid was refined.[8] Eventually the macrosegregation metrics will approach a constant value, as the composition of last liquid to freeze is limited by the eutectic point and further increasing the spatial resolution will not cause the highest solid composition to increase.

Fig. 10
figure 10

The grid dependence of the normalized Weibull deviation and macrosegregation number for the case with a heat transfer coefficient of 500 W/m2K. Plots at right show three examples of the fitted Weibull PDFs (x-axis is composition and y-axis is probability density), increasing in asymmetry with the number of cells

Full size image

One of the disadvantages of the frequency analysis described by Voller and Vušanović[8] is that it strictly applies to a uniform grid. Here, the construction of the Weibull distribution is done by weighting each data point by its associated volume, so that results using non-uniform grids may be analyzed. To demonstrate the generality of the present method, simulations with various non-uniform grids were performed. Control volume faces were located using a power law scheme:

$$ x_{{{\text{face}}}}^{i} = \left( {\frac{{i\;x_{{{\text{tot}}}} }}{{i_{{{\text{max}}}} }}} \right)^{n} , $$
(17)

where \( x_{\text{face}}^{i} \) is the location of control volume face i, \( x_{\text{tot}} \) is the size of the domain in the x-direction, i max is the total number of control volumes in the x-direction, and n is the power law exponent. Eq. [17] is only applied to the x-direction (the direction of the solidification front motion), and the y-direction is left uniform. The grid was refined near the chill to have better resolution of the temperature and velocity gradients where the heat transfer and flow will be the strongest. Various values of n were used to compare the effect of successive grid refinement. Relatively small changes in the macrosegregation levels are expected, since most of the segregation occurs at the end of solidification where the grid resolution is most similar for all n values. Results are shown in Figure 11 for both the normalized Weibull deviation and the macrosegregation number, as well as an example of the power law grid refinement in Eq. [17] with n = 1.5. Both macrosegregation metrics are unaffected by the level of grid non-uniformity as expected, which demonstrates that the Weibull deviation can be used on irregular grids.

Fig. 11
figure 11

The effect of a non-uniform grid on the normalized Weibull deviation and macrosegregation number plotted in (a) for power law grid spacing (in the x-direction) with various exponent values. An example of the non-uniform grids is shown in (b) for n = 1.5

Full size image

3.3 Predicted Segregation in Multicomponent Inconel 625 Ingot

The purpose of this final example is to discuss the relationship among the macrosegregation levels of different chemical species in a complex multicomponent alloy. The model used for this study is the same as the previous Al-4.5 wt pct Cu example, with a 15 × 15 cm2 Cartesian domain. Again, the effect of the cooling condition is examined by varying the heat transfer coefficient from 1000 to 10,000 W/m2K. The properties and solidification path of IN625 are taken from Fezi et al.[7] The nominal compositions and partition coefficients for the primary alloying elements are given in Table I.

Table I Nominal Composition and Partition Coefficients for Simulation of IN625
Full size table

As discussed by Schneider and Beckermann,[5] the macrosegregation number exhibits an interesting relationship for multicomponent alloys in which it is linear with the elemental partition coefficients on either side of k = 1. Considering that the normalized Weibull deviation is equal to the macrosegregation for a symmetric composition distribution, it is not unexpected that a similar trend is seen with higher heat transfer coefficients (more symmetry in composition distribution), but this trend also holds for cases with less symmetric composition distributions (Figure 12). For the case with the highest heat transfer coefficients, where the composition distributions are most symmetric, W is very close to M, and both metrics are linear with partition coefficient. At lower heat transfer coefficients, the normalized Weibull deviation is different from the macrosegregation number, indicating an asymmetric distribution, but retains linearity with partition coefficient, with a slightly different slope than the macrosegregation number. The linear relationship between W and k can be used to simplify numerical predictions of multicomponent solidification by reducing the number of composition equations, as discussed by Schneider and Beckermann.[5] They used the M vs k relationship to reduce the number of composition equations that must be solved in solidification simulations of a ten component steel alloy. However, when reducing the number of composition equations the solutal contribution of all pertinent alloying elements needs to be considered. Considering that the normalized Weibull deviation is a better representation of the composition field, using it to simplify the model in such a way will yield more accurate results than if the macrosegregation number was used.

Fig. 12
figure 12

Normalized Weibull deviation and macrosegregation numbers as a function of partition coefficient for the IN625 cases with different cooling rates. (a) h = 1000 W/m2K, (b) h = 5000 W/m2K, and (c) h = 10,000 W/m2K

Full size image

4 Conclusion

The three-parameter Weibull distribution was proposed as an improved metric for macrosegregation in alloy solidification than the macrosegregation number, Pareto distribution, or power law function. The process of fitting the distribution to a compositional dataset was described and implemented for both experimental and numerical data from statically cast ingots with columnar solidification structures. Different solidification morphologies and casting processes will produce different compositional fields; however, the process of fitting the distribution remains the same. (Composition distribution shapes similar to the static castings here are found in predictions of electroslag remelting.[7]) The utility of the Weibull distribution was demonstrated in numerical simulations over a range of cooling rates which changed the symmetry of the composition distribution and was related to the associated transport phenomena. The normalized Weibull deviation was proposed as a new metric for quantifying macrosegregation and was shown to illuminate trends which are not found with the macrosegregation number. The metric retains the property of being linear with partition coefficient for multicomponent alloys, which can be used to reduce the number of composition equations needed to model multicomponent solidification. The grid dependence of the Weibull deviation was analyzed and it was used to test for grid convergence. Additionally, the Weibull distribution was also able to characterize predicted segregation results using non-uniform grids.