Abstract
The stacking fault energy plays an important role in the transition of deformation microstructure. This energy is strongly dependent on the concentration of alloying elements and the temperature under which the alloy is exposed. Extensive literature review has been carried out and investigated that there are inconsistencies in findings on the influence of alloying elements on stacking fault energy. This may be attributed to the differences in chemical compositions, inaccuracy in measurements, and the methodology applied for evaluating the stacking fault energy. In the present research, a Bayesian neural network model is created to correlate the complex relationship between the extent of stacking fault energy with its influencing parameters in different austenitic grade steels. The model has been applied to confirm that the predictions are reasonable in the context of metallurgical principles and other data published in the open literature. In addition, it has been possible to estimate the isolated influence of particular variables such as nickel concentration, which exactly cannot in practice be varied independently. This demonstrates the ability of the method to investigate a new phenomenon in cases where the information cannot be accessed experimentally.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Stacking fault, two-dimensional planar defects, is one of the most important crystal imperfections, which is mainly introduced in the material by mechanical deformation and this, in turn, plays a crucial role in the plastic deformation behavior of face-centered cubic (fcc) alloys. The differences in deformation behavior of fcc alloys are strongly dependent due to differences in the stacking fault behavior. However, the strengthening of fcc alloys is strongly dependent on the stacking fault energy (SFE), which generally influences splitting of screw dislocations.[1] Splitting of screw dislocations must be pushed back together before they can cross slip. The cross slipping becomes more difficult as the split in the dislocations increases.[1] The SFE for the Al is so large that splitting is less than one Burgers vector, which is defined as dislocation bands. The partial dislocations separate the slipped and non-slipped areas, while in between one another, they fix a partially slipped area as the stacking fault. Due to stacking fault, dislocations are connected to a certain slip plane so that screw dislocations have a defined slip plane.[1] Metals with wide stacking faults (i.e., low SFE) strain harden more rapidly, twin easily on annealing, and show a different temperature dependence of the flow stress than metals with narrow stacking faults. Metals with high SFE have a deformation substructures of banded, linear arrays of dislocations, which has been reported in detail elsewhere.[2]
SFE is very sensitive to chemical composition of the material and the temperature. According to Otte,[3] faulting in austenite (fcc) is in all cases consistent with a high work hardening capacity of the austenite. The SFE in pure metals and alloys is very important for creep deformation behavior.[2] The smaller the SFE, the spacing between two partial dislocations is greater and cross slipping is even more strongly restricted. Thus, softening becomes more difficult and the stationary creep rate is reduced. This explains the large creep resistance of austenitic steels, which has been documented elsewhere.[1] Constrictions in stacking fault ribbon permit cross slipping, but this requires energy. The greater the width of the stacking faults, the more difficult is to produce constrictions in the stacking faults. This explains why the cross slip is quite prevalent in Al, that has a very narrow stacking fault ribbon, while it is not observed usually in Cu, which has a wide stacking fault ribbon.[2]
There is good correlation between SFE and type of texture. High SFE and high temperature deformation favor the Cu-type structure \(\left\{ 112\right\} \left\langle 111\right\rangle \).[2] The SFE plays an important role in determination of critical driving force, \(\Delta G_c\) for the deformation-induced martensitic transformation.[4] A material with a low SFE prefers to follow the mechanism: \(\gamma {(fcc)} \rightarrow \epsilon {(hcp)} \rightarrow \alpha ^{/} {(bcc)}\). Thus, the \(\epsilon (hcp)\) martensite is generated as a precursor during the first stage of phase transformation and is subsequently transformed into \(\alpha^{/} {(bcc)}\) martensite.[4] Present author has already discussed the formation and nucleation mechanisms of deformation-induced martensitic transformation of AISI 304LN stainless steels under different loading conditions through many experimental evidences, which are reported elsewhere.[5–16] There are few cases that have traced this microstructural transformation on multiple scales, ranging from nanometres to several micrometers, during deformation in various loading and temperature environments. There are many techniques available to measure SFE experimentally, i.e., X-ray powder diffraction (XRD), weak-beam dark field (WBDF), TEM etc. Different techniques used to measure the SFE in various metals and alloys are critically reviewed and are listed in briefed in Table I since 1957 to 2015.[17–57]
Several empirical equations for calculating SFE in austenitic stainless steels are also available in the published domain, and the most frequently used equations are listed in Table II.[36,37,58–60] Many studies modeling the SFE in different alloys are available in the open literatures, which has been reviewed and summarized in brief in Table III since 1964 to 2015.[61–101] Different kinds of modeling techniques are extensively developed by various eminent scientists.
There has been a consensus that different deformed microstructural features observed in fcc alloys are closely related to the SFE. Despite lots of investigations (i.e., experimental, theoretical) on the effect of chemical compositions on SFE of austenitic steels, there are inconsistencies in the published literatures regarding the influence of all alloying elements on SFE. It is conceivable that the disagreements among previous researches may arise from the differences in concentrations of chemical composition and techniques employed for evaluating SFE. Due to its practical engineering and theoretical importance, considerable efforts, critical review, analysis, and discussions have been made available to revisit SFE in various grades of steels in the present context.
The literatures related to estimation of SFE by using neural network approach are limited/not available in the published domain. In the present research, neural network has been used to calculate the SFE of many austenitic grade steels. Neural networks are having enormous usefulness in these circumstances, not only to estimate the SFE of the materials but wherever the complexity of the problem is overwhelming from a fundamental perspective and where simplification is unacceptable.[102] Accordingly, the modeling of SFE has to cover a range of concentration of alloying elements, and it is not so easy to predict the extent of SFE of an unknown steel. In this research, in view of the complexity of the phenomenon, neural network techniques under Bayesian framework are applied in place of the usual regression analysis, empirical equations, thermodynamic models, first principal calculations, or physical models. The problem of SFE of a material clearly involves many variables and considerable complexity. The purpose of this research is not only to identify parameters which control the deformation microstructures and the SFE of the steels but also to correlate the complex relationship between the extent of SFE with its influencing parameters.
In the present research, the influence of each individual parameters on SFE in austenitic grade steels has been revisited. In the present context, the optimization of SFE needs access to a quantitative relationship between the concentration of alloying elements and the ultimate value of SFE. A neural network method has been developed to correlate those and applied extensively for other steels within a Bayesian framework.
2 Stacking Fault Mechanisms
The atomic arrangement on \(\left\{ 111\right\} \) plane of an fcc structure and \(\left\{ 0001\right\} \) plane of an hcp structure could be obtained by the stacking of the closed packed planes of spheres. For the fcc structure, the stacking sequence of the planes of atoms is given by ABC ABC ABC. For hcp structure, the stacking sequence is given by AB AB AB. Errors, or faults, in the sequence can be produced in most metals by plastic deformation.[2] Typical stacking faults are shown in Figure 1 when AISI 304 LN austenitic stainless steels are deformed monotonically at strain rate of 0.10/s under tension at ambient temperature. Stacking faults in stainless steels have been shown to have a supplementary displacement, in addition to the expected 1/3 \(\left\langle 111\right\rangle \), which has the same sense and direction as the change in interplanar spacing of the close packed planes which occurs in the \(\gamma {(fcc)} \rightarrow \epsilon {(hcp)}\) transformation.[4] The formation of stacking faults has been schematically represented and explained per example of a fcc lattice in Figure 2. Thus, \({\epsilon}{(hcp)}\) martensite nucleates from irregularly spaced bundles of stacking faults which gradually become perfect hexagonal crystals as it is energetically favorable to generate faults which give rise to the required ABAB stacking.[103] There are two different kinds of stacking faults formed in many systems: intrinsic and extrinsic.
Transmission electron bright-field micrographs showing stacking faults in tensile deformed austenite at room temperature: (a, b) strain rate = 0.10/s of AISI 304LN austenitic stainless steel
Schematic diagram of the stacking arrangement of (111) close packed plane. (a, b) the perfect fcc stacking configuration, and (c, d) intrinsic stacking fault
Intrinsic stacking faults form in fcc crystal lattice as a consequence of the dissociation of a/2 \(\left\langle 110\right\rangle \) perfect dislocations into two a/6 \(\left\langle 211\right\rangle \) partial dislocations, referred to as Shockley partial dislocations.[2] An intrinsic stacking fault is formed between the partials, and consequently, the stacking sequence of \(\left\{ 111\right\} \) planes is changed from regular ABCABCABC to, for instance, ABCACABCA sequence. If two intrinsic stacking faults overlap on successive \(\left\{ 111\right\} \) planes, the resulting stacking sequence will be ABCACBCAB, which has one excess plane with the C stacking. Such a fault is referred to as an extrinsic stacking fault or twins. Thus, stacking faults in fcc metals can also be considered as sub-microscopic twins of nearly atomic thickness. The reason why mechanical twins of microscopically resolvable width are not formed readily when fcc alloys are deformed is that the formation of stacking faults is energetically favorable.[2] Consequently, it is difficult to distinguish between single stacking fault, bundle of overlapping stacking faults, and faulted or perfect \(\epsilon \) (hcp) martensite. Therefore, a collective term “shear band”[104] has often been used to designate the microstructural features originating from the formation and overlapping of stacking faults in austenitic stainless steels.
3 Method
The neural network is a simple regression method in which a flexible non-linear function is fitted with the experimentally measured data, the details of which have been reviewed extensively by many eminent researchers elsewhere.[102,105–107] It is nevertheless worth emphasizing some of the features of the particular method applied in the present context, which is referred by MacKay in his studies reported elsewhere.[108–111]
The Bayesian framework of the network used in the present research is able to indicate two uncertainties. The neural network is trained on a set of examples of inputs and output data. The outcome of this training is a set of coefficient and the specification of the functions which in combination with the weights correlating the inputs to the model output. The training process involves a search for the best optimum non-linear relationship between the inputs and output and is computer intensive. Once the neural network is trained, estimation of model output for any given inputs is rapid. The method recognizes that there are many functions which can be fitted or extrapolated into uncertain regions of input space, without excessively compromising the fit in adjacent regions which are rich in accurate data. Instead of calculating a unique set of weights, a probability distribution of sets of weights is generally used to define the fitting uncertainty. The error bars, therefore, become large when these data are sparse or locally noisy.
This Bayesian framework for neural networks has two further advantages. First, the significance of the input variables is quantified automatically. Consequently, the model perceived significance of each input variable can be compared against established metallurgical theory. Second, the network’s predictions are accompanied by the error bars which strongly depend on the specific position in the input space. This quantifies the model’s certainty about their predictions.
The general form of the model is as follows, with y representing the output variables and \(x_j\) the set of inputs:
The subscript i represents the hidden units (Figure 3), the \(\theta _i\) and \({w}_{ij}\) terms are biases and weights, respectively. The bias is designated \(\theta _i\) and is analogous to the constant that appears in linear regression analysis. The strength of the transfer function is in each case determined by the weight, \({w}_{ij}\). Thus, the statement of Eq. [1] together with the weights and the coefficient defines the function giving the output as a function of inputs.
A typical neural network employed in the present analysis
A potential difficulty with the use of powerful regression technique is the possibility of the over fitting data. To avoid over fitting, total experimental data can be subdivided into two different sets, a training and a testing dataset. The Bayesian neural network model is produced by employing only training dataset. Later the testing data are used to check whether the model behaves itself when presented with previously unseen data. Yescas et al.[112] have demonstrated a similar kind of neural network analysis in their study for estimation of retained austenite in austempered ductile irons. Recently, Das et al.[113,114] have also used Bayesian neural network technique to estimate the extent of deformation-induced martensite in austenitic grade stainless steels. Das et al.[115,116] also used the same technique to estimate the damage accumulation under tensile deformation through the Bayesian neural network analysis.
Bhadeshia[102] has clearly demonstrated in his elegant research that a linear model is too simple and does not capture the real complexity in data, an over complex function accurately models the training data but generalizes very badly. It is the minimum in the test error which enables that model to be chosen which generalizes best to the unseen data. This discussion related to the over fitting is rather brief because the problem does not simply involve the minimization of the test error. There are other parameters which control the complexity, which have been adjusted automatically to try to achieve the right complexity of model that has been reported elsewhere.[108–111]
4 Data
Extensive literature review has been done to understand the stacking fault mechanisms, deformation micro-mechanisms, and their interpretations while explaining the mechanical performance of austenitic steels under various operating conditions. It is indicated that the input parameters are interactive with each other during phase evolution in the microstructure. The analysis is based on the published data and is, therefore, limited to quantities that are readily measured and frequently reported. For example, in order to estimate the SFE, the quantity of all alloying elements has to include as inputs. Therefore, a pragmatic set of variables must be chosen which implicitly contain all information needed to estimate the extent of SFE. The set of inputs (Table IV), therefore, included the detailed test parameters (i.e., alloying elements) and the target is SFE. Table IV represents the statistics of the whole database constructing the model.
For the present model, inputs are chosen according to the knowledge gained from the common published literatures.[3–104] However, due to lack of appropriate data, no explicit account can be taken of initial texture of the material, temperature, stress, strain, etc., and their extent while SFE calculations. Different austenitic grade steels were chosen for this model. A total 75 experimental data (i.e., 75 rows in excel sheet) were collected from several and different published sources.[21,41,60,117–129]
It is emphasized that unlike the linear regression analysis, the ranges stated in Table IV cannot be utilized to define the range of applicability of neural network model. This is because the inputs are in general expected to interact with each other. It is the Bayesian framework of neural network analysis which makes possible the calculation of error bars whose magnitudes vary with the position in input space, that define the range of useful applicability of the trained network. A visual impression of the spread of the data is shown in Figures 4((a) through (h)).
The whole database values (i.e., for creating the model) of each variable vs the extent of SFE in austenitic steels. (a) C, (b) Si, (c) Mn, (d) Cr, (e) Ni, (f) N, (g) Mo, and (h) Al-concentrations. Compositions are in wt pct
5 Analysis
In this present investigation, both the input and output variables were first normalized within the range ±0.5 as obtained quantitatively by using following Eq. [2]:
where x N is the normalized value of x; x min and x max are, respectively, the minimum and maximum values, respectively, of x in the entire dataset (statistics of database, Table IV). The normalization is not necessary for the analysis but facilitates the subsequent comparison of the significance of each of the inputs. The normalization is straightforward for all quantitative variables utilized. The database was randomized and then partitioned equally into test and training datasets. The later was used to create a large variety of models, whereas the test data were used to see how the trained models generalized on unseen data. Figure 3 shows an example of typical network. Each network consists of input nodes (one for each variable x), a number hidden nodes, and an output node. Linear functions of the inputs, x j , are operated on by a hyperbolic tangent transfer function (demonstrated in Eq. [1]) so that each input contributes to every hidden unit. The transfer to the output y is linear (see Eq. [1]).
The specification of the neural network, together with the set of weights, is a complete description of the formula correlated the inputs to the target. The weights are generally determined by training the neural network. The training is performed using a dataset \({D} = \left\{ x^{(m)}, t^{(m)}\right\} \) by adjusting the weights, w, to minimize an error function, e.g.,
The error function, \(E_{D}(w),\) is the sum squared error as follows:
The objective function is a sum of terms, one for each input-target pair \(\left\{ x, t\right\} \), measuring the degree of correlation between the output y \(\left\{ x;w\right\} \) and the target t.[130] The parameter m denotes each input–output pair.
The training for each network is started with a variety of random seeds. The training involves a minimization of the regularized sum of squared errors, \(\sigma _\nu \). The term, \(\sigma _\nu, \) used below is the framework estimate of noise level of the data. The complexity of the model is controlled by the number of hidden units (shown in Figure 5). Figure 5 shows that the inferred noise level decreases as the number of hidden units increases.
Variation of \(\sigma _\nu \) as a function of the number of hidden units. Several values are presented for each set of hidden units because the training for each network was started with a variety of random seeds
The complexity of the model increases with the number of hidden units. The high degree of complexity may not be justified, and in the extreme case, the model runs in a meaningless way, attempting to fit the noise in the measured data. MacKay[108–111,130,131] made a detailed study of this problem and defined a quantity “evidence” which comments on the probability of a model. In circumstances where two models give similar kind of results over the known dataset, the more probable model would be predicted to be that which is simpler; this simple model would have a higher value of “evidence.” The “evidence” framework was used to control the regularization constants and \(\sigma _\nu \). The number of hidden units is set by examining the performance of the model on unseen data. A combination of Bayesian and pragmatic statistical techniques was, therefore, used to control the model complexity. Five hidden units were found to give a reasonable level of complexity to represent the variation in SFE as a function of the input variables. Large number of hidden units did not give significantly lower values of \(\sigma _\nu \); indeed the test set error goes through a minimum value. The test error tends to go through a minimum at an optimum complexity, which has been shown in Figure 6.
The test error as a function of the number of hidden units. Optimum test error: 0.550 at hidden unit: 2
It is possible that a committee of models (represented in Figure 7) can make a reliable and the reasonable estimate than an individual model used which has been discussed elsewhere.[108–111,130,131] Bayesian neural network technique has been employed to solve the problem. In the current formulation, the network architecture has been given in Table V.
Combined test error as a function of the number of models in committee. Suggested model: 1 when minimum test error: 0.5562
The best models are ranked using the values of the test errors. Committees are then formed by combining the predictions of the best L models, where \({L} = 1, 2, 3\ldots \); the size of the committee is, therefore, given by the value of L. A plot of the test error of the committee vs its size L gives a minimum which defines the optimum size of the committee as shown in Figure 7.
Test error, T e, is a measure of the deviation of the predicted value from the experimental one in the test data
where y n is the predicted amount of SFE and t n is the corresponding measured value previously unseen by the model.
It is popular to use the test error (sum squared error) as the default performance measure whereby the model with the lowest test error is considered to be the best.[130] In many applications, there will be an opportunity to make a prediction with error bars rather than a simple scalar prediction, or may be carry out an even more complex predictive procedure. It is then reasonable to compare models in terms of their predictive performance as measured by the log predictive probability of the test data. Under the log predictive error (LPE), as contrasted with the test error, the penalty for making a “wild” prediction is much less if the wild prediction is accompanied by appropriately large error bars. Assuming that for each example m, the model gives a prediction with error \(\left( y^{(m)}, \sigma ^{(m)^2}\right) \), the LPE.
When making the prediction, MacKay[130] has recommended the use of multiple good models instead of just one best model. This is termed “forming a committee.” The committee prediction \(\overline{y}\) is obtained using the following equation:
where L is the size of the committee and \(y_{i}\) is the estimate of a particular model i. The test error of the predictions made by a committee is calculated by replacing the \(y_{i}\) in Eq. [3] with \(\overline{y}\). In the present analysis, a committee of models was used to make more reliable predictions. The models were ranked according to their LPE. Figure 8 shows the variation of LPE as a function of number of hidden units. Committees were then formed by combining the predictions of best L models, where L gives the number of members in a given committee model.
LPE as a function of the number of hidden units. Optimum LPE: 12.78 at hidden unit: 2
However, the committee with one model (i.e., minimum test error = 0.5562) was found to have an optimum membership with the smallest test error (Figure 7). Once the optimum committee is chosen, it is retrained on the entire dataset without changing the complexity of each model, with the exception of the inevitable and relatively small adjustments to the weights. Figures 9 and 10 show the normalized predicted values vs experimental values of SFE for the best model in the training and test datasets, respectively. The predictions made using the optimum committee of models are illustrated in Figure 11.
Plot of the estimated vs measured SFE (normalized value)—training dataset
Plot of the estimated vs measured SFE (normalized value)—testing dataset
Training data for best committee model (training was done on whole dataset)
6 Application
The neural network can capture interactions between the input variables because functions involved are non-linear in nature. The nature of these interactions is implicit in the values of the weights, but the weights are not always easy to interpret. For example, there may exist more than just pair-wise interactions, in which case the problem becomes difficult to visualize from an examination of the weights. A better method is to actually use the network to make predictions and to see how these interactions depend on various combinations of inputs. It is the Bayesian framework of the present method which resolves this problem because it allows the calculation of error bars which defines the range of useful applicability of the trained network. The model can, therefore, be used in extrapolation given that it indicates appropriately large uncertainties when the knowledge is sparse. Figures 12 and 13 show the application of the committee model for unseen and reserved experimental data from other sources, respectively. From these graphs, it is noted that the model is robust enough to predict the total blind data. This means that a good correlation between the measured and calculated data has been obtained for these applications. These figures show that the used network could be capable for prediction with a minimum error. Figure 14 shows the comparison of the present model with the existing empirical equations (given in Table II) estimating SFE. It has been understood from this figure that few data points are over predicting and few are under estimating the perfect line of agreement, but the present model shows better agreement. This may be attributed to the differences in the chemical compositions, their variability, incompleteness, inaccuracy in their concentration, interaction with each other, and the methodology employed for measuring SFE. It is also true that many other variables also influence the SFE, which will be discussed later.
Application of the best committee model for unseen experimental data[117]
Application of the best committee model for unseen experimental data[58]
7 Prediction
The optimized committee model (Figure 11) has been used to predict the influence of all individual input parameters on SFE in many austenitic grade steels and they are discussed in detail with respect to the huge number of literature study in the following subsections. Figures 15((a) through (h)) shows the prediction according to the example shown in Table IV (i.e., last column). When the influence of an alloying element on SFE is investigated, other parameters were kept unaltered to investigate the variation of SFE. The isolated influence of all the individual variables has been quantitatively explained with the support of extensive literature study. The minor changes in concentration of alloying elements have significant effects on SFE. The error bars are not constant for all data points in each graph except Figure 15(a), which strongly depends on the position in the input space, an inherent features of the neural network technique used. The predictions are made without any adjustment of the models, which did not interrogate any SFE data during their creation. The error bars in all graphs corresponds to ±1 σ standard deviation and give an indication of the uncertainty in the experimental data as well as the uncertainty in interpreting those data. These error bars can be used to identify regions of the input space where further experiments would be useful.
7.1 Effect of C on SFE
Figure 15(a) demonstrates the effect of C concentration on the variation of SFE in austenitic grade steels where other variables are kept unaltered. It has been investigated from this figure that with the increase in C content in the austenitic grade steels, the extent of SFE remains constant. According to Brofman et al.,[58] the SFE is relatively insensitive to the small changes in the C concentration in austenitic stainless steels. This is in agreement with the study of Otte.[3] According to him, the influence of C on SFE is difficult to assess, it probably acts as a slight inhibitor. The addition of sufficient amount of C to an Fe-Mn alloy eventually eliminates the formation of hcp phase which occurs in the binary, so that at Hadfield’s composition, only stacking faults can be detected.[3] In stainless steels, the effect of C is similar in so far as it inhibits transformation, but up to about 0.10 pct C, the hcp structures may still be obtained by mechanical deformation.[3] In contrary, Dulieu et al.[23] investigated that the addition of C caused an increase in the SFE in austenitic stainless steels. Petrov et al.[70] had shown from their elegant theoretical calculations and experimentally measured data that C decreased the SFE of austenitic steels at low concentrations but increased the SFE at high C contents. Petrov[70] also investigated that C in austenitic stainless steels increased the SFE but non-monotonous dependence of C was observed in Fe-Mn-C alloys. According to Dai et al.,[60] in cryogenic austenitic stainless steels with a content of C plus N less than 0.10 pct, SFE becomes the dominant factor to affect the type of martensitic transformation. By the investigation of Prokoshkina et al.,[132] it has been realized that the addition of C promotes the \(\gamma (fcc) \rightarrow \alpha ^{/} (bcc)\) phase transformations. The influence of C concentration on SFE has already been investigated by many eminent researchers during 1957 to 2014 and they are critically reviewed in Table VI. Due to lack of experimental data, however, further works on the effect of C on SFE in other steels need to be carried out for the alloys with wider range of C concentration.
7.2 Effect of Si on SFE
From Figure 15(b), it is realized that with the increase in Si concentration, the calculated SFE decreases in most of the austenitic grade steels, where other elements were kept constant. According to Schramm et al.,[36] the additions of Si concentration decrease the SFE of the alloy and sustain the \(\gamma (fcc) \rightarrow \epsilon (hcp)\) transformation sequence during cooling and deformation. Hsu et al.[140] also found that the SFE plays an important role in determination of the critical driving force, \(\Delta G_{\gamma \rightarrow \epsilon }\) for the \(\gamma (fcc) \rightarrow \epsilon (hcp)\) transformation in the ternary Fe-Mn-Si alloys. \(\Delta G_{\gamma \rightarrow \epsilon }\) decreases with the content of the substitutional element Si. The effect of Si on SFE in different grades of austenitic steels is reviewed and is listed in Table VII.
7.3 Effect of Mn on SFE
It has been revisited that with the increase in Mn content in austenitic grade steels, the extent of SFE increases drastically (Figure 15(c)). According to Datta et al.,[4] \(\Delta G_{\gamma \rightarrow \epsilon }\) increases with the content of the substitutional element Mn. Kelly[129] in his pioneer research investigated that as the Fe-Ni and Fe-Ni-C alloys have a relatively high SFE, while alloys containing appreciable amounts of Cr or Mn have low SFE and form lath martensite associated with faulting or the formation of \(\epsilon (hcp)\) martensite. Mishra et al.[154] investigated that high ductility even up to 90 pct elongations has been observed in high Mn austenitic steels with TWIP effect, having SFE of about 20 mJ/m2. This is in accordance with the study of Huang et al.[155] There are literatures available in the open domain reporting that Mn increases SFE of austenite and those reporting decreasing SFE with increasing Mn content, which have been reviewed systematically and are listed in brief in Table VIII. Present investigation clearly reveals the fact.
7.4 Effect of Cr on SFE
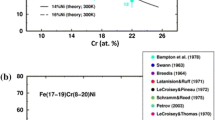
Figure 15(d) shows the effect of Cr concentration on SFE in austenitic grade steels, where the concentration of other elements was kept constant. It has been seen that variation in Cr concentration does not have any influence on the SFE in most of the austenitic grade steels. According to Prokoshkina et al.,[132] Cr alloying in high N steels lowers the SFE that leads to higher strain hardening and lower softening even at a certain development of the dynamic recrystallization at large strains. Bracke et al.[87] in their study reported that Cr and N suppressed the deformation-induced martensitic transformation in austenitic Fe-Mn-Cr-N alloy, and the differences in transformation behavior were attributed to the change in the intrinsic SFE. The influence of Cr content on \(M_S\) temperature cannot be used as a measure of SFE.[39] Since Cr is a bcc stabilizer and the stability (against martensitic transformation) will depend strongly on the relative stability of the fcc and the hcp phases only if the transformation to bcc martensite involves the intermediate hcp phase. The complex effect of Cr on SFE will not then be reflected in the variation of \(M_S\) temperature.[39] The effect of Cr on SFE in different grades of austenitic grade steels is reviewed from the open domain literatures and is briefed in Table IX.
7.5 Effect of Ni on SFE
From Figure 15(e), it is to be noted that with the increase in Ni concentration in austenitic grade steels, the SFE increases drastically. According to Simmons,[159] Ni and C tend to raise the SFE thereby influencing dislocation cross slip, while Cr, Mn, Si, and Ni tend to decrease the SFE of the austenite. In contrast, high SFE fcc materials such as Ni (SFE = 128 mJ/m2) generally exhibit cell-type dislocation structures produced by cross slip which occurs at much lower strains than in low SFE materials.[159] Wang et al.[160] showed that in the Ni-bearing steels, SFE increased with increase of N concentration up to 0.40 pct, and then decreased at higher N content. According to Otte,[3] it has been investigated that Cr and Mn have a marked effect in promoting the formation of stacking faults in the austenite, whereas the influence of Ni is very less. According to Datta et al.,[4] in high Ni austenite stabilizing alloys, \(\epsilon (hcp)\) martensite could be found. In Fe-Ni binary alloys, no hcp structures appear, whereas in Fe-Mn alloy, it happens. The addition of Cr to the Fe-Ni alloys causes, however, a hcp phase structure to appear in the stainless steel composition range. In the similar way, the addition of sufficient amount of Cr to straight Fe-C alloys will cause the appearance of stacking faults on quenching, whereas the addition of Ni in place of Cr produces faulting only after mechanical deformation.[3] The effect of Ni addition on SFE of austenitic grade steels is reviewed and is listed in Table X.
7.6 Effect of N on SFE
It has been investigated from Figure 15(f) that with the increase in N concentration in the austenitic grade steels, the SFE increases slightly. According to Fayeulle et al.,[166] the introduction of N causes the formation of stacking faults in stainless steels. According to them, their number becomes more and more important during ion bombardment which creates an expansion of the lattice and consequently an increase in the strains. When the N quantity becomes significant, \(\gamma {(fcc)} \rightarrow \alpha^{/} {(bcc)}\) transformation becomes enforced in the material. N also promotes the \(\epsilon{(hcp)}\) martensite formation in austenitic stainless steels. Many earlier investigations (Table XI) have provided the experimental measurements in support of the decreasing tendency of SFE with increasing N content in the austenitic alloy. Fawley et al.,[29] Swann,[20] and Dulieu and Nutting[23] experimentally measured the SFE of many Fe-Cr-Ni alloys and reported in their classical studies that the increase in the N content led to the slight decrease in the SFE of those alloys. It is to be noted that most of the previous research have been performed on commercial grades of Fe-Cr-Ni steels, and the N concentration of the steels was in limited levels less than 0.10 pct. Hence, it is not easy to assess the influence of N on SFE measurements of the high N steels where the N concentration is in the range of 0.3 to 1.0 pct, and main composition is the Fe-Cr-Mn alloy system. Recent investigations on austenitic high N steels have shown that N increases the SFE[172] or, in some cases, a non-monotonous relationship between SFE and the N content is also reported by many pioneer researchers.[173] Gavriljuk et al.[173] reported that the SFE of Fe-Cr-Mn alloys increased with increasing N concentration, whereas the SFE of Fe-C-Mn-Ni alloys showed a non-monotonous change with the N content. There are literatures in published domain reporting that N increases SFE of austenite and those reporting decreasing SFE with increasing N content, which have been reviewed systematically and are listed in brief in Table XI.
7.7 Effect of Mo on SFE
Figure 15(g) represents that with the increase in Mo concentration in austenitic grade steels, the calculated SFE increases marginally where the concentration of other elements was kept unaltered. In some of the austenitic stainless steels (i.e., AISI 316L), the addition of Mo content (~2.5 pct) is employed in order to improve both the corrosion resistance and hot deformation (creep) behavior. Mo in solid solution acts as a favorable element in reducing dislocation mobility. There is lower diffusion rate of Mo as compared to other alloying elements in austenite.[128] Hence, Mo influences the annealing behavior of the cold-rolled material.[174] According to Singh,[136] in the 13.0 pct Ni steels containing Mo such as AISI 316L, SFE is relatively higher than that of the AISI 304 stainless steels in which the martensitic transformation can occur. Ni and C tend to raise the SFE thereby influencing dislocation cross slip, while Cr, Mn, Si, and Ni tend to decrease the SFE of the austenite.[70] According to Lagneborg,[141] the effect of Si and Mo on SFE is unknown. According to him, Cr and Mn lower the SFE, while Ni raises it. The effect of Mo on SFE in different grades of austenitic steels is reviewed from the published literatures and is listed in brief in Table XII.
Predictions of SFE in austenitic grade steels as a function of (a) C, (b) Si, (c) Mn, (d) Cr, (e) Ni, (f) N, (g) Mo, and (h) Al-concentrations. Compositions are in wt pct. Note: the small error bars indicate that the scatter in the database is very small and the large error bars suggest lack of sufficient data in the range examined. All error bars are not really constant and their trend lines are not exactly linear, except (a)
7.8 Effect of Al on SFE
It has been investigated from Figure 15(h) that with the increase in Al content in austenitic grade steels, calculated SFE decreases slightly. Stability of austenite phase decreases with decreasing SFE, the tendency to form the strain-induced features increases with decreasing SFE. Austenitic steels with lower SFE have been reported to form \(\epsilon{(hcp)}\) martensite preferentially to deformation twinning in Fe-Cr-Ni and Fe-Mn-Cr-C alloys.[178,179] It is generally reported that the SFE decreases with decreasing temperature and Al content in Fe-Mn-Cr-C and Fe-Mn-Al alloys.[69,179] The tendency to form \(\epsilon{(hcp)}\) martensite increases, while the tendency to form deformation twins decreases with decreasing temperature and Al content.[180] According to Han et al.,[180] the Al is an austenite stabilizer suppressing the formation of the strain-induced \(\epsilon{(hcp)}\) martensite, while it behaved as a \(\delta \) ferrite stabilizer when added to 3.0 pct to Fe-32Mn-12Cr-xAl-0.4C cryogenic alloys. As the SFE increases with increasing Al content, the elongation peak shifted to lower temperature with increasing Al content in the Fe-32Mn-12Cr-xAl-0.4C alloy.[180] The influence of Al on SFE of different austenitic grade steels is reviewed and is discussed in brief in Table XIII.
7.9 Effect of Other Elements on SFE
In the present research, it was not possible to incorporate other alloying elements (which also influence the SFE) in the model as the quantitative information was very limited in the published domain. It would be worthwhile to discuss some of the important findings of other alloying elements on SFE in austenitic grades steels. According to Huang et al.,[47] the presence of Ti lowers the SFE in AISI 321 stainless steels, compared to AISI 304 stainless steels and thus produces the deformation twins. The measurement of stacking fault probability indicates that the addition of Nb increases the SFE of the alloy, and thus retards the \(\gamma {(fcc)} \rightarrow \epsilon{(hcp)}\) transformation, which increases the elongation of TWIP steels and decreases the tensile strength.[47] The additions of Ti, Mo, and Nb at levels up to 2.0 pct lower the SFE, although direct measurements are reported only on Nb.[22] The \(\epsilon \) (hcp) martensite is formed during H charging as a result of decreasing the SFE.[75] The decrease of the SFE induced by H in austenitic stainless steels was always involved to explain the formation of \(\epsilon (hcp)\) martensite at room temperature during cathodic charging of H.[187] The SFE decrease in austenitic stainless steels could be explained by H–H pairs formation in faulted zone.[75,188] An increase of the thermodynamic stability of the austenite by N can be a reason for higher resistance to the H-induced \(\gamma {(fcc)} \rightarrow \epsilon{(hcp)}\) transformation, and at the same time, the results obtained mean that decrease of SFE by H is not of a segregation nature.[173] The effect of H on the SFE of an austenitic stainless steel was also tested by Ferreira et al.[189] Considerable further information on the variation of SFE on alloying Ni with transition elements was also provided by the rolling texture studies of Beeston and France.[190]
7.10 Effect of Temperature on SFE
This parameter could not be included in the present analysis as the quantitative information correlating SFE was limited in the published domain. But it is an important parameter for SFE. It would be worthwhile to report some of the interesting findings by other researchers in this present context.
Temperature influences the SFE of austenitic grade steels. According to Byun,[191] deformation structures in austenitic stainless steels can be classified by equivalent stress, strain, defect density, and temperature. Few researchers[191] reported in their studies that the SFE of austenitic stainless steels increases with increasing temperature. The influence of temperature and SFE on the deformation characteristics of austenitic steels has been schematically represented in Figure 16.[179] It has been found that the twinning is an intermediate mode of deformation between the formation of \(\epsilon \)(hcp) martensite and dislocation cells, corresponding to the SFE of 10 to 40 mJ/m2. In the work of Hwan et al.,[192] the change in the M S temperature of \(\gamma {(fcc)} \rightarrow \alpha^{/} {(bcc)}\) transformation with austenite grain size (AGS) was investigated in relation to the SFE in a Fe to 18 pctMn alloys. A good linear relationship is established between the M S temperature and the inverse of the SFE. According to Datta et al.,[4] the variation in M S temperature with AGS depends strongly on the change in SFE. The effect of temperature on SFE in austenitic grade steels is reviewed and is listed in brief in Table XIV.
Effect of temperature and SFE on the deformation microstructures of austenitic Fe-Mn-Cr-C alloys[179]
According to Olson and Cohen,[207] the strain-induced martensitic transformation mechanism assumes that martensite nucleates only at micro-shear band intersections, and the implications are that because these micro-shear bands are stacking fault-free energy dependent as well as temperature (and strain rate) dependent, the number of intersections will also vary with strain rate. Assuming that the SFE decreases linearly with decreasing temperature by the amount of 0.08 mJ/m2 per degree as reported in Fe-Mn-Cr-C alloy[180] and Fe-Cr-Ni alloys,[180] the SFE of Fe-32Mn-12Cr-xAl-0.4C alloys was calculated at various temperatures. The SFE of 0-Al alloy was calculated as 21.7 mJ/m2 at 77 K (i.e., −196 °C), while the SFE of 1-Al alloys was calculated as 34.0 mJ/m2 at 77K (i.e., −196 °C). These results are strongly in agreement with the previous result that the formation of strain-induced \(\epsilon \)(hcp) martensite was predominant when the SFE is below about 20 mJ/m2 in Fe-Mn-Cr-C alloys.[180]
7.11 Effect of Stress, Strain, Grain Size, and Texture on SFE
Due to limited number of literatures available in the published domain, the effect of these variables also on SFE of austenitic steels could not be included in the present analysis. In these circumstances, it would be worthwhile to discuss and mention some of the important findings by other researchers influencing these variables on SFE. This would be helpful for other scientists to carry out further researches in this field.
According to Goodchild et al.,[208] the effect of stress on stacking fault width plays an important part in determining the dislocation distribution in metals of low SFE and in addition influences the formation of extended stacking faults. They showed that in the separation of Shockley partials, the contribution due to an applied stress is of about the same magnitude as that due to the SFE. Hsu[140] reported that the driving force for solid-state phase transformation is primarily concerned with the SFE of the material.
According to Breedis’s[21] investigation, the driving force for the phase transformation increases monotonically as the SFE increases. In low SFE materials like austenitic stainless steels, the effect of applied stress on the partial dislocation separation and dislocation substructure is significant.[191] A quantitative estimate of the magnitude of the effect of an applied stress on stacking fault separation may be made by means of the equation due to Copley and Kear.[209] Later Kestenbach[210] showed that the applied stress can make an average contribution of ±17.0 pct to an effective SFE in a AISI 304 stainless steel. According to Copley and Kear,[209] if a reasonable value of the SFE is assumed as 10 ergs/cm2, then the contribution due to an applied stress is of about the same magnitude as that due to the SFE. It therefore seems probable that the effect of stress on the stacking fault width plays an important role in estimating the dislocation distribution in alloys of low SFE and in addition influences the formation of extended stacking faults and \(\epsilon{(hcp)}\) martensite.
El-Danaf et al.[211] investigated that in low SFE materials, the flow stress is approximately inversely proportional to the homogeneous deformation zone size (shear bands) in austenitic steels. Byun[191] had shown the twinning stress as a function of SFE, from there possible deformation microstructure can be predicted. At a given strength and SFE, the possible dominant deformation microstructure can be predicted. According to Jun and Choi,[73] the change in the M S temperature of \(\gamma {(fcc)} \rightarrow \epsilon{(hcp)}\) martensitic transformation with AGS was investigated in relation to the SFE in Fe-18 pctMn alloys.[4] The effect of grain size on SFE in austenitic grade steels is reviewed in Table XV.
Karaman et al.[212] studied the stress-strain behavior of N containing AISI 316L stainless steels with different crystallographic orientations; and suggested that the overall mechanical response was strongly dependent on the crystallographic orientation. The influence of N on SFE of AISI 316L is non-monotonous; it first increases with N, and thus, suppresses twinning, and then decreases with the further addition of N, triggering twinning at ambient temperature. According to Karaman et al.,[212] the orientation close to [111] experiences a decrease in the effective SFE under tension of austenitic stainless steels. According to Smallman et al.,[213] the observed rolling textures of AISI 316L stainless steels upto 40 pct reduction are relatively weak in intensity and are consistent with the SFE level of this material. According to Dillamore,[64] the texture method of estimating SFE is purely empirical, and its principal virtue and justification is that it works and is applicable over the widest range of SFEs, provided that the available thermal energy is adjusted appropriately.
8 Significance
In the present model, it has been possible to show the isolated influence of individual input parameters. The Bayesian neural network modeling has an excellent advantage to calculate the significance of the input variables which has been clearly demonstrated by MacKay[108–111] in his studies. Figure 17 shows the model perceived significance of the input variables for the best model (Committee model). The parameter is rather like a partial correlation coefficient in linear regression analysis in that it represents the amount of variation in the output that can be attributed to any particular input parameter and does not necessarily represent the sensitivity of the output to each of the input parameters. It should be noted that it does not indicate the sensitivity of the output to the input. The ranking number is indicated in Figure 17 for each variable that has been perceived to have a significance or rank of elements influencing SFE. It is clearly understood that the effect of Ni and C concentrations is more predominant than the rest. From this graph, the importance of each input variables on revisiting SFE of steels is drawn.
Bar chart showing a measure of the model perceived significance of each of the input variables on influencing SFE. The number denotes the rank
9 Conclusions
A neural network model has been created to enable the estimation of SFE in vast majority of austenitic grade steels as a function of its alloying elements. Nevertheless, it would have been better model if temperature, stress, defect density, etc., could be included. The model successfully reproduces experimentally observed trends. It can be exploited in two ways, first in the design of austenitic steels and their deformation microstructures, but also to identify whether experiments are needed in the future. If the model prediction is associated with a large uncertainty then an experiment can be considered to be novel and useful. The influence of all individual variables on SFE has been convincingly revealed. C and Cr do not have any contribution in SFE. Mn, Ni, N, Mo increase SFE of the austenitic steels. Si and Al decrease the SFE of the alloy. The present author’s experience of the neural network technique suggests that it has considerable potential for useful applications in materials science.
Nevertheless, the neural network can be created more effectively in discovering better trends while ignoring the noise in the data with sufficiently larger database. Therefore, there is scope for further research to be done in order to broaden the sensitivity analysis using a larger and comprehensive database including other important variables like temperature, stress, strain, grain size, texture, etc., which could be generated by suitable experimentation and extensive literature reviews.
References
W. Bleck: Material Testing—Textbook for RWTH Students. Aachen University, Mainz, 2007
G.E. Dieter, Mechanical Metallurgy, SI Metric Edition. Springer, Berlin, 1993
H.M. Otte, Acta Metall. 6, 614 (1957)
K. Datta, R. Delhez, P.M. Bronsveld, J. Beyer, H.J.M. Geijselaers, J. Post. Acta Mat 57, 3321 (2009)
A. Das, S. Sivaprasad, M. Ghosh, P.C. Chakraborti, S. Tarafder, Mater Sci Eng A 486, 283 (2008)
A. Das, S. Sivaprasad, P.C. Chakraborti, S. Tarafder, Mater Sci Eng A 528, 7909 (2011)
A. Das, S. Tarafder, Int J Plast 25, 2222 (2009)
A. Das, J Mag Mag Mater 361, 232 (2014)
A. Das, Int J Fat 70, 473 (2015)
A. Das, S. Sivaprasad, P.C. Chakraborti, S. Tarafder, Phil Mag Lett 91, 664 (2011)
A. Das, Scripta Mater 68, 514 (2013)
A. Das, S. Tarafder, Scripta Mater 59, 1014 (2008)
A. Das, Philos Mag 95, 844 (2015)
A. Das, Philos Mag 95, 2210 (2015)
A. Das, Metall Mater Trans A 45, 2927 (2014)
A. Das: PhD Thesis, Jadavpur University, Kolkata, 2013
R.E. Smallman, K.H. Westmacott, Phil. Mag. 2, 669 (1957)
M.J. Whelan, P.B. Hirsch, R.W. Home, W. Bollmann, Proc Roy Soc A 240, 524 (1957)
M.J. Whelan, Proc Roy Soc A 249, 114 (1959)
P.R. Swann, Corrosion 19, 102 (1963)
J.F. Breedis, Trans. TMS-AIME 230, 1583 (1964)
D.L. Douglass, G. Thomas, W.R. Roser, Corrosion 20, 15 (1964)
D. Dulieu and J. Nutting: Special Report 86, pp. 140–145, The Iron and Steel Institute, London, 1964.
O. Vingsbro, Acta Metall. 15, 615 (1967)
P. Hirsch et al.: Electron Microscopy of Thin Crystals, Butterworths, London (1965)
J.M. Silcock, R.W. Rookes, J. Barford, J. Iron Steel Inst. 204, 623 (1966)
A. Clement, N. Clement, P. Coulomb, Phys. Status Solidi 21, K97 (1967)
B. Thomas, G. Henry, Mem Sci Rev Met 64, 625 (1967)
R.F. Fawley, M.A. Quader, R.A. Dodd, Trans. TMS-AIME 242, 771 (1968)
R.M. Latanision, A.W. Ruff Jr, J Appl Phys 40, 2716 (1969)
R.M. Latanision, A.W. Ruff Jr, Metall. Trans. 2, 505 (1971)
L.E. Murr, Thin Solid Films 4, 389 (1969)
F. LeCroisey, B. Thomas, Phys. Status Solidi 2, K217 (1970)
P.C.J. Gallagher: Ph.D. Thesis, Cambridge University, England, 1964.
E.D. Butakova, K.A. Malyshev, N.I. Noskova, Fiz Metal Metalloved 35, 662 (1973)
R.E. Schramm, R.P. Reed, Metall. Trans. A 6, 1345 (1975)
C.G. Rhodes, A.W. Thompson, Metall. Trans. A 8, 1901 (1977)
L. Remy, Acta Metall. 25, 173 (1977)
C.C. Bampton, I.P. Jones, M.H. Loretto, Acta Metall. 26, 39 (1978)
M.J. Carr, J.R. Strife, G.S. Ansell, Metall. Trans. A 9, 857 (1978)
R.E. Stoltz, J.B. Vander Sande, Metall. Trans. A 11, 1033 (1980)
A.E. Pontini, J.D. Hermida, Scripta Mater. 37, 1831 (1997)
K. Rosolankova, J.S. Wark, E.M. Bringa, J. Hawreliak, J. Phys. Condens. Mater. 18, 6749 (2006)
P. Sahu, A.S. Hamada, R.N. Ghosh, L.P. Karjalainen, Metall. Trans. A 38, 1991 (2007)
S.K. Huang, N. Li, Y.H. Wen, J. Teng, S. Ding, Y.G. Xu, Mater. Sci. Eng. A 479, 223 (2008)
X. Tian, H. Li, Y. Zhang, J. Mater. Sci. 43, 6214 (2008)
B.X. Huang, X.D. Wang, L. Wang, Y.H. Rong, Metall. Mater. Trans. A 39, 717 (2008)
T.H. Lee, H.Y. Ha, B. Hwang, S.J. Kim, E. Shin, Metall. Mater. Trans. A 43, 4455 (2012)
H. Idrissi, K. Renard, L. Ryelandt, Acta Mater 58, 2464 (2010)
J.Y. Kim, B.C. De Cooman, Metall. Mater. Trans. A 42, 932 (2011)
J.Y. Kim, S.J. Lee, B.C. De Cooman, Scripta Mater. 65, 363 (2011)
J.S. Jeong, W. Woo, K.H. Oh, S.K. Kwon, Y.M. Koo, Acta Mater 60, 2290 (2012)
J.E. Jin, Y.K. Lee, Acta Mater 60, 1680 (2012)
D.T. Pierce, J.A. Jimenez, J. Bentley, D. Raabe, Acta Mater 68, 238 (2014)
S.J. Lee, Y.S. Jung, S. Baik, Y.W. Kim, M. Kang, W. Woo, Y.K. Lee, Scripta Mater. 92, 23 (2014)
M. Moallemi, A.Z. Hanzaki, A. Mirzaei, J. Mater. Eng. Perform. 24, 2335 (2015)
B. Mahato, S.K. Shee, T. Sahu, S.G. Chowdhury, P. Sahu, D.A. Porter, L.P. Karjalainen, Acta Mater 86, 69 (2015)
P.J. Brofman, G.S. Ansell, Metall Trans A 9, 879 (1978)
F.B. Pickering, In Stainless Steels (The Institute of Metals, London, UK, 1985)
Q.X. Dai, X.N. Cheng, X.M. Luo, Y.T. Zhao, Mater. Charact. 49, 367 (2003)
L.M. Brown, A.R. Tholen, Discuss. Faraday Soc. 38, 35 (1964)
A.W. Ruff, L.K. Ives, Acta Metall. 15, 189 (1967)
I.L. Dillamore, R.E. Smallman, W.T. Roberts, Phil Mag 9, 517 (1964)
I.L. Dillamore, Metall. Trans. 1, 2463 (1970)
G.B. Olson, M. Cohen, Metall Trans A 7, 1897 (1976)
K. Ishida, Scripta Metall 11, 237 (1977)
Y.V. Konobeev, S.I. Rudnev, Atomnaya Energiya 53, 107 (1982)
K. Sato, M. Ichinose, Y. Hirotsu, Y. Inoue, ISIJ Int 29, 868 (1989)
W.S. Yang, C.M. Wan, J. Mater. Sci. 25, 1821 (1990)
N.Y. Petrov, I.A. Yakubtsov, Phys. Met. Metall. 8, 889 (1990)
S. Takaki, H. Nakatsu, Y. Tokunaga, Mater. Trans. JIM 34, 489 (1993)
P. Mullner, P.J. Ferreira, Phil Mag Lett 73, 289 (1996)
J.H. Jun, C.S. Choi, Mater. Sci. Eng. A 257, 353 (1998)
P.J. Ferreira, P. Mllner, Acta Mater. 46, 4479 (1998)
J.D. Hermida, A. Roviglione, Scripta Mater. 39(8), 1145 (1998)
Y.K. Lee, C.S. Choi, Metall. Mater. Trans. A 31, 355 (2000)
Y. Mishin, M.J. Mehl, D.A. Papaconstantopoulos, A.F. Voter, J.D. Kress, Phys. Rev. B 63, 224106 (2001)
E.H. Lee, M.H. Yoo, T.S. Byun, J.D. Hunn, K. Farrell, L.K. Mansur, Acta Mater. 49, 3277 (2001)
S. Vercammen, B.C. De Cooman, N. Akdut, B. Blanpain, P. Wollants, Steel Res 74, 370 (2003)
S. Vercammen: Doctoral Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2004.
S. Allain, J.P. Chateau, O. Bouaziz, S. Migot, N. Guelton, Mater. Sci. Eng. A 387–389, 158 (2004)
L. Vitos, J.O. Nilsson, B. Johansson, Acta Mater 54, 3821 (2006)
L. Vitos and B. Johansson: in Lecture Notes in Computer Science, vol. 4699, Springer, Berlin/Heidelberg, 2007, p. 510
S. Kibey, J.B. Liu, M.J. Curtis, D.D. Johnson, H. Sehitoglu, Acta Mater. 54, 2991 (2006)
P.L. Williams, Y. Mishin, J.C. Hamilton, Model Simul Mater Sci Engg 14, 817 (2006)
C. Brandl, P.M. Derlet, H. Van Swygenhoven, Phys. Rev. B 76, 1 (2007)
L. Bracke, J. Penning, N. Akdut, Metall. Mater. Trans. A 38, 520 (2007)
A. Dumay, J.P. Chateau, S. Allain, S. Migot, O. Bouaziz, Mater Sci Engg A 483, 184 (2008)
T. Hickel, A. Dick, B. Grabowski, F. Kormann, J. Neugebauer, Steel Res Int 80, 4 (2009)
J. Yu, S.B. Sinnott, S.R. Phillpot, Philos. Mag. Lett. 89, 136 (2009)
A. Saeed-Akbari, J. Imlau, U. Prahl, W. Bleck, Metall. Mater. Trans. A 40, 3076 (2009)
A. Saeed-Akbari, L. Mosecker, A. Schwedt, W. Bleck, Metall Mater Trans A 43, 1688 (2012)
J. Nakano and J.P. Jacques: CALPHAD 34 (2010) 167
J. Nakano, Sci Technol Adv Mater 14, 014207 (2013)
X.Z. Wu, R. Wang, S.F. Wang, Q.Y. Wei, Appl. Surf. Sci. 256, 6345 (2010)
S.L. Shang, W.Y. Wang, Y. Wang, Y. Du, J.X. Zhang, A.D. Patel, Z.K. Liu, J. Phys. Condens. Mater. 24, 155402 (2012)
L. Mosecker, A. Saeed-Akbari, Sci Technol Adv Mater 14, 033001 (2013)
D. Geissler, J. Freudenberger, A. Kauffmann, S. Martin, D. Rafaja, Phil Mag 94, 2967 (2014)
R. Xiong, H. Peng, H. Si, W. Zhang, Y. Wen. Mater. Sci. Eng. A 598 (2014) 376
S. Huang, W. Li, S. Lu, F. Tian, J. Shen, E. Holmstrom, L. Vitos, Scripta Mater., 2015, vol. 108, p. 44.
K.R. Limmer, J.E. Medvedeva, D.C. Van Aken, N.I. Medvedeva, Comp Mat Sci 99, 253 (2015)
H.K.D.H. Bhadeshia: ISIJ Int., 1999, vol. 39 (10), p. 966.
J.W. Brooks, M.H. Loretto, R.E. Smallman, Acta Metall. 27(912), 1829 (1979)
J. Talonen: PhD Thesis, Helsinki University of Technology, Espoo, Finland, 2007.
H. Fujii, D.J.C. Mackay, H.K.D.H. Bhadeshia, ISIJ Int 36(11), 1373 (1996)
R.C. Eberhart, R.W. Dobbins, Neural Networks PC tools (Academic Press, California, 1990)
A.Y. Badmos, H.K.D.H. Bhadeshia, D.J.C. MacKay, Mat Sci Tech 14, 793 (1998)
D.J.C. MacKay, Neural Compu 4, 415 (1992a)
D.J.C. MacKay, Neural Comput. 4, 448 (1992b)
D.J.C. MacKay, ASHRAE Trans 100(2), 1053 (1994)
D.J.C. MacKay. Netw. Comput. Neural Syst. 6 (1995) 469
M.A. Yescas, H.K.D.H. Bhadeshia, D.J.C. MacKay, Mater. Sci. Eng. A 311, 162 (2001)
A. Das, P.C. Chakraborti, S. Tarafder, H.K.D.H. Bhadeshia, Mat Sci and Tech 27(1), 366 (2011)
A. Das, S. Tarafder, P.C. Chakraborti, Mat Sci and Engg A 529, 9 (2011)
A. Das, S.K. Das, S. Sivaprasad, M. Tarafder, S. Tarafder, Proc Engg 55, 786 (2013)
A. Das, S. Sivaprasad, M. Tarafder, S.K. Das, S. Tarafder, Appl Soft Compu 13(2), 1033 (2013)
T.H. Lee, E. Shin, C.S. Oh, H.Y. Ha, S.J. Kim. Acta Mater 58, 3173 (2010)
J. Talonen, H. Hanninen, Acta Mat 55, 108 (2007)
M. Ojima, Y. Adachi, Y. Tomota, Y. Katada, Y. Kaneko, K. Kuroda, Steel Res Inst 80, 477 (2009)
V.G. Gavriljuk, Y. Petrov, B. Shanina, Scripta Mater. 55, 537 (2006)
Q.X. Dai, Iron Steel 30(8), 52 (1995)
T.Y. Hsu, Martensitic Transformation and Martensite (Science Press, Beijing, 1999)
O. Umezawa, K. Nagal, Metall. Trans. A 29, 809 (1998)
Y.S. Zhang, Acta Metall. Sin.19(4), 262 (1983)
T. Boriuchi, R. Ogawa, and M. Shimada: in Proceedings of ICMC Kobe, Japan, 1985, p. 7
Z. Zhou, Z. Xing, Y. Gao, Acta Metall. Sin.24, 94 (1988)
Q.X. Dai, A.D. Wang, X.N. Cheng, Mat Sci and Engg A 311(1/2), 205 (2001)
J.H. Yang, M. Wayman, Mater. Charact. 28(1), 23 (1992)
P.M. Kelly, Acta Metall. 13, 635 (1965)
D.J.C. MacKay: in Mathematical Modelling of Weld Phenomena, 3rd ed., H. Cerjak and H.K.D.H. Bhadeshia, eds., The Institute of Materials, London, 1997, pp. 359–89
D.J.C. MacKay, Trans Am Soc Heat Refrig Air-Cond Engg 100, 1053 (1994)
V. Prokoshkina, L. Kaputkina, Mat Sci and Engg A 481–482, 762 (2008)
G. Thomas, Acta Metall. 11, 1369 (1963)
PYu. Volosevich, V.N. Grindnev, Y.N. Petrov, Phys Met Metallogr 42, 126 (1976)
W. Charnock, J. Nutting, Metal Science Journal 1, 123 (1967)
J. Singh, J. Mater. Sci. 20, 3157 (1985)
L.M. Kaputkina, V.G. Prokoshkina, N.A. Krysina, Metals 6, 80 (2001)
YuN Petrov, Z Metallkd 94, 1012 (2003)
N.I. Medvedeva, M.S. Park, D.C. Van Aken, and J.E. Medvedeva: [cond-mat.mtrl-sci], 2012, arXiv:1208.0310v1
T.Y. Hsu, X. Zuyao, Mat Sci and Engg A 273–275, 494 (1999)
R. Lagneborg, Acta Metall. 7, 823 (1964)
B.J. Thomas, Metaux. Corrosion lndustrie 532, 405 (1969)
P.C.J. Gallagher, Metall. Mater. Trans. A 1, 2429 (1970)
X. Tian, Y. Zhang, Mater Sci Engg A 516, 73 (2009)
M. Koyama, T. Sawaguchi, K. Tsuzaki, Phil Mag 92, 3051 (2012)
K. Jeong, J.-E. Jin, Y.-S. Jung, S. Kang, Y.-K. Lee, Acta Mater 61, 3399 (2013)
G.R. Lehnhoff, K.O. Findley, JOM 66, 756 (2014)
D.I. Dooley and J. Nutting: in High-Alloy Steels [Russian translation], Moscow, 1969, p. 287
H. Schumann, J Kristall Technik 10, 1141 (1974)
B.K. Zuidema, D.K. Subramanyam, W.C. Leslie, Metall Trans A 18, 1629 (1987)
S.W. Lee, H.C. Lee, Metall. Trans. A 24, 1333 (1993)
J.E. Jin, Y.K. Lee, Acta Mater 60, 1680 (2012)
S. Hong, S.Y. Shin, J. Lee, D.H. Ahn, H.S. Kim, S.K. Kim, K.G. Chin, S. Lee, Metall. Mater. Trans. A 45, 633 (2014)
R.D.K. Misra, S. Nayak, S.A. Mali, J.S. Shah, M.C. Somani, L.P. Karjalainen, Met and Mat Trans A 40, 2498 (2009)
B.X. Huang, X.D. Wang, Y.H. Rong, L. Wang, L. Jin, Mat Sci and Engg A 438–440, 306 (2006)
K.R. Williams, J. Mater. Sci. 8, 109 (1973)
Z.Y. Xu, Sci China Ser E 27, 289 (1997). (in Chinese)
L. Bracke, G. Mertens, J. Penning, B.C. De Cooman, M. Liebeherr, N. Akdut, Metall. Mater. Trans. A 37, 307 (2006)
J.W. Simmons, Mat Sci and Engg A 207, 159 (1996)
S. Wang, K. Yang, Y. Shan, L. Li, Mat Sci and Engg A 490, 95 (2008)
G. Thomas, J Aust Inst Metals 8, 80 (1963)
P. Coulomb, N. Gibert, A. Clement, A. Coufou, Z Phys Suppl C3(27), 94 (1966)
P.C.J. Gallagher, Trans. TMS-AIME 242, 103 (1968)
M. Grujicic, J.O. Nilsson, W.S. Owen, and T. Thorvaldsson: in HNS 88, Lille, France, May 1988 J. Foct and A. Hendry, eds., The Institute of Metals, London, 1989, p. 151
J. Sassen, A.J. Garratt-Reed, and W.S. Owen: in HNS 88, Lille, France, May 1988 J. Foct and A. Hendry, eds., The Institute of Metals, London, 1989, p. 159
S. Fayeulle, D. Treheux, C. Esnouf, Appl Surf Sci 25, 288 (1986)
M. Fujikura, K. Takada, K. Ishida, Trans ISIJ 15, 464 (1975)
R. Taillard and J. Foct: in High Nitrogen Steels, HNS 88, J. Foct and A. Hendry, eds., The Institute of Metals, London, 1989, p. 387
N.D. Afanasiev, V.G. Gavrilyuk, V.A. Duz, V.M. Nadutov, Physics of Metals and Metnllogracow phy 8, 121 (1990). (in Russian)
I.A. Yakubtsov, A. Ariapour, D.D. Perovic, Acta Mater 47, 1271 (1999)
J. Talonen, H. Hanninen, Metall. Mater. Trans. A 35, 2401 (2004)
T.-H. Lee, C.-S. Oh, S.-J. Kim, S. Takaki, Acta Mat 55, 3649 (2007)
V.G. Gavriljuk, H. Hanninen, A.V. Tarasenko, A.S. Tereshchenko, K. Ullakko, Acta Metall. Mater. 43(2), 559 (1995)
C. Donadille, R. Valle, P. Dervin, R. Penelle, Acta Metall. 37(6), 1547 (1989)
S.M. Abbasi, A. Shokuhfar, N. Ehsani, and M. Morakabatt: Association of Metallurgical Engineers of Serbia, UDC:669.265.018.15.001.26:620.18–20, pp. 55-65
H. Monajati, G.R. Razavi, M. Saboktakin, M. Razavi. (2011). doi:10.1115/1.859810
G.R. Razavi, M.S. Rizi, H.M. Zadeh, Mat Tech 47, 611 (2013)
F. Lecroisey, A. Pineau, Metall Trans 3, 387 (1972)
L. Remy, A. Pineau, Mater Sci Engg A28, 99 (1977)
Y.S. Han, S.H. Hong, Mat Sci and Engg A 222, 76 (1997)
K. Ishida, T. Nishizawa, Trans Jpn Inst Met 15, 225 (1974)
O. Grassel, G. Frommeyer, C. Derder, H. Hofman. J Phys IV France c5 (1997) 383
Z.H. Guo, Y.H. Rong, S.C. Chen, Trans JIM 40, 328 (1999)
G. Frommeyer, U. Brux, P. Neumann, ISIJ Int 43, 438 (2003)
G. Frommeyer, U. Brux, Steel Res Int 77, 627 (2006)
M.C. Mcgrath, D.C.V. Aken, N.I. Medvedeva, J.E. Medvedeva, Metall. Mater. Trans. A 44, 4634 (2013)
M.L. Holtz Worth, M.R. Lanthan Jr. Corrosion 24 (1968) 110
A. Juan, L. Moro, G. Brizuela, E. Pronsato, Int. J. Hydro. Engg., 2002, vol. 27, p. 333.
P.J. Ferreira, I.M. Robertson, H.K. Birnbaum, Mater Sci Forum 207–209, 93 (1996)
B.E.P. Beeston, L.K. France, J. Inst Metals 96, 105 (1968)
T.S. Byun, Acta Mat 51, 3063 (2003)
J.J. Hwan, C.C. Sool, Mat Sci and Engg A 257(2), 353 (1998)
P.R. Thornton, P.B. Hirsch, Phil Mag 3, 738 (1958)
A. Seeger, R. Berner, H. Wolf, Z Physik 155, 247 (1959)
R. Berner, Z Naturforsohung 15a (1960) 689
P. Haasen, A. King, Z. Metallkunde 51, 702 (1960)
P.R. Swann, J. Nutting, J Inst Metals 90, 133 (1961)
M. Ahlers, P. Haasen, Z Metallkunde 53, 302 (1962)
T. Eriekson, Acta Metall. 14, 853 (1966)
F. Abrassart, Metall. Trans. 4, 2205 (1973)
I.Ya. Georgieva: Metallovedenie Termicheskaya Obrabotka Metallov, 1976, p. 18
L.S. Malinov and V.I. Konop: Metallovedenie Termicheskaya Obrabotka Metallov, 1978, p. 10
S.W. Yang, J.E. Spruiell, J. Mater. Sci. 17, 677 (1982)
Y. Kaneko, K. Kaneko, A. Nohara, H. Saka, Phil Mag 71, 399 (1995)
J. Wan, S. Chen, Z. Xu, Sci China 44, 345 (2001)
X.D. Wang, B.X. Huang, Y.H. Rong, Phil Mag Lett 88, 845 (2008)
G.B. Olson, and M. Cohen. Metall. Trans., 1976, vol. 7A, p. 1897.
D. Goodchild, W.T. Roberts, D.V. Wilson, Acta Metall. 18, 1137 (1970)
S.M. Copley, B.H. Kear, Acta Metall. 16, 227 (1968)
H.J. Kestenbach, Phil Mag 36, 1509 (1977)
E. El-Danaf, S.R. Kalidindi, R.D. Doherty, Metall Mater Trans 30A, 1223 (1999)
I. Karaman, H. Sehitoglu, Y.I. Chumlyakov, H.J. Maier. JOM (2002) 31
R.E. Smallman, D. Green, Acta Metall. 12, 145 (1964)
Acknowledgments
I am extremely grateful to Professor Sir H.K.D.H. Bhadeshia, Phase Transformation & Complex Properties Research Group, Department of Materials Science and Metallurgy, University of Cambridge, UK for the provision of Neuromat Neural Network software for the present analysis. I would also like to thank all the respected reviewers for their positive and constructive recommendations which helped a lot to prepare this revised manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript submitted February 19, 2015.
Rights and permissions
About this article
Cite this article
Das, A. Revisiting Stacking Fault Energy of Steels. Metall Mater Trans A 47, 748–768 (2016). https://doi.org/10.1007/s11661-015-3266-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-015-3266-9