1 Introduction

Nanocrystalline materials exhibit many unique properties which are normally superior to their coarse-grained counterparts, and therefore have great potentials in a variety of applications.[1–5] However, due to a high volume fraction of grain boundaries (GBs), the driving force for grain coarsening of the nanocrystalline materials is rather high, and the thermal stability of this kind of materials is poor. Many pure nanocrystalline metals, e.g., Sn, Pb, Al, Mg, Cu, and Pd, etc.,[6–9] are subjected to apparent grain coarsening even at room temperature. This strongly hinders the applications of these materials. Therefore, enhancing thermal stability of nanocrystalline materials is a fundamentally important issue regarding the applications of nanocrystalline materials.

According to the classical grain growth theory,[10,11] the velocity of grain growth (dD/dt) is expressed by the product of driving force (P = γ/D) and GB mobility (M GB),

$$ \frac{{{\text{d}}D}}{{{\text{d}}t}} = M^{\text{GB}} \cdot P = M^{\text{GB}} \cdot \frac{\gamma }{D} $$
(1)

Accordingly, the enhanced thermal stability of nanocrystalline materials can be achieved by either reducing the driving force or reducing the GB mobility. It has been demonstrated widely that both of the above two strategies can be achieved by alloying foreign elements.[11–13] Therefore, understanding the alloying effects on grain growth of nanocrystalline materials will be essentially important for enhancing their thermal stability. So far, plenty of efforts and progresses[12–26] have been reported in evaluating the alloying effects both thermodynamically and kinetically. However, several issues are still required to be clarified, which are summarized briefly below.

1.1 Thermodynamic Description for Grain Growth of Nanocrystalline Alloy System

Thermodynamic descriptions of a nanocrystalline alloy system have been carried out by Weissmüller,[12,27] and other authors,[13–19,28–33] yielding a conclusion that the minimum of Gibbs energy of a system corresponds to a zero GB energy caused by solute segregation. Basically, the reported models assume an equilibrium solute distributionFootnote 1 in the bulk and GB phases, and thus follow the equilibrium GB segregation equation, e.g., Mclean’s model.[34] This means, at a given state, namely, a given D, the solute molar fractions in the bulk (X b) and GBs (X GB) are determined by the equilibrium GB segregation equation. However, for an actual grain growth process, the nonequilibrium system prevails, and in turn, the solute distribution will no longer follow the equilibrium GB segregation equation, thus leading to deviations of X b and X GB from their equilibrium values.[20,35] As a consequence, the above-mentioned thermodynamic descriptions will not be suitable for the actual grain growth. Hence, how the nonequilibrium solute distribution affects the thermodynamics of an actual grain growth process will need a detailed analysis.

1.2 Solute Drag in an Actual Grain Growth Process

It is generally accepted that, kinetically, for an actual grain growth process, the asymmetric distribution of solute in the vicinity of GBs causes the solute drag effect on migration of GBs.[20,21] By incorporation of the solute drag force P solute into Eq. [1], the grain growth equation considering the solute drag effect can be expressed as[22,24,36]

$$ \frac{{{\text{d}}D}}{{{\text{d}}t}} = M^{\text{GB}} \cdot \left( {P - P_{\text{solute}} } \right) $$
(2)

However, this kind of approaches incorporates arbitrarily the kinetic effect (solute drag force) into the thermodynamic term (driving force). Whether this treatment is physically meaningful deserves a further analysis.

A widely accepted form of solute drag force was defined by Cahn[20] as

$$ P_{\text{solute}} = - N_{\text{v}} \int\limits_{ - \infty }^{ + \infty } {\left( {X^{\text{GB}} - X^{\text{b}} } \right)\frac{{{\text{d}}E}}{{{\text{d}}y}}{\text{d}}y} $$
(3)

where N v, dE/dy, X GB, X b, and y are the number of atoms in the GB phase, the interaction energy between solute and GB, the compositional profile of solute at GB, an constant solute molar fraction, and the distance of an atom from GB, respectively. Since it is difficult to solve analytically the compositional profile at the GB, Eq. [3] is hardly used to describe quantitatively the solute drag effect on grain growth. Although some simplified solute drag models are subsequently proposed by assuming the difference between solute molar fractions in the bulk and GB phases is proportional to D, and then used to describe the solute drag effect on the nanoscale grain growth.[23,24] However, this assumption actually lacks of theoretical supports and on the other hand, brings unclear constants to the models.[22,23]

1.3 Evolution of Thermodynamic and Kinetic Parameters upon an Actual Grain Growth

For an ideal parabolic grain growth of pure polycrystalline metals, the thermodynamic and kinetic parameters involved in grain growth equation, i.e., the GB energy and the GB mobility, are constant. When solute elements are introduced, solute distributions in the system will be changing during grain growth. In this case, interactions between the solute and the GB are bound to change these thermodynamic and kinetic parameters. This has been modeled extensively both thermodynamically[12–15] and kinetically.[20–23] However, early investigations on the thermodynamic and kinetic effects are more or less independent, without considering the interplay in between. This may limit the understanding of the effects of the thermodynamic and kinetic parameters on the grain growth of nanocrystalline materials. As stated by Borisov,[37] upon grain growth, GB mobility is related to GB energy, which implies that during grain growth thermodynamics and kinetics of a system may actually be linked. Recently, Chen et al.[26] established a thermokinetic model for the grain growth in nanocrystalline alloy systems and linked the GB energy with the activation energy. On this basis, the authors found that upon grain growth a decrease of GB energy is accompanied with an increase of activation energy. However, Chen et al.’s work does not consider the effect of the difference between the solute molar fractions in bulk and GB (i.e., X GB − X b). As suggested by Molodov et al.,[38] the change of X GB − X b also plays a role in determining the GB mobility. A further quantitative analysis on the evolution of thermodynamic and kinetic parameters during an actual grain growth is, therefore, essential for understanding the effects of these parameters on the grain growth behaviors.

In order to clarify the above-mentioned issues, the thermodynamic and kinetic effects of alloying on the nanoscale grain growth of substitutional binary alloy systems will be analyzed in this work. First, adopting a regular solution model proposed by Trelewicz[17] and Saber,[18,19] the molar Gibbs free energy of mixing for an actual grain growth process is constructed in Section II. Then, the driving force for grain growth considering nonequilibrium solute distribution is derived in Section III. On this basis, a new grain growth equation in combination with the changed GB mobility is obtained in Section III. In Section IV, applying the derived model, the grain growth behaviors of two nanocrystalline substitutional alloys, i.e., Fe-4at. pct Zr and Pd-19at. pct Zr, are analyzed and the effects of the thermodynamic and kinetic parameters on the grain growth are illuminated.

2 Gibbs Free Energy of Mixing

According to References 17 and 18, for nanocrystalline alloy systems, the Gibbs free energy of mixing depends on three variables, i.e., X GB, X b, and D. Upon grain growth, the evolutions of these parameters determine the change of the Gibbs free energy of mixing. In order to illuminate the difference between the equilibrium solute distribution and the nonequilibrium solute distribution upon grain growth, we define two kinds of kinetic grain growth processes.

  1. 1.

    Grain growth assuming equilibrium solute distribution. In this process, the solute distribution in the bulk and GB phases is determined by the equilibrium GB segregation equation.

  2. 2.

    Grain growth considering non equilibrium solute distribution. In this process, the solute distribution in the bulk and GB phases does not follow the equilibrium GB segregation equation. Solute molar fractions in the bulk and GB phases deviate from their equilibrium values.

2.1 Constructions of Gibbs Free Energy of Mixing

2.1.1 Gibbs free energy of mixing assuming equilibrium solute distribution

In order to construct the total Gibbs free energy of the system, the regular solution model proposed by Trelewicz[17] and Saber[18,19] is adopted. Following the approaches of Hillert[39] and Saber,[18] molar Gibbs free energy of mixing (MGFEM) for a polycrystalline alloy system (G mix) is derived as (see Appendix A)

$$ \begin{aligned} G_{\text{mix}} &= \omega zX^{\text{b}} \left( {1 - X^{\text{b}} } \right)\left( {1 - f} \right) + \alpha \omega zX^{\text{GB}} \left( {1 - X^{\text{GB}} } \right)f + \left( {X^{\text{GB}} \sigma_{\text{A}} \gamma_{\text{A}} + \left( {1 - X^{\text{GB}} } \right)\sigma_{\text{B}} \gamma_{\text{B}} } \right)f + H_{\text{elas}} X^{\text{GB}} f \\ & \quad + RT\left\{ {\left( {1 - f} \right)\left[ {X^{\text{b}} \ln X^{\text{b}} + \left( {1 - X^{\text{b}} } \right)\ln \left( {1 - X^{\text{b}} } \right)} \right] + f\left[ {X^{\text{GB}} \ln X^{\text{GB}} + \left( {1 - X^{\text{GB}} } \right)\ln \left( {1 - X^{\text{GB}} } \right)} \right]} \right\} \hfill \\ \end{aligned} $$
(4)

where ω, z, α, σ A, σ B, γ A, γ B, H elas, and f are the interaction energy, the coordination number, the scale factor of bond energy between the bulk and GB, the molar GB areas of solute (A) and solvent (B) atoms, the GB energies of solute (A) and solvent (B) atoms, the elastic energy due to atomic size mismatch, and the volume fraction of GBs, respectively. The terms \( \omega zX^{\text{b}} \left( { 1- X^{\text{b}} } \right)\left( { 1- f} \right) + \omega \alpha zX^{\text{GB}} \left( { 1- X^{\text{GB}} } \right)f, \, \left( {X^{\text{GB}} \gamma_{\text{A}} \sigma_{\text{A}} + \left( { 1- X^{\text{GB}} } \right)\gamma_{\text{B}} \sigma_{\text{B}} } \right)f,H_{\text{elas}} X^{\text{GB}} f\;{\text{and}}\;RT\left\{ {\left( { 1- f} \right)\left[ {X^{\text{b}} { \ln }X^{\text{b}} + \left( { 1- X^{b} } \right){ \ln }\left( { 1- X^{\text{b}} } \right)} \right] + f\left[ {X^{\text{GB}} { \ln }X^{\text{GB}} + \left( { 1- X^{\text{GB}} } \right){ \ln }\left( { 1- X^{\text{GB}} } \right)} \right]} \right\} \) correspond to the contributions of enthalpy of mixing of bulk and GB, the energy penalty required to form GB, the elastic energy induced by atomic size mismatch, and the contributions of entropy of mixing of bulk and GB, respectively. Separating these terms and restructuring them according to their contributions, the MGFEM of bulk (\( G_{\text{mix}}^{\text{b}} \)) and GB (\( G_{\text{mix}}^{\text{GB}} \)) are expressed as

$$ G_{\text{mix}}^{\text{b}} = \omega zX^{\text{b}} \left( {1 - X^{\text{b}} } \right) + RT\left[ {X^{\text{b}} \ln X^{\text{b}} + \left( {1 - X^{\text{b}} } \right)\ln \left( {1 - X^{\text{b}} } \right)} \right] $$
(5a)
$$ G_{\text{mix}}^{\text{GB}} = \alpha \omega zX^{\text{GB}} \left( {1 - X^{\text{GB}} } \right) + \left( {X^{\text{GB}} \sigma_{\text{A}} \gamma_{\text{A}} + \left( {1 - X^{\text{GB}} } \right)\sigma_{\text{B}} \gamma_{\text{B}} } \right) + H_{\text{elas}} X^{\text{GB}} + RT\left[ {X^{\text{GB}} \ln X^{\text{GB}} + \left( {1 - X^{\text{GB}} } \right)\ln \left( {1 - X^{\text{GB}} } \right)} \right] $$
(5b)

Comparing Eq. [4] to Eq. [5], G mix (Eq. [4]) can be rewritten as

$$ G_{\text{mix}} = \left( {1 - f} \right)G_{\text{mix}}^{\text{b}} + fG_{\text{mix}}^{\text{GB}} $$
(6)

2.1.2 Gibbs free energy of mixing considering nonequilibrium solute distribution

For an actual grain growth process, the solute diffusion is slower than the GB motion, so that an asymmetric solute distribution along the GB is always expected.[20,40] In this case, the average solute molar fraction in the bulk and GB phases will deviate from their equilibrium values.[20,35] By introducing two increments of deviations ΔX GB and ΔX b, X GB and X b in the case of nonequilibrium solute distribution will be replaced by X GB + ΔX GB and X b + ΔX b, respectively. Following Eq. [5], MGFEM in the actual grain growth process is then modified as

$$ G_{\text{mix}}^{{\prime {\text{b}}}} = G_{\text{mix}}^{\text{b}} + \Delta G_{\text{mix}}^{\text{b}} $$
(7a)
$$ G_{\text{mix}}^{{\prime {\text{GB}}}} = G_{\text{mix}}^{\text{GB}} + \Delta G_{\text{mix}}^{\text{GB}} $$
(7b)

where \( \Delta G_{\text{mix}}^{\text{b}} \) and \( \Delta G_{\text{mix}}^{\text{GB}} \) represent the additional energy contributions to MGFEM due to ΔX b and ΔX GB, respectively. By comparing Eq. [7] to Eq. [5], \( \Delta G_{\text{mix}}^{\text{b}} \) and \( \Delta G_{\text{mix}}^{\text{GB}} \) are derived asFootnote 2

$$ \Delta G_{\text{mix}}^{\text{b}} = \omega z\Delta X^{\text{b}} \left( {1 - 2X^{\text{b}} } \right) + RT\Delta X^{\text{b}} \ln \frac{{X^{\text{b}} + \Delta X^{\text{b}} }}{{1 - X^{\text{b}} - \Delta X^{\text{b}} }} $$
(8a)
$$ \Delta G_{\text{mix}}^{\text{GB}} = \alpha \omega z\Delta X^{\text{GB}} \left( {1 - X^{\text{GB}} } \right) + \Delta X^{\text{GB}} \left( {\sigma_{\text{A}} \gamma_{\text{A}} - \sigma_{\text{B}} \gamma_{\text{B}} } \right) + H_{\text{elas}} \Delta X^{\text{GB}} {\kern 1pt} {\kern 1pt} {\kern 1pt} + RT\Delta X^{\text{GB}} \ln \frac{{X^{\text{GB}} + \Delta X^{GB} }}{{1 - X^{\text{GB}} - \Delta X^{\text{GB}} }} $$
(8b)

Similar to Eq. [6], the MGFEM \( G^{\prime}_{\text{mix}} \) can be given as

$$ G^{\prime}_{\text{mix}} = \left( {1 - f} \right)G_{\text{mix}}^{{\prime {\text{b}}}} + fG_{\text{mix}}^{{\prime {\text{GB}}}} $$
(9)

By substituting Eq. [7] into Eq. [9] and assuming \( \Delta G_{\text{mix}} = \left( {1 - f} \right)\Delta G_{\text{mix}}^{\text{b}} + f\Delta G_{\text{mix}}^{\text{GB}} \), Eq. [9] is then rewritten as

$$ G^{\prime}_{\text{mix}} = G_{\text{mix}} + \Delta G_{\text{mix}} $$
(10)

2.2 Evolution of Gibbs Free Energy of Mixing upon Grain Growth

Upon grain growth, GB area decreases continuously, leading to the redistribution of solute in the bulk and GB phases, and thus the change of the MGFEM. The solute redistribution in the bulk and GB phases should follow two constraint conditions: (1) mass conservation law, and (2) solute segregation equation.

The mass conservation equation for solute distribution in the bulk and GB phases can be written as

$$ X^{\text{b}} \left( {1 - f} \right) + X^{\text{GB}} f = X^{0} $$
(11)

where X 0 is the total solute molar fraction. For a constant GB thickness 2δ, f can be expressed as a function of D:

$$ f = 1 - \left( {\frac{D - \delta }{D}} \right)^{3} $$
(12)

At a given state (D), X b and X GB can be correlated by the following solute segregation equation:

$$ \frac{{X^{\text{GB}} }}{{1 - X^{\text{GB}} }} = \frac{{X^{\text{b}} }}{{1 - X^{\text{b}} }}\exp \left( {\frac{{H_{\text{seg}} }}{RT}} \right) $$
(13)

In the general treatments, e.g., Mclean’s segregation model,[41] the segregation enthalpy H seg is assumed as a constant. This is practical for a relatively low X GB, where the solute–solute interaction is negligible. However, for a high X GB, the solute–solute interaction may influence H seg, which will no longer be a constant.[41] In Appendix B, an expression of H seg considering the solute–solute interaction is derived as

$$ H_{\text{seg}} = H_{0} - C_1X^{\text{GB}} + C_2X^{\text{b}} $$
(14)

with \( H_{0} = \omega z - \alpha \omega z - \left( {\sigma_{\text{A}} \gamma_{\text{A}} - \sigma_{\text{B}} \gamma_{\text{B}} } \right) - H_{\text{elas}} \), C 1 = −2αωz and C 2 = −2ωz. In the following model derivation, X b and X GB will follow Eq. [13] with the new expression of H seg (Eq. [14]).

On this basis, applying the above two constraint conditions, X b and X GB can be expressed as functions of D by solving Eqs. [11] through [13]. Then, for the grain growth assuming the equilibrium solute distribution, substituting Eq. [12] into Eq. [6], the evolution of MGFEM upon grain growth can be expressed as a function of D:

$$ G_{\text{mix}} \left( D \right) = \left( {\frac{D - \delta }{D}} \right)^{3} G_{\text{mix}}^{\text{b}} + \left( {1 - \left( {\frac{D - \delta }{D}} \right)^{3} } \right)G_{\text{mix}}^{\text{GB}}. $$
(15)

While for the grain growth considering the nonequilibrium solute distribution, Eq. [15] will be replaced by

$$ G_{\text{mix}} \left( D \right) = \left( {\frac{D - \delta }{D}} \right)^{3} G_{\text{mix}}^{{\prime {\text{b}}}} + \left( {1 - \left( {\frac{D - \delta }{D}} \right)^{3} } \right)G_{\text{mix}}^{{\prime {\text{GB}}}} $$
(16)

3 Driving Force for Grain Growth and a New Grain Growth Equation

Driving force for grain growth corresponds to the reduction of Gibbs free energy of the system against volumetric change of the system (dV), which can be given as

$$ {\text{d}}V = V_\text{D} \left( {\frac{{V_{\text{m}} }}{{V_\text{D} }} - \frac{{V_{\text{m}} }}{{V_\text{D + dD} }}} \right) = 3V_{\text{m}} \frac{{{\text{d}}D}}{D} $$
(17)

where V D and V D + dD denote the volume of spherical grain with grain size D and D + dD, respectively. Then the driving force for grain growth assuming the equilibrium solute distribution (P) can be given by

$$ P = - \frac{{{\text{d}}G_{\text{mix}} \left( D \right)}}{{{\text{d}}V}} = - \frac{D}{{3V_{\text{m}} }}\frac{{{\text{d}}G_{\text{mix}} \left( D \right)}}{{{\text{d}}D}} $$
(18)

For grain growth considering the nonequilibrium solute distribution, the driving force (\( P^{'} \)) can be expressed as

$$ P^{\prime} = - \frac{{{\text{d}}G^{\prime}_{\text{mix}} \left( D \right)}}{{{\text{d}}V}} = - \frac{D}{{3V_{\text{m}} }}\frac{{{\text{d}}G_{\text{mix}} \left( D \right) + {\text{d}}\Delta G_{\text{mix}} \left( D \right)}}{{{\text{d}}D}} $$
(19)

3.1 Driving Force Assuming Equilibrium Solute Distribution

Before proceeding with the following derivations, it is necessary to clarify two different definitions of the chemical potential of solute in GB (\( \mu_{\text{A}}^{\text{GB}} \)) and bulk (\( \mu_{\text{A}}^{\text{b}} \)) in the literature.[12,15,39] When solute distribution between GB and bulk reaches equilibrium state, according to References 15 and 39, \( \mu_{\text{A}}^{\text{GB}} \) and \( \mu_{\text{A}}^{\text{b}} \) follow the following relationship:

$$ \mu_{\text{A}}^{\text{GB}} - \mu_{\text{A}}^{\text{b}} = \gamma A^{\text{GB}} $$
(20)

with A GB as the molar GB area.

By solving Eq. [18] mathematically (see Appendix C), the driving force for grain growth can be obtained as

$$ P = \frac{\delta }{{V_{\text{m}} }}\left( {\frac{{\partial G_{\text{mix}} \left( D \right)}}{\partial f} - \lambda \left( {X^{\text{GB}} - X^{\text{b}} } \right)} \right)\frac{1}{D} $$
(21)

where λ is the Lagrangian multiplier (see Appendix B).

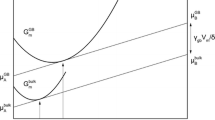
Following the approaches of Hillert[39] and Krill,[15] the Gibbs free energy of bulk and GB for a binary polycrystalline alloy system is illustrated in Figure 1, where two identical slopes of tangents at X GB and X b for GB and bulk, i.e., \( \frac{{\partial G^{\text{GB}} }}{{\partial X^{\text{GB}} }} \) and \( \frac{{\partial G^{\text{b}} }}{{\partial X^{\text{b}} }} \), correspond to the Lagrangian multipliers as defined in Appendix B (see Eq. [B3]). Then, \( \mu_{\text{A}}^{\text{b}} \) and \( \mu_{\text{A}}^{\text{GB}} \) can be written as

Fig. 1
figure 1

Gibbs free energy diagram for a binary polycrystalline alloy system. G b and G GB represent the molar Gibbs free energies of bulk and GB, respectively. \( \mu_{\text{A}}^{\text{b}} \), \( \mu_{\text{A}}^{\text{GB}} \), \( \mu_{\text{B}}^{\text{b}} \), and \( \mu_{\text{B}}^{\text{GB}} \) are chemical potentials. The superscripts A and B, and the subscripts b and GB represent solute and solvent, bulk, and grain boundary, respectively

Full size image
$$ \mu_{\text{A}}^{\text{b}} = G^{\text{b}} + \frac{{\partial G^{\text{b}} }}{{\partial X^{\text{b}} }}\left( {1 - X^{\text{b}} } \right),\qquad\mu_{\text{A}}^{\text{GB}} = G^{\text{GB}} + \frac{{\partial G^{\text{GB}} }}{{\partial X^{\text{GB}} }}\left( {1 - X^{\text{GB}} } \right) $$
(22)

Substituting Eqs. [22] and [B3] into Eq. [20], one can obtain

$$ \gamma = \frac{1}{{A^{\text{GB}} }}\left( {\frac{\partial G}{\partial f} - \lambda \left( {X^{\text{GB}} - X^{\text{b}} } \right)} \right) $$
(23)

where G (=fG GB + (1 − f)G b) denotes the Gibbs free energy of system. According to References 17 and 18, G and G mix follow the energy conservation equation, i.e., −G mix + G = G total, where G total represents the total Gibbs free energy of system before mixing. Differentiating this equation yields \( \frac{\partial G}{\partial f} = \frac{{\partial G_{\text{mix}} }}{\partial f} \). Accordingly, Eq. [23] can be rewritten as

$$ \gamma = \frac{1}{{A^{\text{GB}} }}\left( {\frac{{\partial G_{\text{mix}} \left( D \right)}}{\partial f} - \lambda \left( {X^{\text{GB}} - X^{\text{b}} } \right)} \right) $$
(24)

Since A GB = V m/δ, by comparing Eq. [24] to Eq. [21], the driving force for grain growth in the case of equilibrium solute distribution can be obtained as

$$ P = \frac{\gamma }{D} $$
(25)

Equation [25] has the similar form to the classical definition of driving force for grain growth. However, the classical grain growth equation (Eq. [1]) is developed for pure polycrystalline metals, where γ is a constant; in alloy system, γ becomes no longer a constant, but a function of D, cf. Eq. [24].

3.2 Driving Force Considering Nonequilibrium Solute Distribution

Equation [25] is obtained by assuming the equilibrium solute distribution during grain growth, and therefore cannot represent the driving force for an actual grain growth where the nonequilibrium solute distribution prevails. Substituting Eq. [18] into Eq. [19], the driving force for grain growth considering the nonequilibrium solute distribution can be expressed as

$$ P^{\prime} = \left[ {\frac{{\partial G_{\text{mix}} \left( D \right)}}{\partial f} - \lambda \left( {X^{\text{GB}} - X^{\text{b}} } \right)} \right]\frac{\delta }{{V_{\text{m}} }}\frac{1}{D} - \frac{D}{{3V_{\text{m}} }}\frac{{{\text{d}}\Delta G_{\text{mix}} \left( D \right)}}{{{\text{d}}D}} = \frac{\gamma }{D} - \frac{D}{{3V_{\text{m}} }}\frac{{{\text{d}}\Delta G_{\text{mix}} \left( D \right)}}{{{\text{d}}D}} $$
(26)

Compared to Eq. [25], one additional term \( \frac{D}{{3V_{\text{m}} }}\frac{{{\text{d}}\Delta G_{\text{mix}} \left( D \right)}}{{{\text{d}}D}} \) appears in Eq. [26]. This term is defined as ΔP, which is totally due to the existence of ΔX GB and ΔX b in the case of nonequilibrium solute distribution. Therefore, this additional term actually corresponds to the energy required to adjust the nonequilibrium solute distribution to the equilibrium one. Since the nonequilibrium solute distribution is always expected in an actual grain growth process, the driving force for the actual grain growth should not conform its classical definition, i.e., P = γ/D, but be separated into the part to drive GB migration and the part to adjust solute molar fractions from their nonequilibrium values to the equilibrium ones. The additional term ΔP can thus be considered as the force impeding GB migration, in other words, the solute drag force. This is compatible with the combination of driving force and drag force as Eq. [2]. So far, it becomes clear that the incorporation of solute drag force into driving force in the grain growth equation (Eq. [2]) is physically meaningful.

3.3 A New Grain Growth Equation

By incorporating the driving force for grain growth considering the nonequilibrium solute distribution (Eq. [26]) into Eq. [1], the grain growth equation can be presented as

$$ \frac{{{\text{d}}D}}{{{\text{d}}t}} = M^{\text{GB}} P^{\prime} = M^{\text{GB}} \left( {\frac{\gamma }{D} - \Delta P} \right), $$
(27)

where the effect of solute segregation on M GB has been well accounted for using a model established by Molodov et al.,[38] viz.,

$$ M^{\text{GB}} = \frac{{V_{\text{m}} D^{\text{GB}} }}{{\delta RT\left( {X^{\text{GB}} - X^{\text{b}} } \right)}} $$
(28)

where D GB (=\( D_{0}^{\text{GB}} \exp \left( { - \frac{{Q^{\text{GB}} }}{RT}} \right) \)) represents the solute diffusion coefficient in the GB phase. As referred to in Chen’s work,[26] the activation energy for GB diffusion Q GB is not a constant but related to the activation energy for bulk diffusion Q b and GB energy γ by the following equation:

$$ Q^{\text{GB}} = Q^{\text{b}} - \gamma A^{\text{GB}} $$
(29)

Combining Eqs. [27] through [29] thus gives an improved grain growth equation:

$$ \frac{{{\text{d}}D}}{{{\text{d}}t}} = \frac{{D_{0}^{\text{GB}} \exp \left( { - \frac{{Q^{\text{b}} - \gamma A^{\text{GB}} }}{RT}} \right)}}{{RT\left( {X^{\text{GB}} - X^{\text{b}} } \right)}}\frac{{V_{\text{m}} }}{\delta }\left( {\frac{\gamma }{D} - \Delta P} \right) $$
(30)

Compared to the classical grain growth equation (Eq. [1]), this new equation considers the concurrent changes of GB energy, solute drag force, and GB mobility, as well as the nonequilibrium solute distribution during grain growth, and therefore, will be more appropriate to describe the actual grain growth behaviors of nanocrystalline alloy systems.

4 Analyses of Actual Grain Growth Behaviors of Nanocrystalline Substitutional Binary Alloys

In this section, the present model will be used to describe the experimental results obtained in nanocrystalline Fe-4at. pct Zr[42] and Pd-19at. pct Zr[15] alloys, where Zr is substitutional solute element. Evolution of three controlling parameters, i.e., the driving force, the solute drag force, and the GB mobility, upon grain growth will be evaluated and discussed.

4.1 Comparison of Model Calculations with Experimental Results

The values of the physical parameters are listed in Table I. Due to lack of reference sources, two fitting parameters, i.e., Q b and α are taken. By using δ = 0.4 nm,[18] the D-t curves for nanocrystalline Fe-4at. pct Zr and Pd-19at. pct Zr alloys were calculated by solving Eq. [30] numerically, Figures 2(a) and (b). It is shown that the calculated D-t curves (the solid lines) exhibit fairly good agreements with the experimental data for both alloys. For the two alloys, the grain size increases rapidly in the early stage of grain growth; as the annealing time increases further, the grain grows slowly; in the late stage of grain growth, the grain size approaches a saturated value (marked by the dash lines in Figures 2(a) and (b)).

Table I The Values of the Physical Parameters of Fe-4at. Pct Zr and Pd-19at. Pct Zr Alloys (A = Solute and B = Solvent)
Full size table
Fig. 2
figure 2

Evolution of grain size (D) as a function of annealing time (t) for (a) Fe-4at. pct Zr alloy at 1073 K and (b) Pd-19at. pct Zr alloy at 873 K. The solid lines were calculated by Eq. [30]. The closed squares are experimental data cited from Refs. [15, 42]. The dash lines mark the calculated saturated grain sizes

Full size image

For Fe-4at. pct Zr alloy, Q b is fitted as 242 kJ/mol which is similar to the activation energy for bulk self-diffusion of Fe (251-282 kJ/mol[48]). The slight deviation between the two values may be caused by the promotion of Fe diffusion by Zr.[48,49] For Pd-19at. pct Zr alloy, the fitted Q b (225 kJ/mol) is again close to the activation energy for bulk self-diffusion of Pd (266 kJ/mol),[48] and the small deviation can be ascribed to the same reason for Fe-4at. pct Zr alloy. In addition, α is fitted as 0.758 for Fe-4at. pct Zr and 0.616 for Pd-19 at. pct Zr alloys, which are in a reasonable scale of agreement with 0.33-1 suggested in Reference 18.

4.2 Evolution of Driving Force upon Grain Growth

4.2.1 Driving force assuming equilibrium solute distribution

Assuming the equilibrium solute distribution, the driving force for grain growth corresponds to P(=γ/D), where, using Eqs. [24] and [25], γ and P were calculated and are shown in Figures 3 and 4, respectively. With the increasing D, both γ and P decrease continuously and approach zero in the late stage of grain growth.

Fig. 3
figure 3

Evolution of γ as a function of D for Fe-4at. pct Zr and Pd-19at. pct Zr alloys calculated using Eq. [24]. The physical parameters adopted in the calculations are listed in Table I

Full size image
Fig. 4
figure 4

Evolution of P, P′, and ΔP as functions of D for (a) Fe-4at. pct Zr and (b) Pd-19at. pct Zr alloys. The dash, solid, and dot lines were calculated using Eqs. [25], [26], and [31], respectively. The calculated parameters are listed in Table I

Full size image

The approach of P to zero upon grain growth can be ascribed to the reduction of GB energy, which has been discussed extensively and is attributed to the solute segregation in GBs.[14,15,50–52] The kinetic reduction of GB energy during grain growth has been less studied. The only relevant research was reported in Reference 26, wherein the evolution of GB energy with time was performed but involved an assumption that X GB − X b is proportional to D. This assumption is to some extent arbitrary and may not be suitable for true cases. This defect has been overcome in the present model, because X GB and X b can be obtained directly by solving Eqs. [11] through [13] numerically. As shown in Figures 5(a) and (b), X GB and X b, as well as X GB − X b increase continuously with the increasing D, indicating that the solute segregation in GBs is enhanced during grain growth. Along with the increases of X GB, X b, and X GB − X b, the GB energies of the two alloys decrease continuously, Figure 3. Once D reaches the calculated saturated grain size marked in Figures 2(a) and (b), the GB energy drops to zero. This suggests that the stagnation of grain growth can be attributed to the vanished GB energy/driving force. Apparently, during grain growth, the continuous increase of X GB − X b enhances the solute segregation in GBs, and, in turn, leads to the continuous reduction of GB energy and final attainment of zero GB energy. It is further noted from Figures 5(a) and (b) that the evolution of X GB with D does not follow a linear law shown by Krill et al.,[15] This is probably caused by the solute–solute interaction which reduces the GB segregation enthalpy and leads to a smaller X GB compared with the case of linear law.

Fig. 5
figure 5

Evolution of X GB, X b, and X GB − X b as functions of D for (a) Fe-4at. pct Zr and (b) Pd-19at. pct Zr alloys. The curves were calculated by solving Eqs. [11] through [13]. The physical parameters adopted in the calculations are listed in Table I

Full size image

4.2.2 Driving force considering nonequilibrium solute distribution

Considering the nonequilibrium solute distribution during grain growth, the driving force for grain growth corresponds to P′(=γ/D − ΔP). Using Eq. [26], P′ as a function of D for the two alloys was calculated and is shown in Figures 4(a) and (b). In contrast to P, P′ increases first, then decreases continuously, and approaches zero in the late stage of grain growth. Once grain growth starts, P′ is only about 35 pct of P for Fe-4at. pct Zr and about 45 pct of P for Pd-19at. pct Zr. As grain growth proceeds, the difference between P and P′ decreases and vanishes finally.

Since P′ consists of two parts, P and ΔP, the deviation of P from P′ is certainly caused by ΔP. As mentioned before, ΔP stands for the energy required to adjust the nonequilibrium solute distribution to the equilibrium solute distribution. Therefore, the magnitude of ΔP depends on the degree of deviation from the nonequilibrium to the equilibrium solute distribution. At a higher grain growth velocity, this deviation becomes more significant, and thus, a higher energy (i.e., ΔP) will be predicted. From Figures 2(a) and (b), in the beginning of grain growth, the grain growth velocity is rather high, which results in a high ΔP and, in turn, a small P′, Figures 4(a) and (b). With the time being, the velocity reduces rapidly. As a consequence, \( \Delta P \) decreases fast, and its impact on P′ becomes weak and vanishes finally in the late stage of grain growth. Consequently, the difference between P and P′ reduces continuously and vanishes in the end.

The above analyses clearly show that in the early stage of an actual grain growth, owing to the pronounced nonequilibrium solute distribution, a large fraction of energy will be spent on adjusting the solute distribution from its nonequilibrium state to its equilibrium state. Therefore, for an actual grain growth, P′ is more practical to stand for the driving force for grain growth rather than P.

4.3 Effects of Solute Drag on Grain Growth

It has been mentioned in Section III that the difference between P and P′, i.e., ΔP, can be considered as a force impeding the GB migration, namely, the solute drag force. Also, in Section IV–B–2, it was shown that ΔP is strongly related to the grain growth velocity; a higher velocity results in a larger ΔP. Then, in this section, it is proposed to correlate ΔP to the grain growth velocity \( \left(\upsilon\right)\), to study its impact on the grain growth, and accordingly, demonstrate its kinetic character.

4.3.1 Kinetic character of solute drag force

ΔP can be formulated by solving \( \frac{{{\text{d}}\Delta G_{\text{mix}} \left( D \right)}}{{{\text{d}}D}} \) (see Appendix D) as

$$ \Delta P = - \frac{{2\alpha \omega zV_{\text{m}} }}{{3R^{2} T^{2} }}\frac{\gamma }{D}\left[ {\left( {2f + \frac{{3\delta \left( {D - \delta } \right)^{2} }}{{D^{3} }}} \right)\frac{\gamma }{D} + 2f\frac{{{\text{d}}\gamma }}{{{\text{d}}D}}} \right] $$
(31)

Differentiating γ over D using Eq. [24], we will have

$$ \Delta P = - \frac{{2\alpha \omega zV_{\text{m}} }}{{3R^{2} T^{2} }}\frac{\gamma }{D}\left[ {\left( {2f + \frac{{3\delta \left( {D - \delta } \right)^{2} }}{{D^{3} }}} \right)\frac{\gamma }{D} + 2f\left( { - 2\alpha \omega z + \frac{RT}{{X^{\text{GB}} \left( {1 - X^{\text{GB}} } \right)}}} \right)\frac{{\delta \left( {X^{\text{GB}} - X^{\text{b}} } \right)}}{{V_{\text{m}} }}\frac{{\partial X^{\text{GB}} }}{\partial D}} \right] $$
(32)

Combining Eqs. [1] and [28], γ can be given as

$$ \gamma = \frac{{\delta RT\left( {X^{\text{GB}} - X^{\text{b}} } \right)}}{{V_{\text{m}} D^{\text{GB}} }}D\upsilon $$
(33)

Substituting Eq. [33] into Eq. [32], ΔP will be correlated with \( \upsilon\) by the following equation:

$$ \Delta P = - \frac{{2\alpha \omega z\delta \left( {X^{\text{GB}} - X^{\text{b}} } \right)}}{{3D^{\text{GB}} RT}}\left[ \begin{aligned} 2f\left( { - 2\alpha \omega z + \frac{RT}{{X^{\text{GB}} \left( {1 - X^{\text{GB}} } \right)}}} \right)\frac{{\delta \left( {X^{\text{GB}} - X^{\text{b}} } \right)}}{{V_{\text{m}} }}\frac{{\partial X^{\text{GB}} }}{\partial D} \hfill \\ + \left( {2f + \frac{{3\delta \left( {D - \delta } \right)^{2} }}{{D^{3} }}} \right)\frac{{\delta RT\left( {X^{\text{GB}} - X^{\text{b}} } \right)}}{{V_{\text{m}} D^{\text{GB}} }}\upsilon \hfill \\ \end{aligned} \right]\upsilon $$
(34)

It is suggested from Eq. [34] that ΔP, thermodynamically originating from ΔX GB and ΔX b, is related to \( \upsilon\) in nature. Since ΔX GB and ΔX b fulfill the mass conservation law (i.e., ΔX GB f = −ΔX b(1 − f)), the change of ΔX GB and ΔX b should be responsible for the evolution of ΔP. Figures 6(a) and (b) display the calculated ΔX GB and ΔP as functions of \( \upsilon\) for the two alloys, wherein, apparently, the enhanced ΔX GB with the increasing υ leads to the increase of ΔP, because higher ΔX GB corresponds to larger energy required to adjust the solute distribution as addressed above. This is compatible with the general statement that upon grain growth, the increase of velocity enhances the solute drag force.[20] Therefore, ΔP exhibits its kinetic character.

Fig. 6
figure 6

Evolution of ΔX GB and ΔP as functions of υ for (a) Fe-4at. pct Zr and (b) Pd-19at. pct Zr alloys. The solid lines (ΔX GB) and dash lines (ΔP) were calculated by Eqs. [D7] and [34], respectively. The values of the physical parameters used in the calculations are listed in Table I

Full size image

4.3.2 Effect due to solute drag

From the analyses above, the solute drag force occurs in the actual grain growth process where the nonequilibrium solute distribution prevails; no solute drag force occurs for the equilibrium solute distribution. The effect of solute drag on the actual grain growth can be illuminated by comparing the case considering the solute drag effect to the case neglecting the effect.

Neglecting ΔP in Eq. [30], a grain growth equation without considering solute drag effect can be obtained as

$$ \frac{{{\text{d}}D}}{{{\text{d}}t}} = \frac{{D_{0}^{\text{GB}} \exp \left( { - \frac{{Q^{\text{b}} - \gamma A^{\text{GB}} }}{RT}} \right)}}{{RT\left( {X^{\text{GB}} - X^{\text{b}} } \right)}}\frac{{V_{\text{m}} }}{\delta }\frac{\gamma }{D} $$
(35)

Using Eq. [35], the evolutions of D with t for Fe-4at. pct Zr and Pd-19at. pct Zr alloys were calculated and are shown in Figures 7(a) and (b), respectively, where the curves calculated by Eq. [30] (including solute drag effect) are also plotted for comparison. It is shown that when the solute drag effect is involved, the grain coarsening is slowed down. In the early stage of grain growth, the difference of grain sizes between the two cases is relatively large, indicating a relatively strong solute drag effect. While in the late stage of grain growth, such a difference becomes rather small, suggesting a rather weak, even negligible solute drag effect.

Fig. 7
figure 7

Comparison of the D-t curves calculated by Eq. [30] (including solute drag effect) and Eq. [35] (neglecting solute drag effect) for (a) Fe-4at. pct Zr alloy and (b) Pd-19at. pct Zr alloy. The values of physical parameters used in the calculations are listed in Table I

Full size image

The solute drag effect on grain growth behaviors is closely related to ΔP. That is to say, a high grain growth velocity corresponds to a large ΔP and a strong solute drag effect in the early stage of grain growth, Figures 6(a) and (b). As the grain growth proceeds, ΔP is becoming small due to a continuous decrease of υ, which will certainly lead to the weakening of solute drag effect. The calculations further show the same saturated grain sizes predicted by Eqs. [30] and [35]. As the grain growth becomes saturated, the grain growth velocity approaches zero, and thus the solute drag force vanishes (Figures 6(a) and (b)), which will, then, lead to the convergence of the saturated grain sizes in the two cases (Figures 7(a) and (b)). One may note further from Figures 7(a) and (b) that the differences between the grain size evolutions considering the solute drag force and the case neglecting the solute drag force are sufficiently small, suggesting that ΔP plays only a minor role in grain growth of the two alloys. This is in accordance with the conclusion in Reference 24.

4.4 Grain Boundary Mobility

In general, upon modeling real grain growth, M GB in the grain growth equation was taken as a fitting parameter and assumed as a constant, cf. References 24 and 25. Following Eqs. [28] and [29], however, M GB is correlated with several parameters which are changing upon grain growth, e.g., X GB, X b, and Q GB. Therefore, for an actual grain growth process, M GB would be taken as a variable rather than a constant. Substituting the calculated X GB, X b, and γ, as well as the values of the essential physical parameters listed in Table I, into Eqs. [28] and [29], the evolutions of M GB with D for Fe-4at. pct Zr and Pd-19at. pct Zr alloys were calculated, Figures 8(a) and (b), respectively. It is shown that M GB decreases continuously upon grain growth. Different from the driving force, a zero M GB is never attained during the whole grain growth process, implying that the inhibition of grain growth should not be ascribed to the zero M GB as stated in References 22,53 through 55.

Fig. 8
figure 8

Evolutions of GB mobility (M GB) as a function of grain size (D) for (a) Fe-4at. pct Zr. (b) Pd-19at. pct Zr alloys. The curves were calculated by Eq. [28]. The solid lines correspond to a changed X GB − X b upon grain growth, while the dash lines were calculated by assuming a constant X GB − X b (the initial values of X GB − X b in Figs. 5(a) and (b)). The values of physical parameters used in the calculations are listed in Table I

Full size image

Following Eq. [28], the change of M GB upon grain growth is related to X GB − X b and Q GB. The influence of Q GB on M GB has been discussed preciously,[26,56,57] where it was demonstrated that during grain growth, the increase of Q GB will reduce M GB. Due to the negligible change of Q b upon grain growth, the increase of Q GB can be ascribed to the reduction of γ caused by solute segregation in GBs,[26,56,57] cf. Eq. [29]. The effect of X GB − X b on M GB was neglected in previous models,[26,56,57] although the factor of X GB − X b reflects the number of atoms required to adjust their positions to suit the migration of GB.[38,58] However, the calculations performed in this work indicate that during grain growth, X GB − X b increases continuously (Figures 5(a) and (b)), which, according to Eq. [28], will surely reduce M GB. For a higher X GB − X b, more atoms will be required to adjust their positions to suit GB migration. This kinetic process will retard the GB migration and, therefore, reduce M GB. Figures 8(a) and (b) display the calculated M GB values with varied and constant X GB − X b, where it is shown that the change of X GB − X b during grain growth influences M GB significantly. With the increasing D, X GB − X b is enhanced (Figures 5(a) and (b)); therefore, the resulting reduction of M GB becomes more and more significant compared with the case of constant X GB − X b.

5 Conclusions

Based on the regular solution model proposed by of Trelewicz and Schuh[17] and Saber,[18] the Gibbs free energy of mixing for substitutional binary alloy systems considering nonequilibrium solute distribution was established. Accordingly, the relevant thermodynamic and kinetic parameters, i.e., the driving force and the solute drag, influencing the grain growth in substitutional binary alloy systems were derived and compared with their generally accepted definitions and interpretations. The improved model was used to analyze the grain growth behaviors of nanocrystalline Fe-4at. pct Zr[42] and Pd-19at. pct Zr[15] alloys. Evolutions of these thermodynamic and kinetic parameters influencing grain growth were evaluated and discussed. The main conclusions are summarized as follows:

  1. 1.

    For grain growth occurring in substitutional binary alloy system, assuming equilibrium solute distribution, the driving force for grain growth is in accordance with its classical definition, i.e., P = γ/D. While for an actual grain growth, where nonequilibrium solute distribution prevails, the driving force should be replaced by P = γ/D − ΔP.

  2. 2.

    ΔP represents the energy required to adjust nonequilibrium solute distribution to equilibrium solute distribution in the system. This parameter is equivalent to the generally accepted solute drag force impeding the GB migration. Since ΔP is correlated to υ, this quantity possesses kinetic character and can be enhanced by increasing υ.

  3. 3.

    For nanocrystalline Fe-4at. pct Zr and Pd-19at. pct Zr alloys, both the thermodynamic and kinetic parameters, i.e., P, ΔP, and M GB, are changing upon grain growth. With the increasing D, P and ΔP decrease and approach zero at the late stage of grain growth, and meanwhile, M GB decreases as well; however, it does not reach zero in the whole grain growth process.