The Effect of Solute Atoms on Grain Boundary Migration: A Solute Pinning Approach

Abstract

The effect of solute atoms on grain boundary migration has been modeled on the basis of the idea that solute atoms will locally perturb the collective rearrangements of solvent atoms associated with boundary migration. The consequence of such perturbations is cusping of the boundary and corresponding stress concentrations on the solute atoms which will promote thermal activation of these atoms out of the boundary. This thermal activation is considered to be the rate-controlling mechanism in boundary migration. It is demonstrated that the current statistical approach is capable of explaining, in phenomenological terms, the known effects of solute atoms on boundary migration. The experimental results of the effect of copper on boundary migration in aluminum, due to Gordon and Vandermeer, have been well accounted for.

1 Introduction

It has been known for a long time that impurity solid solution atoms have a tendency of segregation to grain boundaries, an effect which may strongly retard the grain boundary mobility and thus the kinetics of recrystallization and grain growth in pure metals, even when present in the ppm range. The first quantitative treatment of this phenomenon, usually referred to as solute drag, was presented by Lücke and Detert,[1] where they concluded that the effect is due to a direct interaction between the solute atoms and the moving grain boundaries.

Since the first quantitative treatment of Lücke and Detert, two main theoretical approaches of the solute drag effect on grain boundary mobility have come to dominate the literature. These are the treatments of Cahn[2] (commonly referred as the solute drag force approach) and Hillert and Sundman[3] (commonly referred as the dissipation approach). Typical application examples for the force and dissipation approaches are found elsewhere.[4–6] In the force approach, the solute drag is estimated by summing the forces that the solute atoms exert on the boundary and in the dissipation approach, by evaluating the amount of free energy dissipated due to diffusion when the boundary goes through a volume containing one mole of material. Over the last few decades, a lot of efforts has been made to generalize these approaches to a migrating phase boundary into a multicomponent system.[3,7–9] Indeed, in the initial treatment of the solute drag effect by Cahn and by Lücke and Stüwe,[10] the equation used for evaluating the solute drag does not apply to phase transformations. It only applies to the migration of grain boundaries, i.e., to one-phase materials.

The force approach and the dissipation approach both have a sound physical basis and should therefore be equivalent. However, the formula for calculating the solute drag for a migrating phase boundary into a multicomponent system in steady-state conditions has been a subject of debates over the years, and it was only recently that a valid expression has been found with a remarkable amount of empirical insight.[11] The general expression has also been derived in a deductive and completely independent way by applying the principle of maximum dissipation in Reference 12.

Even if in the recent years more complex situations than the one treated in the initial studies of Cahn[2] and Lücke and Stüwe[10] could be tackled, as two different types of solute,[13,14] curved interfaces,[15] solute drag occurring in a regular solid solution,[16] during massive phase transformations[12,17–20] or in nonsteady-state condition,[21,22] they rely on the same framework: the composition profile of the solute atoms around the migrating phase boundary is calculated by solving Fick’s law for diffusion and then the solute drag stems from the solute profile by applying the appropriate equation. In the current article, however, we will limit our discussion to the initial case treated by Cahn[2] and Lücke and Stüwe[10]: a moving grain boundary in a binary solid solution which is supposed to be ideal.

2 Background Theories

2.1 The Classical Treatment

Lücke and Detert[1] were the first to present a quantitative theory of grain boundary mobility which took into account the interaction between the grain boundary and solute atoms. Their approach was further developed by Cahn[2] and Lücke and Stüwe,[10,23] to be referred to as the CLS theory. This theory rests on the assumption that a solute atom near a grain boundary interacts with the boundary, the interaction force being

$$ F(x) = - \frac{dU(x)}{dx} $$

(1)

where x is the distance between the solute atom and the boundary, and U(x) is the free energy of interaction. For a boundary at rest, this interaction will result in a symmetrically shaped solute concentration profile across the boundary region. For dilute alloys (solute concentrations c ≪ 1), it follows from Boltzmann-statistics that the boundary concentration c _b becomes

$$ c_{\text{b}} = c\;\exp \left( { - \frac{U\left( x \right)}{kT}} \right) $$

(2)

where $U(x = 0) = - U_{0}$, T is the temperature, and k is Boltzmann’s constant. If a pressure P causes the boundary to migrate at a rate $\text v_{\text{b}}$, then a consequence of this migration will be a redistribution of the solute concentration in the vicinity of the boundary. This solute atom redistribution will result in a net dynamic drag force P _s opposing the migration. And, it follows from the treatment of Lücke and Stüwe[10] that the boundary migration rate becomes

$$ {\text v_{\text{b}}} = m(P - P_{\text{s}} ) $$

(3)

where m is the intrinsic boundary mobility (i.e., that corresponding to c = 0). The treatments by Cahn[2] and Lücke and Stüwe[10,23] are derived on the basis of the assumption that the effects on boundary mobility due to the cusp formation resulting from the solute-boundary interaction can be neglected; the validity of this assumption is discussed later in this section. Another necessary assumption to derive Eq. [3] is that a migrating boundary in a solute-containing metal can be assigned a mobility equal to that of the boundary in the pure metal. Or, it means that the diffusivity of solute atoms across the boundary is approximately equal to that of the solvent ones. The consequence of relaxing this latter assumption has been addressed by Westengen and Ryum.[24] They demonstrated that by assuming different boundary diffusion coefficients for solute and solvent atoms, a drag force of similar nature to that introduced above will result, even if U(x) = 0 for all values of x.

An important question to be addressed becomes as follows: Is it acceptable, as proposed by Lücke and Stüwe,[10] to reduce the effect of solute atoms on grain boundary migration into a drag only, ignoring the effects due to in situ interactions between solute atoms and the boundary? We will try to answer this question later by considering the phenomenon of solute-induced cusping of a migrating boundary. First, however, the main predictions and the general applicability of the CLS-theory will briefly be considered.

2.2 Theory vs Experimental Results

In qualitative terms, the CLS theory predicts that a grain boundary, subjected to a driving pressure (in a solute-containing alloy), will migrate at a rate which will depend on solute concentration, driving pressure and temperature as schematically outlined in Figures 1(a) through (c), respectively. A characteristic feature displayed in these diagrams is the discontinuous speed changes commonly referred to as break-away or loading phenomena. For instance, by increasing the solute content, Figure 1(a), the drop is caused by a discontinuous increase in the boundary solute content (loading), while by increasing the pressure, Figure 1(b), the rapid increase in speed is caused by a discontinuous decrease in solute content (break-away). However, these loading/break-away phenomena are not as precisely defined as that shown by the fully drawn curves in Figure 1. Rather, the CLS theory predicts an S-shaped behavior as indicated by the broken lines. The physical interpretation of this effect is that within these S-regions, where the theory has no unique solution, a general state of boundary solute instability exists. Only in the extreme cases, the CLS theory is capable of quantitative predictions: For low solute contents, high driving pressures, and high-temperature situations, there is no solute effect or the boundary is free and has the property of that in the pure metal, while in the other extreme of a loaded boundary this theory predicts a migration rate as given by

Fig. 1

Some possible types of transitions (schematically) from free to loaded boundary; for details, see the text

$$ {\text v_{\text{b}}} = \Upgamma b\nu_{\text{D}} c^{ - 1} \;\left( {\frac{{\mathop {Pb}\nolimits^{3} }}{kT}} \right)\;\exp \;\left( { - \frac{{U_{\text{s}} + U_{0} }}{kT}} \right) $$

(4)

where the concentration c is given as atomic fraction, U _s is the activation energy for solute diffusion, b is a typical inter-atomic spacing, ν _D is the Debye frequency and Γ is a constant.

This relationship was derived for the first time by Lücke and Detert.[1] While the CLS theory seems to provide a reasonable description, as shown above (Figure 1), of the effects of solute atoms on grain boundary mobility, there are important aspects which are not satisfactorily covered. The following three comments seem relevant in this context. First, in the low solute regime where a break-away situation predicts no solute-boundary interaction, the classic experiments of Aust and Rutter[25–28] do indicate the existence of such an effect as illustrated in Figure 2. Second, within the relatively broad instability region of the CLS theory where no predictions can be made, experimental investigations reveal no similar scatter in migration rate observations as also evident from Figure 2 or, in other words, reproducible results can be obtained even in regions of rapidly changing migration rates. Third, for solute atoms which have activation energies of diffusion (within the boundary) different from that of the solvent atoms, a solute effect on boundary mobility is to be expected even if the interaction energy U ₀ is negligible or zero,[24] in contrast to the prediction of the CLS theory.

Fig. 2

Comparison of the grain boundary migration rates at 573.15 K (300 °C) as a function of solute concentration for tin and gold as solutes in high-purity lead, from Refs. [25] and [26]. The solid lines outline the trend displayed by the experimental points

2.3 Boundary Pinning

Machlin[29] considered that a moving grain boundary should become cusped at a point where it meets a solute atom, Figure 3(a), and he derived an expression for the pinning force by applying a Zener-drag type analysis. He supposed that the rate-controlling step in the migration process was diffusion of impurity atoms along the cusped parts of the boundary. Lücke and Stüwe[23] also considered this effect of cusping, but they concluded that the Zener-drag treatment was not very satisfactory from a theoretic point of view. It requires that the thickness of the boundary is small in comparison with the diameter of the solute atom, Figure 3(b), where, as argued by Lücke and Stüwe, for an individual solute atom, just the opposite is true, Figure 3(c). Lücke and Stüwe’s conclusion is probably correct in terms of the applicability of a Zener-drag type analysis to obtain the pinning action of individual solute atoms on a migration boundary. On the other hand, even if a Zener type analysis has to be rejected, it does not necessarily follow from such a conclusion that the solute cusping effect is insignificant or can be ignored. Roy and Bauer[30] were thinking along similar lines when suggesting a 2D model where diffusion, both parallel and perpendicular to the boundary, was considered in terms of causing nonuniform solute distribution and associated shape changes and clustering. Their model indicated that clustering of impurities in the boundary and subsequent break away of the boundary from the clusters are natural consequences of grain boundary migration.

Fig. 3

(a) Formation of a cusp on a migrating grain boundary due to interactions with solute atoms (redrawn from Machlin[29]). (b) and (c) for boundary thickness small and large, respectively, compared with the atomic diameter (redrawn from Lücke and Stüwe[10])

The objective of the following treatment is to reconsider the Machlin idea that solute atom cusping will retard the migration of grain boundaries. The approach taken, however, differs from that of both Machlin[29] and Roy and Bauer.[30] The main effect of cusping in the current treatment is assumed to be “stress-concentration” on the cusp-forming atoms and a corresponding change in the activation volume associated with the thermal activation of these atoms.

3 The Effect of Solute Pinning on Boundary Migration

3.1 General Considerations

The migration of a high angle grain boundary in a pure metal has been treated in terms of different approaches, a review of which has been given by Humphreys and Hatherly.[31] All treatments, however, assume that if a pressure, P, acts on a boundary, then it will migrate at a rate

$$ {\text v_{\text{b}}} = mP = \Upgamma_{\text{p}} b\nu_{\text{D}} \frac{{P\mathop b\nolimits^{3} }}{kT}\;\exp \left( { - \frac{{U_{\text{SD}}^{\text{b}} }}{kT}} \right). $$

(5)

In this equation, $\Upgamma_{\text{p}}$ is a constant and $U_{\text{SD}}^{\text{b}}$ is an activation energy associated with boundary migration. This activation energy is typically found to have a value half that of self-diffusion.

If solute atoms are added to the metal, then the situation will change. These atoms will interact with both a stationary and a migrating boundary, as defined by Eq. [1]. The current treatment assumes a boundary region potential for the boundary solute interaction as schematically outlined in Figure 4(a), i.e., $U\left( x \right) = - U_{0}$ for $\left( {x\left( t \right) - \frac{\lambda }{2}} \right) \le x(t) \le \left( {x(t) + \frac{\lambda }{2}} \right)$ and U(x) = 0 for all other values of x, where x(t) is the instantaneous position of the boundary and λ its thickness. Outside the boundary region, thermal activation of the solute atoms is associated with an energy U _s (i.e., that of solute bulk diffusion) except for jumping into the boundary where the activation barrier may be somewhat less ($U_{\text{s}}^{*}$ in Figure 4(a)); however, such an energy profile refinement will not be included in the current treatment at this stage. It follows that in the static case, Figure 4(a), the solute atom concentration in the boundary will be given by Eq. [2].

Fig. 4

Schematic representation of the interactions between (a) a stationary and (b) a migrating grain boundary and solute atoms; for details, see the text

If a pressure acts on the boundary, then the boundary may start to migrate, and this boundary concentration will change. In the current model, the basic idea is that the effect of the solute atoms on the boundary migration rate will be determined by the rate at which such atoms are activated out of the boundary region. The pressure P driving the boundary results in a cusping force F _C on each solute atom, which reduces the activation barrier out of the boundary by F _C b, as illustrated by the “jumping out of the boundary” energy profile in Figure 4(b). To calculate the size of this pinning force F _C in mechanical terms, a breaking-angle analysis is required, and as demonstrated by Lücke and Stüwe,[23] the conclusions which can be drawn from such an analysis are uncertain indeed. In the current treatment, however, F _C is calculated in a different way making such an analysis unnecessary; see later.

The presence of the work-term, F _C b, may influence the boundary migration rate as qualitatively described in the following: Imagine a situation where a pressure P is applied on a statically saturated boundary at time t = 0. On the assumption of a dilute solid solution, the boundary regions far away (in terms of atomic dimensions) from boundary solute atoms will respond by migrating at a rate as determined by Eq. [5]. Such a migration of the boundary is inhibited at the solute atom sites with the consequence that these atoms cusp the boundary. Let us assume, for a moment, that these atoms have infinite interaction energy with the boundary, in which case, the boundary bulges out until the local curvatures generated counterbalance the applied pressure. If, on the other hand, the boundary solute atoms are associated with a local energy situation as illustrated by the “jumping out of the boundary” energy profile in Figure 4(b), then one alternative becomes an unpinning of the cusps by thermal activation of solute atoms out of the boundary (evaporation into the lattice) and another alternative becomes un-cusping by boundary rearrangements of solvent atoms. Which of these mechanisms will be rate controlling is difficult to decide, but that will depend on the effect a solute atom has on the local collective solvent atom rearrangements associated with boundary migration. However, the current treatment of solute–boundary interaction rests on the postulation that the first alternative above, i.e., “cusping-pressure-biased” thermal activation of boundary solute atoms out of the boundary, is the rate-controlling step for the migration of the boundary. The objective of the following becomes to explore the consequence of such a thermal activation mechanism on grain boundary migration in dilute solid solutions. This approach represents a 2D analogy to similar treatments for the corresponding 1D situation, i.e., migration of dislocations where solute pinning may control the migration rate; see Hirth and Lothe.[32]

3.2 The Model

Consider a boundary which migrates because of a constant driving pressure P. Some time after the pressure P has been applied, a steady-state boundary solute concentration c _b will be established, to which corresponds a steady-state boundary migration rate v_b. This steady-state solute concentration will be defined by

$$ \phi^{ - } + \phi^{ + } = 0 $$

(6)

where $\phi^{ - }$ is the rate per unit area at which the solute atoms leave the boundary and $\phi^{ + }$ is the corresponding arrival rate. It should be noticed that only the atoms jumping behind the boundary contribute to the leaving rate $\phi^{ - }$. Indeed, the atoms jumping forward will be immediately recaptured by the migrating boundary. Then, the leaving rate $\phi^{ - }$ is proportional to the backward jump frequency out of the boundary $\nu^{ - }$:

$$ \phi^{ - } = c_{\text{b}} n_{\text{b}} \lambda \nu^{ - } $$

(7)

where the boundary concentration c _b is given in terms of atomic fraction, and n _b is the number of atoms per unit volume inside the boundary. Within the context of the schematic energy profiles in Figure 4(b), the backward jump frequency $\nu^{ - }$ can be expressed, in terms of thermal activations, as follows:

$$ \nu^{ - } = \Upgamma^{ - } \nu_{\text{D}} \;\exp \;\left( { - \frac{{U_{\text{s}} + U_{0} - F_{\text{C}} b}}{kT}} \right) $$

(8)

with $\Upgamma^{ - }$ a constant. The work $F_{\text{C}} b$ done by the force F _C decreases the energy barrier $U_{\text{s}} + U_{0}$, even if the atom does not jump in the direction of the force F _C because the displacement of the grain boundary releases the stress accumulated at the pinning atom. Finally, the leaving rate is given by

$$ \phi^{ - } = \Upgamma^{ - } c_{\text{b}} n_{\text{b}} \lambda \nu_{\text{D}} \;\exp \left( { - \frac{{U_{\text{s}} + U_{0} - F_{\text{C}} b}}{kT}} \right). $$

(9)

The arrival rate $\phi^{ + }$ can be written as follows:

$$ \phi^{ + } = - \left[ {\Upgamma^{ + } cnb\nu_{\text{D}} \exp \left( { - \frac{{U_{\text{s}} }}{kT}} \right) + cn\text v_{\text{b}} } \right] $$

(10)

where c is the bulk solute concentration (in atomic fraction), n the number of atoms per unit volume in the bulk of the material, and $\Upgamma^{ + }$ is a constant. The first term in Eq. [10] represents thermal activation of bulk atoms into the boundary, and the second “sweeping term” reflects the constant flux of solute atoms arriving in the boundary because of its migrating at a rate $\text v_{\text{b}}$ into a lattice containing a solute concentration c.

Balancing the expressions for $\phi^{ + }$ and $\phi^{ - }$ (Eq. [6]) makes it possible to calculate $c_{\text{b}} (c,T,F_{\text{C}} )$, provided an expression for the boundary migration rate ${\text v_{\text{b}}} (c,T,F_{\text{C}} )$ is obtained. A characteristic of a steady-state conditions (Eq. [6]) is that when a solute atom ‘evaporates’ from the grain boundary, another necessarily will arrive and pin it again. Consequently, as a statistical average, the distance the boundary will move in between thermal activation and repinning typically becomes an atomic distance of size b. And, it follows that in terms of thermal activations, the boundary speed can be written:

$$ {\text v_{\text{b}}} = b\left[ {\nu^{ - } - \Upgamma^{ - } \nu_{\text{D}} \exp \left( { - \frac{{U_{\text{s}} + U_{0} + F_{\text{C}} b}}{kT}} \right)} \right]. $$

(11)

The second term inside the parenthesis is required to take into account the statistical probability that solute atoms may jump against the cusping induced bias, F _C b, as illustrated schematically in Figure 5. So, a solute atom has to overcome an energy barrier equal to the energy barrier when there is no cusping effect $U_{\text{s}} + U_{0}$ plus the necessary energy F _C b to compensate for the work done by the force F _C during the backward jump, as illustrated by the “jumping with the boundary” energy profile in Figure 4(b). In this case, the solute atom will remain in the boundary and consequently the jump has no effect on the $\nu^{ - }$-term. Similar backward jumps are also included in Hirth and Lothe’s treatment of solute drag of moving dislocations.[32]

Fig. 5

Schematic representation of an atom jumping against the cusping bias F _C b

Combination of Eqs. [8] and [11] gives the following expressions for the boundary velocity $\text v_{\text{b}}$:

$$ {\text v_{\text{b}}} = 2\Upgamma^{ - } b\nu_{\text{D}} \exp \left( { - \frac{{U_{\text{s}} + U_{0} }}{kT}} \right)\sinh \left( {\frac{{F_{\text{C}} b}}{kT}} \right) $$

(12)

and by combining this relationship with Eq. [10], an expression for $\phi^{ + }$ is obtained and it then follows from Eq. [6] that the boundary solute concentration c _b can be written:

$$ c_{\text{b}} = c\frac{nb}{{n_{\text{b}} \lambda }}\exp \left( {\frac{{U_{0} - F_{\text{C}} b}}{kT}} \right)\left[ {1 + 2\left( {\exp \left( { - \frac{{U_{0} }}{kT}} \right)} \right)\sinh \left( {\frac{{F_{\text{C}} b}}{kT}} \right)} \right]. $$

(13)

In deriving this expression, the constants $\Upgamma^{ - }$ and $\Upgamma^{ + }$ have been assumed to be of approximately the same size and have consequently been represented by a common symbol, $\Upgamma_{s}$, in the following. It is easily seen that Eq. [13] is consistent with the required boundary conditions that for low driving pressures/high solute concentrations, i.e., $F_{\text{C}} b/kT \ll 1$, the boundary concentration becomes the equilibrium level $c_{\text{b}} = c\exp \left( {\frac{{U_{0} }}{kT}} \right)$ assuming the ratio $\frac{nb}{{n_{\text{b}} \lambda }}$ nearly equal to 1, and for high pressures/low solute concentrations, i.e., $F_{\text{C}} b/kT \gg 1$, $c_{\text{b}} = c$, conditions referred to as loaded and break-away situations, respectively, in the solute drag theory.

In order to achieve complete solutions of Eqs. [12] and [13], an expression for the pinning force F _C is needed, or more exactly for the ratio $\frac{{F_{\text{C}} b}}{kT}$. Fortunately, it is possible to calculate this force because an alternative expression to Eq. [12] for the migration rate can be formulated. By having two independent relationships for the same migration rate the pinning force problem can be solved.

A second expression for the boundary speed is obtained by considering a boundary subjected to a driving pressure P and which also experiences a restraining pressure $P_{\text{C}} = F_{\text{C}} /A = F_{\text{C}} \lambda c_{\text{b}} n_{\text{b}}$, Figure 4. In between these restraining points the boundary is free of solute atoms with a mobility, m, typical of that of a pure metal, Eq. [5], and it follows that boundary speed now can be written:

$$ {\text v_{\text{b}}} = m\left( {P - \frac{2\gamma }{R} - P_{\text{C}} } \right) $$

(14)

with R the effective radius of the boundary curvature between the restraining points. The pressure stemming from the grain boundary curvature will be neglected in the following treatment, which assumes that the grain boundary remains macroscopically planar during its migration. It should be remarked that this treatment is different from the one of Cahn[2] and Lücke and Stüwe[10] in which the relationship ${\text v_{\text{b}}} = m\left( {P - P_{\text{s}} } \right)$ is applied regardless of whether the grain boundary is free of solute atoms or not.

By equating the two expressions for the boundary migration rate, Eqs. [12] and [14], and by replacing m by its expression, Eq. [5], the pinning force is obtained. Unfortunately it is not possible to give this force in terms of an analytical expression; only an implicit expression can be given:

$$ c = \frac{1}{{nb^{3} }}\frac{{\left( {\frac{{Pb^{3} }}{kT} - 2\frac{{\Upgamma_{\text{s}} }}{{\Upgamma_{\text{p}} }}\exp \left( { - \frac{{U_{\text{s}} + U_{0} - U_{\text{SD}}^{\text{b}} }}{kT}} \right)\sinh \left( {\frac{{F_{\text{C}} b}}{kT}} \right)} \right)\exp \left( {\frac{{F_{\text{C}} b}}{kT}} \right)}}{{\frac{{F_{\text{C}} b}}{kT}\left( {\exp \left( {\frac{{U_{0} }}{kT}} \right) + 2\sinh \left( {\frac{{F_{\text{C}} b}}{kT}} \right)} \right)}}. $$

(15)

However, by numerical treatments, it becomes possible to calculate $F_{\text{C}} (c,P,T),\;c_{\text{b}} (c,P,T)$ and ${\text v_{\text{b}}} (c,P,T)$ for any given combination of materials’ specific parameters $n,\;b,\;c,\;\Upgamma_{p} ,\;\Upgamma_{s} ,\;U_{\text{SD}}^{\text{b}} ,\;U_{0} ,$ and U _s if it is assumed the ratio $\frac{nb}{{n_{\text{b}} \lambda }}$ close to 1. In computing the boundary solute concentration c _b and the migration rate v_b, the size of the pinning force F _C is monitored to check that this force does not exceed that expected from a mechanical breaking-angle analysis. As argued by Lücke and Stüwe,[23] such an analysis is very uncertain, but an estimate for the maximum possible force F _C is obtained from a Zener-drag type argument, i.e., $F_{\hbox{max} } = \pi \gamma b$, where $\gamma$ is the boundary energy. In the subsequent numerical treatment, the pinning force F _C is always smaller, or much smaller than this maximum value; see also Appendix.

In the special case of a low driving pressure/high solute concentration, i.e., $F_{\text{C}} b/kT \ll 1$, a good approximate solution for the migration rate of a loaded boundary becomes

$$ {\text v_{\text{b}}} = \frac{2}{{nb^{3} }}\Upgamma_{\text{s}} b\nu_{\text{D}} c^{ - 1} \left( {\frac{{Pb^{3} }}{kT}} \right)\exp \left( { - \frac{{U_{\text{s}} + 2U_{0} }}{kT}} \right) $$

(16)

where $\Upgamma_{\text{s}}$ is a constant. This expression for the boundary migration rate is, except for the numerical factors $\frac{2}{{nb^{3} }}$ and 2 in front of $U_{0}$, similar to Eq. [4], i.e., the one which was originally derived by Lücke and Detert.[1] The origin of the factor 2 in front of $U_{0}$ stems from the fact that in the current model, the interaction energy $U_{0}$ appears twice: (i) in the boundary solute concentration in the fully loaded case (Eq. [2]) and (ii) in the activation frequency of atoms jumping out of the boundary (Eq. [8]).

3.3 Model Predictions

In contrast to the solute drag theory, the current analytical treatment is simple indeed. The predictions for the boundary solid solution contents c _b and the migration rates v_b for grain boundaries, acted upon by a pressure P in a generic solid solution alloy of various solute contents c, are illustrated qualitatively in Figures 6(a) and (b), respectively. The metal studied is assumed to have a close-packed spacing b equal to 3 Å (typical value in metals). Then, the atomic density n is estimated as $\frac{1}{{b^{3} }}$ and the ratio $\frac{nb}{{n_{\text{b}} \lambda }}$ as close to 1. The values of the input parameters used are given in Figure 6(a), except for the activation energy for boundary migration $U_{\text{SD}}^{\text{b}}$, which for the sake of simplicity is taken as the half of the activation energy for solute diffusion U _S, and for the constants $\Upgamma_{\text{p}} \;{\text{and}}\;\Upgamma_{\text{s}}$ for which numerical values 18 and 82, respectively, have been selected (the procedure adopted for the quantification of these parameters in an experimental case is explained later). Figure 6(a) shows the grain boundary concentration c _b as a function of the matrix concentration c for various values of the interaction energy U ₀. The corresponding variation in the boundary migration rate $\text v_{\text{b}}$ is illustrated in Figure 6(b). Note that for values of U ₀ larger than some critical level, the c _b vs c curves become S shaped, and consequently the v_b vs c curve takes the form of a similarly shaped configuration, broken lines in the figures. A similar behavior is predicted also by the CLS theory and is interpreted as an instability phenomenon associated with either break-away or loading; see Section I. The physics, however, behind this peculiar behavior is more transparent in the current treatment where the break-away/loading phenomenon is reduced to a well-defined discontinuity (fully drawn lines), the reason for which can be explained in free energy terms as follows: by increasing the c-values from the lower side in Figure 6(a), one eventually reaches the point marked A where the system spontaneously can lower its free energy by a discontinuous increase in boundary concentration, point B, i.e., a concentration close to the equilibrium one defined by Eq. [2].

Fig. 6

Model predictions for: (a) solute atom concentration in the boundary c _b vs that in the bulk c in a migrating boundary under constant driving pressure, for the U ₀-values given (b) the corresponding variation in the migration rate v_b

In terms of comparing the predictions which follow from the current solute pinning approach to that of the CLS theory, two important differences emerge: (i) The current model predicts a c-dependence in the boundary migration rate v_b also for c-values below the break-away level in accordance with experimental observations, e.g., Figure 2, in contrast to the CLS theory, and (ii) a strong solute-pinning effect may, according to the current approach, prevail even in cases where the interaction energy U ₀ = 0. It appears as intuitively obvious that in cases where the activation energy for solute diffusion in the boundary is significantly different from that of boundary self-diffusion, the solute atoms will disturb the solvent redistribution pattern and restrict boundary migration even if the “long range” elastic interaction is negligible. A similar $U_{0}$-effect is found in the model by Westengen and Ryum.[24] The effect of varying the main variables P and T on the boundary migration rate is illustrated in Figures 7(a) and (b), respectively. While the CLS theory is capable of making quantitative predictions only in the low pressure/high concentration/low temperature (fully loaded) regime, the current model gives equally good predictions for any combination of driving pressure, solute concentration and temperature, as will be demonstrated in the application section below.

Fig. 7

Model predictions for the variations in the boundary migration rate v_b vs (a) the driving pressure P and (b) the inverse temperature 1/T

4 Applications

The current model will now be tested on the bases of some classical experimental investigations, of which the most notable ones are those due to Aust and Rutter[25–28] and Gordon and Vandermeer.[33–36] The latter work, on the effect of small additions of Cu on grain boundary migration in aluminum, is the most carefully conducted experiment of its kind, and will therefore be examined first.

To allow some flexibility in the model, a tuning parameter has been introduced. The area acted upon by the restraining pressure P _C was taken only as a fraction $\kappa$ of the geometrical area A initially assigned:

$$ a = \kappa A = \frac{\kappa }{{c_{\text{b}} n_{\text{b}} \lambda }}. $$

(17)

The physical meaning is that the activation volume related to the work of the force F _C is actually smaller than the one predicted geometrically. This parameter modifies the restraining pressure in the following way: $P_{\text{C}} = \frac{{F_{\text{C}} }}{a} = \frac{1}{\kappa }F_{\text{C}} c_{\text{b}} n_{\text{b}} \lambda$. The consequence of this takes the form of introducing $\kappa$ as a multiplication factor in the right-hand side of Eq. [15], whereas the expressions for the boundary velocity v_b (Eq. [12]) and the boundary solute concentration c _b (Eq. [13]) in function of F _C are unaffected. It also slightly modifies the expression of the migration rate v_b of a loaded boundary (Eq. [16]) which now takes the form:

$$ {\text v_{\text{b}}} = 2\frac{\kappa }{{nb^{3} }}\Upgamma_{\text{s}} b\nu_{\text{D}} c^{ - 1} \frac{{Pb^{3} }}{kT}\exp \left( { - \frac{{U_{\text{s}} + 2U_{0} }}{kT}} \right). $$

(18)

4.1 The Experiments of Gordon and Vandermeer

These researchers investigated the effect of adding copper (range 2 to 250 ppm to zone-refined aluminum) on grain boundary migration.[33–36] The experimental procedure adopted was to cold roll the various compositions to a reduction of 40 pct and subsequently follow the initial stage of recrystallization at various temperatures, carefully monitoring initial growth rate of the largest grain. Great care was exercised to assure that this initial stage of growth in all investigated conditions occurred under constant driving pressure.[36] Their results, in terms of migration rates vs solute concentration, are shown in Figure 8. From these results it follows that in the extremes the boundary migration rates are well represented by Eqs. [5] and [18]. Equation [5] applies to zone-refined aluminum with an activation energy $U_{\text{SD}}^{\text{b}} = 65\;{\text{kJ/mol}}$. The results in the ultimate (high concentration) range satisfy Eq. [16] with U _s + 2U ₀ = 131 kJ/mol. Further, it follows from the behavior in these extremes that the two pre-exponential constants can be identified as: $\Upgamma_{\text{P}} = 2.5 \times 10^{9} /P$ and $\Upgamma_{\text{s}} = 1.2 \times 10^{10} \kappa /P$. A test of the current model now is to find out if it is capable of accounting for the effect of solute atoms on boundary migration also in between these extremes.

Fig. 8

Experimental[33] and theoretically predicted variation in migration rate vs composition for the temperatures given (filled symbols, actual data points; open symbols, extrapolated values). As velocities for a pure metal could not be reported in a log–log plot, they have been plotted at an arbitrary abscise of $2 \times 10^{ - 7}$

In order to apply the current model to the results in Figure 8, the driving pressure involved needs to be quantified. Gordon and Vandermeer estimated the driving pressure on the basis of a relationship of the form P = 4Z/Na ³₀ , where Z is the stored free energy per mole, N is Avogadros number, and a ₀ is the lattice parameter. On the basis of calorimetric measurements, Z was estimated to 16.7 J/mol which gives P = 1.7 MPa, which again corresponds to a dislocation density estimate (P = 0.5 Gb ² ρ, where G is the shear modulus and ρ is the dislocation density) at ρ = 1.6 × 10¹⁵ m⁻². This is indeed a high density to be the result of a 40 pct rolling reduction of zone-refined-grades of aluminum. In terms of a shear flow stress estimate ($\tau = \tau_{0} + 0.5Gb\sqrt \rho$), such a dislocation density corresponds to a stress level of about 150 MPa, which is about an order of magnitude larger than expected. In commercial 5N grades of aluminum, the shear flow stress (in multiple slip, at 40 pct elongation) is found to be about 15 MPa.[37] The typical value for $\tau_{0}$ is about 5 MPa, which again gives the following estimates for the dislocation density and the stored energy: ρ = 7 × 10¹² m⁻² and P = 7500 Pa, respectively. Gordon and Vandermeer, however, investigated aluminum with Cu-contents in the atomic fraction range from $2 \times 10^{ - 6}$ to $3 \times 10^{ - 4}$. This variation in solute content will result in a corresponding variation in flow stress and driving pressure at a constant rolling reduction (Table I). This effect is illustrated in Figure 9 where the driving pressure for three low solute variants (5N, 4N, and commercial purity aluminum) indicates an approximate power relationship in this solute regime. The model predictions illustrated in Figure 8 are based on this driving pressure relationship. Note that this fit also requires $\kappa = 0,4$ and $U_{0} = 3\,{\text{kJ/mol}}$, from which it follows that the activation energy U _s becomes 125 kJ/mol, which is also a reasonable value, close to the activation energy for bulk diffusion of Cu in Al; 135 kJ/mol.[38] From the diagram in Figure 8, $\text v_{\text{b}}$ vs 1/T-plots at constant concentrations can be generated, from which the theoretically predicted variation in the (partly apparent) activation energy in Figure 10 is obtained. In contrast to what is observed, no maximum in the apparent activation energy is predicted by the model. As this region does not correspond to a simple physical mechanism, it is quite difficult to give an explanation to this discrepancy. The conclusion becomes that the current theory is able to adequately account for the Gordon and Vandermeer observations by means of a fitting parameter.

Table I Values of the Flow Stress and the Driving Pressure for Different Purity Degrees of Aluminum at 40 Pct Elongation Taken from Ref. [37]

Fig. 9

Variation of the estimated driving force for recrystallisation in function of the purity degree of aluminum

Fig. 10

Activation energy (partially apparent) for boundary migration as a function of atomic fraction of copper, experimental data from Gordon and Vandermeer[33]

4.2 The Experiments of Aust and Rutter

These experiments pertain to the effects of small additions of Ag, Au, and Sn on grain boundary migration in melt-grown single crystals of lead,[25–28] the driving pressure for boundary migration in this case being the grown-in striation (subgrain) structure. The claimed advantage of this approach is the thermal stability of the substructure which assured a constant driving pressure throughout the experiment. How accurate this claim is will be further discussed below. The authors did mention, however, the problems of reproducing the striation structure from wire to wire and of maintaining a constant structure along the wire. This problem probably explains the considerable scatter (a factor of 5) in the measured migration rates, especially for low solute contents; see Figure 2.

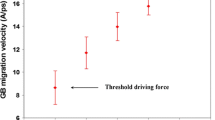
Let us first consider the results on the effect of Sn in Pb, given in Figure 11. The diagram gives the boundary migration rate as a function of Sn-concentration at 573.15 K (300 °C) at a constant driving pressure P. By applying the modeling approach described above using $\kappa = 1$, $U_{\text{SD}}^{\text{b}} = 54\;{\text{kJ/mol}}$, $U_{0} = 5\;{\text{kJ/mol}}$ and $U_{\text{s}} + 2\,U_{0} = 100\;{\text{kJ/mol}}$ the pre-exponential factors become $\Upgamma_{\text{P}} = 4.4\,10^{5} /P$ and $\Upgamma_{s} = {{218} \mathord{\left/ {\vphantom {{218} P}} \right. \kern-0pt} P}$. As can be seen from Figure 11, the best fit is obtained with a driving pressure P = 15,000 Pa. This value is more than two orders of magnitude larger than the driving pressure estimate made by Aust and Rutter (400 Pa). Keeping this low driving pressure and adjusting the fitting parameter $\kappa$ lead to an extremely high value ($\kappa = 32$), which seems unreasonable to adopt. However, before considering the possible reasons for this discrepancy, some other observations on the effects of Sn on grain boundary migration in zone-refined lead need to be brought to the attention. Some interesting results on grain growth due to Bolling and Winegard[39,40] are shown in Figure 12. These results are often quoted as demonstrating that the effect of these solute elements on the boundary migration rate increases in the order Sn-Ag-Au. The effect of Sn is not included in Figure 12, the reason being that these researchers apparently could not find any effect of Sn on grain growth at all. It is difficult to precisely quantify the driving pressure in grain growth experiments, but at a grain size of about 1 mm, this pressure ($P \simeq 2\gamma_{\text{GB}} /R$ where $\gamma_{\text{GB}}$ is the grain boundary energy and R the average grain radius) is expected to be of approximately the same order as in the experiments of Aust and Rutter. It is, however, very difficult to understand why an addition of around 100 ppm of Sn to Pb has only a marginal effect on grain growth, but causing a 4 orders of magnitude change in the migration rate in the experiments of Aust and Rutter, Figure 11. A possible explanation will be offered below, but first the effects of the other solute additions need to be considered.

Fig. 11

Model predictions of the boundary migration rate as a function of solute atom concentration for the given driving pressures, as compared with the results on tin in lead by Aust and Rutter[25]

Fig. 12

Grain diameter vs annealing time at 573.15 K (300 °C) for zone-refined lead (top), zone-refined lead with 100 ppm silver added (middle), and zone-refined lead with 200 ppm gold added (bottom), from Bolling and Winegard[39,40]

A total representation of the Aust and Rutter data is given in Figure 2. Although the scatter in the Sn and Au data is considerable, the trend seems clear, indicating a several orders of magnitude drop in the boundary migration rate for a solute concentration larger than a few ppm. Again, this is in total conflict with the grain growth observations by Bolling and Winegard,[39,40] showing that the average growth rates at a grain size of 1 mm are $7 \times 10^{ - 6}$ m/s, $4 \times 10^{ - 6}$ m/s, and $3 \times 10^{ - 6}$ m/s taken in the order pure Pb, Pb-Ag and Pb-Au (Figure 12). While the driving pressure in grain growth experiments is difficult to assess, one cannot dispute the fact that these growth rates all refer to approximately the same driving pressure. An interesting speculation becomes to which extent, if at all, the observations of Aust and Rutter really reflect a constant driving pressure. An important argument in favor of such a constant pressure has traditionally been that the striation structure is stable during the migration experiments. One has to bear in mind, however, that we are here talking about experimenting with single crystal wires a few mm in radius and containing, according to Aust and Rutter, an average dislocation density of about 7 × 10⁷ m⁻², i.e., handling thin lead wires having a shear flow stress of about 0.5 MPa. Doing that without introducing dislocations in an amount many times larger than those grown in will be a problem in itself. Bolling and Winegard reported that as the solute content increased, so did the flow stress of the material (of course). An interesting speculation then becomes, if by increasing the solute content, the lead wires become stronger and easier to handle without introducing additional dislocations, and accordingly the drop in migration speed in Figure 2 or 11 is partly due to a decrease in driving pressure. The studies by Aust and Rutter provide no answer to such a speculation. It is, however, the opinion of the current authors that the observations of Bolling and Winegard cannot be overlooked in this context. They have convincingly demonstrated that the effects of additions of about 100 ppm of Sn, Ag, or Au on the grain boundary migration rates in zone-refined lead at a constant driving pressure caused migration speed reductions compared with the pure metal of at most a factor of 3. From these observations, it seems appropriate to question the more spectacular results by Aust and Rutter in Figures 2 and 11. The current conclusion then becomes that their results in general are not suited as a basis for applications in quantitative modeling.

5 Concluding Remarks

The solute-pinning approach developed in the current article rests on the assumption that solute atoms within a migrating boundary perturb the collective rearrangements of solvent atoms associated with boundary migration, the consequence of which is cusping of the boundary and a pinning force on the solute atoms. This pinning force will promote thermal activation of solute atoms out of the boundary, a reaction which is believed to be the rate-controlling step for grain boundary migration in solute-containing metals. It has been demonstrated that this mechanism is capable of explaining the known effects due to solute atoms on grain boundary migration in relation to recrystallization and grain growth phenomena. The experimental results on the effect of copper on boundary migration in aluminum due to Gordon and Vandermeer[33–36] have been described successfully by this new model.

Appendix

The information contained in Eqs. [6] through [15] can be condensed into the following three analytical expressions:

$$ \begin{aligned} c & = \frac{\kappa }{{nb^{3} }}\frac{{\left( {\frac{{Pb^{3} }}{kT} - 2\frac{{\Upgamma_{\text{s}} }}{{\Upgamma_{\text{p}} }}\exp \left( { - \frac{{U_{\text{s}} + U_{0} - U_{\text{SD}}^{\text{b}} }}{kT}} \right)\sinh \left( x \right)} \right)\exp \left( x \right)}}{{x\left( {\exp \left( {\frac{{U_{0} }}{kT}} \right) + 2\sinh \left( x \right)} \right)}} \\ c_{\text{b}} & = c\frac{nb}{{n_{\text{b}} \lambda }}\exp \left( {\frac{{U_{0} }}{kT}} \right)\left( {1 + 2\exp \left( { - \frac{{U_{0} }}{kT}} \right)\sinh \left( x \right)} \right)\exp \left( { - x} \right) \\ \text v_{\text{b}} & = 2\Upgamma_{\text{s}} b\nu_{\text{D}} \exp \left( { - \frac{{U_{\text{s}} + U_{0} }}{kT}} \right)\sinh \left( x \right) \\ \end{aligned} $$

where $x = \frac{{F_{\text{C}} b}}{kT}$ and $\kappa$ is the tuning parameter introduced in the application section. The computational procedure now becomes to find the value of x which satisfies the first equation, and then the solute concentration in the boundary c _b and the interface velocity v_b could be deduced from the value of x. It should be noted that the possible values of x are in the interval $\left[ {0,x_{\hbox{max} } } \right]$ where $x_{\hbox{max} }$ is obtained from the necessary requirement that the nominator in the first equation has to be larger than 0. Making it equal to zero gives

$$ x_{\hbox{max} } = \sinh^{ - 1} \left( {\frac{1}{2}\;\frac{{\Upgamma_{\text{p}} }}{{\Upgamma_{\text{s}} }}\;\frac{{Pb^{3} }}{kT}\exp \left( {\frac{{U_{\text{s}} + U_{0} - U_{\text{SD}}^{\text{b}} }}{kT}} \right)} \right). $$

Expression of the interface velocity where $\frac{{F_{\text{C}} b}}{kT} \ll 1$:

This corresponds to the case of a low driving pressure or a high solute concentration. If the expression of c is expanded to the lowest order, then we obtain

$$ c = \frac{\kappa }{{nb^{3} }}\frac{{\frac{{Pb^{3} }}{kT}}}{{x\exp \left( {\frac{{U_{0} }}{kT}} \right)}}. $$

From this expression we simply get the value of x:

$$ x = \frac{\kappa }{{nb^{3} }}\frac{{\frac{{Pb^{3} }}{kT}}}{{c\exp \left( {\frac{{U_{0} }}{kT}} \right)}}. $$

By substituting the expression of x into the expression of the boundary velocity and using the approximation $\sinh \left( x \right) \approx x$ for small value of x, we easily obtain

$$ {\text v_{\text{b}}} = 2\frac{\kappa }{{nb^{3} }}\Upgamma_{\text{s}} b\nu_{\text{D}} c^{ - 1} \frac{{Pb^{3} }}{kT}\exp \left( { - \frac{{U_{\text{s}} + 2U_{0} }}{kT}} \right). $$

It can also be easily demonstrated that $c_{\text{b}} \approx c\,\exp \left( {\frac{{U_{0} }}{kT}} \right)\;\frac{nb}{{n_{\text{b}} \lambda }}$.

It should be noted that in this case, the pinning force could be expressed in an analytical way:

$$ F_{\text{C}} = \frac{{n_{\text{b}} \lambda }}{nb}Pa. $$

Everything behaves as if the grain boundary is planar: It is pinned in so many places that the curvature between two pinning atoms is small.

Expression of the interface velocity where $\frac{{F_{\text{C}} b}}{kT} \gg 1.$

This corresponds to the case of high driving pressure or low solute concentration. In this case, $x$ is close to $x_{\hbox{max} }$:

$$ x \sim x_{\hbox{max} } = \sinh^{ - 1} \left( {\frac{1}{2}\;\frac{{\Upgamma_{\text{p}} }}{{\Upgamma_{\text{s}} }}\;\frac{{Pb^{3} }}{kT}\exp \left( {\frac{{U_{\text{s}} + U_{0} - U_{\text{SD}}^{\text{b}} }}{kT}} \right)} \right). $$

The interface velocity is given by

$$ \begin{aligned} {\text v_{\text{b}}} \left( x \right) \approx{\text{v}_{\text{b}}} \left( {x_{\hbox{max} } } \right) =b\Upgamma_{\text{s}} \nu_{\text{D}} \exp \left( { -\frac{{U_{\text{s}} + U_{0} }}{kT}} \right)2\sinh \left({x_{\hbox{max} } } \right) \\ {\text v_{\text{b}}} \left( x\right) = \frac{{\Upgamma_{\text{p}} \nu_{\text{D}} b^{4}}}{kT}\exp \left( { - \frac{{U_{\text{SD}}^{\text{b}} }}{kT}}\right)\,P. \\ \end{aligned} $$

This expression is the same expression of the velocity of a pure boundary.

For $x \gg 1$, $\sinh \left( x \right) \approx \frac{{e^{x} }}{2} \gg 1$ and the solute concentration in the boundary c _b is given by

$$ \begin{aligned} c_{\text{b}} & \approx c\exp \left( {\frac{{U_{0} }}{kT}} \right)\frac{nb}{{n_{\text{b}} \lambda }}2\frac{1}{2}\exp \left( { - \frac{{U_{0} }}{kT}} \right)\exp \left( x \right)\exp \left( { - x} \right) \\ c_{\text{b}} & \approx c\frac{nb}{{n_{\text{b}} \lambda }}. \\ \end{aligned} $$

For this case, there is almost no segregation at the moving interface.