Prediction of the Mixing Enthalpies of the Al-Cu-Ni-Zr Quaternary Alloys by the Molecular Interaction Volume Model

Abstract

The mixing enthalpies of the Al-Cu-Ni-Zr quaternary alloys are calculated by the molecular interaction volume model (MIVM) using only the coordination numbers and the binary infinite dilute enthalpies. The average relative error and the average standard deviation of prediction are ±19.6 pct and ±7.5 kJ/mol, respectively. The results calculated with the optimal interaction parameters are ±14.0 pct and ±4.4 kJ/mol. The results indicate that the model is reliable and convenient.

The Al-Cu-Ni-Zr quaternary system has gained popular interest in recent years; it possesses an extraordinary glass-forming ability and is widely used for the production of bulk amorphous materials.[1] The mixing enthalpy is very important in order to understand their extremely good glass-forming ability in multicomponent metallic systems as well as for processing improvements. However, the experimental investigation of thermodynamic properties of binary and higher component systems is rather difficult and very expensive. Therefore, a convenient and effective method to predict multicomponent systems from theories or from thermodynamic models, which depend on less experimental data, is required. In the past century, the mixing enthalpy of liquid alloys has been investigated by many researchers.[2–6]

In an earlier article,[7] the molecular interaction volume model (MIVM) was obtained from a physical basis. It is a two-parameter model and is able to predict some component activities in liquid alloys and solid solutions.[8,9] The main purpose of this article is to calculate the mixing enthalpies of the Al-Cu-Ni-Zr quaternary amorphous alloys by the model and to present its convenience and reliability.

For a multicomponent system, its molar excess Gibbs energy, $G^{E}_{m}$, of the MIVM is

$$ \frac{{G^{E}_{m} }} {{R{\rm T}}} = {\sum\limits_{i = 1}^n {x_{i} \ln \frac{{V_{{mi}} }} {{{\sum\nolimits_{j = 1}^n {x_{j} V_{{mj}} B_{{ji}} } }}}} } - \frac{1} {2}{\sum\limits_{i = 1}^n {Z_{i} x_{i} {\left( {\frac{{{\sum\nolimits_{j = 1}^n {x_{j} B_{{ji}} \ln B_{{ji}} } }}} {{{\sum\nolimits_{k = 1}^n {x_{k} B_{{ki}} } }}}} \right)}} } = - \frac{{S^{E}_{m} }} {R} + \frac{{H^{E}_{m} }} {{{\text{R}}T}} $$

(1)

Further, one can obtain its molar mixing enthalpy

$$ \frac{{\Delta H^{M}_{m} }} {{R{\text{T}}}} = - \frac{1} {2}{\sum\limits_{i = 1}^n {Z_{i} x_{i} } }{\left( {\frac{{{\sum\nolimits_{j = 1}^n {x_{j} B_{{ji}} \ln B_{{ji}} } }}} {{{\sum\nolimits_{k = 1}^n {x_{k} B_{{ki}} } }}}} \right)} $$

(2)

where Z _i is the nearest molecule or first coordination numbers; x _i , x _j , and x _k are the molar fractions; and the pair-potential energy interaction parameters B _ij and B _ji are, respectively, defined as

$$ B_{{ij}} = \exp [ - {\left( {\varepsilon _{{ij}} - \varepsilon _{{jj}} } \right)}/{\text{k}}T]\quad B_{{ji}} = \exp [ - {\left( {\varepsilon _{{ji}} - \varepsilon _{{ii}} } \right)}/{\text{k}}T] $$

(3)

where ε _ii , ε _jj , and ε _ij are the i-i, j-j, and i-j pair-potential energies, and ε _ij  = ε _ji , k is the Boltzmann constant, and T is the absolute temperature. The mixing enthalpy of a binary mixture i-j is

$$ \frac{{\Delta H^{M}_{m} }} {{R{\text{T}}}} = - \frac{1} {2}{\left[ {Z_{i} x_{i} {\left( {\frac{{x_{j} B_{{ji}} \ln B_{{ji}} }} {{x_{i} + x_{j} B_{{ji}} }}} \right)} + Z_{j} x_{j} {\left( {\frac{{x_{i} B_{{ij}} \ln B_{{ij}} }} {{x_{i} B_{{ij}} + x_{j} }}} \right)}} \right]} $$

(4)

It is necessary to determine the coordination numbers of liquid metals before applying the new model to liquid alloys. The coordination number Z _i can be estimated from the literature,[10] in which there was a mistake noticed in that a part of the exponential term in Eq. [6], (T – T _mi ), should be corrected as (T _mi  – T).

In order to determine the required binary parameters B _ij and B _ji , the infinite dilute enthalpies of the binary liquid alloys and the related parameters of their components must be determined for the model, as shown in Tables I and II. The parameters B _ij and B _ji can be determined by the procedure as follows.

Table I Related Parameters of the Components[11,12]

Table II Values of $\Delta \overline{H} ^{\infty }_{i}$,$\Delta \overline{H} ^{\infty }_{j}$, B _ij , B _ji , $B^{*}_{{ij}}$, and $B^{*}_{{ji}}$ of the Binary Alloys i-j at the Required Temperatures ($B^{*}_{{ij}}$and $B^{*}_{{ji}}$ Are Obtained by Fitting Experimental Data of Binary Systems)

The partial molar mixing enthalpy of component i is obtained from Eq. [2]:

$$ \frac{{\Delta \overline{H} ^{M}_{i} }} {{R{\text{T}}}} = - \frac{1} {2}{\left[ {\frac{{Z_{i} {\sum\nolimits_{j = 1}^n {x_{j} B_{{ji}} \ln B_{{ji}} } }}} {{{\sum\nolimits_{l = 1}^n {x_{l} {\rlap{-}{B}}_{{li}} } }}} + {\sum\limits_{j = 1}^n {\frac{{Z_{j} x_{j} B_{{ij}} }} {{{\sum\nolimits_{l = 1}^n {x_{l} {B}_{{lj}} } }}}} } \times {\left( {\ln B_{{ij}} - \frac{{{\sum\nolimits_{t = 1}^n {x_{t} B_{{tj}} \ln B_{{tj}} } }}} {{{\sum\nolimits_{l = 1}^n {x_{l} B_{{lj}} } }}}} \right)}} \right]} $$

(5)

When x _i or x _j approaches zero, the infinite dilution enthalpies $\Delta \overline{H} ^{\infty }_{i}$ and $\Delta \overline{H} ^{\infty }_{j}$ are derived from Eq. [5]:

$$ \frac{{\Delta \overline{H} ^{\infty }_{i} }} {{R{\text{T}}}} = - \frac{1} {2}{\left( {Z_{i} \ln B_{{ji}} + Z_{j} B_{{ij}} \ln B_{{ij}} } \right)} $$

(6)

$$ \frac{{\Delta \overline{H} ^{\infty }_{j} }} {{R{\text{T}}}} = - \frac{1} {2}{\left( {Z_{j} \ln B_{{ij}} - Z_{i} B_{{ji}} \ln B_{{ji}} } \right)} $$

(7)

The parameter B _ij is solved by Eq. [7]:

$$ B_{{ij}} = e^{Y} $$

(8)

$$ {{Y= - \left( {\frac{{2\Delta \overline H _j^\infty }}{{R{\text{T}}}} + Z_i B_{ji} \ln B_{ji} } \right)} \mathord{\left/ {\vphantom {{Y = - \left( {\frac{{2\Delta \overline H _j^\infty }}{{R{\text{T}}}} + Z_i B_{ji} \ln B_{ji} } \right)} {Z_j }}} \right. \kern-\nulldelimiterspace} {Z_j }} $$

(9)

Let a function and its derivative be, respectively,

$$ f(B_{{ji}} ) = \frac{{\Delta H^{\infty }_{i} }} {{R{\text{T}}}} + \frac{1} {2}{\left( {Z_{i} \ln B_{{ji}} + Z_{j} e^{Y} Y} \right)} $$

(10)

$$ {f}'(B_{{ji}} ) = \frac{1} {2}{\left[ {\frac{{Z_{i} }} {{B_{{ji}} }} + Z_{j} Y'e^{Y} {\left( {1 + Y} \right)}} \right]} $$

(11)

$$ Y' = - \frac{{Z_{i} }} {{Z_{j} }}(1 + \ln B_{{ji}} ) $$

(12)

According to the Newton formula,

$$ B_{{ji(n + 1)}} = B_{{ji(n)}} - \frac{{f[B_{{ji(n)}} ]}} {{{f}'[B_{{ji(n)}} ]}} $$

(13)

The initial values of B _ij and B _ji can be obtained from the data of $\Delta \overline{H} ^{\infty }_{i}$ and $\Delta \overline{H} ^{\infty }_{j}$ through computing repeatedly (n + 1) times until |B _ji(n) – B _ji(n+1)|≤ 10⁻⁸. On the other hand, when the values of B _ij and B _ji are known, the values of B _ij and B _ji at the required temperatures can be obtained from Eq. [3] in which the pair-potential energy interaction parameters (ε _ij  – ε _jj )/kT and (ε _ji  − ε _ii )/kT may be assumed to be independent of temperature. Substituting the corresponding B _ij and B _ji into Eq. [4], the enthalpies of mixing of liquid alloys have been calculated, in which the average relative error is

$$ S = \pm \frac{{100}} {m}{\sum\limits_{i = 1}^m {{\left| {\frac{{\Delta H_{{pre}} - \Delta H_{{\exp }} }} {{\Delta H_{{{\text{exp}}}} }}} \right|}} } $$

(14)

and the average standard error is

$$ \overline{S} = \pm {\left[ {\frac{1} {m}{\sum\limits_{i = 1}^m {{\left( {\Delta H_{{{\text{pre}}}} - \Delta H_{{\exp }} } \right)}^{2} } }} \right]}^{{1/2}} $$

(15)

where ΔH _exp is the mixing enthalpies of experimental data and ΔH _pre is the calculated results by the MIVM, and m is the number of experimental data.

In addition, if there are no infinite dilution enthalpies of binary systems, the initial values of $B^{*}_{{ij}}$ and $B^{*}_{{ji}}$ can be obtained by fitting experimental data of binary systems. An object function is chosen to calculate the optimal $B^{*}_{{ij}}$ and $B^{*}_{{ji}}$. The object function is

$$ OF = \pm {\left[ {\frac{1} {m}{\sum\limits_{i = 1}^m {{\left( {\Delta H^{{}}_{{\exp }} - \Delta H^{{\text{*}}}_{{{\text{pre}}}} } \right)}^{2} } }} \right]}^{1/2} \le \varepsilon _{a} $$

(16)

where $\Delta H^{*}_{{{\text{pre}}}}$ represents the results calculated with the optimal parameters $B^{*}_{{ij}}$ and $B^{*}_{{ji}}$, and ε _a the maximal value of the object function.

The mixing enthalpies of liquid alloys of six constituent binary systems, i.e., Al-Cu, Al-Ni, Al-Zr, Cu-Ni, Cu-Zr, and Ni-Zr, have been calculated by the MIVM. The experimental data and predicted values are shown in Figures 1(a) through (f). For the Al-Ni system, the only $\Delta H^{*}_{{{\text{pre}}}}$ can be calculated using Eq. [16] due to the lack of the partial molar infinite dilute enthalpies of Al and Ni at 1700 K. Because the infinite dilute enthalpies of Cu and Ni are positive and the mixing enthalpy as a function of concentration seems to be symmetrical, the calculated mixing enthalpies of the Cu-Ni system are coincident with those of Hultgren et al.[15] at 1473 K. For the Al-Cu, Al-Zr, Cu-Zr, and Ni-Zr systems, the predicted values are not in good agreement with the experimental data, and their errors are in the range of 10 to 20 pct. This fact may be attributed to the existence of chemical short-range order, as pointed out by Stoz et al.,[13] and the asymmetry of mixing enthalpy as a function of concentration. The errors are also derived from the infinite dilution enthalpy. In Figure 1, a large deviation of ΔH _pre can be observed in a range of x = 0.4 to 0.6, where there is a strong interaction between unlike atoms. From Reference 18, the coordination number in amorphous alloys was so large (e.g., Z = 17) that some clusters with Z may be formed in those systems. However, a primary feature of the MIVM is suitable for the situation of considering the nearest interaction only in the first coordination shell; namely, it does not describe the cluster formation. Consequently, further investigation is required to modify the calculation of the coordination number as well as this model. Nevertheless, the average relative errors of $\Delta H^{*}_{{{\text{pre}}}}$ of those six binary systems are less than ±10.0 pct. This shows that the fitting effects of the model for the liquid alloys are still excellent.

Fig. 1

Comparison of the predicted values with experimental data of binary systems: (a) Al-Cu at 1467 K,[13] (b) Al-Ni at 1700 K,[13] (c) Al-Zr at 2045 K,[14] (d) Cu-Ni at 1473 K,[15] (e) Cu-Zr at 1485 K,[16] and (f) Ni-Zr at 1565 K[17]

Substituting the corresponding interaction parameters B into Eq. [4], the enthalpies of mixing of the ternary Al-Cu-Ni, Al-Cu-Zr, Al-Ni-Zr, and Cu-Ni-Zr alloys have been calculated. From Table III, the present calculations using the model are in agreement with experimental data (the discrepancy ratios are less than 30 pct), except for the Cu-Ni-Zr system. The reason may arise from the predictions that the corresponding binary systems will impact the multicomponent systems. In addition, for a ternary alloy, only the binary interactions between atoms are considered, and the ternary atomic interactions between the constituents are neglected when the MIVM extends to the ternary alloys. Compared with the Zhang et al.[6] calculation of the Al-Cu-Ni alloy system using an extended Miedema model, in which the average relative error is around 60 pct, the MIVM proposed here also shows better results.

Table III Average Relative Error and the Average Standard Deviation of Prediction of Al-Cu-Ni at 1700 K,[19] Al-Ni-Zr at 1565 K,[20] Al-Cu-Zr at 1450, 1485, and 2010 to 2080 K,[14] and Cu-Ni-Zr at 1565 K[17] (±S ^* and $\pm \overline{{S^{*} }}$ are Calculated by Optimal Interaction Parameters B ^*)

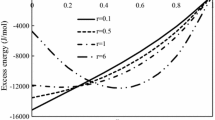
From Figures 2(a) and (b), it can be seen that the mixing enthalpies of liquid Al-Cu-Ni-Zr alloys have been calculated with the MIVM and the associate model[21] in an entire composition range at 1565 K for comparison with the experimental data of Witusiewicz et al.[20] The average relative error and the average standard deviation of ΔH _pre and $\Delta H^{*}_{{{\text{pre}}}}$ are ±19.6 pct, ±7.5 kJ/mol and ±14.0 pct, ±4.4 kJ/mol, respectively.

Fig. 2

Comparison of the predicted values with experimental data[20] and the associated model[21] of the Al-Cu-Ni-Zr: (a) Cu₄₁Ni₂₄Zr₃₅-Al at 1565 K and (b) Cu₁₉Ni₁₁Zr₇₀-Al at 1565 K (ΔH _ass: calculated by the associated model)

As shown previously, it can be seen clearly that based on the good predicted results of the binary systems, the mixing enthalpies of the Al-Cu-Ni-Zr quaternary system and four ternary systems should be also reasonable and reliable relatively. During the prediction procedure, the MIVM has introduced certain errors that are more obvious in the ternary systems than in a multicomponent system, perhaps due to a counterbalance of various errors that results in the predicted effect being good.

In conclusion, a significant advantage of the model lies in its ability to predict the mixing enthalpies of multicomponent liquid alloys using only the binary infinite dilute enthalpies or binary experimental data, and the predicted values are in agreement with the experimental data, which show that the model is reliable and convenient.