1 Introduction

When a metal is mixed with other metals or nonmetals, it usually results in the formation of new material with enhanced properties that can be used in different applications including domestic, medical, military and industrial. Since the mixing takes place in the liquid phase of the constituent elements, information about energetics and structure of the initial melt is required to set up devices and experimental procedures. As a result, a large group of researchers working in the field of material science and engineering including materials design are attempting to assess the energetics of metallic mixtures.

Since last few decades, shape memory alloys (SMAs) developed considering Cu as substrate atom have emerged as a promising material for a wide range of applications, including high damping materials, sensors and actuators (Ref 1, 2). Cu-Al-Ni SMAs, for example, have high thermal stability, good thermal and electrical conductivity, tailored microstructures including thermoelastic martensitic transformation, and thus can be used as sensors and actuators at temperatures around 200 °C (Ref 1,2,3,4). Furthermore, applying the concept of multiple primary alloying elements, Al-Cu-Ni alloys are commonly used as high-entropy alloys (Ref 5,6,7,8). Using this process, new designed and/or optimized alloys offering higher quality products with respect to those processed by traditional alloying procedures can be developed (Ref 5,6,7,8). On the other side, excluding Al-rich corner of the Al-Cu-Ni system, its alloys have relatively high melting temperatures (> 1000 K) implying experimental difficulties related to high temperature measurements (Ref 9, 10). Therefore, to compensate the lack of experimental properties data, modeling in the framework of different theoretical approaches represents an alternative. Accordingly, in the present work, to calculate the mixing properties of liquid Al-Cu-Ni alloys, the thermodynamic approach that combines thermodynamic datasets of constituent binary subsystems was applied.

Several research groups have investigated the binary Al-Cu (Ref 11,12,13,14,15,16,17,18,20), Cu-Ni (Ref 16, 21,22,23,24) and Ni-Al (Ref 19, 25,26,27,28,29,30,31) subsystems of the Al-Cu-Ni. The most reliable and widely used thermodynamic description of the Al-Cu system is that of Witusiewicz et al. (Ref 14), and thus, its Redlich–Kister (R–K) (Ref 32) coefficients for the liquid phase were selected for the current calculations. On the other hand, using the experimental data of Srikanth and Jacob (Ref 21) and Desai (Ref 25), respectively, the energetic terms of the Cu-Ni and Ni-Al liquid phases, both in (R–K) polynomials form were optimized.

Several researchers (Ref 1, 6, 33,34,35,36,37,38,39,40) have studied the thermodynamic properties and phase equilibria of the Al-Cu-Ni system using different approaches. Indeed, Stolz et al. (Ref 34) experimentally measured the enthalpy of mixing of the system using a high-temperature mixing calorimeter at 1700 K. They also calculated the enthalpy of mixing using the associated solution model, and it showed a small deviation from the experimental results. Later, Kundin et al. (Ref 40) reported DTA experimental datasets, solidification analysis of the Al-Cu-Ni alloy system for T < 1300 K and the Scheil simulations that combine CALPHAD (Calculation of Phase Diagram) method and phase-field modeling. To this aim, the thermodynamic descriptions for the free energies of the phases involved including the Al-Cu-Ni liquid phase of Al-rich alloys as functions of the concentration and the temperature were done (Ref 40). Recently, Wang et al. (Ref 6) have summarized the literature review regarding the phase equilibria and thermodynamics of the Al-Cu-Ni ternary system. They also evaluated a set of self-consistent thermodynamic parameters for the Gibbs free energy of mixing of this ternary system including those of the individual phases and performed Ab initio calculations to validate the assessment of these phases. In addition to these, Rodrigues et al. (Ref 41) have investigated the effects of Ni-addition on the macro-segregation, solidification route and microstructural characteristics as well as resulting tensile and corrosion properties of the Al-Cu-Ni system. The different thermal processing techniques for Al-Cu-Ni SMAs have been summarized by Agrawal and Dube (Ref 1). Based on the literature review, it is possible to conclude that the Al-Cu-Ni ternary system has a variety of properties data, but to the best of the authors' knowledge, until now, neither the thermodynamic nor the surface properties of liquid Al-Cu-Ni alloys for high temperatures (T > 1600 K) are available.

In this regard, the thermodynamic (excess Gibbs free energy of mixing and activity) and surface properties (surface tension and surface concentration) of the liquid ternary system were theoretically evaluated using the thermodynamic database of its binary subsystems. Using available experimental and theoretical data, the linear temperature-dependent coefficients of the R–K polynomial for the excess Gibbs free energy of mixing of the binary subsystems were firstly optimized. The thermodynamic properties of the ternary system were then calculated using the general solution model (GSM) (Ref 20, 42, 43), the Kohler model (Ref 20, 44, 45) and the Toop model (Ref 20, 44,45,46,47). The Butler equation (Ref 20, 47, 48) was used to compute the surface properties of the binaries and ternary systems. Previously obtained interaction energy parameters were the input data for the calculations of the mixing properties of the Al-Cu-Ni system for the temperatures of 1773, 1873, 1973 and 2073 K.

2 Theory

The expression for the excess Gibbs free energy of mixing \((\Delta G_{ij}^{xs} )\) of a binary subsystem in terms of R–K polynomial can be given as (Ref 20, 32, 44)

$$\Delta G_{ij}^{xs} = x_{i} x_{j} \mathop \sum \limits_{\nu = 0}^{n} A_{ij}^{\nu } \left( {x_{i} - x_{j} } \right)^{\nu }$$
(1)

where \({x}_{i}\) and \({x}_{j}\) are mole fractions of the components of a binary subsystem with \(x_{i} + x_{j} = 1\), while \(A_{ij}^{\nu }\) (\(= a_{ij}^{\nu } + b_{ij}^{\nu } *T\)) are linear temperature dependent coefficients of R–K polynomial for \(\Delta G_{ij}^{xs}\). Herein, \(a_{ij}^{\nu }\) (in J mol−1) is the enthalpy of mixing (\(\Delta H_{M}\)) and \(b_{ij}^{\nu }\) (in J mol−1 K−1) excess entropy of mixing (\(\Delta S_{M}^{xs}\)) contribution terms to \(\Delta G_{ij}^{xs} .\) The values of \(A_{ij}^{\nu }\) have to be optimized using the database of the thermodynamic functions of the binary subsystems.

According to general solution model (GSM) (Ref 20, 42, 43), the expression for the excess Gibbs free energy of mixing \((\Delta G_{123}^{xs} )\) of a ternary alloy can be given as

$$\begin{aligned} \Delta G_{123}^{xs} = & \;\;\frac{{x_{1} x_{2} }}{{X_{{1\left( {12} \right)}} X_{{2\left( {12} \right)}} }}\Delta G_{12}^{xs} \left( {X_{{1\left( {12} \right)}} ,X_{{2\left( {12} \right)}} } \right) \\ + & \;\;\frac{{x_{2} x_{3} }}{{X_{{2\left( {23} \right)}} X_{{3\left( {23} \right)}} }}\Delta G_{23}^{xs} \left( {X_{{2\left( {23} \right)}} ,X_{{3\left( {23} \right)}} } \right). \\ + & \;\;\frac{{x_{3} x_{1} }}{{X_{{3\left( {31} \right)}} X_{{1\left( {31} \right)}} }}\Delta G_{31}^{xs} \left( {X_{{3\left( {31} \right)}} ,X_{{1\left( {31} \right)}} } \right) \\ \end{aligned}$$
(2)

where \(x_{1}\), \(x_{2}\) and \(x_{3}\) are the mole fractions of the elements of ternary system. \({X}_{i(ij)}\) and \({X}_{j(ij)}\) are the concentrations of components of binary subsystems present in the ternary alloy such that \({X}_{i(ij)}+{X}_{j(ij)}=1\) and defined by the relations (Ref 20, 42, 43)

$$X_{{i\left( {ij} \right)}} = x_{i} + \xi_{ij} \left( {1 - x_{i} - x_{j} } \right)$$
(3)

where \(\xi_{ij}\) are called the similarity index and are dined as

$$\xi_{12} = \frac{{\eta_{I} }}{{\eta_{I} + \eta_{II} }}, \xi_{23} = \frac{{\eta_{II} }}{{\eta_{II} + \eta_{III} }} \;\;\;{\text{and}} \xi_{31} = \frac{{\eta_{III} }}{{\eta_{III} + \eta_{I} }}$$
(4)

Herein, the terms \(\eta\) are called deviation sum of squares and are expressed as

$$\begin{aligned} \eta_{I} & = \frac{1}{30}\left( {A_{12}^{0} - A_{13}^{0} } \right)^{2} + \frac{1}{210}\left( {A_{12}^{1} - A_{13}^{1} } \right)^{2} + \frac{1}{630}\left( {A_{12}^{2} - A_{13}^{2} } \right)^{2} + \frac{1}{1386}\left( {A_{12}^{3} - A_{13}^{3} } \right)^{2} + \frac{1}{105}\left( {A_{12}^{0} - A_{13}^{0} } \right)\left( {A_{12}^{2} - A_{13}^{2} } \right) \\ & \quad + \frac{1}{315}\left( {A_{12}^{1} - A_{13}^{1} } \right)\left( {A_{12}^{3} - A_{13}^{3} } \right) \\ \end{aligned}$$
(5a)
$$\begin{aligned} \eta_{II} & = \frac{1}{30}\left( {A_{23}^{0} - A_{21}^{0} } \right)^{2} + \frac{1}{210}\left( {A_{23}^{1} - A_{21}^{1} } \right)^{2} + \frac{1}{630}\left( {A_{23}^{2} - A_{21}^{2} } \right)^{2} \\ & \quad + \frac{1}{1386}\left( {A_{23}^{3} - A_{21}^{3} } \right)^{2} + \frac{1}{105}\left( {A_{23}^{0} - A_{21}^{0} } \right)(A_{23}^{2} - A_{21}^{2}) + \frac{1}{315}\left( {A_{23}^{1} - A_{21}^{1} } \right)\left( {A_{23}^{3} - A_{21}^{3} } \right). \\ \end{aligned}$$
(5b)
$$\begin{aligned} \eta_{III} & = \frac{1}{30}\left( {A_{31}^{0} - A_{32}^{0} } \right)^{2} + \frac{1}{210}\left( {A_{31}^{1} - A_{32}^{1} } \right)^{2} \\ & \quad + \frac{1}{630}\left( {A_{31}^{2} - A_{32}^{2} } \right)^{2} + \frac{1}{1386}\left( {A_{31}^{3} - A_{32}^{3} } \right)^{2} \\ & \quad + \frac{1}{105}\left( {A_{31}^{0} - A_{32}^{0} } \right)\left( {A_{31}^{2} - A_{32}^{2} } \right) + \frac{1}{315}\left( {A_{31}^{1} - A_{32}^{1} } \right)\left( {A_{31}^{3} - A_{32}^{3} } \right) \\ \end{aligned}$$
(5c)

Including ternary interaction parameter GSM model can be expressed as (Ref 6, 42)

$$G_{123}^{xs} = x_{1} x_{2} \mathop \sum \nolimits_{\nu = 0}^{n} {\text{A}}_{12}^{\nu } \left( {x_{1} - x_{2} } \right)^{\nu } + x_{2} x_{3} \mathop \sum \nolimits_{\nu = 0}^{n} {\text{A}}_{23}^{\nu } \left( {x_{2} - x_{3} } \right)^{\nu } + x_{3} x_{1} \mathop \sum \nolimits_{\nu = 0}^{n} {\text{A}}_{31}^{\nu } \left( {x_{3} - x_{1} } \right)^{\nu } + fx_{1} x_{2} x_{3}$$
(5d)

where the term f is the ternary interaction term and it can be given as

$$\begin{aligned} f & = \left( {2\xi_{12} - 1} \right)[A_{12}^{3} \left( {3\left( {x_{1} - x_{2} } \right)^{2} x_{3} + 3\left( {x_{1} - x_{2} } \right)x_{3}^{2} \left( {2\xi_{12} - 1} \right) + x_{3}^{3} \left( {2\xi_{12} - 1} \right)^{2 } } \right) \\ & \quad + A_{12}^{2} \left( {\left( {2\xi_{12} - 1} \right)x_{3} + 2\left( {x_{1} - x_{2} } \right)} \right) + A_{12}^{1} ] \\ & \quad + \left( {2\xi_{23} - 1} \right)[A_{23}^{3} \left( {3\left( {x_{2} - x_{3} } \right)^{2} x_{1} + 3\left( {x_{2} - x_{3} } \right)x_{1}^{2} \left( {2\xi_{23} - 1} \right) + x_{1}^{3} \left( {2\xi_{23} - 1} \right)^{2 } } \right) \\ & \quad + A_{23}^{2} \left( {\left( {2\xi_{23} - 1} \right)x_{1} + 2\left( {x_{2} - x_{3} } \right)} \right) + A_{23}^{1} ] \\ & \quad + \left( {2\xi_{31} - 1} \right)[A_{31}^{3} \left( {3\left( {x_{3} - x_{1} } \right)^{2} x_{2} + 3\left( {x_{3} - x_{1} } \right)x_{2}^{2} \left( {2\xi_{31} - 1} \right) + x_{2}^{3} \left( {2\xi_{31} - 1} \right)^{2 } } \right) \\ & \quad + A_{31}^{2} \left( {\left( {2\xi_{31} - 1} \right)x_{2} + 2\left( {x_{3} - x_{1} } \right)} \right) + A_{31}^{1} ] \\ \end{aligned}$$
(5e)

Based on the Kohler model, the expression for \(\Delta G_{123}^{xs}\) of a ternary system (Ref 20, 44, 45) is described by

$$\begin{aligned} \Delta G_{123}^{xs} & = \left( {x_{1} + x_{2} } \right)^{2} \Delta G_{12}^{xs} \left( {\frac{{x_{1} }}{{x_{1} + x_{2} }}, \frac{{x_{2} }}{{x_{1} + x_{2} }}} \right) \\ & \quad + \left( {x_{2} + x_{3} } \right)^{2} \Delta G_{23}^{xs} \left( {\frac{{x_{2} }}{{x_{2} + x_{3} }}, \frac{{x_{3} }}{{x_{2} + x_{3} }}} \right) \\ & \quad + \left( {x_{3} + x_{1} } \right)^{2} \Delta G_{31}^{xs} \left( {\frac{{x_{3} }}{{x_{3} + x_{1} }}, \frac{{x_{1} }}{{x_{3} + x_{1} }}} \right) \\ \end{aligned}$$
(6)

Since the Kohler model is symmetrical, the mole fraction of any of the three components can be chosen as \({x}_{1}\), \({x}_{2}\) and \({x}_{3}\). On the contrarily, the Toop model is asymmetrical and hence asymmetrical element has to be chosen to perform the calculations. According to this model, the expression for \(\Delta G_{123}^{xs}\) considering \(x_{1} = x_{Al}\) as the asymmetric element (Ref 20, 44,45,46,47) can be given as

$$\begin{aligned} \Delta G_{123}^{xs} & = \left( {\frac{{x_{2} }}{{x_{2} + x_{3} }}} \right)\Delta G_{12}^{xs} \left( {x_{1} ,1 - x_{1} } \right) \\ & \quad + \left( {x_{2} + x_{3} } \right)^{2} \Delta G_{23}^{xs} \left( {\frac{{x_{2} }}{{x_{2} + x_{3} }}, \frac{{x_{3} }}{{x_{2} + x_{3} }}} \right) \\ & \quad + \left( {\frac{{x_{3} }}{{x_{2} + x_{3} }}} \right)\Delta G_{31}^{xs} \left( {x_{1} ,1 - x_{1} } \right) \\ \end{aligned}$$
(7)

The expressions for partial excess free energy (\({G}_{i}^{xs}\)) of ith component in the binary and ternary alloys (Ref 20, 45, 47) can be obtained by using the relation

$${G}_{i}^{xs}={G}_{ij}^{xs}+{\sum }_{j=1}^{m}({\delta }_{ij}-{x}_{j})\frac{\partial {G}^{xs}}{\partial {x}_{j}}$$
(8)

where \({\delta }_{ij}\) is Kronecker delta symbol defined as \({\delta }_{ij}=1\) for \(i=j\) and \({\delta }_{ij}=0\) for \(i\ne j\). The value of \(m=2\) for the binary sub-systems and \(m=3\) for the ternary system. The activity \(({a}_{i})\) of \({i}^{th}\) component of the systems can be expressed in terms of \({G}_{i}^{xs}\) by the relation

$${a}_{i}={x}_{i}{\text{exp}}(\frac{{G}_{i}^{xs}}{RT})$$
(9)

where R (in \({\text{J}} {{\text{mol}}}^{-1}{{\text{K}}}^{-1}\)) is universal gas constant and T (in K) is the absolute temperature.

The surface concentration \(({x}_{i}^{s})\) of ith component and the surface tension \((\sigma )\) of binary and ternary liquid alloys can be computed using the Butler equations (Ref 20, 47, 48), expressed as

$$\sigma = \sigma_{1} + \frac{RT}{{\alpha_{1} }}\ln \frac{{x_{1}^{s} }}{{x_{1}^{b} }} + \frac{{G_{s,1}^{xs} - G_{b,1}^{xs} }}{{\alpha_{1} }} = \sigma_{2} + \frac{RT}{{\alpha_{2} }}\ln \frac{{x_{2}^{s} }}{{x_{2}^{b} }} + \frac{{G_{s,2}^{xs} - G_{b,2}^{xs} }}{{\alpha_{2} }} = \sigma_{3} + \frac{RT}{{\alpha_{3} }}\ln \frac{{x_{3}^{s} }}{{x_{3}^{b} }} + \frac{{G_{s,3}^{xs} - G_{b,3}^{xs} }}{{\alpha_{3} }}$$
(10)

where \({\sigma }_{i}\) \((i=1,2,3)\) is the surface tension of a pure component \(i\) of the liquid mixture and \({\alpha }_{i}\) is the monolayer surface area of one mole of individual components in an alloy. The partial excess free energy for surface phase \(({G}_{s,i}^{xs})\) and bulk phase \(({G}_{b,i}^{xs})\) of the components (Ref 20, 45, 49, 50) are related as

$$\beta = \frac{{G_{s,i}^{xs} }}{{G_{b,i}^{xs} }}$$
(11)

\(\beta\) value is a reduced coordination that depends on the coordination number of the atoms on the surface and bulk phases of the liquid alloy. Its value varies between 0.5 and 0.84 and for close packed structures, its value is usually 0.75 (Ref 20, 50) and 0.82 for simple liquid metals. The monolayer surface area \(({\alpha }_{i})\) of one mole of the individual component (Ref 47, 49, 50) can be determined using the relation

$$\alpha_{i} = fN_{A}^{\frac{1}{3}} \left( {\frac{{M_{i} }}{{\rho_{i} }}} \right)^{2/3}$$
(12)

where \(f\) is the geometric factor, that in this work was taken as \(f=\) 1.00 (Ref 20, 50). The terms \({N}_{A}\), \({M}_{i}\) and \({\rho }_{i}\) are the Avogadro’s number, molar mass and density of the ith component, respectively. The surface tension and the molar volume (Ref 51) of pure alloy components obey the linear law and for working temperature \((T)\) can be computed using the relations

$$\sigma = \sigma_{0} + \frac{\partial \sigma }{{\partial T}}\left( {T - T_{0} } \right)\quad {\text{and}}\quad V_{l,T} = V_{l,m} \left[ {1 +\lambda_{l} \left( {T - T_{m} } \right)} \right]$$
(13)

where \({\sigma }_{0}\) and \({V}_{l,m}\) are the surface tension and molar volume of \({i}^{th}\) pure component at its melting temperature (\({T}_{0}\)). \(\frac{\partial \sigma }{\partial T}\) and \(\lambda_{l}\) are the surface tension and volume temperature coefficients of \({i}^{th}\) component, respectively.

3 Results and Discussion

3.1 Thermodynamic Properties

Using theoretical approaches, the calculations of mixing properties of binary and ternary liquid alloys require fitting model parameters. In general, these parameters are optimized using the thermodynamic datasets. These parameters are considered reliable and consistent if they can well explain the reference thermodynamic data as well as reproduce activity of the systems. Using the aforementioned geometric models, temperature dependent interaction parameters for the excess Gibbs free energy of mixing (\(\Delta G_{ij}^{xs}\)) of binary subsystems are required to compute the mixing properties of Al-Cu-Ni liquid alloys. For the Al-Cu binary subsystem, R–K coefficients of \(\Delta G_{Al - Cu}^{xs}\) were taken from Witusiewicz et al. (Ref 14), while for the Cu-Ni, these parameters were optimized inserting into Eq 1 the empirical expressions for enthalpy of mixing (\(\Delta H_{M}\)) and excess entropy of mixing (\(\Delta S_{M}^{xs}\)) at 1673 K (Ref 21). The values obtained for the binary subsystems are given in Table 1.

Table 1 Optimized R–K coefficients for the excess Gibbs free energies of mixing (\({{\text{Jmol}}}^{-1}\)) of binary subsystems of liquid Al-Cu-Ni alloys
Full size table

Similarly, to optimize the interaction energy parameters of liquid Ni-Al alloys, the experimental values of \(\Delta H_{M}\) and \(\Delta S_{M}^{xs}\) of the Ni-Al system (Ref 25) were used. The optimized parameter \(b_{0}\) for \(A_{31}^{0}\) calculated assuming linear temperature dependence of interaction parameters was found to be greater than 2R (Table 1), but it should be less than 2R (Ref 52, 53). Therefore, these parameters were re-optimized considering the interaction energy parameters to be exponential temperature dependent. In this frame, the interaction parameters are expressed as \(A_{ij}^{\nu } = h_{ij}^{\nu } \exp \left( { - T/\tau_{ij}^{\nu } } \right)\), where \(h_{ij}^{\nu }\) (in J mol−1) is the enthalpy contribution and \(\tau_{ij}^{\nu }\) (in J mol−1 K−1) is the entropy contribution term to \(\Delta G_{ij}^{xs}\) (Ref 52, 53). For the calculations of the thermodynamic and surface properties, exponential parameters were preferred.

Once the R–K coefficients were obtained (Table 1), the model predicted values of \(\Delta G_{ij}^{xs}\) were computed by using Eq 1. To validate the predictive ability of the model used, for each binary subsystem the computed values of \(\Delta G_{ij}^{xs}\) are compared with the available literature data, as shown in Fig. 1(a), (b), (c) and (d).

Fig. 1
figure 1

(a-d) Compositional dependence of the excess Gibbs free energy of mixing (\(\Delta G_{ij}^{xs} /RT\)), partial excess free energy (\(\Delta G_{i}^{xs} /RT\)) and activities (\(a_{i}\)) of alloy components for binary subsystems of liquid Al-Cu-Ni ternary alloys: (a) \(\Delta G_{{\text{Al - Cu}}}^{xs} /RT\) (x1 = Al) at 1373 K and \(\Delta G_{{\text{Ni - Al}}}^{xs} /RT\) (x1 = Ni) at 1873 K; (b) \(\Delta G_{{\text{Cu - Ni}}}^{xs} /RT\), \(a_{{{\text{Cu}}}}\) and \(a_{{{\text{Ni}}}}\) for Cu-Ni at 1823 K; (c) \(\Delta G_{i}^{xs} /RT\) of Al-Cu at 1373 K; (d) \(\Delta G_{i}^{xs} /RT\) of Ni-Al at 1873 K

Full size image

Using the interaction energy parameters of Witusiewicz et al. (Ref 14), the \({\Delta G}_{{\text{Al}}-{\text{Cu}}}^{xs}\) values of liquid Al-Cu alloys computed at 1373 K are in excellent agreement with the data of Kanibolotsky et al. (Ref 13) and good agreement with the experimental (Ref 11) and literature datasets (Ref 12, 18) (Fig. 1a). The maximum negative value of \(\Delta G_{{\text{Al - Cu}}}^{xs}\) is found to be − 14.38 kJ mol−1 at \(x_{Al} = 0.4\), indicating that the system is moderately interacting in nature. The computed values of \(\Delta G_{{\text{Cu - Ni}}}^{xs}\) obtained at 1673 K using the optimized parameters for liquid Cu-Ni alloys agree fairly well with the data described by the empirical expressions of Srikanth and Jacob (Ref 21), and this plot has not been included in the present work. The values of \(\Delta G_{{\text{Cu - Ni}}}^{xs}\) were then computed for 1823 K using the R–K parameters given in Table 1 and subsequently compared with the available experimental (Ref 11) and literature data (Ref 12, 23, 24) (Fig. 1b). Positive values of \(\Delta G_{{\text{Cu - Ni}}}^{xs}\) are found and thus, liquid Cu-Ni alloys are segregating in nature. Concerning Ni-Al liquid alloys, the computed values of \(\Delta G_{{\text{Ni - Al}}}^{xs}\) at 1873 K are in excellent agreement with the reference data (Ref 25) and in good agreement with that of Ansara et al. (Ref 27) (Fig. 1a). The model predicted values of the present work are also in excellent agreement with that of Yadav et al. (Ref 30, 31). Contrarily, the \(\Delta G_{{\text{Ni-Al}}}^{xs}\) datasets reported by Huang and Chang (Ref 28) and those of Zhang et al. (Ref 29) exhibit around equiatomic composition (\(x_{{{\text{Ni}}}} = 0.5\)) significant scattering from the present results. Moreover, the maximum negative value of \(\Delta G_{{\text{Ni-Al}}}^{xs} = - 32.05 \,{\text{kJ}}\,{\text{mol}}^{ - 1}\) at \(x_{{{\text{Ni}}}} = 0.5\) classifies the Ni-Al system as strongly interacting in nature (Fig. 1a). Therefore, it can be concluded that the temperature dependent optimized coefficients of interaction energy parameters, considered in the present work, have successfully described \(\Delta G_{ij}^{xs}\) of the three binary subsystems.

Activity (\(a\)) of the alloys is an important thermodynamic function, which is calculated directly from the experimental measurements. The activity of individual components (\(a_{i}\)) in an alloy melt is directly related to its partial excess Gibbs free energy (\(\Delta G_{i}^{xs}\)). Therefore, the optimized coefficients will gain validity only if they successfully reproduce the activity of a pure component (\(a_{i}\)) of each binary subsystem. Using Eqs (1) and (8) with the corresponding input data (Table 1), theoretical values of \(\Delta G_{i}^{xs}\) of binary subsystems were computed. To compute the activity \(a_{i}\) of the respective component of Al-Cu binary subsystem, the values previously obtained were inserted into Eq 9. The computed values of \(a_{i}\) along with the available literature data as a function of composition for Cu-Ni subsystem are shown in Fig. 1(b). The computed values of \(a_{i}\) for the components of Al-Cu and Ni-Al binary subsystems were found to be very small. Thus, the computed values of \(\Delta G_{i}^{xs}\) were preferred for the graphical representations (Fig. 1c, and d). The computed values of \(a_{i}\) and \(\Delta G_{i}^{xs}\) of present work and the literature datasets are in good agreement (Fig. 1b-d). Therefore, R–K coefficients (Table 1) were further used for the computations and predictions of mixing properties of the Al-Cu-Ni ternary system. The computed values of \(\Delta G_{i}^{xs}\) of the pure components of liquid Al-Cu and Ni-Al alloys were found to be negative at all compositions indicating these systems to be ordering in nature (Fig. 1c, d). Meanwhile, the computed values of \(a_{i}\) for the components of Cu-Ni alloy showed positive deviation from their ideal values indicating the system to be segregating in nature (Fig. 1b). These findings substantiate the nature of mixing of liquid binary alloys as predicted by \(\Delta G_{ij}^{xs}\).

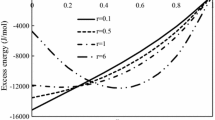
The excess Gibbs free energy of mixing (\(\Delta G_{123}^{xs}\)) of liquid Al-Cu-Ni ternary alloys was computed inserting previously determined values of \(\Delta G_{ij}^{xs}\) into Eq 2-8. To this aim, nine vertical sections of the Al-Cu-Ni phase diagram representing the alloys with the constant composition of one component, and the ratio of other two components was considered. Therefore, the compositional dependence of \(\Delta G_{123}^{xs}\) was calculated taking into account Al, Cu and Ni vertices of the Gibbs triangle, and three vertical sections passing through each vertex having the ratios of \({x}_{i}:{x}_{j}\) = 3:1 (curve \({\text{A}}\)), 1:1 (curve \(B\)) and 1:3 (curve \(C\)) of the other two components, as shown in Fig. 2(a), (b) and (c). Considering ternary Al-Cu-Ni alloys that belong to the three vertical sections from Al-vertex, the variations of \(\Delta G_{123}^{xs}\), calculated by the three geometric models, are symmetric with respect to \({x}_{Al}\) = 0.5 (Fig. 2a). Moreover, it can be observed that the negative values of \(\Delta G_{123}^{xs}\) gradually increase with an increase in Ni-content. This may be attributed to the Ni-Al system being strongly interacting one and the Al-Cu system being moderately interacting, whereas the Cu-Ni system exhibits weak demixing. The perusal of Fig. 2b corresponds that the negative value of \(\Delta G_{123}^{xs}\) rapidly decreases at the higher Ni-content (\({x}_{{\text{Ni}}}:{x}_{{\text{Al}}}=3:1 (\mathrm{curve A})\)), whereas the rate of decrement is rather slow at a higher Al-content (\({x}_{{\text{Ni}}}:{x}_{{\text{Al}}}=1:3 (\mathrm{curve C})\)) with the increase in the concentration of Cu. From Fig. 2c, it can be observed that the negative value of \(\Delta G_{123}^{xs}\) gradually decreases at a higher Cu-content (\({x}_{{\text{Al}}}:{x}_{{\text{Cu}}}=1:3 (\mathrm{curve C})\)) with the increase of Ni-content. Additionally, the curve of \(\Delta G_{123}^{xs}\) gradually shallows down with an increase in Al-content from Ni-corner and tends to attain symmetry at/around \({x}_{Ni}=0.5\) (Fig. 2c). Using GSM, Kohler’s and Toop’s models, the model predicted values of \(\Delta G_{123}^{xs}\) for liquid Al-Cu-Ni alloys were obtained, and the results were compared among them due to the lacking of the experimental/literature thermodynamic data. Among the computed values of \(\Delta G_{123}^{xs}\), the maximum deviation of about \(6.6 \%\) was found for the \({{\text{Al}}}_{10}{{\text{Cu}}}_{60}{{\text{Ni}}}_{30}\) alloy and thus, the model predicted values are in reasonable agreement. The present investigations predict that the interaction between the binary pairs (Al-Cu and Ni-Al) govern the mixing behavior of liquid Al-Cu-Ni alloys.

Fig. 2
figure 2

(a-e) The computed values of \(\Delta G_{123}^{xs}\) of liquid Al-Cu-Ni ternary alloys for T = 1773 K: (a) three vertical sections passing through Al-vertex and having the ratios of Cu and Ni components: \({x}_{i}:{x}_{j}\) = 3:1 (curve \(A\)), 1:1 (curve \(B\)) and 1:3 (curve \(C\)); (b) three vertical sections passing through Cu-vertex and having the ratios of Ni and Al components: \({x}_{i}:{x}_{j}\) = 3:1 (curve \(A\)), 1:1 (curve \(B\)) and 1:3 (curve \(C\)); (c) three vertical sections passing through Ni-vertex and having the ratios of Al and Cu components: \({x}_{i}:{x}_{j}\) = 3:1 (curve \(A\)), 1:1 (curve \(B\)) and 1:3 (curve \(C\)); (d) iso-Gibbs free energy curves, \(\Delta G_{123}^{xs}\) [\(\mathrm{k J}{{\text{mol}}}^{-1}]\) at 1773 K; (e) variation of \(\Delta G_{123}^{xs}\) with temperature in the range of 1773-2073 K

Full size image

Wang et al. (Ref 6) assessed the thermodynamic properties, \(\Delta G_{123}^{xs}\) and constituent binary and ternary phases of the Al-Cu-Ni system using CALPHAD and ab initio computer based software. For the purpose, they used the available literature data of temperature-dependent interaction energy parameters for \(\Delta G_{123}^{xs}\) of binary subsystems. Further, they presented the temperature-dependent self-consistent parameters for \(\Delta G_{123}^{xs}\) and compared the computed isothermal sections of different phases present in the ternary liquid alloys with the available experimental values. For the similar process, we computed the values of \(\Delta G_{123}^{xs}\) using the binary (Ref 12, 23, 27) and ternary (Ref 6) parameters tabulated by Wang et al. Significant disagreements in \(\Delta G_{123}^{xs}\) can be observed among the values computed using parameters of Wang et al. and this work from all three corners and cross-sections (Fig. 2a-c). The deviations were found to be more prominent from Al and Ni corners in compared to those of Cu corners. These disagreements appeared due to different input parameters of binary subsystems and ternary system in these two approaches.

Iso-Gibbs free energy curves, calculated for 1773 K using the GSM to represent \({\Delta G}_{123}^{xs}\) of liquid Al-Cu-Ni ternary alloys are shown in Fig. 2(d). \(\Delta G_{123}^{xs}\) of the ternary system exhibits strong variations at the lower concentration of Al. For the \({{\text{Cu}}}_{50}{{\text{Ni}}}_{50}\) (in at.%) binary alloy, the value positive of \(\Delta G_{123}^{xs}\) = \(3.40 \mathrm{k J}{{\text{mol}}}^{-1}\) is found changing its sign to negative with small Al-addition, even at 4 at.%, as observed for the \({{{\text{Al}}}_{4}{\text{Cu}}}_{48}{{\text{Ni}}}_{48}\) alloy. Then, with an increase in Al-content, the negative values of \(\Delta G_{123}^{xs}\) increase rapidly and shift towards the Al-Ni axis. The maximum negative value of \(\Delta G_{123}^{xs}\) for T = 1773 K is obtained for the \({{\text{Al}}}_{50}{{\text{Ni}}}_{50}\) (in at.%) alloy (Fig. 2d).

The present model predicted values of \(\Delta G_{123}^{xs}\) suggest a strong complex forming tendency in Al-Cu-Ni melts as detailed for its binary Ni-Al subsystem (Ref 54). Following the abovementioned procedure, the \(\Delta G_{123}^{xs}\) values for ternary Al-Cu-Ni alloys were also calculated for temperatures ranging from 1773 to 2073 K. For all alloy compositions with an increase in temperature, the computed values of \(\Delta G_{123}^{xs}\) gradually decrease indicating a decreasing complex formation tendency in alloy melts (Fig. 2e). Similar results were also obtained for other binary and ternary liquid alloy systems as reported in (Ref 45, 47, 55).

In order to compute \({a}_{{\text{Al}}}\), \({a}_{{\text{Cu}}}\) and \({a}_{{\text{Ni}}}\) activities of the alloy components in ternary Al-Cu-Ni melts, firstly the partial Gibbs free energies \(\Delta G_{123}^{xs}\) of the binaries were determined. Indeed, the GSM (Eq 2-5) calculated values along with the R–K coefficients given in Table 1 were inserted into Eq 6. Subsequently, the computed values were then used in Eq 9 to obtain \({a}_{\text{Al}}, \;{a}_{\text{Cu}}\; \text{and}\; {a}_{\text{Ni}}\) of the ternary system. As an example, the variation of \({a}_{{\text{Al}}}, \;{a}_{{\text{Cu}}} \;{\text{and}} \;{a}_{{\text{Ni}}}\) of the alloys belonging to the vertical section defined by Ni vertex and the ratio \({x}_{{\text{Al}}}:{x}_{{\text{Cu}}}=1:1\), is displayed in Fig. 3(a). It can be depicted that with a gradual increase in Ni-content in the alloys, \({a}_{{\text{Cu}}}\) gradually increases up to \({x}_{{\text{Ni}}}=0.5\) and then start to decrease even though Cu-content decreases over the entire composition range (Fig. 3a). Due to strong interactions between Ni and Al atoms in Ni-Al melts (Ref 54), when the Ni-content is increased, then Al atoms prefer to make pairs with Ni atoms producing free Cu atoms and, because of the formation of NiAl complexes, \({a}_{{\text{Cu}}}\) may be significantly increased.

Fig. 3
figure 3

(a-d) The computed \({a}_{Al}\), \({a}_{{\text{Cu}}}\) and \({a}_{{\text{Ni}}}\) activities of the alloy components in liquid Al-Cu-Ni ternary alloys for T = 1773 K: (a) \({a}_{{\text{Al}}}, \;{a}_{{\text{Cu}}} \;{\text{and}}\; {a}_{{\text{Ni}}}\) for the alloys of the vertical section passing through Ni-vertex and with the ratio \({x}_{{\text{Al}}}:{x}_{{\text{Cu}}}=1:1\); (b) iso-activity lines for \({a}_{{\text{Al}}}\); (c) iso-activity lines for \({a}_{{\text{Cu}}}\); (d) iso-activity lines for \({a}_{{\text{Ni}}}\)

Full size image

The iso-activity lines for \({a}_{{\text{Al}}}, \;{a}_{{\text{Cu}}}\;{\text{and}}\; {a}_{{\text{Ni}}}\) of the Al-Cu-Ni ternary system are shown in Fig. 3(b), (c) and (d). Taking into account that the Al-Cu and Ni-Al are compound forming systems (Ref 9, 11), thus Al makes complexes with both Cu and Ni in the alloy melts, indicating the exothermic reactions in both alloy systems. Therefore, the \({a}_{Al}\) model predicted values of the ternary system are significantly lower with respect to those of the ideal values, can be supported by the abovementioned considerations (Fig. 3b). On the other side, a dual activity behavior of \({a}_{{\text{Cu}}}\) was observed: for higher Ni-content, \({a}_{{\text{Cu}}}\) values are higher than those of the ideal mixture, while for higher Al and Cu-content, the \({a}_{{\text{Cu}}}\) values are lower in comparison with the ideal values. Negative deviations of \({a}_{{\text{Cu}}}\) from ideality at a higher concentration Al as Cu atoms is due to the formation of complexes only with Al atoms (Fig. 3c). A similar trend was also observed for \({a}_{{\text{Ni}}}\) in Al-Cu-Ni melts as the Ni-Al is compound forming system, whereas the Cu-Ni is segregating in nature (Fig. 3d).

3.2 Surface Properties

Knowledge of the surface properties offers insight into a variety of metallurgical processes such as casting, joining, crystal growth, composites production and others that involve the presence of the liquid phase. In view of material's design and new processes development, the surface tensions (\(\sigma\)) of the Al-Cu-Ni system and its binary subsystems were calculated using the Butler equation (Eq 10-12) and Eq 13 and inserting the reference data given in Table 2. The temperature dependent coefficients of volume expansion (\(\lambda_{l}\)) for the components of the system were computed using Eq 13 and the reference data (Ref 58). These values slightly deviated from those reported by Kaptay (Ref 51). The surface tensions of the binary subsystems as a function of composition are displayed in Fig. 4.

Table 2 Reference data of the density and surface tension of individual element of binary subsystems (Ref 58)
Full size table
Fig. 4
figure 4

Surface tension isotherms of liquid Al-Cu (x1 = Al) at 1373 K, Cu-Ni (x1 = Cu) at 1546 K and Ni-Al (x1 = Ni) at 1673 K alloys calculated by Butler’s and the ideal solution model and comparison with experimental data (Ref 16, 54, 56, 57)

Full size image

The calculated surface tension isotherms of all the constituent binary subsystems show negative deviations from the corresponding ideal isotherms. The calculated surface tension isotherms of liquid Ni-Al, Al-Cu and Cu-Ni alloys were compared to the literature data (Ref 16, 54, 56, 57), respectively. A comparison between the calculated isotherms and experimental data exhibit similar trend at all concentration for all binary subsystems (Fig. 4). Moreover, the computed surface tension values of Al-Cu and Cu-Ni melts gradually decrease with an increase in Al and Cu-content, respectively. Contrarily, the surface tension of liquid Ni-Al alloys gradually increases with an increase in Ni-content.

The variations of the Al, Cu and Ni surface concentrations, calculated with respect to the bulk concentrations of the same alloy components are shown in Fig. 5(a)-(d). Liquid Al-Cu-Ni ternary alloys at T = 1773 K, belonging to three vertical sections defined by the constant composition of one component and 1:1 ratio of other two components were considered. For the \({{\text{Al}}}_{33.3}{{\text{Cu}}}_{33.3}{{\text{Ni}}}_{33.3}\) alloy with the equiatomic composition, the surface concentrations of Al, Cu and Ni of about 72, 23 and 5 at.%, respectively, were obtained. These observations predict prevalent segregation of the component with the lowest surface tension to the surface of ternary melts. Regular variations of the surface concentrations for the vertical sections passing through Al and Cu vertices are shown in Fig. 5(a) and (b) in which surface concentrations of each component are proportional with respect to its bulk concentration. In the case of liquid Al-Cu-Ni ternary alloys belonging to the vertical section from Ni-vertex, an opposite trend of Cu surface concentration was found (Fig. 5c). Indeed, an increase in Cu surface concentration with increasing Ni bulk concentration up to \({x}_{{\text{Ni}}}<0.6\) even though the bulk concentration of Cu gradually decreases in this range.

Fig. 5
figure 5

(a-d) The variations of \({x}_{{\text{Al}}}^{s}\), \({x}_{{\text{Cu}}}^{s}\) and \({x}_{{\text{Ni}}}^{s}\) surface concentrations of the alloy components of the Al-Cu-Ni system with composition and temperature: (a) \({x}_{{\text{Al}}}^{s}\), \({x}_{{\text{Cu}}}^{s}\) and \({x}_{{\text{Ni}}}^{s}\) from Al vertex at \({x}_{{\text{Cu}}}:{x}_{{\text{Ni}}}=1:1\); (b) \({x}_{{\text{Al}}}^{s}\), \({x}_{{\text{Cu}}}^{s}\) and \({x}_{{\text{Ni}}}^{s}\) from Cu vertex at \({x}_{{\text{Ni}}}:{x}_{{\text{Al}}}=1:1\); (c) \({x}_{{\text{Al}}}^{s}\), \({x}_{{\text{Cu}}}^{s}\) and \({x}_{{\text{Ni}}}^{s}\) from Ni vertex at \({x}_{{\text{Al}}}:{x}_{{\text{Cu}}}=1:1\); (d) variations of \({x}_{Al}^{s}\), \({x}_{Cu}^{s}\) and \({x}_{Ni}^{s}\) with temperature in the range 1773-2073 K

Full size image

At 1773 K, the surface tensions of liquid Al, Cu and Ni are \({\sigma }_{{\text{Ni}}}=1.760 {{\text{Nm}}}^{-1}\), \({\sigma }_{{\text{Al}}}=0.620 {{\text{Nm}}}^{-1}\) and \({\sigma }_{{\text{Cu}}}=1.207 {{\text{Nm}}}^{-1}\). Having the highest surface tension, Ni remains in the bulk phase of the ternary solutions, whereas Al segregates to the surface as it has the lowest surface tension. When the bulk concentration of Ni is gradually increased, there is a preferable association between Ni and Al atoms to form complexes and thereby breaking the association between Al and Cu atoms. As a result, Cu surface concentration seems to be relatively increased representing an unusual trend mentioned above.

The temperature variations of Al, Cu and Ni surface concentrations of the Al-Cu-Ni system is shown in Fig. 5(d). It can be observed that Al surface concentration decreases whereas that of Ni increases with the temperature rise, while Cu surface concentration remains almost constant. This shows that with the temperature rise, the surface concentrations of alloy components tend to shift toward the ideal values (bulk concentration).

The iso-surface tension lines for liquid Al-Cu-Ni alloys at 1773 K are shown in Fig. 6(a). The surface tension of the ternary alloys increases with an increase in Ni concentration whereas it decreases with an increase in Al concentration. The observed variations appear due to the lowest Al surface tension and the highest Ni surface tension. For all alloy compositions, the surface tension of liquid Al-Cu-Ni alloys decreases linearly with the rise in temperature (Fig. 6b). Temperature dependent linear variations of the surface tension of liquid Al-Cu-Ni alloys is due to the same behavior of the surface tensions of alloy components (Eq 13) as well as the assumption of linear temperature dependence of the interaction energy parameters for the excess Gibbs free energy of mixing (Table 1).

Fig. 6
figure 6

(a, b) The surface tension [N/m] computed values of liquid Al-Cu-Ni ternary alloy. (a) Iso-surface tension lines at 1773 K. (b) Variations of the surface tension [N/m] over the temperature range of 1773-2073 K

Full size image

4 Conclusions

The following important conclusions can be drawn from the present work:

  1. (a)

    The values of the excess Gibbs free energies of mixing and the activities of binary subsystems, calculated using optimized R–K coefficients agree well with experimental and literature data. This ensures the validity of optimization procedure and thus these parameters were then used to compute other physical quantities.

  2. (b)

    The maximum negative value of the excess Gibbs free energy of mixing for liquid Al-Cu-Ni ternary alloys at 1773 K is found to be at equiatomic composition of Al and Ni (\(50 {\text{at}}.\% {\text{Al}}, 50 {\text{at}}. \% {\text{Ni}},0 {\text{at}}. \% {\text{Cu}}\)). This result substantiates a strong tendency of NiAl complexes formation even in ternary melts. As the temperature of the system rises, the excess Gibbs free energy of mixing decreases, reducing a complex forming tendency in it.

  3. (c)

    The activities of Al and Ni components increase with an increase in their respective bulk concentrations of the ternary liquid alloys. However, an unusual the variation of Cu activity has been observed for ternary alloys belonging to the vertical section defined by Ni vertex and the ratio \({x}_{Al}:{x}_{Cu}=1:1\), in which its activity is found to increase at first and then decreases, despite the fact that its bulk concentration is decreasing continuously.

  4. (d)

    The surface tension of liquid Al-Cu-Ni ternary alloys decreases as Al content of the bulk increases, whereas it increases with an increase of Ni content in the bulk alloys. Furthermore, increasing the temperature, the surface tension of the system decreases linearly.