1 Introduction

Finite mixtures of Gaussian linear regression models allow to perform linear regression analysis in the presence of a finite number of heterogeneous populations, each of which is characterised by a Gaussian linear regression model whose parameters are different from the ones of the other populations (see, e.g., Quandt and Ramsey 1978; De Sarbo and Cron 1988; De Veaux 1989). Examples of fields in which they have been successfully employed are agriculture, education, quantitative finance, social sciences and transport systems (see, e.g., Turner 2000; Ding 2006; Tashman and Frey 2009; Dyer et al. 2012; Van Horn et al. 2015; McDonald et al. 2016; Elhenawy et al. 2017). These models naturally arise when relevant categorical predictors are omitted from a regression model (see, e.g., Hosmer 1974). They can also be used in outlier detection or robust regression estimation (see, e.g., Aitkin and Tunnicliffe Wilson 1980). In the multivariate scenario, this approach to linear regression analysis makes it possible to take into account the correlation among the dependent variables that typically occur in longitudinal data, time-series data or repeated measures (Jones and McLachlan 1992). In most of the multivariate models developed so far the same vector of regressors has to be used for all dependent variables. This restriction does not affect the class of linear regression models based on a finite Gaussian mixture recently proposed in Galimberti et al. (2016). However, in this class, the effect of the regressors on the responses is assumed to be the same for all populations.

This paper introduces a more flexible class of finite mixtures of multivariate Gaussian linear regression models in which a different vector of regressors can be used for each dependent variable, as in the seemingly unrelated regression context (see, e.g., Srivastava and Giles 1987). Such an approach can be particularly useful in the modelling of multivariate economic data, where different economic variables may be expected to be relevant in the prediction of different aspects of economic behaviour. A classical example is given by Zellner (1962), who applied such an approach to explain investment on the part of two large corporations; his application is based on an investment equation in which a firm’s current gross investment is assumed to depend on the firm’s beginning-of-year capital stock and the value of its outstanding shares at the beginning of the year. Other classical applications dealing with the explanation of a certain economic activity in different geographical locations are due to Giles and Hampton (1984), who considered Cobb-Douglas production functions for five regions of New Zealand in the period 1935-1948, Donnelly (1982), who analyzed the regional demand for petrol in six different Australian states, and White and Hewings (1982) who estimated emolyment equations for five multi-county regions for each of several industrial categories within the State of Illinois. Other fields in which the seemingly unrelated approach to multivariate regression can be successfully employed are medicine (see, e.g., Keshavarzi et al. 2012) and food quality (see, e.g., Cadavez and Hennningsen 2012). In addition, in the models proposed in this paper the effect of the regressors on the responses changes with the populations, thus leading to finite mixtures of seemingly unrelated Gaussian linear regression models. For these new models, the paper addresses the model identification and maximum likelihood (ML) estimation. Parsimonious models are included into the proposed class, where parsimony is attained by constraining the covariance matrices of the responses for the different populations using a parameterisation for such matrices which is based on their spectral decomposition (see, e.g., Celeux and Govaert 1995). The usefulness of the new methods proposed in this paper is shown through the analysis of a real dataset in which the goal is the evaluation of the effect of prices and promotional activities on sales of canned tuna. In addition, the paper provides simple assumptions ensuring some regularity conditions that make it possible to prove the consistency of the ML estimator under the examined models. In order to provide some insight into the behaviour of the ML estimator also with finite samples, an extensive Monte Carlo study has been carried out, based on datasets generated from models belonging to the proposed model class. In particular, this study has focused on evaluating the effects of the sample size and the level of overlap among the linear regressions in the mixture on the behaviour of the ML estimator.

The key contributions of this paper are:

  • The introduction of methods for multivariate linear regression analysis based on seemingly unrelated Gaussian regression mixtures that let the researcher free to use a different vector of regressors for each dependent variable;

  • A proof of the consistency of the ML estimator under the proposed class of models;

  • A numerical study of the behaviour of the ML estimator under correctly specified models with varying sample sizes and varying overlap levels among population regression models.

The paper is organised as follows. Section 2.1 defines the proposed class of linear regression models. Section 2.2 shows how the models belonging to this class relate to some existing models. Details about the ML estimation are described in Sect. 2.3. Parsimonious models are introduced in Sect. 2.4. Methods to perform model selection are reported in Sect. 2.5. Results of the analysis of the real dataset are summarised in Sect. 2.7. A theorem providing conditions for the model identifiability is given in Sect. 3.1. The simple assumptions on the elements and parameters of the model class are detailed in Sect. 3.2. Theorems and lemmas used to prove the consistency of the ML estimator are reported in Sect. 3.3. The main results of the Monte Carlo study are summarised in Sect. 3.4. Section 4 provides some concluding remarks. The proofs of two theorems can be found in the Online Resource.

2 Regression models based on finite Gaussian mixtures

2.1 Seemingly unrelated Gaussian clusterwise linear regression models

A convenient way of introducing the class of models examined in this paper is to exploit the structure that typically characterises seemingly unrelated linear regression models (see, e.g., Srivastava and Giles 1987). Let \({\mathbf {Y}}_i=(Y_{i1}, \ldots , Y_{id}, \ldots , Y_{iD})'\) be the vector of the D dependent variables for the ith observation, \(i=1, \ldots , I\), and let \(\mathbf {{\mathbf {X}}}_i\) be the vector of G regressors employed for the overall prediction of \({\mathbf {Y}}_i\). Furthermore, suppose that only \(P_d\) regressors (\(P_d \le G\)) are relevant for the prediction of the dth dependent variable, and this assumption holds true for each dependent variable. Thus, let \({\mathbf {x}}_{id}\) be the \(P_d \times 1\) vector composed of the observed values of \({\mathbf {X}}_{id}\), which is the subvector of \(\mathbf {{\mathbf {X}}}_i\) with the \(P_d\) regressors for the ith observation to be used in the equation for the dth dependent variable, \(d=1, \ldots , D\). A seemingly unrelated linear regression model for the conditional distributions of \(Y_{id}|{\mathbf {X}}_{id}={\mathbf {x}}_{id}\), \(d=1, \ldots , D\), can be defined through the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{l} Y_{i1} = \lambda _1 + {\mathbf {x}}_{i1}'{\varvec{\beta }}_1 + \epsilon _{i1}, \\ \vdots \\ Y_{id} = \lambda _{d} + {\mathbf {x}}_{id}'{\varvec{\beta }}_d + \epsilon _{id}, \\ \vdots \\ Y_{iD} = \lambda _{D} + {\mathbf {x}}_{iD}'{\varvec{\beta }}_D + \epsilon _{iD}, \end{array} \right. \ \ i = 1, \ldots , I, \end{aligned}$$
(1)

where \(\lambda _{d}\), \({\varvec{\beta }}_d\) and \(\epsilon _{id}\) are the intercept, the regression coefficient vector and the error term for the ith observation in the equation for the dth dependent variable, respectively. Namely, the vector \({\varvec{\beta }}_d\) contains the \(P_d\) regression coefficients that express the joint linear effect of the \(P_d\) regressors on \(Y_d\). A classical assumption for this model is that the \(D-\)dimensional error vectors \({\varvec{\epsilon }}_{i}=(\epsilon _{i1}, \ldots , \epsilon _{id}, \ldots , \epsilon _{iD})'\) for the I sample observations are independent and identically distributed (i.i.d.), and that \({\varvec{\epsilon }}_{i} \sim N_D({\mathbf {0}},{\varvec{\varSigma }})\); \(N_D({\varvec{\mu }},{\varvec{\varSigma }})\) denotes the \(D-\)dimensional normal distribution with \(D \times 1\) mean vector \({\varvec{\mu }}\) and \(D \times D\) covariance matrix \({\varvec{\varSigma }}\); \(\phi \left( \cdot ; {\varvec{\mu }},{\varvec{\varSigma }}\right) \) is the corresponding probability density function (p.d.f.). Equations in (1) can be written in compact form as follows:

$$\begin{aligned} {\mathbf {Y}}_i= {\varvec{\lambda }} + \tilde{{\mathbf {X}}}_{i}'{\varvec{\beta }}+{\varvec{\epsilon }}_{i}, \ \ i = 1, \ldots , I, \end{aligned}$$

where \({\varvec{\lambda }}=\left( \lambda _{1}, \ldots , \lambda _{d}, \ldots , \lambda _{D}\right) '\), \({\varvec{\beta }}=\left( {\varvec{\beta }}'_1, \ldots , {\varvec{\beta }}'_d, \ldots , {\varvec{\beta }}'_D\right) '\) and \(\tilde{{\mathbf {X}}}_{i}\) is the following \(P \times D\) partitioned matrix:

$$\begin{aligned} \tilde{{\mathbf {X}}}_{i} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\mathbf {x}}_{i1} &{} {\mathbf {0}}_{P_1} &{} \cdots &{} {\mathbf {0}}_{P_1} \\ {\mathbf {0}}_{P_2} &{} {\mathbf {x}}_{i2} &{} \cdots &{} {\mathbf {0}}_{P_2} \\ \vdots &{} \vdots &{} &{} \vdots \\ {\mathbf {0}}_{P_D} &{} {\mathbf {0}}_{P_D} &{} \cdots &{} {\mathbf {x}}_{iD} \\ \end{array} \right] , \end{aligned}$$

with \({\mathbf {0}}_{P_d}\) denoting the \(P_d\)-dimensional null vector and \(P=\sum _{d=1}^D P_d\). \({\varvec{\beta }}\) is a \(P \times 1\) vector containing all the regression coefficients. This model is useful whenever the error terms in the D equations of the system (1) are correlated (i.e.: \({\varvec{\varSigma }}\) is not a diagonal matrix) and, thus, those equations have to be jointly considered. It differs from the classical multivariate linear regression model because it allows to use a specific vector of regressors for each dependent variable.

Mixtures of K Gaussian seemingly unrelated linear regression models can be introduced as follows:

$$\begin{aligned} {\mathbf {Y}}_i={\left\{ \begin{array}{ll} {\varvec{\lambda }}_1 + \tilde{{\mathbf {X}}}_{i}'{\varvec{\beta }}_1+{\varvec{\epsilon }}_{i}, \ {\varvec{\epsilon }}_{i} \sim N_D({\mathbf {0}},{\varvec{\varSigma }}_1), \ \ \text { with probability } \pi _1,\\ \quad \vdots \\ {\varvec{\lambda }}_k + \tilde{{\mathbf {X}}}_{i}'{\varvec{\beta }}_k+{\varvec{\epsilon }}_{i}, \ {\varvec{\epsilon }}_{i} \sim N_D({\mathbf {0}},{\varvec{\varSigma }}_k), \ \ \text { with probability } \pi _k,\\ \quad \vdots \\ {\varvec{\lambda }}_K + \tilde{{\mathbf {X}}}_{i}'{\varvec{\beta }}_K+{\varvec{\epsilon }}_{i}, \ {\varvec{\epsilon }}_{i} \sim N_D({\mathbf {0}},{\varvec{\varSigma }}_K), \ \ \text { with probability } \pi _K, \end{array}\right. } \end{aligned}$$
(2)

where the probabilities \(\pi _1, \ldots , \pi _K\) are assumed to be positive and summing to one. \({\varvec{\lambda }}_k\) and \({\varvec{\beta }}_k\) are vectors composed of D intercepts and P regression coefficients, respectively, for \(k=1, \ldots , K\); namely, \({\varvec{\lambda }}_k=\left( \lambda _{k1}, \ldots , \lambda _{kd}, \ldots , \lambda _{kD}\right) '\); \({\varvec{\beta }}_k = \left( {\varvec{\beta }}'_{k1}, \ldots , {\varvec{\beta }}'_{kd}, \ldots , {\varvec{\beta }}'_{kD}\right) '\). The covariance matrix \({\varvec{\varSigma }}_k\) is \(D \times D\)\(\forall k\). If all these K matrices are positive definite, it is possible to write the conditional p.d.f. of \({\mathbf {Y}}_i|{\mathbf {X}}_{i}={\mathbf {x}}_{i}\) as a weighted average of K Gaussian seemingly unrelated linear regression models with weights \(\pi _k\), \(k=1, \ldots , K\). Namely:

$$\begin{aligned} f({\mathbf {y}}_i|{\mathbf {x}}_i; {\varvec{\theta }}) = \sum _{k=1}^K \pi _k \phi \left( {\mathbf {y}}_i;{\varvec{\mu }}_{ik},{\varvec{\varSigma }}_{k}\right) , \ {\mathbf {y}}_i \in {\mathbb {R}}^{D}, \end{aligned}$$
(3)

where

$$\begin{aligned} {\varvec{\mu }}_{ik} = {\varvec{\lambda }}_k + \tilde{{\mathbf {X}}}_{i}'{\varvec{\beta }}_k, \end{aligned}$$
(4)

\({\varvec{\theta }}= ({\varvec{\pi }}',{\varvec{\theta }}'_{1}, \ldots , {\varvec{\theta }}'_{k}, \ldots , {\varvec{\theta }}'_{K})' \in {\varvec{\varTheta }}\), \({\varvec{\pi }}=\left( \pi _{1},\dots ,\pi _{K-1}\right) '\) such that \(\pi _k>0\)\( \ \forall k\), \(\sum _{k=1}^K \pi _k =1\), \({\varvec{\theta }}_{k}=\left( {\varvec{\lambda }}'_{k}, {\varvec{\beta }}'_{k}, ({\mathrm {v}}\left( {\varvec{\varSigma }}_{k}\right) )' \right) '\). The definition of \({\varvec{\theta }}_{k}\) involves the \({\mathrm {v}}(.)\) operator. Namely, \({\mathrm {v}}({\mathbf {B}})\) denotes the column vector obtained by eliminating all supradiagonal elements of a symmetric matrix \({\mathbf {B}}\) (thus, \({\mathrm {v}}({\mathbf {B}})\) contains only the distinct elements of \({\mathbf {B}}\)) (see, e.g., Magnus and Neudecker 1988). Note that the dependence of the p.d.f. \(f({\mathbf {y}}_i|{\mathbf {x}}_i; {\varvec{\theta }})\) on \({\mathbf {x}}_i\) in Eq. (3) is due to the linear term \(\tilde{{\mathbf {X}}}_{i}'{\varvec{\beta }}_k\) that affects \({\varvec{\mu }}_{ik}\) in Eq. (4).

2.2 Comparisons with other linear regression mixtures

When specific conditions are met, some special linear regression models can be obtained from Eq. (3).

  • If \(D=1\) (only one dependent variable is considered), Eq. (3) reduces to a mixture of univariate Gaussian linear regression models (see, e.g., Quandt and Ramsey 1978; De Sarbo and Cron 1988; De Veaux 1989).

  • If \(D=1\) and \({\varvec{\beta }}_k = {\varvec{\beta }}\)\(\forall k\) (only one dependent variable is considered and the regression coefficients are constrained to be equal among all components), the resulting model coincides with a univariate linear regression model with error terms distributed according to a mixture of K univariate Gaussian distributions (Bartolucci and Scaccia 2005).

  • If \(D>1\) and \({\mathbf {X}}_{id}={\mathbf {X}}_i\)\(\forall d\), the following equality holds:

    $$\begin{aligned} \tilde{{\mathbf {X}}}_i={\mathbf {I}}_D\otimes {\mathbf {x}}_i, \end{aligned}$$

    where \({\mathbf {I}}_D\) is the identity matrix of order D and \(\otimes \) denotes the Kronecker product operator (see, e.g., Magnus and Neudecker 1988). Equation (4) can be rewritten as

    $$\begin{aligned} {\varvec{\mu }}_{ik}={\varvec{\lambda }}_k+\left( {\mathbf {I}}_D\otimes {\mathbf {x}}_i\right) '{\varvec{\beta }}_k={\varvec{\lambda }}_k+{\mathbf {B}}_k'{\mathbf {x}}_i, \ k=1, \ldots , K, \end{aligned}$$

    where \({\mathbf {B}}_k=\left[ {\varvec{\beta }}_{k1} \cdots {\varvec{\beta }}_{kd} \cdots {\varvec{\beta }}_{kD}\right] \), thus leading to a finite mixture of Gaussian linear regression models with the same vector of predictors for all the dependent variables (see, e.g., Jones and McLachlan 1992).

  • If \(D>1\), \({\mathbf {X}}_{id}={\mathbf {X}}_i\)\(\forall d\) and \({\varvec{\beta }}_k = {\varvec{\beta }}\)\(\forall k\), multivariate linear regression models with a multivariate Gaussian mixture for the distribution of the error terms are obtained (Soffritti and Galimberti 2011).

  • If \(D>1\) and \({\varvec{\beta }}_k = {\varvec{\beta }}\)\(\forall k\), the resulting model coincides with a multivariate seemingly unrelated linear regression model whose error terms are assumed to follow a multivariate Gaussian mixture model (Galimberti et al. 2016).

Thus, the models proposed in this paper encompass all the linear regression mixture models just mentioned. It is also worth noting that seemingly unrelated regression models can be considered as multivariate regression models in which prior information about the absence of certain regressors from certain regression equations is explicitly taken into consideration (Srivastava and Giles 1987). Thus, Eq. (3) can also be seen as a constrained multivariate mixture of K Gaussian linear regression models with \(\mathbf {{\mathbf {X}}}_{id}={\mathbf {X}}_{i}\) as regressors in all the equations of the system (1) but with some regression coefficients constrained to be a priori equal to zero.

2.3 ML estimation

Similarly to any other finite mixture model, the ML estimation is carried out for a fixed value of K. Let \({\mathcal {Z}}=\left\{ ({\mathbf {x}}_{1}, {\mathbf {y}}_{1}), \ldots , ({\mathbf {x}}_{I}, {\mathbf {y}}_{I})\right\} \) be a sample of I observations. The log-likelihood of model (3) is equal to

$$\begin{aligned} l_I({\varvec{\theta }})=\sum _{i=1}^I \ln \left( \sum _{k=1}^K \pi _k \phi \left( {\varvec{y}}_{i};{\varvec{\lambda }}_{k}+\tilde{{\mathbf {X}}}_i'{\varvec{\beta }}_{k},{\varvec{\varSigma }}_{k}\right) \right) . \end{aligned}$$
(5)

The ML estimate \(\hat{{\varvec{\theta }}}_I\) can be computed using an EM algorithm (Dempster et al. 1977). Let \(u_{ik}\) be a binary variable equal to 1 when the ith observation has been generated from the kth component \(\phi \left( {\varvec{y}}_{i};{\varvec{\lambda }}_{k}+\tilde{{\mathbf {X}}}_i'{\varvec{\beta }}_{k},{\varvec{\varSigma }}_{k}\right) \) of the mixture (3), and 0 otherwise, for \(k=1, \ldots ,K\). Thus, \(\sum _{k=1}^K u_{ik}=1\). Furthermore, let \({\mathbf {u}}_{i+}\) be the K-dimensional vector whose kth element is \(u_{ik}\). Since vectors \({\mathbf {u}}_{i+}\)’s are generally unknown, the observed data \({\mathcal {Z}}\) can be considered incomplete, and Eq. (5) is the incomplete-data log-likelihood. If we knew both the observed data and the component-label vectors \({\mathbf {u}}_{i+}\)’s, we could obtain the so-called complete log-likelihood. By assuming that the component label vectors \({\mathbf {u}}_{1+}, \ldots , {\mathbf {u}}_{I+}\) are I i.i.d. random vectors whose unconditional distribution is multinomial consisting of one draw on K categories with probabilities \(\pi _1, \ldots , \pi _K\), the complete log-likelihood is equal to

$$\begin{aligned} l_{Ic}({\varvec{\theta }})=\sum _{i=1}^I \sum _{k=1}^K u_{ik} [\ln \pi _k + \ln \phi ({\mathbf {y}}_i;{\varvec{\mu }}_{ik},{\varvec{\varSigma }}_{k})]. \end{aligned}$$

Since the \(u_{ik}\)’s are missing, in the EM algorithm they are substituted with their conditional expected values. More specifically, the EM algorithm consists of iterating the following two steps until convergence:

E step on the basis of the current estimate \(\hat{{\varvec{\theta }}}^{(r)}\) of the model parameters \({\varvec{\theta }}\), the expected value of the complete log-likelihood given the observed data, \({\mathbb {E}}\left[ l_{Ic}({\varvec{\theta }})|{\mathcal {Z}}\right] \), is computed. In practice, this consists in substituting any \(u_{ik}\) with its conditional expected value \({\mathbb {E}}\left[ u_{ik}|{\mathcal {Z}}\right] \), which is equal to

$$\begin{aligned} p_{ik}^{(r)}=\frac{{\hat{\pi }}^{(r)}_k \phi \left( {\mathbf {y}}_i;\hat{{\varvec{\mu }}}^{(r)}_{ik},\hat{{\varvec{\varSigma }}}^{(r)}_{k}\right) }{\sum _{h=1}^K {\hat{\pi }}^{(r)}_h \phi \left( {\mathbf {y}}_i;\hat{{\varvec{\mu }}}^{(r)}_{ih},\hat{{\varvec{\varSigma }}}^{(r)}_{h}\right) }. \end{aligned}$$

M step\(\hat{{\varvec{\theta }}}^{(r)}\) is updated by maximising \(\mathrm {E}\left[ l_{Ic}({\varvec{\theta }})|{\mathcal {Z}}\right] \) with respect to \({\varvec{\theta }}\). This leads to the following solutions for the prior probabilities:

$$\begin{aligned} {\hat{\pi }}^{(r+1)}_k = \frac{1}{I}\sum _{i=1}^I p^{(r)}_{ik}, k=1, \ldots , K. \end{aligned}$$

As far as the solutions for \(\hat{{\varvec{\lambda }}}^{(r+1)}_k\), \(\hat{{\varvec{\beta }}}^{(r+1)}_k\) and \(\hat{{\varvec{\varSigma }}}^{(r+1)}_k\) are concerned, they depend on each other; thus, in order to obtain such solutions an iterative updating scheme is needed within each M step. Let \(\tilde{{\varvec{\lambda }}}^{(0)}_k=\hat{{\varvec{\lambda }}}^{(r)}_k\), \(\tilde{{\varvec{\beta }}}^{(0)}_k=\hat{{\varvec{\beta }}}^{(r)}_k\) and \(\tilde{{\varvec{\varSigma }}}^{(0)}_k=\hat{{\varvec{\varSigma }}}^{(r)}_k\) be the starting values within the \((r+1)\)th M step; the \((j+1)\)th updates are given by:

$$\begin{aligned} \tilde{{\varvec{\lambda }}}^{(j+1)}_k= & {} \frac{\sum _{i=1}^I p^{(r)}_{ik}\left( {\mathbf {y}}_i-\tilde{{\mathbf {X}}}_i'\tilde{{\varvec{\beta }}}_k^{(j)}\right) }{\sum _{i=1}^I p^{(r)}_{ik}}, \\ \tilde{{\varvec{\beta }}}_k^{(j+1)}= & {} \left( \sum _{i=1}^I p^{(r)}_{ik}\tilde{{\mathbf {X}}}_i\left( \tilde{{\varvec{\varSigma }}}_k^{(j)}\right) ^{-1}\tilde{{\mathbf {X}}}_i'\right) ^{-1}\sum _{i=1}^I p^{(r)}_{ik}\tilde{{\mathbf {X}}}_i\left( \tilde{{\varvec{\varSigma }}}_k^{(j)}\right) ^{-1}\left( {\mathbf {y}}_i-\tilde{{\varvec{\lambda }}}_k^{(j+1)}\right) ,\\ \tilde{{\varvec{\varSigma }}}_k^{(j+1)}= & {} \frac{\sum _{i=1}^I p^{(r)}_{ik}\left( {\mathbf {y}}_i-\tilde{{\varvec{\lambda }}}^{(j+1)}_k-\tilde{{\mathbf {X}}}_i'\tilde{{\varvec{\beta }}}_k^{(j+1)}\right) \left( {\mathbf {y}}_i-\tilde{{\varvec{\lambda }}}^{(j+1)}_k-\tilde{{\mathbf {X}}}_i'\tilde{{\varvec{\beta }}}_k^{(j+1)}\right) '}{\sum _{i=1}^I p^{(r)}_{ik}}, \end{aligned}$$

for \(k=1,\ldots ,K\). It is worth mentioning that these solutions for the M step admit as special cases the ones already derived for mixtures of univariate and multivariate Gaussian linear regression models (see, e.g., De Veaux 1989; Jones and McLachlan 1992).

Similarly to Gaussian mixture models (see, e.g. Kiefer and Wolfowitz 1956; Day 1969), the maximisation of \(l_I({\varvec{\theta }})\) might be affected by problems arising from its unboundedness on \({\varvec{\varTheta }}\) and by the presence of local spurious modes. A way to deal with these problems is to introduce suitable constraints on the parameter space \({\varvec{\theta }}\) and to perform the estimation under a constrained \({\varvec{\theta }}\). Methods developed for Gaussian mixtures (see, e.g. Ingrassia and Rocci 2011; Rocci et al. 2018) could be exploited also for the models defined by Eqs. (3) and (4). An approach based on the maximisation of the posterior distribution of the model parameters within a Bayesian framework could also be employed (see, e.g., Frühwirth-Schnatter 2006, chapter 3).

2.4 Parsimonious models

The number of free parameters for models described in Sect. 2.1 is given by \(npar=K-1+K\cdot \left( P+D\right) +K\dfrac{D(D+1)}{2}\). It is evident that this number increases quadratically with the number of dependent variables. In order to overcome this issue, parsimonious models can be obtained by introducing constraints on the component covariance matrices \({\varvec{\varSigma }}_{k}\) (\(k=1,\ldots ,K\)). In particular, denoting the determinant of \({\varvec{\varSigma }}_{k}\) as \(|{\varvec{\varSigma }}_{k}|\) and following the approach described in Celeux and Govaert (1995), these constraints can be introduced on the eigenstructure \({\varvec{\varSigma }}_{k}=\alpha _{k}{\mathbf {D}}_{k}{\mathbf {A}}_{k}{\mathbf {D}}'_{k}\), where \(\alpha _{k}=|{\varvec{\varSigma }}_{k}|^{1/D}\), \({\mathbf {A}}_{k}\) is the diagonal matrix containing the eigenvalues of \({\varvec{\varSigma }}_{k}\) (normalised in such a way that \(|{\mathbf {A}}_{k}|=1\)) and \({\mathbf {D}}_{k}\) is the matrix of eigenvectors of \({\varvec{\varSigma }}_{k}\). These three parameters determine the geometrical features of \({\varvec{\varSigma }}_{k}\) in terms of volume, shape and orientation (see Celeux and Govaert 1995, for more details). A family of 14 parameterisations can be obtained by constraining one or more of the three elements of the eigenstructure to be equal among components. Some details about these parameterisations can be found in Table 1. Once a parameterisation is selected, the EM algorithm described in Sect. 2.3 must be modified in order to obtain the corresponding parameter estimates. Namely, this modification involves only the M step updates \(\hat{{\varvec{\varSigma }}}_k^{(r+1)}\). Depending on the parameterisation, these updates can be computed in closed form or using iterative procedures (see Celeux and Govaert 1995, for more details).

Table 1 Parsimonious parameterisations for the covariance matrices \({\varvec{\varSigma }}_k\)
Full size table

2.5 Model selection

The EM algorithm described in Sect. 2.3 requires to specify in advance a value for K. In most practical applications, however, the number of components is not known and must be determined from the data. A common solution to this task is obtained by exploiting model selection techniques (see, e.g., McLachlan and Peel 2000, chapter 6). In particular, the Bayesian Information Criterion (Schwarz 1978), defined as

$$\begin{aligned} BIC_M=2l_M(\hat{{\varvec{\theta }}})-npar_M\ln I, \end{aligned}$$
(6)

is a model selection criterion that has been used extensively in the context of Gaussian mixture models and of mixtures of Gaussian regression models (see, e.g., Fraley and Raftery 2002; Soffritti and Galimberti 2011; Dang and McNicholas 2015). This criterion allows to trade-off the fit (measured by \(l_M(\hat{{\varvec{\theta }}})\), the maximum of the incomplete loglikelihood of model M) and complexity (given by \(npar_M\), the number of free parameters in model M): the larger the BIC, the better the model. The BIC can be used not only to select the optimal number of components, but also to choose the optimal parameterisation (among those described in Sect. 2.4). Furthermore, in Sect. 2.7 this criterion is exploited to perform variable selection.

2.6 Initialisation and convergence of the EM algorithm

A specific function implementing the ML estimation of the parameters of the model defined in Eqs. (3) and (4) through the EM algorithm described in Sect. 2.3 has been developed in the R environment (R Core Team 2019). This function also allows the estimation of the parsimonious models illustrated in Sect. 2.4. The starting estimates \(\hat{{\varvec{\theta }}}^{(0)}\) of the model parameters in the analyses reported in Sect. 2.7 have been obtained through the following two-step strategy.

Step 1:

Use the sample \({\mathcal {Z}}\) to estimate the seemingly unrelated linear regression model defined in Eq. (1) and consider the I sample residuals \({\mathcal {E}}=(\hat{{\varvec{\epsilon }}}_{1}, \cdots , \hat{{\varvec{\epsilon }}}_{I})\) of this model. Then, fit a Gaussian mixture model with K components and the desired parameterisation to the residuals \({\mathcal {E}}\). The estimated weights and covariance matrices of this mixture model are \({\hat{\pi }}_k^{(0)}\) and \(\hat{{\varvec{\varSigma }}}_k^{(0)}\), \(k=1, \ldots , K\).

Step 2:

Consider the partition \({\mathcal {P}}=\{{\mathcal {Z}}_1, \ldots , {\mathcal {Z}}_K\}\) of the sample \({\mathcal {Z}}\) obtained from the highest estimated component posterior probabilities of the mixture model fitted to \({\mathcal {E}}\) at Step 1. Estimate K different seemingly unrelated linear regression models, one for each of the K elements of \({\mathcal {P}}\). The estimated intercepts and regression coefficients of these regression models are \(\hat{{\varvec{\lambda }}}_k^{(0)}\) and \(\hat{{\varvec{\beta }}}_k^{(0)}\), \(k=1, \ldots , K\).

In the implementation of this initialisation strategy the R packages mclust (Scrucca et al. 2017) and systemfit (Henningsen and Hamann 2007) have been exploited. It is worth noting that all the elements of the partition \({\mathcal {P}}\) examined at Step 2 have to be nonempty in order for this initialisation strategy to work properly. If this does not happen, an approach based on multiple random initialisations and multiple executions of the EM algorithm could be adopted. Furthermore, the R function implementing the EM algorithm has been devised to manage situations in which the mixture model to be fitted at Step 1 is affected by estimating problems. In those situations, mixture models with K components were fitted for all possible parameterisations, and \({\hat{\pi }}_k^{(0)}\) and \(\hat{{\varvec{\varSigma }}}_k^{(0)}\) were obtained by picking the weights and covariance matrices from the fitted model with the larger value of BIC.

As far as the convergence of the EM algorithm is concerned, the following criteria have been implemented. The EM algorithm is stopped when the number of iterations reaches 500 or \(|l_\infty ^{(r+1)}-l^{(r)}|<10^{-8}\), where \(l^{(r)}\) is the log-likelihood value from iteration r, and \(l_\infty ^{(r+1)}\) is the asymptotic estimate of the log-likelihood at iteration \(r+1\) (Dang and McNicholas 2015). The stopping rules for the iterative scheme within the M step are either when the mean Euclidean distance between two consecutive estimated vectors of the model parameters is lower than \(10^{-8}\) or when the number of iterations reaches the maximum of 500.

In order to avoid difficulties arising when matrices \(\hat{{\varvec{\varSigma }}}_{k}^{(r)}\) are singular or nearly singular, the R function implementing the EM algorithm embeds suitable constraints on the eigenvalues of \(\hat{{\varvec{\varSigma }}}_{k}^{(r)}\) for \(k=1, \ldots , K\). Namely, all estimated covariance matrices have been required to have eigenvalues greater than \(10^{-20}\); furthermore, the ratio between the smallest and the largest eigenvalues of such matrices is required to be not lower than \(10^{-10}\).

2.7 Analysis of canned tuna sales

In order to show the usefulness of the proposed methodology in comparison with other existing methods, data taken from Chevalier et al. (2003) and available within the R package bayesm (Rossi 2012) have been employed. This dataset contains the volume of weekly sales for seven of the top 10 U.S. brands in the canned tuna product category for \(I=338\) weeks between September 1989 and May 1997, together with a measure of the display activity and the log price of each brand. Analyses have been focused on \(D=2\) products: Bumble Bee Solid 6.12 oz. (BBS) and Bumble Bee Chunk 6.12 oz. (BBC). The goal is to study the effect of prices and promotional activities on sales for these two products. Thus, the following variables have been examined: the log unit sale (\(Y_{i1}\)), the measure of the display activity (\(x_{i1}\)) and the log price (\(x_{i2}\)) registered in week i for BBS; \(Y_{i2}\), \(x_{i3}\) and \(x_{i4}\) denote the same information for BBC. Results from analyses of other brands can be found, for example, in Rossi et al. (2005) and Galimberti et al. (2016).

Table 2 Maximised log-likelihood and BIC value for the best models fitted to the tuna dataset in the first analysis within subclasses of models defined by the examined values of K
Full size table

A first analysis has been performed by assuming that prices and promotional activities for each of the two examined products can only affect sales of the same product. Thus, \({\mathbf {x}}'_{i1}= (x_{i1}, x_{i2})\) and \({\mathbf {x}}'_{i2}= (x_{i3}, x_{i4})\) are the vectors with the regressors that have been used in the equations for \(Y_{i1}\) and \(Y_{i2}\), respectively, in all the models fitted to the data in this analysis. The "R" function illustrated in Sect. 2.6 has been used to estimate models defined in Eqs. (3) and (4) with a value of K from 1 to 4. For each \(K>1\), fourteen different parsimonious models have been fitted to the dataset, one for each of the possible structures of the covariance matrices (see Sect. 2.4). When \(K=1\), \({\varvec{\varSigma }}_1\) can only be fully unconstrained, diagonal with D unequal variances or diagonal with equal variances; thus, only three models with \(K=1\) have been fitted. Models have been estimated for the values \(K=2, 3, 4\) also under the constraint \({\varvec{\beta }}_k={\varvec{\beta }} \ \forall k\), thus leading to the models proposed by Galimberti et al. (2016). Table 2 provides some model fitting results within the four subclasses of models identified by the examined values of K for each of the two sets of unconstrained and constrained models just mentioned. According to the BIC, the best model for studying the effect of prices and promotional activities on sales for BBS and BBC canned tuna is obtained with a mixture of \(K=3\) unconstrained seemingly unrelated linear regression models. Parameter estimates of this model are reported in the upper part of Table 3. By focusing the attention on the estimated regression coefficients, there is a clear evidence of differential effects of the log prices on the log unit sales for both products when we compare the three clusters of weeks detected by the model. As far as promotional activities are concerned, their effects on the log unit sales seem to be slightly positive only in the smallest cluster of weeks.

Table 3 Parameter estimates of the overall best models fitted to the tuna dataset in the first and second analyses
Full size table

In order to discover whether taking account of the correlation between the errors in the bivariate regression model for the log unit sales of BBC and BBS really allows to obtain a better model for this dataset, also mixtures of K linear regression models composed of two separate univariate regression equations have been examined, in which (conditional) independence between the log unit sales of BBC and BBS is assumed. Such mixtures have been estimated for \(K\in {1,2,3,4}\), both with and without the constraint \({\varvec{\beta }}_k={\varvec{\beta }} \ \forall k\). For each \(K>1\), two parameterisations have been considered: equal or unequal variances among components. A model with \(K=2\) components, unconstrained regression coefficients and unequal variances has been selected for both BBS and BBC, with BIC values equal to \(-165.56\) and \(-510.14\), respectively. The overall BIC value under the independence assumption is thus given by \(-675.70\). Note that this BIC value is smaller than the one obtained using mixtures of seemingly unrelated regression models. This seems to suggest that the conditional distributions of \(Y_{i1}\) and \(Y_{i2}\) should not be modelled separately and that the seemingly unrelated regression setting actually leads to a better model for the data in this analysis.

Since BBS and BBC products are produced by the same brand, prices and promotional activities for one product could have an impact on the sales of the other product. Thus, additional models should be examined, in which each of the \(G=4\) regressors \(x_{i1}, x_{i2}, x_{i3}, x_{i4}\) can enter into either of the two regression equations for \(Y_{i1}\) and \(Y_{i2}\). For these reasons, for each K (\(K=1,2,3,4\)) and each dependent variable, an exhaustive search for the relevant regressors has been performed. For each value of K and each possible structure of the component-covariance matrices, \(2^{G \cdot D}=256\) different bivariate regression models can be specified. In this second analysis, the overall number of estimated models, as defined in Eqs. (3) and (4), is 11520 (\(256 \cdot 3 + 256 \cdot 14 \cdot 3)\). This same set of models for \(K=2,3,4\) has been estimated also under the constraint \({\varvec{\beta }}_k={\varvec{\beta }} \ \forall k\). In this situation, the BIC defined in Sect. 2.5 can be employed to choose not only the best model but also the best subset of regressors for each dependent variable. Table 4 provides some model fitting results for the two sets of models just illustrated. According to the BIC, the best model for studying the effect of prices and promotional activities on sales for BBS and BBC canned tuna is still obtained with a mixture of \(K=3\) unconstrained linear seemingly unrelated regression models. In this model, the log unit sales of BBS canned tuna are simply regressed on the log prices of BBS canned tuna; thus, \({\mathbf {x}}_{i1}= (x_{i2})\). As far as the regressors for the BBC log unit sales are concerned, only the log price of BBC canned tuna has been selected, that is \({\mathbf {x}}_{i2}= (x_{i4})\). From the parameter estimates (see the lower part of Table 3) it emerges that the effects of log prices on the log unit sales for both products are negative within each cluster detected by this model. However, these effects are stronger in the first cluster of weeks (especially for BBS canned tuna) and weaker in the third cluster. This seems to suggest that the effect of log price on log unit sales is not homogeneous during the examined period of time for both dependent variables. Heterogeneity over time appears to emerge also in the correlations between log sales of BBS and BBC products: they are almost zero within the second and third cluster, while in the first cluster these variables show a mild negative correlation. According to the highest estimated posterior probabilities, 19, 94 and 225 weeks are assigned to these three clusters, respectively. An interesting feature of this partition is that 17 out of the 19 weeks in the first cluster are consecutive from week 58 to week 74, which correspond to the period from mid-October 1990 to mid-February 1991 (see the additional information about the canned tuna dataset available at the University of Chicago website http://research.chicagobooth.edu/kilts/marketing-databases/dominicks/). That period was characterised by a worldwide boycott campaign (promoted by the U.S. nongovernmental organisation Earth Island Institute) encouraging consumers not to buy Bumble Bee tuna because Bumble Bee was found to be buying yellow-fin tuna caught by dolphin-unsafe techniques (Baird and Quastel 2011). The selected model seems to suggest that such events may be one of the sources of the unobserved heterogeneity that affected both the correlation between log sales of BBS and BBC and the effects of log price on log unit sales.

Table 4 Maximised log-likelihood and BIC value for the best models fitted to the tuna dataset in the second analysis within subclasses of models defined by the examined values of K
Full size table

3 Consistency of the ML estimator

Although in a regression context the primary interest is on the conditional p.d.f. of \({\mathbf {Y}}_i|{\mathbf {X}}_{i}={\mathbf {x}}_{i}\), the regularity conditions ensuring the consistency of the ML estimator of \({\varvec{\theta }}\) developed in this paper concern the joint distribution of the regressors and dependent variables. Let \({\mathbf {Z}}_i=(\varvec{{\mathbf {X}}}_i',{\mathbf {Y}}_i')'\). The density of \({\mathbf {Z}}_i\) is supposed to have the form

$$\begin{aligned} h({\mathbf {z}}_i; {\varvec{\psi }}) = q({\mathbf {x}}_i; {\varvec{\vartheta }}) f({\mathbf {y}}_i|{\mathbf {x}}_i; {\varvec{\theta }}), \ {\mathbf {z}}_i=({\mathbf {x}}_i',{\mathbf {y}}_i')' \in {\mathbb {R}}^{G+D}, \end{aligned}$$
(7)

for some \({\varvec{\psi }}=({\varvec{\vartheta }}', {\varvec{\theta }}')' \in {\varvec{\varPsi }}={\varvec{\varUpsilon }} \times {\varvec{\varTheta }}\). The function \(q({\mathbf {x}}; {\varvec{\vartheta }})=d Q\left( {\mathbf {x}}; {\varvec{\vartheta }}\right) /d\mu \) is the Radon-Nikodym density of \(Q\left( {\mathbf {x}}; {\varvec{\vartheta }}\right) \), the joint distribution of \({\mathbf {X}}\), with \(Q\left( {\mathbf {x}}; {\varvec{\vartheta }}\right) \in {\mathcal {B}}=\{Q\left( {\mathbf {x}}; {\varvec{\vartheta }}\right) ; {\varvec{\vartheta }} \in {\varvec{\varUpsilon }}\}\). The conditional p.d.f. of \({\mathbf {Y}}| \varvec{{\mathbf {X}}} = {\mathbf {x}}\) is given in Eq. (3). It is also assumed that the marginal density of the predictors \(q({\mathbf {x}}; {\varvec{\vartheta }})\) is a parametric function whose parameters \({\varvec{\vartheta }}\) do not involve the parameters \({\varvec{\theta }}\) that characterise the conditional density function of \({\mathbf {Y}} | {\mathbf {X}} = {\mathbf {x}}\). Hereafter the class of finite mixtures of Gaussian linear regression models with random predictors just defined is denoted as \({\mathfrak {F}}_K = \{h({\mathbf {z}}; {\varvec{\psi }}), {\varvec{\psi }} \in {\varvec{\varPsi }}\}\), where K is the order of the mixture model (3).

This section provides a study of the behaviour of the ML estimator for the model class \({\mathfrak {F}}_K\) as the sample size increases. Properties of the ML estimator have been analytically investigated with \(I \rightarrow \infty \). A numerical evaluation has been carried out with increasing finite sample sizes. Section 3.1 provides conditions for model identifiability, that represents a preliminary requirement to study consistency. Section 3.2 contains simple assumptions ensuring the consistency of the ML estimator. The proof of the consistency reported in Sect. 3.3 is based on a general consistency theorem that holds true for the extremum estimators of parametric models in the presence of i.i.d. random variables (see Newey and McFadden 1994, Theorem 2.1). The assumptions on the elements and parameters of \({\mathfrak {F}}_K\) are defined so as to ensure that the conditions required by that theorem are fulfilled and, thus, the theorem can be applied to the ML estimator of the models examined in Sect. 2.1. As suggested by Newey and McFadden (1994, p. 2122), the assumptions are formulated to be explicit and primitive in the sense that they are easy to interpret.

3.1 Identifiability

Consider the class of models \({\mathfrak {F}} = \{{\mathfrak {F}}_K, K=1, \ldots , K_{max}\}\), where \(K_{max}\) denotes the maximum order specified by the researcher for the mixture in Eq. (3). This class is said to be identifiable if, for any two models M, \(M^* \in {\mathfrak {F}}\) with parameters \({\varvec{\psi }}=({\varvec{\vartheta }}',{\varvec{\theta }}')'\) and \({\varvec{\psi }}^*=({\varvec{\vartheta }}'^*,{\varvec{\theta }}'^*)'\), respectively,

$$\begin{aligned} q({\mathbf {x}}; {\varvec{\vartheta }}) \sum _{k=1}^K \pi _k \phi \left( {\mathbf {y}};{\varvec{\mu }}_{k},{\varvec{\varSigma }}_{k}\right) = q({\mathbf {x}}; {\varvec{\vartheta }}^*) \sum _{k=1}^{K^*} \pi ^*_k \phi \left( {\mathbf {y}};{\varvec{\mu }}^*_{k},{\varvec{\varSigma }}^*_{k}\right) \forall ({\mathbf {x}},{\mathbf {y}}) \in {\mathbb {R}}^{G+D} \end{aligned}$$

implies that \({\varvec{\vartheta }}={\varvec{\vartheta }}^*\), \(K=K^*\) and \({\varvec{\theta }}={\varvec{\theta }}^*\).

Several types of non-identifiability can affect the model class \({\mathfrak {F}}\). A first type is due to invariance to relabeling the components (also known as label-switching). Furthermore, non-identifiability is caused by potential overfitting associated with empty components or equal components. These types of non-identifiability are common to any finite mixture model (see, e.g., Frühwirth-Schnatter 2006, p. 15). For mixtures of univariate and multivariate Gaussian linear regression models with random regressors, another type of non-identifiability arises when the marginal density \(q({\mathbf {x}}; {\varvec{\vartheta }})\) assigns positive probability on a \((G-1)\)-dimensional hyperplane (Hennig 2000). A similar issue can occur also for the model class \({\mathfrak {F}}\).

Under mild conditions, the identifiability of the model class \({\mathfrak {F}}\) is ensured by the following theorem (see Section A of the Online Resource for a proof).

Theorem 1

  1. (I1)

    Let \(\mathcal {{\bar{B}}}=\{Q\left( {\mathbf {x}}; {\varvec{\vartheta }}\right) ; {\varvec{\vartheta }} \in \varvec{{\bar{\varUpsilon }}}\}\) be a class of identifiable models composed of parametric joint distributions for \({\mathbf {X}}\), such that the marginal distributions of \({\mathbf {X}}_{d}\) do not give positive probability to any \((P_d-1)\)-dimensional hyperplane of \({\mathbb {R}}^{P_d}\), for \(d=1,\ldots ,D\). Let \(q({\mathbf {x}}; {\varvec{\vartheta }})=d Q\left( {\mathbf {x}}; {\varvec{\vartheta }}\right) /d\mu \) be the corresponding Radon-Nikodym density.

Furthermore, let \({\varvec{\varPsi }}=\varvec{{\bar{\varUpsilon }}} \times {\varvec{\varTheta }}\) be a parameter space associated with the model class \({\mathfrak {F}}\) whose elements \({\varvec{\psi }}=({\varvec{\vartheta }}',{\varvec{\theta }}')'\) fulfil the following conditions:

$$\begin{aligned}&\displaystyle {\pi _k>0 \ \forall k}; \end{aligned}$$
(8)
$$\begin{aligned}&\displaystyle {\varvec{\lambda }}_k \ne {\varvec{\lambda }}_{k'} \vee {\varvec{\beta }}_k \ne {\varvec{\beta }}_{k'} \vee {\varvec{\varSigma }}_{k} \ne {\varvec{\varSigma }}_{k'} \ \forall \ k \ne k'. \end{aligned}$$
(9)

Let \(M \in {\mathfrak {F}}_K\) and \(M^* \in {\mathfrak {F}}_{K^*}\) be two finite mixtures of Gaussian linear regression models with orders K and \(K^*\), respectively. If \({\varvec{\psi }}_M = ({\varvec{\vartheta }}'_M,{\varvec{\theta }}'_M)' \in {\varvec{\varPsi }}_M\) and \({\varvec{\psi }}^*_{M^*} = ({\varvec{\vartheta }}'^*_{M^*},{\varvec{\theta }}'^*_{M^*})' \in {\varvec{\varPsi }}_{M^*}\) exist such that \(q({\mathbf {x}}; {\varvec{\vartheta }}_M) f({\mathbf {y}}|{\mathbf {x}}; {\varvec{\theta }}_M) = q({\mathbf {x}}; {\varvec{\vartheta }}^*_{M^*}) f({\mathbf {y}}|{\mathbf {x}}; {\varvec{\theta }}^*_{M^*})\) with \({\varvec{\vartheta }}_M,{\varvec{\vartheta }}^*_{M^*} \in \varvec{{\bar{\varUpsilon }}}\)\( \forall ({\mathbf {x}}',{\mathbf {y}}')' \in {\mathbb {R}}^{G+D}\), then \(K=K^*\) and \({\varvec{\psi }}_M={\varvec{\psi }}^*_{M^*}\).

The condition \(\pi _k >0, k=1, \ldots , K\) in Eq. (8) allows to avoid non-identifiability due to empty components. The constraints on \({\varvec{\varTheta }}\) defined by the Eq. (9) make it possible to avoid non-identifiability caused by equal components. Furthermore, Eq. (9) implies that any two parameter vectors \({\varvec{\theta }}_k\) and \({\varvec{\theta }}_{k'}\) differ in at least one element which need not be the same for all components. As noted by Frühwirth-Schnatter (2006, p. 20), constraints defined by Eq. (9) force a unique labeling of the components, thus preventing label switching. In particular, if all K vectors \({\varvec{\theta }}_{1}, \ldots ,{\varvec{\theta }}_{k}, \ldots , {\varvec{\theta }}_{K}\) differ in the same qth element \(\theta _{k,q}\), then a unique labeling can be obtained by considering a strict order constraint on that element:

$$\begin{aligned} \theta _{1,q}< \theta _{2,q}< \cdots < \theta _{K,q}. \end{aligned}$$
(10)

This strict order constraint imposes \(K-1\) strict inequalities between pairs \(\theta _{k,q}\) and \(\theta _{k+1,q}\) for all \(k=1,\ldots ,K-1\). When such an element does not exist, it is possible to replace some of these strict inequalities by constraints on different elements of \({\varvec{\theta }}_k\) (for further details, see Frühwirth-Schnatter 2006, pp. 19-20). Conditions (I1) on the marginal distributions of \({\mathbf {X}}_{d}\) generalise the identifiability conditions introduced by Hennig (2000) for mixtures of univariate Gaussian linear regression models with random covariates. It is worth noting that these latter conditions may be violated in applications with dummy or categorical regressors and, more generally, with regressors taking a small number of values.

3.2 Assumptions

Let the true density function of \({\mathbf {Z}}\) be denoted as \(g({\mathbf {z}})\). The conditions required in this paper for the consistency of the ML estimator can be partitioned into two classes: i) conditions on the parameters \({\varvec{\theta }}\) that characterise the conditional p.d.f. of \({\mathbf {Y}}|{\mathbf {X}}={\mathbf {x}}\); ii) conditions concerning the predictors \({\mathbf {X}}\).

Consider the model class \({\mathfrak {F}}_K = \{h({\mathbf {z}}; {\varvec{\psi }}), {\varvec{\psi }} \in \varvec{{\bar{\varPsi }}}\}\), with \(\varvec{{\bar{\varPsi }}}=\varvec{{\bar{\varUpsilon }}} \times \varvec{{\bar{\varTheta }}}\) denoting a compact metric subspace of \({\varvec{\varPsi }}\) whose elements fulfil the following conditions:

  1. (C1)

    \({\varvec{\varSigma }}_{k} \in {\mathcal {D}}\)\(\forall k\), where \({\mathcal {D}}\) denotes the set of the \(D \times D\) positive definite matrices with eigenvalues in [a, b], with \(0< a< b < \infty \);

  2. (C2)

    \({\varvec{\beta }}_{k} \in {\mathcal {B}}(\eta ,P)\)\(\forall k\), where \({\mathcal {B}}(\eta ,r)=\{{\mathbf {a}} \in {\mathbb {R}}^r: \Vert {\mathbf {a}}\Vert \le \eta \}\), \(\eta >0\);

  3. (C3)

    \({\varvec{\lambda }}_{k} \in {\mathcal {B}}(\eta ,D)\)\(\forall k\),

where \(\Vert .\Vert \) denotes the Euclidean norm. From Eq. (7) it is possible to write

$$\begin{aligned} \ln [h({\mathbf {z}}; {\varvec{\psi }})] = \ln [q({\mathbf {x}}; {\varvec{\vartheta }})] + \ln [ f({\mathbf {y}}|{\mathbf {x}}; {\varvec{\theta }})]. \end{aligned}$$
(11)

For the function \(\ln [q({\mathbf {x}}; {\varvec{\vartheta }})]\) in Eq. (11) it is supposed that

$$\begin{aligned} h_0 + h_1 \Vert {\mathbf {x}}\Vert ^2 \le \ln [q({\mathbf {x}}; {\varvec{\vartheta }})] \le h_2 + h_3 \Vert {\mathbf {x}}\Vert ^2 \ \forall {\mathbf {x}} \in {\mathbb {R}}^{G}, \ \forall {\varvec{\vartheta }} \in \varvec{{\bar{\varUpsilon }}}, \end{aligned}$$
(12)

where \(h_0\), \(h_1\), \(h_2\) and \(h_3\) are real constants, and

$$\begin{aligned} \ln [q({\mathbf {x}}; {\varvec{\vartheta }})] \text { is continuous at each } {\varvec{\vartheta }} \in \varvec{{\bar{\varUpsilon }}} \text { with probability one}. \end{aligned}$$
(13)

It is also assumed that \(g({\mathbf {x}})\), the true density function of \({\mathbf {x}}\), fulfils the following condition:

$$\begin{aligned} \int \Vert {\mathbf {x}}\Vert ^2 g({\mathbf {x}})d{\mathbf {x}} < \infty . \end{aligned}$$
(14)

Finally, it is required that

  1. (C4)

    a unique model \(M^0 \in {\mathfrak {F}}_{K^0}\) exists such that \(g({\mathbf {z}})=h({\mathbf {z}}; {\varvec{\breve{\psi }}}_{M^0})\) for some parameter value \({\varvec{\breve{\psi }}}_{M^0} \in {\varvec{{\bar{\varPsi }}}}\), where the order \(K^0\) of model \(M^0\) is known.

Conditions (C1)-(C3) and assumption (12) are required to ensure a boundedness inequality for the function \(\ln [h({\mathbf {z}}; {\varvec{\psi }})]\). The constraints on the component-covariance matrices illustrated in the condition (C1) can also avoid degeneracies and spurious local solutions in the maximisation of the log-likelihood function. Condition (C4) and assumption (14) are necessary for the second part of the proof of Theorem 2 (see Section B in the Online Resource). In particular, condition (C4) states that the model class \({\mathfrak {F}}_K\) is correctly specified. It is worth mentioning that conditions (C1)-(C4) are similar to the ones described in Maugis et al. (2009).

3.3 Derivation of the consistency result

For the proof of the consistency of the ML estimator \(\hat{{\varvec{\psi }}}_I\), some preliminary theorems and lemmas are needed. Namely, Theorem 2 states that, under some of the just introduced assumptions, it is possible to obtain an envelope function \(e({\mathbf {z}})\) for the model class \({\mathfrak {F}}_K\) and that this function is g-integrable (see Section B of the Online Resource for a proof). Lemmas 1 and 2 ensure some conditions that are required from the general consistency theorem in Newey and McFadden (1994). Namely, under the conditions stated in Lemma 1, \({\mathbb {E}}\left( \ln [h({\mathbf {Z}}; {\varvec{\psi }})]\right) \) has a unique maximum at \({\varvec{\psi }}_0\), where \({\varvec{\psi }}_0\) denotes the true value of the model parameter; furthermore, if the conditions required by Lemma 2 are fulfilled, \({\mathbb {E}}\left( \ln [h({\mathbf {Z}}; {\varvec{\psi }})]\right) \) is continuous and \(\frac{1}{I} \sum _{i=1}^I \ln [h({\mathbf {z}}_i; {\varvec{\psi }})]\) uniformly converges in probability to \({\mathbb {E}}\left( \ln \left[ h({\mathbf {Z}}; {\varvec{\psi }})\right] \right) \).

Theorem 2

Given the conditions (C1)–(C4) and assumptions (12) and (14) there exists a function \(e({\mathbf {z}})\), \({\mathbf {z}} \in {\mathbb {R}}^{G+D}\), such that

$$\begin{aligned}&\displaystyle |\ln [h({\mathbf {z}}; {\varvec{\psi }})]| \le e({\mathbf {z}}) \ \forall {\varvec{\psi }} \in \varvec{{\bar{\varPsi }}}, \forall {\mathbf {z}} \in {\mathbb {R}}^{G+D}, \end{aligned}$$
(15)
$$\begin{aligned}&\displaystyle \int e({\mathbf {z}}) g({\mathbf {z}}) d{\mathbf {z}} < \infty . \end{aligned}$$
(16)

Lemma 1

Given the conditions (I1), (C1)–(C4), (8), (9) and assumptions (12) and (14) and if \({\varvec{\psi }}_0 \in \varvec{{\bar{\varPsi }}}\), then \({\mathbb {E}}\left( \ln [h({\mathbf {Z}}; {\varvec{\psi }})]\right) \) has a unique maximum at \({\varvec{\psi }}_0\).

Proof

Conditions (I1), (8) and (9) ensure that \({\varvec{\psi }}_0\) is identified. Under the conditions (C1)–(C4) and assumptions (12) and (14), from Theorem 2 it follows that

$$\begin{aligned} {\mathbb {E}} \left( |\ln [h({\mathbf {Z}}; {\varvec{\psi }})]| \right) \le {\mathbb {E}} \left( e({\mathbf {Z}}) \right) \ \forall {\varvec{\psi }} \in \varvec{{\bar{\varPsi }}}. \end{aligned}$$

Finally, Lemma 2.2 of Newey and McFadden (1994) leads to the result given in Lemma 1. \(\square \)

Lemma 2

If \({\mathbf {z}}_{1}, \ldots , {\mathbf {z}}_{I}\) are i.i.d. sample observations of \({\mathbf {Z}}\), \(\varvec{{\bar{\varPsi }}}\) is compact and the conditions (C1)–(C4) and assumptions (12) and (14) are fulfilled, then \({\mathbb {E}}\left( \ln [h({\mathbf {Z}}; {\varvec{\psi }})]\right) \) is continuous and

$$\begin{aligned} \sup _{{\varvec{\psi }} \in \varvec{{\bar{\varPsi }}}} \left| \frac{1}{I} \sum _{i=1}^I \ln [h({\mathbf {z}}_i; {\varvec{\psi }})] - {\mathbb {E}}\left( \ln \left[ h({\mathbf {Z}}; {\varvec{\psi }}) \right] \right) \right| \xrightarrow {p} 0. \end{aligned}$$
(17)

Proof

The results given in Lemma 2 follow immediately from Theorem 2 and Lemma 2.4 of Newey and McFadden (1994). \(\square \)

Corollary 1

Given the conditions (I1), (C1)–(C4), (8), (9) and assumptions (12)–(13) and if \({\varvec{\breve{\varPsi }}}\) is compact, then the following convergence in probability holds true:

$$\begin{aligned} \hat{{\varvec{\psi }}}_I \xrightarrow {p} {\varvec{\psi }}_0. \end{aligned}$$
(18)

Proof

The result (18) follows immediately from Theorem 2 and Theorem 2.1, Lemmas 2.2 and 2.4 of Newey and McFadden (1994). \(\square \)

3.4 Results from the analysis of finite samples

Given an i.i.d. random sample \({\mathcal {Z}}=\left\{ ({\mathbf {x}}_{1}, {\mathbf {y}}_{1}), \ldots , ({\mathbf {x}}_{I}, {\mathbf {y}}_{I})\right\} \) of \(({\mathbf {X}},{\mathbf {Y}})\), the log-likelihood of a model from the class \({\mathfrak {F}}_K\) is equal to \(l_I({\varvec{\psi }})=l_I({\varvec{\vartheta }})+l_I({\varvec{\theta }})\), where \(l_I({\varvec{\vartheta }})=\sum _{i=1}^I \ln q({\mathbf {x}}_i; {\varvec{\vartheta }})\) and \(l_I({\varvec{\theta }})\) is given in Eq. (5). Thus, \(\hat{{\varvec{\psi }}}_I=(\hat{{\varvec{\vartheta }}}_I', \hat{{\varvec{\theta }}}_I')'\), the ML estimator of \({\varvec{\psi }}\) based on I sample observations, can be obtained by a separate maximisation of \(l_I({\varvec{\vartheta }})\) and \(l_I({\varvec{\theta }})\). As far as \({\varvec{\vartheta }}\) is concerned, its estimator will depend on the probability distribution specified for the predictors. In this Section, the attention is focused on the behaviour of \(\hat{{\varvec{\theta }}}_I\) under correctly specified models for \(f({\mathbf {y}}_i|{\mathbf {x}}_i; {\varvec{\theta }})\).

In this study, two experimental factors have been examined: the sample size (I) and the level of overlap among the linear regressions in the model. This latter factor has been measured as the classification error rate (ER) associated with the model used to generate the datasets. The considered factors’ levels are 1000, 2000, 3000, 4000, 5000 and 6000 for the sample size, and \(1\%, 5\%\) and \(10\%\) for the error rate, thus leading to 18 different experimental situations.

Datasets have been simulated under some models from the class defined by Eqs. (2)–(4) according to three different scenarios. In the first scenario the models used to generate datasets are mixtures of two (\(K=2\)) bivariate (\(D=2\)) seemingly unrelated linear regression models with \(X_1\), \(X_2\) and \(X_3\) as regressors for \(Y_1\), \(X_1\), \(X_4\) and \(X_5\) as regressors for \(Y_2\). The specific values of the model parameters \({\varvec{\theta }}=({\varvec{\pi }}', {\varvec{\theta }}'_1, {\varvec{\theta }}'_2)'\) employed in this first scenario are: \(\pi _1=0.4\), \(\pi _2=0.6\), \({\varvec{\beta }}_1 = (1,2,3,4,5,6)'\),

$$\begin{aligned} {\varvec{\lambda }}_1 = \left( \begin{array}{c@{\quad }c} 2 \\ 2\end{array}\right) , {\varvec{\varSigma }}_1 = \left( \begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad 1.5\end{matrix}\right) , \ {\varvec{\varSigma }}_2 = \left( \begin{matrix} 1.2 &{}\quad 0\\ 0 &{}\quad 1.8\end{matrix}\right) . \end{aligned}$$

As far as \({\varvec{\lambda }}_2\) and \({\varvec{\beta }}_2\) are concerned, their values have been computed as \({\varvec{\lambda }}_2= {\varvec{\lambda }}_1 + {\varvec{\zeta }}_2\) and \({\varvec{\beta }}_2= {\varvec{\beta }}_1 + {\varvec{\zeta }}_6\), respectively, where \({\varvec{\zeta }}_j\) denotes a vector of j independent realizations of the uniform random variable in the interval \((a, a+1)\) of the real line, \(a>0\). Clearly, the larger the value of a is, the lower the ER associated with the model is. Three different values of \(a>0\) have been employed in the first scenario; they are \(a_1=1\), \(a_2=2\) and \(a_3=5.5\). Such values have been selected so as to obtain models whose classification error rates are approximately equal to 10%, 5% and 1%, respectively. The specific realizations of vectors \({\varvec{\zeta }}_2\) and \({\varvec{\zeta }}_6\) used to compute \({\varvec{\lambda }}_2\) and \({\varvec{\beta }}_2\) with \(a_1\) are \({\varvec{\zeta }}_2=(1.9387,1.6060)'\) and \({\varvec{\zeta }}_6=(1.4187, 1.6560, 1.9459, 1.1949, 1.7602, 1.0397)'\). Each element of these latter vectors has been translated by \(a_j-a_1\) in order to obtain the specific realizations to be used with the values \(a_j\), \(j=2,3\).

In the second scenario the datasets are generated from mixtures of three (\(K=3\)) bivariate (\(D=2\)) seemingly unrelated linear regression models, where \(\pi _1=0.15\), \(\pi _2=0.35\), \(\pi _3=0.5\), \((X_1, X_2, X_3)\) and \((X_1, X_4, X_5)\) are the vectors of the regressors for \(Y_1\) and \(Y_2\), respectively. As far as model parameters \({\varvec{\beta }}_1\), \({\varvec{\lambda }}_1\), \({\varvec{\varSigma }}_1\) and \({\varvec{\varSigma }}_2 \) are concerned, they are set equal to the same values employed in the first scenario. The remaining parameters have been obtained as follows: \({\varvec{\lambda }}_2= {\varvec{\lambda }}_1 + {\varvec{\zeta }}_2\), \({\varvec{\beta }}_2= {\varvec{\beta }}_1 + {\varvec{\zeta }}_6\), \({\varvec{\lambda }}_3= {\varvec{\lambda }}_2 + {\varvec{\zeta }}_2\), \({\varvec{\beta }}_3= {\varvec{\beta }}_2 + {\varvec{\zeta }}_6\),

$$\begin{aligned} {\varvec{\varSigma }}_3 = \left( \begin{matrix} 1.8 &{}\quad 0\\ 0 &{}\quad 1.2\end{matrix}\right) . \end{aligned}$$

The realizations of \({\varvec{\zeta }}_j\) have been obtained using the same strategy employed in the first scenario. The values of a leading to model classification error rates ER approximately equal to 10%, 5% and 1% are \(a_1=1.3125\), \(a_2=2.3125\) and \(a_3=6.3125\), respectively. The specific realizations of vectors \({\varvec{\zeta }}_2\) and \({\varvec{\zeta }}_6\) generated from a uniform random variable in the interval \((a_1, a_1+1)\) are \({\varvec{\zeta }}_2=(2.2512, 1.9185)'\) and \({\varvec{\zeta }}_6=(1.7312, 1.9684, 2.2584, 1.5074, 2.0727, 1.3522)'\).

The setting of the third scenario coincides with the one of the first scenario except for a different choice of the weights; here, weights are set as follows: \(\pi _1=\pi _2=0.5\). In order to obtain models with an approximated ER of 10%, \({\varvec{\lambda }}_2\) and \({\varvec{\beta }}_2\) have been computed as follows: \({\varvec{\lambda }}_2= {\varvec{\lambda }}_1 + {\varvec{\zeta }}_2\), where \({\varvec{\zeta }}_2=(2.0012, 1.6685)'\), and \({\varvec{\beta }}_2= {\varvec{\beta }}_1 + {\varvec{\zeta }}_6\), where \({\varvec{\zeta }}_6=(1.4812, 1.7184, 2.0084, 1.2574, 1.8227, 1.1022)'\). These specific realizations of \({\varvec{\zeta }}_2\) and \({\varvec{\zeta }}_6\) have been obtained using \(a_1=1.0625\). As far as the choice of the parameters in association with \(ER=5\%\) and \(ER=1\%\) are concerned, the values \(a_2=1.9375\) and \(a_3=5.4375\) have been employed. In all scenarios, the realizations of each regressor have been generated by the standard normal distribution.

For each scenario and each combination of factors’ levels, \(R = 1000\) datasets have been generated. Then, each dataset has been used to compute \(\hat{{\varvec{\theta }}}\), the ML estimate of the data-generating model. Since the main goal of these analyses is to study the behaviour of the ML estimator under correctly specified models, for each simulated dataset only the ML estimate of the true generating model parameters has been computed. This task has been carried out through the package FlexMix (Grün and Leisch 2008) for the R software environment (R Core Team 2019), that allows to fit not only mixtures of univariate Gaussian regression models but also mixtures of multivariate and seemingly unrelated Gaussian regression models with diagonal component covariance matrices. In particular, function initFlexmix has been used for the initialisation of the model parameters. To this end, 10, 60 and 30 random initialisations have been employed for each dataset in the first, second and third scenarios, respectively.

In order to study the behaviour of the ML estimator, the following measure has been examined: \(d_r=\Vert \hat{{\varvec{\theta }}}_r - {\varvec{\theta }}\Vert \), where \(\hat{{\varvec{\theta }}}_r\) is the ML estimate of \({\varvec{\theta }}\) obtained from the \(r-\)th simulated dataset. This measure has been chosen because of the equivalence between the convergence in probability of each component of \(\hat{{\varvec{\theta }}}\) to the corresponding element of \({\varvec{\theta }}\) and the convergence in probability of the vector \(\hat{{\varvec{\theta }}}\) to the vector \({\varvec{\theta }}\) based on \(\Vert \hat{{\varvec{\theta }}} - {\varvec{\theta }}\Vert < \delta \), \(\forall \delta >0\) (see, e.g., Lehmann 1999, p. 278). Thus, for each scenario and each combination of factors’ levels, an estimate of the sample distribution of the Euclidean distance between \(\hat{{\varvec{\theta }}}\) and \({\varvec{\theta }}\) has been obtained, based on \(R=1000\) samples. In order to avoid problems associated with the labeling of the K regression models in the mixture, the Euclidean distances \(d_r\) have been computed after relabeling the K estimated regression models. In the first two scenarios, this task has been carried out according to the estimated prior probabilities taken in non-decreasing order. As far as the third scenario is concerned, the K estimated regression models have been labeled in order of the estimated intercepts in the regression models for the first dependent variable (i.e., the first elements of \({\varvec{\lambda }}_1, \ldots , {\varvec{\lambda }}_K\)). No problem while labeling the K regressions in the mixture based on such criteria have emerged from any scenario. Labelling methods incorporating the information about the true labels \({\mathbf {u}}_{1+}, \ldots , {\mathbf {u}}_{I+}\) in simulation studies have been recently proposed (see, e. g., Yao 2015). With such methods, the researcher avoids putting order constraints on a specific model parameter, which will lead to undesirable results when the chosen parameter does not contain enough information about the true labels of the sample observations.

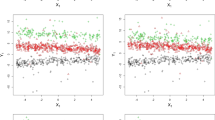
In the first scenario, the estimated sample distributions of the Euclidean distance between \(\hat{{\varvec{\theta }}}\) and \({\varvec{\theta }}\) tend towards zero as the sample size increases for each examined classification error rate (see Fig. 1, upper part). A similar behaviour emerges also in the second and third scenarios (see Fig. 1, central and lower parts). By focusing the attention on the median, the 95% and 99% percentiles of the \(d_r\)s (Table 5), it emerges that, for each scenario and each sample size, such distances are slightly closer to zero when the classification error rate is lower. In addition, the percentiles obtained when the datasets are generated from models with three components are higher than the ones obtained using models with two components for every sample size and every error rate. Furthermore, the impact of using equal weights on the results of the first scenario appears to be negligible.

Fig. 1
figure 1

Boxplots of the Euclidean distances \(d_r\) for the six sample sizes within the three error rates in the first (upper part), second (central part) and third (lower part) scenarios

Full size image
Table 5 50%, 95% and 99% percentiles of the sample Euclidean distances \(d_r\) in the three scenarios, for the 18 examined experimental situations
Full size table

In order to gain a deeper understanding of the effects of the sample size and the classification error rate on \(\Vert \hat{{\varvec{\theta }}} - {\varvec{\theta }}\Vert \), three regression analyses have been performed. For each scenario, the Euclidean distances \(d_r\) obtained on the \(R^*=18 \cdot R\) simulated samples have been regressed on the sample size and the classification error rate. Preliminary results (not shown here) have revealed that \(d_r\) is characterised by conditional heteroscedasticity, given the values of the two regressors, and that the natural logarithm proves to be a suitable variance-stabilising transformation in all scenarios. For these reasons, the following regression model has been specified:

$$\begin{aligned} \ln d_r = \delta _0+\delta _1z_{r1}+\delta _2z_{r2}+\delta _3z_{r3}+\delta _4z_{r4}+\delta _5z_{r5}+\varepsilon _r, \ \ \ r=1,\ldots , R^*,\nonumber \\ \end{aligned}$$
(19)

where \(z_{r1}=\ln I_r-\ln 3500\), \(I_r\) is the sample size of the dataset employed to compute \(d_r\), \(z_{r1}\) and \(z_{r2}\) are two dummy variables used to numerically code the error rate (with \(ER=0.01\) as reference category) and \(z_{r4}=z_{r1}z_{r2}\) and \(z_{r5}=z_{r1}z_{r3}\) allow for possible interaction between sample size and error rate. Note that \(\ln I_r-\ln 3500\) is considered instead of \(I_r\) in order to reduce collinearity with the interaction terms. As far as the errors are concerned, it is assumed that they have Gaussian distributions with expected value equal to zero and their variances may vary with the overlap level: \(\mathrm {Var}\left[ \varepsilon _r\right] =\sigma ^2\left[ 1+\left( \omega _1-1\right) z_{r2}+\left( \omega _2-1\right) z_{r3}\right] \). Thus, \(\sigma ^2\) is the error variance when \(ER=1\%\), and \(\omega _1, \omega _2\) are scale factors for \(\sigma ^2\) when \(ER=5\%\) and \(ER=10\%\), respectively. It is worth mentioning that assuming a conditional Gaussian distribution for \(\ln d_r\) is equivalent to assume a conditional lognormal distribution for \(d_r\). Thus, a Gaussian linear model for \(\ln d_r\) implies a lognormal regression model for \(d_r\). Furthermore, given the properties of lognormal distributions, \(\mathrm {E}[d_r]\le \mathrm {med}[d_r]=\exp \left\{ \mathrm {med}[\ln d_r]\right\} =\exp \left\{ \mathrm {E}[\ln d_r]\right\} \) (see, e. g., Aitkin et al. 2009, p. 125). Thus, model (19) implies the following multiplicative model for the median Euclidean distances:

$$\begin{aligned} \mathrm {med}\left[ d_r\right] =\left( \frac{I_r}{3500}\right) ^{\left( \delta _1+\delta _4z_{r2}+\delta _5z_{r3}\right) }e^{\left( \delta _0+\delta _2z_{r2}+\delta _3z_{r3}\right) }, \ r=1,\ldots , R^*. \end{aligned}$$
(20)

Parameters of model (19) have been estimated by exploiting generalised least squares and using the R package nlme (Pinheiro et al. 2017). The obtained results for the three scenarios are reported in Tables 6,  7 and  8. For the regression coefficients \(\delta _h\), \(h=1, \ldots , 5\), these tables also contain the estimated standard errors, the t-test statistics (for the null hypothesis \(H_0: \delta _h=0\), \(h=1, \ldots , 5\)) and the corresponding p values. According to these results, it appears that not only the sample size but also the error rate has a significant effect on \(\ln \Vert \hat{{\varvec{\theta }}}-{\varvec{\theta }}\Vert \). Namely, on average \(\ln \Vert \hat{{\varvec{\theta }}}-{\varvec{\theta }}\Vert \) tends to be larger as the error rate increases. The boxplots of the standardised residuals versus the fitted values for the two regression models are represented in Fig. 2. In particular, each figure contains 18 boxplots (one for each possible combination of the factors’ levels). As shown by these boxplots, in each scenario the distributions of the standardised residuals are approximately symmetric around zero and show a fairly similar variability. This behaviour suggests that the regression models can be considered adequately specified.

Table 6 Estimated parameters for the regression model (19) in the first scenario
Full size table
Table 7 Estimated parameters for the regression model (19) in the second scenario
Full size table
Table 8 Estimated parameters for the regression model (19) in the third scenario
Full size table
Fig. 2
figure 2

Boxplots of the standardised residuals versus fitted values for the regression model (19) in the first (left part), second (central part) and third (right part) scenarios

Full size image

By focusing the attention on the interaction between I and ER, the p-values for the Wald statistic to test the null hypothesis \(H_0: \delta _4=\delta _5=0\) in the three scenarios (see the last column in Table 9) suggest that there is not a significant interaction between sample size and error rate in any of the considered scenarios. As far as the two estimated main effects of the sample size are concerned (see the column \({\hat{\delta }}_1\) in Table 9), it emerges that they are approximately equal. In addition, all 95% confidence intervals for \(\delta _1\) contain the value −0.5. Thus, in each examined scenario, the median Euclidean distance between \(\hat{{\varvec{\theta }}}\) and \({\varvec{\theta }}\) tends to decrease approximately at the same rate as \(I^{-0.5}\), regardless of the overlap level.

Table 9 Estimated effects of the sample size from model (19) in the three scenarios and p values for the Wald statistic to test for the absence of interaction between sample size and classification error rate (\(H_0:\delta _4=\delta _5=0\))
Full size table

4 Conclusions

The paper has introduced a flexible and rich class of models for multivariate linear regression analysis based on finite mixtures of seemingly unrelated Gaussian linear regression models. These models are able to deal with correlated response variables in the presence of data coming from heterogeneous populations. In addition, with these models it is possible to specify a different vector of regressors for each dependent variable. This class encompasses several other types of Gaussian mixture-based linear regression models previously proposed in the literature. The paper has addressed both the model identification and ML estimation; this latter task is accomplished by means of an EM algorithm. Similarly to any other regression analysis based on Gaussian finite mixtures, also the proposed models and methods are affected by some practical issues, such as the choice of a proper value for K and the unboundedness of the mixture likelihood. This latter problem could be dealt with by constrained ML estimation. As far as the choice of K is concerned, several model selection techniques could be employed also in the framework proposed in this paper. A comparison among different linear regression models has been carried out in a study of the effects of prices and promotional activities on sales between September 1989 and May 1997 for two top U.S. brands in the canned tuna product category; the obtained results have demonstrated the practical usefulness of the proposed models in highlighting the presence of unobserved heterogeneity.

Furthermore, the paper has provided a range of specific conditions and assumptions for the model identifiability and regularity. Such regularity conditions and assumptions are easy to interpret, do not involve any derivatives of the model p.d.f. and ensure the consistency of the ML estimator given i.i.d. observations. As far as model identification and consistency of the ML estimator are concerned, it is important to note that there can be problems in applications where the regressors can only take a small number of values. The proof of the consistency property exploits general asymptotic results that hold true for extremum estimators of parametric models given i.i.d. observations (Newey and McFadden 1994). In particular, a theorem providing a weak consistency result has been used. In order to ensure the strong consistency of the ML estimator it is necessary to replace the result about the uniform convergence in probability given in Eq. (17) with a similar result concerning the almost sure uniform convergence. In addition, the behaviour of the ML estimator in the presence of finite samples has been evaluated through an estimate of the sample distribution of the Euclidean distance between \(\hat{{\varvec{\theta }}}\) and \({\varvec{\theta }}\), based on 1000 simulated datasets. This evaluation has been carried out for three types of models belonging to the proposed model class and for varying values of both the sample size and the classification error rate associated with the examined models. The obtained results have shown that such distance decreases with the sample size for each examined classification error rate. In addition, the interaction between the sample size and error rate on the logarithm of the Euclidean distance between \(\hat{{\varvec{\theta }}}\) and \({\varvec{\theta }}\) has resulted to be not significant. Finally, the median value of this distance decreases with the sample size at the same rate (\(I^{-0.5}\)) for every examined classification error rate; these results hold true for each of the three types of models considered in the Monte Carlo study.