1 Introduction

“Seemingly unrelated regression equations” is an expression first used by Zellner (1962). It indicates a set of equations for modelling the dependence of D variables (\(D \ge 1\)) on one or more regressors in which the error terms in the different equations are allowed to be correlated and, thus, the equations should be jointly considered. The range of situations for which models composed of seemingly unrelated regression equations are appropriate is wide, including cross-section data, time-series data and repeated measures (see, e.g., Srivastava and Giles 1987; Park 1993). For example, these models can be used to study the effect of prices and promotional activities on sales for different brands of a given product. In particular, when \(D=2\) brands (A and B) are considered, the following system of equations can be defined:

$$\begin{aligned} \left\{ \begin{array}{l} Y_{i1} = \beta _{01} + \beta _{11}x_{i1} + \beta _{12}x_{i2} + \epsilon _{i1} \\ Y_{i2} = \beta _{02} + \beta _{21}x_{i3} + \beta _{22}x_{i4} + \epsilon _{i2} \end{array} \right. \ \ i = 1, \ldots , I, \end{aligned}$$
(1)

where \(Y_{i1}\), \(x_{i1}\) and \(x_{i2}\) are the log unit sale, the measure of a display activity and the log price, respectively, registered in week i for brand A; \(Y_{i2}\), \(x_{i3}\) and \(x_{i4}\) provide the same information for brand B. In this situation, in order to account for a possible correlation between the error terms \(\epsilon _{i1}\) and \(\epsilon _{i2}\), the linear regression models that compose system (1) should be jointly examined.

Seemingly unrelated regression models have been studied through many approaches. In Zellner (1962, 1963) feasible generalized least squares estimators are introduced and their properties are analysed. The maximum likelihood estimator from a Gaussian distribution for the error terms is investigated, for example, in Kmenta and Gilbert (1968), Oberhofer and Kmenta (1974), Magnus (1978), Park (1993). Further developments have been obtained by using bootstrap methods (see, e.g., Rocke 1989; Rilstone and Veall 1996) and a likelihood distributional analysis (Fraser et al. 2005). Many studies have been performed also in a Bayesian framework (see, e.g., Zellner 1971; Percy 1992; Ando and Zellner 2010; Zellner and Ando 2010a). Most of these methods have been developed under the assumption that the distribution of the error terms is Gaussian. Some of them are implemented in the R package systemfit (Henningsen and Hamann 2007).

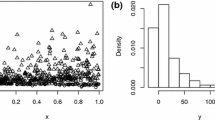
As an example, the above-mentioned methods can be employed to estimate parameters of system (1) using data taken from Chevalier et al. (2003) and available within the R package bayesm (Rossi 2012). This dataset contains the weekly sales for seven of the top 10 U.S. brands in the canned tuna product category for \(I=338\) weeks between September 1989 and May 1997, together with a measure of the display activity and the log price of each brand. In particular, two brands are examined: Star Kist 6 oz. (brand A) and Bumble Bee Solid 6.12 oz. (brand B). Figure 1 shows the standardized residuals obtained from model (1); it is evident that they have a non-Gaussian behavior. In particular, both marginal distributions are skewed. Furthermore, a subset of observations is characterised by strongly negative residuals for the equation describing Bumble Bee sales.

Fig. 1
figure 1

Canned tuna dataset: scatterplot and Q–Q plots of the standardized residuals

Full size image

The problem of dealing with non-Gaussian errors in seemingly unrelated regression models has already been tackled in the statistical literature. For example, properties of the feasible generalized least squares estimators under non-Gaussian errors are investigated in Srivastava and Maekawa (1995) and Kurata (1999). Solutions obtained using elliptical distributions are described in Ng (2002). The use of multivariate Student t errors is suggested in Kowalski et al. (1999) and Zellner and Ando (2010b).

The aim of this paper is to propose the use of Gaussian mixtures for modelling the error term distribution in a seemingly unrelated linear regression model. Finite mixtures represent a convenient and flexible framework for dealing with distributions of unknown shapes, as they can account for skewness, kurtosis and multimodality. They are widely employed in many areas of multivariate analysis, especially for model-based cluster analysis, discriminant analysis and multivariate density estimation (see, e.g., McLachlan and Peel 2000). Recently, finite mixtures of Gaussian and Student t distributions have been employed also in multiple and multivariate linear regression analysis (see, e.g., Bartolucci and Scaccia 2005; Soffritti and Galimberti 2011; Galimberti and Soffritti 2014) to handle non-normal error terms. In this context, the use of finite mixture has the advantage of capturing the effect of omitted nominal regressors from the model and obtaining robust estimates of the regression coefficients when the distribution of the error terms is non-normal.

The paper is organized as follows. Section 2 illustrates the theory behind the new methodology. Namely, the novel models are presented in Sect. 2.1. Theorem 1 provides conditions for the model identifiability (Sect. 2.2). The score vector and the Hessian matrix for the model parameter are reported in Sect. 2.3 (Theorems 2 and 3). Details about the maximum likelihood (ML) estimation through an Expectation–Maximisation (EM) algorithm are given in Sect. 2.4. Section 2.5 addresses model selection issues. Results obtained from the analysis of real datasets using the proposed approach are presented in Sect. 3, together with the results derived from models with multivariate Gaussian or Student t error terms. In particular, Sect. 3.1 describes the results for the above-mentioned canned tuna dataset. In Sect. 4 some concluding remarks are provided. Proofs of Theorems 2 and 3 and other technical results are in Appendix. Finally, further experimental results obtained from real and simulated datasets are provided in the online Supplementary material.

2 Seemingly unrelated regression models with a Gaussian mixture for the error terms

2.1 The general model

The novel model can be introduced as follows. Let \(\mathbf {Y}_i=(Y_{i1}, \ldots , Y_{id}, \ldots , Y_{iD})^{\prime }\) be the vector of the D dependent variables for the ith observation, \(i=1, \ldots , I\). Furthermore, let \(\mathbf {x}_{id}\) be the vector composed of the fixed values of the \(P_d\) regressors for the ith observation in the equation for the dth dependent variable, \(d=1, \ldots , D\). A seemingly unrelated regression model can be defined through the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{l} Y_{i1} = \beta _{01} + \mathbf {x}_{i1}'\varvec{\beta }_1 + \epsilon _{i1} \\ \vdots \\ Y_{id} = \beta _{0d} + \mathbf {x}_{id}'\varvec{\beta }_d + \epsilon _{id} \\ \vdots \\ Y_{iD} = \beta _{0D} + \mathbf {x}_{iD}'\varvec{\beta }_D + \epsilon _{iD} \end{array} \right. \ \ i = 1, \ldots , I, \end{aligned}$$
(2)

where \(\beta _{0d}\), \(\varvec{\beta }_d\), and \(\epsilon _{id}\) are the intercept, the regression coefficient vector and the error term for the ith observation in the equation for the dth dependent variable, respectively. Equation (2) can be written in compact form using the following matrix notation:

$$\begin{aligned} \mathbf {Y}_i= \varvec{\beta }_0 + \mathbf {X}_{i}'\varvec{\beta }+\varvec{\epsilon }_{i}, \quad i = 1, \ldots , I, \end{aligned}$$
(3)

where \(\varvec{\beta }_0=\left( \beta _{01}, \ldots , \beta _{0d}, \ldots , \beta _{0D}\right) ^{\prime }\), \(\varvec{\beta }=\left( \varvec{\beta }^{\prime }_1, \ldots , \varvec{\beta }^{\prime }_d,\right. \left. \ldots , \varvec{\beta }^{\prime }_D\right) ^{\prime }\), \(\varvec{\epsilon }_{i}=\left( \epsilon _{i1}, \ldots , \epsilon _{id}, \ldots , \epsilon _{iD}\right) ^{\prime }\), and \(\mathbf {X}_{i}\) is the following \(P \times D\) partitioned matrix:

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \mathbf {x}_{i1} &{} \mathbf {0}_{P_1} &{} \cdots &{} \mathbf {0}_{P_1} \\ \mathbf {0}_{P_2} &{} \mathbf {x}_{i2} &{} \cdots &{} \mathbf {0}_{P_2} \\ \vdots &{} \vdots &{} &{} \vdots \\ \mathbf {0}_{P_D} &{} \mathbf {0}_{P_D} &{} \cdots &{} \mathbf {x}_{iD} \\ \end{array} \right] , \end{aligned}$$
(4)

with \(\mathbf {0}_{P_d}\) denoting the \(P_d\)-dimensional null vector and \(P=\sum _{d=1}^D P_d\).

Remark 1

This definition of seemingly unrelated regression model differs from the one originally introduced by Zellner (1962); however, these two definitions are equivalent (see, for example, Park 1993). The choice of the model definition given in Eq. (3) is motivated by its analytical convenience in deriving some technical results described in this paper.

The proposed model is based on the assumption that the I error terms are independent and identically distributed, and that

$$\begin{aligned} \varvec{\epsilon }_i \sim \sum _{k=1}^K \pi _k N_D(\varvec{\nu }_{k},\varvec{\varSigma }_{k}), \quad i = 1, \ldots , I, \end{aligned}$$
(5)

where \(\pi _k\)’s are positive weights that sum to 1, the \(\varvec{\nu }_{k}\)’s are D-dimensional mean vectors that satisfy the constraint \(\sum _{k=1}^K \pi _k \varvec{\nu }_{k}= \varvec{0}_D\), the \(\varvec{\varSigma }_{k}\)’s are \(D \times D\) positive definite symmetric matrices and \(N_D(\varvec{\nu }_{k},\varvec{\varSigma }_{k})\) denotes the D-dimensional Gaussian distribution with parameters \(\varvec{\nu }_{k}\) and \(\varvec{\varSigma }_{k}\).

Given Eqs. (3) and (5), the conditional probability density function (p.d.f.) of the D-dimensional random vector \(\mathbf {Y}_i\) given \(\mathbf {X}_{i}\) is

$$\begin{aligned} \sum _{k=1}^K \pi _k \phi _D(\mathbf {y}_i; \varvec{\lambda }_{k}+ \mathbf {X}_{i}^{\prime }\varvec{\beta }, \varvec{\varSigma }_{k}), \ \ \mathbf {y}_i \in \mathbb {R}^D, \ \ i=1, \ldots , I,\nonumber \\ \end{aligned}$$
(6)

where \(\phi _D(\mathbf {y}_i;\varvec{\mu },\varvec{\varSigma })\) is the p.d.f. of the D-dimensional Gaussian distribution \(N_D(\varvec{\mu },\varvec{\varSigma })\) evaluated at \(\mathbf {y}_i\), and \(\varvec{\lambda }_{k}=\varvec{\beta }_0+\varvec{\nu }_{k}\). Differently from the \(\varvec{\nu }_{k}\)’s, the \(\varvec{\lambda }_{k}\)’s are not subject to any constraint. For this reason, in this paper the attention is focused on the vector of the model parameters given by \(\varvec{\theta }=\left( \varvec{\pi }^{\prime }, \varvec{\beta }^{\prime }, \varvec{\theta }^{\prime }_1, \ldots , \varvec{\theta }^{\prime }_K\right) ^{\prime }\), where \(\varvec{\pi }=(\pi _1, \ldots , \pi _{K-1})^{\prime }\), \(\varvec{\theta }_k =\left( \varvec{\lambda }^{\prime }_k, \mathrm {v}\left( \varvec{\varSigma }_k\right) ^{\prime }\right) ^{\prime }\) for \(k=1, \ldots , K\), with \(\mathrm {v}(\varvec{\varSigma }_{k})\) denoting the \(\frac{1}{2}D(D+1)\)-dimensional vector formed by stacking the columns of the lower triangular portion of \(\varvec{\varSigma }_{k}\) (see, e.g., Schott 2005).

Suppose that the ith observation was drawn from the kth component of the mixture. Then, the equation for such an observation would be

$$\begin{aligned} \mathbf {Y}_i=\varvec{\lambda }_k+\mathbf {X}_{i}^{\prime }\varvec{\beta }+\tilde{\varvec{\epsilon }}_{ik}, \end{aligned}$$
(7)

where \(\tilde{\varvec{\epsilon }}_{ik} \sim N_D(\varvec{0}_D,\varvec{\varSigma }_k)\). Thus, the model defined by Eq. (6) can be seen as a mixture of K seemingly unrelated linear regression models with Gaussian error terms. This property of the proposed model makes it possible to establish a link with finite mixtures of regression models (see, e.g., Frühwirth-Schnatter 2006). This kind of mixtures constitutes a flexible tool for the identification of K unknown sub-populations of observations (clusters), each of which is characterised by a specific relationship between the dependent variables and the regressors. In these models it is generally assumed that each component of the mixture is associated with a cluster. It is worth noting that, according to model (6), the K clusters of observations differ in the intercepts for the D dependent variables and in the covariance matrices for the error terms, while the regression coefficients are equal across clusters. Thus, the K unknown sub-populations can also be interpreted as the categories of an unobserved (and, thus, omitted) nominal regressor that affects both the conditional expected values and covariances of the dependent variables.

In the special case where \(K=1\), model (6) results in the classical seemingly unrelated regression model with Gaussian errors. If \(\mathbf {x}_{id}=\mathbf {x}_{i}\) \(\forall d\) (the vectors of the regressors for the D equations coincide), the following equality holds:

$$\begin{aligned} \mathbf {X}_{i}=\mathbf {I}_D\otimes \mathbf {x}_{i}, \end{aligned}$$

where \(\mathbf {I}_D\) is the identity matrix of order D and \(\otimes \) denotes the Kronecker product operator (see, e.g., Schott 2005). Thus, Eq. (7) can be rewritten as

$$\begin{aligned} \mathbf {Y}_i=\varvec{\lambda }_k+\left( \mathbf {I}_D\otimes \mathbf {x}_{i}\right) ^{\prime }\varvec{\beta }+\tilde{\varvec{\epsilon }}_{ik}=\varvec{\lambda }_k+\varvec{B}^{\prime }\mathbf {x}_{i}+\tilde{\varvec{\epsilon }}_{ik}, \end{aligned}$$
(8)

where \(\varvec{B}=\left[ \varvec{\beta }_1 \cdots \varvec{\beta }_d \cdots \varvec{\beta }_D\right] \). Equation (8) corresponds to the model described in Soffritti and Galimberti (2011). Furthermore, the model proposed by Bartolucci and Scaccia (2005) can be obtained when \(D=1\). Finally, if \(P_d=0\) \(\forall d\), model (6) results in the mixture model with K Gaussian components (see, e.g., McLachlan and Peel 2000).

2.2 Model identifiability

As any finite mixture model, also model (6) is invariant under permutations of the labels of the K components (see, e.g., McLachlan and Peel 2000). For the proposed model, whose parameter is \(\varvec{\theta }=\left( \varvec{\pi }^{\prime }, \varvec{\beta }^{\prime }, \varvec{\theta }^{\prime }_1, \ldots , \varvec{\theta }^{\prime }_K\right) ^{\prime }\), the following theorem holds:

Theorem 1

Model (6) is identifiable, provided that, for \(d=1, \ldots , D\), vectors \(\{\mathbf {x}_{id}, i=1, \ldots , I\}\) do not lie on a common \((P_d-1)\)-dimensional hyperplane.

Proof

The identifiability condition described in Theorem 1 is a generalization of the usual condition for the identifiability of a multiple linear regression model. It is required in order to guarantee identifiability of the parameters \(\varvec{\beta }\) and \(\varvec{\lambda }_1, \ldots , \varvec{\lambda }_K\) that characterise the conditional expectations for the D dependent variables.

Furthermore, consider the joint conditional p.d.f. of a random sample \(\mathbf {y}_1, \ldots , \mathbf {y}_I\) from the model (6), given the fixed values of the regressors contained in \(\mathbf {X}_{1}, \ldots , \mathbf {X}_{I}\):

$$\begin{aligned}&f(\mathbf {y}_1, \ldots , \mathbf {y}_I; \mathbf {X}_{1}, \ldots , \mathbf {X}_{I}, \varvec{\theta })\nonumber \\&\quad =\prod _{i=1}^I \left[ \sum _{k=1}^K \pi _k \phi _D\left( \mathbf {y}_i; \varvec{\lambda }_{k}+ \mathbf {X}_{i}^{\prime }\varvec{\beta }, \varvec{\varSigma }_{k}\right) \right] . \end{aligned}$$
(9)

Formula (9) can be re-written as follows:

$$\begin{aligned}&f\left( \mathbf {y}_1, \ldots , \mathbf {y}_I; \mathbf {X}_{1}, \ldots , \mathbf {X}_{I}, \varvec{\theta }\right) \nonumber \\&\quad = \sum _{j=1}^J \pi _j \phi _{D \cdot I}\left( \mathbf {y}; \varvec{\lambda }_{j}+ \mathbf {X}\varvec{\beta }, \varvec{\varSigma }_{j}\right) , \end{aligned}$$
(10)

where \(J=K^I\), \(\mathbf {y}=\left( \mathbf {y}^{\prime }_1, \ldots , \mathbf {y}^{\prime }_I\right) ^{\prime }\), \(\mathbf {X}=\left[ \mathbf {X}_{1} \ldots \mathbf {X}_{I}\right] ^{\prime }\), \(\pi _j=\prod _{i=1}^I \pi _{k_i^{(j)}}\), \({\varvec{\lambda }}_j = \left( \varvec{\lambda }_{k_1^{(j)}}^{\prime }, \ldots , {\varvec{\lambda }}_{k_I^{(j)}}^{\prime }\right) ^{\prime }\), \(\varvec{\varSigma }_j=\) \(diag(\varvec{\varSigma }_{k_1^{(j)}},\) \(\ldots , \varvec{\varSigma }_{k_I^{(j)}})\) is a block diagonal matrix, and \(\mathbf k ^{(j)}=\left( k_1^{(j)}, \ldots , k_I^{(j)}\right) ^{\prime }\) is the jth element of the set \(A_{K,I}=\{(k_1, \ldots , k_I)^{\prime }: k_i \in \{1, \ldots , K\}, \ i=1, \ldots , I\}\) containing the J arrangements of the first K positive integers amongst I with repetitions. The proof can be completed by showing that mixtures (10) are identifiable. The proof of this latter result can be found in Soffritti and Galimberti (2011).

2.3 Score vector and Hessian matrix

Given a random sample \(\mathbf {y}_1, \ldots , \mathbf {y}_I\) from the model (6), the log-likelihood is

$$\begin{aligned} l(\varvec{\theta })=\sum _{i=1}^I \ln \left( \sum _{k=1}^K \pi _k \phi _D(\mathbf {y}_i; \varvec{\lambda }_{k}+ \mathbf {X}_{i}^{\prime }\varvec{\beta }, \varvec{\varSigma }_{k})\right) . \end{aligned}$$
(11)

The log-likelihood (11) can be used to derive the ML estimator of \(\varvec{\theta }\). Furthermore, Redner and Walker (1984) showed that, under suitable conditions, an estimate of the asymptotic variance of the ML estimator of the parameters in a finite mixture model can be obtained using the Hessian matrix. In order to obtain the score vector and the Hessian matrix the following notation is introduced. Let

$$\begin{aligned} f_{ki}= & {} \frac{\pi _k}{(2\pi )^{D/2}\det \left( \varvec{\varSigma }_k\right) ^{1/2}}\exp \left[ -\frac{1}{2}\left( \mathbf {y}_i-\varvec{\lambda }_k-\mathbf {X}^{\prime }_{i}\varvec{\beta } \right) ^{\prime }\right. \\&\quad \left. \times \varvec{\varSigma }_k^{-1}\left( \mathbf {y}_i-\varvec{\lambda }_k-\mathbf {X}^{\prime }_{i}\varvec{\beta } \right) \right] ; \end{aligned}$$

\(\alpha _{ki}=\frac{f_{ki}}{\left( \sum _{l=1}^K f_{li}\right) }\); \(\mathbf {a}_k=\frac{1}{\pi _k}\mathbf {e}_k\) for \(k=1,\ldots ,K-1\) and \(\mathbf {a}_K=-\frac{1}{\pi _K}\varvec{1}_{(K-1)}\), where \(\mathbf {e}_k\) is the kth column of \(\mathbf {I}_{(K-1)}\) and \(\varvec{1}_{(K-1)}\) denotes the \((K-1)\)-dimensional vector having each component equal to 1; \(\mathbf {b}_{ki}=\varvec{\varSigma }_k^{-1}\left( \mathbf {y}_i-\varvec{\lambda }_k-\mathbf {X}_{i}^{\prime }\varvec{\beta } \right) \); \(\mathbf {B}_{ki}=\varvec{\varSigma }_k^{-1}-\mathbf {b}_{ki}\mathbf {b}^{\prime }_{ki}\);

$$\begin{aligned} \mathbf {c}_{ki}=\left[ \begin{array}{c} \mathbf {b}_{ki} \\ -\frac{1}{2} \mathbf {G}^{\prime } \mathrm {vec}\left( \mathbf {B}_{ki}\right) \end{array}\right] , \end{aligned}$$

where \(\mathbf {G}\) denotes the duplication matrix and \(\mathrm {vec}(\mathbf {B}_{ki})\) denotes the vector formed by stacking the columns of the matrix \(\mathbf {B}_{ki}\) one underneath the other (see, e.g., Schott 2005).

Theorem 2

The score vector for the parameters of model (6) is composed of the sub-vectors \(\frac{\partial }{\partial \varvec{\pi }^{\prime }}l\left( \varvec{\theta }\right) \), \(\frac{\partial }{\partial \varvec{\beta }^{\prime }}l\left( \varvec{\theta }\right) \), \(\frac{\partial }{\partial \varvec{\theta }^{\prime }_1}l\left( \varvec{\theta }\right) , \ldots , \frac{\partial }{\partial \varvec{\theta }^{\prime }_K}l\left( \varvec{\theta }\right) \), where

$$\begin{aligned} \frac{\partial }{\partial \varvec{\pi }}l\left( \varvec{\theta }\right)= & {} \sum _{i=1}^I\bar{\mathbf {a}}_i,\\ \frac{\partial }{\partial \varvec{\beta }}l\left( \varvec{\theta }\right)= & {} \sum _{i=1}^I\mathbf {X}_{i}\bar{\mathbf {b}}_i, \\ \frac{\partial }{\partial \varvec{\theta }_k}l\left( \varvec{\theta }\right)= & {} \sum _{i=1}^I \alpha _{ki}\mathbf {c}_{ki}, \ \ k=1, \ldots , K, \end{aligned}$$

with \(\bar{\mathbf {a}}_i=\sum _{k=1}^K \alpha _{ki}\mathbf {a}_k\) and \(\bar{\mathbf {b}}_i=\sum _{k=1}^K \alpha _{ki}\mathbf {b}_{ki}\).

Theorem 3

The Hessian matrix \(H(\varvec{\theta })\) for the parameters of model (6) is equal to

$$\begin{aligned} \left[ \begin{array}{ccccc} \frac{\partial ^2}{\partial \varvec{\pi }\partial \varvec{\pi }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\pi }\partial \varvec{\beta }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\pi }\partial \varvec{\theta }_1^{\prime }}l\left( \varvec{\theta }\right) &{} \cdots &{} \frac{\partial ^2}{\partial \varvec{\pi }\partial \varvec{\theta }_K^{\prime }}l\left( \varvec{\theta }\right) \\ \frac{\partial ^2}{\partial \varvec{\beta }\partial \varvec{\pi }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\beta }\partial \varvec{\beta }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\beta }\partial \varvec{\theta }_1^{\prime }}l\left( \varvec{\theta }\right) &{} \cdots &{} \frac{\partial ^2}{\partial \varvec{\beta }\partial \varvec{\theta }_K^{\prime }}l\left( \varvec{\theta }\right) \\ \frac{\partial ^2}{\partial \varvec{\theta }_1\partial \varvec{\pi }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\theta }_1\partial \varvec{\beta }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\theta }_1\partial \varvec{\theta }_1^{\prime }}l\left( \varvec{\theta }\right) &{} \cdots &{} \frac{\partial ^2}{\partial \varvec{\theta }_1\partial \varvec{\theta }_K^{\prime }}l\left( \varvec{\theta }\right) \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{\partial ^2}{\partial \varvec{\theta }_K\partial \varvec{\pi }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\theta }_K\partial \varvec{\beta }^{\prime }}l\left( \varvec{\theta }\right) &{} \frac{\partial ^2}{\partial \varvec{\theta }_K\partial \varvec{\theta }_1^{\prime }}l\left( \varvec{\theta }\right) &{} \cdots &{} \frac{\partial ^2}{\partial \varvec{\theta }_K\partial \varvec{\theta }_K^{\prime }}l\left( \varvec{\theta }\right) \end{array} \right] , \end{aligned}$$
(12)

where

$$\begin{aligned}&\frac{\partial ^2}{\partial \varvec{\pi }\partial \varvec{\pi }^{\prime }}l\left( \varvec{\theta }\right) = -\sum _{i=1}^I \bar{\mathbf {a}}_i\bar{\mathbf {a}}^{\prime }_i,\\&\frac{\partial ^2}{\partial \varvec{\pi }\partial \varvec{\beta }^{\prime }}l\left( \varvec{\theta }\right) = \sum _{i=1}^I \left[ \left( \sum _{k=1}^K\alpha _{ki}\mathbf {a}_k \mathbf {b}^{\prime }_{ki}\right) -\bar{\mathbf {a}}_i \bar{\mathbf {b}}^{\prime }_{i}\right] \mathbf {X}^{\prime }_{i},\\&\frac{\partial ^2}{\partial \varvec{\pi }\partial \varvec{\theta }_k^{\prime }}l\left( \varvec{\theta }\right) = \sum _{i=1}^I \alpha _{ki}\left( \mathbf {a}_{k}-\bar{\mathbf {a}}_i\right) \mathbf {c}^{\prime }_{ki}, \ \ k=1, \ldots , K,\\&\frac{\partial ^2}{\partial \varvec{\beta }\partial \varvec{\beta }^{\prime }}l\left( \varvec{\theta }\right) = - \sum _{i=1}^I \mathbf {X}_{i}\left[ \bar{\mathbf {B}}_{i}+\bar{\mathbf {b}}_{i}\bar{\mathbf {b}}^{\prime }_{i}\right] \mathbf {X}^{\prime }_{i},\\&\frac{\partial ^2}{\partial \varvec{\beta }\partial \varvec{\theta }_k^{\prime }}l\left( \varvec{\theta }\right) = - \sum _{i=1}^I \alpha _{ki}\mathbf {X}_{i}\left[ \mathbf {F}_{ki}-\left( \mathbf {b}_{ki}-\bar{\mathbf {b}}_{i}\right) \mathbf {c}^{\prime }_{ki}\right] ,\\&\quad \qquad \quad k=1, \ldots , K,\\&\frac{\partial ^2}{\partial \varvec{\theta }_k\partial \varvec{\theta }_k^{\prime }}l\left( \varvec{\theta }\right) = - \sum _{i=1}^I \alpha _{ki}\left[ \mathbf {C}_{ki}-\left( 1-\alpha _{ki}\right) \mathbf {c}_{ki}\mathbf {c}^{\prime }_{ki}\right] ,\\&\quad \qquad \quad k=1, \ldots , K,\\&\frac{\partial ^2}{\partial \varvec{\theta }_k\partial \varvec{\theta }^{\prime }_h}l\left( \varvec{\theta }\right) = - \sum _{i=1}^I \alpha _{ki}\alpha _{hi}\mathbf {c}_{ki}\mathbf {c}^{\prime }_{hi}, \ \ \forall k \ne h, \end{aligned}$$

with \(\bar{\mathbf {B}}_{i}=\sum _{k=1}^K\alpha _{ki}\left( \varvec{\varSigma }_k^{-1}-\mathbf {b}_{ki}\mathbf {b}^{\prime }_{ki}\right) \), \(\mathbf {F}_{ki}=\left[ \begin{array}{cc} \varvec{\varSigma }_k^{-1}&\left( \mathbf {b}^{\prime }_{ki}\otimes \varvec{\varSigma }_k^{-1}\right) \mathbf {G} \end{array}\right] \) and

$$\begin{aligned} \mathbf {C}_{ki}=\left[ \begin{array}{cc} \varvec{\varSigma }_k^{-1} &{} \left( \mathbf {b}^{\prime }_{ki}\otimes \varvec{\varSigma }_k^{-1}\right) \mathbf {G}\\ \mathbf {G}^{\prime }\left( \mathbf {b}_{ki}\otimes \varvec{\varSigma }_k^{-1}\right) &{} \frac{1}{2}\mathbf {G}^{\prime }\left[ \left( \varvec{\varSigma }_k^{-1}-2\mathbf {B}_{ki}\right) \otimes \varvec{\varSigma }_k^{-1}\right] \mathbf {G}\end{array}\right] . \end{aligned}$$

Proofs of Theorems 2 and 3 are provided in Appendix 1 and 2, respectively.

Remark 2

After some suitable simplifications, Theorems 2 and 3 provide the score vector and the Hessian matrix also for the models introduced in Bartolucci and Scaccia (2005) and Soffritti and Galimberti (2011). Furthermore, they represent a generalization of Theorem 1 in Boldea and Magnus (2009).

2.4 An EM algorithm for maximum likelihood estimation

The score vector and the Hessian matrix described in Sect. 2.3 can be used to compute the ML estimates of the model parameter \(\varvec{\theta }\) through a Newton-Raphson algorithm for the maximisation of \(l(\varvec{\theta })\) in Eq. (11). However, the evaluation of the Hessian matrix at each iteration can be computationally expensive, especially with large samples. In order to avoid this problem, in this Section an EM algorithm is developed by resorting to the approach for incomplete-data problems (Dempster et al. 1977; McLachlan and Krishnan 2008). This approach is widely employed in finite mixture models, where the source of unobservable information is the specific component of the mixture model that generates each sample observation. Specifically, this unobservable information for the ith observation can be described by the K-dimensional vector \(\mathbf {z}^{\prime }_i=\left( z_{i1}, \ldots , z_{iK}\right) \), where \(z_{ik}=1\) when \(\mathbf {y}_i\) is generated from the kth component, and \(z_{ik}=0\) otherwise, for \(k=1, \ldots , K\). Thus, \(\sum _{k=1}^K z_{ik}=1\), \(i=1, \ldots , I\).

Consider the following hierarchical representation for \(\mathbf {y}_i|\mathbf {X}_i\):

$$\begin{aligned}&\mathbf {z}_i \sim mult(1, \pi _1, \ldots , \pi _K),\\&\mathbf {y}_i|(\mathbf {X}_i, z_{ik}=1) \sim N_D\left( \varvec{\lambda }_k+ \mathbf {X}^{\prime }_i \varvec{\beta }, \varvec{\varSigma }_k\right) , \end{aligned}$$

where \(mult(1, \pi _1, \ldots , \pi _K)\) denotes the K-dimensional multinomial distribution with parameters \(\pi _1, \ldots , \pi _K\), and assume that this representation independently holds for \(i=1, \ldots , I\). Then, the complete-data log-likelihood \(l_c(\varvec{\theta })\) of model (6) can be expressed as

$$\begin{aligned} l_c\left( \varvec{\theta }\right) =\sum _{i=1}^I \sum _{k=1}^K z_{ik}\ln f_{ki}. \end{aligned}$$
(13)

The first order differential of \(l_c(\varvec{\theta })\) is

$$\begin{aligned} \mathrm {d}l_c\left( \varvec{\theta }\right)= & {} \sum _{i=1}^I \sum _{k=1}^K z_{ik} \mathrm {d}\ln f_{ki}\nonumber \\= & {} \left( \mathrm {d}\varvec{\pi }\right) ^{\prime }\sum _{k=1}^K z_{\cdot k}\mathbf {a}_k + \left( \mathrm {d}\varvec{\beta }\right) ^{\prime }\sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{i}\mathbf {b}_{ki}\nonumber \\&+\sum _{k=1}^K \left( \mathrm {d}\varvec{\theta }_k\right) ^{\prime }\sum _{i=1}^I z_{ik}\mathbf {c}_{ki}\nonumber \\= & {} \left( \mathrm {d}\varvec{\pi }\right) ^{\prime }\sum _{k=1}^K z_{\cdot k}\mathbf {a}_k \nonumber \\&+ \sum _{i=1}^I \sum _{k=1}^K z_{ik}\left[ \left( \mathrm {d}\varvec{\lambda }_k\right) ^{\prime }+ \left( \mathrm {d}\varvec{\beta }\right) ^{\prime }\mathbf {X}_{i}\right] \mathbf {b}_{ki} \end{aligned}$$
(14)
$$\begin{aligned}&-\frac{1}{2}\sum _{k=1}^K \mathrm {d}\left( \mathrm {v}\varvec{\varSigma }_k\right) ^{\prime }\mathbf {G}^{\prime }\mathrm {vec}\left( \sum _{i=1}^I z_{ik}\mathbf {B}_{ki}\right) \end{aligned}$$
(15)

where the second and third equalities are obtained using Eq. (34) in Appendix 1, and \(z_{\cdot k}=\sum _{i=1}^I z_{ik}\).

To determine the solution of each M step of the EM algorithm, it is convenient to introduce the following notation. Let \(\mathrm {d}l_{c2}\) and \(\mathrm {d}l_{c3}\) denote the expressions in Eqs. (14) and (15), respectively. Let \(\varvec{\gamma }=\left( \varvec{\lambda }^{\prime }_{1}, \ldots , \varvec{\lambda }^{\prime }_{K}, \varvec{\beta }^{\prime }\right) {^\prime }\) be the \((D \cdot K +P)\)-dimensional vector comprising the intercepts of all components and regression coefficients for all dependent variables. \(\mathbf {O}_k\) is a matrix of dimension \((D\cdot K)\times D\) obtained by extracting the columns of the matrix \(\mathbf {I}_{(D\cdot K)}\) from the \((1+(k-1)\cdot D)\)th to the \((D+(k-1)\cdot D)\)th, for \(k=1,\ldots , K\). Furthermore, let \(\mathbf {X}_{ki}=\left[ \begin{array}{c} \mathbf {O}_k\\ \mathbf {X}_i \end{array}\right] \); this is a matrix of dimension \(\left( D\cdot K+P\right) \times D\) such that \(\mathbf {X}^{\prime }_{ki}\varvec{\gamma }=\varvec{\lambda }_k+\mathbf {X}^{\prime }_{i}\varvec{\beta }\) and \(\mathbf {X}^{\prime }_{ki}\mathrm {d}\varvec{\gamma }=\mathrm {d}\varvec{\lambda }_k+\mathbf {X}^{\prime }_{i}\mathrm {d}\varvec{\beta }\). Using this latter notation, the expressions of \(\mathrm {d}l_{c2}\) and \(\mathrm {d}l_{c3}\) in Eqs. (14) and (15) turn into

$$\begin{aligned} \mathrm {d}l_{c2}= & {} \sum _{i=1}^I \sum _{k=1}^K z_{ik}\left( \mathrm {d}\varvec{\gamma }\right) ^{\prime }\mathbf {X}_{ki}\mathbf {b}_{ki}\nonumber \\= & {} \left( \mathrm {d}\varvec{\gamma }\right) ^{\prime }\sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\left( \mathbf {y}_i-\mathbf {X}^{\prime }_{ki}\varvec{\gamma }\right) \nonumber \\= & {} \left( \mathrm {d}\varvec{\gamma }\right) ^{\prime }\sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {y}_i\nonumber \\&-\left( \mathrm {d}\varvec{\gamma }\right) ^{\prime }\left( \sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {X}^{\prime }_{ki}\right) \varvec{\gamma },\end{aligned}$$
(16)
$$\begin{aligned} \mathrm {d}l_{c3}= & {} -\frac{1}{2}\sum _{k=1}^K \mathrm {d}\left( \mathrm {v}\varvec{\varSigma }_k\right) ^{\prime }\mathbf {G}^{\prime } \mathrm {vec}\left( \sum _{i=1}^I z_{ik}\varvec{\varSigma }_k^{-1}-\sum _{i=1}^I z_{ik}\mathbf {b}_{ki}\mathbf {b}^{\prime }_{ki}\right) \nonumber \\= & {} -\frac{1}{2}\sum _{k=1}^K \mathrm {d}\left( \mathrm {v}\varvec{\varSigma }_k\right) ^{\prime }\mathbf {G}^{\prime } \mathrm {vec}\left( z_{\cdot k}\varvec{\varSigma }_k^{-1}-\varvec{\varSigma }_k^{-1}\mathbf {S}_k\varvec{\varSigma }_k^{-1}\right) , \end{aligned}$$
(17)

where \(\mathbf {S}_k=\sum _{i=1}^I z_{ik}\left( \mathbf {y}_i-\mathbf {X}^{\prime }_{ki}\varvec{\gamma }\right) \left( \mathbf {y}_i-\mathbf {X}^{\prime }_{ki}\varvec{\gamma }\right) ^{\prime }\). Using Eq. (17) and some properties of the vec operator (see, in particular, Schott 2005, Theorem 8.11) it is also possible to write

$$\begin{aligned} \mathrm {d}l_{c3}= & {} \frac{1}{2}\sum _{k=1}^K \mathrm {d}\left( \mathrm {v}\varvec{\varSigma }_k\right) ^{\prime }\mathbf {G}^{\prime } \mathrm {vec}\left[ \varvec{\varSigma }_k^{-1}\left( \mathbf {S}_k-z_{\cdot k}\varvec{\varSigma }_k\right) \varvec{\varSigma }_k^{-1}\right] \nonumber \\= & {} \frac{1}{2}\sum _{k=1}^K \mathrm {d}\left( \mathrm {v}\varvec{\varSigma }_k\right) ^{\prime }\mathbf {G}^{\prime } \left( \varvec{\varSigma }_k^{-1}\otimes \varvec{\varSigma }_k^{-1}\right) \mathbf {G}\mathrm {v}\left( \mathbf {S}_k-z_{\cdot k}\varvec{\varSigma }_k\right) .\nonumber \\ \end{aligned}$$
(18)

Thus, the following alternative expression for \(\mathrm {d}l_c\left( \varvec{\theta }\right) \) holds:

$$\begin{aligned} \mathrm {d}l_c\left( \varvec{\theta }\right)= & {} \left( \mathrm {d}\varvec{\pi }\right) ^{\prime }\sum _{k=1}^K z_{\cdot k}\mathbf {a}_k+ \left( \mathrm {d}\varvec{\gamma }\right) ^{\prime }\sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {y}_i\nonumber \\&-\left( \mathrm {d}\varvec{\gamma }\right) ^{\prime }\left( \sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {X}^{\prime }_{ki}\right) \varvec{\gamma }\nonumber \\&+ \frac{1}{2}\sum _{k=1}^K \mathrm {d}\left( \mathrm {v}\varvec{\varSigma }_k\right) ^{\prime }\mathbf {G}^{\prime } \left( \varvec{\varSigma }_k^{-1}\otimes \varvec{\varSigma }_k^{-1}\right) \mathbf {G}\mathrm {v}\left( \mathbf {S}_k-z_{\cdot k}\varvec{\varSigma }_k\right) .\nonumber \\ \end{aligned}$$
(19)

The first derivatives of \(l_c\left( \varvec{\theta }\right) \) with respect to the parameters \(\varvec{\pi }\), \(\varvec{\gamma }\) and \(\mathrm {v}\varvec{\varSigma }_k\) (\(k=1, \ldots , K)\) are:

$$\begin{aligned}&\frac{\partial }{\partial \varvec{\pi }}l_c\left( \varvec{\theta }\right) = \sum _{k=1}^K z_{\cdot k}\mathbf {a}_k,\\&\frac{\partial }{\partial \varvec{\gamma }}l_c\left( \varvec{\theta }\right) = \sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {y}_i\\&\quad - \left( \sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {X}^{\prime }_{ki}\right) \varvec{\gamma },\\&\frac{\partial }{\partial \left( \mathrm {v}\varvec{\varSigma }_k\right) }l_c\left( \varvec{\theta }\right) = \frac{1}{2}\mathbf {G}^{\prime } \left( \varvec{\varSigma }_k^{-1}\otimes \varvec{\varSigma }_k^{-1}\right) \mathbf {G}\mathrm {v}\left( \mathbf {S}_k-z_{\cdot k}\varvec{\varSigma }_k\right) ,\\&\quad \qquad \quad k=1, \ldots , K. \end{aligned}$$

In order to maximise \(l_c\left( \varvec{\theta }\right) \) these derivatives are set equal to zero. By solving the resulting system of equations the following expressions are obtained:

$$\begin{aligned} \pi ^*_k=z_{\cdot k}/I, \ \ k=1, \ldots , K, \end{aligned}$$
(20)

and, provided that the matrix \(\sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {X}^{\prime }_{ki}\) is non-singular,

$$\begin{aligned} \varvec{\gamma }^*= & {} \left( \sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {X}^{\prime }_{ki}\right) ^{-1}\sum _{i=1}^I \sum _{k=1}^K z_{ik}\mathbf {X}_{ki}\varvec{\varSigma }_{k}^{-1}\mathbf {y}_i, \nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned} \varvec{\varSigma }_k^*= & {} z_{\cdot k}^{-1}\mathbf {S}_k, \ \ k=1, \ldots , K. \end{aligned}$$
(22)

Using some initial value for \(\varvec{\theta }\), say \(\varvec{\theta }^{(0)}\), the E-step on the \((r+1)\)th iteration of the EM algorithm is effected by simply replacing \(z_{ik}\) by \(E_{\varvec{\theta }^{(r)}}(z_{ik}|\mathbf {y}_i, \mathbf {x}_i)= P_{\varvec{\theta }^{(r)}}(z_{ik}=1|\mathbf {y}_i, \mathbf {x}_i)=p_{ik}^{(r)}\), which is the posterior probability that \(\mathbf {y}_i\) is generated from the kth component of the mixture. Namely:

$$\begin{aligned} p_{ik}^{(r)}=\frac{\pi ^{(r)}_k \phi _D\left( \varvec{y}_i;\varvec{\lambda }^{(r)}_{k}+\mathbf {X}^{\prime }_{i}\varvec{\beta }^{(r)},\varvec{\varSigma }^{(r)}_{k}\right) }{\sum _{h=1}^K \pi ^{(r)}_h \phi _D\left( \varvec{y}_i;\varvec{\lambda }^{(r)}_{h}+\mathbf {X}^{\prime }_{i}\varvec{\beta }^{(r)},\varvec{\varSigma }^{(r)}_{h}\right) }. \end{aligned}$$
(23)

On the M-step at the \((r+1)\)th iteration of the EM algorithm, the updated estimates of the model parameters \(\pi ^{(r+1)}_k\), \(\varvec{\gamma }^{(r+1)}\) and \(\varvec{\varSigma }^{(r+1)}_{k}\) are computed using Eqs. (20), (21) and (22), respectively, where \(z_{ik}\) is replaced by \(p_{ik}^{(r)}\). As Eq. (21) depends on the \(\varvec{\varSigma }_{k}\)’s and Eq. (22) depends on \(\varvec{\gamma }\), the updated estimates of such parameters at the \((r+1)\)th iteration are obtained through an iterative process in which the estimate of \(\varvec{\gamma }\) is updated, given an estimate of the \(\varvec{\varSigma }_{k}\)’s, and vice versa, until convergence.

Once the convergence is reached, in addition to the parameter estimates the EM algorithm also provides estimates of the posterior probabilities using Eq. (23). These estimated posterior probabilities can be used to partition the I observations into K clusters, by assigning each observation to the component showing the highest posterior probability.

A crucial point of any application of an EM algorithm is the choice of \(\varvec{\theta }^{(0)}\). In general, convergence with the EM algorithm is slow, and this problem can be worsened by a poor choice of \(\varvec{\theta }^{(0)}\) (see, e.g., McLachlan and Peel 2000). Furthermore, since in a mixture model the likelihood function usually has multiple maxima, different starting values for the model parameters can lead to different estimates. A way to deal with the latter problem is to consider multiple random initializations and then to select the parameter estimate leading to the largest likelihood value. For the model described in this paper, starting values for the EM algorithm can be chosen by adapting the strategies described in Galimberti and Soffritti (2014). \(\varvec{\beta }^{(0)}\) can be obtained by fitting the standard seemingly unrelated regression model; the sample residuals of this model can be used to derive starting values for the remaining parameters. For example, the estimates from the fitting of a Gaussian mixture model with K components to the sample residuals can be employed. Alternatively, a random initialisation can be obtained by randomly partitioning the sample residuals into K groups and by computing the corresponding relative group sizes, group mean vectors and group covariance matrices. Further details and a practical comparison of these two different approaches to initialising \(\varvec{\pi }\), \(\varvec{\theta }_1, \ldots , \varvec{\theta }_K\) are provided in the online Supplementary material (see Sect. A).

2.5 Model selection

In the EM algorithm described in Sect. 2.4 the value of K is considered to be fixed and known. However, in most situations such value is not known and has to be estimated from the data. Several approaches dealing with this problem have been investigated in the framework of finite mixture models; most of them are model selection techniques which seek to find a parsimonious model that adequately describes the observed data (see, e.g., McLachlan and Peel 2000, chapter 6). An example is given by the Bayesian Information Criterion (Schwarz 1978):

$$\begin{aligned} BIC_M=2 \max \left[ l_M \right] -\mathrm {npar}_M\log (I), \end{aligned}$$

where \(\max \left[ l_M \right] \) is the maximum of the log-likelihood of a model M for the given sample of I observations, and \(\mathrm {npar}_M\) is the number of unconstrained parameters to be estimated for that model. This criterion allows to trade-off the fit and parsimony of a given model: the greater the BIC, the better the model. In the following Sections, this criterion is used not only to establish the most appropriate value of K to be used in model (6) but also to compare models characterised by different error term distributions.

3 Experimental results

The usefulness and effectiveness of the methods described in Sect. 2 are illustrated through some examples based on real and simulated datasets. The main results obtained on two real datasets are summarised in the following Sections. Further results are reported in the online Supplementary material. In particular, a numerical evaluation of properties of the ML estimates is carried out on both simulated and real datasets, with a special emphasis on the regression coefficients (see Sects. B and C).

All analyses are performed in the R environment (R Core Team 2013). A specific function is used, that implements the ML estimation through the EM algorithm described in Sect. 2.4 and the calculation of the Hessian matrix defined in Theorem 3. For each examined dataset, parameters of model (6) are estimated with a value of K from 1 to \(K_{max}\) (the values of \(K_{max}\) used in the experiments are described in the following Sections). For the results illustrated in this Section, the starting values of the model parameters are obtained through a strategy that fits Gaussian mixture models to the sample residuals of the classical seemingly unrelated linear regression model. The package mclust (Fraley and Raftery 2002; Fraley et al. 2012) is used without imposing any restriction on the component-covariance matrices. The EM algorithm is stopped when the number of iterations reaches 500 or \(|l_\infty ^{(r+1)}-l^{(r)}|<10^{-8}\), where \(l^{(r)}\) is the log-likelihood value from iteration r, and \(l_\infty ^{(r+1)}\) is the asymptotic estimate of the log-likelihood at iteration \(r+1\) (McNicholas and Murphy 2008). The stopping rules for each M step are either when the mean Euclidean distance between two consecutive estimated vectors of the model parameters is lower than \(10^{-8}\) or when the number of iterations reaches the maximum of 500. Estimates of the standard errors of the ML estimators of the regression coefficients are computed as the square root of the diagonal elements of \(H(\hat{\varvec{\theta }})^{-1}\) that refer to \(\varvec{\beta }\). Asymptotic confidence intervals for the regression coefficients are also obtained by assuming an asymptotic normal distribution for the ML estimators.

Model (2) under the assumption of multivariate Student t error terms is also fitted. In order to perform this latter task, a modified version of the EM algorithm described in Lange et al. (1989) is developed and implemented in a specific R function. This function selects starting values for \(\varvec{\beta }_0\) and \(\varvec{\beta }\) by fitting univariate Student t linear regression models for each dependent variable. Starting values of all the other model parameters are obtained by fitting a multivariate Student t distribution to the residuals derived from the D univariate regression models. The EM stopping rules described above are exploited also in this second function.

3.1 Canned tuna dataset

In this example, in which \(D=2\), \(P_1=P_2=2\), the parameters of the system of Eq. (1) for the canned tuna brands Star Kist 6 oz. and Bumble Bee Solid 6.12 oz. (see Sect. 1) are estimated. The value of \(K_{max}\) used in this experiment is 4. Table 1 provides some model fitting results.

Table 1 Maximised log-likelihood and BIC value for the models fitted to the tuna dataset
Full size table

According to the BIC, the model with \(K=3\) components provides the best description of the joint linear dependence of the log unit sales on the display activity and the log price for the two examined brands. The estimates of the prior probabilities of this model are 0.744, 0.195 and 0.061. Tables 2 and 3 report the estimates of the remaining parameters.

Table 2 Estimates of parameters \(\varvec{\lambda }_k\) and \(\varvec{\varSigma }_k\) obtained from the best model fitted to the canned tuna dataset
Full size table
Table 3 Estimates of the regression coefficients (RC) calculated from the best model fitted to the canned tuna dataset and their estimated SE
Full size table

By comparing the three components it emerges that the second component shows the highest value of the intercepts for both dependent variables (Table 2); this component is also highly homogeneous with respect to the log unit sales of Bumble Bee Solid 6.12 oz. A slightly lower estimated intercept and a very high estimated variance for the log unit sales of Bumble Bee Solid 6.12 oz. are the main specific features of the third component together with a negative estimated correlation between the log unit sales of the two brands.

As far as the effects of the regressors on the dependent variables are concerned (Table 3), they can be considered all significant (none of the 95 % asymptotic confidence intervals contains 0). The impact of the display activity on the log unit sales for Star Kist 6 oz. seems to be slightly higher than for Bumble Bee Solid 6.12 oz. The opposite result holds true for the effect of the log price.

The 338 weeks can be partitioned into three clusters by assigning each week to the component of the mixture that register the highest posterior probability. Most of the weeks (278) are assigned to the first cluster (CL1), while only 19 weeks are classified in the third cluster (CL3). Figure 2 shows the scatterplot of the log unit sales for the two brands in all weeks after removing the estimated effects of the two regressors. Weeks are labelled according to the cluster they are assigned. An interesting feature of the obtained classification emerging from this plot is that the third cluster is composed of weeks in which Bumble Bee Solid 6.12 oz. tuna sales register a relatively low mean level. Furthermore, it is also relevant to highlight that 17 out of the 19 weeks in the third cluster are consecutive from week 58 to week 74. According to additional information about the canned tuna dataset available at the University of Chicago website (http://research.chicagobooth.edu/kilts/marketing-databases/dominicks/), these weeks correspond to the period from mid-October 1990 to mid-February 1991. It is worth noting that in that same period the U.S. nongovernmental organization Earth Island Institute promoted a worldwide boycott campaign encouraging consumers not to buy Bumble Bee tuna because Bumble Bee was found to be buying yellow-fin tuna caught by dolphin-unsafe techniques (Baird and Quastel 2011).

Fig. 2
figure 2

Canned tuna dataset: scatterplot of the weekly log unit sales for the two brands after removing the estimated effects of the two regressors. Weeks are labelled according to their cluster membership

Full size image

3.2 AIS dataset

This Section describes some results obtained from the analysis of the Australian Institute of Sport (AIS) dataset (Cook and Weisberg 1994). Namely, the interest is focused on studying the joint linear dependence of \(D=4\) biometrical variables (\(Y_1\): body mass index (BMI), \(Y_2\): sum of skin folds (SSF), \(Y_3\): percentage of body fat (PBF), \(Y_4\): lean body mass (LBM)) on three variables providing information about blood composition (red cell count (RCC), white cell count (WCC), plasma ferritine concentration (PFC)). The same problem was investigated by Soffritti and Galimberti (2011) using multivariate linear regression models.

Seemingly unrelated linear regression models from Eq. (6) are estimated for \(K=1, 2, 3\). Since the choice of the regressors to be used for each biometrical variable may be questionable, for each value of K and each dependent variable an exhaustive search for the relevant regressors is performed. Thus, for each value of K, \(2^{3 \cdot D}=4096\) different regression models are fitted to the dataset. The same exhaustive search is carried out using seemingly unrelated regression models with multivariate Student t error terms. Thus, a total number of 16384 different models are examined. The total number P of regressors included in a model is between 0 and 12. The EM algorithm has failed due to the singularity of some matrices for two models when \(K=2\) and 40 models when \(K=3\).

In this situation, the BIC defined in Sect. 2.5 can be used not only to choose the best distribution for the error terms (multivariate Gaussian, Student t or Gaussian mixture in this study), but also the best subset of regressors for each equation in the system (2). Figure 3 shows the BIC values of the fitted models with the best trade-off (i.e., the maximum value of the BIC) among all the models having the same error distribution (Gaussian mixture with \(K=1, 2, 3\) and Student t) and the same number of regressors (\(P=0, \ldots , 12\)). By comparing models having the same value of P it emerges that the best performance is obtained using Gaussian models with three components when the total number of regressors is low (\(P=0, 1, 2\)); otherwise, Gaussian models with two components should be preferred. Thus, the introduction of a finite mixture for the distribution of the error terms allows to obtain a relevant improvement with respect to seemingly unrelated regression models with both Gaussian and Student t errors, for all P. Note that Student t models achieve a slightly better performance than classical models with Gaussian errors.

Fig. 3
figure 3

AIS dataset: best BIC values by total number of regressors and number of components

Full size image

If models are compared by controlling the error distribution, \(P=7\) regressors should be used when \(K=1,2\) and with Student t errors. Namely, for these three cases, the selected regressors for the equations of the dependent variables BMI, PBF and LBM are RCC and PFC; only RCC is selected as a relevant regressor for the equation of SSF. Hence, the numbers of regressors in the \(D=4\) equations associated with these three cases are \(P_1=P_3=P_4=2\) and \(P_2=1\). When \(K=3\), the best trade-off is obtained using a model without regressors (\(P_1=P_2=P_3=P_4=0\)). Some results concerning these four latter models are illustrated in Table 4. Overall, according to the BIC the best model is the one with \(K = 2\). In this model, the estimates of the parameters \(\pi _1\) and \(\pi _2\) are 0.619 and 0.381. Tables 5 and 6 report the estimates of the remaining parameters. Compared to the second component, the first component is characterised by lower values of the intercepts for all dependent variables and lower variances for BMI, SSF and PBF. Further differences between components concern some correlations (see the lower triangular parts of \(\hat{\varvec{\varSigma }}_1\) and \(\hat{\varvec{\varSigma }}_2\) in Table 5). The asymptotic confidence intervals for the regression coefficients are reported in Table 6, along with the estimated standard errors of the corresponding ML estimators. None of such confidence intervals contains the 0 value.

Table 4 Maximised log-likelihood and BIC value for the best models fitted to the AIS dataset
Full size table
Table 5 Estimates of parameters \(\varvec{\lambda }_k\) and \(\varvec{\varSigma }_k\) obtained from the best model fitted to the AIS dataset
Full size table
Table 6 Estimates of the regression coefficients (RC) calculated from the best model fitted to the AIS dataset and their estimated SEs
Full size table

The best model can be used to assign each athlete to the component of the mixture that register the highest posterior probability, thus producing a partition of the sample into two clusters. Most of the athletes assigned to the second cluster are female (79.2 %), while 68.8 % of the athletes classified in the first cluster are male (Table 7). This classification of the athletes is statistically associated with athletes’ gender (\(\chi ^2=43.96\), \(p\,value=3.36\cdot 10^{-11}\)). Thus, the omitted regressor captured by the selected model is strongly connected with athletes’ gender. However, the partition discovered by the model has a misclassification rate equal to 0.27. Using multivariate regression models (by including RCC, WCC and PFC in each equation), Soffritti and Galimberti (2011) obtained a partition with a slightly lower misclassification rate (0.25). Note that this latter result was obtained by estimating a model with a larger number of parameters but a lower BIC value (\(-4905.44\)).

Table 7 AIS dataset: joint classification of the athletes according to gender and cluster membership estimated by the best model
Full size table

4 Concluding remarks

In this paper, multivariate Gaussian mixtures are used to model the error terms in seemingly unrelated linear regressions. This allows to exploit the flexibility of mixtures for dealing with non-Gaussian errors. In particular, the resulting models are able to handle asymmetric and heavy-tailed errors and to detect and capture the effect of relevant nominal regressors omitted from the model. Furthermore, by setting the number of components equal to one or by constraining all the equations to have the same regressors, some solutions already described in the statistical literature can be obtained as special cases.

The approach described in this paper can be extended by considering other parametric families for the mixture components. For example, similarly to Galimberti and Soffritti (2014), mixtures of multivariate Student t distributions could be used to define a more general class of models, which contains model (6) as a limiting case.

Parsimonious seemingly unrelated linear regression models can be obtained by introducing some constraints on the component covariance matrices \(\varvec{\varSigma }_{k}\)’s, based on the spectral decomposition (see, e.g., Banfield and Raftery 1993; Celeux and Govaert 1995; McLachlan et al. 2003; McNicholas and Murphy 2008). Such models could provide a good fit for some datasets by using a lower number of parameters; they could be useful especially in the presence of a large number of dependent variables.

In Sect. 3 the BIC is used to select the relevant regressors in each equation as well as the number of mixture components. The use of this criterion can be motivated on the basis of both theoretical and practical results (see, e.g., Cutler and Windham 1994; Keribin 2000; Ray and Lindsay 2008; Maugis et al. 2009a, b). Clearly, other model selection criteria could be used, such as the ICL (Biernacki et al. 2000), which additionally takes into account the uncertainty of the classification of the sample units to the mixture components.

Some computational issues could arise when using the models proposed in this paper. For example, when the number of candidate regressors is large, an exhaustive search for the relevant regressors for each equation could be unfeasible. A possible solution could be obtained by resorting to stochastic search techniques, such as genetic algorithms (see, e.g., Chatterjee et al. 1996). As far as the EM algorithm is concerned, different initialisation strategies may be considered and evaluated (see, e.g., Biernacki et al. 2003; Melnykov and Melnykov 2012). Although these issues are not the main focus of this paper, they could deserve further investigation.