1 Introduction

Glass manufacturing processes have very long dynamic response time and are complex processes with high energy usage. Especially, large furnaces with multiple port burners cause glass manufacturing industries to consume high energies in glass production. Most glass industries are operating at maximum daily throughput to fulfil the market requirement. Therefore, glass furnace operations are facing great challenges in reducing fuel consumption by applying well tuned control strategies. Apart from high energy consumption, undesirable emissions from glass industries is another setback to consider as the entire world is greatly concerned about green house effects. Tight environmental regulations are now applied to reduce gases and particles that are undesirable emissions associated with burning fossil fuels.

Generally, the glass industries are operating within the emission guideline which is regulated by environmental agencies[1]. Thus, most glass industries are not emphasising on continuous monitoring and control strategies for emissions. At maximum operating conditions, the likelihood of producing undesirable emission is high. If there is any occurrence of sudden undesirable disturbances, this can result in more problems for existing furnaces which may be already operating in poor thermal conditions around the world. The control of excess oxygen emissions, as well as glass temperature, is therefore also considered in this paper.

For such a complex multivariable process, a decentralised control strategy is generally applied and has always been in the attention of many researchers for developing a precise control strategy to enhance the performance of multivariable processes. However, difficulties are encountered in designing the decentralised control due to loop interactions.

A literature search reveals that there are several classified tuning methods suggested to tune decentralised controllers for multivariable processes such as detuning[2], sequential design[3], independent design[4] and iterative[5] methods. These tuning methods have achieved a certain degree of success in the design approach. However, these tuning methods do exhibit weaknesses and can suffer in compensating the couplings between loop interactions of a multivariable system. To improve the compensation of loop interactions, the effective open-loop (EOL) method was introduced[6]. The EOL method considers all other loop interactions while adapting the i-th control parameters for the i-th EOL. But, the EOL method produces model approximation error, due to mathematical complications, as the model dimensions are increased. Thus, the EOL method is mainly applicable for low dimension models. Another successful approach is that of relay auto-tuning, which is a combination of single loop relay auto-tuning and the sequential tuning method[7]. This method appears to perform well, but a multivariable system with large multiple dead time exhibits poor performance. In recent years, to improve the entire control performance and robust stability, a systematical approach based on the generalised internal model control, proportional-integral-derivative (IMC-PID) design method[8] and the reduced effective transfer function (RETF) by inverse response behaviour method[9] have been introduced for multivariable processes. But, both methods involve a complex mathematical approach to design the decentralised controllers. In general, a question always arises about the wellness of control optimisation and the flexibility, due to the application constraints, of these design methods.

Standard genetic algorithms (SGAs) are global search methods by genetics evolution with higher performance in optimisation over traditional methods[10–12]. Due to their superior self-adjustable ability, SGAs have been applied extensively in tuning the PID parameters for single-input single-output (SISO) systems[13–15], curve fitting[16] and fuzzy optimisation[17]. On the other hand, application to multiple-input multiple-output (MIMO) systems is still an open research topic for optimising control parameters by SGAs. A promising decentralised controller by SGAs was proposed for a multivariable process[18]. The controller performance was defined by closed-loop response in terms of time-domain bounds for both reference following and loop interactions. An integrity theorem with SGAs to enhance the closed-loop system stability when certain loops are failing or breaking down was proposed[19]. Recently, improved convergence of genetic algorithms was achieved by introducing the multi-objective evolutionary algorithm (MOEA) which combines two fitness assignment methods (global rank and dominance rank)[20].

This paper investigates the potential of SGAs for optimising the discrete-time PID controller parameters in a decentralised control scheme for a multivariable glass furnace. The paper enhances and expands on initial results presented in [21]. The structure of this paper is as follows. First, an introduction is given about the considered multivariable glass furnace process and the models used for the controller optimisation studies. Second, the approach to optimisation by SGAs of discrete PID controller parameters is presented, with considerations to boundary constraints and particular cost functions. Third, investigations are presented on loop interaction effects and control robustness for the multivariable glass furnace, with controllers optimised by three SGAs tuning approaches. The proposed methods are developed and tested in simulations based on Matlab/Simulink models.

2 Multivariable glass furnace process and modelling

Fig. 1 illustrates the block diagram of the realistic multivariable glass furnace considered in this research, which consists of a state-space furnace model of 24 states with feedback loop and excess oxygen model. f1 and f2 are algebraic expressions, f1 includes controller output and saturation, f2 includes specific heat C p and lower heat value (LHV) for determining the combustion energy, T SET is the primary temperature setting, AFR is air-fuel ratio, T amb is ambient temperature, ṁ is fuel flow in mass, T g is glass temperature, and EO2 is excess oxygen.

Fig. 1
figure 1

Block diagram of realistic multivariable glass furnace process model

Full size image

The realistic glass furnace model that is identified and applied for further research here is representing a real plant combustion chamber from Fenton Art Glass Company, USA[22]. The furnace model is an extended research work by Holladay[23] using a radiative zone method to develop the 24 state space variables (zones) model. The linearised energy balance equations are applied and modified with respect to the 24 state variables for each zone corresponding to temperatures. For example, the energy balance equation of combustion zone α1 can be written as

$$\matrix{{C{a_{\alpha 1}}{{dT{a_{\alpha 1}}} \over {{\rm{d}}t}} = Q{a_{\alpha 1}} =} \hfill \cr {\quad \quad \quad \quad \;\;Qb{w_{\alpha 1}} + Q{c_{\alpha 1}} + Qs{w_{\alpha 1}} + Q{a_{\alpha 2}} +} \hfill \cr {\quad \quad \quad \quad \;\;Q{g_{\beta 1}} + Q{g_{\beta 2}} + Q{g_{\chi 1}} + Q{g_{\chi 2}} +} \hfill \cr {\quad \quad \quad \quad \;\;Q{g_{\delta 1}} + Q{g_{\delta 2}} + {Q_{in}}.} \hfill \cr}$$
(1)

A literature survey reveals that there is no EO2 realistic model for a glass furnace available for research. The realistic EO2 model designed for research here was developed using collected data from an industrial furnace by an open-loop step response technique. SGAs were applied for identification of a higher order transfer function (3rd order) as a realistic model for EO2, and control oriented models for both T g and EO2 for control optimisation. The identified transfer functions by SGAs are as follows:

For EO2 realistic model,

$${{\Delta E{O_2}(s)} \over {\Delta AFR(s)}} = {{1.613} \over {50.3{s^3} + 149.6{s^2} + 142.7s + 1}}{{\rm{e}}^{- 173s}}.$$
(2)

For EO2 control oriented model,

$${{\Delta E{O_2}(s)} \over {\Delta AFR(s)}} = {G_{E{O_2}}}(s) = {{1.6} \over {150s + 1}}{{\rm{e}}^{- 174s}}.$$
(3)

For glass furnace temperature control oriented model,

$$\matrix{{\Delta {T_g}(s) = {G_{{T_g}1}}(s)\Delta \dot m(s) + {G_{{T_g}2}}(s)\Delta {T_{SET}}(s) =} \hfill \cr {\quad \quad \quad \;\;{{4488.4} \over {1.992 \times {{10}^5}s + 1}}\Delta \dot m(s) +} \hfill \cr {\quad \;\;\quad \quad {{- 0.9834} \over {1.992 \times {{10}^5}s + 1}}\Delta {T_{SET}}(s).} \hfill \cr}$$
(4)

According to the collected data of EO2, the model is designed based on a step input of air-fuel ratio (AFR ratio is 17.2:1 in mass). Changes in fuel flow ṁ cause corresponding changes in air flow through the AFR. Since ṁ does not alter the AFR and it is the AFR that affects EO2, there will be no effect on the EO2 when ṁ is changed. However, any variation in air-fuel ratio will affect the outputs of f1 and f2 (Fig. 1) which leads directly to changes in ṁ and hence, T g . Therefore, the multivariable glass furnace process has single loop interaction from AFR to T g under closed-loop influences. The identified control oriented model of the interaction was

$${{\Delta {T_g}(s)} \over {\Delta AFR(s)}} = {G_{AFR}}(s) = {{- 61.5} \over {2 \times {{10}^5}s + 1}}.$$
(5)

The dynamics of the glass furnace process are therefore, represented by the following low order 2 × 3 transfer function matrix which is used for controller optimisation.

$$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {\Delta T_g (s)} \\ {\Delta EO_2 (s)} \\ \end{array} } \right] = } \\ {\left[ {\begin{array}{*{20}c} {G_{Tg1} } & {G_{Tg2} } & {G_{AFR} } \\ 0 & 0 & {G_{EO2} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\Delta \dot m(s)} \\ {\Delta T_{SET} (s)} \\ {\Delta AFR(s)} \\ \end{array} } \right].} \\ \end{array} $$
(6)

For a more complete control realisation of the EO2 process, the realistic model transfer function (2) is associated with an AFR conversion model and EO2 look-up table as illustrated in Fig. 2. The AFR conversion model was particularly designed to convert the real value of AFR(mass) to respective AFR(volumetric) based on the methane gas law. The transfer function (2) and AFR conversion model are linear. But, the EO2 look-up table exhibits some nonlinear effects due to the methane chemical relationship between the stoichiometric AFR(volumetric) input and EO2(%) output.

Fig. 2
figure 2

Block diagram of complete realised EO2 model

Full size image

3 Discrete PID parameters optimisation by SGAs

In general, a classical PID controller can be described as an input-output relation expressed as

$$u(t) = {K_c}\left({e(t) + {1 \over {{T_i}}}\int {e(t){\rm{d}}t + {T_d}{{{\rm{d}}e(t)} \over {{\rm{d}}t}}}} \right)$$
(7)

where u is the control signal, e is the error signal, and K c , T i and T d denote the proportional gain, the integral gain and derivative gain, respectively. By using finite difference approximations, (7) is expressed as its discrete equivalent in positional form. For more accurate approximations, the trapezoidal and backward rules are applied here to develop discrete expressions for the integral and derivative terms, respectively \(({K_I} = {1 \over {{T_i}}})\),

$$\matrix{{{G_c}(z) = {{U(z)} \over {E(z)}} =} \hfill \cr {\quad {K_c}\left({1 + {K_I}{T \over 2} \times {{z + 1} \over {z - 1}} + {T_d}{1 \over T} \times {{z - 1} \over z}} \right).} \hfill \cr}$$
(8)

3.1 Performance criterion formulation

The performance criteria for both T g and EO2 are formulated individually under closed-loop SISO control based on the following desired response characteristics.

  1. 1)

    For T g , overshoot ≤ 2%, settling time (t s ) ≈ 5h.

  2. 2)

    For EO2, overshoot ≤ 2%, settling time (t s ) ≈ 7min.

  3. 3)

    For both variables, zero steady state error to a constant set point.

3.2 SGAs configuration

The SGAs approach used for optimisation of the PID controller parameters is shown in Fig. 3. As illustrated in the flowchart of the SGAs, at initial state, the chromosomes of an array of variable values to be optimised are defined as

$${\rm{Chromosome}} = \{\underbrace {({{K_c}{K_I}{T_d}}),}_{{T_g}}\underbrace {({{K_c}{K_I}{T_d}})\} .}_{E{O_2}}$$
(9)
Fig. 3
figure 3

Flow chart of control optimisation by SGAs

Full size image

Binary coding was selected to encode the discrete controller parameters into binary strings to generate the initial population randomly in the beginning. The length of each chromosome (Lind) is determined based on the binary precision or resolution:

$${\rm{re}}{{\rm{s}}_j} = {{{b_j} - {a_j}} \over {{2^{{m_j}}} - 1}}$$
(10)

where m j is the number of bits, b j is the upper boundary, and a j is the lower boundary of each individual chromosome’s searching parameter. Each chromosome’s binary string is converted into an associated real value of PID parameter to propagate to the discrete PID controller. The decoding process into a real value is done as

$${x_j} = {a_j} + Dec \times {{{b_j} - {a_j}} \over {{2^{{m_j}}} - 1}}$$
(11)

where x j is the respective real value of the chromosome’s search parameter and Dec is the decimal value of the respective binary string. A complete simulated system response of each PID set and its initial fitness value is evaluated by using a defined objective function.

According to the chromosome’s fitness value by a defined objective function, a new generation (offspring) is produced by the process of genetic operators. The genetic operators manipulate the binary strings of the chromosomes directly, by means of selection rate (S rate ), crossover rate (X rate ) and mutation rate M rate to produce fitter chromosomes for the next generation. After completion of the genetic operator process, the new set of binary strings for each chromosome in the population is required to be decoded into real values and propagated again to the discrete PID controller to evaluate the new fitness values. This process is sequentially repeated until a maximum number of generations is reached, where the optimal fitness is attained. Due to no previous information available for genetic operator values for both T g and EO2 control optimisation, several experiments were conducted where variations of the genetic operator values were tested individually for enhancing the searching mechanism. Table 1 illustrates the selected genetic operator parameters for both T g and EO2.

Table 1 Genetic operators of T g and EO2
Full size table

3.3 Objective function and boundary constraint formulation

The control oriented models of both T g and EO2 were used individually to identify the optimum objective function and searching boundaries to achieve the performance criteria. In the first attempt, initial guesses were made for the search boundaries in the SGAs. Improved boundary constraints were subsequently introduced. For better selection of improved boundary values, conventional tuning methods (Ziegler-Nichols and direct synthesis) were analysed to identify PID values. With these identified PID values, b j and a j were adjusted accordingly to ensure an optimal solution for the desired response characteristics.

Two objective functions, integral absolute error (IAE) and integral squared error (ISE),

$${J_i}(IAE) = \sum\limits_{k = 0}^{\max} {\left| {e(k)} \right|}$$
(12)
$${J_i}({ISE}) = \sum\limits_{k = 0}^{\max} {{e^2}(k)}$$
(13)

were used to compare and improve the set-point error for EO2. Fig. 4 and Table 2 illustrates that the SGAs with parameter vectors of improved bound PID, K c ∈ [0, 1], K I ∈ [0, 0.01], T d ∈ [0, 50], for EO2 have better dynamic response and higher degree of accuracy while reducing the performance criterion by adapting the fitness value. Initial optimisation of PID parameters by conventional techniques provides a better suggestion of improved bound ranges than assigning the ranges randomly or arbitrarily. By limiting b j of K c , the SGA consolidates well within the boundary constraints for K I and T d to converge to the global minimum.

Fig. 4
figure 4

Responses of EO2 for conventional techniques and SGAs with random and improved boundaries

Full size image
Table 2 PID parameters for EO2 by different tuning methods
Full size table

However, Fig. 5 and Table 3 illustrate an overshoot of 10% (1555 K) occurred in the transient response with a long settling time of 30 h for T g with improved boundaries. SGAs optimised close to the b j to attain the desired response characteristics, but failed to achieve a global minimum. To enhance the searching mechanism for the control parameters and achieve a global minimum, a modified cost function is applied. A weighting factor λ applied to the integral squared process input (controller output) term u (ISU) is added to the cost function to reduce the fast rising effect of the transient response. The modified cost function applied for T g is given by the relation,

$${J_i}({ISE + {\rm{\lambda}}ISU}) = \sum\limits_{k = 0}^{\max} {\left| {Tg\left(k \right) - 1550} \right| + {\rm{\lambda}}{u^2}(k)}$$
(14)

where k is the sampling number and u is the controller output. The selection of an optimal value of λ is done by trial and error technique by varying λ in the range [100, 1 000]. The weighting factor associated with the desired response characteristics was set to λ = 400 to give more emphasis to the set point tracking objectives.

Fig. 5
figure 5

Responses of T g for a conventional technique and SGAs with improved boundaries and weighting factor

Full size image
Table 3 PID parameters for T g by different tuning methods
Full size table

The simulation results in Fig. 5 and Table 3 illustrate that the SGA with modified cost function, IAE + λISU (14), has a higher level of optimisation mechanism and better dynamic response than the improved searching bound alone. Application of λ with ISU has suppressed the larger overshoot behaviour of the glass temperature response by smoothing the controller output. Overall desired response characteristics, which are reduction of set-point error, overshoot and settling time, are achieved for T g with the IAE + λISU cost function.

4 Simulation results of decentralised control strategies by SGAs

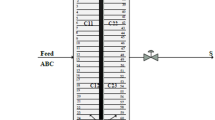
The optimisation of discrete decentralised control strategies is analysed by three SGAs tuning approaches, associated with the 2 × 2 control oriented multivariable glass furnace model as illustrated in Fig. 6. The three SGAs tuning approaches are applied in closed-loop step input tests. The three tuning approaches are:

  • SGAs-1: The discrete PID values of both T g and EO2 are optimised individually with their respective closed-loop control oriented model (independently) without loop interactions as discussed in Section 3.3.

  • SGAs-2: The discrete PID values of both T g and EO2 are optimised individually with their respective closed-loop control oriented model with loop interaction. (C1 (z) is optimised with respective cost function, T SET = 1500K → 1550K, EO2(Ref) is constant (2.45%), C2(z) = default value from SGAs-1 result, C2(z) is optimised with respective cost function, T SET is constant (1500K), EO2(Ref) = 2.45% → 3%, C1(z) = default value from SGAs-1 result.)

  • SGAs-3: The discrete PID value of both T g and EO2 are optimised together by multivariable closed-loop control oriented model with loop interaction. The optimised cost function is modified to include the total effect of T g and EO2 by adding the individual cost functions for both variables for each test as shown in (15). (C1(z) and C2(z) are optimised with modified cost function: T SET = 1 500 K → 1550K at EO2 = steady-state, EO2(ref) = 2.45% → 3% at T SET = steady-state (1550K)).

    $$\matrix{{{J_{i({Tg})}} = {{({ISE + {\rm{\lambda}}ISU})}_{Tg}} + IA{E_{E{O_2}}}} \hfill \cr{{J_{i({E{O_2}})}} = 0 + IA{E_{E{O_2}}}.} \hfill \cr}$$
    (15)
Fig. 6
figure 6

2-input, 2-output multivariable control oriented model under closed-loop discrete decentralised PID control

Full size image

Tables 4 and 5 compare the optimised PID parameters by the respective SGA tuning approaches of T g and EO2, respectively. As discussed in Section 2, any variation in ṁ caused by T SET and EO2(Ref) step inputs does not affect EO2. Thus, Fig. 7 reveals that there is no change in EO2 responses by SGAs-1 and SGAs-2. This can also be noticed in Table 5, where the PID parameters for these two approaches barely have a change.

Fig. 7
figure 7

EO2 responses by three SGAs tuning approaches under loop interaction

Full size image
Table 4 Optimised PID parameters for T g by decentralised techniques
Full size table
Table 5 Optimised PID parameters for EO2 by decentralised techniques
Full size table

On the other hand, Fig. 8 reveals that the optimised PID parameters by SGAs-1 are inadequate to achieve the desired performance criteria for T g under loop interaction. As a result of the G AFR (S)’S long dynamic time constant (2 × 105 s), the T g response rise time (t r ) is lagged about 24 min, hence the settling time (t s )has increased to 7h and produced a steady-state temperature error of 1 K. In contrast, the SGAs-2 method consolidated better with loop interaction and G AFR (s)’s dynamic time constant to maintain the desired performance criteria by increasing the K c and K I parameters accordingly.

Fig. 8
figure 8

T g responses by three SGAs tuning approaches under loop interaction

Full size image

The SGAs-3 tuning approach is tested by applying step inputs on both set points (T g and EO2)at two different time periods in one simulation with the modified (combined) cost function (15). Thus, the total simulation time has increased to optimise both sets of PID parameters. The simulation results of SGAs-3 for T g are shown in Fig. 9. At t1 =0h, T SET = 1500K → 1550K, EO2 = 2.45% (constant). At t2= 61.1 h, T SET = 1550K (constant), EO2 = 2.45% → 3%. From t1 to t2, technically the cost function of T g (IAE + λISU) is optimising the PID parameters of C1 (z) individually without any effect of the EO2 cost function (IAE). Such a long time, gap between t1 and t2 is required in the optimisation considering the effect of G AFR (s)’s long dynamic time constant (2 × 105s). Up to t1, there is no effect on EO2 as this loop interaction is cancelled by the AFR relationship inherent in the process.

Fig. 9
figure 9

T g responses by SGAs-3 with modified (combined) cost function

Full size image

From t2, the total effect of T g and EO2 cost functions \(({J_i}_{({T_g})})\) are compounded together in further optimisation of the C1(z) and C2(z) PID parameters. According to Fig. 9, T g is reduced approximately to 1549.2 K under loop interaction for the increase in EO2 at t2. To maintain the T g response, the K c parameter by SGAs-3 is increased about 5.31% from SGAs-2 (Table 4). But, the K I parameter by SGAs-3 is reduced about 4.58% from SGAs-2. The effect of an increment and reduction of K c and K I is noticeable in Fig. 7 where both gain parameters are consolidating well to achieve a desirable response. Also, the EO2 response and PID parameters vary by a smaller amount with the modified (combined) cost function \(({J_i}_{({T_g})})\) as illustrated in Fig. 8 and Table 5. In the control of both variables, the SGAs-3 method achieves the smallest values of the cost functions and settling times (Tables 4 and 5).

The total set-point error of \({J_i}_{({T_g})}\) is 7.024 9 × 104. Technically, as there is no loop interaction from ṁ to EO2, the cost function of \({J_{i(E{O_2})}}\) (15) is applied to identify the set-point error of EO2. As a result, the set-point error of \({J_{i(E{O_2})}}\) is 178.53. Also, the optimised PID parameters by \({J_i}_{({T_g})}\) for EO2 are very much similar to \({J_{i(E{O_2})}}\). Thus, the set-point error of IAE + λISU (T g ) is 7.007 × 104 by calculation.

As discussed in Section 2, a nonlinearity effect may appear in step input variations due to the methane chemical relationship between stoichiometric AFR (volumetric) and EO2(%). Thus, the loop stability and control robustness are investigated further. Fig. 10 illustrates the robust responses of T g for the three sets of optimised PID parameters (SGAs-1 to SGAs-3) under loop interaction for two EO2 step input tests. The simulations of the two EO2 step input tests are elaborated as follows:

  1. 1)

    EO2, 2.45% → 3.45%: Initial steady state of T g = 1550 K causes an initial reduction in T g , 1550 K → 1548.7 K (approximately).

  2. 2)

    EO2, 2.45% → 1.45%: Initial steady state of T g = 1550 K causes an initial increase in T g , 1550 K → 1551 K (approximately).

Fig. 10
figure 10

Loop interaction of multivariable process under closed-loop discrete decentralised control strategy. Effect of EO2(ref) (Δ1%) on T g

Full size image

The observed disturbances in T g are caused by the changing AFR as a result of the EO2 set points. To compensate the feedback error, controller C1(z) varies ṁ accordingly to sustain T g . In overall, the SGAs-2 method has 17.4% better control robustness than SGAs-1 (as measured by the IAE between T g and the temperature set point). While, the SGAs-3 method has 4.36% better control robustness than SGAs-2.

5 Conclusions

SGAs were applied successfully to identify low order, control oriented models of the plant to be used for subsequent controller optimisation. According to the desired response characteristics, the control parameters optimisation by genetic algorithms was enhanced with an improved cost function and improved searching boundaries. The loop interaction and control robustness within the realistic multivariable glass furnace model were compensated with well optimised PID parameters by SGAs in a decentralised PID control scheme. Lower values of the optimised cost functions and improved robustness to loop interactions were achieved when the controllers were optimised together.