1 Introduction

The applications of machines and robots to assist human in performing their tasks have become increasingly extensive. In industrial applications, the use of robotic system has reached the level which surpasses human ability in terms of speed and accuracy. On the other hand, in the field of domestic robots or service robots, the developments are still far from perfection.

For a service robot to perfectly perform its tasks, it needs to be able to adapt to and cope with the normal human living environment. From the practical point of view, bipedal robot is the most suitable robot structure due to its similarity of physical configuration with human especially in terms of locomotion method. However, the realization of bipedal robot is more challenging compared to other types of mobile robots due to the unstable nature of bipedal walking. Therefore, many studies have been carried out especially to address the concerns of stability sensing and control strategies of bipedal robot.

The complexity of the bipedal walking task becomes a major challenge in realization of bipedal robot. The walking process itself inherently creates a disturbance to destabilize the robot. Therefore, optimal walking algorithms that consider many destabilizing factors, such as handling of major mass of the robot body, possibility of impact at feet landing, sensitivity of control system to the disturbing factors have to be designed to be able to correct and alter the posture and keep the robot stable. This may increase the complexity of the walking algorithms and requires a special decision making process which involves multivariable parameters.

Big companies, such as Honda, Sony, Fujitsu and Alde-baran Robotics, have invested a considerable amount of funds and efforts in the area of bipedal or humanoid robot research[1–4]. However, the applications of the humanoids are still limited to entertainment and research purpose due to the cost and complexity.

The most recent development of bipedal walking robot in the field of military is the utilization of bipedal walking robot in testing the chemical protection clothing used by US Army. The bipedal walking robot, PETMAN, is able to perform human-like walking, crawling and doing a variety of suit-stressing calisthenics during exposure to chemical warfare agents. PETMAN also simulates human physiology within the protective suit by controlling temperature, humidity and sweating when necessary[5].

Despite all the advance features such as object recognition, speech recognition, human-robot interaction[6, 7], the classic problem of how to optimally achieve a stable walk of the humanoid robots with simple minimalist structure still remains challenging.

There are several theories that have been established and applied to the stability control of bipedal robot. Zero moment point (ZMP) was first introduced by Vukobratovi and Juricic[8] in 1968. Since then, the theory has been widely studied and applied by many researchers to the development of several successful walking robots[9–13]. ZMP is defined as the point on the ground at which the net moment of the inertial forces and the gravity forces has no component along the horizontal axes. In application, the position of ZMP reflects the level of robot posture balance in motion. From the control point of view, this information is used as feedback variable to ensure that the robot will stay in the stable region throughout the entire walk gait.

The concept of linear inverted pendulum model (LIPM) was first introduced and implemented by Kajita and Tani[14]. LIPM simplifies the complex shape of the robot model into a single concentrated mass at the centre of mass (CoM). The concentrated mass is linked to a contact point on the ground via a massless rod, which is represented by the supporting leg. The linear model of the pendulum is achieved by applying constraint control so that the body of the robot is restricted to moving in a straight line. During a single support phase, the CoM of the robot is restricted to moving along constraint line and the posture is kept in the upright position. The constraint is implemented by control­ling the knee and the hip joints of the support leg.

Another approach of stability measurement for bipedal robot is by using the angular momentum information of the system. This approach has been increasingly explored for the past few years[15–17]. The usage of angular momentum was first introduced and demonstrated in a physical bipedal robot prototype by Sano and Furusho[15]. The motion control in the sagittal plane is achieved by controlling the ankle torque of the supporting leg in order to follow the provided reference function of angular momentum. The reference function is designed based on the changes in angular momentum undergone by an inverted pendulum in the earth’s field of gravity. For the lateral plane, the motion is formulated as a simple regulator with two equilibrium states, which is a repetition of tilting the body to place the centre of gravity to the left or right supporting leg alternately.

This paper and related research introduce a novel minimalist bipedal robot construction and control strategy with the main objective of decoupling the walking and balancing systems as well as having an optimal control that considers various destabilizing factors. The proposed approaches focus on achieving stable bipedal walking with a simple mechanism and multiple control strategies. This distinguishes the proposed approaches from most of the existing bipedal robots which employ complex mechanism and require heavy computing power in order to achieve a stable walk. By separating the walking and balancing task into two individual subsystems, the task of walking control can be simplified. This research aims to prove the feasibility of decoupling the walking task of a bipedal robot from the stability maintenance task. By dividing task and conquering the problem individually, it is expected that the complexity of the system can be greatly reduced. Due to its simplicity, the decoupling technique provides a great advantage for the practical implementation of bipedal walking algorithms.

This paper mainly discusses the details of the minimalist bipedal robot development which is designed based on the newly proposed algorithms. The viability of the proposed walk and stability control strategies, such as hip-mass carry strategy and the planning of impact-free trajectories, has been theoretically confirmed by the detail mathematical model and computer simulation results. The theoretical details of these strategies have been reported on our previous publications[18,19]. The detail simulation results reported in the latest paper[20] further proved the feasibility of the decoupling technique and the related walk strategies in achieving a stable walk.

The content of this paper is arranged as follows. Section 2 discusses the details on the locomotion systems which include the structural construction as well as the actuation and motion transmission system. Section 3 presents the design of the stability sensing system and the mechanism for restoring the robot posture balance. The technical details of the control systems are presented in Section 4. Section 5 discusses the mathematical model and the simulation result of the proposed design. The experiments and related results are discussed in Section 6. Lastly, the conclusion is provided in Section 7.

2 Locomotion systems

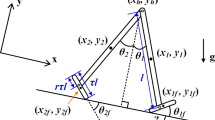
Fig. 1 shows the schematic diagram of a single leg. The leg mechanism is constructed by a series linkage to control the leg motion and also to serve as the main leg structure. Angles θ 1 and θ A are applied by the actuators to control the angular position of the hip and knee joints, respectively. The linkage can be divided into three sets of parallelogram mechanism and their kinematics can be analyzed individually. The first two sets of parallelogram mechanisms are OCFG and CDEF which are used to control the position of the foot link. The third set is the parallelogram mechanism OABC which is used to control the position of the shank link.

Fig. 1
figure 1

Schematic diagram of parallelogram leg mechanism

Full size image

Unlike a conventional bipedal robot configuration, the ankle joint in this design concept of the robot is not actuated by any actuator. Instead, it utilizes a series of parallelogram mechanisms to passively control the ankle joint in order to maintain the horizontal orientation of the foot. The usage of parallelogram mechanism provides an essential benefit due to reduction of the number of actuators required to drive the leg. This, in turn, results in the simplification of the overall mechanical design and reduction of the robot’s weight. Fig. 2 shows the implementation of the parallelogram leg mechanism on the physical prototype.

Fig. 2
figure 2

Physical prototype with different leg configurations

Full size image

For the leg structure shown in Fig. 1, links OG, CF and DE have equal lengths. Links OC and CD are the thigh and shank segments of the leg, and they have lengths equal to links FG and EF, respectively. For the linkage OCFG, links OG and CF will always be aligned in parallel, at any angle of θ 1, due to the characteristics of parallelogram mechanism. Similarly, parallelogram linkage CDEF will force link DE to be always in parallel with link CF regardless of the actual angle θ 2. At any applied angles of θ 1 and θ 2, links OG, C F and ED always remain parallel, therefore the orientation of the foot will always remain parallel to the horizontal surface of the ground.

The knee joint is controlled by an actuator with the power transmitted through an additional linkage mechanism. This configuration allows the actuator to be placed at the stationary platform on the hip plane, which gives several advantages to the design. Firstly, by placing the actuator away from the leg, the total weight of the leg can be greatly reduced, which in turn minimizes the dynamic forces created when the leg starts moving. Secondly, the knee angle is always referenced to the fixed vertical axis of the stationary world coordinate frame regardless of the position of the hip angle. In this case, during the lifting of the leg only the hip joint needs to be actuated, whereas in the case of conventional serial leg structure, both joints need to be manipulated in order to provide some ground clearance for the foot.

From the schematic diagram in Fig. 1, link OA is attached to the knee actuator at point O and it has the same length as link BC. Link OC is the thigh segment of the leg and it is separately actuated by the hip actuator attached at point O. This link has a length equal to that of link AB. The motion of the knee actuator rotates link OA by an angular displacement of θa. Since the linkage OABC is a parallelogram mechanism, angle θ B will be equal to angle θ A . Link BCD is a ternary link with BC perpendicular to CD, therefore, – θ B and φ are complimentary angles and – θ 2 and ϖ are also complimentary angles. The relationship of θ b and θ 2 can be expressed as

$$\begin{array}{*{20}{l}} { - {\theta _B} + \varphi = {{90}^ \circ }} \\ { - {\theta _2} + \varphi = {{90}^ \circ }} \end{array}$$

Hence,

$${\theta _2} = {\theta _B}.$$

3 Balancing systems

3.1 Stability sensing system

In order to perform a stable walk, ideally the robot has to be immune to any sort of disturbance that might occur during the walking cycle. However in reality, every system has its own limitation in sensing and reacting to the disturbance mostly due to physical constraints of the system. One of the important factors is the ability of the system to detect the disturbance and properly interpret the nature of the disturbance.

For the robot to be able to handle the disturbance, the controller has to be provided immediately with accurate information on the stability state of the system. Therefore, it is necessary to have a proper sensing system that can provide that information for the controller. Furthermore, the information provided by the sensing system has to be easily interpreted and processed by the controller. Many works have reported the use of inertial measurement unit (IMU) which is the combination of micro electro mechanical system (MEMS) accelerometer and gyroscope to sense the tilt angle of the robot body[21, 22]. The information of the tilt angle is then used as a measure of the robot stability. However, the information provided by the IMU does not directly reflect the tilt angle of the body, instead, it provides the information of the acceleration and the rate of change of the robot body angle which needs to be processed further. The signal processing of the sensor information requires considerable amount of time and computing power which might lead to slow response of the system.

The proposed design utilizes a new approach of sensing the instability by introducing an additional degree of freedom to the leg structure in the sideway direction next to the ankle joint. This sensing ability significantly improves the sideway stability control of the robot as it provides faster response due to the early warning information obtained straight from the additional sensor. In this study, the stability control is only implemented in the sagittal plane but the concept can be further extended, if necessary, to the case of three-dimensional plane by having an additional set of identical sensors working in the coronal plane.

Fig. 3 shows the structure of the additional degree of freedom where the free rotary joint O on the frontal plane is placed at the ankle between the foot and ankle joints. When there is a disturbance either due to the walk or from other external source, the unconstrained robot body is able to freely tilt in the sideway (sagittal) direction. The body tilt angle can be then measured directly using a simple rotary sensor on the free joint and the controller will be able to instantly detect this instability and react immediately to restore the sideway balance.

Fig. 3
figure 3

Flexible ankle structure

Full size image

In order to maintain the horizontal orientation of the foot plane =F2 = 0). When the robot is tilted to one side (θ ≠ 0) (Fig. 3(b)), one of the spring (F 1) is stretched and exerts a force while the other (F 2) remains un-stretched due to the slack of the chain. Therefore, when the leg is hanging (foot is floating), the foot plate is kept horizontal. In this application, the tension of the spring is chosen to be just sufficient to restore the foot to its neutral position without adding unnecessary rigidity to the free ankle joint. The physical implementation of the additional ankle joint is shown in Fig. 4.

Fig. 4
figure 4

Mechanical assembly of flexible ankle structure

Full size image

3.2 Balancing mechanism

The walking cycle of bipedal robot consists of a single support phase and a double support phase, which are executed in sequence and repeatedly. In the single support phase, the robot is standing on one leg while another leg is transferred forward. During this phase, the robot body will be tilted sideways due to the unbalanced torque generated by the weight of the lifted leg and the inertia forces generated by the leg movement. Besides, during the single support phase, any unknown disturbance may destabilize the robot and cause it to tip over.

In order to maintain the stability, it is necessary to perform a corrective action to counterbalance the detected disturbance. Typically, the corrective action is performed by modifying the physical configuration (posture) of the robot. This can be achieved by altering the step size, foot placement or the speed of the leg in order to recover the state of stability of the robot[23]. These actions will lead to the alteration of the pre-computed walking trajectories that are initially planned to be achieved by the robot. Therefore, any disturbance that occurs during the walking cycle will result in delay of the robot in getting to its destination.

This work proposes a different approach in dealing with the disturbance, i.e., by performing the corrective action without altering the existing walking cycle of the robot. This is actually achieved by adding a separate mechanism to deliberately execute the corrective action whenever in-stability is detected either due to walk or external disturbance. This approach allows the walking subsystem to work independently in executing the planned walking trajectory while the balancing subsystem tends to continuously maintain the balance of the robot. This divide and conquer approach is believed to be more efficient because each subsystem is left to perform its own tasks without interference from the other.

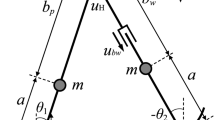
The design of the balancing mechanism is realized by a set of counterbalance masses located at a specific position to compensate at once the unbalanced mass of the lifted leg and any other possible disturbance. Fig. 5 shows the simplified 3-masses model of the bipedal robot, where m L represents the lumped mass of the hanging leg, m B 1 represents the major balancing mass, m B 2 represents the minor balancing mass, and r represents the length of the leg.

Fig. 5
figure 5

Simplified 3-masses model of bipedal robot

Full size image

The major balancing mass is mainly used to compensate for the weight of the lifted leg. This mass is positioned at the pre-calculated position d s in order to balance the torque created by the mass of lifted leg m L . The minor balancing mass m B 2 is designated to compensate for any unknown disturbance that may affect the system during the single support phase. The position a of this mass is continuously changed based on the sensor data and commands from the controller.

Fig. 6 shows the block diagram for the minor balancing mass position controller. The proportion-integral-derivative (PID) controller constantly monitors the tilt angle (θ) from the ankle joint sensor and compares the sensor reading with the desired angle. If there is a disturbance in the sideway direction, the body tends to tilt around the ankle joint. When the controller detects any non-zero value on the tilt angle (θ ≠ 0) in the one sense, it will drive the balancing mass in the opposite sense in order to restore the balance and keep the robot standing in the upright position.

Fig. 6
figure 6

Control block diagram for minor balancing mass control

Full size image

The usage of two separate counterbalance masses provides several advantages, such as

  1. 1)

    Faster response time to minor disturbances can be achieved by only moving small size counterbalancing mass instead of moving a larger one.

  2. 2)

    Energy efficiency can be improved by reducing load of the motor that drives a smaller size counterbalancing mass.

4 Control systems

Fig. 7 shows the overview of the controller design for the bipedal robot. The controller consists of two separate subsystems, namely, walking controller and balancing controller. The walking controller handles the task of controlling the joint actuators based on the predesigned trajectory planning in order to achieve the forward walking. The balancing controller is handling the task of monitoring the stability of the robot and continuously controls the minor balancing mass distance a from the center in order to provide a stable walk for the robot.

Fig. 7
figure 7

Block diagram of the bipedal robot controller

Full size image

In this prototype, the walking motion controller and the balancing controller are physically separated and run independently by different sets of programs. The walking motion is controlled by the microcontroller which controls the leg actuators motion based on the designed walking patterns and also controls the positioning of the major balancing mass based on the current stationary leg. The balancing control is handled by a separate microcontroller which is responsible for maintaining the sideway balance of the robot during a single support phase by varying the position of the minor balancing mass based on the robot tilt angle around the ankle joint.

4.1 Walking controller

Fig. 8 shows the block diagram of the walking controller. The 8-bit Microchip PIC18F2550 microcontroller is used as the main controller. This microcontroller is equipped with comprehensive peripherals, such as pulse width modulation (PWM) generator, timer interrupt, analog to digital converter (ADC) and universal asynchronous receiver transmitter (UART) module. The built-in features of the microcontroller help to reduce the requirement of using external components and hence reduce the complexity of the electronics circuit and overall size of the control circuit hardware.

Fig. 8
figure 8

System block diagram of the walking controller

Full size image

The major task of the walking controller is to control the motion of the leg actuators to achieve the designed walking motion. The actuators used to drive the legs are Dy-namixel RX–64 Smart Actuators from Robotis. These actuators combine the motor, drive and control electronics, sensor and communication module in one package. The onboard controller of the actuator is capable of performing closed-loop position control based on the reference angle sent from the microcontroller.

The communication between the actuator and the microcontroller is implemented by RS–485 protocol which allows more than one device to be controlled by a single host using the daisy chain network. In order for the microcontroller to be able to communicate with the actuator, an RS–485 host has to be setup on the microcontroller side. The RS-485 communication is achieved by converting UART (RS–232) protocol to RS–485 protocol. On the software side, the data streams of RS–485 are still similar to the native UART protocol with an addition of preceding byte to indicate the address of the target device in the daisy chain. On the hardware side, the logic levels of RS–485 and UART are different. UART is using full duplex communication with the common ground as the voltage reference for the signal, and RS–485 is using half duplex differential signal for data transmission. In order to match the signal requirement of RS–485 protocol, a logic level converter chip is used to convert the UART signal from microcontroller to RS–485 signal which is then sent to the actuator.

Besides controlling the motion of the leg actuators, the walking controller is also responsible for controlling the position of the major balancing mass. The position of the major balancing mass depends on whether the right or left leg is the standing one. In order to be able to accurately position the mass, a quadrature encoder is attached to the driving motor to count the number of revolutions of the driving pulley. The limit switch is attached to both end of the sliding rail to prevent the mass from overshooting and also to act as a homing switch for the encoder to start the count.

Fig. 9 shows the logic flowchart of the program for the walking controller. Once started, the controller will initialize the communication with the leg actuators and set the joints angle to standing position and move the major balancing mass to the middle position. Next, the controller will start sending position data to the leg actuators to perform the walking pattern. The position data are pre-calculated and stored the microcontroller in the form of lookup table. The position data are generated with the sampling period of 10 ms and the position command to the actuator is updated regularly by the microcontroller on every timer interrupt with the period of 10 ms.

Fig. 9
figure 9

Program flowchart of the walking controller

Full size image

When the robot is standing on both legs, the major balancing mass will be positioned at the middle of the hip. Before the right leg is lifted, the mass will be moved to a preset position at the left side of the hip. Hence, when the right leg is lifted so that the robot is standing only on the left leg, the balancing mass will pre-compensate for the weight of the hanging right leg. This sequence is executed repeatedly for the right and left standing legs throughout the walking cycle.

4.2 Balancing controller

The sideway balancing controller is a secondary controller which is dedicated to handling the task of maintaining the sideway balance of the robot by controlling the position of the minor balancing mass. The controller receives input from the ankle joint potentiometer which measures the amount of tilt angle of the robot body and will attempt to maintain the body in upright position by moving the mass accordingly.

Fig. 10 shows the block diagram of the sideway balancing controller. The microcontroller used in this balancing controller is Microchip PIC18F2550 similar to one used for the walking controller. Two potentiometers are connected to the ADC port of the microcontroller to provide continuous measurement of the tilt angle from both left and right ankles. Another potentiometer is used for measuring the current position of the minor balancing mass. This potentiometer is a multi-turn potentiometer which is connected in parallel to the shaft of the driving pulley. Therefore, by knowing the diameter and the angular position of the pulley, the linear position of the mass can be easily calculated by the controller.

Fig. 10
figure 10

System block diagram of the sideway balancing controller

Full size image

In order to drive the minor balancing mass, a direct current (DC) motor with the gear reduction from the servo motor is used. The rotation of the DC motor is controlled directly by the microcontroller via a dedicated motor driver. The sideway balancing controller also receives signals from the walking controller which indicate the current side of the standing leg.

Fig. 11 shows the logic flowchart programmed into the sideway balancing controller. At the beginning, the program will check the status signal from the walking controller. The status signals are then sent via two digital inputs indicating the current side of the standing leg. The signals are sent in the form of Boolean logic, one for the left leg and one for the right leg. If the current standing leg is the left leg and the right leg is hanging, the data sent will be “1” for left signal and “0” for right signal. If the current standing leg is the right leg and the left leg is hanging, the data sent will be “0” for the left signal and “1” for the right signal. If both legs are standing (during a double support phase), both left and right signals will be “1”. If both signals are “0”, it indicates that the walking controller is at stopping state and the sideway balancing controller should not perform any task.

Fig. 11
figure 11

Program flowchart of the sideway balancing controller

Full size image

When the current standing leg is the left leg, the controller will move the minor balancing mass above the left leg, read the sensor from the left ankle and start the closed-loop balancing control. When the current standing leg is the right leg, the controller will move the minor balancing mass above the right leg, read the sensor from the right ankle and start the closed-loop balancing control. When the robot is standing on both legs, the controller will move the mass to the middle of the hip and turn off the closed loop control since the robot is statically stable during the double support phase.

Once activated, the closed-loop system (Fig. 6) will continuously monitor the reading from the rotary sensor of the standing leg’s ankle joint. If the detected angle is not equal to the set point (θ = 0°), the PID control will actuate the motor and move the minor mass in order to tilt the body back to the upright position. The closed-loop systems for the left and right standing legs are identical except that the input of the actual tilt angle is read from different sensors depending on which leg the robot is standing on.

5 Mathematical modeling and computer simulation

This section discusses the mathematical model of the proposed design described in the previous sections. Two models are developed separately, namely the forward stability model and the sideway balancing model. The viability ofthe proposed design and the developed model is tested by performing the simulation in Matlab environment.

5.1 Modeling and simulation of forward stable walk

Fig. 12 shows the side view of the robot in the single support phase taking a forward step by performing a stepping motion on the swinging leg from the back to the front of the hip. When standing on one leg, there is a possibility for the robot to lose its balance and fall forward due to the forces created by the swinging leg.

Fig. 12
figure 12

Side view of bipedal robot in single support phase

Full size image

Assuming that there is no slip between the foot and the ground surface, the stability of the robot during this phase can be determined by taking into account all the static and dynamic forces acting on the leg structure. Static forces come from the weight of the robot’s body parts and the dynamic forces can be calculated from the planned trajectories of the legs motion. The acceleration of the knee and the ankle mass for the swinging leg are

$$\begin{array}{*{20}{l}} {{y_{RK}} = {l_{\sin }}{\theta _{RH}}} \\ {{{\dot y}_{RK}} = l{{\dot \theta }_{RH}}\cos {\theta _{RH}}} \\ {{{\ddot y}_{RK}} = l\left( {{{\ddot \theta }_{RH}}\cos {\theta _{RH}} - \dot \theta _{RH}^2\sin {\theta _{RH}}} \right)} \\ {{z_{RK}} = H - l\cos {\theta _{RH}}} \\ {{{\dot z}_{RK}} = l\sin {\theta _{RH}}{{\dot \theta }_{RH}}} \\ {{{\ddot z}_{RK}} = l\left( {\dot \theta _{RH}^2\cos {\theta _{RH}} + {{\ddot \theta }_{RH}}\sin {\theta _{RH}}} \right)} \\ {{y_{RA}} = {y_{RK}} + l{{\dot \theta }_{RK}}\cos {\theta _{RK}}} \\ {{{\dot y}_{RA}} = {{\dot y}_{RK}} + l{{\dot \theta }_{RK}}\cos {\theta _{RK}}} \\ {{{\ddot y}_{RA}} = {{\ddot y}_{RK}} + l\left( {{{\ddot \theta }_{RK}}\cos {\theta _{RK}} - \dot \theta _{RK}^2\sin {\theta _{RK}}} \right)} \\ {{z_{RA}} = {z_{RK}} - l\cos {\theta _{RK}}} \\ {{{\dot z}_{RA}} = {{\dot z}_{RK}} + l{{\dot \theta }_{RK}}\sin {\theta _{RK}}} \\ {{{\ddot z}_{RA}} = {{\ddot z}_{RK}} + l\left( {{{\dot \theta }_{RK}}\cos {\theta _{RK}} + {{\ddot \theta }_{RK}}\sin {\theta _{RK}}} \right)} \end{array}$$

In order for the robot to stay stable, the position of the resultant reaction forces between the foot and the ground R should always fall inside the foot area. From Fig. 12, it is clear that the robot may only rotate about the front edge of the foot in the clockwise direction if and only if the net torque from all the forces acting on the body with respect to that point is not zero or negative (clockwise direction). On the other hand, if the net torque from all the forces with respect to the edge point is not zero but positive (counterclockwise direction), the robot will maintain stability while moving in the forward direction.

In the latter case, the resultant torque can be securely balanced by the foot reaction forces because the resultant force falls within the foot area. Therefore, the forward stability condition solely depends on the position of the resultant force R which changes dynamically based on the position and movement of the leg. If the resultant force is always located within the area of the foot, then the robot is able to maintain its stability. Based on this concept, the distance d from the position of the resultant R to the ankle center point O can be used to indicate the degree of stability of the robot while walking in the forward direction.

Based on the diagram in Fig. 12, taking the net torque balance about point O yields

$$\begin{gathered} \sum {{T_O} = 0} \hfill \\ - {m_{LK}}g \times {y_{LK}} - {m_{RK}}\left( {g + {{\ddot z}_{RK}}} \right){y_{RK}} - \hfill \\ {m_{RA}}\left( {g + {{\ddot z}_{RA}}} \right){y_{RA}} + {m_{RK}} \times {{\ddot y}_{RK}} \times {z_{RK}} + \hfill \\ {m_{RA}} \times {{\ddot y}_{RA}} \times {z_{RA}} + R \times d = 0. \hfill \\ \end{gathered} $$
(1)

The total of vertical forces acting on R is

$$\begin{gathered} R = {m_{LA}}g + {M_g} + {m_{LK}}g + {m_{RK}}\left( {g + {{\ddot z}_{RK}}} \right) + \hfill \\ \quad \;\;{m_{RA}}\left( {g + {{\ddot z}_{RA}}} \right). \hfill \\ \end{gathered} $$
(2)

Substituting (2) into (1) yields

$$\begin{gathered} d = [{m_{LK}}g{y_{LK}} + {m_{RK}}(g + {{\ddot z}_{RK}}){y_{RK}} + \hfill \\ \quad \,\,\,{m_{RA}}(g + {{\ddot z}_{RA}}){y_{RA}} - {m_{RK}}{{\ddot y}_{RK}}{z_{RK}} - \hfill \\ \quad \,\,\,{m_{RA}}{{\ddot y}_{RA}}{z_{RA}}]/[{m_{LA}}g + Mg + {m_{LK}}g + \hfill \\ \quad \,\,{m_{RK}}(g + {{\ddot z}_{RK}}) + {m_{RA}}\left( {g + {{\ddot z}_{RA}}} \right)]. \hfill \\ \end{gathered} $$
(3)

If D F is the actual length of the foot in front of the ankle, the forward balance conditions for the robot can be defined as follows: When d < D F robot is stable, d = D F robot is critically stable, d > D F robot is unstable.

The stability of the robot while walking in the forward direction can be measured by the stability margin S M , which is the ratio of the reaction force position d and the actual length of the foot in front of the ankle D F . The stability margin S M can be derived as

$${S_M} = \frac{{{D_F} - d}}{{{D_F}}}.$$
(4)

The stability margin S M is a dimensionless value that can be used to measure the stability state of the robot. The value close to one indicates that the robot is in a stable condition and the value close to zero indicates that the robot is approaching the critically stable condition.

Fig. 13 shows the simulated result of the stability margin S M when the swinging leg of the robot is taking a step forward based on the model described in (3) and (4). The plot shows that the robot is able to maintain the forward stability throughout the entire single support phase.

Fig. 13
figure 13

Forward stability margin during single support phase

Full size image

5.2 Modeling and simulation of independent sideway stability

A simplified model of the bipedal robot during the single support phase is shown in Fig. 14. The inverted pendulum approach is adopted in deriving equations of sideway angular motion of the robot about the free rotary joint O at the ankle. Fig. 14 shows all the major point masses distributed accordingly on the leg structure and contributions to the instability of the single degree of freedom model either in the form of static gravity force or dynamic inertia force. The modeled inertia forces are due to the masses accelerating independently within the system, such as masses driven by the leg’s hip, knee motors or counterbalance mass m B 2 driven by the linear actuator located on the hip plane.

Fig. 14
figure 14

Front view of bipedal robot in single support phase

Full size image

Therefore, the net torque of all the gravity and inertia forces with respect to free rotary pin O can be expressed as

$$\begin{gathered} \sum {{T_O} = {T_{{\text{dist}}}} + {m_A} \times g \times {x_{RA}} + {m_K} \times g \times {x_{RK}} + } \hfill \\ \quad \;\;\;{m_H} \times g \times {x_{RH}} + M \times g \times {x_M} + {m_H} \times g \times {x_{LH}} + \hfill \\ \quad \;\;\;{m_K} \times g \times {x_{LK}} + {m_{B2}} \times \ddot a \times r - {m_{B2}} \times g \times {x_{B2}} - \hfill \\ \quad \;\;\;{m_{B1}} \times g \times {x_{B1}} - {m_K} \times {{\ddot z}_{RK}} \times d - {m_A} \times {{\ddot z}_{RA}} \times d - \hfill \\ \quad \;\;\;c \times \dot \theta - k \times \theta \hfill \\ \end{gathered} $$

where m A is the point mass of the ankle joint, m K is the point mass of the knee joint, m H is the point mass of the hip joint, M is the total of the hip platform, m B 1 is the major balancing mass placed at the fix location, m B 2 is the minor balancing mass whose position changes dynamically to maintain the balance, c and k are the damping and spring coefficients of the components associated with the rotary joint O.

The complete dynamic equation of motion of the single degree of freedom system about point O that includes all the moments of inertia from point masses is

$$\begin{gathered} {T_{{\text{dist}}}} - {m_{B2}} \times g \times a\cos \theta + g\sin \theta ({m_A}\left( {r - {d_{RA}}} \right) + \hfill \\ \quad \;\;\;{m_K}\left( {r - {d_{RK}}} \right) + {m_A}r + Mr + 2{m_H}r + {m_K}\left( {r - {z_{LK}}} \right) + \hfill \\ \quad \;\;\;{m_{B2}}r + {m_{B1}}r) + {m_{B2}}\ddot ar - {m_K}{{\ddot z}_{RK}}d - {m_A}{{\ddot z}_{RA}}d - \hfill \\ \quad \;\;\;({m_{B2}}{a^2} + {m_A}{r^2}_{RA} + {m_K}{r^2}_{RK})\ddot \theta = \hfill \\ \quad \;\;\;({m_K}{(r - {z_{LK}})^2} + {m_H}{r^2} + Mr_M^2 + {m_H}r_{RH}^2 + {m_{B2r}}^2 + \hfill \\ \quad \;\;\;{m_{B1}}r_{B1}^2)\ddot \theta + c\dot \theta + k\theta . \hfill \\ \end{gathered} $$
(5)

The differential equation above has two distinct parts. The right-hand side consists of the ordinary differential equation with constant time invariant coefficients and the left-hand side presents all other remaining components of the equation which includes:

  1. 1)

    Non-linear trigonometric functions of the main dependent argument θ, i.e., sin θ and cos θ;

  2. 2)

    Additional but independent from the main argument θ time varying parameter a and its derivatives, due to the linear independent motion of the minor balancing mass;

  3. 3)

    The parameters that comprise both a and θ arguments, namely \({m_{B2}}{a^2}\ddot \theta \)

  4. 4)

    Time varying kinematics parameters of the swinging leg lumped masses ma and m K .

Based on the model shown in (5), the stability of the side-way balancing system is tested by applying random disturbance to mimic the push on the robot body in the sideway direction. Fig. 15 shows the simulation result of the sideway balancing control response.

Fig. 15
figure 15

System response of sideway balancing system with external disturbance

Full size image

6 Experimental results

In order to verify the viability of the proposed concept, experiments were carried out on a physical prototype that is fabricated based on the design discussed in earlier sections. The overall height of the robot is 0.9 m with the total weight of 7 kg. The length for both thigh and shank are 0.3 m and the spacing between the two legs is 0.15 m.

6.1 Forward walking motion performance

During the testing, the bipedal robot demonstrated the ability to walk in a straight direction on a flat ground. It also demonstrated the ability of maintaining the forward balance during the single support phase. The real-time measurements of the step length taken by the robot agree with the results obtained the the simulated walking trajectories.

Fig. 16 shows the sequential snapshots of the robot when performing a forward walking motion. The snapshots are taken for the following sequence of the motions: Foot lifting, foot landing, and hip mass carry stages. Then, the cycle was repeated for the motion of the other leg. The tests show that the robot is able to walk in the forward direction for an indefinite distance.

Fig. 16
figure 16

Force sensors on the foot sole for reaction force measurement

Full size image

The reliability of the forward walking stability has been proven by the result of the simulation in the previous section. Due to the proper positioning of the dominant hip mass during the single support phase, the stability margin in the forward direction only varies between 87 %–98 % throughout the walking cycle. In order to further verify this condition, the actual reaction force on the foot of the physical robot was measured during the walk. The measurement is achieved by attaching a series of force sensors at each corner of the foot (Fig. 17). From the recorded forces at each sensor, the position of the reaction force from the ankle can be calculated as

Fig. 17
figure 17

Force sensors on the foot sole for reaction force measurement

Full size image
$$d = \frac{{\left( {{F_1} + {F_2}} \right)\left( { - {x_R}} \right) + \left( {{F_3} + {F_4}} \right)\left( {{x_F}} \right)}}{{\left( {{F_1} + {F_2} + {F_3} + {F_4}} \right)}}.$$
(6)

Fig. 18 shows the distribution of the reaction force position d during the single support phase while the swinging leg is moved forward to make a step as described in (3). Fig. 19 shows the plot of the actual stability margin calculated from the measured reaction force and the simulated stability margin (4) during a single support phase. There is a slight difference between the simulated and actual results obtained from the prototype. The possible cause of this discrepancy is because in the simulation work, the masses of the links are assumed to be point masses in order to reduce the complexity of the calculation, whereas, the masses of the links are distributed in reality.

Fig. 18
figure 18

Distribution of reaction force positions during single support phase

Full size image
Fig. 19
figure 19

Actual versus simulated stability margin during single support phase

Full size image

6.2 Sideway walking motion performance

The sideway balancing system has been proven to be able to handle the small disturbance created by the dynamic forces while the leg is swinging during the forward walking experiment. The balancing system is working independently to adjust the position of the mass in order to maintain the standing posture of the robot throughout the entire walking cycle.

The robustness of the sideway balancing system is further tested by applying an external disturbance while the robot is standing in the single support phase. The disturbance is created by applying a quick push on the side of the hip to simulate an impulse input that will destabilize the robot in the sideway direction. The magnitude of the pushing force is measured by a force sensor at a fixed point on the hip plane (Fig. 20). Based on the measured force, the disturbance torque about the ankle joint can be calculated by multiplying the force by the horizontal distance to the fixed point to the standing leg.

Fig. 20
figure 20

Force sensor at the edge of the hip to measure the magnitude of the external disturbance

Full size image

Fig. 21 shows the plot of the body tilt angle θ, minor balancing mass distance a and the sideway disturbance applied to the robot body T dist. The disturbance was applied manually by operator in a random manner. Once the disturbance is applied, the robot body starts to rotate sideway about the ankle joint. The amount of rotation is sensed by the rotary sensor and sent to the sideway balancing controller which controls the position of the minor balancing mass and ultimately restores the balance. The results from several trials show that the robot is able to cope with the disturbance less than 1 Nm (5N push at the edge of the hip).

Fig. 21
figure 21

Response of the robot in sideway direction when external disturbance is applied

Full size image

The plot shown in Fig. 22 records the event when the disturbance of more than 1 Nm is applied to the robot. It can be seen that the controller is reacting to correct the disturbance by moving the minor mass, but the weight of the mass is not enough to create a sufficient counter torque to rotate the robot back to the upright position.

Fig. 22
figure 22

Response of the robot in sideway direction when excessive external disturbance is applied

Full size image

7 Conclusions

The proposed design of the bipedal robot is successfully implemented in the form of a physical prototype. As an experimental platform, the prototype of the robot has successfully performed the tasks as it was expected in the proposed design.

The forward walking experiment on the robot shows that the walking task can be performed independently based on the preplanned trajectory while the sideway balancing controller continuously compensates for any possible disturbance and constantly maintains the standing posture of the robot.

A separate experiment is carried out in order to further verify the capability of the robot in handling external disturbance. The results of the experiments conclude that the system is able to handle and correct the unknown external disturbance up to a certain intensity. This limitation is related to the limitations of hardware components, such as the weight of the balancing mass and the actuator response.

In general, the reported experimental results prove the advantages of new theoretical and mechanical concepts implemented in the design of minimalist robots, such as smooth and impact-free trajectory planning, hip-mass carry strategies in planning the gaits, improvement of the control system sensitivity and response to the walk disturbances by introducing a single degree of freedom joint at the ankle, decoupling of walk and stability functions of the controller to improve its efficiency.