Abstract
This paper deals with the synthesis of fuzzy controller applied to the induction motor with a guaranteed model reference tracking performance. First, the Takagi-Sugeno (T-S) fuzzy model is used to approximate the nonlinear system in the synchronous d-q frame rotating with field-oriented control strategy. Then, a fuzzy state feedback controller is designed to reduce the tracking error by minimizing the disturbance level. The proposed controller is based on a T-S reference model in which the desired trajectory has been specified. The inaccessible rotor flux is estimated by a T-S fuzzy observer. The developed approach for the controller design is based on the synthesis of an augmented fuzzy model which regroups the model of induction machine, fuzzy observer, and reference model. The gains of the observer and controller are obtained by solving a set of linear matrix inequalities (LMIs). Finally, simulation and experimental results are given to show the performance of the observer-based tracking controller.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In the last two decades, the problem of tracking control for nonlinear systems has been dealt by several classic approaches, and many studies have been developed around this subject. However, there are a few works based on the Takgi-Sugeno (T-S) fuzzy model relating to the tracking control problem which have been studied for continuous-time systems[1–5]
In our work, we are interested in the design of fuzzy observer-based tracking controller for an induction motor with H ∞ performance. Induction motors are highly nonlinear systems, having uncertain time-varying parameters and subjected to unknown load disturbance. In addition, the rotor flux is inaccessible for state feedback control. Taking these difficulties into account, various control strategies, such as vector control method using proportional-integral (PI) controllers, input-output decoupling, control via geometric techniques, fuzzy adaptive control, and sliding mode control are proposed. A classical PI controller is a simple regulator used in the control of induction motor drives. However, the main drawback of this kind of controller is its sensitivity to the system-parameter variations and load changes[6, 7]. Thus, based on loop-shaping technique, a new control technique is proposed[8] to assure the disturbances rejection and lowering of tracking error. Wai and Chang[9] presented an adaptive observation system with an inverse rotor time-constant observer, based on a model reference adaptive system (MRAS) theory. The proposed adaptive system introduced in the control scheme guarantees the accurate estimation of the slip angular velocity, and preserves the decoupling control characteristic. In the last decade, many publications concerning the use of nonlinear input-output linearization techniques for the control of induction motors have been appeared. However, these approaches lose their performance when the motor parameters vary from their nominal values and when a load torque is applied. As a result, Marino et al.[10, 11] proposed a direct adaptive controller for speed regulation, in which the motor model is input-output decoupled by a feedback-linearizing technique, while the load torque and rotor resistance are adapted in real time. The major inconvenience of this approach is the inability to ensure the asymptotic convergence of the system states and the estimated parameters. In the same context, a mixed H 2/H ∞ optimized controller is used[12] to minimize the tracking error and to ensure the load torque disturbance rejection. A robust stability analysis method is presented via a parameter dependant Lyapunov function, in which the robust stability of the overall uncertain linearized closed-loop system is tested. The sliding mode technique has been widely used in induction motor control and proved to have a small tracking error[13–15], but the chattering phenomenon is inevitable, which degrades the performance of the system and may even lead to instability.
Recently, fuzzy techniques have been widely and successfully used in induction motor modeling and control[16–18]. Among various fuzzy modeling methods, the well-known T-S fuzzy model is considered as a popular and powerful tool in approximating a complex nonlinear system[19, 20]. The basic idea of this approach is to decompose the model of the nonlinear system into a series of linear models involving nonlinear weighting functions. The equivalent T-S fuzzy model describes the dynamic behavior of the system. The weighting functions checks the convex sum property.
In this paper, the tracking problem for an induction motor is studied using the T-S fuzzy approach. First, a fuzzy augmented model is constructed by regrouping the T-S fuzzy model of the induction motor, a fuzzy observer, and the T-S reference model. Then, a fuzzy observer-based tracking controller is developed. The proposed T-S controller is dynamic and it has the characteristic to be adjustable through the insertion of the nonlinear weighting functions associated for every local controller. This property allows to adapt the global fuzzy controller inside the polytope region \(\left[ {{i_{{s_{{\text{min}}}}}},{i_{{s_{{\text{max}}}}}}} \right] \times \left[ {{\omega _{{m_{{\text{min}}}}}},{\omega _{{m_{{\text{max}}}}}}} \right]\) operating at various load torque and reference speed in order to improve the tracking performance. It also has the ability to achieve the favorable decoupling control and precision speed tracking property, even if the machine is subject to parametric variations. In addition, the tracking control design problem is parameterized in terms of a linear matrix inequality (LMI) problem which can be solved very efficiently using the convex optimization techniques.
This paper is organized as follows. Section 2 presents an open-loop control strategy, which includes a physical model of the induction motor. Section 3 deals with the synthesis of a fuzzy control law with H ∞ performance. To specify the desired trajectory, a T-S reference model is designed. The gains of the observer and controller are obtained by solving a set of LMIs. Section 4 gives the simulation and experimental results to highlight the effectiveness of the proposed control law. Section 5 gives conclusions on the main themes developed in this paper.
2 Open-loop control strategy
2.1 Physical model of induction motor
Under the assumptions of the linearity of the magnetic circuit, the electromagnetic dynamic model of the induction motor in the synchronous d-q reference frame can be described as
where

where ω m is the rotor speed, ω s is the electrical speed of stator, (Ψ rd ,Ψ rq ) are the rotor fluxes, (i sd ,i sq ) are the stator currents, and (u sd ,u sq ) are the stator voltages. The load torque C r is considered as an unknown disturbance. The motor parameters are moment of inertia J, rotor and stator resistances (R s ,R r ), rotor and stator inductances (L s ,L r ), mutual inductance M, friction coefficient f, and number of pole pairs n p .
2.2 Open-loop control
In this section, the structure of the open-loop control strategy is explored, which will be modified in the next section to design the closed-loop T-S reference model. If we replace the state variables of the motor [i sd i sq Ψ rd Ψ rq ω m ]T by the corresponding reference signals [i sdc i sqc Ψ rdc 0 ω mc ]T in (1), we obtain[21]
The last two equalities in (2) lead to the open-loop reference stator currents as
According to (2), the electrical speed reference of the stator is given as
From the first two equalities in (2), we obtain the expression of the open-loop control as
3 Fuzzy observer-based tracking control
The nonlinear model (1), described in the synchronous d-q frame, is transformed into an equivalent T-S fuzzy model using the linear sector transformation[22]. The global linear fuzzy model is composed of a set of linear models which are interpolated by membership functions. The synthesis of a fuzzy controller requires the construction of the augmented fuzzy model, which regroups the T-S fuzzy model of the induction motor, the fuzzy observer, and the reference model. The premise variables are assumed to be measurable.
3.1 T-S fuzzy model of induction motor
The field-oriented strategy when is implemented relative to the synchronously rotating frame of reference, allows for an independent control of the torque and of the rotor flux. In this case, the dynamics of the induction motor is similar to the separately excited DC motor. In this condition, the rotor flux vector (Ψ rd , Ψ rq ) is aligned to the d-axis, and the results can be obtained as
To assure condition (6), the electrical speed of the stator in the rotating synchronous d-q frame must be chosen as
If we replace the electrical speed of the stator (7) in the physical model (1), the nonlinear model of the induction motor can be written as the state space form:
where
and v(t) represents the measurement noise.
Considering the sector of nonlinearities of the terms z k (t) = x k (t) ∈ [z k min, z k max] of the matrix A(x(t)) with k = 1, 2, 3 yields
Thus, we can transform the nonlinear terms into the following shape:
where the membership functions can be written as
The fuzzy model is described by fuzzy If-Then rules and will be employed here to deal with the control design problem for the induction motor. The i-th rule of the fuzzy model for the nonlinear system is described in the following form:
Rule R i :
If ( z 1(t) is F 1,l ) and (z 2(t) is F 2 f ) and (z 3(t) is F 3,h ) Then \(\dot x\)(t) = A i x(t) + Bu(t) + w(t) with l,f , ,h ∈ {min, max}, and i = 1, 2, ⋯ , 8.
The global fuzzy model is inferred as
with
where h i(z(t)) is regarded as the normalized weight of each model rule, and F ik (z(t)) is the grade of membership of z k (t) in Fi k .
3.2 T-S reference model
The open-loop response of the induction motor defined by the control input (5) is characterized by an important overshoot of the d-axis rotor flux (see Appendix D). In order to improve the transient performance of the system, we consider a nonlinear reference model via a T-S fuzzy approach. The designed T-S reference model is a piecewise interpolation of several linear models through membership functions. The dynamics of the closed-loop system is modified through the insertion of positive parameters K i and K Ψ in the T-S reference model, which has the desired dynamics behavior. Therefore, we define the new control input vector as
Consider the reference state of the closed-loop system x r (t) = [i sdr i sqr Ψ rdr Ψ rqr ωmr]T. It is the desired trajectory for x(t) to follow.
The above equality (15) can be written as
This is equivalent to
Given the new control input (17) in the physical model (1), and replacing the state x(t) by x r (t), the nonlinear model of the induction motor leads to the state space reference model:
where
K 1 = (γ + K i), K 2 = \((\frac{{{K_s}}}{{{\tau _r}}} - \frac{{M{K_\Psi }}}{{{L_s}{\tau _r}}})\), and ω sr = npω mr + \(\frac{M}{{{\tau _r}{\Psi _{rdc}}}}{i_{sqr}}\). r(t) is a bounded input given as
where U r = [ u sdr u sqr ]T.
The reference model (18) is nonlinear and can be described via a T-S fuzzy model.
Rule R j :
If (z r 1(t) is N 1,l ) and (z r 2(t) is N 2,f ) and (z r 3(t) is N 3,h ) Then \({\dot x_r}(t)\) = A rj x r (t) + r(t) with l,f,h ∈ {min, max}, i = 1, 2, ⋯ , 8, z r 1(t), z r 2(t) and z r 3(t) are the measurable premise variables defined as
$$\left\{ {\begin{array}{*{20}{c}} {{z_{r1}} = {i_{sdr}}(t)} \\ {{z_{r2}} = {i_{sqr}}(t)} \\ {{z_{r3}} = {\omega _{mr}}(t)} \end{array}} \right.$$((19))where N 1,l ,N 2,f and N 3,h are the fuzzy sets which have the same structure as (11).
The global fuzzy reference model is inferred as
with
For all h rj (z r (t)) > 0, and \(\sum\nolimits_{j = 1}^8 {{h_{rj}}({z_r}(t))} = 1.\,\;{h_{rj}}({z_r}(t))\) is regarded as the normalized weight of each reference rule. N jk (z r (t)) is the grade of membership of z rk (t) in N jk .
Define the tracking error as
Then, the objective is to design a T-S fuzzy model-based controller which stabilizes the closed-loop fuzzy system and achieves the H ∞ tracking performance related to the tracking error e r (t) given by

where \(\bar \phi \) = [v(t) w(t) r(t)]T for all reference input r(t), external disturbance w(t), and measurement noise v(t). t f represents the terminal time of control, Q is a positive definite weighting matrix, and ρ a prescribed attenuation level.
3.3 Tracking control design
To design an observer-based tracking controller, a new parallel distributed compensation (PDC) controller is proposed. The main difference from the ordinary PDC controller described in [23] is to have a term of x r (t) in the feedback control law. Then, the new PDC fuzzy controller is designed as[24]
Sub-controller A rule R i :
If (z 1(t) is F 1,l ) and (z 2(t) is F 2,f ) and (z 3(t) is F 3,h ) Then u A (t) = K i \(\hat x\)(t) for i = 1, , 2, ⋯ , 8.
Sub-controller B rule R j :
If (z r 1(t) is N 1,l ) and (z r 2(t is N 2,f ) and (z r 3(t) is N 3,h ) Then u B (t) = −K j x r (t) for j = 1, 2, ⋯ , 8.
Hence, the overall fuzzy controller is given by
$$u(t) = {u_A}(t) + {u_B}(t)$$((25))$$u(t) = \sum\limits_{i = 1}^8 {{h_i}(z(t)){K_i}\hat x(t)} - \sum\limits_{j = 1}^8 {{h_{rj}}} ({z_r}(t)){K_j}{x_r}(t).$$((26))
However, the fuzzy tracking control law (26) requires that all state variables are available. In this condition, a fuzzy observer of Luenberger type is constructed to estimate the immeasurable states of the rotor flux. According to the fuzzy model (12), the fuzzy observer is given as
If (z 1(t) is F 1,l ) and (z 2(t) is F 2,f ) and (z 3(t) is F 3,h ) Then \(\mathop {\hat x}\limits^{\;.} (t) = ({A_i}\hat x(t) + Bu(t) + {L_i}(y(t) - \hat y(t)))\) where L i is the gain of the observer.
The overall fuzzy observer is represented as
Define the observation error
From systems (12), (27) and (28), we can obtain the error dynamics as
The augmented system composed of equalities (12), (20) and (29) can be expressed as
where
Hence, the H ∞ tracking performance in (24) can be modified as follows, if the initial condition is also considered[2, 25, 26]:

where
and \(\bar P\) is a symmetric positive definite weighting matrix.
Now, the objective is to determine the controller's and observer's gains K i and L i for the augmented model (30) with the guaranteed H ∞ tracking performance (24) for all \(\bar \phi (t)\) . The main result of fuzzy observer-based tracking control for the T-S fuzzy model of the induction motor is summarised in the following theorem:
Theorem 1. If there exists a symmetric and positive definite matrix \(\bar P = {\bar P^{\text{T}}} > 0\) and a prescribed positive constant ρ 2 such that

then the performance of H ∞ tracking control for the prescribed ρ 2 is guaranteed, and the quadratic stability for the closed-loop system is assured.
Proof. Consider the Lyapunov function \(V(\bar x(t)) = {\bar x^{\text{T}}}(t)\bar P\;\bar x(t)\) where \(\bar P = {\bar P^{\text{T}}} > 0\). The time derivative of \(V(\bar x(t))\) is

Lemma 1. For any matrices X and Y with appropriate dimensions, the following property holds:

where ρ is a real value which is assumed to be positive.
Applying the statement of Lemma to the term

we obtain

Substituting (34) into (33) yields

From (32), we get

Integrating (35) from t = 0 to t = t f yields

This is equivalent to

As a result, the H ∞ tracking control performance is achieved with a prescribed attenuation level ρ.
It is noted that Theorem 1 gives the sufficient condition of ensuring the stability of the augmented fuzzy system (30) and achieving the tracking performance (24). However, it does not give the methods of obtaining the solution of the common positive matrices, the gains of fuzzy controller and fuzzy observer. Inequality (32) presents bilinear matrix inequality (BMI) conditions. For this reason, we propose a method that consists of solving these BMI’s in two stages, such that every stage is considered as a standard LMI[2, 25]. To facilitate the resolution, the matrix variable \(\bar P\) is chosen diagonal with respect to appropriate matrix blocks:
By substituting (38) into (32), we obtain
where

We consider the change of variable Z i = P 1 L i. Using the Schur complement, inequality (39) is equivalent to

where

Using LMI tools, there are several parameters that should be determined from (40). There are no effective algorithms for solving them simultaneously. However, we can solve them by the following two-step procedure. First, we can find P 2 and K i from the diagonal blocks D 44, then P 1, P 3 and L i from the inequality (40). Indeed, after congruence of (40) with diag{I, I, I, \(P_2^{ - 1}\), I,I}, considering the change of variable N 2 = \(P_2^{ - 1}\), Y i = K iN2, and using the Schur’s complement, D 44 is equivalent to the following LMI:

The parameters \({P_2} = N_2^{ - 1}\) and \({K_i} = {Y_i}N_2^{ - 1}\) are obtained by solving the LMIs in (41). In the second step, by substituting P 2 and K i into inequality (40), the last condition becomes a standard LMI, and we can easily solve P 1, P 3 and the observer’s gains L i.
4 Simulation and experimental results
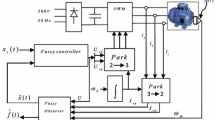
The proposed fuzzy tracking control law has first been tested in simulation as shown in Fig. 1.
4.1 Simulation results
Figs. 2 and 3 present the simulation results of the proposed fuzzy control law. The controller parameters for the T-S reference model are chosen as K i = 20 and K ψ = 100. The reference flux starts from zero at t = 0 and increases to the rated constant value 1 Wb. The speed reference goes from 0 to 100 rad/s at t = 1 s and increases to 150 rad/s at t = 10s. From time t = 14s to t = 18s, a constant load torque of 5 N•m value is applied.
The simulation results illustrated in the Fig. 2 show the performance of the developed approach in terms of tracking error and state estimation. Indeed, Fig. 2 (a) shows the convergence of the estimated rotor speed toward the real speed and then toward the desired trajectory, which shows that the tracking performance is assured as well as the observer's convergence. In addition, a smaller tracking error for speed is observed in Fig. 2 (c) in spite of the load torque being applied. Fig. 2 (d) and (e) shows that when the value of the rotor speed reference changes, the d-axis rotor flux undergoes a weak fluctuation and remains close to its T-S reference value, while the q-axis rotor flux remains null in Fig. 2(f).
In order to evaluate the performance of the proposed fuzzy control law, simulation results for reversing speed from 150rad/s to -150rad/s are also presented in Fig. 3.
A similar level of performance is obtained characterized by a small rotor speed tracking error which does not pass 1.5rad/s (Fig 3(b)) and a good reconstruction of the machine states. The d-axis rotor flux tracks the reference trajectory (Fig. 3(c)), and the decoupling control characteristic between the rotor flux and the torque is achieved.
4.2 Experimental results
Experimental tests are carried out to verify the effectiveness of our proposed fuzzy controller. The test bench (Fig.4) is made up of a three-phase induction motor (IM), an insulated gate bipolar transistor (IGBT) source voltage inverter, a digital signal processor (DSP) controller card, an incremental encoder, and three hall-effect current sensors for the measurement of stator currents. The fuzzy observer as well as the whole control algorithm has been implemented on Dspace carte DS1104 with a TMS320F240 processor. This control card is composed of two processors. The master processor allows the application to be managed while the slave processor generates the pulse width modulated (PWM) signals of the controls. It constitutes the hardware part of Dspace. The software is based on a Matlab/Simulink program, which permits an easy programming of the real time application under simulink environment with the use of specific blocks included in the real time interface (RTI) toolbox. The second program, control desk, is a graphic interface allowing for observing online the evolution of the measured data.
In addition, a set of I/O modules are constructed in the card connector panel CP1104 for the voltage/current measurement, encoder interface, and the protection of the power inverter. The pulse width modulation (PWM) signals are generated with switching frequency of 5 kHz. The experiments have been performed for the rated speed of 100 rad/s at t = 2s and increased to 150 rad/s at t = 10 s as shown in Fig. 5 (a).
It is clear that the rotor speed tracks the reference trajectory perfectly (Fig. 5 (a)). The rotor flux is aligned with the d-axis, and the estimation error remains very small. Consequently, we can note that the experiment response is close to the simulated one, which confirms the effectiveness of the proposed fuzzy state feedback controllers.
5 Conclusions
In this paper, we present a fuzzy H ∞ model reference tracking control scheme applied to a field oriented induction motor drive. The shape of the designed fuzzy control law is similar to the parallel distributed compensation (PDC) control techniques except that the proposed fuzzy controller is expressed with the tracking error. The T-S fuzzy model is used to represent the induction motor by a set of local state space models which are interpolated by nonlinear functions. Based on the T-S fuzzy model, a fuzzy observer based fuzzy controller is developed to reduce the tracking error as much as possible by minimizing the effect of the disturbance level. The stability of the fuzzy closed-loop system has been analyzed using Lyapunov theory combined with an LMI approach. A two-step LMI method has been given to solve the coupled matrix inequality. The effectiveness of the proposed controller and fuzzy observer are demonstrated through numerical simulations and experimental results. Thus, this work offers the perspective to develop a fuzzy robust tracking control applied to the induction motor which takes the parametric variation into account.
Appendix
A. The premise variables are bounded as
B. Solving LMIs (41) and (40) by LMI optimization algorithm, we have the gains of the observer and controller as follows.
C. The three-phase induction motor is characterized by the following parameters:
Motor rated power: 1.1 kW
Pole pair number (p): 2
Stator resistance: 10.5 Ω
Rotor resistance: 4.3047 Ω
Stator inductance: 0.4718 mH
Rotor inductance: 0.4718 mH
Motor inertia J 0.0293 kg•m2
Friction coefficient f: 0.001 N•m•rad−1.
D. The simulation results of the open-loop control law defined by (5) are shown in Fig. 6. We consider a step reference speed of value 100 rad/s.
References
S. C. Tong, T. Wang, H. X. Li. Fuzzy robust tracking control for uncertain nonlinear systems. International Journal of Approximate Reasoning, vol. 30, no.2, pp. 73–90, 2002.
C. S. Tseng, B. S. Chen, H. J. Uang. Fuzzy tracking control design for nonlinear dynamic system via T-S fuzzy model. IEEE Transactions on Fuzzy Systems, vol. 9, no. 3, pp. 381–392, 2001.
F. Zheng, Q. G. Wang, T. H. Lee. Output tracking control of MIMO fuzzy nonlinear systems using variable structure control approach. IEEE Transactions on Fuzzy Systems, vol. 10, no. 6, pp. 686–697, 2002.
C. Lin, Q. G. Wang, T. H. Lee. H ∞ output tracking control for nonlinear systems via T-S fuzzy model approach. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, vol. 36}, no. 2}, pp. 450–457, 2
Y. Yi, H. Shen, L. Guo. Statistic PID tracking control for non-Gaussian stochastic systems based on T-S fuzzy model. International Journal of Automation and Computing, vol. 6, no.1, pp. 81–87, 2009.
Z. Ibrahim, E. Levi. A comparative analysis of fuzzy logic and PI speed control in high-performance AC drives using experimental approach. IEEE Transactions on Industry Applications, vol. 38, no. 5, pp. 1210–1218, 2002.
F. Betin, D. Depernet, P. Flozeck, A. Faqir, D. Pinchon, C. Goeldel. Control of induction machine drive using fuzzy logic approach: Robustness study. In Proceedings of IEEE International Symposium on Industrial Electronics, IEEE, Italy, vol. 2, pp. 361–366, 2002.
E. Larochea, Y. Bonnassieuxb, H. Abou-Kandilc, J. P Louisc. Controller design and robustness analysis for induction machine-based positioning system. Control Engineering Practice, vol. 12, no. 6, pp. 757–767, 2004.
R. J. Wai, L. J. Chang. Decoupling and tracking control of induction motor drive. IEEE Transactions on Aerospace and Electronic Systems, vol. 38, no. 4, pp. 1357–1369, 2002.
R. Marino, S. Peresada, P. Tomei. Global adaptive output feedback control of induction motors with uncertain rotor resistance. IEEE Transactions on Automatic Control, vol. 44, no. 5, pp. 967–983, 1993.
R. Marino, S. Peresada, P. Tomei. Adaptive output feedback control of current-fed induction motors with uncertain rotor resistance and load torque. Automatica, vol. 34, no. 5, pp. 617–624, 1998.
S. Cauet, L. Rambault, O. Bachelier, D. Mehdi. Robust control and stability analysis of linearized system with parameter variation: Application to induction motor. In Proceedings of the 40th IEEE Conference on Decision and Control, IEEE, Oriendo, FL, USA, pp. 2645–2650, 2001.
H. Rehman, R. Dhaouadi. A fuzzy learning - Sliding mode controller for direct field-oriented induction machine. Neurocomputing, vol. 71, no. 13-15, pp. 2693–2701, 2008.
T. J. Fu, W. F. Xie. A novel sliding-mode control of induction motor using space vector modulation technique. ISA Transactions, vol. 44, no. 4, pp. 481–490, 2005.
O. Barambones, A. J. Garrido. A sensorless variable structure control of induction motor drives. Electric Power Systems Research, vol. 72, no. 1, pp. 21–32, 2004.
S. M. Kima, W. Y. Han. Induction motor servo drive using robust PID-like neuro-fuzzy controller. Control Engineering Practice, vol. 14, no. 5, pp. 481–487, 2006.
M. Boussak, M. Bauer. Robust speed and position control of an indirect field oriented controlled induction motor drive using fuzzy logic regulator. In Proceedings of International Conference on Electrical Machines, pp. 219–224, Spain, 1996.
L. Baghli, H. Razik, A. Rezzoug. Comparison between fuzzy and classical speed control within a field oriented method for induction motor. In Proceedings of the European Conference on Power Electrics and Applications, Trondheim, Norway, vol. 2, pp. 2444–2448, 1997.
H. O. Wang, K. Tanaka, M. F. Griffin. An approach to fuzzy control of nonlinear systems: Stability and design issues. IEEE Transactions on Fuzzy Systems, vol. 4, no. 1, pp. 14–23, 1996.
Y.Morre. Mise en uvre de lois de commande pour les modles flous de type Takagi-Sugeno, Thse de doctorat, Universit de Valenciennes et du Hainaut Cambrsis, 2000. (Y. Morre. Implementation of control laws for a Takagi-Sugeno fuzzy models, Ph. D. dissertation, University of Valenciennes and Hainaut Cambresis, France, 2000.)
R. Marino, P. Tomei, C. M. Verrelli. A global tracking control for speed-sensorless induction motors. Automatica, vol. 40, no. 6, pp. 1071–1077, 2004.
D. Maquin. State estimation and fault detection for systems described by Takagi-Sugeno nonlinear models. In Proceedings of the 10th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering, Tunisia, pp. 20–22, 2009.
K. Tanaka, S. Hori, H. O. Wang. Multiobjective control of a vehicle with triple trailers. IEEE/ASME Transactions on Mechatronics, vol.7, no. 3, pp. 357–368, 2002.
T. Taniguchi, K. Tanaka, K. Yamafuji, H. O. Wang. A new PDC for fuzzy reference models. In Proceedings of IEEE International Fuzzy Systems Conference, IEEE, Seoul, Korea, pp. 898–903, 1999.
B. Mansouri, N. Manamanni, K. Guelton, A. Kruszewski, T. M. Guerra. Output feedback LMI tracking control conditions with H? criterion for uncertain and disturbed T-S models. Information Sciences, vol. 179, no.4, pp. 446–457, 2009.
Y. Z. Cai, L. Xu, J. X. Gao, X. M. Xu. Study on robust H? filtering in networked environments. International Journal of Automation and Computing, vol. 8, no. 4, pp. 465–471, 2011.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by AECID Projects (Nos. A/023792/09, A/030410/10 and AP/034911/11)
M. Allouche received the M.Sc. degree from National Engineering School of Sfax, Tunisia in 2006. Also, he obtained the Ph. D. degree in electrical engineering from the National Engineering School of Sfax, Tunisia in 2010. Currently, he is an assistant professor in High Institute of Industrial Systems of Gabes.
His research interests include robust control, fuzzy logic control, D-stability analysis, neutral networks, and renewable energies (solar energies).
M. Chaabane received the Ph.D. degree in electrical engineering from the University of Nancy, French in 1991. He was associate professor at the University of Nancy, and is a researcher at Center of Automatic Control of Nancy (CRAN) from {dy1988} to 1992. He is currently a professor in National School of Engineers of Sfax, and he is editor-in-chief of the International Journal on Sciences and Techniques of Automatic Control and Computer Engineering (IJSTA). Since {dy1997}, he is holding a research position at Automatic Control Unit, National School of Engineers of Sfax.
His research interests include robust control, delay systems, and descriptor systems.
M. Souissi received his Ph.D. degree in physical sciences from the University of Tunis, Tunisia in 2002. He is a professor in automatic control at Preparatory Institute of Engineers of Sfax, Tunisia. Since {dy2003}, he is holding a research position at Automatic Control Unit, National School of Engineers of Sfax, Tunisia. He is a member of the organization committees of several national and international conferences (STA, CASA).
His research interests include robust control, optimal control, fuzzy logic, linear matrix inequalities, and applications of these techniques to agriculture systems.
D. Mehdi is currently a professor at Institute of Technology of Poitiers, France. He is the head of the research group "Multivariable Systems and Robust Control" in Laboratory of Automatic and Industrial Informatics of Poitiers. para]His research interests include robust control, delay systems, robust root-clustering, descriptor systems, and control of industrial processes. F. Tadeo graduated from the same university, in physics in {dy1992}, and in electronic engineering in 1994. After received M. Sc. degree in control engineering in the University of Bradford, UK, he went back to Valladolid, where he received his Ph. D. degree. Currently, he is a professor at the Department of Systems Engineering and Automation.
His research interests include observation and control of positive systems, l1 optimal control, two degree freedom structures, constrained systems with delays, neutralization processes, greenhouses, hydrogen reformers, membranes, and renewable energies.
Rights and permissions
About this article
Cite this article
Allouche, M., Chaabane, M., Souissi, M. et al. State Feedback Tracking Control for Indirect Field- oriented Induction Motor Using Fuzzy Approach. Int. J. Autom. Comput. 10, 99–110 (2013). https://doi.org/10.1007/s11633-013-0702-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11633-013-0702-4