1 Introduction

The induction motor (IMs) is commonly employed in industries because of its reliability, less cost and maintenance free (Deng et al. 2019; Lopes et al. 2017). The dynamics of the induction motors is complicated and is disturbed by variation in rotor resistance and changes in load torque and so on Guedes et al. (2019). Then the control problem of the induction motors has attained great attention in recent years. Various control methods have been applied to the control of IMs. The proposed methods are classified in three categories. In the first category, some simple and ordinary control schemes have been designed for IMs. For instance, the field-oriented control approach is designed for the speed control of IMs (Kubota and Matsuse 1994). In Yu et al. (2001), the vector controller is developed for IMs. The other simple controller which is frequently applied on IMs is PID control method (Lim et al. 2013). Many optimization methods and algorithms have been applied to optimize the PID control for IMs such as genetic algorithm, particle swarm optimization, fuzzy systems, imperialist competitive algorithm and so on (Thangaraj et al. 2011; Ustun and Demirtas 2008; Uddin et al. 2002; Ali 2015).

The next main approach for the control of IMs is the classical control methods. For instance, the predictive control is developed for IMs (Zhang and Yang 2015; Zhang et al. 2016). In Lascu et al. (2016), the feedback linearzation method designed for IMs and its performance is compared with the sliding mode approach. The backstepping control technique is studied for IMs in Regaya et al. (2018), and its robustness against variation of rotor resistance is investigated. The immersion and invariance control strategy is studied for IMs in Sabzalian et al. (2019b), and its robustness is investigated. The other most common controller that is frequently used to control of IMs is the sliding model control (SMC) approach. Various version of sliding mode control technique has been studied for IMs such as traditional SMC, adaptive exponential SMC, second-order SMC, terminal SMC, integral SMC, and so on (Xu et al. 2019; Ponce et al. 2018).

The main drawback of the reviewed studies is that the dynamic model of IM is considered to be certain and known. To cope with uncertainties of the mathematical model of IM, some intelligent control methods have been proposed (Kalat 2019). In third category, some control approaches have been presented based on the fuzzy systems, neural networks and evolutionary optimization algorithm. For example, in Guazzelli et al. (2018), a predictive controller is designed by genetic algorithm, in which a cost function is minimized to obtain the weighting factors of the conventional predictive controller. The super-twisting technique is employed to improve the field oriented control method (Kali et al. 2018). A simple neuro-fuzzy control method is suggested for IMs, and it is proved that the designed controller has desirable performance in contrast to the conventional PI controller (Gopal and Shivakumar 2019). In Xu et al. (2019), the conventional backstepping strategy is combined with the type-1 fuzzy system to cope with uncertainties. The predictive controller is combined with the Takagi–Sugeno fuzzy system, and it is shown that the performance of the model predictive control is improved (Ammar et al. 2019). The adaptive controller on basis of fuzzy systems, the command filtering and backstepping technique is studied for IMs (Zhao et al. 2018). In Farah et al. (2019), a simple self-evolving fuzzy controller is proposed to improve the performance of indirect field-oriented control scheme. The dynamics of IM is approximated with the fuzzy system in kind of type-1, and then, the feedback controller is designed and its stability is investigated using \(L_2\) optimization (Zina et al. 2018).

In the most of the aforementioned papers, type-1 fuzzy systems and simple neural networks are used to cope with the uncertainties of the dynamics of IMs. Also the robustness of the controller with respect to main faults such as perturbation in the rotor resistance and sudden changes in load torque need more researches. In recent years, it is demonstrated that interval and general type-2 fuzzy systems result in more desirable and more effective performance in approximation of uncertainties (Mohammadzadeh et al. 2019a; Melin et al. 2019; Ontiveros-Robles and Melin 2020; Jana et al. 2019; Zhao et al. 2019). Most recently, the generalized type-2 fuzzy system (GT2FSs) is successfully applied in various applications (Castillo and Atanassov 2019; Castillo et al. 2019). For instance, in Zarandi et al. (2019), GT2FSs are employed for diagnosis of depression. The improved fuzzy systems are used in ship steering systems (Chang et al. 2019). The type-2 fuzzy systems are used to green solid transportation problem (Das et al. 2018). In Sabzalian et al. (2019a), Mohammadzadeh and Kaynak (2019), Jhang et al. (2018), Mohammadzadeh and Zhang (2019) and Mohammadzadeh et al. (2019b) the GT2FSs are used in forecasting and control problems. GT2FSs are used in fault detection and time-series prediction (Boumella et al. 2012; Shabanian and Montazeri 2011). Many learning techniques have been suggested to optimize the type-2 fuzzy systems such as bee colony optimization (Zhang et al. 2019), particle swarm optimization (Boumella et al. 2012), among many others. However, the stable optimization of GT2FSs has been rarely studied. In this paper, the proposed GT2FSs are learned on basis of the tuning laws that are extracted through the robustness analysis.

Based on the aforementioned discussion and motivations, in this study a novel fault-tolerant control scheme is presented. The main innovations of this study are:

  1. 1.

    Unlike the most studies, in this paper dynamic model of IM is considered to be unknown and also it is supposed the dynamics of IM to be disturbed by main faults such as perturbation in the rotor resistance and suddenly changes of load torque.

  2. 2.

    In addition to the dynamic uncertainties and abrupt faults, the effect of measurement errors is also considered.

  3. 3.

    A GT2FS is presented to cope with the uncertainties.

  4. 4.

    The robustness of the suggested control approach is analyzed and a novel compensator is developed to insure the stability and robustness.

The remain structure of this study is as follows. The dynamics of IM is described in Sect. 2. The proposed GT2FS is illustrated in Sect. 3. The control signals and stability analysis are given in Sect. 4. Simulations are presented in Sect. 5, and the conclusion is summarized in Sect. 6.

Fig. 1
figure 1

The general view on the suggested controller

Full size image

2 Problem formulation

The mathematical dynamics of the IM are given as:

$$\begin{aligned} \begin{array}{l} \hbox {d}\omega /\hbox {d}t = - {n_\mathrm{p}}{T_\mathrm{r}}/J + \mu {\phi _\mathrm{r}}{i_\mathrm{sq}}\\ \hbox {d}{\phi _\mathrm{r}}/\hbox {d}t = \frac{{{M_\mathrm{sr}}}}{{{\tau _\mathrm{r}}}}{i_\mathrm{sd}} - \frac{1}{{{\tau _\mathrm{r}}}}{\phi _\mathrm{r}}\\ \hbox {d}{i_\mathrm{sd}}/\hbox {d}t = \beta \omega {\phi _\mathrm{rq}} + \frac{\beta }{{{\tau _\mathrm{r}}}}{\phi _\mathrm{rd}} + {\omega _\mathrm{s}}{i_\mathrm{sq}}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{1}{{{\tau _1}}}{i_\mathrm{sd}} + {V_\mathrm{sd}}/{L_1}\\ \hbox {d}{i_\mathrm{sq}}/\hbox {d}t = - \beta \omega {\phi _\mathrm{rd}} + \beta /{\tau _\mathrm{r}}{\phi _\mathrm{rq}} - {\omega _\mathrm{s}}{i_\mathrm{sd}}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{1}{{{\tau _1}}}{i_\mathrm{sq}} + {V_\mathrm{sq}}/{L_1} \end{array} \end{aligned}$$
(1)

where the subscripts q, d, r and s refer to quadrature component, direct component, rotor and stator, respectively. \(\phi \), V and i, are the flux, voltage and current, respectively. \(\omega \) represents the rotor speed and \({\omega _\mathrm{s}}\) is frequency of stator angular. \({T _\mathrm{r}}\) is the load torque and it is considered to be unknown. The other parameters are defined as follows:

$$\begin{aligned} {\tau _\mathrm{r}}= & {} {L_\mathrm{r}}/{R_\mathrm{r}}\nonumber \\ {L_1}= & {} {L_\mathrm{s}} - \frac{{{M_\mathrm{sr}}^2}}{{{L_\mathrm{r}}}}\nonumber \\ {R_1}= & {} {R_\mathrm{s}} + {R_\mathrm{r}}{\left( {\frac{{{M_\mathrm{sr}}}}{{{L_\mathrm{r}}}}} \right) ^2}\nonumber \\ \beta= & {} \frac{{{M_\mathrm{sr}}}}{{{L_\mathrm{r}}{L_1}}}\nonumber \\ \mu= & {} n_\mathrm{p}^2\left( {\frac{{{M_\mathrm{sr}}}}{{J{L_\mathrm{r}}}}} \right) \nonumber \\ {\tau _1}= & {} \frac{{{L_1}}}{{{R_1}}} \end{aligned}$$
(2)

where J express moment of inertia, the number of pole pairs is represented by \(n_\mathrm{p}\) , \({L_\mathrm{r}}/{L_\mathrm{s}}\) is the rotor/stator inductances, \({R_\mathrm{r}}/{R_\mathrm{s}}\) is the rotor/stator resistance and \(M_\mathrm{sr}\) represents the mutual inductance.

The dynamics of IM in (1) are rewritten as follows:

(3)

where

(4)
(5)

By using the suggested GT2FS, the dynamics of IM in (3) are online estimated as follows:

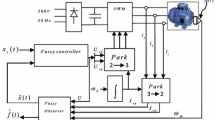
$$\begin{aligned} \begin{array}{*{20}{l}} {{{\dot{\hat{y}}}_1} = {{\hat{y}}_4}}+{{\hat{f}}_1}\left( {\underline{\hat{y}} |{{ \theta }_1}} \right) \\ {{{\dot{\hat{y}}}_2} = {{\hat{y}}_3}}+{{\hat{f}}_2}\left( {\underline{\hat{y}} |{{ \theta }_2}} \right) \\ {{{\dot{\hat{y}}}_3} = {{\hat{f}}_3}\left( {\underline{\hat{y}} |{{ \theta }_3}} \right) + \frac{1}{{{L_1}}}{u_1}}\\ {{{\dot{\hat{y}}}_4} = {{\hat{f}}_4}\left( {\underline{\hat{y}} |{{ \theta }_4}} \right) + \frac{1}{{{L_1}}}{u_2}} \end{array} \end{aligned}$$
(6)

where \({{{\hat{f}}}_i},\,i = 1,\ldots ,4\) are the suggested GT2GSs and . \({{\hat{f}}_1}\), \({{\hat{f}}_2}\), \({{\hat{f}}_3}\) and \({{\hat{f}}_4}\) are the estimation of \({f_1}\left( {{\underline{y}} } \right) \), \({f_2}\left( {{\underline{y}} } \right) \), \({f_3}\left( {{\underline{y}} } \right) \) and \({f_4}\left( {{\underline{y}} } \right) \), respectively. A general view on the proposed control scheme shown in Fig. 1.

Fig. 2
figure 2

The structure of the generalized type-2 fuzzy system

Full size image
Fig. 3
figure 3

The proposed non-singleton fuzzification

Full size image

3 Suggested fuzzy system

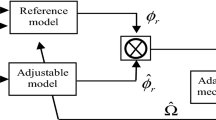
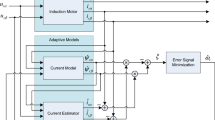
In this section, the suggested GT2FS is explained. The suggested structure is displayed in Fig. 2. Consider the ith GT2FS, the details are described in below.

  1. 1.

    The estimated states \({{{\hat{y}}}_k},\,k = 1,\ldots ,4\) are the inputs of GT2FS \({\hat{f}}_i\).

  2. 2.

    Consider the nth membership function (MF) for the kth input as \({\tilde{A}}_k^n\); by conventional singleton fuzzification, the upper membership and the lower membership of \({\tilde{A}}_k^n\) at the horizontal slice level \(\alpha \) are computed as follows:

    $$\begin{aligned} {\bar{\mu }} _{k|\alpha }^n= & {} \exp \left( { - \frac{{{{\left( {{{{\hat{y}}}_k} - {c_{{\tilde{A}}_k^n}}} \right) }^2}}}{{{\bar{\sigma }} _{{\tilde{A}}_{k|\alpha }^n}^2}}} \right) \nonumber \\ {\underline{\mu }} _{k|\alpha }^n= & {} \exp \left( { - \frac{{{{\left( {{{{\hat{y}}}_k} - {c_{{\tilde{A}}_k^n}}} \right) }^2}}}{{{\underline{\sigma }} _{{\tilde{A}}_{k|\alpha }^n}^2}}} \right) \end{aligned}$$
    (7)

    where \({{c_{{\tilde{A}}_k^n}}}\), \({{\bar{\sigma }} _{{\tilde{A}}_{k|\alpha }^n}}\) and \({{\underline{\sigma }} _{{\tilde{A}}_{k|\alpha }^n}}\), express the center, upper standard division and lower standard division of the Gaussian MF \({\tilde{A}}_{k|\alpha }^n\), respectively. \({{{{\hat{y}}}_k}}\) is the \(k-th\) input. \({\bar{\mu }} _{k|\alpha }^n\) and \({\underline{\mu }} _{k|\alpha }^n\) are the upper ad lower membership of \({\tilde{A}}_k^n\). By the proposed non-singleton fuzzfication, the upper membership and the lower membership of \({\tilde{A}}_k^n\) at the horizontal slice level \(\alpha \) are computed as follows:

    $$\begin{aligned} \begin{array}{*{20}{l}} {\bar{\mu }_{k|\alpha }^n = \exp \left( { - \frac{{{{\left( {\hat{\bar{y}}_k^n - {c_{\tilde{A}_k^n}}} \right) }^2}}}{{\bar{\sigma }_{\tilde{A}_{k|\alpha }^n}^2}}} \right) }\\ {\underline{\mu }_{k|\alpha }^n = \exp \left( { - \frac{{{{\left( {\underline{\hat{y}} _k^n - {c_{\tilde{A}_k^n}}} \right) }^2}}}{{\underline{\sigma }_{\tilde{A}_{k|\alpha }^n}^2}}} \right) } \end{array} \end{aligned}$$
    (8)

    where \({\hat{{\bar{y}}}_k^n}\) and \({\underline{{\hat{y}}} _k^n}\) are computed as (see Fig. 3):

    $$\begin{aligned} \hat{{\bar{y}}}_k^n= & {} \frac{{\sigma _{{B_k}}^2{c_{{\tilde{A}}_i^j}} + {\bar{\sigma }} _{{\tilde{A}}_{k|\alpha }^n}^2{{{\hat{y}}}_k}}}{{\sigma _{{B_k}}^2{c_{{\tilde{A}}_i^j}} + {\bar{\sigma }} _{{\tilde{A}}_{k|\alpha }^n}^2{{{\hat{y}}}_k}}} \end{aligned}$$
    (9)
    $$\begin{aligned} \underline{{\hat{y}}} _k^n{}= & {} \frac{{\sigma _{{B_k}}^2{c_{{\tilde{A}}_i^j}} + {\underline{\sigma }} _{\tilde{A}_{k|\alpha }^n}^2{{{\hat{y}}}_k}}}{{\sigma _{{B_k}}^2{c_{\tilde{A}_i^j}} + {\underline{\sigma }} _{{\tilde{A}}_{k|\alpha }^n}^2{{{\hat{y}}}_k}}} \end{aligned}$$
    (10)

    where \({\sigma _{{B_k}}}\) is a parameter in the membership function \({B_k}\) for kth input. The membership of \({B_k}\) is obtained as:

    $$\begin{aligned} {\mu _{{B_k}}} = \left[ {1 + \frac{{{{\left( {y - {{{\hat{y}}}_k}} \right) }^2}}}{{\sigma _{{B_k}}^2}}} \right] \exp \left[ { - \frac{{{{\left( {y - {{{\hat{y}}}_k}} \right) }^2}}}{{\sigma _{{B_k}}^2}}} \right] \end{aligned}$$
    (11)
  3. 3.

    The rule firing are obtained as follows:

    $$\begin{aligned} {{{\bar{\psi }} }_{n|\alpha }}= & {} {\bar{\mu }} _{1|\alpha }^n \times \cdots \times {\bar{\mu }} _{4|\alpha }^n\nonumber \\ {{\underline{\psi }} _{n|\alpha }}= & {} {\underline{\mu }} _{1|\alpha }^n \times \cdots \times {\underline{\mu }} _{4|\alpha }^n \end{aligned}$$
    (12)

    where \({{{\bar{\psi }} }_{n|\alpha }}\) and \({{\underline{\psi }} _{n|\alpha }}\) represent upper rule firing and lower rule firing of nth rule at level \(\alpha \)-cut.

  4. 4.

    On the basis of the Nie-Tan type-reduction (Fekih 2008), one has:

    $$\begin{aligned} {f_i} = {{\sum \limits _{j = 1}^{{N_\alpha }} {{\alpha _j}\,\theta _i^T{\xi _{i|{\alpha _j}}}} } \big / {\sum \limits _{j = 1}^{{N_\alpha }} {{\alpha _j}} }} \end{aligned}$$
    (13)
    $$\begin{aligned} \begin{array}{l} {\xi _{i|{\alpha _j}}} = \frac{1}{{\sum \nolimits _{n = 1}^{{N_\mathrm{r}}} {{{\bar{\psi }}_{n|{\alpha _j}}} + {{\underline{\psi }}_{n|{\alpha _j}}}} }}\\ {\left[ {{{\bar{\psi }}_{1|{\alpha _j}}} + {{\underline{\psi }}_{1|{\alpha _j}}},\ldots ,{{\bar{\psi }}_{{N_\mathrm{r}}|{\alpha _j}}} + {{\underline{\psi }}_{{N_\mathrm{r}}|{\alpha _j}}}} \right] ^\mathrm{T}} \end{array} \end{aligned}$$
    (14)

    where \({\hat{f}}_i\) is the output, \({{N_\mathrm{r}}}\) represents the rule numbers, \({{N_\alpha }}\) is the number of \(\alpha \)-cuts and \({\theta _i}\) is the vector of the consequent parameters. \({f_i}\) can be rewritten as follows:

    $$\begin{aligned} {f_i} = \,\theta _i^T{\zeta _i} \end{aligned}$$
    (15)

    where

    $$\begin{aligned} {\zeta _i} = {{\sum \limits _{j = 1}^{{N_\alpha }} {{\xi _{i|{\alpha _j}}}} } \big / {\sum \limits _{j = 1}^{{N_\alpha }} {{\alpha _j}} }} \end{aligned}$$
    (16)

4 Main results

The main outcomes of the study are given in the following theorem.

Theorem 1

The system (3) is stable, asymptotically, if the controllers and the tuning rules of the fuzzy systems are designed as follows:

$$\begin{aligned} \frac{1}{{{L_1}}}{u_2}= & {} {{\dot{z}}_1} - {k_1}{\chi _1} - {{\hat{f}}_4}\nonumber \\ \frac{1}{{{L_1}}}{u_1}= & {} {{\dot{z}}_2} - {k_2}{\chi _2} - {{\hat{f}}_3} \end{aligned}$$
(17)
$$\begin{aligned} \dot{\theta _1^{}}= & {} \eta {{\tilde{e}}_1}{\zeta _1}\nonumber \\ \dot{\theta _2^{}}= & {} \eta {{\tilde{e}}_2}{\zeta _2}\nonumber \\ \dot{\theta _3^{}}= & {} \eta {{\tilde{e}}_3}{\zeta _3}\nonumber \\ \dot{\theta _4^{}}= & {} \eta {{\tilde{e}}_4}{\zeta _4} \end{aligned}$$
(18)

where \(k_1\) and \(k_2\) are constants with positive values and the variables \({\chi _i}\), \({z_i}\), \(i=1,2\) are defined as follows:

$$\begin{aligned}&\begin{array}{l} {\chi _2} = {{\hat{y}}_3} - {z_2}\,\,\,\,\,\,\,\,\,{\chi _1} = {{\hat{y}}_4} - {z_1} \end{array} \end{aligned}$$
(19)
$$\begin{aligned}&\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{z_1} = - {{\hat{f}}_1}\left( {\underline{\hat{y}} |{{ \theta }_1}} \right) + {{\dot{r}}_1} - {\lambda _1}{{\hat{e}}_1}}\\ {\,\,\,\,\,\,\,\,\,\, - \left( {{{\bar{\varepsilon }}_3}\left| {{{\tilde{e}}_3}} \right| + {{\bar{\varepsilon }}_1}\left| {{{\tilde{e}}_1}} \right| + {{\tilde{e}}_1}\left| {{{\tilde{e}}_4}} \right| } \right) /\left( {{{\hat{e}}_1} - \delta \mathrm{{sign}}\left( {{{\hat{e}}_1}} \right) } \right) } \end{array}}\\ {\begin{array}{*{20}{l}} {{z_2} = - {{\hat{f}}_2}\left( {\underline{\hat{y}} |{{ \theta }_2}} \right) + {{\dot{r}}_2} - {\lambda _2}{{\hat{e}}_2}}\\ {\,\,\,\,\,\,\,\,\,\, - \left( {{{\bar{\varepsilon }}_4}\left| {{{\tilde{e}}_4}} \right| + {{\bar{\varepsilon }}_2}\left| {{{\tilde{e}}_2}} \right| + {{\tilde{e}}_2}\left| {{{\tilde{e}}_3}} \right| } \right) /\left( {{{\hat{e}}_2} - \delta \mathrm{{sign}}\left( {{{\hat{e}}_2}} \right) } \right) } \end{array}} \end{array} \end{aligned}$$
(20)

where , \(i=1,\ldots ,4\) are proposed fuzzy system, \({{ r}_1}\) and \({{ r}_2}\) are the reference signals, \({\lambda _1}\) and \({\lambda _2}\) are constant variables with the positive values, \(\delta \) is small positive constant, \({{\hat{e}}_i}\) and \({{\tilde{e}}_i},\,i = 1,\ldots ,4\) are defined as \({{\hat{e}}_i} = {{\hat{y}}_i} - {r_i},\,\,{{\tilde{e}}_i} = {y_i} - {{\hat{y}}_i}\), \({{{\bar{\varepsilon }} }_i},\,i = 1,\ldots ,4\) are the upper bounds of \({{ \varepsilon }_i}\) where are defined as follows:

$$\begin{aligned} \begin{array}{l} {\varepsilon _1} = \left[ {{f_1}\left( {{\underline{y}} } \right) - {\hat{f}}_1^*\left( {\underline{{\hat{y}}} | \theta _1^*} \right) } \right] \\ {\varepsilon _2} = \left[ {{f_2}\left( {{\underline{y}} } \right) - {\hat{f}}_2^*\left( {\underline{{\hat{y}}} | \theta _2^*} \right) } \right] \\ {\varepsilon _3} = \left[ {{f_3}\left( {{\underline{y}} } \right) - {\hat{f}}_3^*\left( {\underline{{\hat{y}}} | \theta _3^*} \right) } \right] \\ {\varepsilon _4} = \left[ {{f_4}\left( {{\underline{y}} } \right) - {\hat{f}}_4^*\left( {\underline{{\hat{y}}} | \theta _4^*} \right) } \right] \end{array} \end{aligned}$$
(21)

where are the proposed type-2 fuzzy system with optimal parameters \({ \theta _i^ * }\). Also \({{\tilde{\theta }} _i}\), \(i=1,\ldots ,4\) are defined as:

$$\begin{aligned} \begin{array}{l} {{{\tilde{\theta }} }_1} = \theta _1^* - {\theta _1}\\ {{{\tilde{\theta }} }_2} = \theta _2^* - {\theta _2}\\ {{{\tilde{\theta }} }_3} = \theta _3^* - {\theta _3}\\ {{{\tilde{\theta }} }_4} = \theta _4^* - \theta _4 \end{array} \end{aligned}$$
(22)

Proof

Substituting (20) into (6), yields:

$$\begin{aligned} \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{{\dot{{\hat{e}}}}_1} = - {\lambda _1}{{{\hat{e}}}_1}}\\ {\,\,\,\,\,\,\,\,\, - \left( {{{{\bar{\varepsilon }} }_3}\left| {{{{\tilde{e}}}_3}} \right| + {{{\bar{\varepsilon }} }_1}\left| {{{\tilde{e}}_1}} \right| + \left| {{{{\tilde{e}}}_1}} \right| \left| {{{\tilde{e}}_4}} \right| } \right) /\left( {{{{\hat{e}}}_1} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_1}} \right) } \right) } \end{array}}\\ {\begin{array}{*{20}{l}} {{{\dot{{\hat{e}}}}_2} = - {\lambda _2}{{{\hat{e}}}_2}}\\ {\,\,\,\,\,\,\,\,\,\, - \left( {{{{\bar{\varepsilon }} }_4}\left| {{{{\tilde{e}}}_4}} \right| + {{{\bar{\varepsilon }} }_2}\left| {{{\tilde{e}}_2}} \right| + \left| {{{{\tilde{e}}}_2}} \right| \left| {{{\tilde{e}}_3}} \right| } \right) /{{{\hat{e}}}_2} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_2}} \right) } \end{array}} \end{array} \end{aligned}$$
(23)

The dynamics of \({{{\tilde{e}}}_1}\), \({{{\tilde{e}}}_2}\), \({{{\tilde{e}}}_3}\) and \({{{\tilde{e}}}_4}\) are obtained as follows:

$$\begin{aligned} \begin{array}{l} {{\dot{{\tilde{e}}}}_1} = {\hat{f}}_1^*\left( {\underline{{\hat{y}}} | \theta _1^*} \right) - {{{\hat{f}}}_1}\left( {\underline{{\hat{y}}} |{{ \theta }_1}} \right) + \left[ {{f_1}\left( {{\underline{y}} } \right) - {\hat{f}}_1^*\left( {\underline{{\hat{y}}} | \theta _1^*} \right) } \right] + {{{\tilde{e}}}_4}\\ {{\dot{{\tilde{e}}}}_2} = {\hat{f}}_2^*\left( {\underline{{\hat{y}}} | \theta _2^*} \right) - {{{\hat{f}}}_2}\left( {\underline{{\hat{y}}} |{{ \theta }_2}} \right) + \left[ {{f_2}\left( {{\underline{y}} } \right) - {\hat{f}}_2^*\left( {\underline{{\hat{y}}} | \theta _3^*} \right) } \right] + {{{\tilde{e}}}_3}\\ \begin{array}{*{20}{l}} {{{\dot{{\tilde{e}}}}_3} = {\hat{f}}_3^*\left( {\underline{{\hat{y}}} | \theta _1^*} \right) - {{{\hat{f}}}_3}\left( {\underline{{\hat{y}}} |{{ \theta }_3}} \right) + \left[ {{f_3}\left( {{\underline{y}} } \right) - {\hat{f}}_3^*\left( {\underline{{\hat{y}}} | \theta _3^*} \right) } \right] }\\ {{{\dot{{\tilde{e}}}}_4} = {\hat{f}}_4^*\left( {\underline{{\hat{y}}} | \theta _4^*} \right) - {{{\hat{f}}}_4}\left( {\underline{{\hat{y}}} |{{ \theta }_2}} \right) + \left[ {{f_4}\left( {{\underline{y}} } \right) - {\hat{f}}_4^*\left( {\underline{{\hat{y}}} | \theta _4^*} \right) } \right] } \end{array} \end{array}\nonumber \\ \end{aligned}$$
(24)

By substituting (21) into equation (24), one has:

$$\begin{aligned} \begin{array}{l} {{\dot{{\tilde{e}}}_1}} = {\tilde{\theta }} _1^T{\zeta _1} + {\varepsilon _1} + {{{\tilde{e}}}_4}\\ {{\dot{{\tilde{e}}}_2}} = {\tilde{\theta }} _2^T{\zeta _2} + {\varepsilon _2} + {{{\tilde{e}}}_3}\\ {{\dot{{\tilde{e}}}_3}} = {\tilde{\theta }} _3^T{\zeta _3} + {\varepsilon _3}\\ {{\dot{{\tilde{e}}}_4}} = {\tilde{\theta }} _4^T{\zeta _4} + {\varepsilon _4} \end{array} \end{aligned}$$
(25)

Time derivative of \({\chi _2}\) and \({\chi _1}\) in (19), are obtained as follows:

$$\begin{aligned} \begin{array}{l} {{{\dot{\chi }} }_1} = {{{\hat{f}}}_4} + \frac{1}{{{L_1}}}{u_2} - {{\dot{z}}_1}\\ {{{\dot{\chi }} }_2} = {{{\hat{f}}}_3} + \frac{1}{{{L_1}}}{u_1} - {{\dot{z}}_2} \end{array} \end{aligned}$$
(26)

From (17) and (26), the dynamics of \(\chi _1\) and \(\chi _2\) can be written as follows:

$$\begin{aligned} \begin{array}{l} {{{\dot{\chi }} }_1} = - {k_1}{\chi _1} \\ {{{\dot{\chi }} }_2} = - {k_2}{\chi _2} \end{array} \end{aligned}$$
(27)

To prove the closed-loop stability, the following Lyapunov function is considered:

$$\begin{aligned} V= & {} \frac{1}{2}{\hat{e}}_1^2 + \frac{1}{2}{\hat{e}}_2^2, + \frac{1}{2}{\tilde{e}}_1^2 + \frac{1}{2}{\tilde{e}}_2^2+ \frac{1}{2}{\tilde{e}}_3^2 + \frac{1}{2}{\tilde{e}}_4^2 + \frac{1}{2}\chi _1^2 + \frac{1}{2}\chi _2^2\nonumber \\&+ \frac{1}{{2\eta }}{\tilde{\theta }} _1^T{\tilde{\theta }} _2^{} + \frac{1}{{2\eta }}{\tilde{\theta }} _2^T{\tilde{\theta }} _2^{} + \frac{1}{{2\eta }}{\tilde{\theta }} _3^T{\tilde{\theta }} _3^{} + \frac{1}{{2\eta }}{\tilde{\theta }} _4^T{\tilde{\theta }} _4^{}\nonumber \\ \end{aligned}$$
(28)

where \(\eta \) is the tuning rate. By taking time derivative of (28), one has:

$$\begin{aligned} \dot{V}= & {} {{{\hat{e}}}_1}\dot{{\hat{e}}}_1^{} + {{{\hat{e}}}_2}\dot{{\hat{e}}}_2^{} + {{{\tilde{e}}}_1}\dot{{\tilde{e}}}_1^{} + {{{\tilde{e}}}_2}\dot{{\tilde{e}}}_2^{} + {{{\tilde{e}}}_3}\dot{{\tilde{e}}}_3^{} + {{{\tilde{e}}}_4}\dot{{\tilde{e}}}_4^{}\nonumber \\&+ {\chi _1}{\dot{\chi }} _1^{} + {\chi _2}{\dot{\chi }} _2^{} - \frac{1}{\eta }{\tilde{\theta }} _1^T{\dot{\theta }} _1^{} - \frac{1}{\eta }{\tilde{\theta }} _2^T{\dot{\theta }} _2^{}\\&- \frac{1}{\eta }{\tilde{\theta }} _3^T{\dot{\theta }} _3^{} - \frac{1}{\eta }{\tilde{\theta }} _4^T{{\dot{\theta }}} _4^{}\nonumber \end{aligned}$$
(29)

Substituting \(\dot{{\hat{e}}}_1\) and \(\dot{{\hat{e}}}_2\) from (23), \(\dot{{\tilde{e}}}_i\) \(i=1,\ldots ,4\) from (25) and \({{\dot{\chi }}} _1\) and \({{\dot{\chi }}} _2\) from (27), yields:

$$\begin{aligned} {\dot{V}}= & {} {{{{\hat{e}}}_1}\left[ { - {\lambda _1}{{{\hat{e}}}_1} - \frac{{{{{\bar{\varepsilon }} }_3}\left| {{{{\tilde{e}}}_3}} \right| + {{{\bar{\varepsilon }} }_1}\left| {{{{\tilde{e}}}_1}} \right| + \left| {{{{\tilde{e}}}_1}} \right| \left| {{{{\tilde{e}}}_4}} \right| }}{{{{{\hat{e}}}_1} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_1}} \right) }}} \right] }\nonumber \\&+ {{{\hat{e}}}_2}\left[ { - {\lambda _2}{{{\hat{e}}}_2} - \frac{{{{{\bar{\varepsilon }} }_4}\left| {{{{\tilde{e}}}_4}} \right| + {{{\bar{\varepsilon }} }_2}\left| {{{{\tilde{e}}}_2}} \right| + \left| {{{{\tilde{e}}}_2}} \right| \left| {{{{\tilde{e}}}_3}} \right| }}{{{{{\hat{e}}}_2} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_2}} \right) }}} \right] \nonumber \\&+ {{{\tilde{e}}}_1}\left( {{\tilde{\theta }} _1^T{\zeta _1} + {\varepsilon _1} + {{{\tilde{e}}}_4}} \right) + {{{\tilde{e}}}_2}\left( {{\tilde{\theta }} _2^T{\zeta _2} + {\varepsilon _2} + {{{\tilde{e}}}_3}} \right) \nonumber \\&+ {{{\tilde{e}}}_3}\left( {{\tilde{\theta }} _3^T{\zeta _3} + {\varepsilon _3}} \right) + {{{\tilde{e}}}_4}\left( {{\tilde{\theta }} _4^T{\zeta _4} + {\varepsilon _4}} \right) \\&+ {\chi _1}\left( { - {k_1}{\chi _1}} \right) + {\chi _2}\left( { - {k_2}{\chi _2}} \right) \nonumber \\&- \frac{1}{\eta }{\tilde{\theta }} _1^T{{\dot{\theta }}} _1^{} - \frac{1}{\eta }{\tilde{\theta }} _2^T{{\dot{\theta }}} _2^{}\nonumber \\&- \frac{1}{\eta }{\tilde{\theta }} _3^T{{\dot{\theta }}} _3^{} - \frac{1}{\eta }{\tilde{\theta }} _4^T{{\dot{\theta }}} _4^{}\nonumber \end{aligned}$$
(30)

Equation (30) can be rewritten as follows:

$$\begin{aligned} \begin{array}{*{20}{l}} {\dot{V} = - {\lambda _1}{\hat{e}}_1^2 - {\lambda _2}{\hat{e}}_2^2 - {k_1}\chi _1^2 - {k_2}\chi _2^2}\\ {\,\,\,\,\,\,\,\,\, + \left( {{\varepsilon _1}{{{\tilde{e}}}_1} + {{{\tilde{e}}}_1}{{{\tilde{e}}}_4} + {\varepsilon _3}{{{\tilde{e}}}_3}} \right) }\\ {\,\,\,\,\,\,\,\,\, - {{{\hat{e}}}_1}\left( {{{{\bar{\varepsilon }} }_3}\left| {{{{\tilde{e}}}_3}} \right| + {{{\bar{\varepsilon }} }_1}\left| {{{{\tilde{e}}}_1}} \right| + \left| {{{{\tilde{e}}}_1}} \right| \left| {{{{\tilde{e}}}_4}} \right| } \right) /\left( {{{{\hat{e}}}_1} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_1}} \right) } \right) }\\ {\,\,\,\,\,\,\,\,\, + \left( {{\varepsilon _2}{{{\tilde{e}}}_2} + {{{\tilde{e}}}_2}{{{\tilde{e}}}_3} + {\varepsilon _4}{{{\tilde{e}}}_4}} \right) }\\ {\,\,\,\,\,\,\,\,\, - {{{\hat{e}}}_2}\left( {{{{\bar{\varepsilon }} }_4}\left| {{{{\tilde{e}}}_4}} \right| + {{{\bar{\varepsilon }} }_2}\left| {{{{\tilde{e}}}_2}} \right| + \left| {{{{\tilde{e}}}_2}} \right| \left| {{{{\tilde{e}}}_3}} \right| } \right) /\left( {{{{\hat{e}}}_2} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_2}} \right) } \right) }\\ {\,\,\,\,\,\,\,\,\, + {{{\tilde{e}}}_1}{\tilde{\theta }} _1^T{\zeta _1} - \frac{1}{\eta }{\tilde{\theta }} _1^T{{\dot{\theta }}} _1^{} + {{{\tilde{e}}}_2}{\tilde{\theta }} _2^T{\zeta _2} - \frac{1}{\eta }{\tilde{\theta }} _2^T{{\dot{\theta }}} _2^{}}\\ {\,\,\,\,\,\,\,\,\, + {{{\tilde{e}}}_3}{\tilde{\theta }} _3^T{\zeta _3} - \frac{1}{\eta }{\tilde{\theta }} _3^T{{\dot{\theta }}} _3^{} + {{\tilde{e}}_4}{\tilde{\theta }} _4^T{\zeta _4} - \frac{1}{\eta }{\tilde{\theta }} _4^T{{\dot{\theta }}} _4^{}} \end{array} \end{aligned}$$
(31)

Substituting the adaptation laws of \( \theta _i, \, i=3,4\) form (18) into (31), results in:

$$\begin{aligned} \begin{array}{l} \dot{V} = - {\lambda _1}{\hat{e}}_1^2 - {\lambda _2}{\hat{e}}_2^2 - {k_1}\chi _1^2 - {k_2}\chi _2^2\\ \,\,\,\,\,\,\,\,\, + \left( {{\varepsilon _1}{{{\tilde{e}}}_1} + {{{\tilde{e}}}_1}{{{\tilde{e}}}_4} + {\varepsilon _3}{{{\tilde{e}}}_3}} \right) \\ \,\,\,\,\,\,\,\,\, - {{{\hat{e}}}_1}\left( {{{{\bar{\varepsilon }} }_3}\left| {{{{\tilde{e}}}_3}} \right| + {{{\bar{\varepsilon }} }_1}\left| {{{{\tilde{e}}}_1}} \right| + \left| {{{{\tilde{e}}}_1}} \right| \left| {{{{\tilde{e}}}_4}} \right| } \right) /\left( {{{{\hat{e}}}_1} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_1}} \right) } \right) \\ \,\,\,\,\,\,\,\,\, + \left( {{\varepsilon _2}{{{\tilde{e}}}_2} + {{{\tilde{e}}}_2}{{{\tilde{e}}}_3} + {\varepsilon _4}{{{\tilde{e}}}_4}} \right) \\ \,\,\,\,\,\,\,\,\, - {{{\hat{e}}}_2}\left( {{{{\bar{\varepsilon }} }_4}\left| {{{{\tilde{e}}}_4}} \right| + {{{\bar{\varepsilon }} }_2}\left| {{{{\tilde{e}}}_2}} \right| + \left| {{{{\tilde{e}}}_2}} \right| \left| {{{{\tilde{e}}}_3}} \right| } \right) /\left( {{{{\hat{e}}}_2} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_2}} \right) } \right) \end{array} \end{aligned}$$
(32)

From (32), one has:

$$\begin{aligned} \dot{V}\le & {} - {\lambda _1}{\hat{e}}_1^2 - {\lambda _2}{\hat{e}}_2^2 - {k_1}\chi _1^2 - {k_2}\chi _2^2 \nonumber \\&+ \left( {\left| {{\varepsilon _1}} \right| \left| {{{{\tilde{e}}}_1}} \right| + \left| {{{{\tilde{e}}}_1}{{{\tilde{e}}}_4}} \right| + \left| {{\varepsilon _3}} \right| \left| {{{{\tilde{e}}}_3}} \right| } \right) \nonumber \\&- {{{\hat{e}}}_1}\left( {{{{\bar{\varepsilon }} }_3}\left| {{{{\tilde{e}}}_3}} \right| + {{{\bar{\varepsilon }} }_1}\left| {{{{\tilde{e}}}_1}} \right| + \left| {{{{\tilde{e}}}_1}} \right| \left| {{{{\tilde{e}}}_4}} \right| } \right) /\left( {{{{\hat{e}}}_1} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_1}} \right) } \right) \nonumber \\&+ \left( {\left| {{\varepsilon _2}} \right| \left| {{{{\tilde{e}}}_2}} \right| + \left| {{{{\tilde{e}}}_2}{{{\tilde{e}}}_3}} \right| + \left| {{\varepsilon _4}} \right| \left| {{{{\tilde{e}}}_4}} \right| } \right) \nonumber \\&- {{{\hat{e}}}_2}\left( {{{{\bar{\varepsilon }} }_4}\left| {{{\tilde{e}}_4}} \right| + {{{\bar{\varepsilon }} }_2}\left| {{{{\tilde{e}}}_2}} \right| + \left| {{{{\tilde{e}}}_2}} \right| \left| {{{{\tilde{e}}}_3}} \right| } \right) /\left( {{{{\hat{e}}}_2} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_2}} \right) } \right) \nonumber \\ \end{aligned}$$
(33)

From (33) and considering the fact that:

$$\begin{aligned} \begin{array}{l} {{{\hat{e}}}_1}/\left( {{{{\hat{e}}}_1} - \delta {\mathop \mathrm{sign}\nolimits } \left( {{{{\hat{e}}}_1}} \right) } \right) \ge 1\\ {{{\hat{e}}}_2}/\left( {{{{\hat{e}}}_2} - \delta {\mathop \mathrm{sign}\nolimits } \left( {{{{\hat{e}}}_2}} \right) } \right) \ge 1 \end{array} \end{aligned}$$
(34)
Table 1 The IM parameters
Full size table
Table 2 The simulation parameters
Full size table
Fig. 4
figure 4

Scenario 1: the tracking performance of rotor speed

Full size image

One has:

$$\begin{aligned} \begin{array}{*{20}{l}} {\left( {\left| {{\varepsilon _1}} \right| \left| {{{{\tilde{e}}}_1}} \right| + \left| {{{{\tilde{e}}}_1}{{{\tilde{e}}}_4}} \right| + \left| {{\varepsilon _3}} \right| \left| {{{{\tilde{e}}}_3}} \right| } \right) - }\\ {{{{\hat{e}}}_1}\left( {{{{\bar{\varepsilon }} }_3}\left| {{{{\tilde{e}}}_3}} \right| + {{{\bar{\varepsilon }} }_1}\left| {{{{\tilde{e}}}_1}} \right| + \left| {{{{\tilde{e}}}_1}} \right| \left| {{{{\tilde{e}}}_4}} \right| } \right) /\left( {{{{\hat{e}}}_1} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_1}} \right) } \right) \le 0}\\ {\left( {\left| {{\varepsilon _2}} \right| \left| {{{{\tilde{e}}}_2}} \right| + \left| {{{{\tilde{e}}}_2}{{{\tilde{e}}}_3}} \right| + \left| {{\varepsilon _4}} \right| \left| {{{{\tilde{e}}}_4}} \right| } \right) - }\\ {{{{\hat{e}}}_2}\left( {{{{\bar{\varepsilon }} }_4}\left| {{{{\tilde{e}}}_4}} \right| + {{{\bar{\varepsilon }} }_2}\left| {{{{\tilde{e}}}_2}} \right| + \left| {{{{\tilde{e}}}_2}} \right| \left| {{{{\tilde{e}}}_3}} \right| } \right) /\left( {{{{\hat{e}}}_2} - \delta \mathrm{{sign}}\left( {{{{\hat{e}}}_2}} \right) } \right) \le 0} \end{array}\nonumber \\ \end{aligned}$$
(35)

From (35), the inequality (33), becomes:

$$\begin{aligned} \dot{V} \le - {\lambda _1}{\hat{e}}_1^2 - {\lambda _2}{\hat{e}}_2^2 - {k_1}\chi _1^2 - {k_2}\chi _2^2 \end{aligned}$$
(36)

Since the \({{\hat{e}}_1^{}}\), \({{\hat{e}}_2^{}}\), \(\chi _1^{}\) and \(\chi _2^{}\) are limited, then \({{\ddot{V}}}\) is bounded and then on the basis Barbalat’s lemma the asymptotic stability is proved and the proof is completed. \(\square \)

5 Simulation

This section presents the examination of the performance of the designed control scheme on an induction motor by 1.5 kW cage rotor and (220–380 V) power supply. The parameters of simulation are given in Tables 1 and 2. The performance of the suggested controller is evaluated in three scenarios, and finally a comparison with other popular control techniques is presented.

Fig. 5
figure 5

Scenario 1: the tracking performance of rotor flux

Full size image
Fig. 6
figure 6

Scenario 1: the trajectory of the tracking error (rotor speed)

Full size image
Fig. 7
figure 7

Scenario 1: the trajectory of the tracking error (rotor flux)

Full size image
Fig. 8
figure 8

Scenario 1: the stator current (direct component)

Full size image

Scenario 1 In the first scenario, it is assumed that there is no fault but the dynamics of IM is unknown. The trajectory of output \(y_1\) (rotor speed) is shown in Fig. 4 and the trajectory of the second output \(y_2\) (rotor flux) is depicted in Fig. 5. The tracking errors \(e_1\) and \(e_2\) are shown in Figs. 6 and 7, respectively. The trajectories of the direct component and the quadrature component of the stator current are given in Figs. 8 and 9, respectively. The direct component and the quadrature component of the control signals are provided in Figs. 10 and 11. One can see that the trajectories of \(y_1\) and \(y_2\) are well reached to the reference values in a finite time.

Fig. 9
figure 9

Scenario 1: the stator current (quadrature component)

Full size image
Fig. 10
figure 10

Scenario 1: the control signal (\(V_\mathrm{sd}\))

Full size image
Fig. 11
figure 11

Scenario 1: the control signal (\(V_\mathrm{sq}\))

Full size image

Scenario 2 In second scenario in addition to the fact that dynamics of IM is unknown, the main faults, such as perturbation in the rotor resistance and sudden changes of load torque, are considered as below. The perturbation of the rotor resistance is considered as \({R_\mathrm{r}} = {R_\mathrm{rN}}\left( {2 - \exp \left( { - 1.5t} \right) } \right) \), where \(R_\mathrm{rN}\) represents the nominal case of \(R_\mathrm{r}\) and the load torque is assumed to be suddenly changed from (5 N\(_\mathrm{m}\)) at \(t=3\) s as depicted in Fig. 12. The rotor speed \(y_1\) is given in Fig. 13, and the trajectory of the second output \(y_2\) (rotor flux) is depicted in Fig. 14. The tracking errors \(e_1\) and \(e_2\) are shown in Figs. 15 and 16, respectively. The trajectories of the stator current (direct component and the quadrature component) are given in Figs. 17 and 18. The direct/quadrature component of input voltage is displayed in Fig. 19/Fig. 20. One can see that the proposed controller could overcome the changes of the load torque, and variation of rotor resistance and the trajectories of rotor speed \(y_1\) and rotor flux \(y_2\) well track the desired reference under faulty conditions.

Fig. 12
figure 12

Scenario 2: the variation of the load torque

Full size image
Fig. 13
figure 13

Scenario 2: the tracking performance of rotor speed

Full size image
Fig. 14
figure 14

Scenario 2: the tracking performance of rotor flux

Full size image
Fig. 15
figure 15

Scenario 2: the trajectory of the tracking error of the rotor speed

Full size image

Scenario 3 In third scenario in addition to the unknown dynamics of IM and presence of the main faults such as considered in Scenario 2, the measurement errors are also considered. The measurement errors are considered to white noise that are added to the output signals. The results are given in Table 3. One can see that the proposed controller using GT2FS and non-singleton fuzzification could better overcome the measurement errors, changes of the load torque and variation of rotor resistance, in contrast to T1FS, IT2FS and singleton fuzzification.

Fig. 16
figure 16

Scenario 2: the trajectory of the tracking error (rotor flux)

Full size image
Fig. 17
figure 17

Scenario 2: the stator current (direct component)

Full size image
Fig. 18
figure 18

Scenario 2: the stator current (quadrature component)

Full size image
Fig. 19
figure 19

Scenario 2: the control signal (\(V_\mathrm{sd}\))

Full size image
Fig. 20
figure 20

Scenario 2: the control signal (\(V_\mathrm{sq}\))

Full size image

Comparison To demonstrate the capability of the suggested controller, a comparison with the other control techniques is provided. The control methods such as the fault tolerant control method (FTAC) (Fekih 2008), field oriented control approach (FOC) (Fekih 2008), the adaptive sliding mode controller (ASMC) (Dong et al. 2016) and type-2 fuzzy sliding mode control technique (T2FSC) (Masumpoor and Khanesar 2015) are considered. The root-mean-square errors (RMSEs) of different control approaches are provided in Table 4. One can see that suggested method performance is more better than the other techniques. It must be taken to account that in contrary to the other approaches, the mathematical dynamics model of the IM is considered to be fully unknown in the suggested control method.

Table 3 Scenario 3: comparison of root-mean-square error in the presence of different level of measurement errors
Full size table
Table 4 Comparison of the root-mean-square of the tracking error for different control methods
Full size table

6 Conclusion

In this paper, a new robust control approach is proposed for the control of induction motors (IM) based on the generalized type-2 fuzzy system. The dynamics of IM is unknown and is disturbed by the changes in rotor resistance and load torque. A new robust compensator is proposed to cope with approximation errors and disturbances. The type-2 fuzzy systems are optimized through the adaptation laws that are derived from Lyapunov robustness analysis. The simulations exhibit that the suggested controller has good and desired performance. Also the comparison with some other control techniques verify the strong effectiveness of the suggested control method. Furthermore, the comparison of the tracking performance of the suggested control system with other kind of fuzzy systems and fuzzification methods demonstrates that the suggested fuzzy control system has better capability in the presence of measurement errors, abrupt faults and unknown time-varying dynamics. The main limitation is that the actuator failures have not been considered. For our future studies, this problem in practical application is taken to account. .