Modeling seismic wave propagation in TTI media using multiaxial complex frequency shifted nearly perfectly matched layer method

Abstract

The nearly perfectly matched layer (NPML) is a non-split perfectly matched layer that directly transforms the wave field. Compared to other non-split perfectly matched layers, NPML is computationally efficient and has advantages such as not changing the form of the equation and being easy to implement. However, in TTI medium simulations it is found that the NPML is very unstable and cannot absorb near-grazing incident waves. This explains why the CPML is currently used more frequently. In this study, the complex frequency shifted transform is used to enhance the absorption of near-grazing incident waves with NPML and to avoid the generation of low-frequency singular values. At the same time, the double damping profile is used to improve the stability of the boundary we called MCFS-NPML. Subsequently, this method is also applied to seismic wave equations in poroelastic media. In order to further improve the absorption capacity of the boundary and weaken the deviation caused by the discrete difference, a new attenuation function is proposed.

Introduction

Anisotropy is widely found in subsurface media such as fractured reservoirs, dense shale formations, and mudstone formations. Thomsen (1986) proposed the Thomsen coefficient to represent this anisotropy Igel et al. (1995) and Dong et al. (1995) have performed forward modeling of anisotropic media using the staggered-grid finite difference method. Anisotropic seismic imaging is usually based on the vertical transversely isotropic (VTI) assumption, which is a good representation of the inherent anisotropy of shales in sedimentary basins (Tsvankin 2001). More complex tectonic environments involving tilted structures must account for a tilted symmetry axis in TTI media (Charles et al. 2008).

Special treatments are needed at the edges of the numerical model to absorb waves propagating outwardly when we simulate seismic wave propagation in TTI media. Such situations include paraxial conditions (e.g., Clayton and Engquist 1977; Engquist and Majda 1977; Reynolds 1978; Higdon 1991) and damping layers or sponge zones’ (e.g., Cerjan et al. 1985; Sochacki et al. 1987). However, all of the local conditions behave poorly under some circumstances, e.g., with spurious energy at grazing incidence or low-frequency energy at all angles of incidence. Berenger proposed the perfectly matched layer (PML) for electromagnetic equations, which has proven to be extremely efficient compared with classical conditions and has become very popular. The original model has been simplified and reformulated in terms of a split field with complex coordinate stretching (e.g., Chew and Weedon 1994; Collino and Monk 1998b) and interpreted as an artificial anisotropic medium (Sacks et al. 1995; Gedney 1996). The PML has been successfully applied to seismic wave modeling in elastic media (Chew and Liu 1996; Hastings et al. 1996), anisotropic media (Collino and Tsogka 2001), and poroelastic media (Zeng and Liu 2001). In addition, Komatitsch and Tromp have demonstrated the use of PML for the elastic wave equation written as a second-order system in displacement. This method splits each variable into two variables, requires high cost for memory storage, and is computationally inefficient. Furthermore, the split PML can generate large spurious reflections for near-grazing incident waves or low-frequency waves.

Kuzuoglu (1996) and Roden and Gedney (2000) proposed complex frequency shifted-PML (C-PML) in electromagnetic wave modeling. This method has been used in seismic wave modeling in elastic media (Komatitsch and Martin 2007) and poroelastic media (Martin et al. 2008). Drossaert and Giannopoulos (2007) used recursive integration to avoid convolution terms. Festa (2005) pointed out that the PML boundary will generate numerical instabilities when absorbing surface waves and Komatitsch and Martin (2007) used numerical simulation to demonstrate that C-PML does not solve all of the instability problems for elastic anisotropic media. Meza-Fajardo (2008) proved that traditional PML fails to satisfy strict asymptotic stability in both isotropic and anisotropic media and introduced attenuation factors operating simultaneously in multiple orthogonal directions; the result is called the multiaxial perfectly matched layer.

Cummer (2003) proposed the NPML by transforming the wave field directly. Unlike other PMLs, NPML does not change the form of the wave equation (Hu et al. 2007) and has the features of implementation simplicity and computational efficiency (Bérenger 2004). The NPML was used to solve various practical problems in electromagnetics (Ramadan 2005), and the method has been applied to seismic wave propagation in acoustic (Hu et al. 2007), elastic (Chen and Zhao 2011), and poroelastic media (Chen 2012).

In this paper, we extend the NPML to TTI media and poroelastic media. It is found that considerable energy is returned into the main domain in the form of spurious reflected waves at grazing incidence. The NPML is extremely unstable in some complex media and models. We give five simulation cases, all of which show unstable phenomena. Even though NPML has its own advantages in computing and application, C-PML is still mainly used in forward and inverse modeling.

The accumulation of seismic wave energy sends spurious energy back into the main domain under the long-time simulation, dramatically increases the number of false reflections, and makes the system unstable even make seismic wave simulation data unavailable. The purpose of this paper is to improve the stability and absorption performance of NPML. In this study, two mutually perpendicular damping profiles are used for NPML called M-NPML. However, the addition of the damping profiles generates false reflections. Therefore, a frequency-dependent term is introduced to M-NPML and the result is named complex frequency shifted-MNPML (MCFS-NPML). The resulting method is implemented to simulate seismic wave propagation in poroelastic media so as to study and verify the performance of MCFS-NPML. Finally, the MCFS-NPML is similar to other PMLs, in that it is impossible to avoid false reflections caused by discrete difference. In this paper, we also study the damping function with TTI media and propose a new decay function that can control the gradient value of the attenuation curve and enhance further the absorptive capacity of PML. Compared with NPML, MCFS-NPML introduced three additional factors (η, β, and P). We further study the influence of three factors on the new decay function and give a new scheme for the values of scaling factor and stability factor based on the attenuation function.

Methods

Governing equations

Assuming the external force is zero, the elastodynamics problem can be described by Cauchy's equation and generalized Hooke's law:

$$\rho \partial_{t}^{2} {{u}} = \nabla \cdot {{{\uptau}}},\,\,{{{\uptau}}} = {{C}}:{{E}},$$

(1)

where u is the displacement field, T is the stress tensor, E is the strain tensor and E = 1/2[▽u + (▽u)^T], ρ is the mass density, and C is the elastic coefficient tensor matrix. Velocity is the first-order derivative of displacement with respect to time. Equation 1 is transformed into a first-order velocity stress equation with a velocity variable:

$$\begin{gathered} \rho \partial_{t} {{v}} = \nabla \cdot {{{\uptau}}} \hfill \\ \partial_{t} {{{\uptau}}} = {{C}}:\nabla {{v}}. \hfill \\ \end{gathered}$$

(2)

The elastic matrix of the TTI medium can be obtained by rotating the elastic matrix of the VTI through a Bond transformation by a certain angle:

$$C_{{{\text{VTI}}}} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{21} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{31} } & {C_{32} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]$$

(3)

$$C_{{{\text{TTI}}}} = M_{\phi } M_{\theta } C_{{{\text{VTI}}}} M_{\theta }^{T} M_{\phi }^{T} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & {C_{14} } & {C_{15} } & {C_{16} } \\ {C_{21} } & {C_{22} } & {C_{23} } & {C_{24} } & {C_{25} } & {C_{26} } \\ {C_{31} } & {C_{32} } & {C_{33} } & {C_{34} } & {C_{35} } & {C_{36} } \\ {C_{41} } & {C_{42} } & {C_{43} } & {C_{44} } & {C_{45} } & {C_{46} } \\ {C_{51} } & {C_{52} } & {C_{53} } & {C_{54} } & {C_{55} } & {C_{56} } \\ {C_{61} } & {C_{62} } & {C_{64} } & {C_{64} } & {C_{65} } & {C_{66} } \\ \end{array} } \right].$$

(4)

θ and φ are the polarization and azimuth angles, respectively, and M_θ and M_φ are defined as follows:

$$M_{\theta } = \left[ {\begin{array}{*{20}c} {\cos^{2} \theta } & 0 & {\sin^{2} \theta } & 0 & { - \sin 2\theta } & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ {\sin^{2} \theta } & 0 & {\cos^{2} \theta } & 0 & {\sin 2\theta } & 0 \\ 0 & 0 & 0 & {\cos \theta } & 0 & {\sin \theta } \\ {\frac{1}{2}\sin 2\theta } & 0 & { - \frac{1}{2}\sin 2\theta } & 0 & {\cos 2\theta } & 0 \\ 0 & 0 & 0 & { - \sin \theta } & 0 & {\cos \theta } \\ \end{array} } \right]$$

(5)

$$M_{\phi } = \left[ {\begin{array}{*{20}c} {\cos^{2} \phi } & {\sin^{2} \phi } & 0 & 0 & 0 & { - \sin 2\phi } \\ {\sin^{2} \phi } & {\cos^{2} \phi } & 0 & 0 & 0 & {\sin 2\phi } \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\cos \phi } & {\sin \phi } & 0 \\ 0 & 0 & 0 & { - \sin \phi } & {\cos \phi } & 0 \\ {\frac{1}{2}\sin 2\phi } & { - \frac{1}{2}\sin 2\phi } & 0 & 0 & 0 & {\cos 2\phi } \\ \end{array} } \right].$$

(6)

To derive a new equation under the NPML, Eq. (2) is transformed into the frequency domain:

$$\begin{gathered} i\omega \rho {{V}}_{f} = \nabla \cdot {{T}} \hfill \\ i\omega {{T}} = {{C}}:\nabla {{V}}_{f}, \hfill \\ \end{gathered}$$

(7)

where V_f is the velocity component in the frequency domain, and T is the stress tensor in the frequency domain. The form of complex coordinate stretching (CCS) is (x direction):

$$\tilde{x}(x) = x - \frac{i}{\omega }\int\limits_{0}^{x} {\alpha (s)} {\text{d}}s$$

(8)

$$\partial \tilde{x} = \frac{1}{{s_{x} }}\partial x, \, s_{x} = 1 + \frac{{\alpha_{x} }}{i\omega }.$$

(9)

By substituting Eqs. (9) into (7), the equations after CCS transformation are obtained:

$$\begin{gathered} i\omega \rho {{V}}_{f} = \nabla \cdot {\overline{{T}}} \hfill \\ i\omega {{T}} = {{C}}:\nabla {\overline{{V}}}_{f} \hfill \\ {{\overline{T} = T/s}} \hfill \\ {\overline{{V}}}_{f} = {{V}}_{f} {{/s}}. \hfill \\ \end{gathered}$$

(10)

Combining Eqs. (9, 10) yields (taking T_xx as an example):

$$\left( {1 + \frac{{\alpha_{x} }}{i\omega }} \right)\overline{T}^{x}_{xx} = T_{xx}$$

(11)

$$i\omega \overline{T}^{x}_{xx} { + }\alpha_{x} \overline{T}^{x}_{xx} { = }i\omega T_{xx}.$$

(12)

In the same way, using the same method for other variables and converting back to the time domain:

$$\begin{gathered} \partial_{t} \rho {{v}} = \nabla \cdot {\overline{{\tau }}} \hfill \\ \partial_{t} {{{\uptau}}} = {{C}}:\nabla {\overline{{v}}}. \hfill \\ \end{gathered}$$

(13)

The variables after the transformation can be obtained with the following equation:

$$\begin{gathered} \partial_{t} \overline{\xi }^{m} + \alpha_{m} \overline{\xi }^{m} = \partial_{t} \xi ; \hfill \\ \xi = \tau_{xx} ,\tau_{zx} ,\tau_{zz} ,v_{x} ,v_{z} ;m = x,z. \hfill \\ \end{gathered}$$

(14)

In the staggered second-order leapfrog scheme, Eq. (14) can be discretized as:

$$\begin{gathered} \frac{{\left( {\bar{\xi }^{m} } \right)^{{k + 1/2}} - \left( {\bar{\xi }^{m} } \right)^{{k - 1/2}} }}{{\Delta t}} \hfill \\ + \alpha _{m} \frac{{\left( {\bar{\xi }^{m} } \right)^{{k + 1/2}} + \left( {\bar{\xi }^{m} } \right)^{{k - 1/2}} }}{2} \hfill \\ = \frac{{\left( {\xi ^{m} } \right)^{{k + 1/2}} - \left( {\xi ^{m} } \right)^{{k - 1/2}} }}{{\Delta t}}. \hfill \\ \end{gathered}$$

(15)

And we get:

$$\begin{aligned} \left( {\overline{\xi }^{m} } \right)^{k + 1/2} = &\, \frac{1}{{\frac{1}{\Delta t} + \frac{{\alpha_{m} }}{2}}} \times \left[ {\left( {\frac{1}{\Delta t} - \frac{{\alpha_{m} }}{2}} \right)\left( {\overline{\xi }^{m} } \right)^{k - 1/2} } \right. \\ & \left. { + \left( {\frac{1}{\Delta t}} \right)\left( {\xi^{m} } \right)^{k + 1/2} - \left( {\frac{1}{\Delta t}} \right)\left( {\xi^{m} } \right)^{k - 1/2} } \right]. \\ \end{aligned}$$

(16)

From Eq. (13), we can see that the form of the reformulated wave equations with NPML has not changed and we are able to find the auxiliary variables. Then, we can use Eq. (14) to update the variables.

Complex frequency shifted-NPML (CFS-NPML)

The NPML is obtained using complex frequency shifted transformation, and the complex frequency shifted transformation equation is modified as follows:

$$s_{x} (x) = \beta_{x} (x) + \frac{{\alpha_{x} (x)}}{{\eta_{x} (x) + i\omega }}.$$

(17)

Comparing Eqs. (17, 9), the 1 on the right side of Eq. (9) becomes a function related to x and is called the scaling factor (β_x). Adding a frequency shifted factor to the denominator (η_x) and transforming Eqs. (7) with (17) yields:

$$[\eta_{x} (x) + i\omega ]\beta_{x} (x)\overline{T}_{xx}^{x} + \alpha_{x} (x)\overline{T}_{xx}^{x} = [\eta_{x} (x) + i\omega ]T_{xx}$$

(18)

$$[\eta_{x} (x)\beta_{x} (x){ + }\alpha_{x} (x)]\overline{T}_{xx}^{x} + i\omega \beta_{x} (x)\overline{T}_{xx}^{x} { = }\,\eta_{x} (x)T_{xx} + i\omega T_{xx}.$$

(19)

Converting back to the time domain, one obtains:

$$[\eta_{x} (x)\beta_{x} (x){ + }\alpha_{x} (x)]\overline{\tau }_{xx}^{x} + \beta_{x} (x)\partial_{t} \overline{\tau }_{xx}^{x} { = }\,\eta_{x} (x)\tau_{xx} + \partial_{t} \tau_{xx}.$$

(20)

Using the same method for the remaining variables, we obtain the transformation equation:

$$\begin{gathered} [\eta_{m} \beta_{m} { + }\alpha_{m} ]\overline{\xi }^{m} + \beta_{m} \partial_{t} \overline{\xi }^{m} { = }\,\eta_{m} \xi + \partial_{t} \xi ; \hfill \\ \xi = \tau_{xx} ,\tau_{zx} ,\tau_{zz} ,v_{x} ,v_{z} ;\,m = x,z. \hfill \\ \end{gathered}$$

(21)

Replacing Eqs. (14) with (21), we obtain a wave equation based on CFS-NPML. Same to Eq. (14), we can deduce the following discrete scheme:

$$\begin{gathered} [\eta_{m} \beta_{m} + \alpha_{m} ]\frac{{\left( {\overline{\xi }^{m} } \right)^{k + 1/2} + \left( {\overline{\xi }^{m} } \right)^{k - 1/2} }}{2} + \beta_{m} \frac{{\left( {\overline{\xi }^{m} } \right)^{k + 1/2} - \left( {\overline{\xi }^{m} } \right)^{k - 1/2} }}{\Delta t} \hfill \\ =\, \eta_{m} \frac{{\left( {\xi^{m} } \right)^{k + 1/2} + \left( {\xi^{m} } \right)^{k - 1/2} }}{2} + \frac{{\left( {\xi^{m} } \right)^{k + 1/2} - \left( {\xi^{m} } \right)^{k - 1/2} }}{\Delta t} \hfill \\ \end{gathered}$$

(22)

and

$$\begin{aligned} \left( {\bar{\xi }^{m} } \right)^{{k + 1/2}} = & \frac{1}{{\frac{{\beta _{m} }}{{\Delta t}} + \frac{{\eta _{m} \beta _{m} + \alpha _{m} }}{2}}} \times \left[ {\left( {\frac{{\beta _{m} }}{{\Delta t}} - \frac{{\eta _{m} \beta _{m} + \alpha _{m} }}{2}} \right)} \right. \\ & \left( {\bar{\xi }^{m} } \right)^{{k - 1/2}} + \left( {\frac{1}{{\Delta t}} + \frac{{\eta _{m} }}{2}} \right)\left( {\xi ^{m} } \right)^{{k + 1/2}} \\ & \left. { + \left( {\frac{{\eta _{m} }}{2} - \frac{1}{{\Delta t}}} \right)\left( {\xi ^{m} } \right)^{{k - 1/2}} } \right]. \\ \end{aligned}$$

(23)

Multiaxial complex frequency shifted-NPML (MCFS-NPML)

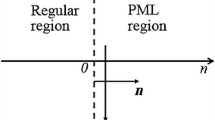
As Fig. 1 shows, in region 1, α_z = α_z^(z) and α_x = 0. In this region, the damping factor increases exponentially in the primary direction, but the value is 0 in the direction perpendicular to the primary direction. In region 3, the damping profiles at the right and top overlap; thus, there are two mutually perpendicular damping profiles. Therefore, it is only necessary to treat regions 1 and 2 when introducing a new profile:

$$\begin{gathered} \alpha_{z} = \alpha_{z}^{\left( z \right)} (z), \, \alpha_{x} = \alpha_{x}^{\left( z \right)} (z) \hfill \\ \alpha_{x}^{\left( z \right)} (z) = p^{(x/z)} \alpha_{z}^{\left( z \right)} (z). \hfill \\ \end{gathered}$$

(24)

Fig. 1

Schematic of different PML layers

As shown in Eq. (24), the primary direction in region 1 is the z direction. The value of α_x is no longer zero and is proportional to the original damping function, and the proportional coefficient P^(x/z) is the stability factor. The multiaxial NPML (M-NPML) is derived below:

$$\begin{gathered} \partial_{t} \overline{\xi }^{z} + \alpha_{z}^{z} \overline{\xi }^{z} = \partial_{t} \xi \hfill \\ \partial_{t} \overline{\xi }^{x} + \alpha_{x}^{(z)} \overline{\xi }^{x} = \partial_{t} \xi = \partial_{t} \overline{\xi }^{x} + p^{(x/z)} \alpha_{z}^{\left( z \right)} \overline{\xi }^{x}. \hfill \\ \end{gathered}$$

(25)

For CFS-NPML, the processing in regions 1 and 2 is different from that of NPML. The transformation function is as follows:

$$\left\{ {\begin{array}{*{20}l} {s_{z} (z) = \beta_{z} (z) + \frac{{\alpha_{z}^{(z)} (z)}}{{\eta_{z} (z) + i\omega }};\, \bot {\text{PML}}} \hfill \\ {s_{x} (x) = 1 + \frac{{\alpha_{x}^{(z)} (x)}}{i\omega };\,\parallel {\text{PML}}}. \hfill \\ \end{array} } \right.$$

(26)

Substituting Eqs. (26) into (10), one obtains:

$$\begin{gathered} \partial_{t} \overline{\xi }^{z} + \alpha_{{_{z} }}^{x} \overline{\xi }^{z} = \partial_{t} \xi ;\,\parallel PML \hfill \\ \partial_{t} \overline{\xi }^{x} + \alpha_{{_{x} }}^{z} \overline{\xi }^{x} = \partial_{t} \xi ;\,\parallel PML \hfill \\ [\eta_{m} \beta_{m} + \alpha_{m}^{m} ]\overline{\xi }^{m} + \beta_{m} \partial_{t} \overline{\xi }^{m} = \eta_{m} \xi + \partial_{t} \xi ;\, \bot PML. \hfill \\ \end{gathered}$$

(27)

The above is the derivation process and transformation equation for NPML, M-NPML, and MCFS-NPML. The scaling factor and frequency shifted factor equations are as follows:

$$\beta_{x} = 1 + (\beta_{0} - 1)\left( {l/L} \right)^{{P_{\beta } }} ,\eta_{x} = \eta_{0} \pi f\left[ {1 - \left( {l/L} \right)^{{P_{\eta } }} } \right],$$

(28)

where L is the thickness of the NPML, and l is the distance between the calculated point and the inner boundary of the PML area. The value of the stability factor should be less than 1, and it changes depending on the complexity of the medium. It should not be too large or it will lead to an increase in the number of false reflections.

Absorption effect and stabilityr analysis

Absorption effect analysis

The solution to Eq. (1) has the following form:

$${{u = u}}_{0} \exp [i(\omega t - k_{x} \cdot x)].$$

(29)

When the complex frequency shifted transformation is performed, a new wave solution is obtained:

$${{u = u}}_{0} \exp \left[ { - {\text{i}}(k_{x} \cdot x - \omega t)} \right]\exp \left[ { - k_{x} /\omega \int\limits_{0}^{x} {\alpha_{x} (s){\text{d}}s} } \right].$$

(30)

The wave solution after the complex frequency shifted transformation (Eq. 30) has an additional term (not present in the original wave solution, Eq. 29) related to the damping function, and α_x grows exponentially. The wave solution decreases rapidly with the increase of the integral value of α_x, and finally tends to zero. From Eq. (30), we can see two problems that exist in the NPML. First, the ω in the denominator of the attenuation term produces a singular value when the incident wave frequency is very low and causes instability. Second, the absorption capacity of PML for waves is related to ∫α_x, and the integral value is related to the value of x. The waves with grazing incidence do not penetrate very deep in the PML, travel longer in a direction parallel to the layer, and cannot be absorbed effectively. At the same time, unabsorbed waves form dissipative waves in the boundary, resulting in instability. When η_x and β_x are introduced, the attenuation term is expressed as follows:

$$\exp \left[ { - \cos \theta /c\int\limits_{0}^{x} {\omega^{2} /(\eta_{x}^{2} + \omega^{2} )\alpha_{x} /\beta_{x} {\text{d}}s} } \right],$$

(31)

where u₀ is the polarization vector, k_x is the wave vector, k_x = cos θ/c, c is the phase velocity depending on the propagation direction, and θ is the angle between the normal direction of the wavefront and the x-axis. In Eq. (31), η_x in the denominator precludes the generation of singular values. β_x reduces the wave propagation speed and bends the wavefront toward the normal direction of the PML, thereby decreasing the slowness angle and increasing the damping of waves with near-grazing incidence angles (Zhang 2010).

Damping factor

Although the MCFS-NPML can enhance the absorption capacity, false reflections at the boundary are unavoidable because the boundary and damping factor are discretized and there are discrete differences between the two layers. The simplest solution to this problem is to increase the number of layers to weaken the discrete difference, but this increases storage space and reduces computing efficiency. The two most widely used decay functions are the exponential and the trigonometric decay function. The equation is defined as follows:

$$\left\{ \begin{gathered} \alpha (x) = \alpha_{0} (l/L)^{4} \hfill \\ \alpha_{0} = \frac{{3v_{p} \ln (1/R)}}{2L}, \hfill \\ \end{gathered} \right.$$

(32)

where L is the thickness of the PML, R is the theoretical reflection coefficient, vP is the P-wave velocity, and l is the distance between the target point and inner boundary. Groby improved the attenuation function in Eq. (32) as:

$$\alpha (x) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {l < 0} \hfill \\ {\ln (1/R)(l/L)^{n} \frac{{(n + 1)\sqrt {\mu /\rho } }}{2L}} \hfill & {l \ge 0}. \hfill \\ \end{array} } \right.$$

(33)

The damping function, in Eq. (33), is equal to Eq. (32) when n = 2. Chen (2010) proposed sine-type and cosine-type functions to increase the rate of growth of α at the interface boundary. The cosine-type function is:

$$\alpha (x) = B\left[ {1 - \cos \frac{\pi (L - l)}{{2L}}} \right].$$

(34)

The sine-type function is:

$$\alpha (x) = B\left( {1 - \sin \frac{\pi l}{{2L}}} \right),$$

(35)

where B is the attenuation amplitude factor.

As Fig. 2a, b show, the exponential function grows too rapidly at the inner boundary in the case of n = 1. Conversely, it grows too slowly at the interface boundary and too quickly at the outer boundary if n > 1. The rapid growth at the inner boundary limits wave propagation into the boundary. If the growth rate is too slow, the remaining energy is greater when the wave propagates to other parts of the boundary. Further, the discrete difference of α is large here, so spurious reflections will be enhanced. Therefore, Chen (2010) proposed sine-type and cosine-type functions with inner boundary growth rates between the exponential functions n = 1 and n = 2 in order to improve the absorption effect. To find the most favorable damping function for boundary absorption, it is necessary to design a function that can flexibly control the gradient values of each part. The new function is:

$$\begin{gathered} \alpha (x) = K[\alpha_{b} + \alpha_{e} ] \hfill \\ \alpha_{e} = \gamma \exp ( - \delta L/l), \hfill \\ \end{gathered}$$

(36)

where α_b is a basic function; it must be increased progressively from the inner boundary to the outer boundary. We can choose exponential functions, trigonometric functions, or other functions that satisfy this condition. The gradient value of α at each part of the boundary is mainly controlled by α_e. As shown in Fig. 2c, d the values of δ and γ were modified to observe their effects. The parameter δ controls the position of the maximum value of the gradient of αe, as shown in Fig. 2c. As the value of δ increases, the maximum moves toward the outer boundary and its value decreases. The other parameter γ controls the magnitude of the maximum in Fig. 2d. The coefficients δ and γ together control the position and value of the maximum so as to regulate the damping curve. As a result, we may fine tune the growth of each part of α to make it more conducive to absorption at the boundary and further diminish the number of spurious reflections caused by the discrete difference. To compare the effects of the two damping functions, Eq. (36) can be written as:

$$\begin{gathered} \alpha (x) = K[\alpha_{b} + \alpha_{e} ],K = \ln (1/R)\frac{{(n + 1)\sqrt {\mu /\rho } }}{2L} \hfill \\ \alpha_{b} = (l/L)^{n} ,\alpha_{e} = \gamma \exp ( - \delta L/l). \hfill \\ \end{gathered}$$

(37)

Fig. 2

Decay function curve and gradient curve of α_e

Stability analysis

For the stability factor, the introduced attenuation profile is orthogonal to the original attenuation profile and is capable of further absorbing the wave at the boundary, even a near-grazing incidence wave. The cluster energy remaining in the boundary will make PML unstable, send spurious energy back into the main domain, and reduce the absorption of the boundary.

Next, the role of stability factors in NPML was studied separately. In order to derive the stability of the entire system of equations, we must combine Eqs. (13, 30). It should be noted that, when α_x is 0, the equations under NPML are still written in the form of Eq. (1). The system can be cast in the following form:

$$\partial_{t} {{{\uppsi}}} = A_{x} \partial_{x} {{{\uppsi}}} + A_{z} \partial_{z} {{{\uppsi}}}$$

(38)

$${{{\uppsi}}} = [{{v}}_{x} \, {{v}}_{z} {{{\uptau}}}_{xx} {{{\uptau}}}_{zz} {{{\uptau}}}_{zx} ]^{T}.$$

(39)

Performing the Fourier transform on the space and merging the right side of the equation into one, we obtain:

$$\partial_{t} {{U}} = A{{U}}$$

(40)

$$U = \int\limits_{ - \infty }^{ + \infty } \psi \exp (ik_{x} x + ik_{z} z){\text{d}}x{\text{d}}z.$$

(41)

A has the following form:

$$A = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {\frac{1}{\rho }ik_{x} } \hfill & 0 \hfill & {\frac{1}{\rho }ik_{z} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\frac{1}{\rho }ik_{z} } \hfill & {\frac{1}{\rho }ik_{x} } \hfill \\ {C_{11} ik_{x} + C_{15} ik_{z} } \hfill & {C_{13} ik_{z} + C_{15} ik_{x} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {C_{13} ik_{x} + C_{35} ik_{z} } \hfill & {C_{33} ik_{z} + C_{35} ik_{x} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {C_{15} ik_{x} + C_{55} ik_{z} } \hfill & {C_{35} ik_{z} + C_{55} ik_{x} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right].$$

(42)

The coefficients matrix A is independent of the time variable, and system 40 is a linear time-invariant or autonomous system. Meanwhile, the matrix A is non-singular, and the only equilibrium point of the autonomous system is the origin U(t) = 0. We study the stability by investigating the behavior of the solutions close to the equilibrium points. The equilibrium solution at the origin U is asymptotically stable if all the eigenvalues have negative real parts. The eigenvalues are as follows:

$$ \sigma = \left\{ \begin{gathered} 0, \pm \frac{i}{\rho }\sqrt {\begin{array}{*{20}c} {(0.5(C_{11} + C_{55} )k_{x}^{2} \rho + (C_{15} + C_{35} )k_{x} k_{z} \rho + 0.5(C_{33} + C_{55} )k_{z}^{2} \rho } \\ {\sqrt[{ - 0.5}]{{\begin{array}{*{20}l} {((((C_{11} + C_{55} )k_{x}^{2} + 2(C_{15} + C_{35} )k_{x} k_{z} + (C_{33} + C_{55} )k_{z}^{2} ) - } \hfill \\ {4( - C_{15}^{2} k_{x}^{4} + C_{11} k_{x}^{2} (C_{55} k_{x}^{2} + k_{z} (2C_{35} k_{x} + C_{33} k_{z} )) + C_{15} } \hfill \\ {k_{x} k_{z} ( - 2C_{13} k_{x}^{2} + k_{z} (2C_{35} k_{x} + 2C_{33} k_{z} )) + k_{z}^{2} ( - C_{13}^{2} k_{x}^{2} + } \hfill \\ {( - C_{35}^{2} + C_{33} C_{55} )k_{z}^{2} + C_{13} k_{x} ( - 2C_{55} k_{x} - 2C_{35} k_{z} ))))\rho^{2} ))} \hfill \\ \end{array} }}} \\ \end{array} } \hfill \\ \pm \frac{i}{\rho }\sqrt {\begin{array}{*{20}c} {(0.5(C_{11} + C_{55} )k_{x}^{2} \rho + (C_{15} + C_{35} )k_{x} k_{z} \rho + 0.5(C_{33} + C_{55} )k_{z}^{2} \rho } \\ {\sqrt[{ + 0.5}]{{\begin{array}{*{20}l} {((((C_{11} + C_{55} )k_{x}^{2} + 2(C_{15} + C_{35} )k_{x} k_{z} + (C_{33} + C_{55} )k_{z}^{2} ) - } \hfill \\ {4( - C_{15}^{2} k_{x}^{4} + C_{11} k_{x}^{2} (C_{55} k_{x}^{2} + k_{z} (2C_{35} k_{x} + C_{33} k_{z} )) + C_{15} } \hfill \\ {k_{x} k_{z} ( - 2C_{13} k_{x}^{2} + k_{z} (2C_{35} k_{x} + 2C_{33} k_{z} )) + k_{z}^{2} ( - C_{13}^{2} k_{x}^{2} + } \hfill \\ {( - C_{35}^{2} + C_{33} C_{55} )k_{z}^{2} + C_{13} k_{x} ( - 2C_{55} k_{x} - 2C_{35} k_{z} ))))\rho^{2} ))} \hfill \\ \end{array} }}} \\ \end{array} } \hfill \\ \end{gathered} \right\} $$

(43)

The four nonzero eigenvalues in 43 correspond to the propagating quasi-S and quasi-P modes and the real part of all eigenvalues is zero. Based on this, we may study the change of eigenvalues after introducing the boundary in order to understand the change in its stability. We write the transformation equations and wave equations in the form of Eq. (40). After adding NPML, Eq. (38) is written as follows:

$$\partial_{t} {{{\uppsi}}} = A_{x} \partial_{x} {{{\uppsi}}} + A_{z} \partial_{z} {{{\uppsi}}} + A_{t} \partial_{t} {{{\uppsi}}} + A_{c} {{{\uppsi}}}.$$

(44)

Because there are partial derivatives of time variables on both sides of the equation, it cannot be written in the form of Eq. (40) directly and Eq. (44) must be modified:

$$\partial_{t} {{U}}^{n} = A^{n} {{U}}^{n}$$

(45)

$$U^{n} = \int\limits_{ - \infty }^{ + \infty } {{{{\uppsi}}}^{n} } \exp (ik_{x} x + ik_{z} z){\text{d}}x{\text{d}}z$$

(46)

$$\begin{gathered} {{{\uppsi}}}^{n} = [{{v}}_{x} \, {{v}}_{z} {{{\uptau}}}_{xx} {{{\uptau}}}_{zz} {{{\uptau}}}_{zx} \, {{v}}_{x}^{x} {{ - v}}_{x} \, {{v}}_{x}^{z} {{ - v}}_{x} \, {{v}}_{z}^{x} {{ - v}}_{z} \hfill \\ {{v}}_{z}^{z} {{ - v}}_{z} {{{\uptau}}}_{xx}^{x} {{ - \tau }}_{xx} {{{\uptau}}}_{zz}^{z} {{ - \tau }}_{zz} {{{\uptau}}}_{zx}^{x} {{ - \tau }}_{zx} {{{\uptau}}}_{zx}^{z} {{ - \tau }}_{zx} ]^{T}. \hfill \\ \end{gathered}$$

(47)

The coefficients matrix Aⁿ is shown in Appendix B (Eqs. 60, 61).

After applying a Fourier transform and introducing the stability factor, we obtain the system of Eq. (45) for the M-NPML. The eigenvalues for NPML with no α are as follows:

$$\sigma = \left\{ {\begin{array}{*{20}l} {0^{(9)} , \pm \frac{i}{\rho }\sqrt {\begin{array}{*{20}c} {(0.5(C_{11} + C_{55} )k_{x}^{2} \rho + (C_{15} + C_{35} )k_{x} k_{z} \rho + 0.5(C_{33} + C_{55} )k_{z}^{2} \rho } \\ { - 0.5\sqrt {\begin{array}{*{20}l} {((((C_{11} + C_{55} )k_{x}^{2} + 2(C_{15} + C_{35} )k_{x} k_{z} + (C_{33} + C_{55} )k_{z}^{2} ) - } \hfill \\ {4( - C_{15}^{2} k_{x}^{4} + C_{11} k_{x}^{2} (C_{55} k_{x}^{2} + k_{z} (2C_{35} k_{x} + C_{33} k_{z} )) + C_{15} } \hfill \\ {k_{x} k_{z} ( - 2C_{13} k_{x}^{2} + k_{z} (2C_{35} k_{x} + 2C_{33} k_{z} )) + k_{z}^{2} ( - C_{13}^{2} k_{x}^{2} + } \hfill \\ {( - C_{35}^{2} + C_{33} C_{55} )k_{z}^{2} + C_{13} k_{x} ( - 2C_{55} k_{x} - 2C_{35} k_{z} ))))\rho^{2} ))} \hfill \\ \end{array} } } \\ \end{array} } } \hfill \\ { \pm \frac{i}{\rho }\sqrt {\begin{array}{*{20}c} {(0.5(C_{11} + C_{55} )k_{x}^{2} \rho + (C_{15} + C_{35} )k_{x} k_{z} \rho + 0.5(C_{33} + C_{55} )k_{z}^{2} \rho } \\ { + 0.5\sqrt {\begin{array}{*{20}l} {((((C_{11} + C_{55} )k_{x}^{2} + 2(C_{15} + C_{35} )k_{x} k_{z} + (C_{33} + C_{55} )k_{z}^{2} ) - } \hfill \\ {4( - C_{15}^{2} k_{x}^{4} + C_{11} k_{x}^{2} (C_{55} k_{x}^{2} + k_{z} (2C_{35} k_{x} + C_{33} k_{z} )) + C_{15} } \hfill \\ {k_{x} k_{z} ( - 2C_{13} k_{x}^{2} + k_{z} (2C_{35} k_{x} + 2C_{33} k_{z} )) + k_{z}^{2} ( - C_{13}^{2} k_{x}^{2} + } \hfill \\ {( - C_{35}^{2} + C_{33} C_{55} )k_{z}^{2} + C_{13} k_{x} ( - 2C_{55} k_{x} - 2C_{35} k_{z} ))))\rho^{2} ))} \hfill \\ \end{array} } } \\ \end{array} } } \hfill \\ \end{array} } \right\}.$$

(48)

There are 13 eigenvalues and five of the eigenvalues are identical to those given in Eq. (43) for the undamped system. The additional eight eigenvalues that are equal to zero are introduced. Next, we obtain the eigenvalues of the matrix Aⁿ:

$$\sigma = \left\{ \begin{gathered} 0^{(5)} ,{\text{Root}}\frac{1}{\rho }[a_{9} \sigma^{8} + a_{8} \sigma^{7} + a_{7} \sigma^{6} + a_{6} \sigma^{5} + \hfill \\ a_{5} \sigma^{4} + a_{4} \sigma^{3} + a_{3} \sigma^{2} + a_{2} \sigma^{1} + a_{1} ] \hfill \\ \end{gathered} \right\},$$

(49)

where the coefficient a is shown in Appendix B (Eq. 62).

After introducing α, only five eigenvalues remain. There are no general closed-form expressions for the remained of the eight eigenvalues, because they are the roots of the eighth-order polynomial in Eq. (49). We forecast the direction on the complex plane in which those eight eigenvalues would move due to the introduction of α after applying the eigenvalue sensitivity analysis (Adhikari and Friswell 2001). The method consists of obtaining the first derivatives of the eigenvalues with respect to α, evaluated at the point at which that α is zero. All eigenvalues have a zero-valued real part when the α is zero. Therefore, if the real part of the first derivatives for all eigenvalues is greater than 0, a small α will induce motion of the eigenvalues toward the positive half complex plane, causing the system to become unstable. Conversely, if the real part of the first derivatives is less than 0, the system is asymptotically stable.

$$\begin{aligned} \left. {\frac{{d\sigma }}{{d\alpha _{x} }}} \right|_{{\alpha _{x} = 0}} = & - \frac{1}{Q}\left( {\rho \left( {2\sigma _{u} ^{4} \left( {1 + p^{{(z/x)}} } \right)} \right.} \right. \\ & + \sigma _{u} ^{2} \rho C_{{11}} k_{x} ^{2} \left( {1 + 2p^{{(z/x)}} } \right) \\ & + k_{z} (3C_{{15}} k_{x} \left( {1 + p^{{(z/x)}} } \right) + 3C_{{35}} k_{x} \left( {1 + p^{{(z/x)}} } \right) \\ & \left. { + C_{{33}} k_{z} \left( {2 + p^{{(z/x)}} } \right)} \right) + C_{{55}} \left( {k_{z} ^{2} \left( {2 + p^{{(z/x)}} } \right)} \right. \\ & + k_{x} ^{2} \left. {\left. {\left( {1 + 2p^{{(z/x)}} } \right)} \right)} \right) + \rho ^{2} \left( { - 2\left( {C_{{35}} ^{2} - C_{{33}} C_{{55}} } \right)k_{z} ^{4} } \right. \\ & + C_{{15}} k_{x} k_{z} ^{2} \left( {2C_{{35}} k_{x} + 3C_{{33}} k_{z} } \right) + C_{{15}} k_{x} \left( { - 2C_{{15}} k_{x} ^{3} } \right. \\ & \left. { + k_{z} ^{2} \left( {2C_{{35}} k_{x} + C_{{33}} k_{z} } \right)} \right)p^{{(z/x)}} - C_{{13}} ^{2} k_{x} ^{2} k_{z} ^{2} \left( {1 + p^{{(z/x)}} } \right) \\ & + C_{{11}} k_{x} ^{2} \left( {2C_{{55}} k_{x} ^{2} p^{{(z/x)}} + C_{{33}} k_{z} ^{2} \left( {1 + p^{{(z/x)}} } \right)} \right. \\ & \left. { + C_{{35}} k_{z} k_{x} \left( {1 + 3p^{{(z/x)}} } \right)} \right) - C_{{13}} k_{x} k_{z} \\ & \left( {C_{{15}} k_{x} ^{2} \left( {1 + 3p^{{(z/x)}} } \right) + k_{z} \left( {2C_{{55}} k_{x} \left( {1 + p^{{(z/x)}} } \right)} \right.} \right. \\ & \left. {\left. {\left. {\left. {\left. { + C_{{35}} k_{z} \left( {1 + p^{{(z/x)}} } \right)} \right)} \right)} \right)} \right)} \right) \\ \end{aligned}$$

$$\begin{aligned} \left. {\frac{{d\sigma }}{{d\alpha _{z} }}} \right|_{{\alpha _{z} = 0}} = & - \frac{1}{Q}\left( {\rho \left( {2\sigma _{u} ^{4} \left( {1 + p^{{(x/z)}} } \right)} \right.} \right. \\ & + \sigma _{u} ^{2} \rho C_{{11}} k_{x} ^{2} \left( {2 + p^{{(x/z)}} } \right) + k_{z} \left( {3(C_{{15}} + C_{{35}} )k_{x} } \right. \\ & \left. { + C_{{33}} k_{z} + 3(C_{{15}} + C_{{35}} )k_{x} p^{{(x/z)}} + 2C_{{33}} k_{z} p^{{(x/z)}} } \right) \\ & \left. {\left. { + C_{{55}} (k_{z} ^{2} (1 + 2p^{{(x/z)}} ) + k_{x} ^{2} (2 + p^{{(x/z)}} )} \right)} \right) \\ & + \rho ^{2} \left( { - 2C_{{15}} ^{2} k_{x} ^{4} + C_{{11}} k_{x} ^{2} \left( {2C_{{55}} k_{x} ^{2} } \right.} \right. \\ & \left. { + C_{{33}} k_{z} ^{2} \left( {1 + p^{{(x/z)}} } \right) + C_{{35}} k_{z} k_{x} \left( {3 + p^{{(x/z)}} } \right)} \right) \\ & + C_{{15}} k_{x} k_{z} \left( { - C_{{13}} k_{x} ^{2} \left( {3 + p^{{(x/z)}} } \right) + k_{z} \left( {2C_{{35}} k_{x} \left( {1 + p^{{(x/z)}} } \right)} \right.} \right. \\ & \left. {\left. {\left. { + C_{{33}} k_{z} \left( {1 + 3p^{{(x/z)}} } \right)} \right)} \right)} \right) + k_{z} ^{2} \left( { - 2\left( {C_{{35}} ^{2} - C_{{55}} C_{{33}} } \right)k_{z} ^{2} p^{{(x/z)}} } \right. \\ & - C_{{13}} ^{2} k_{x} ^{2} \left( {1 + p^{{(x/z)}} } \right) - C_{{13}} k_{x} \left( {2C_{{55}} k_{x} \left( {1 + p^{{(x/z)}} } \right)} \right. \\ & \left. {\left. {\left. {\left. { + C_{{35}} k_{z} \left( {1 + 3p^{{(x/z)}} } \right)} \right)} \right)} \right)} \right) \\ \end{aligned}$$

$$\begin{aligned} Q = & 4\sigma _{u} ^{4} + 3\left( {(C_{{11}} + C_{{55}} )k_{x} ^{2} + 2(C_{{15}} + C_{{35}} )k_{x} k_{z} } \right. \\ & \left. { + (C_{{33}} + C_{{55}} )k_{z} } \right)\sigma _{u} ^{2} \rho + 2\left( {( - C_{{15}} ^{2} + C_{{11}} C_{{55}} )k_{x} ^{4} } \right. \\ & + 2( - C_{{13}} C_{{15}} + C_{{11}} C_{{35}} )k_{x} ^{3} k_{z} + \left( {C_{{11}} C_{{33}} + 2C_{{15}} C_{{35}} } \right. \\ & \left. { - C_{{13}} (C_{{13}} + 2C_{{55}} )} \right)k_{x} ^{2} k_{z} ^{2} + 2( - C_{{13}} C_{{35}} + C_{{15}} C_{{33}} )k_{z} ^{3} k_{x} \\ & \left. { + ( - C_{{35}} ^{2} + C_{{33}} C_{{55}} )k_{x} ^{4} )\rho ^{2} } \right) \\ \end{aligned}$$

(50)

As shown in Eq. (50), eigenvalues are related to the elastic coefficient tensor, direction of wave propagation, and stability factors. Substituting Eqs. (51) into (47), we eliminate the wave number:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{u} = \frac{{\sigma_{u} }}{\left| k \right|},n_{x} = \frac{{k_{x} }}{\left| k \right|},n_{z} = \frac{{k_{z} }}{\left| k \right|}.$$

(51)

Introducing the small α in the elastodynamic equation causes the system to become unstable. The eigenderivatives are determined by the elastic constants, the direction of propagation, and the ratios p^(x/z) and p^(z/x). The eigenvalue sensitivity curve and the eigenderivatives equation at a specific angle are given below:

$$\begin{aligned} \left. {Qp:\frac{{d\sigma }}{{d\alpha _{z} }}} \right|_{{\alpha _{z} = 0}} = & - 1.68859 \times 10^{{ - 20}} \left( { - 4.45842 \times 10^{{16}} } \right. \\ & + 1.18442 \times 10^{{23}} p^{{(x/z)}} - 5.16756 \\ & \left. { \times 10^{{16}} \left( {0.5 + p^{{(x/z)}} } \right)} \right) \\ \left. {\frac{{d\sigma }}{{d\alpha _{z} }}} \right|_{{\alpha _{z} = 0}} = & - 199.999(p^{{(x/z)}} = 0.1,n_{x} = 0) \\ \left. {\frac{{d\sigma }}{{d\alpha _{z} }}} \right|_{{\alpha _{z} = 0}} = & - 599.999(p^{{(x/z)}} = 0.3,n_{x} = 0) \\ \left. {\frac{{d\sigma }}{{d\alpha _{z} }}} \right|_{{\alpha _{z} = 0}} = & 0.00118914(p^{{(x/z)}} = 0,n_{x} = 0). \\ \end{aligned}$$

(52)

In the case of M-NPML for anisotropic media, the difference in eigenderivatives corresponding to the quasi-S, quasi-P modes and the situation of σ = 0 is small, and their curves basically overlap in Fig. 3. To observe the effect of p^(x/z), we utilize the eigenderivatives equation (Eq. 52) related to quasi-P mode when the angle of incidence is 90°. As Eq. (52) shows, the value of eigenderivative is greater than 0 with p^(x/z) = 0. When we introduce the α, the eigenvalues move toward the positive half complex plane and the system is unstable. After introducing the p^(x/z), the eigenvalues will tend to move toward the negative half complex plane and the p^(x/z) can enhance the stability of the system. As shown in Eq. (52) and Fig. 3, the larger the p^(x/z), the farther the first derivative is from 0 on the negative half complex plane. This ensures that, when the attenuation factor is introduced, the real part of the eigenvalue does not move to the positive half complex plane.

Fig. 3

M-NPML eigenderivatives for TI media

Numerical tests results and discussion

Model 1 (normal incidence)

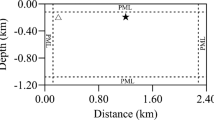
We applied several PMLs and damping factors to the simulations of seismic waves. The time step used is 0.6 ms, and the source-time function is a Ricker wavelet with a center frequency of 25 Hz. We consider two models to study the propagations of waves at normal incidence and grazing incidence. The grid spacing is 5 m, and the size of the first model is 1100 × 1100 m. The elastic parameters of TI media, C11, C33, C13, C44, and C66, are 26.4 × 10⁹ N/m², 15.6 × 10⁹ N/m², 6.11 × 10⁹ N/m², 4.38 × 10⁹ N/m², and 6.84 × 10⁹ N/m², respectively. The polarization and azimuth angles are 60° and 25°. The source is applied at (550, 550) m, 10 cells away from the PML-interior interface.

The snapshots in Fig. 4 of the v_x component correspond to various NPMLs and two damping functions. The rightmost snapshots marked with ‘#’ are wavefield simulations obtained with the new damping function. The maps in Fig. 4b labeled solely with the stability factor P correspond to M-NPML, those marked with frequency shifted factor (η) or scaling factor (β) (Fig. 4c and d) are snapshots obtained with CFS-NPML, and those in Fig. 4e marked with all three factors correspond to the MCFS-NPML. From a comparison of Fig. 4b and d, it is clear that the stability factor and scaling factor have little effect on the spurious reflections of the wave field at normal incidence. Fortunately, the frequency shifted factor can significantly reduce false reflections at the boundary and, the larger the factor value, the better the absorption effect. As shown in Fig. 4c and e, the absorption effect of MCFS-NPML is similar to that of CFS-NPML with the same η, and this confirms that the effect of stability and scale factors on absorption is weak. The absorption effect of all boundaries was further improved when the α was replaced by Eq. (32).

Fig. 4

Wavefield snapshots. a NPML. b M-NPML includes the stability factors p^(x/z) and p^(z/x). c CFS-NPML includes the frequency shifted factor (η). d CFS-NPML includes the scaling factor (β). e MCFS-NPML includes p^(x/z), p^(z/x), η and β simultaneously

Model 2 (grazing incidence)

Next, we design another model to study the propagation of waves at grazing incidence.

Compared with Figs. 4 and 5, there is a large false reflection at the upper boundary of Fig. 5, which is caused by large angle incidence and is consistent with the conclusion of Eq. (26). The seismic waves at grazing incidence cannot be absorbed along the edges of the model and generate dissipative waves. The accumulation of seismic wave energy sends spurious energy back into the main domain, dramatically increases the number of false reflections, and makes the system unstable. There is little change inside the upper PML layers resulting from the application of the new damping factor, because the false reflection enhancement and instability at grazing incidence are problems inherent in CCS transformation and have little to do with the attenuation function in this case.

Fig. 5

source location parameters. The size of the model is 2600 × 600 m, the source is applied at (130055)m, and the waves propagate along a path nearly parallel to the boundary

Wavefield snapshots. This model adopts parameters similar to those used for the normal incidence model, except for the size and

When we introduce the stability factors p^(x/z) and p^(z/x), the accumulated cluster energy inside the upper NPML layers is diminished and, the larger the stability factors, the more the residual energy in the boundary is reduced. However, the stability factors also increase the number of false reflections in this case. Although introduction of the factors can enhance the absorption of energy, the use of the damping profile corresponding to the stability factor prevents the waves from propagating into NPML layers to a certain degree; the larger the angle, the stronger is the energy of false reflections. When the parameter η is introduced, the energy in the boundary and the false reflections returning into the main domain are greatly weakened; the β can suppress the instability in NPML. When the p, η, and β are introduced simultaneously, not only is the false reflection weakened, but the residual energy in the boundary is also the weakest observed. The new damping function attenuates false reflections in all cases but strengthens the residual energy inside the upper NPML layers.

The energy decay curve corresponds to the second model in Fig. 6, and the dashed and solid lines correspond to the energy curves of the entire domain and main domain, respectively. The difference between the two curves represents the energy remaining inside the NPML layers. If the stability factor is large, the two curves appear to be nearly identical, as Fig. 6a shows. The divergence point of the energy curves demonstrates the effect of the scaling factor in repressing instability. The scaling factor dramatically improves the stability of the boundary but, when it is set to a large value, it will generate energy disturbances in the second half of the decay curve; this means that it will bring about another unstable phenomenon while enhancing the boundary stability. In the meantime, the difference between the two curves is still large, and only the stability factor can eliminate the residual energy and suppress the energy disturbance caused by the parameter η. Similarly, the parameter η resolves the problem of enhanced false reflections caused by the stability factor.

Fig. 6

Energy decay curves. a NPML and M-NPML. b CFS-NPML includes the frequency shifted factor (η). c CFS-NPML includes the scaling factor (β). d MCFS-NPML, M-NPML and CFS-NPML

We present the results of numerical tests with the two damping functions in Fig. 7. Although the new α can weaken the false reflections, the residual energy inside the NPML layers is higher than that of the original α after introduction of P and β in model 2. For this reason, we treat P and η specially and the problem is solved. First, the P parameter prevents the waves from propagating into NPML layers in a direction approximately parallel to the boundary. Therefore, P must be as small as possible while still ensuring the stability of the system. The new damping function moderates the attenuation profile perpendicular to the boundary direction, allowing more effective absorption of seismic waves by fine-tuning the gradient of the function. After fine-tuning, the new function increases faster than does the original function at the inner boundary. As a consequence, the new damping profile approximately parallel to the boundary further hinders waves from entering the layers and raises the second half of the decay curve above that of the original function in Fig. 7a and b. In this paper, γ in the additional profile is set to 0 and the results in Fig. 7c marked with ‘*’ demonstrate that this method is effective. We must rewrite Eq. (20) when using the new α:

$$\begin{gathered} \alpha_{z} { = }\,\alpha_{z}^{\left( z \right)} (z), \, \alpha_{z}^{\left( z \right)} = K[\alpha_{b} + \alpha_{e} ],K = \ln (1/R)\frac{{(n + 1)\sqrt {\mu /\rho } }}{2L} \hfill \\ \alpha_{b} = (l/L)^{n} ,\alpha_{e} = \gamma \exp ( - \delta L/l) \hfill \\ \alpha_{x} = \alpha_{x}^{\left( z \right)} (z),\alpha_{x}^{\left( z \right)} (z) = p^{(x/z)} \ln (1/R)\frac{{(n + 1)\sqrt {\mu /\rho } }}{2L}(l/L)^{n}. \hfill \\ \end{gathered}$$

(53)

Fig. 7

Energy decay curves. a Total energy. b Energy of main domain. c Total energy in α, new α and new α with special treatment

As shown in Fig. 7a and b, if we apply the β as in Eq. (28) and use the new damping function, the total energy curve rises above that of the original function and the main domain energy curve is lower. A combination of Eqs. (28, 36) results in a new equation for β:

$$\begin{gathered} \beta_{x} = 1 + (\beta_{0} - 1)\left( {\alpha_{b} + \alpha_{e} } \right)^{{P_{\beta } }} , \hfill \\ \alpha_{b} = \left( {l/L} \right)^{{P_{\beta } }} ,\alpha_{e} = \gamma \exp ( - \delta L/l). \hfill \\ \end{gathered}$$

(54)

The test results using Eq. (53) are shown in Fig. 7c and marked with ‘*’, and the energy in the NPML layers is suppressed. The phenomenon of instability accompanied by strong false reflections occurs, not only in seismic wave simulation in TTI media, but also in different media and models.

Model 3 (Marmousi model in an elastic isotropic medium)

Next, the wave equations and simulation results in other media or models are presented to verify the importance of MCFS-NPML.

Figure 8 depicts simulation results derived from application of the Marmousi model in an elastic isotropic medium. We take a snapshot of the wave field in part of the region, and the figures from left to right correspond to several NPMLs identified from top to bottom in the inset box in Fig. 8c. The wave field energy marked with the blue oval begins to accumulate after a certain period of time and returns to the main domain with the NPML. This simulation corresponding to the black energy curve in Fig. 8c begins to diverge at a time of about 4 s. The other three NPMLs can suppress the system instability, and only the introduction of the stability factor can completely clear the energy disturbance in NPML layers; this is shown by the area marked with a red rectangle in Fig. 8b. Regardless of the values of β and η for CFS-NPML, large amounts of wave energy exist inside the upper NPML layers and they cause a certain degree of instability. However, as shown in the red ellipses, the false reflection is still strong prior to the introduction of the stability factor and it weakens considerably with CFS-NPML and MCFS-NPML. The false waves caused by instability and boundary reflection seriously interfere with experimental results, so we must introduce the NPML boundary and all three factors at the same time (MCFS-NPML).

Fig. 8

Wavefield snapshots and energy decay curves

Model 4 (poroelastic VTI medium)

The theory of seismic wave propagation in a poroelastic medium is described by Biot’s theory (Biot 1962). We provide the first-order partial differential equations for poroelastic VTI media after applying the MCFS-NPML in Appendix C.

Here the time step is 0.5 ms, and the source-time function is a Ricker wavelet with a center frequency of 40 Hz. The grid spacing is 5 m, and the size of the first model is 3100 × 600 m. vp, vs, ζ, γ, and δ are 4167 m/s, 2612 m/s, 0.17, 0.16, and − 0.2, respectively. Values of ρf, ρs, and ρa are 1040 kg/m³, 2500 kg/m³, and 200 kg/m³, respectively. The values of bx and bz are 7.45 kg·m⁻³·s⁻¹ and 3 kg·m⁻³·s⁻¹. Q1, Q3, and R are 2.15 × 10⁹ kg·m⁻¹·s⁻², 2.45 × 10⁹ kg·m⁻¹·s⁻², and 1 × 10⁹ kg·m⁻¹·s⁻². The source is applied at (1550, 55) m, 10 cells away from the PML-interior interface.

In Fig. 9, the NPML is unstable and has strong false reflection for near-grazing incident waves, especially the slow P-waves. However, the MCFS-NPML can suppress instability and enhance absorption. This demonstrates that the MCFS-NPML is highly effective for seismic wave modeling in poroelastic VTI media, as it is in elastic isotropic and TTI media.

Fig. 9

Wavefield snapshots and energy decay curves in poroelastic VTI media

Model 5 (free surface)

Free surface conditions were used for the upper surface, and NPML was used for the left, right, and bottom boundaries. The size of this model is 1330 × 2660 m, and homogeneous medium model has the same parameters as model 1 (Fig. 10). The parameters of the anticline model are shown in Table 1

Table 1 The anticline model parameters

.

Fig. 10

The anticline model

Compared with Fig. 5, because the surface is simulated by free surface conditions, surface waves are generated at the upper boundary shown by the area marked with a blue rectangle in Fig. 11a.

Fig. 11

Wavefield snapshots. a, c, e, g, NPML. b, d, f, h MCFS-NPML p = 0.05, η₀ = 3 and β₀ = 2. a, b, e, f 0.36 s. c, d, g, h 0.84 s

Such a boundary model is more consistent with the actual situation of seismic wave propagation, but for NPML, there are still problems of poor absorption effect and instability. When the seismic wave propagation is simulated for a long time, the unstable energy accumulation in the boundary will return to the main domain and pollute the whole wave field. Therefore, it is necessary to adopt the MCFS-NPML.

Conclusions

We have improved the behavior of the NPML at grazing incidence and normal incidence for the differential seismic wave equation and made the NPML more stable. Although the NPML has the advantages of implementation simplicity and computational efficiency, it will produce strong spurious reflections and is extremely unstable in some complex media and models, e.g., the poroelastic VTI media, the TTI medium, and the Marmousi model in elastic isotropic media. We also derived the M-NPML, but it has the limitation of predicting excess absorption; CFS-NPML still produces instability phenomena shown in Figs. 6c, d and 8a. The MCFS-NPML can solve all of the above problems. We designed a new damping function to enhance further the absorption of NPML, and the new function is perfectly implemented in MCFS-NPML by specially treating the scaling factor (β) and stability factors (P).

Appendix

Appendix A: the discrete format of the fifinite-difference operator for cfs-npml equation

The velocity-stress Eq. (13) is first-order partial-differential equations with respect to time and space and can be discretized as (take Formula 55 as an example):

$$\partial_{t} \tau_{xx} = C_{11} \partial_{x} v_{x} + C_{13} \partial_{z} v_{z} + C_{15} \left( {\partial_{z} v_{x} + \partial_{x} v_{z} } \right)$$

(55)

$$\begin{aligned} \left( {\tau _{{xx}} } \right)_{{i,j}}^{k} = & \left( {\tau _{{xx}} } \right)_{{i,j}}^{{k - 1}} + \vartriangle t\left[ {C_{{11}} D_{x}^{{2M,2}} \left( {v_{x} } \right)_{{i,j}}^{{k - 1/2}} + C_{{13}} D_{z}^{{2M,2}} \left( {v_{z} } \right)_{{i,j}}^{{k - 1/2}} \partial _{z} } \right. \\ & \left. { + C_{{15}} \left( {D_{z}^{{2M,2}} \left( {v_{x} } \right)_{{i,j}}^{{k - 1/2}} + D_{x}^{{2M,2}} \left( {v_{z} } \right)_{{i,j}}^{{k - 1/2}} } \right)} \right], \\ \end{aligned}$$

(56)

where $D_{x}^{2M,2}$ and $D_{z}^{2M,2}$ are finite-difference operators have 2Mth-order accuracy in space and second-order accuracy in time along x- and z-axis, respectively. Term $\left( {\tau_{xx} } \right)_{i,j}^{k}$ represents the discretized pressure wavefield p(x + i∆x, z + j∆z, k∆t), and $\left( {v_{x} } \right)_{i,j}^{k - 1/2}$ denote the discretized velocity wavefield.$D_{x}^{2M,2}$ is described by the following formula:

$$D_{x}^{2M,2} v_{i,j}^{k - 1/2} = 1/\Delta x\sum\limits_{m = 1}^{M} {d_{m,j} } \left( {v_{{i + \left( {2m - 1} \right)/2,j}}^{k - 1/2} - v_{{i - \left( {2m - 1} \right)/2,j}}^{k - 1/2} } \right).$$

(57)

In this paper, the scheme with twelfth-order accuracy in space and second-order accuracy in time is adopted. The traditional high-order staggered finite-difference method has high-order accuracy in space, but only the second-order accuracy in time. Some new methods with sixth-order accuracy are proposed (Tan and Huang 2014; Chen, H. M., et al., 2017).

Tan and Huang determine the coefficients of the finite-difference operator in the joint time–space domain to achieve high-order accuracy in time while preserving high-order accuracy in space. The finite-difference operators have fourth-order accuracy in time $D_{x}^{2M,4}$ is described as follows:

$$\begin{gathered} D_{x}^{2M,4} v_{i,j}^{k - 1/2} = 1/\Delta x[\sum\limits_{m = 1}^{M} {d_{m,j} } \left( {v_{{i + \left( {2m - 1} \right)/2,j}}^{k - 1/2} - v_{{i - \left( {2m - 1} \right)/2,j}}^{k - 1/2} } \right) \hfill \\ \, + d_{1,j} \left( {v_{i + 1/2,j + 1}^{k - 1/2} - v_{i - 1/2,j + 1}^{k - 1/2} + v_{i + 1/2,j - 1}^{k - 1/2} - v_{i - 1/2,j - 1}^{k - 1/2} } \right)]. \hfill \\ \end{gathered}$$

(58)

The CFS-NPML Eq. (19) has no partial derivation to space, so we can deduce the following discrete scheme:

$$\begin{aligned} \left( {\overline{\xi }^{m} } \right)^{k + 1/2} = & \frac{1}{{\frac{{\beta_{m} }}{\Delta t} + \frac{{\eta_{m} \beta_{m} + \alpha_{m} }}{2}}} \times \left[ {\left( {\frac{{\beta_{m} }}{\Delta t} - \frac{{\eta_{m} \beta_{m} + \alpha_{m} }}{2}} \right)\left( {\overline{\xi }^{m} } \right)^{k - 1/2} } \right. \\ & \, \left. { + \left( {\frac{1}{\Delta t} + \frac{{\eta_{m} }}{2}} \right)\left( {\xi^{m} } \right)^{k + 1/2} + \left( {\frac{{\eta_{m} }}{2} - \frac{1}{\Delta t}} \right)\left( {\xi^{m} } \right)^{k - 1/2} } \right]. \\ \end{aligned}$$

(59)

Appendix B: stability factors analysis

$$A^{n} = \left[ {\begin{array}{*{20}c} {0_{22} } & {A_{2} } & {0_{24} } & {C_{2} } \\ {A_{1} } & {0_{33} } & {C_{1} } & {0_{34} } \\ {D_{3} } & {0_{43} } & {D_{1} } & {0_{44} } \\ {0_{42} } & {D_{4} } & {0_{44} } & {D_{2} } \\ \end{array} } \right]$$

(60)

$$A_{2} = \left[ {\begin{array}{*{20}l} {i\frac{1}{\rho }k_{x} } \hfill & 0 \hfill & {i\frac{1}{\rho }k_{z} } \hfill \\ 0 \hfill & {i\frac{1}{\rho }k_{z} } \hfill & {i\frac{1}{\rho }k_{x} } \hfill \\ \end{array} } \right]\,\,A_{1} = \left[ {\begin{array}{*{20}l} {C_{11} ik_{x} + C_{15} ik_{z} } \hfill & {C_{13} ik_{z} + C_{15} ik_{x} } \hfill \\ {C_{13} ik_{x} + C_{35} ik_{z} } \hfill & {C_{33} ik_{z} + C_{35} ik_{x} } \hfill \\ {C_{15} ik_{x} + C_{55} ik_{z} } \hfill & {C_{35} ik_{z} + C_{55} ik_{x} } \hfill \\ \end{array} } \right]$$

$$C_{1} = \left[ {\begin{array}{*{20}l} {C_{11} ik_{x} } \hfill & {C_{15} ik_{z} } \hfill & {C_{15} ik_{x} } \hfill & {C_{13} ik_{z} } \hfill \\ {C_{13} ik_{x} } \hfill & {C_{35} ik_{z} } \hfill & {C_{35} ik_{x} } \hfill & {C_{33} ik_{z} } \hfill \\ {C_{15} ik_{x} } \hfill & {C_{55} ik_{z} } \hfill & {C_{55} ik_{x} } \hfill & {C_{35} ik_{z} } \hfill \\ \end{array} } \right]\,\,C_{2} = \left[ {\begin{array}{*{20}l} {i\frac{1}{\rho }k_{x} } \hfill & 0 \hfill & 0 \hfill & {i\frac{1}{\rho }k_{z} } \hfill \\ 0 \hfill & {i\frac{1}{\rho }k_{z} } \hfill & {i\frac{1}{\rho }k_{x} } \hfill & 0 \hfill \\ \end{array} } \right]$$

$$D_{1} = \left[ {\begin{array}{*{20}c} { - \alpha_{x}^{\left( x \right)} } & 0 & 0 & 0 \\ 0 & { - p^{(z/x)} \alpha_{x}^{\left( x \right)} } & 0 & 0 \\ 0 & 0 & { - \alpha_{x}^{\left( x \right)} } & 0 \\ 0 & 0 & 0 & { - p^{(z/x)} \alpha_{x}^{\left( x \right)} } \\ \end{array} } \right],D_{2} = D_{1}$$

$$D_{3} = \left[ {\begin{array}{*{20}l} { - \alpha_{x}^{\left( x \right)} } \hfill & 0 \hfill \\ { - p^{(z/x)} \alpha_{x}^{\left( x \right)} } \hfill & 0 \hfill \\ 0 \hfill & { - \alpha_{x}^{\left( x \right)} } \hfill \\ 0 \hfill & { - p^{(z/x)} \alpha_{x}^{\left( x \right)} } \hfill \\ \end{array} } \right]D_{4} = \left[ {\begin{array}{*{20}l} { - \alpha_{x}^{\left( x \right)} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - p^{(z/x)} \alpha_{x}^{\left( x \right)} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - \alpha_{x}^{\left( x \right)} } \hfill \\ 0 \hfill & 0 \hfill & { - p^{(z/x)} \alpha_{x}^{\left( x \right)} } \hfill \\ \end{array} } \right]$$

(61)

$$\begin{aligned} a_{1} & = \rho ^{6} \left( { - C_{{15}} ^{2} \alpha _{z} ^{4} k_{x} ^{4} + \alpha _{x} ^{2} \left( {k_{z} ^{2} ( - C_{{13}} (C_{{13}} + 2C_{{55}} )\alpha _{z} ^{2} k_{x} ^{2} } \right.} \right. \\ & \left. { - 2C_{{13}} C_{{35}} \alpha _{z} k_{x} \alpha _{x} k_{z} + \,( - C_{{35}} ^{2} + C_{{33}} C_{{55}} )\alpha _{x} ^{2} k_{z} ^{2} } \right) \\ & + \alpha _{z} ^{2} \left( {C_{{55}} \alpha _{z} ^{2} k_{x} ^{2} + 2C_{{35}} \alpha _{z} k_{x} \alpha _{x} k_{z} + (C_{{33}} + C_{{55}} )\alpha _{x} ^{2} k_{z} ^{2} } \right)\rho \\ & \left. { + \,\alpha _{z} ^{2} \alpha _{x} ^{2} \rho } \right)^{2} + 2C_{{15}} \alpha _{z} k_{x} \alpha _{x} k_{z} \left( { - C_{{13}} \alpha _{z} ^{2} k_{x} ^{2} + \alpha _{x} (C_{{35}} \alpha _{z} k_{x} k_{z} } \right. \\ & \left. { + C_{{33}} \alpha _{x} k_{z} ^{2} + \alpha _{x} \alpha _{z} ^{2} \rho )} \right) + \,C_{{11}} \alpha _{z} ^{2} k_{x} ^{2} \left( {C_{{55}} \alpha _{z} ^{2} k_{x} ^{2} } \right. \\ & \left. {\left. { + \alpha _{x} \left( {2C_{{35}} \alpha _{z} k_{x} k_{z} + C_{{33}} \alpha _{x} k_{z} ^{2} + \alpha _{x} \alpha _{z} ^{2} \rho } \right)} \right)} \right) \\ \end{aligned}$$

$$\begin{aligned} a_{2} = & \,2\rho^{5} \left( { - 2C_{15}^{2} \alpha_{z}^{3} k_{x}^{4} + \alpha_{x} k_{z}^{2} ( - C_{13} (C_{13} + 2C_{55} )\alpha_{z} (\alpha_{z} + \alpha_{x} )k_{x}^{2} } \right. \\ & \left. { - \,C_{13} C_{35} \alpha_{x} (3\alpha_{z} + \alpha_{x} )k_{x} k_{z} - 2(C_{35}^{2} - C_{33} C_{55} )\alpha_{x}^{2} k_{z}^{2} } \right) \\ & + \,\alpha_{x} \alpha_{z} \left( {C_{55} \alpha_{z}^{2} (\alpha_{z} + 2\alpha_{x} )k_{x}^{2} + 3C_{35} \alpha_{x} \alpha_{z} (\alpha_{z} + \alpha_{x} )k_{x} k_{z} } \right. \\ & \left. { + \,(C_{33} + C_{55} )\alpha_{x}^{2} (2\alpha_{z} + \alpha_{x} )k_{z}^{2} } \right)\rho + 2\alpha_{x}^{3} \alpha_{z}^{3} (\alpha_{z} + \alpha_{x} )\rho^{2} \\ & + \,C_{11} \alpha_{z} k_{x}^{2} \left( {2C_{55} \alpha_{z}^{2} k_{x}^{2} + \left( {C_{35} \alpha_{z} (\alpha_{z} + 3\alpha_{x} )k_{x} k_{z} + C_{33} \alpha_{x} (\alpha_{z} + \alpha_{x} )k_{z} } \right)} \right. \\ & \left. { + \,\alpha_{x} \alpha_{z}^{2} (\alpha_{z} + 2\alpha_{x} )\rho } \right) + C_{15} k_{x} k_{z} \left( { - C_{13} \alpha_{z}^{2} (\alpha_{z} + 3\alpha_{x} )k_{x}^{2} } \right. \\ & + \,\alpha_{x} \left( {k_{z} (2C_{35} \alpha_{z} (\alpha_{z} + \alpha_{x} )k_{x} + C_{33} \alpha_{x} (3\alpha_{z} + \alpha_{x} )} \right. \\ & \left. {\left. {\left. { + \,3\alpha_{x} \alpha_{z}^{2} (\alpha_{z} + \alpha_{x} )\rho } \right)} \right)} \right) \\ \end{aligned}$$

$$\begin{aligned} a_{3} = & \,\rho^{4} ( - 6C_{15}^{2} \alpha_{z}^{2} k_{x}^{4} + k_{z}^{2} ( - C_{13} (C_{13} + 2C_{55} )(\alpha_{z}^{2} + 4\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{x}^{2} \\ & - \,6C_{13} C_{35} \alpha_{x} (\alpha_{z} + \alpha_{x} )k_{x} k_{z} - 6(C_{35}^{2} - C_{33} C_{55} )\alpha_{x}^{2} k_{z}^{2} ) \\ & + \,(C_{55} \alpha_{z}^{2} (\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + 6\alpha_{x}^{2} )k_{x}^{2} + 6C_{35} \alpha_{x} \alpha_{z} (\alpha_{z}^{2} + 3\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{x} k_{z} \\ & + \,(C_{33} + C_{55} )\alpha_{x}^{2} (6\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{z}^{2} )\rho \\ & + \,2\alpha_{x}^{2} \alpha_{z}^{2} (3\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + 3\alpha_{x}^{2} )\rho^{2} + 2C_{15} k_{z} k_{x} ( - 3C_{13} \alpha_{z} (\alpha_{z} + \alpha_{x} )k_{x}^{2} \\ & + \,k_{z} (C_{35} (\alpha_{z}^{2} + 4\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{x} + 3C_{33} \alpha_{x} (\alpha_{z} + \alpha_{x} )k_{z} ) + 3\alpha_{x} \alpha_{z} (\alpha_{z}^{2} + 3\alpha_{x} \alpha_{z} + 3\alpha_{x}^{2} )\rho ) \\ & + \,C_{11} k_{x}^{2} \left( {6C_{55} \alpha_{z}^{2} k_{x}^{2} + k_{z} } \right.\left( {6C_{55} \alpha_{z}^{2} k_{x}^{2} + k_{z} } \right.\left( {6C_{35} \alpha_{z} (\alpha_{z} + \alpha_{x} )k_{x} } \right. \\ & \left. {\left. { + \,C_{33} (\alpha_{z}^{2} + 4\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{z} } \right) + \alpha_{z}^{2} (\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + 6\alpha_{x}^{2} )\rho )} \right) \\ \end{aligned}$$

$$\begin{aligned} a_{4} = & 2\rho^{3} ( - 2C_{15}^{2} \alpha_{z} k_{x}^{4} + k_{z}^{2} ( - C_{13} (C_{13} + 2C_{55} )(\alpha_{z} + \alpha_{x} )k_{x}^{2} \\ & - C_{13} C_{35} (\alpha_{z} + 3\alpha_{x} )k_{x} k_{z} - 2(C_{35}^{2} - C_{33} C_{55} )\alpha_{x} k_{z}^{2} ) \\ & + (2C_{55} \alpha_{z} (\alpha_{z}^{2} + 3\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{x}^{2} + C_{35} (\alpha_{z} + \alpha_{x} )(\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{x} k_{z} \\ & + 2(C_{33} + C_{55} )\alpha_{x} (\alpha_{z}^{2} + 3\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{z}^{2} )\rho + 2\alpha_{x} \alpha_{z} (\alpha_{z}^{2} + 5\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )\rho^{2} \\ & + C_{11} k_{x}^{2} (2C_{55} \alpha_{z} k_{x}^{2} + k_{z} (C_{35} (3\alpha_{z} + \alpha_{x} )k_{x} + C_{33} (\alpha_{z} + \alpha_{x} )k_{z} ) \\ & + 2\alpha_{z} (\alpha_{z}^{2} + 3\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )\rho ) + C_{15} k_{x} k_{x} ( - C_{13} (3\alpha_{z} + \alpha_{x} )k_{x}^{2} \\ & + k_{z} (2C_{35} (\alpha_{z} + \alpha_{x} )k_{x} + C_{33} (\alpha_{z} + 3\alpha_{x} )k_{z} ) + (\alpha_{z} + \alpha_{x} )(\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )\rho )) \\ \end{aligned}$$

$$\begin{aligned} a_{5} = & \rho^{2} ( - C_{15}^{2} k_{x}^{4} + C_{11} C_{15} k_{x}^{4} + 2C_{11} C_{35} k_{x}^{3} k_{z} - C_{13}^{2} k_{x}^{2} k_{z}^{2} \\ & + C_{11} C_{13} k_{x}^{2} k_{z}^{2} - 2C_{55} C_{13} k_{x}^{2} k_{z}^{2} - 2C_{13} C_{35} k_{z}^{3} k_{x} - C_{35}^{2} k_{z}^{4} \\ & + C_{33} C_{55} k_{z}^{4} + ((C_{11} + C_{55} )(6\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{x}^{2} \\ & + 6C_{35} (\alpha_{z}^{2} + 3\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )k_{x} k_{z} + (C_{33} + C_{55} )(\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + 6\alpha_{x}^{2} )k_{x}^{2} )\rho \\ & + (\alpha_{z}^{4} + 16\alpha_{x}^{3} \alpha_{z} + 36\alpha_{x}^{2} \alpha_{z}^{2} + 16\alpha_{x} \alpha_{z}^{3} + \alpha_{x}^{4} )\rho^{2} + 2C_{15} k_{x} k_{z} ( - C_{13} k_{x}^{2} \\ & + k_{z} (C_{35} k_{x} + C_{33} k_{z} ) + 3(\alpha_{z}^{2} + 3\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )\rho )) \\ \end{aligned}$$

$$\begin{aligned} a_{6} = & 2\rho^{2} (C_{11} (2\alpha_{z} + \alpha_{x} )k_{x}^{2} + C_{55} (2\alpha_{z} + \alpha_{x} )k_{x}^{2} \\ & + C_{55} (\alpha_{z} + 2\alpha_{x} )k_{z}^{2} + k_{z} (3(C_{11} + C_{35} )(\alpha_{z} + \alpha_{x} )k_{x} \\ & + C_{33} (\alpha_{z} + 2\alpha_{x} )k_{z} + 2(\alpha_{z} + \alpha_{x} )(\alpha_{z}^{2} + 5\alpha_{x} \alpha_{z} + \alpha_{x}^{2} )\rho ) \\ \end{aligned}$$

$$\begin{aligned} a_{7} = & \rho ((C_{11} + C_{35} )k_{x}^{2} + 2(C_{15} + C_{35} )k_{x} k_{z} \\ & + (C_{33} + C_{55} )k_{z}^{2} + 2(3\alpha_{z}^{2} + 8\alpha_{x} \alpha_{z} + 3\alpha_{x}^{2} )\rho ) \\ \end{aligned}$$

$$a_{8} = 4\rho (\alpha_{z} + \alpha_{x} )\rho$$

$$a_{9} = 1$$

(62)

Appendix C: the first-order partial differential equations for poroelastic VTI media after applying the MCFS-NPML

$$\begin{gathered} (\rho_{11} \rho_{22} - \rho_{12}^{2} )\partial_{t} v_{x} = \rho_{22} \left( {\partial_{x} \overline{\tau }_{xx}^{x} + \partial_{z} \overline{\tau }_{xz}^{z} } \right) - \rho_{12} \partial_{x} \overline{s}^{x} + (\rho_{12} + \rho_{22} )b_{x} (V_{x} - v_{x} ) \hfill \\ (\rho_{11} \rho_{22} - \rho_{12}^{2} )\partial_{t} v_{z} = \rho_{22} \left( {\partial_{z} \overline{\tau }_{zz}^{z} + \partial_{x} \overline{\tau }_{xz}^{x} } \right) - \rho_{12} \partial_{z} \overline{s}^{z} + (\rho_{12} + \rho_{22} )b_{z} (V_{z} - v_{z} ) \hfill \\ (\rho_{12}^{2} - \rho_{11} \rho_{22} )\partial_{t} V_{x} = \rho_{12} \left( {\partial_{x} \overline{\tau }_{xx}^{x} + \partial_{z} \overline{\tau }_{xz}^{z} } \right) - \rho_{11} \partial_{x} \overline{s}^{x} + (\rho_{12} + \rho_{11} )b_{x} (V_{x} - v_{x} ) \hfill \\ (\rho_{12}^{2} - \rho_{11} \rho_{22} )\partial_{t} V_{z} = \rho_{12} \left( {\partial_{z} \overline{\tau }_{zz}^{z} + \partial_{x} \overline{\tau }_{xz}^{x} } \right) - \rho_{11} \partial_{z} \overline{s}^{z} + (\rho_{12} + \rho_{11} )b_{z} (V_{z} - v_{z} ) \hfill \\ \partial_{t} \tau_{xx} = c_{11} \partial_{x} \overline{v}_{x}^{x} + c_{13} \partial_{z} \overline{v}_{z}^{z} + Q_{1} (\partial_{x} \overline{V}_{x}^{x} + \partial_{z} \overline{V}_{z}^{z} ) \hfill \\ \partial_{t} \tau_{zz} = c_{13} \partial_{x} \overline{v}_{x}^{x} + c_{33} \partial_{z} \overline{v}_{z}^{z} + Q_{3} (\partial_{x} \overline{V}_{x}^{x} + \partial_{z} \overline{V}_{z}^{z} ) \hfill \\ \partial_{t} \tau_{xx} = c_{55} \partial_{z} \overline{v}_{x}^{z} + c_{55} \partial_{x} \overline{v}_{z}^{x} \hfill \\ \partial_{t} s = Q_{1} \partial_{x} \overline{v}_{x}^{x} + Q_{3} \partial_{z} \overline{v}_{z}^{z} + R(\partial_{x} \overline{V}_{x}^{x} + \partial_{z} \overline{V}_{z}^{z} ) \hfill \\ \end{gathered}$$

(63)

and

$$\begin{gathered} \partial_{t} \overline{\xi }^{z} + \alpha_{{_{z} }}^{x} \overline{\xi }^{z} = \partial_{t} \xi ;\,\parallel PML \hfill \\ \partial_{t} \overline{\xi }^{x} + \alpha_{{_{x} }}^{z} \overline{\xi }^{x} = \partial_{t} \xi ;\,\parallel PML \hfill \\ \left[ {\eta_{m} \beta_{m} + \alpha_{m}^{m} } \right]\overline{\xi }^{m} + \beta_{m} \partial_{t} \overline{\xi }^{m} = \eta_{m} \xi + \partial_{t} \xi ;\, \bot PML \hfill \\ \xi = \tau_{xx} ,\tau_{zz} ,\tau_{xz} ,v_{x} ,v_{z} ,V_{x} ,V_{z} ,s;m = x,z, \hfill \\ \end{gathered}$$

(64)

where v is the velocity vector for the solid, V is the velocity vector for the fluid, and s is the pore fluid pressure. This results in:

$$\begin{gathered} \rho_{11} + \rho_{12} = (1 - \varphi )\rho_{s} = \rho_{1} \hfill \\ \rho_{22} + \rho_{12} = \varphi \rho_{f} = \rho_{2} ;\rho_{12} = - \rho_{a}, \hfill \\ \end{gathered}$$

(65)

where ρ_f and ρ_s are the densities of the fluid and solid, ρ_a is the macroscopic density of the fluid saturated medium, φ is the porosity, b is the dissipation coefficient, Q is the coupling parameter between the solid and the fluid, and R is the poroelastic coefficient of effective stress. For VTI media, there are five independent elastic coefficients: v_p represents the P-wave velocity, v_s the S-wave velocity, and ζ, γ and δ the Thomsen anisotropy parameters.

$$\begin{gathered} c_{11} = (2\zeta + 1)\rho_{1} v_{p}^{2} ;c_{33} = \rho_{1} v_{p}^{2} ;c_{55} = \rho_{1} v_{s}^{2} \hfill \\ c_{13} = \rho_{1} (\sqrt {\left[ {\left( {2\delta + 1} \right)v_{p}^{2} - v_{s}^{2} } \right](v_{p}^{2} - v_{s}^{2} )} - v_{s}^{2} ) \hfill \\ c_{66} = (2\gamma + 1)c_{55} ;c_{12} = c_{11} - 2c_{66} \hfill \\ \end{gathered}$$

(66)