Introduction

It is increasingly important for climatologists to provide better and more accurate information regarding climatic conditions at a given place and time. This may be problematic in watersheds located in semi-arid to arid areas where complex topography and highly spatially differentiated climates make it difficult to estimate small-scale precipitation and temperature patterns. In addition, such watersheds often have few meteorological monitoring sites and are only at point locations (e.g., climatological or synoptic weather stations) (Skirvin et al. 2003). To address this problem, interpolation techniques are used to produce meteorological data estimates for areas lacking monitoring infrastructure and instruments. Many interpolation techniques have been tested for spatial interpolation of daily meteorological data (e.g., Dodson and Marks 1997; Thornton et al. 1997; Bolstad et al. 1998; Courault and Monestiez 1999; Shen et al. 2001; Xia et al. 2001; Jarvis and Stuart, 2001; Hasenauer et al. 2003; Garen and Marks 2005).

Choosing among the vast range of interpolation techniques to use in weather data estimation is a complex and sensitive process. The software, Geographic Information System (ArcGIS), is useful in this case as it allows users to compare the different interpolation techniques, including both deterministic [Inverse Distance Weighting (IDW), Spline, Natural Neighbor (NN), Local Polynomial (LP), Global Polynomial (GP), Radius Basis Function (RBF)] and geostatistical [Kriging and Co-Kriging (CK)] (Xiao et al. 2016). Deterministic techniques are directly based on the surrounding data points. Geostatistical theory as applied to interpolation is based on a stochastic model, which allows for optimal estimations at any location in a selected area (Wamwling 2003).

The applicability and accuracy of deterministic and geostatistical interpolation methods have been the focus of numerous studies. Mutua and Kuria (2012) evaluated kriging, CK, GP, and IDW methods for precipitation interpolation based on root mean square error (RMSE) values in Kenya’s Nyando River basin and concluded that the Kriging and CK methods to be the most accurate. Delbari et al. (2013) applied different univariate [IDW and Ordinary Kriging (OK)] and multivariate [linear regression, Ordinary Co-Kriging (O-CK), Simple Kriging (SK) with varying local mean and Kriging with an External Drift (KED)] interpolation methods to map monthly and annual rainfall in northeast Iran. Results showed that OK provided the most accurate estimates. De Amorim et al. (2016) studied spatial interpolation methods involving IDW, OK, Multivariate Regression with interpolation of residuals by IDW (MRegIDW) and Multivariate Regression with interpolation of residuals by OK (MRegOK) for the estimation of precipitation distribution in Distrito Federal, Brazil. Their research showed MRegOK had the lowest errors and highest correlation and Nash–Sutcliffe efficiency criteria. Fadavi et al. (2016) investigated several interpolation methods, including IDW, Kriging, Co-K, Kriging-Regression (K-R), multiple regression and Spline in the regionalization of daily \(T_{ \min }\) data from 30 meteorological stations in 1992 and 54 meteorological stations in 2007 in Isfahan, Iran. They found that multiple regression and K-R were the most accurate methods. Fadavi and Bazarafshan (2016) also compared regional estimation methods for daily \(T_{ \max }\) including IDW, Kriging, Co-K, K-R, multiple regression and Spline in Isfahan. They found that multiple regression, OK and K-R had better performances than other methods. The potential of deterministic and geostatistical rainfall interpolation was examined under high rainfall variability and dry spells in Kenya’s Central Highlands by Kisaka et al. (2016). The kriging interpolation method emerged as the most appropriate geostatistical interpolation technique and was found to be suitable for spatial rainfall map generation in the study region. Das et al. (2017) concluded that the IDW method was the best spatial interpolation method in West Bengal, India. Xu et al. (2018) used P-BSHADE for temperature spatial interpolation based on sparse historical stations in China. Results were compared with kriging, IDW and combined Spline with Kriging (TPS-KRG), and it was found that the P-BSHADE method had the smallest error.

Interpolation techniques are algorithms used to solve the problem of missing geo-based data. Although these techniques encounter some limitations, including estimating errors, they are still useful. These techniques are used to predict unrecorded climatic data at each station in a catchment (e.g., semi-arid catchments, etc.) containing sufficient weather stations and climatic variable records such as precipitation and temperature. These predicted data are then used to study water resources management in the catchment area through hydrologic models.

The uncertainties associated with interpolation techniques are particularly important in arid and semi-arid watersheds where unstable weather is affected by seasonal variation, a large difference between maximum and minimum temperatures and a vast diversity of topography. Generally, finding techniques that have the best conformity to a region’s specific conditions, and which can be accurately used in computing interpolated data to match with regional characteristics, is difficult. In addition, a method that performs well at one site may perform poorly at another and therefore its effectiveness needs to be examined on a site-by-site basis.

Due to the occurrence of multiple droughts and a frequent lack of sufficient meteorological data in semi-arid areas, a study was deemed necessary to determine which interpolation methods could be used for water resources management. As droughts, common to semi-arid areas, result in large changes in temperature and precipitation patterns in specific locations, previous studies on mapping would not necessarily be appropriate.

Although some methods such as IDW, NN, Regularized Spline (RS), Tension Spline (TS), OK and Universal Kriging (UK) have been individually used around the world, a comparison of these methods has never been performed in semi-arid areas simultaneously to determine the best interpolation method for mapping temperature and precipitation (Karamouz et al. 2007; Zareian et al. 2015; Eslamian et al. 2017).

The accuracy of climatic maps of mean annual minimum temperature (\(T_{ \min }\)), maximum temperature (\(T_{ \max }\)), and precipitation prepared using six deterministic and geostatistic spatial interpolation methods was compared. The best method was then selected for each climatic variable in the Zayandeh-Rud River basin, Iran, a large semi-arid area with high variations in temperature and rainfall. The selection of a site-appropriate method and its relative accuracy were determined by statistical indices (e.g., Root Mean Square Error (RMSE), Mean Absolute Error (MAE), etc.) derived through a cross-validation technique.

Study area

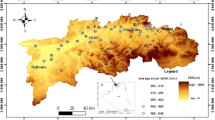
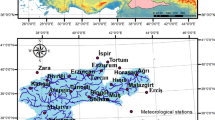
The study was carried out in the 26,917 km2 Zayandeh-Rud River basin located in semi-arid central Iran (lat. 31°15′–33°45′, long 50°02′–53° 20′; Fig. 1). The Zayandeh-Rud River is about 350 km long and is the most important river in the basin. It flows from the Zagros Mountains in the east of Chaharmahal province (3974 m A.M.S.L.) toward the Gav-Khouni Marsh in the east of Isfahan province (1470 m A.M.S.L.) (Zareian et al. 2015).

Fig. 1
figure 1

The location of the Zayandeh-Rud River basin and distribution of selected weather stations

Full size image

Basin precipitation varies from about 50 mm year−1 in the eastern plains to about 1500 mm year−1 in the western mountainous region and has an average of 140 mm year−1. The average monthly temperature for the basin ranges from 3 °C (in January) to 30 °C (in July) and the average annual temperature is 14.5 °C. The Zayandeh-Rud River had an average flow of about 850 × 106 m3 year−1 between 1970 and 2009 (Madani and Marino 2009). Further characteristics of this region and the distribution of selected weather stations within the basin are shown in Table 1 and Fig. 1, respectively.

Table 1 Characteristics of the selected weather stations
Full size table

Methods

As the Zayandeh-Rud basin has a semi-arid climate and is a complicated and strategic region from the point of view of its water resources, continuous monitoring of those resources is key to sustainable water management. Thus, data obtained by the regionalized meteorological techniques could be very useful.

Data and meteorological stations

In the present study, average monthly precipitation and average monthly minimum and maximum temperature data (1970–2014) were recorded by 18 and 27 meteorological stations, respectively. The accuracy of several interpolation methods was compared via a cross-validation technique.

Spatial interpolation techniques

Within the ArcGIS environment, spatial distribution maps allowing for the analysis of spatial variation and zoning in precipitation, \(T_{ \min }\), and \(T_{ \max }\) values were created through geostatistical (kriging) and deterministic (IDW, NN, and Spline) methods.

Inverse Distance Weighting (IDW) method

The IDW technique assumes the value at an unsampled point can be approximated by a weighted average of values at measured points within a local neighborhood surrounding the unsampled location. The local neighborhood radius can be defined by the range of a fixed number of points or a fixed distance surrounding the unsampled point. The value of any point can be calculated as shown by Burrough and McDonnell (1998).

This method places a greater weight on points closer (vs. farther) to unsampled points and accordingly these have a greater effect on interpolation calculations. The weight parameter controls the effect of measured point values on the interpolated value based on their distance from the unsampled point (Erdoğan 2009).

Natural neighbor (NN) method

The NN method is the most general and robust method of interpolation. Based on a local weighted average approach, the NN method uses a Voronoi diagram to determine the relative contribution of measured points. Weights are defined as a ratio of the area “stolen” from unsampled points in the Voronoi and Delaunay diagrams by adding an interpolated point divided by the area assigned to the new point. The general relationship of interpolation by the natural neighborhood method is defined by Sibson (1981) and Watson and Phillip (1987).

Kriging method

The existence of a spatial structure, where measured points close to each other are more similar than those that are far apart (spatial autocorrelation), is a prerequisite for the application of geostatistics. These use semi-variograms as a descriptive tool to specify the spatial pattern of a feature (Goovaerts 1999). The semi-variance is a value of spatial dependence between measured points calculated on the basis of the distance between them (Tatalovich et al. 2006). The semi-variogram model that best fits the data is used to generate optimum interpolation weights (Burrough and McDonnell 2000a). Therefore, kriging is a geostatistical interpolation method that considers the spatial correlation between measured points to predict attribute values at unsampled locations using information related to other attributes (Goovaerts 1999).

After analysis of the experimental semi-variogram, a compatible model that is fitted by a parametric smooth model implying stationarity, isotropy and the best-fitting parametric model, is used to build up the auto-covariance matrix of the regression residuals (in UK). In this case, OK and SK models can be defined as described by Attorre et al. (2007).

When the measured points are modeled as the sum of constant trend and intrinsic stationary error, a more diverse batch of models is obtained. In the UK model (Ver Hoef 1993), such a trend can be modeled as a linear function in explanatory variables (i.e., climatic, geographical and topographical covariates).

While kriging is well known to be the best linear unbiased (spatial) predictor (BLUP), its applications can be limited by the existence of problems of nonstationarity in real-world data-sets. Accordingly, some authors (e.g., Agnew and Palutikof 2000; Ninyerola et al. 2000; Antonić et al. 2001), instead of using the UK with a trend function modeled via a set of covariates, have proposed a simpler approach based on RK, i.e., kriging after de-trending, such that the trend function and estimated residuals are modeled separately.

Ordinary Kriging (OK) and Universal Kriging (UK) methods

OK and UK are two common univariate kriging methods and two typically general linear regression models. The UK method assumes that spatial variation in measured point values includes a drift or structural component that can be arrived at through the variation of locations, allowing the locational information to then be incorporated into the kriging process. Unlike the OK method, where the weights of data points are determined by a stationary random function model, the weights under the UK method are taken from a nonstationary random function model (Burrough and McDonnell 2000). The OK method requires a constant but unknown mean, whereas the UK method assumes a spatially varying mean, which has proven helpful when it is necessary to account for trends observed in exploratory data analysis (Krivoruchko and Gotway 2004).

Spline method

Spline interpolation consists of the approximation of a function by means of a series of polynomials over adjacent intervals, with continuous derivatives at the end point of the intervals. The method is based on two basic assumptions: (i) The interpolating function should pass through the data points; (ii) it should be as smooth as possible.

Two types of spline techniques (TS and RS) were tested in the present study. The TS method defines a function that passes through the input data points concurrently and minimizes the curving energy function (Franke 1982; Mitas and Mitasova 1988).

Among the types of spline that can be used (see Merwade et al. 2006), the RS method improves the analytical properties of splines by adding and applying third-order and higher order derivatives.

Sensitivity analysis

Sensitivity analysis was used to determine how independent parameter values would affect particular dependent parameters under a given set of assumptions. Their usage depended on one or more input parameters within specific boundaries, such as the search neighborhood, and power and weight of smoothness that changes the prediction of a variable obtained by interpolation methods. Sensitive parameters were determined separately for each interpolation method in order to predict variables accurately.

Evaluation and comparison criteria

Cross-validation

Cross-validation is a common method for validating the accuracy of interpolation techniques (Voltz and Webster 1990). In this technique, information regarding one point is removed temporarily, the removed information is estimated from the remaining data points, and the difference between the actual and estimated values is calculated. This operation is repeated for the remainder of the points (Davis 1987).

Comparative analysis of interpolation techniques

Six different interpolation methods were validated independently for monthly \(T_{ \min }\), \(T_{ \max }\), and precipitation using cross-validation. Validation was performed for each month from 1970 to 2014, and the accuracy of the interpolation method was evaluated on the basis of Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Bias Error (MBE) and the coefficient of determination (R2).

$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{i = N} \left( {x_{i}^{\text{intp}} - x_{i}^{\text{meas}} } \right)^{2} }}{n}}$$
(1)
$${\text{MAE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{i = N} \left| {x_{i}^{\text{intp}} - x_{i}^{\text{meas}} } \right|}}{n}$$
(2)
$${\text{MBE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{i = N} \left( {x_{i}^{\text{intp}} - x_{i}^{\text{meas}} } \right)}}{n}$$
(3)
$$R^{2} = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{i = N} \left( {x_{i}^{\text{intp}} - \overline{{x^{\text{intp}} }} } \right)\left( {x_{i}^{\text{meas}} - \overline{{x^{\text{meas}} }} } \right)}}{{n\left( {s_{{x^{\text{intp}} }} } \right)\left( {s_{{x^{\text{meas}} }} } \right)}}} \right]^{2}$$
(4)

where N is the number of evaluated data points, \(x_{i}^{\text{intp}}\) is the ith interpolated value of the variable studied, \(x_{i}^{\text{meas}}\) is the ith measured value of the variable studied, \(\overline{{x^{\text{intp}} }}\) is the average of interpolated values of the variable studied, and \(\overline{{x^{\text{meas}} }}\) is the average of measured values of the variable studied.

Results and discussion

Sensitivity analysis

The optimum values of parameters for all spatial interpolation methods were obtained by implementing sensitivity analysis. These parameters were selected using the RMSE index, except for the NN method, which does not require user-specified parameters (e.g., search neighborhood, power (P), and weight of smoothness) to participate in interpolations (Figs. 2, 3 and 4). The search neighborhood was determined by the number of points (N) for all methods. The selection of the optimal parameter in interpolation by each of the methods, except for NN, can have a significant effect on the estimation error. It is important to note that these parameters are valid only for the interpolation of data points in a specific area and may be different for data points from other regions. Sensitivity analysis results are presented for the \(T_{ \min }\), \(T_{ \max }\), and precipitation variables in Table 2.

Fig. 2
figure 2

Variations in RMSE for Tmin with a number of points (N) for IDW, b power (P) for IDW, c number of points for RS, d weight of third-order derivatives for RS, e number of points (n) for TS, f weight of first-order derivatives for TS, g number of points for OK, h number of points for UK

Full size image
Fig. 3
figure 3

Variations in RMSE for Tmax with a number of points (N) for IDW, b power (P) for IDW, c number of points for RS, d weight of third-order derivatives for RS, e number of points (N) for TS, f weight of first-order derivatives for TS, g number of points for OK, h number of points for UK

Full size image
Fig. 4
figure 4

Variations in RMSE for precipitation with a number of points (N) for IDW, b power (P) for IDW, c number of points for RS, d weight of third-order derivatives for RS, e number of points (N) for TS, f weight of first-order derivatives for TS, g number of points for OK, h number of points for UK

Full size image
Table 2 Accuracy of spatial interpolation methods with optimal interpolation parameters for \(T_{ \min }\), \(T_{ \max }\), and precipitation as assessed by RMSE
Full size table

For \(T_{ \min }\), the RMSE decreased as the value of N increased for all methods except OK (Fig. 2). For the IDW method, as P increased, the error rate first decreased and then increased significantly. For the RS and TS methods, the error rate increased and then decreased as the value of the weight parameter increased.

For \(T_{ \max }\), the two methods of the spline family showed that increasing N decreased the error rate; otherwise an increase in N led to an increase in the error rate (Fig. 3). For the IDW method, increasing the value of P led to an initial decline in estimation error, followed by an increase. Increasing the weight parameter under the RS and TS methods led to a respective increase and decrease in the error rate.

For precipitation, increasing N reduced the estimation error rate for the TS method, while for the OK method the same increase in N first decreased and then increased the estimation error (Fig. 4). Increasing the value of P when using the IDW method led to a slow decrease in the estimation error. Moreover, for the spline model family, an increase in the weight parameter led to an increase in the error rate.

Accuracy of interpolations

The interpolators applied for \(T_{ \min }\), \(T_{ \max }\) and precipitation were compared by cross-validation based on R2, MAE, MBE and RMSE. The errors for these techniques were estimated by applying an optimal power function. The ranking of all interpolation techniques is shown for \(T_{ \min }\), \(T_{ \max }\), and precipitation in Tables 3, 4 and 5, respectively.

Table 3 Evaluation of interpolation method accuracy using cross-validation for monthly mean \(T_{\min }\) from 1970 to 2014
Full size table
Table 4 Evaluation of interpolation method accuracy using cross-validation for monthly mean \(T_{\max }\) from 1970 to 2014
Full size table
Table 5 Evaluation of interpolation method accuracy using cross-validation for monthly mean precipitation from 1970 to 2014
Full size table

For monthly average \(T_{ \min }\) data, the OK method implementing a Gaussian semi-variogram (MAE = 1.827 °C) and the UK method with a Linear Drift semi-variogram (MAE = 1.821 °C), were the most accurate methods over 45 years (1970–2014) of data, achieving the 1st and 2nd ranks, respectively (Table 3). The interpolation techniques that showed the weakest results were NN (MAE = 1.902 °C) and IDW (MAE = 1.942 °C), which ranked 10th and 11th among all methods. For the spline family of methods, tension type interpolation functions outperformed regularized functions. Daily differences between the maximum and minimum temperatures are strongly influenced by factors such as frequent changes in daily weather, rapid changes in surface temperature and the lack of air humidity, which are common in summer and winter compared to other seasons. Therefore, all interpolation methods showed the highest estimation errors for \(T_{ \min }\) in the summer and winter months and the lowest errors in the spring (Fig. 5).

Fig. 5
figure 5

Variation of monthly MAE for Tmin using different interpolation methods

Full size image

In contrast to the monthly average \(T_{ \min }\) data, the NN method (MAE = 1.178) was the most accurate interpolation method for \(T_{ \max }\) (Table 4; Fig. 6). In a manner similar to \(T_{ \min }\), the OK method with Gaussian semi-variogram (MAE = 1.256) and the UK method with Linear Drift semi-variogram (MAE = 1.286) were also among the more accurate methods. In general, kriging methods provided acceptable results, except for UK with a Quadratic Drift semi-variogram, which, along with SR were among the weaker methods. All interpolation methods presented a higher estimation error in winter and lower errors in spring and autumn (Fig. 6).

Fig. 6
figure 6

Variation of monthly MAE for Tmax using different interpolation methods

Full size image

The results of interpolations of mean monthly precipitation showed that the IDW and RS methods were relatively weak compared to other interpolation techniques (Table 5). All three evaluation criteria ranked them 10th and 11th in accuracy. Among kriging interpolation techniques, OK with Exponential semi-variogram (MAE = 0.546) and UK with Linear with Quadratic Drift semi-variogram (MAE = 0.5) showed the greatest accuracy. Overall, the NN method with the least error value (MAE = 0.241) gave the best estimates among all methods followed by UK with Quadratic Drift (MAE = 0.5) and UK with Linear Drift semi-variogram (MAE = 0.52). It is evident that in all months of the year, the NN method had the lowest MAE among the methods (Fig. 7).

Fig. 7
figure 7

Variation of monthly MAE for precipitation using different interpolation methods

Full size image

Most of the basin’s precipitation occurs during spring and autumn, from October to June. This is related to the seasonal variation in temperature and precipitation, a result of clouds generated in Europe and northern Africa, which bring heavy rains. On the other hand, in the summer, the basin receives little precipitation except for high elevation areas in the west where the mountains are located.

Accordingly, higher estimation errors occurred in the winter and lower errors in the spring and autumn, while in the summer months all interpolation methods studied showed very small estimation errors (Fig. 7).

Mapping of climatic variables

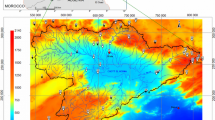
The spatial distribution patterns of optimally interpolated monthly \(T_{ \min }\), \(T_{ \max }\), and precipitation are shown for the month of January (Fig. 8). Plots for \(T_{ \min }\) and \(T_{ \max }\) (Fig. 8a, b) illustrated a temperature gradient from west to east with both variables lowest in the west and highest in the central and eastern portions of the study area. Precipitation increased gradually from the west and southwest to the eastern part of the basin (Fig. 8c). The results obtained in this study confirmed the results of past studies in this area such as Fadavi and Bazarafshan (2016) and Fadavi et al. (2016).

Fig. 8
figure 8

Optimal monthly mean zoning using climatic data (in January) in the study area: aTmin, bTmax and c precipitation

Full size image

Conclusions

The present research was carried out to determine the most accurate spatial monthly patterns for three meteorological variables (\(T_{ \min }\), \(T_{ \max }\) and precipitation) using six spatial interpolation techniques including IDW, NN, RS, TS, OK and UK in the Zayandeh-Rud River basin of Iran using 45 years of data (1970–2014). Among the different spatial interpolation methods, the IDW method was found to be the most sensitive to interpolation variables including \(T_{ \min }\), \(T_{ \max }\), and precipitation. Therefore, choosing correct values of parameters (N and P) is a critical step in the overall process of IDW interpolation.

The best method for spatial pattern analysis of the three climatic variables was identified by applying different error criteria. Among all methods studied, OK with Gaussian semi-variogram was identified as an appropriate technique for spatial analysis and interpolation of \(T_{ \min }\) and NN was found to be the most accurate technique for both \(T_{ \max }\) and precipitation.