Introduction

Interpretation of magnetic anomalies of dikes is often used in mining and oil exploration geophysics. Several researchers interpret these anomalies by separating the anomalies into even and odd components which are origin-symmetric. Among these researchers, Hutchinson (1958) used logarithmic curve fitting, Bhimasankaram et al. (1978) used Fourier transform method, andKara et al. (1996) and Kara (1997) used correlation factors and integration nomograms on the even and odd components. Rao et al. (1973) developed two different methods, applied using the horizontal derivative of the anomaly. Atchuta Rao and Ram Babu (1981) used nomograms, depending whether the anomaly is due to a dike or a fault, for interpretation using the maximum and minimum values of the anomaly.

Additionally, Murthy (1985) applied the midpoint method, and Mohan et al. (1982) and Ram Babu and Atchuta Rao (1991) applied the Hilbert transform method on magnetic anomalies. Atchuta Rao et al. (1981) used complex gradient method, and Ram Babu et al. (1982) derived relation diagrams. Abdelrahman and Essa (2005) estimated depth and shape factors for simple geological models from magnetic data using least squares method. Abdelrahman et al. (2007) developed a least squares approach to determine the depth and width of a thick dipping dike using filters of successive window lengths. Abdelrahman and Essa (2015) developed a method to recover depth and shape properties of simple geological models from second derivative anomalies. Abo-Ezz and Essa (2016) linearized magnetic anomaly formula for simple geological models and estimated model parameters using least squares method. Essa and Elhussein (2017) estimated all the model parameters of a dipping dike by calculating second horizontal gradient anomalies using successive window lengths and minimizing the misfit between observed and predicted data. Essa (2007) obtained the shape factors and depth values for spheres, horizontal cylinders, and vertical infinite cylinders using a procedure similar to the method proposed in this paper.

In this study, a set of curves is obtained using the even component, each by dividing the maximum of the even component to its value for a different distance x. Depth and half-width values of the dike are determined from the intersection point of these curves. The proposed method is tested on a synthetic model and thereafter applied to field data.

Method

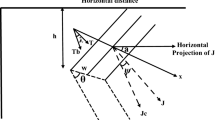
For a Cartesian coordinate system with the Y axis showing the strike of the anomalous structure and X axis showing the profile direction, the magnetic anomaly (ΔF) of a 2D infinite vertical dipping dike (Fig. 1) at any point P(x) is given by the following formula (Parker Gay 1963):

$$\Delta F = C\left\{ {\cos Q\left[ {\tan^{ - 1} \left( {\frac{x + 1}{h}} \right) - \tan^{ - 1} \left( {\frac{x - b}{h}} \right)} \right] + \frac{1}{2}\sin Q \ln \left[ {\frac{{\left( {x + b} \right)^{2} + h^{2} }}{{\left( {x - b} \right)^{2} - h^{2} }}} \right]} \right\}$$
(1)

where x is the distance between the observation point and the origin, h is the depth to the top of the dike, b is the half-width, θ is the dipping angle, k is the susceptibility contrast, and T is the normalized total field strength. C and Q denote the amplitude coefficient and index parameter, respectively, and their values for total, vertical, and horizontal field are given in Table 1. \(I = \tan^{ - 1} \left( {\tan i/\cos \alpha } \right)\), where i is the geomagnetic inclination in the study area, and α is the azimuth of the profile according to the magnetic north (Figs. 2, 3).

Fig. 1
figure 1

a Plan view of a 2D body showing the direction of the profile and magnetic north. b Cross-sectional view of a 2D dike

Full size image
Table 1 Amplitude coefficient and index parameter values for different magnetic field components
Full size table
Fig. 2
figure 2

Flowchart of the proposed method for a single curve. The process should be repeated for different values of x, in order to obtain a set of curves

Full size image
Fig. 3
figure 3

Locating origin of a magnetic anomaly

Full size image

Since Eq. 1 may be given as a summation of even and odd functions, it can be re-written as

$$\Delta F\left( x \right) \, = \, A\left( x \right) \, + \, B\left( x \right),$$
(2)

where

$$A\left( x \right) = C \cdot \cos Q\left[ {\tan^{ - 1} \left( {\frac{x + b}{h}} \right) - \tan^{ - 1} \left( {\frac{x - b}{h}} \right)} \right]\;\left( {\text{even}} \right)$$
(3a)
$$B\left( x \right) = \frac{1}{2}C \cdot \sin Q \cdot \ln \left[ {\frac{{\left( {x + b} \right)^{2} + h^{2} }}{{\left( {x - b} \right)^{2} + h^{2} }}} \right]\;\left( {\text{odd}} \right),$$
(3b)

Anomalies of ΔF(x), A(x), and B(x) may be seen in Fig. 4 for the synthetic example.

Fig. 4
figure 4

Magnetic anomaly and its even and odd components calculated for the theoretical example

Full size image

A(x) takes its maximal value for x = 0 and can be expressed as

$$A\left( 0 \right) = A_{\hbox{max} } = 2 \cdot C \cdot \cos Q \cdot \tan^{ - 1} \left( {\frac{b}{h}} \right)$$
(4)

After dividing the maximal value of the even component by its value for any x, left and right sides of the equation may be given separately as

$$S1 = \frac{A\left( 0 \right)}{A\left( x \right)}$$
(5a)

and

$$S2 = \frac{{2 \cdot \tan^{ - 1} \left( {\frac{b}{h}} \right)}}{{\tan^{ - 1} \left( {\frac{x + b}{h}} \right) - \tan^{ - 1} \left( {\frac{x - b}{h}} \right)}}$$
(5b)

Variable S1 is obtained from the field data, by dividing the maximum of the even component to its value at any x. The first set of S2 values is calculated by assigning a minimal value for the depth (h), and slowly increasing the half-width (b), starting from a minimal value until it reaches its maximum possible value. Different sets of S2 are calculated by slowly increasing the value of h to a maximal value. For each set of S2, values of h and b yield to the S2 closest to S1 are obtained. These values of h and b are plotted as a curve by assigning h to the horizontal axis and b to the vertical axis. The flowchart of the proposed method is given in Fig. 2. Even though the obtained curve depicts a non-uniqueness, after repeating the process for different distances, and plotting resulting curves (each depicting a non-uniqueness) on the same graph, the intersection point of these curves yields to the actual values of h and b.

Location of the origin and the base level

To obtain even and odd components of an anomaly due to a dike, the location of the origin and the base level should be determined in prior. Powell (1967) proposed a method aiming at this need. Accordingly, if the origin is in its actual location, there applies the following equation:

$$x_{1} \cdot y_{1} = x_{2} \cdot y_{2}$$

and if it is not, the equation becomes (Fig. 3),

$$\left( {x_{1} + \Delta } \right) \cdot \left( {y_{1} - \Delta } \right) = \left( {x_{2} + \Delta } \right) \cdot \left( {y_{2} - \Delta } \right)$$

When this equation is solved for Δ,

$$\Delta = \frac{{x_{2} \cdot y_{2} - x_{1} \cdot y_{1} }}{{x_{2} - x_{1} - y_{2} + y_{1} }}$$
(6)

is obtained. The base level is obtained from the equation (Koulomzine et al. 1970)

$$\Delta F\left( 0 \right) \, = \, \Delta F_{ \hbox{max} } \, + \, \Delta F_{ \hbox{min} }$$
(7)

where ΔF(0) is the value of the anomaly at the origin.

Following the determination of the origin and the base level, the even and odd components are calculated using the equations

$$A\left( x \right) = \frac{1}{2}\left[ {\Delta F\left( x \right) + \Delta F\left( { - x} \right)} \right]\;\left( {\text{even}} \right)$$
(8a)

and

$$B\left( x \right) = \frac{1}{2}\left[ {\Delta F\left( x \right) - \Delta F\left( x \right)} \right]\left( {\text{odd}} \right)$$
(8b)

Once the proposed method is implemented on the even component, and the depth (h) and half-width (b) parameters are obtained, the index parameter (Q) should be calculated for determining the dipping angle.

For any x ≠ 0, it is possible to solve Q by using B(x)/A(x) as below:

$$Q = \tan^{ - 1} \left\{ {\frac{{B\left( x \right)\left[ {\tan^{ - 1} \left( {\frac{x + b}{h}} \right) - \tan^{ - 1} \left( {\frac{x - b}{h}} \right)} \right]}}{{A\left( x \right)\left[ {\frac{1}{2}\ln \left[ {\frac{{\left( {x + b} \right)^{2} + h^{2} }}{{\left( {x - b} \right)^{2} + h^{2} }}} \right]} \right]}}} \right\}$$
(9)

Since Q is obtained between 0 and 90 (degrees) from Eq. 9, the following criterions should be applied to calculate Q correctly;

  • Major positive anomaly towards the positive x-axis: \(Q = Q_{n} ;\)

  • Major positive anomaly towards the negative x-axis: \(Q = \, - Q_{n} ;\)

  • Major negative anomaly towards the positive x-axis: \(Q = Q_{n} - 180^\circ ;\)

  • Major negative anomaly towards the negative x-axis: \(Q = - (Q_{n} + 180^\circ ),\)

where Q n is the value of Q obtained using Eq. 9 (Atchuta Rao and Ram Babu 1981).

Since all of the parameters except amplitude coefficient (C) are derived, the value of C can be calculated using Eq. 4.

Theoretical example

The parameters of the theoretical model are as follows: C = 500 nT, h = 8 m, b = 6 m, and Q = −60° (degrees). The calculated anomaly and the even and odd components for the described model are given in Fig. 4. The curves given in Fig. 5a are obtained by implementing the proposed method for x = 3, 6, 9, and 12. According to the method, the intersection point of these curves should correspond to the depth (h) and half-width (b) of the dike. In the figure, it is easy to determine that the intersection point corresponds to h = 8 m, and b = 6 m. The above-mentioned parameters obtained are the same as those of the theoretical model, showing the validity of the proposed method.

Fig. 5
figure 5

a The curves obtained by implementing the proposed method to the anomaly calculated for the theoretical model (Fig. 4); b the same curves in the presence of an erroneously assessed origin. In this case, the curves are not intersecting at a common point as they do in Fig. 5a, and the point of intersection is not leading to the actual values of h and b

Full size image

Before the implementation of the method, regional effects, and density irregularities must be eliminated. Besides, the zero line and particularly the origin must be determined correctly; otherwise, the calculated curves may not intersect at a single point. To show this, the origin shown in Fig. 4 is shifted by 1 unit the right and the curves are re-calculated, as shown in Fig. 5b. One should note that there is no common intersection point for all curves. Besides, for the point the curves for x = 6, 9, and 12 intersect, the values of h and b are different from their actual values.

Field example

For the field example, the vertical field magnetic anomaly data over Marcona district in Peru (Fig. 11 of Parker Gay 1963) is sampled with 50 m intervals and is shown in Fig. 6. The even and odd components calculated for this anomaly are shown in Fig. 7.

Fig. 6
figure 6

The vertical field magnetic anomaly over Marcona district, Peru (Parker Gay 1963) and the calculated anomaly for the model parameters obtained using the proposed method

Full size image
Fig. 7
figure 7

The even and odd components of the field data given in Fig. 6

Full size image

The proposed method is applied on the even component for x = 0, 100, 200, 300, 400 m, and b = 188 m and h = 154 m are obtained (Fig. 8). After using Eq. 9, Q = −50.3° is obtained and since all model parameters except the amplitude coefficient (C) are derived, the value of C is determined by using Eq. 4. The anomaly calculated for these model parameters is shown in Fig. 6. It is easy to note the similarity between the observed and the calculated anomalies. Previous interpretations of the same anomaly by several authors are compared to the results of this study in Table 2.

Fig. 8
figure 8

The curves obtained by the implementation of the proposed method to the field data

Full size image
Table 2 Analysis results of the vertical magnetic anomaly shown in Fig. 6
Full size table

Conclusions

In this study, a method incorporating the even component of magnetic anomalies is presented to obtain depth and half-width of dikes. In the method, a curve is obtained by dividing the maximum of the even component to its value at any distance x. After several curves for different x values are plotted on a graph, the top-depth and half-width of the dike are delineated from the intersection point of these curves. Using this method, the anomaly may be interpreted using the maximum of the even component and its value at two different distances. The previously proposed methods were not applicable for Q = 0° or 90°, whereas the method proposed in this study allows interpretation for Q = 0°. Even though the method has such advantages, the curves would not lead to the actual values in the presence of noise, erroneous assessment of the zero line or the origin.