Inverse optimal value problem on minimum spanning tree under unit $l_{\infty }$ norm

Abstract

We consider the inverse optimal value problem on minimum spanning tree under unit $l_{\infty }$ norm. Given an edge weighted connected undirected network $G=(V, E, {\varvec{w}})$ and a spanning trees $T^0$, we aim to modify the weights of the edges such that $T^0$ is the minimum spanning tree under the new weight vector whose weight is equal to a given value K and the modification cost under unit $l_{\infty }$ norm is minimized. We present a mathematical model of the problem. After analyzing the properties, we propose a sufficient and necessary condition for optimal solutions of the problem. Then we develop a strongly polynomial time algorithm with running time O(|V||E|). Finally, we give an example to demonstrate the algorithm.

1 Introduction

In recent years, spanning tree problems have become an important topic in the field of combinatorial optimization due to many applications in transportation networks, communication networks, etc. Let $G=(V, E, {\varvec{w}})$ be a connected undirected network, where $V=\{1, 2, \ldots , n\}$ and $E=\{e_1, e_2, \ldots , e_m\}$. Each edge $e_i$ is associated with a weight $w_i$. Let ${\varvec{w}}=(w_1, w_2, \ldots , w_m)$ be the weight vector. Let $\varGamma$ be the set of all spanning trees of G. The weight of a spanning tree T is defined as the sum of weights of edges in T, that is, ${\varvec{w}}(T) = \sum _{e_i\in T}w_i$. The minimum spanning tree (MST) problem is to find a spanning tree $T\in \varGamma$ whose weight is minimum.

We consider the inverse optimal value problems on minimum spanning trees under unit $l_{\infty }$ norm (denoted by IOVMST$_\infty$), which can be described as follows. Given a spanning tree $T^0$ of G, we aim to find a new edge weight vector ${\varvec{\bar{w}}}$ such that

• (1) The weight of $T^0$ under ${\varvec{\bar{w}}}$ is equal to a given value K, where $K<{\varvec{w}}( T^0)$;

• (2) $T^0$ is the minimum spanning tree under ${\varvec{\bar{w}}}$, that is, the weight of any spanning tree under ${\varvec{\bar{w}}}$ is not less than K;

• (3) The maximum modification $\max _{e_i\in E} |\bar{w}_i-w_i|$ is minimized.

The problem IOVMST$_\infty$ can be formulated as follows:

$$\begin{aligned} \begin{array}{lll} &{}\min _{{\varvec{\bar{w}}}} &{}\max _{e_i\in E} |\bar{w}_i-w_i|\\ &{}{\text{ s.t. }}&{} \sum \limits _{e_i\in T^{0}}\bar{w}_i= K, \\ &{} &{} \sum \limits _{e_j \in T}\bar{w}_j \ge K, \quad \forall T\in \varGamma . \end{array} \end{aligned}$$

(1.1)

The problem IOVMST$_\infty$ has practical background. An enterprise has n agents in a region, each agent has connection with other agents [2]. Any commercial message passed between agents i and j will fall into hostile hands with certain probability $p_{ij}$. Define the edge weight of edge $e_k$ between agents i and j as $w_k=p_{ij}$. The enterprise leader wants to transmit confidential commercial messages among all the agents through a spanning tree $T^0$ of a safe network. A safe network $T^0$ means the total probability of $T^0$ to be intercepted is minimum and the total probability is small enough to be a constant K. The leader aims to change edge weight ${\varvec{w}}$ to ${{\varvec{\bar{w}}}}$ such that the maximum deviation $|\bar{w}_k-w_k|$ of each edge $e_k$ is minimum. To meet this requirement, the leader needs to arrange some training courses for some agents to decrease the probabilities of interception when transmitting commercial messages among some edges. Notice that more deviation $|\bar{w}_k-w_k|$ of edge $e_k$ needs more cost $c_k$ of training courses for agents i and j. For example, let $c_k=a^{|\bar{w}_k-w_k|}$ and $a=10$. Then the cost $c_k$ is 10US$ when $|\bar{w}_k-w_k|=1$, but $c_k$ is 100 US$ when $|\bar{w}_k-w_k|=2$. This is just an inverse optimal value problem on minimum spanning tree.

Notice that there is another kind of inverse optimal value problems on minimum spanning trees under unit $l_{\infty }$ norm, in which we do not need to preassign a spanning tree $T^0$, but to make the weight ${\varvec{\bar{w}}}(T)$ of any MST under ${{\varvec{\bar{w}}}}$ to be a given value K. The mathematical model is given below.

$$\begin{aligned}&\min _{{\varvec{\bar{w}}}}&\max _{e_i\in E} |\bar{w}_i-w_i| \nonumber \\&{\text{ s.t. }}&\min _{T \in \varGamma }\sum _{e_i \in T}\bar{w}_i =K. \end{aligned}$$

(1.2)

However, the problem (1.2) is trivial to solve. Firstly, we find a minimum spanning tree $T^{*}$ under ${\varvec{w}}$, then solve equation $\sum _{e\in T^{*}}(w_i+\lambda ^{*})=K$ to calculate $\lambda ^{*}=\frac{K-{\varvec{w}}(T^{*})}{n-1}$. If $\lambda ^{*}\ge 0$, then $w^{*}_i=w_i+\lambda ^{*}$ for each $e_i\in E$. If $\lambda ^{*}<0$, then $w^{*}_i=w_i+\lambda ^{*}$ for each $e_i\in T^{*}$, and $w^{*}_i=w_i-\lambda ^{*}$ for each $e_i\not \in T^{*}$. It is not difficult to prove that $T^{*}$ is still a minimum spanning tree under ${\varvec{w^{*}}}$ and ${\varvec{w^{*}}}$ is an optimal solution of the problem (1.2) with objective value $|\lambda ^{*}|$. Thus, in this paper, we consider the problem IOVMST$_\infty$.

Related to the problem IOVMST$_\infty$, the inverse minimum spanning tree problems (1.3) (denoted by IMST) are mostly studied under different norms including $l_1$ and $l_{\infty }$ norms and Hamming distance [3,4,5,6,7,8,9,10, 12,13,14,15,16,17,18].

$$\begin{aligned}&\min&\Vert {\varvec{\bar{w}}}-{\varvec{w}}\Vert \nonumber \\ (\mathbf{IMST} )&{\text{ s.t. }}&\sum \limits _{e_i \in T^{0}}\bar{w}_i\le \sum \limits _{e_j \in T}\bar{w}_j, \quad \forall T\in \varGamma . \end{aligned}$$

(1.3)

Note that in the problem IMST we do not need to preassign a value K to the weight ${\varvec{\bar{w}}}(T^0)$ for the given MST $T^0$ under the new weight vector ${\varvec{\bar{w}}}$, hence the problem IOVMST$_\infty$ is a subproblem of the problem IMST$_\infty$ under unit $l_\infty$ norm. For the problem IMST$_\infty$, Sokkalingam et al. [13] showed that it can be solved in $O(n^2)$ time, and Hochbaum [8] proposed an $O(m\log n)$ algorithm, which is more efficient if the graph is not dense.

For the partial inverse minimum spanning tree problem (denoted by PIMST), in which not a full spanning tree but a part of it (a forest) is given, Lai and Orlin [9] showed that the problem PIMST under the weighted $l_{\infty }$ norm can be solved in strongly polynomial time. Li et al. [10] showed that the capacitated PIMST under $l_{\infty }$ norm can be solved in polynomial time, in which the deviation $|\bar{w}_i-w_i|$ is upper-bounded by given values for each ${e_i\in E}$. Cai et al. [4] considered the capacitated PIMST when weight increasing is forbidden and presented a strongly polynomial time algorithm for a general criterion objective function including $l_1, l_2, l_\infty$ norms.

Ahmed and Guan [1] considered the inverse optimal value (IOVLP) problem on linear programming (LP) problem. Given an LP problem with a desired optimal objective value and a set of feasible cost vectors, they aim to determine a cost vector such that the optimal objective value of the LP is closest to the desired value. They first proved that the general problem IOVLP is NP-hard, then for a concave maximization/minimization problem, they provided sufficient conditions, under which the problem IOVLP is polynomially solvable. When the set of feasible cost vectors is polyhedral, they described an algorithm for the problem IOVLP by solving linear and bilinear programming problems. Lv et al. [11] transformed the problem IOVLP under some conditions into a nonlinear bilevel programming problem, which was transformed into a single-level nonlinear program using the Kuhn–Tucker optimality condition of the lower level problem. They proposed an algorithm based on exact penalty method and analysed its convergence.

The paper is organized as follows. In Sect. 2, we study some properties of optimal solutions of the problem IOVMST$_\infty$ and propose a sufficient and necessary condition. In Sect. 3, we develop a strongly polynomial time algorithm with time complexity O(mn). A computational example of the problem IOVMST$_\infty$ is given in Sect. 4. Finally, conclusion and discussion are given in Sect. 5.

2 Properties of an optimal solution of the problem IOVMST $_\infty$

In this section, we analyze some properties of an optimal solution of the problem IOVMST$_\infty$. Most importantly, we obtain a sufficient and necessary condition for an optimal solution.

We first introduce some notations. For each $e_j \notin T^{0}$, $T^{0}\cup \{e_j\}$ contains a fundamental cycle, and we denote by $P_j$ all edges in this cycle except $e_j$ and define $\varOmega _i=\{e_j\notin T^{0}|e_i\in P_j\}$. If both edge $e_j\not \in T$ and edge $e_i\in T$ are in at least one cycle, then $e_j\in \varOmega _i$. Let $\varOmega ^{0}=\{e_i\in T^{0}| \varOmega _i=\emptyset \}$ be the set of isolated edges in $T_0$, which belongs to every spanning tree of G. If $\varOmega ^{0}\not =\emptyset$, then $\varOmega ^{0}$ is also the set of cut edges of G. If $\varOmega ^{0}=\emptyset$, then each edge in $T^{0}$ belongs to at least one fundamental cycle. Let

$$\begin{aligned} \delta =\max _{e_i\in T^{0}}\max _{e_k\in \varOmega _i}\{w_i-w_k\}\end{aligned}$$

(2.1)

be the maximum deviation between $w_i$ and $w_k$ for each $e_i\in T^{0}$ and $e_k\in \varOmega _i$. Denote $\varTheta _i=\{e_{j_i}\in \varOmega _i| w_i-w_{j_i}=\max _{e_k\in \varOmega _i}\{w_i-w_k\}> 0 \}$ as the set of edges $e_{j_i}\in \varOmega _i$ achieving the maximum value for $e_i$. Let $\varTheta ^{0}=\{e_i\in T^{0}{\setminus }\varOmega ^{0}| \varTheta _i=\emptyset \}$. If $\varTheta ^{0}\not =\emptyset$, then for each $e_i\in \varTheta ^{0}$, if $e_p\in \varOmega _i$, then $w_p\ge w_i$. If $\varTheta ^{0}=\emptyset$, then for each $e_i\in T^{0}{\setminus } \varOmega ^{0}$, there exists an edge $e_p\in \varOmega _i$ such that $w_p<w_i$. In order to explain the meaning of above notations, we give the next example.

Example 1

As shown in Fig. 1, let $V=\{v_1,v_2,\dots ,v_{11}\}$, $E=\{e_1,e_2,\dots ,e_{17}\}$, ${\varvec{w}}=(3,4,3,3,4,3,1,5,5,$ 3, 4, 5, 5, 3, 4, 4, 1), $T^0=\{e_1,e_2,e_3,e_4,e_8,e_9,e_{12},e_{13},e_{15},e_{16}\}$ ($T^0$ is denoted by thick lines in Fig. 1).

Fig. 1

An example to show the meanings of notations

In Example 1 shown in Fig. 1,

(1) for each $e_i\not \in T^{0}$, $P_5=\{e_3,e_4\}$, $P_6=\{e_2,e_4\}$, $P_7=\{e_2,e_4,e_8\}$, $P_{10}=\{e_8,e_9\}$, $P_{11}=\{e_8,e_9,e_{13}\}$, $P_{14}=\{e_8,e_9,e_{12},e_{13}\}$, and $P_{17}=\{e_8,e_9,e_{12},e_{13},e_{15}\}$;

(2) for each $e_i\in T^{0}$, $\varOmega _1=\varOmega _{16}=\emptyset$, $\varOmega _2=\{e_6,e_7\}$, $\varOmega _3=\{e_5\}$, $\varOmega _4=\{e_5,e_6,e_7\}$, $\varOmega _8=\{e_7,e_{10},e_{11},e_{14},e_{17}\}$, $\varOmega _9=\{e_{10},e_{11},e_{14},e_{17}\}$, $\varOmega _{12}=\{e_{14},e_{17}\}$, $\varOmega _{13}=\{e_{11},e_{14},e_{17}\}$, $\varOmega _{15}=\{e_{17}\}$;

(3) for each $e_i\in T^{0}$, $\varTheta _1=\varTheta _{16}=\emptyset$, $\varTheta _2=\{e_7\}$, $\varTheta _3=\emptyset$, $\varTheta _4=\{e_7\}$, $\varTheta _8=\{e_7,e_{17}\}$, $\varTheta _9=\{e_{17}\}$, $\varTheta _{12}=\{e_{17}\}$, $\varTheta _{13}=\{e_{17}\}$, $\varTheta _{15}=\{e_{17}\}$;

(4) $\varOmega ^{0}=\{e_1,e_{16}\}$ and $\varTheta ^{0}=\{e_3\}$;

(5) $e_{j_2}=e_7$, $e_{j_4}=e_7$, $e_{j_8}=e_7$ or $e_{j_8}=e_{17}$, $e_{j_9}=e_{17}$, $e_{j_{12}}=e_{17}$, $e_{j_{13}}=e_{17}$, $e_{j_{15}}=e_{17}$; $\delta =w_8-w_{j_8}=w_8-w_7=4$;

Next, we analyze some properties of a feasible solution of the problem IOVMST$_\infty$.

Lemma 1

[2] $T^0$ is a minimum spanning tree with respect to the weight vector ${\varvec{\bar{w}}}$ if and only if the following optimality conditions are satisfied:

$$\begin{aligned} \bar{w}_i\le \bar{w}_j \quad \hbox {for each}\ e_j\notin T^{0}\ \hbox {and} \ e_i\in P_j. \end{aligned}$$

(2.2)

Lemma 2

If ${\varvec{\bar{w}}}$ is a feasible solution of problem (1.1) with objective value $\bar{\lambda }$, then ${\varvec{\hat{w}}}$ is also a feasible solution of (1.1) with objective value $\hat{\lambda }=\bar{\lambda }$, where

$$\begin{aligned} \hat{w}_k =\left\{ \begin{array}{ll} \bar{w_k},&{}\quad {\text{ if } } e_k\in T^{0}, \\ w_k+\bar{\lambda },&{}\quad {\text{ if } } e_k\notin T^{0}. \end{array} \right. \end{aligned}$$

(2.3)

Proof

We first prove the feasibility of ${\varvec{\hat{w}}}$. It follows from (2.2) and (2.3) that $\hat{w}_j=w_j+\bar{\lambda }\ge \bar{w}_j\ge \bar{w}_i=\hat{w}_i$ for $e_i\in P_j$ and $e_j\notin T^{0}$, where the first inequality follows from the feasibility of ${\varvec{\bar{w}}}$ and the definition of $\bar{\lambda }$, and the second inequality follows from the feasibility of ${\varvec{\bar{w}}}$. Moreover, $\sum _{e_i\in T^0}\hat{w}_i=\sum _{e_i\in T^0}\bar{w}_i=K$. To calculate the objective value, we have $|\hat{w}_i-w_i|=|\bar{w}_i-w_i|\le \bar{\lambda }$ for each $e_i\in T^{0}$, and $|\hat{w}_j-w_j|=|w_j+\bar{\lambda }-w_j|=\bar{\lambda }$ for $e_j\notin T^{0}$. So $\hat{\lambda }=\max _{e_k\in E}|\hat{w}_k-w_k|=\bar{\lambda }$. $\square$

By Lemma 2, we know that the weight of edge $e_j\notin T^0$ in an optimal solution can be increased to the maximum weight $\hat{w}_j= w_j+\hat{\lambda }$ if the optimal objective value $\hat{\lambda }$ is obtained. In the following part of the paper, we find an optimal solution of the problem (1.1) satisfying (2.3).

By using the notation of $\varOmega _i$ for $e_i\in T^{0}$, the problem (1.1) is equivalent to

$$\begin{aligned} \begin{array}{llll} &{}\min &{} \max |\bar{w}_i-w_i|&{}\\ &{}{\text{ s.t. }}&{}\bar{w}_i\le \bar{w}_j, &{} e_i\in T^{0}\ \text{ and }\ e_j\in \varOmega _i, \\ &{} &{}\bar{w}_j\ge w_j, &{} e_j\not \in T^{0},\\ &{} &{} \sum \limits _{e_i\in T^{0}}\bar{w}_i= K. &{} \end{array} \end{aligned}$$

(2.4)

Lemma 3

If ${\varvec{\bar{w}}}$ is a feasible solution of problem (2.4) with objective value $\bar{\lambda }$, then $\bar{\lambda }\ge \frac{\delta }{2}$, where $\delta$ is defined as in (2.1).

Proof

We only consider $\delta >0$. In fact, if $\delta \le 0$, then $T^0$ is a minimum spanning tree of G under weight ${\varvec{w}}$, hence $\bar{\lambda }\ge 0\ge \frac{\delta }{2}$. It follows from Lemma 2 that ${\varvec{\hat{w}}}$ defined as in (2.3) is a feasible solution of problem (2.4). Let $\delta =\delta _p=w_p-w_{j_p}$ for some edge $e_p\in T^{0}$ and $e_{j_p}\in \varTheta _p$. Then

$$\begin{aligned} \delta =w_p-w_{j_p}=w_p-\hat{w}_p+(\hat{w}_p-w_{j_p})\le (w_p-\hat{w}_p)+(\hat{w}_{j_p}-w_{j_p})\le 2\bar{\lambda }, \end{aligned}$$

where the first inequality follows from the feasibility of ${\varvec{\hat{w}}}$ and the second inequality follows from the definition of ${\varvec{\hat{w}}}$ and $\bar{\lambda }$. Hence $\bar{\lambda }\ge \frac{\delta }{2}$. $\square$

Let ${\varvec{\hat{w}}}$ be a feasible solution of problem (2.4) which satisfies (2.3) and its value is $\hat{\lambda }$. It follows from (2.3) that $\hat{w}_j=w_j+\hat{\lambda }$ for $e_j\notin T^0$. For edge $e_i\in T^0$, the weight ${w}_i$ may be increased, decreased, or be unchanged to $\hat{w}_i$. If $\varOmega ^0\not =\emptyset$ and $e_i\in \varOmega ^0$, then $e_i$ is an isolated edge belonging to any tree including $T^{0}$ and thus $w_i$ may be increased in an optimal solution in some cases (see Fig. 4b).

2.1 Properties of an optimal solution of the problem IOVMST $_\infty$ when $\varTheta ^{0}=\emptyset$ and $\varOmega ^{0}=\emptyset$

In this subsection, we analyze some properties of an optimal solution of the problem IOVMST$_\infty$ when $\varTheta ^{0}=\emptyset$ and $\varOmega ^{0}=\emptyset$, then we propose a sufficient and necessary condition for an optimal solution of the problem IOVMST$_\infty$.

If $\varTheta ^{0}=\emptyset$, then $w_i-\hat{\lambda }\le \hat{w}_i\le w_{j_i}+\hat{\lambda }$ for $e_i\in T^0, e_{j_i}\in \varTheta _i$. Define

$$\begin{aligned} \left\{ \begin{array}{ll} EU({\varvec{\hat{w}}})=&{}\{e_i\in T^{0}|~ \hat{w}_i=w_{j_i}+\hat{\lambda }, e_{j_i}\in \varTheta _i\}, \\ ED({\varvec{\hat{w}}})=&{}\{e_i\in T^{0}|~ \hat{w}_i=w_i-\hat{\lambda }\}, \\ EM({\varvec{\hat{w}}})=&{}\{e_i\in T^{0}|~ w_i-\hat{\lambda }<\hat{w}_i<w_{j_i}+\hat{\lambda }, e_{j_i}\in \varTheta _i\}. \end{array}\right. \end{aligned}$$

(2.5)

Obviously, $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})\cup EU({\varvec{\hat{w}}})=T^0$. Let $N_U=|EU({\varvec{\hat{w}}})|, N_D=|ED({\varvec{\hat{w}}})|, N_M=|EM({\varvec{\hat{w}}})|$. Define

$$\begin{aligned} \left\{ \begin{array}{ll}\gamma ({\varvec{\hat{w}}})=&{}\min \{\hat{w}_i-(w_i-\hat{\lambda })|~e_i\in EM({\varvec{\hat{w}}})\},\\ \eta ({\varvec{\hat{w}}})=&{}\min \{(w_{j_i}+\hat{\lambda })-\hat{w}_i|~e_i\in EM({\varvec{\hat{w}}})\}. \end{array}\right. \end{aligned}$$

(2.6)

In order to explain the meaning of above notations, we give the next example.

Example 2

As shown in Fig. 2, let $V=\{v_1,v_2,\dots ,v_{9}\}$, $E=\{e_1,e_2,\dots ,e_{15}\}$, ${\varvec{w}}=(1,4,5,3,4,3,1,5,5,$ 3, 4, 5, 5, 3, 4), $T^0=\{e_2,e_3,e_4,e_8,e_9,e_{12},e_{13},e_{15}\}$ ($T^0$ is denoted by thick lines in Fig. 2), $K=22$, ${\varvec{\hat{w}}}=\{3.5, {\varvec{3.5}},{\varvec{2.5}},{\varvec{2}},6.5,3.5,{\varvec{3.5}},{\varvec{3}},5.5,6.5,{\varvec{3.5}},{\varvec{2.5}},5.5,{\varvec{1.5}}\}$.

Fig. 2

An example to explain the meanings of $ED({\varvec{\hat{w}}}), EM({\varvec{\hat{w}}}), EU({\varvec{\hat{w}}}), \gamma ({\varvec{\hat{w}}})$ and $\eta ({\varvec{\hat{w}}})$

In Example 2 shown in Fig. 2, ${\varvec{w}}(T^{0})=36$, and it is easy to check that ${\varvec{\hat{w}}}$ is a feasible solution of problem (2.4) satisfying (2.3) with objective value $\hat{\lambda }=2.5$.

• (1) $EU({\varvec{\hat{w}}})=\{e_2,e_8,e_{12}\}$. For example, $e_{j_2}=e_7$ and $\hat{w}_2=w_7+\hat{\lambda }$, so $e_2\in EU({\varvec{\hat{w}}})$.

• (2) $ED({\varvec{\hat{w}}})=\{e_3,e_{13},e_{15}\}$. For example, $e_{j_{13}}=e_{1}$ and $\hat{w}_{13}=w_{13}-\hat{\lambda }$, so $e_{13}\in ED({\varvec{\hat{w}}})$.

• (3) $EM({\varvec{\hat{w}}})=\{e_4,e_9\}$. For example, $e_{j_9}=e_1$ and $w_{9}-\hat{\lambda }<\hat{w}_{9}<w_1+\hat{\lambda }$, so $e_{9}\in EM({\varvec{\hat{w}}})$.

• (4) $\gamma ({\varvec{\hat{w}}})=\min \{\hat{w}_4-(w_4-2.5),\hat{w}_9-(w_9-2.5)\}=\hat{w}_9-(w_9-2.5)=0.5$, $\eta ({\varvec{\hat{w}}})=\min \{(w_{j_4}+2.5)-\hat{w}_4,(w_{j_9}+2.5)-\hat{w}_9\}=(w_{j_9}+2.5)-\hat{w}_9=0.5$.

It is not difficult to see that ${\varvec{\hat{w}}}$ is not an optimal solution and $EM({\varvec{\hat{w}}})=\{e_4,e_9\}\not =\emptyset$ in Example  2.

Next, we use the notations given above to analyze some properties of an optimal solution.

Theorem 4

Suppose $\varOmega ^{0}=\emptyset$ and $\varTheta ^{0}=\emptyset$. Let ${\varvec{\hat{w}}}$ be a feasible solution of problem (2.4) satisfying (2.3) and $\hat{\lambda }>\frac{\delta }{2}$. If $EM({\varvec{\hat{w}}})\ne \emptyset$, then ${\varvec{\hat{w}}}$ is not an optimal solution of (2.4), where $EM({\varvec{\hat{w}}})$ is defined as in (2.5).

Proof

We consider four cases, in which we find a better feasible solution ${\varvec{w^*}}$ than ${\varvec{\hat{w}}}$ satisfying $\lambda ^*<\hat{\lambda }$. If $EM({\varvec{\hat{w}}})\ne \emptyset$, then $\eta ({\varvec{\hat{w}}})>0, \gamma ({\varvec{\hat{w}}})>0$. Let $\alpha =\min \{\eta ({\varvec{\hat{w}}}),\gamma ({\varvec{\hat{w}}})\}$, then $\alpha >0$.

Case 1 $EU({\varvec{\hat{w}}})=\emptyset , ED({\varvec{\hat{w}}})=\emptyset .$

Then $EM({\varvec{\hat{w}}})=T^0$ and $\hat{\lambda }\ge \alpha$. Next we show that the weight vector ${\varvec{w^*}}$ defined below is a feasible solution of problem (2.4) whose objective value is $\lambda ^*=\hat{\lambda }-\alpha <\hat{\lambda }$.

$$\begin{aligned} w^*_k =\left\{ \begin{array}{ll} \hat{w}_k,&{}\quad {\text{ if } }e_k\in T^{0},\\ \hat{w}_k-\alpha ,&{}\quad {\text{ if } }e_k\notin T^{0}. \end{array} \right. \end{aligned}$$

For each $e_i\in EM({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, and $e_{j_i}\in \varTheta _i$, then $w_k\ge w_{j_i}$ and $e_k, e_{j_i}\notin T^0$.

$$\begin{aligned} w^*_k\ge w^*_{j_i}= & {} \hat{w}_{j_i}-\alpha =w_{j_i}+\hat{\lambda }-\alpha \\ {}= & {} (w_{j_i}+\hat{\lambda }-\hat{w}_i)+\hat{w}_i-\alpha \ge \eta ({\varvec{\hat{w}}})+\hat{w}_i-\alpha \ge \hat{w}_i=w^*_i, \end{aligned}$$

where the first inequality follows from the definition of $w^*$, ${\hat{w}}$ and $e_{j_i}$, the second inequality follows from the definition of $\eta (\hat{w}$) and the third inequality follows from the definition of $\alpha$.

Furthermore, $w^*_k = \hat{w}_k-\alpha =w_k+\hat{\lambda }-\alpha \ge w_k$ for $e_k\notin T^0$ and $\sum _{e_i\in T^{0}}w^*_i=\sum _{e_i\in T^{0}}\hat{w}_i= K.$ Hence, ${\varvec{w^*}}$ is a feasible solution of problem (2.4).

Now we calculate the objective value $\lambda ^*$. Firstly, for each $e_j\notin T^{0}$, $|w^*_j-w_j|=|w_j+\hat{\lambda }-\alpha -w_j|=|\hat{\lambda }-\alpha |=\lambda ^*$. Secondly, we show that $|w^*_i-w_i|\le \lambda ^*$ for each $e_i\in T^{0}=EM({\varvec{\hat{w}}})$. (a) $w^*_i-w_i\le w^*_{j_i}-w_i=w_{j_i}+(\hat{\lambda }-\alpha )-w_i\le \hat{\lambda }-\alpha =\lambda ^*$; (b) Notice that $\hat{w}_i-w_i+\hat{\lambda }\ge \gamma ({\varvec{\hat{w}}})$. Then $w^*_i=\hat{w}_i\ge w_i-\hat{\lambda }+\gamma ({\varvec{\hat{w}}})\ge w_i-\hat{\lambda }+\alpha$, hence $w^*_i-w_i\ge -\hat{\lambda }+\alpha =-\lambda ^*$. Thus ${\varvec{w^*}}$ is a better feasible solution than ${\varvec{\hat{w}}}$ satisfying $\lambda ^*=\hat{\lambda }-\alpha <\hat{\lambda }$.

Case 2 $EU({\varvec{\hat{w}}})=\emptyset , ED({\varvec{\hat{w}}})\not =\emptyset .$

Then $0<N_D<n-1$, $EM({\varvec{\hat{w}}})=T^{0}{\setminus } ED({\varvec{\hat{w}}})$ and $N_M=n-N_D-1>0$. Let

$$\begin{aligned} w^*_k =\left\{ \begin{array}{ll} \hat{w}_k+\xi ,&{}\quad {\text{ if } }e_k\in ED({\varvec{\hat{w}}}),\\ \hat{w}_k-\beta ,&{}\quad {\text{ if } }e_k\in EM({\varvec{\hat{w}}}),\\ \hat{w}_k-\xi ,&{}\quad {\text{ if } }e_k\notin T^{0}, \end{array} \right. \end{aligned}$$

where $\xi , \beta$ are solutions of the following equation system

$$\begin{aligned} \left\{ \begin{array}{ll} \xi \cdot N_D=(n-N_D-1)\cdot \beta ,\\ \xi +\beta =\mu ({\varvec{\hat{w}}})=\min \{\gamma ({\varvec{\hat{w}}}),\eta ({\varvec{\hat{w}}}),\hat{\lambda }-\frac{\delta }{2} \}. \end{array} \right. \end{aligned}$$

Then $\xi =\frac{n-N_D-1}{n-1}\mu ({\varvec{\hat{w}}}), \beta =\frac{N_D}{n-1}\mu ({\varvec{\hat{w}}})$. Notice that $\beta >0$ and $\xi >0$ as $\mu ({\varvec{\hat{w}}})>0$.

For each $e_i\in EM({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, $e_{j_i}\in \varTheta _i$, then

$$\begin{aligned} w^*_k\ge w^*_{j_i}= \hat{w}_{j_i}-\xi \ge \hat{w}_{j_i}-\eta ({\varvec{\hat{w}}})\ge \hat{w}_{j_i}+\hat{w}_i-({w}_{j_i}+\hat{\lambda })= \hat{w}_i>\hat{w}_i-\beta =w^*_i, \end{aligned}$$

where the second inequality follows from $0<\xi \le \mu ({\varvec{\hat{w}}})\le \eta ({\varvec{\hat{w}}})$, the third inequality follows from the definition of $\eta ({\varvec{\hat{w}}})$ and the fourth inequality follows from $\beta >0$.

For each $e_i\in ED({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, notice that $w_i-w_{j_i}\le \delta$ and $\xi <\hat{\lambda }-\frac{\delta }{2}$, then

$$\begin{aligned} w^*_k\ge w^*_{j_i}=(w_{j_i}+\hat{\lambda })-\xi \ge w_{j_i}+\frac{\delta }{2}\ge w_i-\frac{\delta }{2}\ge w_i-(\hat{\lambda }-\xi )=w^*_i. \end{aligned}$$

Furthermore,

$$\begin{aligned} \begin{array}{ll}\sum \limits _{e_i\in T^{0}}w^*_i&{}=\sum \limits _{e_i\in ED({\varvec{\hat{w}}})}w^*_i+\sum \limits _{e_i\in EM({\varvec{\hat{w}}})}w^*_i= \sum \limits _{e_i\in ED({\varvec{\hat{w}}})}(\hat{w}_i+\xi )+\sum \limits _{e_i\in EM({\varvec{\hat{w}}})}(\hat{w}_i-\beta )\\ &{}=\sum \limits _{e_i\in ED({\varvec{\hat{w}}})}\hat{w}_i+\sum \limits _{e_i\in EM({\varvec{\hat{w}}})}\hat{w}_i+\xi \cdot N_D-\beta \cdot (n-N_D-1)=\sum \limits _{e_i\in T^{0}}\hat{w}_i=K. \end{array} \end{aligned}$$

Then ${\varvec{w^*}}$ is a feasible solution of problem (2.4).

Now we show that the objective value $\lambda ^*=\hat{\lambda }-\xi <\hat{\lambda }$. Firstly, we show that $|w^*_i-w_i|\le \lambda ^*$ for each $e_i\in EM({\varvec{\hat{w}}})$. (a) $w^*_i-w_i\le w^*_{j_i}-w_i=w_{j_i}+(\hat{\lambda }-\xi )-w_i\le \hat{\lambda }-\xi =\lambda ^*$, (b) Notice that $\xi +\beta \le \gamma ({\varvec{\hat{w}}})\le \hat{w}_i+\hat{\lambda }-w_i$, then $\hat{w}_i-\beta -w_i\ge \xi -\hat{\lambda }$. Hence $w^*_i-w_i=\hat{w}_i-\beta -w_i\ge -\hat{\lambda }+\xi =-\lambda ^*$. Secondly, for each $e_i\in ED({\varvec{\hat{w}}})$, $|w^*_i-w_i|=|w_i-\hat{\lambda }+\xi -w_i|=|-\hat{\lambda }+\xi |=\lambda ^*$. Thirdly, for each $e_j\notin T^{0}$, $|w^*_j-w_j|=|w_j+\hat{\lambda }-\xi -w_j|=|\hat{\lambda }-\xi |=\lambda ^*$.

Case 3 $EU({\varvec{\hat{w}}})\not =\emptyset , ED({\varvec{\hat{w}}})=\emptyset .$

Then $0<N_U<n-1$, $EM({\varvec{\hat{w}}})=T^{0}{\setminus } EU({\varvec{\hat{w}}})$ and $N_M=n-N_U-1>0$. Let

$$\begin{aligned} w^*_k =\left\{ \begin{array}{ll} \hat{w}_k-\xi ,&{}\quad {\text{ if } }e_k\in EU({\varvec{\hat{w}}}),\\ \hat{w}_k+\beta ,&{}\quad {\text{ if } }e_k\in EM({\varvec{\hat{w}}}),\\ \hat{w}_k-\xi ,&{}\quad {\text{ if } }e_k\notin T^{0}, \end{array} \right. \end{aligned}$$

where $\xi =\frac{n-N_U-1}{n-1}\mu ({\varvec{\hat{w}}})>0, \beta =\frac{N_U}{n-1}\mu ({\varvec{\hat{w}}})>0$ are defined the same as in Case 2.

For each $e_i\in EU({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, we have $w^*_k\ge w^*_{j_i}=\hat{w}_{j_i}-\xi = \hat{w}_i-\xi =w^*_i.$ By using the same discussion as in Case 2, we can know that ${\varvec{w^*}}$ is a better feasible solution than ${\varvec{\hat{w}}}$ satisfying $\lambda ^*=\hat{\lambda }-\xi <\hat{\lambda }$.

Case 4 $EU({\varvec{\hat{w}}})\not =\emptyset , ED({\varvec{\hat{w}}})\not =\emptyset .$

Then $0<N_D<n-1$, $0<N_U<n-1-N_D$, $EM({\varvec{\hat{w}}})=T^{0}{\setminus } (ED({\varvec{\hat{w}}})\cup EU({\varvec{\hat{w}}}))$, and $N_M=n-N_D-N_U-1>0$. Let

$$\begin{aligned} w^*_k =\left\{ \begin{array}{ll} \hat{w}_k+\tau ,&{}\quad {\text{ if } }e_k\in ED({\varvec{\hat{w}}}),\\ \hat{w}_k-\rho ,&{}\quad {\text{ if } }e_k\in EU({\varvec{\hat{w}}}),\\ \hat{w}_k,&{}\quad {\text{ if } }e_k\in EM({\varvec{\hat{w}}}),\\ \hat{w}_k-\xi ,&{}\quad {\text{ if } }e_k\notin T^{0}, \end{array} \right. \end{aligned}$$

where $\xi =\min \{\tau , \rho \}$, and $\tau , \rho$ are solutions of the following equation system

$$\begin{aligned} \left\{ \begin{array}{ll} \rho \cdot N_U=\tau \cdot N_D,\\ \rho +\tau =\mu ({\varvec{\hat{w}}})=\min \{\gamma ({\varvec{\hat{w}}}),\eta ({\varvec{\hat{w}}}),\hat{\lambda }-\frac{\delta }{2}\}. \end{array} \right. \end{aligned}$$

Then $\tau =\frac{N_U}{N_D+N_U}\mu ({\varvec{\hat{w}}})>0, \rho =\frac{N_D}{N_D+N_U}\mu ({\varvec{\hat{w}}})>0$.

For each $e_i\in EM({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, $e_{j_i}\in \varTheta _i$, then

$$\begin{aligned} w^*_k\ge w^*_{j_i}= \hat{w}_{j_i}-\xi \ge \hat{w}_{j_i}-\eta ({\varvec{\hat{w}}}) \ge \hat{w}_{j_i}+\hat{w}_i-({w}_{j_i}+\hat{\lambda })= \hat{w}_i=w^*_i, \end{aligned}$$

where the second inequality follows from $\xi \le \tau \le \mu ({\varvec{\hat{w}}})\le \eta ({\varvec{\hat{w}}})$ and the third inequality follows from the definition of $\eta ({\varvec{\hat{w}}})$.

For each $e_i\in ED({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, notice that $w_i-w_{j_i}\le \delta$, $\xi <\hat{\lambda }-\frac{\delta }{2}$ and $\tau <\hat{\lambda }-\frac{\delta }{2}$, then

$$\begin{aligned} w^*_k\ge w^*_{j_i}=w_{j_i}+(\hat{\lambda }-\xi )\ge w_{j_i}+\frac{\delta }{2}\ge w_i-\frac{\delta }{2}\ge w_i-(\hat{\lambda }-\tau )=\hat{w}_i+\tau =w^*_i. \end{aligned}$$

For each $e_i\in EU({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, then $w^*_k\ge w^*_{j_i}=\hat{w}_{j_i}-\xi \ge \hat{w}_i-\rho =w^*_i.$ Furthermore,

$$\begin{aligned} \begin{array}{ll}\sum \limits _{e_i\in T^{0}}w^*_i&{}=\sum \limits _{e_i\in ED({\varvec{\hat{w}}})}w^*_i+\sum \limits _{e_i\in EU({\varvec{\hat{w}}})}w^*_i+\sum \limits _{e_i\in EM({\varvec{\hat{w}}})}w^*_i\\ &{}= \sum \limits _{e_i\in ED({\varvec{\hat{w}}})}(\hat{w}_i+\tau )+\sum \limits _{e_i\in EU({\varvec{\hat{w}}})}(\hat{w}_i-\rho )+\sum \limits _{e_i\in EM({\varvec{\hat{w}}})}\hat{w}_i\\ &{}=\sum \limits _{e_i\in T^{0}}\hat{w}_i+\tau \cdot N_D-\rho \cdot N_U=\sum \limits _{e_i\in T^{0}}\hat{w}_i=K. \end{array} \end{aligned}$$

Now we show that the objective value $\lambda ^*=\hat{\lambda }-\xi <\hat{\lambda }$. Firstly, we show that $|w^*_i-w_i|\le \lambda ^*$ for each $e_i\in EM({\varvec{\hat{w}}})$. (a) $w^*_i-w_i\le w^*_{j_i}-w_i=(w_{j_i}+\hat{\lambda }-\xi )-w_i\le \hat{\lambda }-\xi =\lambda ^*$, (b) notice that $\xi \le \gamma ({\varvec{\hat{w}}})\le \hat{w}_i+\hat{\lambda }-w_i$ and $\hat{w}_i=w^*_i$, then $\hat{w}_i-w_i\ge \xi -\hat{\lambda }$, hence $w^*_i-w_i\ge -\hat{\lambda }+\xi =-\lambda ^*$. Then $|w^*_i-w_i|\le \lambda ^*$ for each $e_i\in EM({\varvec{\hat{w}}})$. Secondly, for each $e_i\in ED({\varvec{\hat{w}}})$, $|w^*_i-w_i|=|w_i-\hat{\lambda }+\tau -w_i|=|\hat{\lambda }-\tau |\le |\hat{\lambda }-\xi |=\lambda ^*$. Thirdly, for each $e_i\in EU({\varvec{\hat{w}}})$, $|w^*_i-w_i|=|w_i+\hat{\lambda }-\rho -w_i|=|\hat{\lambda }-\rho |\le |\hat{\lambda }-\xi |=\lambda ^*$. Finally, for each $e_j\not \in T^{0}$, $|w^*_j-w_j|=|w_j+\hat{\lambda }-\xi -w_j|=|\hat{\lambda }-\xi |=\lambda ^*$.

Thus ${\varvec{w^*}}$ is a better feasible solution than ${\varvec{\hat{w}}}$ satisfying $\lambda ^*=\hat{\lambda }-\xi <\hat{\lambda }$. $\square$

By using the similar proof as in Case 4 of Theorem 4, we can prove the following corollary.

Corollary 5

Suppose $\varOmega ^{0}=\emptyset$ and $\varTheta ^{0}=\emptyset$. Let ${\varvec{\hat{w}}}$ be a feasible solution of problem (2.4) satisfying (2.3) and $\hat{\lambda }>\frac{\delta }{2}$. If $ED({\varvec{\hat{w}}})\not =\emptyset$ and $EU({\varvec{\hat{w}}})\not =\emptyset$, then ${\varvec{\hat{w}}}$ is not an optimal solution of (2.4).

Define

$$\begin{aligned} \lambda _1=\frac{{\varvec{w}}(T^0)-K}{n-1}, \ \ \ \ \lambda _2=\frac{K-\sum \limits _{e_i\in T^{0}{\setminus } \varTheta ^{0}, e_{j_i}\in \varTheta _i}w_{j_i}-\sum \limits _{e_i\in \varTheta ^{0}}w_i}{n-1}. \end{aligned}$$

(2.7)

In order to reduce ${\varvec{w}}(T^0)$ to K, we have two possible cases depending on the values of $\lambda _1$ and $\lambda _2$. The first case is to reduce each weight $w_i$ of $e_i\in T^{0}$ to $w_i-\lambda _1$. The second case is to change weight $w_i$ to $w_{j_i}+\lambda _2$ if $\varTheta _i\not =\emptyset$ and to $w_i+\lambda _2$ if $e_i\in \varTheta ^{0}$, for each $e_i\in T^{0}$.

Lemma 6

Suppose $\varOmega ^{0}=\emptyset$. If $\lambda _1$ and $\lambda _2$ are defined as in (2.7), then $\lambda _1+\lambda _2\le \delta$.

Proof

$$\begin{aligned} \lambda _1+\lambda _2= & {} \frac{{\varvec{w}}(T^0)-K}{n-1}+\frac{K-\sum \limits _{e_i\in T^{0}{\setminus } \varTheta ^{0}, e_{j_i}\in \varTheta _i}w_{j_i}-\sum \limits _{e_i\in \varTheta ^{0}}w_i}{n-1}\\= & {} \frac{\sum \limits _{e_i\in T^{0}{\setminus } \varTheta ^{0}, e_{j_i}\in \varTheta _i}(w_i-w_{j_i})}{n-1} \\\le & {} \frac{|T^0{\setminus } \varTheta ^0|}{n-1}\cdot \max \{w_i-w_{j_i}|e_i\in T^{0}{\setminus } \varTheta ^{0}, e_{j_i}\in \varTheta _i\}\\\le & {} \frac{|T^0{\setminus } \varTheta ^0|}{n-1}\cdot \delta =\frac{(n-1-|\varTheta ^{0}|)}{n-1}\cdot \delta \le \delta \end{aligned}$$

The lemma holds. $\square$

Now we prove the sufficient and necessary condition of an optimal solution of problem (2.4).

Theorem 7

Suppose $\varOmega ^{0}=\emptyset$ and $\varTheta ^{0}=\emptyset$. Let ${\varvec{\hat{w}}}$ be a feasible solution of problem (2.4) which satisfies (2.3). If its objective value is $\hat{\lambda }>\frac{\delta }{2}$, then ${\varvec{\hat{w}}}$ is an optimal solution of problem (2.4) if and only if either $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$ or $EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$.

Proof

(Necessity) Let ${\varvec{\hat{w}}}$ be an optimal solution of problem (2.4) satisfying (2.3) and $\hat{\lambda }>\frac{\delta }{2}$, then we know that $EM({\varvec{\hat{w}}})=\emptyset$ by Theorem 4, and either $ED({\varvec{\hat{w}}})=\emptyset$ or $EU({\varvec{\hat{w}}})=\emptyset$ by Corollary 5. Hence, $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$ or $EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$.

(Sufficiency) Firstly, at least one of $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})$ and $EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})$ is nonempty. Otherwise, $T^0=\emptyset$. Notice that $\varTheta ^{0}=\emptyset$, then $\lambda _2=\frac{K-\sum _{e_i\in T^{0}, e_{j_i}\in \varTheta _i}w_{j_i}}{n-1}$ and $\sum _{e_i\in T^{0}, e_{j_i}\in \varTheta _i}w_{j_i}+(n-1)\lambda _2=K$.

Case 1 If $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$ and $EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})\not =\emptyset$, then $T^0=EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})\cup ED({\varvec{\hat{w}}})=EU({\varvec{\hat{w}}})$. Due to the feasibility of ${\varvec{\hat{w}}}$ and $\hat{\lambda }>\frac{\delta }{2}$, we have

$$\begin{aligned} \sum \limits _{e_i\in T^0}\hat{w}_i=\sum \limits _{e_i\in T^0,e_{j_i}\in \varTheta _i}(w_{j_i}+\hat{\lambda })=\sum \limits _{e_i\in T^0,e_{j_i}\in \varTheta _i}w_{j_i}+(n-1)\hat{\lambda }=K. \end{aligned}$$

(2.8)

Thus, $\lambda _2=\hat{\lambda }>\frac{\delta }{2}$ and $\lambda _1<\frac{\delta }{2}$ by definition of $\lambda _1$, $\lambda _2$ and Lemma 6.

If ${\varvec{\hat{w}}}$ is not an optimal solution of problem (2.4), suppose ${\varvec{w^{*}}}$ is an optimal solution with $\lambda ^{*}<\hat{\lambda }$, then $ED({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$ or $EU({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$ by the necessity of Theorem 7.

(a) If $EU({\varvec{w^{*}}})=EM({\varvec{w^{*}}})=\emptyset$ and $ED({\varvec{w^{*}}})=T^0$, then

$$\begin{aligned} \sum \limits _{e_i\in T^0}w^{*}_i=\sum \limits _{e_i\in T^0}({w}_i-\lambda ^{*})={\varvec{w}}(T^0)-(n-1)\lambda ^{*}=K={\varvec{w}}(T^0)-(n-1)\lambda _1. \end{aligned}$$

Hence, $\lambda ^{*}=\lambda _1$, which contradicts that $\lambda ^{*}\ge \frac{\delta }{2}> \lambda _1$ by Lemma 3.

(b) If $ED({\varvec{w^{*}}})=EM({\varvec{w^{*}}})=\emptyset$ and $EU({\varvec{w^{*}}})=T^0$, then by (2.8) we have

$$\begin{aligned} \sum \limits _{e_i\in T^0}w^{*}_i= & {} \sum \limits _{e_i\in T^0}(w_{j_i}+\lambda ^{*})=\sum \limits _{e_i\in T^0,e_{j_i}\in \varTheta _i}w_{j_i}+(n-1)\lambda ^{*}=K\\= & {} \sum \limits _{e_i\in T^0,e_{j_i}\in \varTheta _i}w_{j_i}+(n-1)\hat{\lambda }. \end{aligned}$$

Hence, $\lambda ^{*}=\hat{\lambda }$, which contradicts $\lambda ^{*}<\hat{\lambda }$.

(c) If $ED({\varvec{w^{*}}})=EM({\varvec{w^{*}}})=EU({\varvec{w^{*}}})=\emptyset$, then $T^0=\emptyset$, which is impossible.

Thus, ${\varvec{\hat{w}}}$ is an optimal solution of problem (2.4).

Case 2 If $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})\not =\emptyset$ and $EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$, then $T^0=ED({\varvec{\hat{w}}})$. Due to the feasibility of ${\varvec{\hat{w}}}$ and $\hat{\lambda }>\frac{\delta }{2}$, we have

$$\begin{aligned} \begin{array}{lr} \sum \limits _{e_i\in T^0}\hat{w}_i=\sum \limits _{e_i\in T^0}({w}_i-\hat{\lambda })={\varvec{w}}(T^0)-(n-1)\hat{\lambda }=K={\varvec{w}}(T^0)-(n-1){\lambda _1}.&\end{array}\nonumber \\ \end{aligned}$$

(2.9)

Thus, $\lambda _1=\hat{\lambda }>\frac{\delta }{2}$ and $\lambda _2<\frac{\delta }{2}$ by definition of $\lambda _1$, $\lambda _2$ and Lemma 6.

Suppose ${\varvec{w^{*}}}$ is an optimal solution of problem (2.4) with $\lambda ^{*}<\hat{\lambda }$, then $ED({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$ or $EU({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$ by the necessity of Theorem 7.

(a) If $EU({\varvec{w^{*}}})=EM({\varvec{w^{*}}})=\emptyset$ and $ED({\varvec{w^{*}}})=T^0$, then

$$\begin{aligned} \sum \limits _{e_i\in T^0}w^{*}_i=\sum \limits _{e_i\in T^0}({w}_i-\lambda ^{*})={\varvec{w}}(T^0)-(n-1)\lambda ^{*}=K={\varvec{w}}(T^0)-(n-1)\hat{\lambda }. \end{aligned}$$

Hence, $\lambda ^{*}=\hat{\lambda }$, which contradicts $\lambda ^{*}<\hat{\lambda }$.

(b) If $ED({\varvec{w^{*}}})=EM({\varvec{w^{*}}})=\emptyset$ and $EU({\varvec{w^{*}}})=T^0$, then

$$\begin{aligned} \sum \limits _{e_i\in T^0}w^{*}_i= & {} \sum \limits _{e_i\in T^0}(w_{j_i}+\lambda ^{*})=\sum \limits _{e_i\in T^0,e_{j_i}\in \varTheta _i}w_{j_i}+(n-1)\lambda ^{*}=K\\= & {} \sum \limits _{e_i\in T^0,e_{j_i}\in \varTheta _i}w_{j_i}+(n-1)\lambda _2. \end{aligned}$$

Hence, $\lambda ^{*}=\lambda _2<\frac{\delta }{2}$, which contradicts Lemma 3 that $\lambda ^{*}\ge \frac{\delta }{2}$.

(c) If $ED({\varvec{w^{*}}})=EM({\varvec{w^{*}}})=EU({\varvec{w^{*}}})=\emptyset$, then $T^0=\emptyset$, which is impossible.

Thus, ${\varvec{\hat{w}}}$ is an optimal solution of problem (2.4).

Hence, under the condition $\varOmega ^{0}=\emptyset$, $\varTheta ^0= \emptyset$, and $\hat{\lambda }>\frac{\delta }{2}$, if $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$ or $EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$, then ${\varvec{\hat{w}}}$ is an optimal solution of problem (2.4). $\square$

2.2 Properties of an optimal solution of the problem IOVMST $_\infty$ when $\varTheta ^0\ne \emptyset$ and $\varOmega ^{0}=\emptyset$

For the feasible solution ${\varvec{\hat{w}}}$ satisfying (2.3) of problem (2.4) with objective value $\hat{\lambda }$, if $\varTheta ^{0}\not =\emptyset$, then we define a new weight vector ${\varvec{\tilde{w}}}$ and three sets $EU({\varvec{\hat{w}}}), ED({\varvec{\hat{w}}}), EM({\varvec{\hat{w}}})$.

$$\begin{aligned}&\tilde{w}_i=\left\{ \begin{array}{ll} w_{j_i}+\hat{\lambda }, &{}\quad { \text{ if } }e_i\in T^{0}{\setminus }\varTheta ^{0}, e_{j_i}\in \varTheta _i,\\ w_i+\hat{\lambda }, &{}\quad { \text{ if } } e_i\in \varTheta ^{0}, \\ \hat{w}_i=w_i+\hat{\lambda }, &{}\quad { \text{ if } } e_i\not \in T^{0}, \end{array} \right. \end{aligned}$$

(2.10)

$$\begin{aligned}&\left\{ \begin{array}{ll} EU({\varvec{\hat{w}}})=\{e_i\in T^{0}| \hat{w}_i=\tilde{w}_i\},&{}\\ ED({\varvec{\hat{w}}})=\{e_i\in T^{0}|\hat{w}_i=w_i-\hat{\lambda }\},&{} \\ EM({\varvec{\hat{w}}})=\{e_i\in T^{0}| w_i-\hat{\lambda }<\hat{w}_i<\tilde{w}_i\}.&{} \end{array} \right. \end{aligned}$$

(2.11)

Obviously, if $\hat{\lambda }>\frac{\delta }{2}$, then $ED({\varvec{\hat{w}}})\cap EU({\varvec{\hat{w}}})=\emptyset$ and $T^0 = EM({\varvec{\hat{w}}})$.

Theorem 8

Suppose $\varOmega ^{0}=\emptyset$. Let ${\varvec{\hat{w}}}$ be a feasible solution of problem (2.4) satisfying (2.3) with objective value $\hat{\lambda }>\frac{\delta }{2}$. If $EM({\varvec{\hat{w}}})\not =\emptyset$, then ${\varvec{\hat{w}}}$ is not an optimal solution of problem (2.4), where $EM({\varvec{\hat{w}}})$ is defined as in (2.11) and ${\varvec{\tilde{w}}}$ used as in $EM({\varvec{\hat{w}}})$ is defined as in (2.10).

Proof

Note that when $\varTheta ^0=\emptyset$, the sets $ED({\varvec{\hat{w}}}), EM({\varvec{\hat{w}}}), EU({\varvec{\hat{w}}})$ defined as in (2.11) are the same as in (2.5), then the result holds obviously due to Theorem 4. If $\varTheta ^0\ne \emptyset$, we can prove similarly by considering four cases depending on the two sets $EU({\varvec{\hat{w}}}), ED({\varvec{\hat{w}}})$ empty or not. In each case, we can find a better feasible solution ${\varvec{w^*}}$ than ${\varvec{\hat{w}}}$ with $\lambda ^*<\hat{\lambda }$. Notice that the only difference in the proof of two theorems is the result related to edges $e_i\in EU({\varvec{\hat{w}}})$, for which we should study two different cases: (i) $e_i\in T^{0}{\setminus }\varTheta ^{0}$ and (ii) $e_i\in \varTheta ^{0}$. Next we only take the proof of Case 4 as an example and omit the similar proof in the other three cases.

Case 4 $EU({\varvec{\hat{w}}})\not =\emptyset , ED({\varvec{\hat{w}}})\not =\emptyset$, we can get a better feasible solution ${\varvec{w^*}}$ with $\lambda ^*<\hat{\lambda }$.

Let $|ED({\varvec{\hat{w}}})|=N_D<n-1$, $|EU({\varvec{\hat{w}}})|=N_U<n-1-N_D$, $EM({\varvec{\hat{w}}})=T^{0}{\setminus } (ED({\varvec{\hat{w}}})\cup EU({\varvec{\hat{w}}}))$, thus $|EM({\varvec{\hat{w}}})|=n_M=n-N_D-N_U-1>0$. Let

$$\begin{aligned} w^*_k =\left\{ \begin{array}{ll} \hat{w}_k+\tau ,&{}\quad {\text{ if }}\ e_k\in ED({\varvec{\hat{w}}}),\\ \hat{w}_k-\rho ,&{}\quad {\text{ if }}\ e_k\in EU({\varvec{\hat{w}}}),\\ \hat{w}_k,&{}\quad {\text{ if } }e_k\in EM({\varvec{\hat{w}}}),\\ \hat{w}_k-\xi ,&{}\quad {\text{ if }}\ e_k\notin T^{0},\\ \end{array} \right. \end{aligned}$$

where $\xi =\min \{\tau , \rho \}$, and $\tau =\frac{N_U}{N_D+N_U}\mu ({\varvec{\hat{w}}})>0, \rho =\frac{N_D}{N_D+N_U}\mu ({\varvec{\hat{w}}})>0$.

For each $e_i\in EM({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, $e_{j_i}\in \varTheta _i$, then

$$\begin{aligned} w^*_k\ge w^*_{j_i}= \hat{w}_{j_i}-\xi \ge \hat{w}_{j_i}-\eta ({\varvec{\hat{w}}}) \ge \hat{w}_{j_i}+\hat{w}_i-({w}_{j_i}+\hat{\lambda })= \hat{w}_i=w^*_i. \end{aligned}$$

For each $e_i\in ED({\varvec{\hat{w}}})$, if $e_k\in \varOmega _i$, notice that $w_i-w_{j_i}\le \delta$, $\xi <\hat{\lambda }-\frac{\delta }{2}$ and $\tau <\hat{\lambda }-\frac{\delta }{2}$, then

$$\begin{aligned} w^*_k\ge w^*_{j_i}=w_{j_i}+(\hat{\lambda }-\xi )\ge w_{j_i}+\frac{\delta }{2}\ge w_i-\frac{\delta }{2}\ge w_i-(\hat{\lambda }-\tau )=\hat{w}_i+\tau =w^*_i. \end{aligned}$$

For each $e_i\in EU({\varvec{\hat{w}}})$, (1) if $e_i\in T^{0}{\setminus }\varTheta ^{0}$, $e_k\in \varOmega _i$ and $e_{j_i}\in \varTheta _i$, then $w^*_k\ge w^*_{j_i}=\hat{w}_{j_i}-\xi \ge \hat{w}_i-\xi \ge \hat{w}_i-\rho =w^*_i.$ (2) If $e_i\in \varTheta ^{0}$, $e_k\in \varOmega _i$, then $w^*_k=\hat{w}_k-\xi \ge \hat{w}_i-\xi \ge \hat{w}_i-\rho =w^*_i.$ Furthermore,

$$\begin{aligned} \begin{array}{ll}\sum \limits _{e_i\in T^{0}}w^*_i&{}= \sum \limits _{e_i\in ED({\varvec{\hat{w}}})}(\hat{w}_i+\tau )+\sum \limits _{e_i\in EU({\varvec{\hat{w}}})}(\hat{w}_i-\rho )+\sum \limits _{e_i\in EM({\varvec{\hat{w}}})}\hat{w}_i\\ &{}={\varvec{\hat{w}}}(T^{0})+\tau \cdot N_D-\rho \cdot N_U={\varvec{\hat{w}}}(T^{0})=K.\\ \end{array} \end{aligned}$$

Now we show that the objective value $\lambda ^*=\hat{\lambda }-\xi <\hat{\lambda }$. Firstly, we show that $|w^*_i-w_i|\le \lambda ^*$ for each $e_i\in EM({\varvec{\hat{w}}})$. (a) $w^*_i-w_i\le w^*_{j_i}-w_i=(w_{j_i}+\hat{\lambda }-\xi )-w_i\le \hat{\lambda }-\xi =\lambda ^*$, (b) Notice that $\xi \le \gamma ({\varvec{\hat{w}}})\le \hat{w}_i+\hat{\lambda }-w_i$ and $\hat{w}_i=w^*_i$, then $\hat{w}_i-w_i\ge \xi -\hat{\lambda }$, hence $w^*_i-w_i\ge -\hat{\lambda }+\xi =-\lambda ^*$. Secondly, for each $e_i\in ED({\varvec{\hat{w}}})$, $|w^*_i-w_i|=|w_i-\hat{\lambda }+\tau -w_i|=|\hat{\lambda }-\tau |\le |\hat{\lambda }-\xi |=\lambda ^*$. Thirdly, for each $e_i\in EU({\varvec{\hat{w}}})$, (1) if $e_i\in T^{0}{\setminus }\varTheta ^{0}$, then $|w^*_i-w_i|=|\hat{w}_i-\rho -w_i|=|w_{j_i}+\hat{\lambda }-\rho -w_i|\le |\hat{\lambda }-\rho | \le |\hat{\lambda }-\xi |=\lambda ^*$. (2) If $e_i\in \varTheta ^{0}$, then $|w^*_i-w_i|=|w_i+\hat{\lambda }-\rho -w_i|=|\hat{\lambda }-\rho |\le |\hat{\lambda }-\xi |=\lambda ^*$. Finally, for each $e_j\not \in T^{0}$, $|w^*_j-w_j|=|w_j+\hat{\lambda }-\xi -w_j|=|\hat{\lambda }-\xi |=\lambda ^*$. $\square$

By using the similar proof as in Theorem 7, we can prove the following theorem.

Theorem 9

Suppose $\varOmega ^{0}=\emptyset$. Let ${\varvec{\hat{w}}}$ be a feasible solution of problem (2.4) satisfying (2.3) and $\hat{\lambda }>\frac{\delta }{2}$. ${\varvec{\hat{w}}}$ is an optimal solution of problem (2.4) if and only if either $ED({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$ or $EU({\varvec{\hat{w}}})\cup EM({\varvec{\hat{w}}})=\emptyset$, where $EM({\varvec{\hat{w}}})$, $EU({\varvec{\hat{w}}})$ and $ED({\varvec{\hat{w}}})$ are defined as in (2.11) and ${\varvec{\tilde{w}}}$ used in $EM({\varvec{\hat{w}}})$ and $EU({\varvec{\hat{w}}})$ is defined as in (2.10).

In fact, the results in Theorems 8 and 9 are more general than that in Theorems 4 and 7, since they include the case of $\varTheta ^{0}=\emptyset$. So we omit the condition $\varTheta ^{0}=\emptyset$ in Theorems 8 and 9.

3 An algorithm for the problem IOVMST $_\infty$

In this section, we first propose an algorithm to solve the problem IOVMST$_\infty$ when $\varOmega ^{0}=\emptyset$ and then we propose an algorithm to solve the problem IOVMST$_\infty$ when $\varOmega ^{0}\not =\emptyset$.

3.1 An algorithm for the problem IOVMST $_\infty$ when $\varOmega ^{0}=\emptyset$

In this subsection, we first propose an algorithm to solve the problem IOVMST$_\infty$ when $\varOmega ^{0}=\emptyset$, then prove its optimality and analyze its time complexity.

The main idea of the algorithm is as follows. Firstly, compute $\lambda _1=\frac{{\varvec{w}}(T^0)-K}{n-1}$. If $\lambda _1> \frac{\delta }{2}$, then let $\lambda ^{*}=\lambda _1$, let $w_i^*=w_i-\lambda ^*$ for $e_i\in T^0$ and $w_i^*=w_i+\lambda ^*$ for $e_i\notin T^0$, and then $EU({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$, which means $w^*$ is an optimal solution of problem (2.4) with $\lambda ^*=\lambda _1$ by Theorem 9. Otherwise, compute $\lambda _2$ by (2.7). If $\lambda _2> \frac{\delta }{2}$, then let $\lambda ^{*}=\lambda _2$, let $w_i^*=w_i+\lambda ^*$ for $e_i\in \varTheta ^0$, $w_i^*=w_{j_i}+\lambda ^*$ for $e_i\in T^0\backslash \varTheta ^0$, and $w_i^*=w_i+\lambda ^*$ for $e_i\notin T^0$, and then $ED({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$, hence $w^*$ is an optimal solution of problem (2.4) with $\lambda ^*=\lambda _2$ by Theorem 9. Secondly, if $\max \{\lambda _1,\lambda _2\}\le \frac{\delta }{2}$, we will consider five cases to present an optimal solution $w^*$ with optimal objective value $\lambda ^*=\frac{\delta }{2}$.

Next we present Algorithm 1 to solve the problem IOVMST$_\infty$ when $\varOmega ^{0}=\emptyset$.

Next we prove ${\varvec{w^*}}$ obtained in Algorithm 1 is an optimal solution of problem (2.4).

Theorem 10

Suppose $\varOmega ^{0}=\emptyset$. If $\max \{\lambda _1,\lambda _2\}>\frac{\delta }{2}$, then the optimal objective value is $\max \{\lambda _1,\lambda _2\}$, and ${\varvec{w^*}}$ defined by (3.12) in Algorithm 1 is an optimal solution of problem (2.4).

Proof

If $\max \{\lambda _1,\lambda _2\}> \frac{\delta }{2}$, then at most one of $\lambda _1$ and $\lambda _2$ is not less than $\frac{\delta }{2}$ as $\lambda _1+\lambda _2\le {\delta }$ by Lemma 6.

(1) If $\lambda _1=\lambda ^*> \frac{\delta }{2}$, then $w_i^*=w_i-\lambda ^*$ for $e_i\in T^0$ and $w_i^*=w_i+\lambda ^*$ for $e_i\notin T^0$ according to (3.12). Hence, $EU({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$, then ${\varvec{w^*}}$ is an optimal solution of problem (2.4) with optimal objective value $\lambda _1$ by Theorem 9.

(2) If $\lambda _2=\lambda ^*> \frac{\delta }{2}$, then $w_i^*=w_i+\lambda ^*$ for $e_i\in \varTheta ^0$, $w_i^*=w_{j_i}+\lambda ^*$ for $e_i\in T^0\backslash \varTheta ^0$, and $w_i^*=w_i+\lambda ^*$ for $e_i\notin T^0$ according to (3.12). Hence $ED({\varvec{w^{*}}})\cup EM({\varvec{w^{*}}})=\emptyset$, then ${\varvec{w^*}}$ is an optimal solution of problem (2.4) with optimal objective value $\lambda _2$ by Theorem 9. $\square$

Theorem 11

Suppose $\varOmega ^{0}=\emptyset$. If $\max \{\lambda _1,\lambda _2\}\le \frac{\delta }{2}$, then the optimal objective value of problem (2.4) is $\lambda ^*=\frac{\delta }{2}$ and ${\varvec{w^*}}$ outputted by Algorithm 1 is an optimal solution.

Proof

We consider five cases according to lines 4-40 of Algorithm 1. In each case, we show that ${\varvec{w^*}}$ obtained in the algorithm is an optimal solution of problem (2.4) with objective value $\frac{\delta }{2}$.

Case 1 If $U^{s}={\varvec{w}}(T^0)-K$, then we first show that ${\varvec{w^{*}}}$ defined as in (3.13) satisfies $w^{*}_k\ge w^{*}_i$ for each $e_i\in T^{0}$ and $e_k\in \varOmega _i$.

(1) If $e_i\in EU^s$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_{j_i}+\frac{\delta }{2}=w^*_i$.

(2) If $e_i\in EU^b$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_{j_i}+\frac{\delta }{2}\ge w_i=w^*_i$.

(3) If $e_i\in \varTheta ^{0}$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_i+\frac{\delta }{2}>w_i=w^*_i$.

Notice that $\sum \nolimits _{e_i\in EU^s}(w_{j_i}+\frac{\delta }{2})=\sum \nolimits _{e_i\in EU^s}w_i-U^s$, then $\sum \nolimits _{e_i\in T^{0}}w^*_i=\sum \nolimits _{e_i\in EU^s}(w_{j_i}+\frac{\delta }{2})+\sum \nolimits _{e_i\in EU^b\cup \varTheta ^{0}}w_i=\sum \nolimits _{e_i\in EU^s}w_i+\sum \nolimits _{e_i\in EU^b\cup \varTheta ^{0}}w_i-U^s={\varvec{w}}(T^0)-U^s=K.$ Then ${\varvec{w^*}}$ is a feasible solution of problem (2.4).

Furthermore, for each $e_i\in EU^{s}$, $|w^*_i-w_i|= |w_i-w_{j_i}-\frac{\delta }{2}| \le \frac{\delta }{2}$, and for each $e_k\notin T^{0}$, $|w^*_k-w_k|=\frac{\delta }{2}$.

Hence ${\varvec{w^*}}$ is an optimal solution of problem (2.4) with $\lambda ^*=\frac{\delta }{2}$.

Case 2 If $U^{s}>{\varvec{w}}(T^0)-K$, we first show that ${\varvec{w^{*}}}$ obtained by (3.14) satisfies $w^{*}_k\ge w^{*}_i$ for each $e_i\in T^{0}$ and $e_k\in \varOmega _i$.

(1) If $e_i=e_c$. (a) If $e_c\in \varTheta ^0$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_c+\frac{\delta }{2}\ge w_c+Rest=w^*_c=w^*_i$. (b) If $e_c\in EU^b$, notice that $Rest\le w_{j_c}+\frac{\delta }{2}-w_c$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_{j_c}+\frac{\delta }{2}=(w_{j_c}+\frac{\delta }{2}-Rest)+Rest\ge w_c+Rest=w^*_c=w^*_i$. Thus, if $e_i=e_c$, then $w^*_k\ge w^*_i$.

(2) If $e_i\in D_\delta$, we know that $e_i\in \varTheta ^0$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_i+\frac{\delta }{2}=w^*_i$.

(3) If $e_i\in EU^s\cup D_d$, then $e_i\in T^0{\setminus }\varTheta ^0$, and $w^*_k=w_k+\frac{\delta }{2}\ge w_{j_i}+\frac{\delta }{2}=w^*_i$.

(4) If $e_i\in (EU^b\cup \varTheta ^{0}){\setminus }(D_\delta \cup D_d\cup \{e_c\})$. (a) If $e_i\in \varTheta ^0$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_i+\frac{\delta }{2}>w_i=w^*_i$. (b) If $e_i\in EU^b$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_{j_i}+\frac{\delta }{2}\ge w_i=w^*_i$.

Now we show that $\sum _{e_i\in T^{0}}w^*_i=K$. Let $e_c$ be the critical edge and Rest be the critical value outputted by lines 9-23 of Algorithm 1. Then $Rest^0=Rest+\frac{\delta }{2}\cdot |D_\delta |+\sum \limits _{e_i\in D_d}[(w_{j_i}+\frac{\delta }{2})-w_i]=U^s-({\varvec{w}}(T^0)-K)$. Notice that $U^{s}=\sum _{e_i\in EU^{s}}(w_i-(w_{j_i}+\frac{\delta }{2}))$, then we have

$$\begin{aligned}&\sum \limits _{e_i\in EU^s}\left[ w_i-\left( w_{j_i}+\frac{\delta }{2}\right) \right] -Rest-\frac{\delta }{2}\cdot |D_\delta |-\sum \limits _{e_i\in D_d}\left[ \left( w_{j_i}+\frac{\delta }{2}\right) -w_i\right] \\&\quad ={\varvec{w}}(T^0)-K. \end{aligned}$$

Now we can calculate the value

$$\begin{aligned} \sum \limits _{e_i\in T^{0}}w^*_i=&(w_c+Rest)+\sum \limits _{e_i\in D_{\delta }}\left( w_i+\frac{\delta }{2}\right) +\sum _{e_i\in EU^s\cup D_d}\left( w_{j_i}+\frac{\delta }{2}\right) \\&+\sum \limits _{e_i\in (EU^{b}\cup \varTheta ^{0}){\setminus }((D_\delta \cup D_d\cup \{e_c\})}w_i\\&=(w_c+Rest)+\sum \limits _{e_i\in D_{\delta }}w_i+\sum \limits _{e_i\in D_{\delta }}\frac{\delta }{2}+\sum \limits _{e_i\in EU^s\cup D_d}w_i\\&\ \ +\sum \limits _{e_i\in EU^s\cup D_d}(w_{j_i}+\frac{\delta }{2}-w_i)+\sum \limits _{e_i\in (EU^{b}\cup \varTheta ^{0}){\setminus }((D_\delta \cup D_d\cup \{e_c\})}w_i\\&={\varvec{w}}(T^0)+\{Rest+\frac{\delta }{2}\cdot |D_\delta |+\sum \limits _{e_i\in D_d}[(w_{j_i}+\frac{\delta }{2})-w_i]\\&-\sum \limits _{e_i\in EU^s}[w_i-(w_{j_i}+\frac{\delta }{2})]\}\\&={\varvec{w}}(T^0)+(-{\varvec{w}}(T^0)+K)=K. \end{aligned}$$

Hence ${\varvec{w^{*}}}$ obtained in Algorithm 1 is a feasible solution of problem (2.4).

Furthermore, (1) If $e_i=e_c$, then $|w_i- w_i^*|=|w_c- w_c^*|=Rest\le \frac{\delta }{2}$. (2) If $e_i\in D_\delta$, $|w_i- w_i^*|=\frac{\delta }{2}$. (3) $e_i\in EU^s\cup D_d$. If $e_i\in EU^s$ then $|w_i- w_i^*|=w_i-w_{j_i}-\frac{\delta }{2}\le \delta -\frac{\delta }{2}=\frac{\delta }{2}$. If $e_i\in D_d$, $|w_i- w_i^*|=w_{j_i}+\frac{\delta }{2}-w_i\le \frac{\delta }{2}$ (4) If $e_i\in (EU^b\cup \varTheta ^{0}){\setminus }(D_\delta \cup D_d\cup \{e_c\})$, then $|w_i- w_i^*|=w_i-w_i=0<\frac{\delta }{2}$. (5) If $e_i\not \in T^{0}$, then $|w_i- w_i^*|=\frac{\delta }{2}$.

Hence ${\varvec{w^*}}$ is an optimal solution of problem (2.4) with $\lambda ^*=\frac{\delta }{2}$.

Case 3 If $U^{s}<{\varvec{w}}(T^0)-K$ and $D^s={\varvec{w}}(T^0)-K$, then we first show that ${\varvec{w^{*}}}$ defined as in (3.15) satisfies $w^{*}_k\ge w^{*}_i$ for each $e_i\in T^{0}$, $e_k\in \varOmega _i$. (1) If $e_i\in EU^s$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_{j_i}+\frac{\delta }{2}\ge w_i-\frac{\delta }{2}=w^*_i$. (2) If $e_i\in EU^b$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_{j_i}+\frac{\delta }{2}\ge w_i=w^*_i$. (3) If $e_i\in \varTheta ^{0}$, then $w^*_k=w_k+\frac{\delta }{2}\ge w_i+\frac{\delta }{2}>w_i=w^*_i$. Notice that $D^{s}=\frac{\delta }{2}\cdot |EU^s|={\varvec{w}}(T^0)-K$, then $\sum \limits _{e_i\in T^{0}}w^*_i=\sum \nolimits _{e_i\in EU^s}(w_i-\frac{\delta }{2})+\sum \nolimits _{e_i\in EU^b\cup \varTheta ^{0}}w_i={\varvec{w}}(T^0)-\frac{\delta }{2}\cdot |EU^s|=K.$ Then ${\varvec{w^*}}$ is a feasible solution of problem (2.4). Furthermore, $|w^*_i-w_i|= \frac{\delta }{2}$ for each $e_i\in EU^{s}$, and $|w^*_k-w_k|=\frac{\delta }{2}$ for each $e_k\notin T^{0}$. Hence ${\varvec{w^*}}$ is an optimal solution of problem (2.4) with $\lambda ^*=\frac{\delta }{2}$.

Case 4 If $U^{s}<{\varvec{w}}(T^0)-K$ and $D^s<{\varvec{w}}(T^0)-K$. Using the same analyses as in Case 1, we can prove that ${\varvec{w^{*}}}$ defined as in (3.16) satisfies $w^*_k\ge w^*_i$ for each $e_i\in T^{0}$ and $e_k\in \varOmega _i$. Notice that $\chi =\frac{{\varvec{w}}(T^0)-K-D^{s}}{|EU^{b}\cup \varTheta ^{0}|}$ and $D^{s}=\frac{\delta }{2}\cdot |EU^s|$. If $\chi > \frac{\delta }{2}$, then ${\varvec{w}}(T^0)-K-D^{s}> \frac{\delta }{2}\cdot |EU^b\cup \varTheta ^{0}|$, and $\sum _{e_i\in T^{0}}(w_i-\frac{\delta }{2})> K=\sum _{e_i\in T^{0}}(w_i-\lambda _1)$, which means $\lambda _1>\frac{\delta }{2}$ and contradicts $\lambda _1\le \frac{\delta }{2}$. Thus, $\chi \le \frac{\delta }{2}$. Moreover,

$$\begin{aligned} \sum \limits _{e_i\in T^{0}}w^*_i= & {} \sum \limits _{e_i\in EU^s}\left( w_i-\frac{\delta }{2}\right) +\sum \limits _{e_i\in EU^b\cup \varTheta ^{0}}(w_i-\chi )\\= & {} {\varvec{w}}(T^0)-\left( \frac{\delta }{2}\cdot |EU^s|+\chi \cdot |EU^b\cup \varTheta ^{0}|\right) =K. \end{aligned}$$

Furthermore, it is obvious that $|w_i^*-w_i|\le \frac{\delta }{2}$ for each $e_i\in T^0$ and $|w^*_k-w_k|=\frac{\delta }{2}$ for each $e_k\notin T^{0}$. Hence ${\varvec{w^*}}$ is an optimal solution of problem (2.4) with $\lambda ^*=\frac{\delta }{2}$.

Case 5 If $U^{s}<{\varvec{w}}(T^0)-K$, and $D^s>{\varvec{w}}(T^0)-K$, then we can similarly prove that ${\varvec{w^{*}}}$ defined as in (3.17) satisfies $w^*_k\ge w^*_i$ for each $e_i\in T^{0}$ and $e_k\in \varOmega _i$. Let $e_p$ be the critical edge and Rest be the critical value outputted by Line 35. Then $Rest^0=Rest+\sum \limits _{e_k\in D_{\delta }}(\delta -w_k+w_{j_k})=Rest-\sum \limits _{e_k\in D_{\delta }}(w_k-(w_{j_k}+\frac{\delta }{2})-\frac{\delta }{2})={\varvec{w}}(T^0)-K-U^s$. Notice that $U^{s}=\sum _{e_i\in EU^{s}}(w_i-(w_{j_i}+\frac{\delta }{2}))$, then we have

$$\begin{aligned}&Rest+\frac{\delta }{2}\cdot |D_\delta |+\left[ w_p-\left( w_{j_p}+\frac{\delta }{2}\right) \right] +\sum \limits _{e_i\in EU^s{\setminus }\left( \{e_p\}\cup D_{\delta }\right) }\left[ w_i-\left( w_{j_i}+\frac{\delta }{2}\right) \right] \\&\quad ={\varvec{w}}(T^0)-K. \end{aligned}$$

Now we can calculate the value

$$\begin{aligned} \begin{array}{ll} \sum \limits _{e_i\in T^{0}}w^*_i&{}=\left( w_{j_p}+\frac{\delta }{2}-Rest\right) +\sum \limits _{e_i\in D_{\delta }}\left( w_i-\frac{\delta }{2}\right) +\sum \limits _{e_i\in EU^s{\setminus }\left( \{e_p\}\cup D_{\delta }\right) }\left( w_{j_i}\right. \\ &{}\quad \left. +\frac{\delta }{2}\right) +\sum \limits _{e_i\in EU^b\cup \varTheta ^{0}}w_i\\ &{}=\{w_p-[w_p-(w_{j_p}+\frac{\delta }{2})]-Rest\}+\sum \limits _{e_i\in D_{\delta }}\left( w_i-\frac{\delta }{2}\right) \\ &{}\quad +\sum \limits _{e_i\in EU^s{\setminus }\left( \{e_p\}\cup D_{\delta }\right) }\left( w_i-\left[ w_i-\left( w_{j_i}+\frac{\delta }{2}\right) \right] \right) +\sum \limits _{e_i\in EU^b\cup \varTheta ^{0}}w_i\\ &{}={\varvec{w}}(T^0)-\left\{ Rest+\frac{\delta }{2}\cdot |D_\delta |+\left[ w_p-\left( w_{j_p}+\frac{\delta }{2}\right) \right] \right. \\ &{}\quad \left. +\sum \limits _{e_i\in EU^s{\setminus }\left( \{e_p\}\cup D_{\delta }\right) }\left[ w_i-\left( w_{j_i}+\frac{\delta }{2}\right) \right] \right\} \\ &{}={\varvec{w}}(T^0)-{\varvec{w}}(T^0)+K=K. \end{array} \end{aligned}$$

Furthermore, it is obvious that $|w_i^*-w_i|\le \frac{\delta }{2}$ for each $e_i\in T^{0}$ and $|w^*_k-w_k|=\frac{\delta }{2}$ for each $e_k\notin T^{0}$. Hence ${\varvec{w^*}}$ is an optimal solution of problem (2.4) with $\lambda ^*=\frac{\delta }{2}$. $\square$

Finally, we analyze the time complexity of Algorithm 1.

Theorem 12

Suppose $\varOmega ^{0}=\emptyset$, the problem (2.4) can be solved in O(mn) time by Algorithm 1.

Proof

In Algorithm 1, it is clear that line 1 takes O(mn) time. Lines 3–41 take O(m) time. Thus, Algorithm 1 runs in O(mn) in the worst-case and hence it is a strongly polynomial time algorithm. $\square$

3.2 An algorithm for IOVMST $_\infty$ problem when $\varOmega ^{0}\not =\emptyset$

In this subsection, we consider the case when $\varOmega ^{0}\not =\emptyset$, which means that there is at least one edge belonging to every spanning tree of G. In this case, the algorithm to solve problem (2.4) is similar to Algorithm 1 and we only replace $\varTheta ^{0}$ in Algorithm 1 with $\varPhi ^{0}=\varOmega ^{0}\cup \varTheta ^{0}$. Hence, we have the following corollary.

Corollary 13

If $\varOmega ^{0}=\{e_i|e_i\in T^{0}, \varOmega _i=\emptyset \}\ne \emptyset$, ${\varvec{w^*}}$ obtained in Algorithm 1 by replacing $\varTheta ^{0}$ with $\varPhi ^{0}=\varOmega ^{0}\cup \varTheta ^{0}$ is an optimal solution of problem (2.4). Furthermore, the time complexity is still O(mn).

4 A computational example of IOVMST $_\infty$ problem

In this section, we use Example 1 to demonstrate the computing process of seven cases in Algorithm 1. Notice that in Example 1, $\varOmega ^{0}\ne \emptyset$ and $\varTheta ^{0}\ne \emptyset$.

Example 3

As shown in Fig. 3, let $V=\{v_1,v_2,\dots ,v_{11}\}$, $E=\{e_1,e_2,\dots ,e_{17}\}$, ${\varvec{w}}=(3,4,3,3,4,3,1,5,5,$ 3, 4, 5, 5, 3, 4, 4, 1), $T^0=\{e_1,e_2,e_3,e_4,e_8,e_9,e_{12},e_{13},e_{15},e_{16}\}$ ($T^0$ is denoted by thick lines in Fig. 3).

Fig. 3

An example of the IOVMST$_\infty$ problem

After running Step 1 of Algorithm 1, we have

(I) ${\varvec{w}}(T^0)=41$; $\varOmega _1=\varOmega _{16}=\emptyset$, $\varOmega _2=\{e_6,e_7\}$, $\varOmega _3=\{e_5\}$, $\varOmega _4=\{e_5,e_6,e_7\}$, $\varOmega _8=\{e_7,e_{10},e_{11},e_{14},e_{17}\}$, $\varOmega _9=\{e_{10},e_{11},e_{14},e_{17}\}$, $\varOmega _{12}=\{e_{14},e_{17}\}$, $\varOmega _{13}=\{e_{11},e_{14},e_{17}\}$, $\varOmega _{15}=\{e_{17}\}$;

(II) $\varOmega ^{0}=\{e_1,e_{16}\}$ and $\varTheta ^{0}=\{e_3\}$; $\varTheta _1=\varTheta _{16}=\emptyset$, $\varTheta _2=\{e_7\}$, $\varTheta _3=\emptyset$, $\varTheta _4=\{e_7\}$, $\varTheta _8=\{e_7,e_{17}\}$, $\varTheta _9=\{e_{17}\}$, $\varTheta _{12}=\{e_{17}\}$, $\varTheta _{13}=\{e_{17}\}$, $\varTheta _{15}=\{e_{17}\}$;

(III) $w_{j_2}=w_7=1$, $w_{j_4}=w_7=1$, $w_{j_8}=w_7=1$, $w_{j_9}=w_{17}=1$, $w_{j_{12}}=w_{17}=1$, $w_{j_{13}}=w_{17}=1$, $w_{j_{15}}=w_{17}=1$; and $\delta =w_8-w_{j_8}=w_8-w_7=4$;

(IV) $EU^s=\{e_2,e_8,e_9,e_{12},e_{13},e_{15}\}$, $EU^b=\{e_4\}$.

Seven cases are considered based on K.

$$\begin{aligned} \lambda _1= & {} \frac{{\varvec{w}}(T^0)-K}{n-1}=\frac{41-K}{10},\\ \lambda _2= & {} \frac{K-\sum \limits _{e_i\in T^{0}{\setminus } (\varTheta ^{0}\cup \varOmega ^{0}), e_{j_i}\in \varTheta _i}w_{j_i}-\sum \limits _{e_i\in \varTheta ^{0}\cup \varOmega ^{0}}w_i}{n-1}=\frac{K-17}{10}. \end{aligned}$$

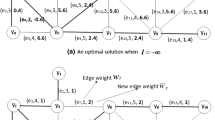
(1) If $K=20$. $\lambda _1=2.1>\frac{\delta }{2}=2$, $\lambda _2=0.3<\frac{\delta }{2}=2$. Then run line 3 of Algorithm 1, obtain ${\varvec{w^*}}= (0.9, 1.9, 0.9, 0.9, 6.1, 5.1, 3.1, 2.9, 2.9, 5.1, 6.1, 2.9, 2.9, 5.1, 1.9, 1.9, 3.1)$ and optimal objective value $\lambda ^*=2.1$ (see Fig. 4a).

(2) If $K=38$. $\lambda _1=0.3<\frac{\delta }{2}=2$, $\lambda _2=2.1>\frac{\delta }{2}=2$. Then run line 3 of Algorithm 1, obtain ${\varvec{w^*}}= (5.1, 3.1, 5.1, 3.1, 6.1, 5.1, 3.1, 3.1, 3.1, 5.1, 6.1, 3.1, 3.1, 5.1, 3.1, 6.1, 3.1)$ and $\lambda ^*=2.1$ (see Fig. 4b).

(3) If $K=31$. $\lambda _1=1<\frac{\delta }{2}=2$, $\lambda _2=1.4<\frac{\delta }{2}=2$. Then $\max \{\lambda _1,\lambda _2\}=1.4<2$, and $U^s=10={\varvec{w}}(T^0)-K$. Run line 7 of Algorithm 1, obtain ${\varvec{w^*}}= (3, 3, 3, 3, 6, 5, 3, 3, 3, 5, 6, 3, 3, 5, 3, 4, 3)$ and $\lambda ^*=2$ (see Fig. 4c).

Fig. 4

An optimal solution of Example 1 when $K=20,38,31,27$

(4) If $K=27$. $\lambda _1=1.4<\frac{\delta }{2}=2$, $\lambda _2=1<\frac{\delta }{2}=2$, $\chi =0.5$. Then $\max \{\lambda _1,\lambda _2\}=1.4<2$, $U^s=10<{\varvec{w}}(T^0)-K$ and $D^s=2\cdot |EU^s|=12<{\varvec{w}}(T^0)-K$. Run line 27 of Algorithm 1, obtain ${\varvec{w^*}}= (2.5, 2, 2.5, 2.5, 6, 5, 3, 3, 3, 5, 6, 3, 3, 5, 2, 3.5, 3)$ and $\lambda ^*=2$ (see Fig. 4d).

(5) If $K=35$. $\lambda _1=0.6<\frac{\delta }{2}=2$, $\lambda _2=1.8<\frac{\delta }{2}=2$. Then $\max \{\lambda _1,\lambda _2\}=1.8<2$, $U^s=10>{\varvec{w}}(T^0)-K=6$. Run line 9-23 of Algorithm 1, obtain $Rest=2$, $e_3$ is critical edge, $D_{\delta }=\{e_1\}$, $D_{d}=\emptyset$, ${\varvec{w^*}}= (5, 3, 5, 3, 6, 5, 3, 3, 3, 5, 6, 3, 3, 5, 3, 4, 3)$ and $\lambda ^*=2$ (see Fig. 5a).

(6) If $K=29$. $\lambda _1=1.2<\frac{\delta }{2}=2$, $\lambda _2=1.2<\frac{\delta }{2}=2$. Then $\max \{\lambda _1,\lambda _2\}=1.2<2$, $U^s=10<{\varvec{w}}(T^0)-K$ and $D^s=2\cdot |EU^s|=12={\varvec{w}}(T^0)-K$. Run line 27 of Algorithm 1, obtain ${\varvec{w^*}}= (3, 2, 3, 3, 6, 5, 3, 3, 3, 5, 6, 3, 3, 5, 2, 4, 3)$ and $\lambda ^*=2$ (see Fig. 5b).

(7) If $K=30$. $\lambda _1=1.1<\frac{\delta }{2}=2$, $\lambda _2=1.3<\frac{\delta }{2}=2$. Then $\max \{\lambda _1,\lambda _2\}=1.3<2$, $U^s=10<{\varvec{w}}(T^0)-K$ and $D^s=2\cdot |EU^s|=12>{\varvec{w}}(T^0)-K$. Run line 31-39 of Algorithm 1, obtain $Rest =1$, $e_2$ is critical edge, $EE=\{e_8,e_9,e_{12},e_{13},e_{15}\}$, $D_{\delta }=\emptyset$, ${\varvec{w^*}}= (3, 2, 3, 3, 6, 5, 3, 3, 3, 5, 6, 3, 3, 5, 3, 4, 3)$ and $\lambda ^*=2$ (see Fig. 5c).

Fig. 5

An optimal solution of Example 1 when $K=35,29,30$

5 Conclusions and further research

In this paper, we consider the inverse optimal value problem on minimum spanning tree under unit $l_{\infty }$ norm. A sufficient and necessary condition of optimal solutions of the problem is first obtained, and then a strongly polynomial time algorithm with running time O(mn) is proposed.

As a future research topic, we will study the inverse optimal value problem on minimum spanning tree under weighted $l_\infty$ norm, $l_1$ norm and Hamming distance. It is also meaningful to consider inverse optimal value problems on some other network problems, such as inverse optimal value problems on shortest path, inverse optimal value problems on network flow, inverse optimal value problems on matching, and inverse optimal value problems on center location problems under $l_1$, $l_{\infty }$ norm and Hamming distance.