1 Introduction

In the current communication resource allocation framework, the demand for efficient radio spectrum is increasing rapidly with continuing growth of wireless application. Most spectrum bands have already been exclusively allocated to licensed service providers [1], and the remaining wireless spectrum suitable for wireless communication is being exhausted. In order to improve the spectrum utilization and cope with the immense popularity of wireless devices, the concept of cognitive radio networks (CRNs) emerged [2]. In CRNs, secondary users (SUs) opportunistically exploit the spectrum unused by primary users (PUs) [3, 4]. The design of spectrum allocation strategy is a hot topic in the field of wireless communications [5, 6].

In CRNs with multiple channels, in order to improve the utilization of the spectrum hole, channel bonding technology has been investigated, where contiguous idle channels are bonded as one logical channel for SUs [7]. Channel aggregate technology has also been proposed, where non-contiguous idle channels can be aggregated as one logical channel for SUs or PUs [8, 9]. Mixed aggregate/bonding technology that takes channel handoff into account has been investigated in [10]. Considering the low arrival rate of PUs, many studies have also researched spectrum reservation strategy. With spectrum reservation strategy, part of the licensed spectrum is reserved for SUs, and the remaining spectrum is used by PUs with preemptive priority and used by SUs opportunistically. This method can decrease handoff and lower interruption probability of SUs so as to enhance the system throughput [11]. One study by [12] examined trading off the forced termination probability and the blocking probability against the number of reserved channels. However, this study ignored the retrial of the SUs interrupted by PUs. In [13], a finite buffer capacity and user impatience were considered in spectrum reservation strategy, but the issue that how to reduce the SU’s interference with PUs was not mentioned.

We note that reserving a fixed ratio of the licensed spectrum for SUs is relatively conservative. On the one hand, an overly high arrival rate of PUs will lead to an increase in average latency of PUs, and the quality of service (QoS) for PUs will go down. On the other hand, a too low arrival rate of PUs will cause a great waste of spectrum resources. According to the change in the spectrum environment, it is necessary to adjust the reservation ratio of the licensed spectrum adaptively for SUs. In addition, in CRNs, SUs have cognition, so the SUs interrupted by PUs can return to the buffer to wait for future transmission on the original spectrum. Furthermore, how to control the SU’s interference with PUs is also an significant problem to be solved in spectrum reservation strategy.

To overcome the limitations of previous works, we suggest a novel approach to adjust the reservation ratio of the licensed spectrum for SUs with respect to spectrum reservation strategy. In addition, in order to reduce SU’s interference with PUs, we also set an admission threshold for SUs. The proposed adaptive spectrum reservation strategy is more flexible than the conventional strategy. Aiming at mathematically evaluating and optimizing the spectrum reservation strategy proposed in this paper, we establish a system cost function. The system optimization will involve complicated nonlinear equations and nonlinear optimization problems, and the conventional optimization methods, such as the steepest descent method or Newton’s method, are inappropriate. We therefore turn to intelligent optimization algorithms with a strong global convergence ability. On the basis of a Teaching-learning-based Optimization (TLBO) idea, we give an intelligent algorithm to globally optimize the system parameters in terms of the adaptive control factor and the admission threshold.

The rest of this paper is organized as follows: In Sect. 2, we present an adaptive control approach, and propose a novel spectrum reservation strategy. In Sect. 3, we build a three-dimensional discrete time Markov Chain model, and obtain the steady-state distribution for the system model by using a matrix geometric solution method. In Sect. 4, we derive the formulas for performance measures, and emphatically discuss the influences of the adaptive control factor and the admission threshold on the system performance using numerical results and simulation experiments. In Sect. 5, considering the tradeoff between different performance measures, we build a system cost function, then present an intelligent searching algorithm to globally optimize the system parameters in terms of the adaptive control factor and the admission threshold. The paper is concluded in Sect. 6.

2 A novel spectrum reservation strategy

We consider a licensed spectrum in CRNs. In such networks, the licensed spectrum is separated into two logical channels, namely the reserved channel and the shared channel, respectively. In this paper, we assume that the reserved channel is only used by SUs, and the shared channel is used by two types of users, namely PUs and SUs. PUs have preemptive priority to use the shared channel and can reclaim the shared channel at any time, while SUs use the shared channel opportunistically.

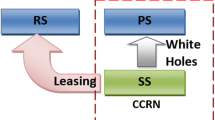
The working principle for the proposed strategy is shown in Fig. 1.

Fig. 1
figure 1

Adaptive spectrum reservation strategy

Full size image

As shown in Fig. 1, we also assume the following:

  1. (1)

    Once a PU arrives at the system, the transmission of the SU on the shared channel is forcibly interrupted, and the terminated SU returns to the buffer set for SUs (called the SU’s buffer). We assume that the capacity of the SU’s buffer is infinite.

  2. (2)

    Considering the low arrival rate of PUs, a buffer (called the PU’s buffer) with a finite capacity \(F (F\ge 0)\) is set for PUs. When a PU arrives at the system, if the shared channel is occupied by a PU and the PU’s buffer is full, the newly arriving PU will be blocked.

  3. (3)

    In order to reduce SU’s interference with PUs, we set an admission threshold \(H (H\ge 0)\) for SUs. That is to say, if the number of SUs waiting in the SU’s buffer is not greater than H, the SU queuing at the head of the SU’s buffer can not access idle shared channel. H is a system parameter.

  4. (4)

    An SU waiting in the SU’s buffer prefers to occupy the idle reserved channel over the idle shared channel.

  5. (5)

    For the sake of clarity, the SUs that are interrupted by PUs and return to the SU’s buffer are termed retrial SUs. The retrial SU has a higher priority than both the newly arriving SU and all the SUs waiting in the SU’s buffer. That is to say, a retrial SU will queue at the head of the SU’s buffer to wait for transmission service. In addition, the transmission of two types of users is supposed to follow a First Come First Service (FCFS) discipline.

In order to describe the strategy more clearly, the ratio of the reserved channel’s bandwidth to the total licensed spectrum’s bandwidth is called the aside spectrum ratio \(\theta \) \( (0 \le \theta \le 1 )\). It is obvious the aside spectrum ratio \(\theta \) may affect the blocking rate of PUs, the interruption rate of SUs and the average latency for the two types of users.

As usual, in order to ensure the QoS of users and achieve system stability, a higher arrival rate of users requires a greater service rate. With our proposed spectrum reservation strategy, a too small aside spectrum ratio \(\theta \) will lead to a strong interference with PUs; Contrary to this, a too large aside spectrum ratio \(\theta \) will lead to a decrease in the QoS of the PUs. Considering both the priority of the PUs, and the need to adapt to the system load, we present an adaptive control approach for the setting aside spectrum ratio \(\theta \) as follows:

$$\begin{aligned} \theta =\frac{\lambda _{su}}{\lambda _{su}+C\lambda _{pu}} \end{aligned}$$
(1)

where C is the adaptive control factor, \(\lambda _{su}\ ( \lambda _{pu})\) is the arrival rate of SUs (PUs). Because the aside spectrum ratio \(\theta \) cannot be greater than 1, the adaptiv control factor \(C\ge 0\). Especially, the adaptive control factor \(C=0\) means that the SUs can occupy the whole licensed spectrum.

Based on Eq. (1), we know that the aside spectrum ratio \(\theta \) decreases as the arrival rate \(\lambda _{pu}\) of PUs increases, and increases as the arrival rate \(\lambda _{su}\) of SUs increases. This control approach is obviously more flexible than that with a fixed aside spectrum ratio. We call this spectrum strategy the adaptive spectrum reservation strategy.

3 System model and model analysis

3.1 System model

In this paper, we assume that the shared channel and the reserved channel act as two servers, that PUs and SUs as two types of customers, and the time axis is slotted. We assume that the arriving intervals for these two types of users are independent random variables. The inter-arrival times of SUs and PUs are supposed to follow geometric distributions with parameters \(\lambda _{su}\) \((0<\lambda _{su}<1,\bar{\lambda }_{su}=1-\lambda _{su})\) and \(\lambda _{pu}\) \((0<\lambda _{su}<1, \bar{\lambda }_{pu}=1-\lambda _{pu})\), respectively. The service times on the shared channel and the reserved channel are geometrically distributed with service rates \(\mu _{sh}\) \((0<\mu _{sh}<1,\bar{\mu }_{sh}=1-\mu _{sh})\) and \(\mu _{re}\) \((0<\mu _{re}<1,\bar{\mu }_{re}=1-\mu _{re})\), respectively. We also assume that the system is an early arrival system (EAS) in this paper.

It is well known that if the Signal to Noise Ratio (SNR) in a channel is fixed, the channel capacity increases linearly with channel bandwidth [14]. We further assume that if the shared channel and the reserved channel are homogeneous and have the same SNR, then the service rate \(\mu _{sh}\) on the shared channel is linearly decreased with the aside spectrum ratio \(\theta \). Conversely, the service \(\mu _{re}\) on the reserved channel is linearly increased with the aside spectrum ratio \(\theta \). Based on the above assumptions, we obtain \(\mu _{sh}=(1-\theta )\times \mu \) and \(\mu _{re}=\theta \times \mu \), where \(\mu \) is the service rate for the whole spectrum.

Let \(X_{n}=i\) \((i=0,1,2,\dots )\) and \(Y_{n}=j\) \((j=0,1)\) indicate the total number of SUs in the system and on the reserved channel, respectively, at the instant \(n^+\). Let \(Z_{n}=k\) \((k=-1,0,1,\dots ,F+1)\) indicate the state of the shared channel at instant \(n^+\). \(k=-1\) means that the shared channel is occupied by an SU. \(k \ge 0\) means that there are k PUs in the system at the instant \(n^+\). Using a three-dimensional vector \(\{(X_{n}, Y_{n}, Z_{n}),\ n\ge 1\}\) to record the stochastic behavior of PUs and SUs, we establish a discrete time Markov Chain model to capture our proposed adaptive spectrum reservation strategy. The state space of the Markov Chain is given as follows:

$$\begin{aligned} {\varvec{\Omega }}= & {} \{(i,j,k):\ i= 0,1,2,\dots ;\ j= 0,1;\ k=-1,0,1,\dots , F+1\}. \end{aligned}$$

Let \(\pi _{i,j,k}\) be the steady-state distribution of the three-dimensional discrete time Markov Chain. \(\pi _{i,j, k}\) is then defined as follows:

$$\begin{aligned} \pi _{i,j,k}= & {} \lim \limits _{n \rightarrow \infty } \mathrm Pr \{X_{n}= i, Y_{n}=j, Z_{n}=k\},\ i=\mathrm 0,1,2,\dots ; \ j=\mathrm 0,1;\ \nonumber \\ k= & {} \mathrm -1,0,1,\dots , F+\mathrm 1. \end{aligned}$$
(2)

3.2 Model analysis

Let \(p_{i,j,k;l,m,h}=\mathrm Pr \{X_{n+\mathrm 1}= l,\ Y_{n+\mathrm 1}= m,\ Z_{n+\mathrm 1}= h\ |\ X_{n}=i, \ Y_{n}=j,\ Z_{n}=k\}\), \((i,j,k)\in \varvec{\Omega },\ (l,m,h)\in \varvec{\Omega }\). All the one step transition probabilities from the original state (i, j, k) to the other possible state (l, m, h) are discussed accordingly as follows:

  1. (1)

    When a new SU arrives at the system, if the reserved channel is occupied by an SU, and neither of the SUs in the system departs in one slot, then all the one step transition probabilities from the original state (i, j, k) can be written as follows:

    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j,k-2}=\lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh},\quad i\ge H+2,\quad j=1,\quad k=1.&\end{aligned}$$
    (3)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j,k-1}={\left\{ \begin{array}{ll} \lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}, &{}\quad i\ge H+1,\quad j=1,\quad k=0\\ \lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh}, &{}\quad 1 \le i \le H+1,\quad j=1,\quad k=1\\ \lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh}, &{}\quad i\ge 1,\quad j=1,\ 2 \le k \le F+1.\\ \end{array}\right. }&\end{aligned}$$
    (4)
    $$\begin{aligned} p_{i,j,k;i+1,j,k}={\left\{ \begin{array}{ll} \lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\bar{\mu }_{sh},&{}\quad i \ge 2, \quad j=1, \quad k=-1\\ \lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re},&{}\quad 0 < i \le H+1,\quad j=1,\quad k=0\\ \lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\bar{\mu }_{sh}+\lambda _{su}\lambda _{pu}\bar{\mu }_{re}\mu _{sh},&{}\quad i\ge 1,\ j=1,\quad 1\le k\le F\\ \lambda _{su}\bar{\mu }_{re}\bar{\mu }_{sh}+\lambda _{su}\lambda _{pu}\bar{\mu }_{re}\mu _{sh},&{}\quad i \ge 1,\quad j=1,\quad k=F+1.\\ \end{array}\right. } \end{aligned}$$
    (5)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j,k+1}={\left\{ \begin{array}{ll} \lambda _{su}\lambda _{pu}\bar{\mu }_{re},&{}\quad i \ge 1,\quad j=1, \quad k=0\\ \lambda _{su}\lambda _{pu}\bar{\mu }_{re}\bar{\mu }_{sh},&{}\quad i\ge 1,\quad j=1, \quad 1 \le k\le F. \end{array}\right. }&\end{aligned}$$
    (6)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j,k+2}= \lambda _{su}\lambda _{pu}\bar{\mu }_{re}\bar{\mu }_{sh},\quad i\ge 2,\ j=1,\quad k=-1.&\end{aligned}$$
    (7)
  2. (2)

    When a new SU arrives at the system, if the reserved channel is idle, and neither of the SUs in the system departs in one slot, then all the one step transition probabilities from the original state (i, j, k) can be written as follows:

    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j+1,k-1}=\bar{\lambda }_{pu}\lambda _{su}\mu _{sh},\quad i=0,\quad j=0,\quad 1 \le k \le F+1.&\end{aligned}$$
    (8)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j+1,k}={\left\{ \begin{array}{ll} \bar{\lambda }_{pu}\lambda _{su}\bar{\mu }_{sh},\quad i=1,\quad j=0,\quad k=-1\\ \bar{\lambda }_{pu}\lambda _{su}, \quad i=0,\quad j=0,\quad k=0\\ \bar{\lambda }_{pu}\lambda _{su}\bar{\mu }_{sh}+\lambda _{su}\lambda _{pu}\mu _{sh}, \quad i=0, \quad j=0, \quad 1\le k \le F\\ \lambda _{su}\bar{\mu }_{sh}+\lambda _{su}\lambda _{pu}\mu _{sh},\quad i=0,\quad j=0,\quad k=F+1.\\ \end{array}\right. }&\end{aligned}$$
    (9)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j+1,k+1}=\lambda _{pu}\lambda _{su},\quad i=0,\quad j=0,\quad 0\le k \le F.&\end{aligned}$$
    (10)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i+1,j+1,k+2}=\lambda _{pu}\lambda _{su}\bar{\mu }_{sh},\quad i=1,\quad j=0,\ k=-1.&\end{aligned}$$
    (11)
  3. (3)

    If the number of SUs is fixed in one slot, then all the one step transition probabilities from the original state (i, j, k) can be written as follows:

    $$\begin{aligned}&\ \ p_{i,j,k;i,j,k-2}= \lambda _{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh}+ \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh},\quad i\ge H+2,\quad j=1,\quad k=1.&\end{aligned}$$
    (12)
    $$\begin{aligned}&\ \ p_{i,j,k;i,j,k-1}\nonumber \\&\quad ={\left\{ \begin{array}{ll} \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh}+ \lambda _{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\ 1\le i\le H+1,\ j=1, \quad k=1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh}+\lambda _{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\quad i\ge 1,\quad j=1, \quad 2\le k\le F+1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{sh},\quad i=0,\quad j=0,\quad k\ge 1. \end{array}\right. }&\end{aligned}$$
    (13)
    $$\begin{aligned} p_{i,j,k;i,j,k+1}={\left\{ \begin{array}{ll} \lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh},\quad 1\le i \le H+1, \quad j=1, \quad k=-1\\ \lambda _{su}\lambda _{pu}\mu _{re}+\bar{\lambda }_{su}\lambda _{pu}\bar{\mu }_{re},\quad 1\le i\le H+1,\quad j=1, \quad k=0\\ \lambda _{su}\lambda _{pu}\mu _{re}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\bar{\mu }_{re}\bar{\mu }_{sh},\quad i \ge 1,\quad j=1, \quad 1\le k\le F\\ \bar{\lambda }_{su}\lambda _{pu}\bar{\mu }_{sh},\quad i=0,\quad j=1, \quad k\ge 1\\ \bar{\lambda }_{su}\lambda _{pu}, \quad i=0, \quad j=0,\quad k=0. \end{array}\right. } \end{aligned}$$
    (14)
    $$\begin{aligned}&p_{i,j,k;i,j,k+2}\nonumber \\&\quad =\lambda _{pu}(\bar{\lambda }_{su}\bar{\mu }_{re}\bar{\mu }_{sh}+ \lambda _{su}\mu _{re}\bar{\mu }_{sh}+\lambda _{su}\bar{\mu }_{re}\mu _{sh}), \quad i\ge 2,\quad j=1,\quad k=-1.&\end{aligned}$$
    (15)
    $$\begin{aligned}&\ \ p_{i,j,k;i,j+1,k+2}=\bar{\lambda }_{su}\lambda _{pu}\bar{\mu }_{sh}, \quad i=1,\quad j=0,\quad k=-1.&\end{aligned}$$
    (16)
    $$\begin{aligned}&p_{i,j,k;i,j,k}={\left\{ \begin{array}{ll} \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{sh},\quad i=1,\quad j=0,\quad k=-1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\bar{\mu }_{sh}+\lambda _{su}\bar{\lambda }_{pu}\mu _{re}\bar{\mu }_{sh}, \quad 1\le i \le H+1,\quad j=1, \quad k=-1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\bar{\mu }_{sh}+\lambda _{su}\bar{\lambda }_{pu}\mu _{re}\bar{\mu }_{sh}\\ \quad +\lambda _{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\mu _{sh}, \quad i \ge H+2,\quad j=1, \quad k=-1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu},\quad i=0,\quad j=0,\quad k=0\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{re}+\lambda _{su}\bar{\lambda }_{pu}\mu _{re},\quad 1 \le i \le H+1,\quad j=1,\quad k=0\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\mu _{sh},\quad i=0,\quad j=0,\quad 1\le k \le F\\ \bar{\lambda }_{su}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\mu _{sh},\quad i=0,\quad j=0,\quad k=F+1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\bar{\mu }_{re}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\bar{\mu }_{re}\mu _{sh}\\ \quad +\lambda _{su}\bar{\lambda }_{pu}\mu _{re}\bar{\mu }_{sh}+\lambda _{su}\lambda _{pu}\mu _{re}\mu _{sh},\quad i\ge 1,\quad j=1,\quad 1\le k\le F\\ \bar{\lambda }_{su}\bar{\mu }_{re}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\bar{\mu }_{re}\mu _{sh}\\ \quad +\lambda _{su}\mu _{re}\bar{\mu }_{sh}+\lambda _{su}\lambda _{pu}\mu _{re}\mu _{sh},\quad i\ge 1,\quad j=1,\quad k=F+1\\ \end{array}\right. }&\end{aligned}$$
    (17)
  4. (4)

    If the number of SUs departing from the system is greater than the number of SUs arriving at the system and the reserved channel does not become idle in one slot, then all the one step transition probabilities from the original state (i, j, k) can be written as follows:

    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-1,j,k-2}=\bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\quad i\ge H+2,\ j=1, \quad k=1.&\end{aligned}$$
    (18)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-1,j,k-1}={\left\{ \begin{array}{ll} \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\quad 2\le i\le H+2,\quad j=1,\quad k=1 \\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\quad i\ge 2,\quad j=1,\quad 2\le k \le F+1. \end{array}\right. }&\end{aligned}$$
    (19)
    $$\begin{aligned} \ p_{i,j,k;i-1,j,k}={\left\{ \begin{array}{ll} \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\bar{\mu }_{sh},\quad 2\le i \le H+2,\quad j=1,\quad k=-1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\bar{\mu }_{re}\mu _{sh}\\ \quad +\lambda _{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\quad i\ge H+3,\quad j=1, \quad k=-1\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re},\quad 2\le i\le H+1,\quad j=1,\quad k=0\\ \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\mu _{re}\mu _{sh}, \quad i \ge 2,\quad j=1, \quad 1\le k\le F\\ \bar{\lambda }_{su}\mu _{re}\bar{\mu }_{sh}+\bar{\lambda }_{su}\lambda _{pu}\mu _{re}\mu _{sh},\quad i \ge 2,\ j=1,\ k=F+1. \end{array}\right. } \end{aligned}$$
    (20)
    $$\begin{aligned}&p_{i,j,k;i-1,j,k+1}\nonumber \\&\quad ={\left\{ \begin{array}{ll} \bar{\lambda }_{pu}\mu _{sh}(\bar{\lambda }_{su}\bar{\mu }_{re}+\lambda _{su}\mu _{re}),\quad 2\le i\le H+2,\quad j=1,\quad k=-1\\ \bar{\lambda }_{su}\lambda _{pu}\mu _{re},\quad 2 \le i \le H+1,\quad j=1,\quad k=0\\ \bar{\lambda }_{su}\lambda _{pu}\mu _{re}\bar{\mu }_{sh},\quad i\ge 2,\quad j=1,\quad 1 \le k \le F\\ \bar{\lambda }_{pu}\bar{\lambda }_{su}\mu _{sh},\quad i=1, \quad j=0,\quad k=-1. \end{array}\right. }&\end{aligned}$$
    (21)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-1,j,k+2}={\left\{ \begin{array}{ll} \lambda _{pu}(\lambda _{su}\mu _{re}\mu _{sh}+\bar{\lambda }_{su}\mu _{re}\bar{\mu }_{sh}+ \bar{\lambda }_{su}\bar{\mu }_{re}\mu _{sh}),\\ \quad i\ge 2,\quad j=1,\quad k=-1\\ \lambda _{pu}\bar{\lambda }_{su}\mu _{sh}, \quad i=1,\quad j=0,\quad k=-1. \end{array}\right. }&\end{aligned}$$
    (22)
  5. (5)

    If the number of SUs departing from the system is greater than the number of SUs arriving at the system, and the reserved channel becomes idle in one slot, then all the one step transition probabilities from the original state (i, j, k) can be written as follows:

    $$\begin{aligned}&p_{i,j,k;i-1,j-1,k-1}=\bar{\lambda }_{pu}\bar{\lambda }_{su}\mu _{re}\mu _{sh},\quad i=1,\quad j=1,\quad 1 \le k\le F+1. \nonumber \\ \end{aligned}$$
    (23)
    $$\begin{aligned}&p_{i,j,k;i-1,j-1,k}\nonumber \\&\quad ={\left\{ \begin{array}{ll} \bar{\lambda }_{pu}\bar{\lambda }_{su}\mu _{re},\quad i=1, \ j=1,\quad k=0\\ \bar{\lambda }_{pu}\bar{\lambda }_{su}\mu _{re}\bar{\mu }_{sh}+\lambda _{pu}\bar{\lambda }_{su}\mu _{re}\mu _{sh},\quad i=1, \quad j=1,\quad 1 \le k\le F\\ \bar{\lambda }_{su}\mu _{re}\bar{\mu }_{sh}+\lambda _{pu}\bar{\lambda }_{su}\mu _{re}\mu _{sh},\quad i=1,\quad j=1,\quad k=F+1\\ \bar{\lambda }_{pu}\bar{\lambda }_{su}\mu _{re}\bar{\mu }_{sh},\quad i=2,\quad j=1,\quad k=-1. \end{array}\right. } \end{aligned}$$
    (24)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-1,j-1,k+1}={\left\{ \begin{array}{ll} \lambda _{pu}\bar{\lambda }_{su}\mu _{re},\quad i=1,\quad j=1,\quad k=0\\ \lambda _{pu}\bar{\lambda }_{su}\mu _{re}\bar{\mu }_{sh},\quad i=1,\quad j=1,\quad 1 \le k\le F. \end{array}\right. }&\end{aligned}$$
    (25)
  6. (6)

    When two SUs depart the system and no SU arrives at the system, if the state of the reserved channel does not change in one slot, then the one step transition probabilities from the original state (i, j, k) can be written as follows:

    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-2,j,k}=\bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\quad i\ge H+4,\quad j=1,\quad k=-1.&\end{aligned}$$
    (26)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-2,j,k+1}= \bar{\lambda }_{su}\bar{\lambda }_{pu}\mu _{re}\mu _{sh},\quad 3 \le i\le H+3,\quad j=1,\quad k=-1.&\end{aligned}$$
    (27)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-2,j,k+2}=\bar{\lambda }_{su}\lambda _{pu}\mu _{re}\mu _{sh}, \ i\ge 3,\quad j=1,\quad k=-1.&\end{aligned}$$
    (28)
  7. (7)

    When two SUs depart the system and no SU arrives at the system, if the state of the reserved channel changes in one slot, then all the one step transition probabilities from the original state (i, j, k) can be written as follows:

    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-2,j-1,k+1}=\bar{\lambda }_{pu}\bar{\lambda }_{su}\mu _{re}\mu _{sh},\quad i=2,\quad j=1,\quad k=-1.&\end{aligned}$$
    (29)
    $$\begin{aligned}&\ \ \ \ p_{i,j,k;i-2,j-1,k+2}= \lambda _{pu}\bar{\lambda }_{su}\mu _{re}\mu _{sh},\quad i=2,\quad j=1,\quad k=-1.&\end{aligned}$$
    (30)

Let \(\varvec{P}\) be the state transition probability matrix of the Markov Chain \(\{(X_{n},Y_{n},Z_{n})\), \(n \ge 1\}\). Let \(\varvec{A}_{i,k}\) be the transition probability sub-matrix for the number of SUs in the system changing from \(i\ (i=0, 1, 2, \dots )\) to \(k\ (k=0, 1, 2, \dots )\). The one step transition probability matrix \(\varvec{P}\) can be written as a block matrix as follows:

$$\begin{aligned} {\varvec{P}}= \begin{bmatrix} {\begin{matrix} {\varvec{A}}_{0,0} &{}\quad \! {\varvec{A}}_{0,1}&{}\quad \! &{}\quad \! &{}\quad \! &{}\quad \!&{}\quad \! \\ {\varvec{A}}_{1,0} &{}\quad \! {\varvec{A}}_{1,1} &{}\quad \! {\varvec{A}}_{1,2} &{}\quad \! &{}\quad \!&{}\quad \! &{}\quad \! \\ \varvec{A}_{2,0} &{}\quad \! {\varvec{A}}_{2,1} &{}\quad \! {\varvec{A}}_{2,2} &{}\quad \! {\varvec{A}}_{2,3} &{}\quad \! &{}\quad \!&{}\quad \! \\ &{}\quad \! &{}\quad \! \ddots &{}\quad \! \ddots &{}\quad \! \ddots &{}\quad \!\ddots &{}\quad \! \\ &{}\quad \! &{}\quad \! &{}\quad \! {\varvec{A}}_{H+4,H+2}&{}\quad \! {\varvec{A}}_{H+4,H+3}&{}\quad \! {\varvec{A}}_{H+4,H+4}&{}\quad \!{\varvec{A}}_{H+4,H+5}&{}\quad \! \\ &{}\quad \! &{}\quad \! &{}\quad \! &{}\quad \! {\varvec{A}}_{H+4,H+2}&{}\quad \! {\varvec{A}}_{H+4,H+3}&{}\quad \! {\varvec{A}}_{H+4,H+4}&{}\quad \!{\varvec{A}}_{H+4,H+5}&{}\quad \! \\ &{}\quad \! &{}\quad \! &{}\quad \! &{}\quad \! &{}\quad \! \ddots &{}\quad \! \ddots &{}\quad \! \ddots &{}\quad \!\ddots &{}\quad \! \\ \end{matrix}} \end{bmatrix}.\nonumber \\ \end{aligned}$$
(31)

Employing Eqs. (3)–(30), each sub-matrix \(\varvec{A}_{i,j}\) can be computed. The structure of the one step transition probability matrix \(\varvec{P}\) shows that the three-dimensional discrete time Markov Chain \(\{(X_{n},Y_{n},Z_{n}),\quad n\ge 1\}\) has structure similar to that of the birth-and-death (QBD) process. If the number of SUs is no less than \((H+4)\), the one step probabilities are repeatable. Therefore, we can use a method similar to that of the matrix-geometric solution to obtain the steady-state distribution \(\pi _{i,j,k}\) for the system model.

For the Markov Chain \(\{(X_{n},Y_{n},Z_{n}),\quad n\ge 1\}\) with the one step transition probability matrix \(\varvec{P}\), the necessary and sufficient condition of positive recurrence is that the 3rd order matrix equation:

$$\begin{aligned} \varvec{R}^3 \varvec{A}_{H+4,H+2}+\varvec{R}^2\varvec{A}_{H+4,H+3}+\varvec{R}\varvec{A}_{H+4,H+4}+\varvec{A}_{H+4,H+5}=\varvec{R} \end{aligned}$$
(32)

has a minimal non-negative solution \(\varvec{R}\), and the spectral radius \(SP( \varvec{R})<1\). In order to employ a method similar to that of the matrix geometric solution, we construct new sub-matrices \(\varvec{B}_{0,0}\), \(\varvec{B}_{0,1}\), \( \varvec{B}_{1}\) and \(\varvec{B}_{2}\) as follows:

$$\begin{aligned} \begin{array}{lll} &{}\varvec{B}_{0,0}= \begin{bmatrix} \varvec{A}_{0,0} &{}\quad \! \varvec{A}_{0,1}&{}\quad \! &{}\quad \!&{}\quad \! &{}\quad \!&{}\quad \! \\ \varvec{A}_{1,0} &{}\quad \! \varvec{A}_{1,1} &{}\quad \! \varvec{A}_{1,2} &{}\quad \! &{}\quad \!&{}\quad \! &{}\quad \! \\ \varvec{A}_{2,0} &{}\quad \! \varvec{A}_{2,1} &{}\quad \! \varvec{A}_{2,2} &{}\quad \! \varvec{A}_{2,3} &{}\quad \! &{}\quad \!&{}\quad \! \\ &{}\quad \! &{}\quad \! \ddots &{}\quad \! \ddots &{}\quad \! \ddots &{}\quad \!\ddots &{}\quad \! \\ &{}\quad \! &{}\quad \! &{}\quad \! \varvec{A}_{H+3,H+1}&{}\quad \! \varvec{A}_{H+3,H+2}&{}\quad \! \varvec{A}_{H+3,H+3}&{}\quad \!&{}\quad \! \\ {} &{}\quad \! \end{bmatrix}, \end{array} \end{aligned}$$
$$\begin{aligned} \varvec{B}_{0,1}=[\mathbf 0 ^T,\ \mathbf 0 ^T,\dots ,\ \mathbf 0 ^T, \ \mathbf A _{H+3,H+4}^T]^{T}, \end{aligned}$$
$$\begin{aligned} \varvec{B}_{1}=[\mathbf 0 ,\ \mathbf 0 ,\dots ,\ \mathbf 0 ,\ \mathbf A _{H+4,H+2},\mathbf A _{H+4,H+3}], \end{aligned}$$
$$\begin{aligned} \varvec{B}_{2}=[\mathbf 0 ,\ \mathbf 0 ,\dots ,\ \mathbf 0 ,\ \mathbf A _{H+4,H+2}]. \end{aligned}$$

Furthermore, we construct a stochastic matrix as follows:

$$\begin{aligned} \begin{array}{l@{\quad }ll} B[\varvec{R}]= \begin{bmatrix} \varvec{B}_{0,0} &{}\quad \varvec{B}_{0,1} \\ \varvec{R} \varvec{B}_{2} + \varvec{B}_{1} &{}\quad \varvec{R}^2\varvec{A}_{H+4,H+2}+\varvec{R} \varvec{A}_{H+4,H+3}+\varvec{A}_{H+4,H+4} \\ \end{bmatrix}. \end{array} \end{aligned}$$

Letting \(\varvec{\pi }_{0}=(\pi _{0,0,0},\pi _{0,0,1},\dots ,\pi _{0,0,F+1})\), \(\pi _{1}=(\pi _{1,0,-1},\pi _{1,1,0},\dots ,\pi _{1,1,F+1})\), \(\pi _{i}=(\pi _{i,1,-1},\pi _{i,1,0},\dots ,\pi _{i,1,F+1})\), \( 2 \le i \le (H+1)\) and \(\pi _{i}=(\pi _{i,1,-1},\pi _{i,1,1},\dots ,\pi _{i,1,F+1})\), \( i \ge (H+2)\), then the steady-state distribution for the Markov Chain can be obtained by solving the following system of linear equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{\pi }_{i} = \varvec{\pi }_{H+3}\varvec{R}^{i-H-3},\ (i\ge H+3)\\ (\varvec{\pi }_{0},\varvec{\pi }_{1},\dots ,\varvec{\pi }_{H+2},\varvec{\pi }_{H+3})=(\varvec{\pi }_{0},\varvec{\pi }_{1},\dots ,\varvec{\pi }_{H+2},\varvec{\pi }_{H+3})B[\varvec{R}]\\ (\varvec{\pi }_{0},\varvec{\pi }_{1},\dots ,\pi _{H+3})\varvec{e}+\pi _{H+3}(\varvec{I}-\varvec{R})^{-1}\varvec{e} =1\\ \end{array}\right. } \end{aligned}$$
(33)

where \(\varvec{e} \) is a one’s column vector.

4 Performance measures and system experiments

In this section, we firstly define some performance measures, then we evaluate the system performance by the help of system experiments.

4.1 Performance measures

The interruption rate \(\beta _{su}\) of SUs is defined as the number of SUs which are interrupted by PUs per slot. An SU which is on the shared channel will be interrupted by a newly arriving PU, so the interruption rate \(\beta _{su}\) of SUs is given as follows:

$$\begin{aligned} \beta _{su}=\lambda _{pu}\left( \sum _{i=2}^{\infty }\pi _{i,1,-1}+\pi _{1,0,-1}\right) \bar{\mu }_{sh}. \end{aligned}$$
(34)

The blocking rate \(\beta _{pu}\) of PUs is defined as the number of PUs which are blocked due to the finite capacity of the PU’s buffer per slot. A newly arriving PU will be blocked when the shared channel is occupied by a PU and the PU’s buffer is full. In addition, since the PUs have preemptive priority, the blocking rate \(\beta _{pu}\) of PUs is not influenced by SUs. Therefore, the blocking ratio \(\beta _{pu}\) of PUs can be given as follows:

$$\begin{aligned} \begin{array}{ll} \beta _{pu}&{}=\lambda _{pu}\left( \sum _{i=1}^{\infty }\pi _{i,1,F+1}+\pi _{0,0,F+1}\right) \\ &{}=\dfrac{\dfrac{\lambda _{pu}\bar{\mu }_{re}}{\mu _{re}}\alpha ^{F+1}}{\dfrac{1-\alpha ^{F+1}}{1-\alpha }+ \dfrac{\lambda _{pu}\bar{\mu }_{re}}{\mu _{re}}\alpha ^{F} } \end{array} \end{aligned}$$
(35)

where \(\alpha ={\lambda _{pu}\bar{\mu }_{re}}({\bar{\lambda }_{pu}\mu _{re}})^{-1}\).

The latency of an SU is defined as the time duration from the arrival instant of an SU to its departure instant. By using Little’s law [15], the average latency \(E\left[ T_{su}\right] \) of SUs can be given as follows:

$$\begin{aligned} E\left[ T_{su}\right] =\frac{\sum _{k=0}^{F+1}\sum \nolimits _{j=0}^{1}\sum _{i=0}^{\infty }i\pi _{i,j,k}}{\lambda _{su}}. \end{aligned}$$
(36)

The normalized throughput \(\omega \) is defined as proportion that the number of SUs transmitted actually per unit time to the number of SUs transmitted maximally per unit time on the whole spectrum. With the normalized throughput, we can evaluate the efficiency of the whole spectrum. When both the shared channel and the reserved channel are occupied by users, the efficiency of the whole spectrum is 1; When the shared channel (reserved channel) is idle and the reserved channel (shared channel) is busy, the efficiency of the whole spectrum is \(\theta \) \((\bar{\theta })\). Therefore, the normalized throughput \(\omega \) is given as follows:

$$\begin{aligned} \omega ={\sum \limits _{i=1}^{\infty }\sum \limits _{k=-1,\ k\ne 0}^{F+1}\pi _{i,1,k}+\sum \limits _{i=1}^{\infty }\pi _{i,1,0}\theta +\sum \limits _{k=1}^{F+1}\pi _{0,0,k}\bar{\theta }}. \end{aligned}$$
(37)

4.2 System experiments and illustrations

In this section, we investigate the influences of the adaptive control factor C and the admission threshold H on the system performance. Unless otherwise specified, system parameters in system experiments are set as follows: \(F=2\), \(\lambda _{pu}=0.20\), \(\lambda _{su}=[0.40,\ 0.45,\ 0.50,\ 0.55]\) and \(\mu =0.80\).

Taking the admission threshold \(H=4\) as an example, for different arrival rates \(\lambda _{su}\) of SUs, we show the change trend of the interruption rate \(\beta _{su}\) of SUs with respect to the adaptive control factor C in Fig. 2.

Fig. 2
figure 2

Interruption rate \(\beta _{su}\) of SUs vs. adaptive control factor C

Full size image

In Fig. 2, we find that the interruption rate \(\beta _{su}\) of SUs exhibits two stages as the adaptive control factor C increases.

During the first stage, the interruption \(\beta _{su}\) of SUs increases sharply as the adaptive control factor C increases. When the adaptive control factor is smaller, the dominant element influencing the interruption rate of SUs is the service rate on the reserved channel. Based on Eq. (1), we note that the aside spectrum ratio decreases as the adaptive control factor increases. Therefore, the larger the adaptive control factor is, the lower the service rate on the reserved channel is, and the more SUs enter into the shared channel to receive transmission service. The transmission of SUs on the shared channel may be interrupted by PUs. When this occurs, the interruption rate of SUs will increase.

During the second stage, the interruption rate \(\beta _{su}\) of SUs decreases slowly as the adaptive control factor C increases. When the adaptive control factor is larger, the dominant element influencing the interruption rate of SUs is the service rate on the shared channel. As the adaptive control factor increases, the service rate on the shared channel increases, the PUs on the shared channel are transmitted quickly, and the synthetical service rate for the SUs increases. Therefore, the transmission of SUs on the shared channel is less likely to be interrupted by PUs, so the interruption rate of SUs will decrease.

By setting the adaptive control factor \(C=0.50\) as an example, for different arrival rates \(\lambda _{su}\) of SUs, we show the change trend for the interruption rate \(\beta _{su}\) of SUs in relation to the admission threshold H in Fig. 3.

Fig. 3
figure 3

Interruption rate \(\beta _{su}\) of SUs vs. admission threshold H

Full size image

In Fig. 3, for all the arrival rates \(\lambda _{su}\) of SUs, we find that the interruption rate \(\beta _{su}\) of SUs decreases as the threshold H increases. The obvious reason is that the higher the admission threshold is, the more SUs are transmitted on the reserved channel without interruption. As a result, the interruption rate of SUs will decrease.

Taking the admission threshold \(H=4\) as an example, for different arrival rates \(\lambda _{su}\) of SUs, we show the change trend for the average latency \(E\left[ T_{su}\right] \) of SUs in relation to the adaptive control factor C in Fig. 4.

Fig. 4
figure 4

Average latency \(E\left[ T_{su}\right] \) of SUs vs. adaptive control factor C

Full size image

We discuss the average latency \(E\left[ T_{su}\right] \) of SUs in two cases.

  1. (1)

    For a higher arrival rate of SUs, such as \(\lambda _{su}=0.50\) and \(\lambda _{su}=0.55\), the average latency \(E\left[ T_{su}\right] \) of SUs exhibits two stages as the adaptive control factor C increases.

During the first stage, the average latency \(E\left[ T_{su}\right] \) of SUs increases sharply as the adaptive control factor C increases. When the adaptive control factor is smaller, the service rate on the reserved channel is the dominant element influencing the average latency of SUs. As the adaptive control factor increases, the service rate on the reserved channel decreases. This leads to a decrease in the synthetical service rate for SUs, and so the average latency of SUs will be greater.

During the second stage, as the adaptive control factor C increases, the average latency \(E\left[ T_{su}\right] \) of SUs decreases slowly and tends to be fixed. When the adaptive control factor exceeds a certain value, the service rate on the shared channel is the dominant element influencing the average latency of SUs. The bigger the adaptive control factor is, the higher the service rate on the shared channel is, and the greater the synthetical service rate for SUs is. Therefore, the average latency of SUs will decrease. As the adaptive control factor continuously increases, nearly all the SUs are transmitted on the shared channel, so the average latency of SUs will tend to be fixed.

  1. (2)

    For a lower arrival rate of SUs, such as \(\lambda _{su}=0.40\) and \(\lambda _{su}=0.45\), the average latency \(E\left[ T_{su}\right] \) of SUs increases sharply when the adaptive control factor C is smaller, increases slowly and tends to be fixed when the adaptive control factor C is greater than a certain value. When the arrival rate of SUs is lower, with the constraint of the admission threshold, the average latency of SUs is mainly influenced by the service rate on the reserved channel. The bigger the adaptive control factor is, the lower the service rate on the reserved channel is, so the average latency of SUs will increases sharply. However, when the adaptive control factor exceeds a certain value, some SUs are transmitted opportunistically on the shared channel, so the average latency of SUs will increase slowly. As the adaptive control factor continuously increases, more and more SUs will enter into the shared channel, so the average latency of SUs will tend to be fixed.

By setting the adaptive control factor \(C\mathrm =1\) as an example, for different arrival rates \(\lambda _{su}\) of SUs, we show the change trend for the average latency \(E\left[ T_{su}\right] \) in relation to the admission threshold H in Fig. 5.

Fig. 5
figure 5

Average latency \(E\left[ T_{su}\right] \) of SUs vs. admission threshold H

Full size image

In Fig. 5, we find that, for all the arrival rates of SUs, the average latency \(E\left[ T_{su}\right] \) of SUs increases as the admission threshold H increases. The reason is that the higher the admission threshold is, the fewer SUs are transmitted on the shared channel, and the lower the synthetical service rate for SUs is. This will lead to an increase in the average latency of SUs.

PUs receive service on the shared channel with preemptive priority. The transmission of PUs is only affected by the adaptive control factor and the arrival rate of PUs, so the blocking rate of PUs has nothing to do with the admission threshold. By setting \(\lambda _{pu}=\left[ 0.15,\ 0.20,\ 0.25,\ 0.30 \right] \) and \(H=4\) as examples, we show the change trend for the blocking ratio \(\beta _{pu}\) of PUs in relation to the adaptive control factor C in Fig. 6.

Fig. 6
figure 6

Blocking rate \(\beta _{pu}\) of PUs vs. adaptive control factor C

Full size image

From Fig. 6, we conclude that, for all the arrival rates \(\lambda _{pu}\) of PUs, the blocking rate \(\beta _{pu}\) of PUs decreases as the adaptive control factor C increases. The intuitive reason is that the larger the adaptive control factor is, the smaller the aside spectrum ratio is, and the higher the service rate for the PUs on the shared channel is. This leads to a decrease in the blocking rate of PUs.

By setting the admission threshold \(H=4\) as an example, for different arrival rates \(\lambda _{su}\) of SUs, we show the change trend for the systematic normalized throughput \(\omega \) in relation to the adaptive control factor C in Fig. 7.

Fig. 7
figure 7

Normalized throughput \(\omega \) vs. adaptive control factor C

Full size image

From Fig. 7, we observe that as the adaptive control factor C increases, the normalized throughput \(\omega \) increases firstly when the adaptive control factor C is smaller; and then, when the adaptive control factor C exceeds a certain value, the normalized throughput tends to be fixed. Since the capacity set for the PUs is finite and the capacity set for SUs is infinite, when the adaptive control factor is less than a certain value, the greater the adaptive control factor is, and the higher the service rate on the shared channel is, the lower the blocking rate of PUs is. As a result, normalized throughput will increase. However, as the adaptive control factor further increases, when the adaptive control factor is greater than a certain value, nearly all the users are transmitted on the shared channel, so the normalized throughput tends to be fixed.

In order to clearly show the normalized throughput \(\omega \) in relation to the admission threshold H, we calculate the normalized throughput increment as \(\alpha =\omega -\omega _{0}\), where \(\omega _{0}\) is the normalized throughput by setting the admission threshold \(H=0\). Taking the adaptive control factor \(C=1\) as an example, for different arrival rates \(\lambda _{su}\) of SUs, we investigate the change trend for the normalized throughput increment \(\alpha \) in relation to the admission threshold H in Fig. 8.

Fig. 8
figure 8

Normalized throughput increment \(\alpha \) vs. admission threshold H

Full size image

Looking at Fig. 8, we find that the normalized throughput increment \(\alpha \) exhibits two stages as the admission threshold H increases.

During the first stage, the normalized throughput increment \(\alpha \) increases as the admission threshold H increases. We note that the service rate on the reserved channel is greater than the service rate on the shared channel with the parameters used in this paper. Therefore, when the admission threshold H is smaller, the dominant element influencing the normalized throughput is the service rate on the reserved channel. This means that the higher the admission threshold is, the more SUs access the reserved channel. This will lead to an increase in the normalized throughput increment.

During the second stage, as the admission threshold further increases, when the admission threshold is greater than a certain value, the dominant element influencing the normalized throughput is the service rate on the shared channel, the higher the admission threshold is, the more likely the shared channel is idle, resulting in a decrease in the normalized throughput increment.

5 System cost and system optimization

Based on the experiment results given in Sect. 4.2, we firstly construct a system cost function to trade off different performance measures. Then, we present a searching algorithm based on the philosophy of teaching and learning to optimize the system parameters in terms of the adaptive control factor and the admission threshold.

5.1 System cost

From the experiment results provided in Sect. 4.2, we can draw the following conclusions. The interruption rate of \(\beta _{su}\) of SUs, the average latency \(E[T_{su}]\) of SUs and the normalized throughput \(\omega \) heavily depend on the adaptive control factor C and the admission threshold H. However, the blocking rate \(\beta _{pu}\) of PUs heavily depends on the adaptive control factor C.

In order to get the utmost out of the spectrum resource and meet the demands for QoS requirements of two types of users, considering the tradeoff between the performance measures of two types users, we construct a system cost \(\psi (C,H)\) as follows:

$$\begin{aligned} \psi (C, H)=f_{1}\beta _{pu}+f_{2}E[T_{su}]+\frac{f_{3}}{\omega }+f_{4}\beta _{su}+\frac{f_{5}}{\lambda _{su}} \end{aligned}$$
(38)

where \(f_{1},f_{2},f_{3},f_{4}\) and \(f_{5}\) are cost factors from blocking rate of PUs, the average latency of SUs, normalized throughput, interruption rate of SUs and arrival rate of SUs. By minimizing the system cost, the optimal combination \((C^{*}, H^{*})\) is given as follows:

$$\begin{aligned} (C^{*}, H^{*})={\text {argmin}}\{\psi (C,H)\} \end{aligned}$$
(39)

where “argmin” stands for the argument of the maximum [16].

Taking system parameters \(f_{1}=20.00,\ f_{2}=0.60,\ f_{3}=4.00,\ f_{4}=3.00\), \(f_{5}=0.20\), \(F =2\), \(\mu = 0.80\), \(\lambda _{pu}=[0.10,\ 0.15]\), \(\lambda _{su}=[0.40,\ 0.50,\ 0.60]\), \(H=4\) and \(C=1\) as an example, we investigate the change trend for the system cost \(\psi \mathrm ( C, H\mathrm )\) in relation to the adaptive control factor C and the admission threshold H in Figs. 9 and 10, respectively.

Fig. 9
figure 9

System cost \(\psi \mathrm ( C, H\mathrm )\) vs. adaptive control factor C \((H=4)\)

Full size image
Fig. 10
figure 10

System cost \(\psi \mathrm ( C, H\mathrm )\) vs. admission threshold H \((C=1)\)

Full size image
Table 1 Searching algorithm to obtain optimal combination \((C^*,H^*)\) with global minimum system cost
Full size table

Looking at Figs. 9 and 10, we conclude that there is an optimal adaptive control factor and an optimal admission threshold with local minimum system costs. Based on these local minimum system costs, we can further obtain the global minimum system cost. However, it is difficult to give an analytical expression for the system cost \(\psi (C,H)\) in close form. Conventional optimization methods, such as steepest descent method or Newton’s method, are inappropriate. Therefore, we turn to an intelligent optimization algorithm with a strong global convergence ability to obtain the optimal combination \((C^*,H^*)\) with a global minimum system cost.

5.2 System optimization

The Teaching-learning-based optimization (TLBO) algorithm is a new and efficient meta-heuristic optimization method based on the philosophy of teaching and learning [17]. This algorithm has the advantages of having fewer parameters, being easy to understand and having a high degree of precision. Based on a TLBO algorithm, we optimize the system parameters in terms of the adaptive control factor C and the admission threshold H.

Inspired by the teaching-learning process, we firstly randomly set a group of (C, H) as the students, and the corresponding system costs \(\psi (C,H)\) as academic records. The student who achieves the best academic record is assigned to the teacher. After a period of the teaching-learning process, we can deduce the best student. This means that we can derive the global minimum system cost \(\psi (C^{*}, H^{*})\) and the optimize combination \((C^*,H^*)\). The complexity of the TLBO algorithm depends on the maximum iterations N, the number M of students and the upper bound of the admission threshold \(H_{1}\). The complexity T of this algorithm is \(T=O(N\times M\times H_{1})\). We give the main steps for the searching algorithm to obtain the optimal adaptive control factor \(C^*\) and admission threshold \(H^*\) in Table 1.

By setting the same parameters as used in Figs. 9 and 10, we obtain the optimal combination \((C^*, H^*)\) with the adaptive control factor C and the admission threshold H as shown in Table 2.

Table 2 Numerical results for optimal combination \((C^*, H^*)\) and global minimum system cost
Full size table

6 Conclusions

In this paper, we presented our proposed novel spectrum reservation strategy with an adaptive control approach for the setting the spectrum aside ratio in centralized CRNs. We firstly constructed a three-dimensional discrete time Markov Chain model, and obtained the steady-state distribution for the system model by using a method similar to that of the matrix geometric solution. Accordingly, we evaluated the system performance mathematically. Moreover, we carried out system experiments to investigate the influence of the adaptive control factor and the admission threshold on the system performance. Based on the trade off between different performance measures, we built a system cost function. Finally, we presented a TLBO based intelligent searching algorithm to optimize the adaptive control factor and the admission threshold with global minimum system cost. System experiments show that the proposed spectrum reservation strategy is effective in improving the spectrum utilization and coping with the immense demand from wireless devices. The numerical results obtained by proposed optimization algorithm are reasonable for setting system parameters with global minimum system cost.

In future work, we will investigate the dependence between the adaptive control factor and the capacity of the PU’s buffer.