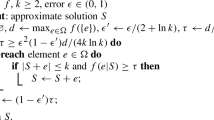New performance guarantees for the greedy maximization of submodular set functions

Abstract

We present new tight performance guarantees for the greedy maximization of monotone submodular set functions. Our main result first provides a performance guarantee in terms of the overlap of the optimal and greedy solutions. As a consequence we improve performance guarantees of Nemhauser et al. (Math Program 14:265–294, 1978) and Conforti and Cornuéjols (Discr Appl Math 7:251–274, 1984) for maximization over subsets, which are at least half the size of the problem domain. As a further application, we obtain a new tight approximation guarantee in terms of the cardinality of the problem domain.

1 Introduction

Let X be a finite set, $X=\{x_1,\dots , x_n\}$, and let T be an integer such that $0 < T\le n$. We consider the cardinality-constrained maximization problem

$$\begin{aligned} \max \{f(S):|S|=T, S \subset X\}, \end{aligned}$$

(1)

where $f:2^X\rightarrow \mathbb R_+$ is a submodular set function. Recall that f is submodular if

$$\begin{aligned} f(S)+f(R)\ge f(S\cup R) + f(S\cap R) \end{aligned}$$

(2)

for all $S,R\subset X$; see, e.g., [1]. We further assume that f is nondecreasing; $f(S) \le f(R)$ for all $S\subset R$, and, without loss of generality, that $f(\emptyset )=0$. We consider the following well-known greedy algorithm for solving problem (1):

Algorithm A has been extensively studied in the literature. It is well known [2, 3], that it finds an optimal solution when f is an additive set function, i.e., when (2) holds with an equality for all $S,R\subset X$. Nemhauser et al. [1] (see also [4, 5]) gave the following performance guarantee for Algorithm A for nonadditive functions f:

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})}\ge 1-\left( 1-\frac{1}{T}\right) ^{T}=:G_{NWF}(T), \end{aligned}$$

(3)

where $S_{opt}$ is an optimal solution to problem (1). Conforti and Cornuéjols [2] improved (3) to

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})}\ge \frac{1}{\alpha }\left( 1-\left( 1-\frac{\alpha }{T}\right) ^{T}\right) =: G_{CC}(T,\alpha ), \end{aligned}$$

(4)

for $\alpha \in (0,1]$, where $\alpha \in (0,1]$ is the total curvature

$$\begin{aligned} \alpha =\max \left\{ 1-\frac{f(X)-f(X{\setminus }\{x\})}{f(\{x\})-f(\emptyset )}:x\in X, f(\{x\})\ne f(\emptyset )\right\} . \end{aligned}$$

It is known that $\alpha \in (0,1]$ if and only if f is nonadditive [2]. We also clearly have $G_{NWT}(T)=G_{CC}(T,1)$ and $G_{CC}(T,\alpha )\rightarrow 1$ as $\alpha \rightarrow 0^+$. The above performance guarantees further satisfy the estimates

$$\begin{aligned} G_{CC}(T,\alpha )\ge \max \left\{ G_{NWF}(T), \frac{1-{\mathrm e}^{-\alpha }}{\alpha }\right\} \ge 1-{\mathrm e}^{-1}, \end{aligned}$$

for all $\alpha$ and T. The guarantees (3) and (4) are tight for suitable choices of parameters T and $\alpha$. For example, for all $\alpha \in (0,1]$ and $T\ge 1$ there is a problem of the type (1) and the corresponding greedy solution $S_{gr}$ such that $f(S_{gr})=G_{CC}(T,\alpha )f(S_{opt})$ [2].

Submodular optimization has played a central role in operations research and combinatorial optimization [6]. By now it has applications in various fields, including computer science [7], economics [8] and, more recently, ecology [9–11]. Problem (1) and the above performance guarantees have been extended to various other settings and problem structures, related to, for example, matroid [2, 12] and knapsack [13, 14] constraints, continuous algorithms [15, 16], nonmonotone functions [17], nonsubmodular functions [18] and supermodular minimization [19, 20].

To authors’ knowledge, previously presented performance guarantees either do not depend on T or n, or, like (3) and (4), they are decreasing in T. However, when $T=n$, it is clear that $S_{opt}=S_{gr}$, so the greedy algorithm returns the optimal solution. This suggests that any performance guarantee should in fact be improving when T approaches and is close enough to n. We show that this is indeed the case. More generally, we show that increasing degree of overlap $m=|S_{opt}\cap S_{gr}|$ between the sets $S_{opt}$ and $S_{gr}$ improves the approximation guarantees. While in applications the overlap m may not be known, we can give this quantity a useful lower bound. In fact, when $T > n/2$, we have $m \ge 2T-n>0$. Our results thus have particular relevance for optimization problems where the maximum is sought over subsets of cardinality larger than n / 2.

Let

$$\begin{aligned} G(T,\alpha ,m)=\frac{1}{\alpha }\left( 1-\left( 1-\frac{\alpha m}{T}\right) \left( 1-\frac{\alpha }{T}\right) ^{T-m}\right) \end{aligned}$$

and $\widetilde{G}(T,\alpha ,n)=G(T,\alpha ,\max \{0, 2T-n\})$. Our main result is the following.

Theorem 1

Let $\alpha \in (0,1]$, let $1\le T \le n$ and let $S_{opt}$ and $S_{gr}$ be an optimal, respectively a greedy, solution to problem (1) and let $m=|S_{opt} \cap S_{gr}|$. Then

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})}\ge G(T,\alpha ,m)\ge \widetilde{G}(T,\alpha ,n). \end{aligned}$$

(5)

Moreover, these bounds are tight in the following sense: for every $\alpha \in (0,1]$ and numbers n and T such that $1\le T\le n$, there is a problem of the type (1) and its greedy solution $S_{gr}$ such that $\max \{0,2T-n \}=|S_{opt} \cap S_{gr}|$ and

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})} = \widetilde{G}(T,\alpha ,n). \end{aligned}$$

We postpone the proof of Theorem 1 to Sect. 2.

Remark 1

Theorem 1 strictly improves (4) and provides further examples of cases where the performance guarantee equals one. Indeed, for all T and n such that $T > n/2$, we have the strict inequality

$$\begin{aligned} \widetilde{G}(T,\alpha ,n) > G_{CC}(T,\alpha ). \end{aligned}$$

For $T=n$, we get $\widetilde{G}(n,\alpha ,n)=1$. Note that, by (4), $\lim _{\alpha \rightarrow 0^+}\widetilde{G}(T,\alpha ,n)=1$. Moreover, in the case $m=T$, we again get $G(T,\alpha ,T)=1$. Note also that $G(T,\alpha ,m)$ is decreasing in $\alpha$, so (5) can be substituted by a weaker but simpler approximation guarantee

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})}\ge 1-\left( 1-\frac{m}{T}\right) \left( 1-\frac{1}{T}\right) ^{T-m}. \end{aligned}$$

Using Theorem 1, one can derive other new performance guarantees for the greedy algorithm. As an example of independent interest, we present the following performance guarantee in terms of n only.

Corollary 1

Let $\alpha \in (0,1]$, $1\le T \le n$, and let $S_{opt}$ and $S_{gr}$ be an optimal, respectively a greedy, solution to problem (1). Then

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})}\ge \frac{1}{\alpha }\left( 1-\left( 1-\frac{\alpha }{\left\lfloor \frac{n}{2}\right\rfloor }\right) ^{\left\lfloor \frac{n}{2}\right\rfloor }\right) \ge \frac{1}{\alpha }\left( 1-\left( 1-\frac{2\alpha }{n}\right) ^{n/2}\right) , \end{aligned}$$

(6)

where $\lfloor x \rfloor$ denotes the largest integer not greater than x. The left-hand estimate is tight in the following sense: for every $\alpha \in (0,1]$ and $n\ge 2$, there is a problem of the type (1) and its greedy solution $S_{gr}$ such that

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})} = \frac{1}{\alpha }\left( 1-\left( 1-\frac{\alpha }{\left\lfloor \frac{n}{2}\right\rfloor }\right) ^{\left\lfloor \frac{n}{2}\right\rfloor }\right) . \end{aligned}$$

Proof

If n is an odd integer, it is easy to check that the minimum of $\widetilde{G}(T,\alpha ,n)$ over all integers T with $0\le T \le n$ is $\widetilde{G}((n-1)/2,\alpha ,n)$. Moreover, when treated as a continuous function of T, $\widetilde{G}(T,\alpha ,n)$ attains its minimum at $T=n/2$. Together with Theorem 1 this yields (6). Tightness of the left-hand inequality in (6) follows from Theorem 1 with the choice $T=\left\lfloor \frac{n}{2}\right\rfloor$.

2 Proof of Theorem 1

In this section we present a proof of Theorem 1. We first prove (5). Note that the right-hand inequality in (5) follows directly from $m=|S_{opt}\cap S_{gr}|\ge \max \{0, 2T-n\}$ and the fact that $G(T,\alpha ,m)$ is increasing in m.

We next prove the left-hand inequality in (5). We may assume that $0< m < T$. Indeed, if $m=T$, then $S_{gr} = S_{opt}$ and the claim is trivial. If $m=0$, the claim follows from (4).

Let $S_0=\emptyset$ and $S_t=\{y_{1},\dots ,y_{t}\}\subset X$ be the successive sets chosen by the greedy algorithm for $t=1,\dots ,T$, so that $S_0\subset S_1\subset \dots \subset S_T$. Let

$$\begin{aligned} a_t=\frac{f(S_t)-f(S_{t-1})}{f(S_{opt})}, \end{aligned}$$

for $t=1,\dots ,T$. Because f is nondecreasing, each $a_t$ is nonnegative and

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})}=\sum _{i=1}^T a_i. \end{aligned}$$

Let $1\le j_1\le \dots \le j_m\le T$ denote the indices for which $S_{gr} \cap S_{opt}=\{y_{j_1},\dots y_{j_m}\}$. Denote $j_0=0$ and $j_{m+1}=T$. We will use the following lemma from [2].

Lemma 1

([2, Lemma 5.1]) We have

$$\begin{aligned} \alpha \sum _{\{i:y_i\in S_{t-1} {\setminus } S_{opt}\}}a_i+ \sum _{\{i:y_i\in S_{t-1}\cap S_{opt}\}}a_i + (T-|S_{t-1}\cap S_{opt}|)a_{t} \ge 1, \end{aligned}$$

for $t=1,\dots ,T$.

Using Lemma 1, we get

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})} \ge B(J), \end{aligned}$$

(7)

where $J = \{j_1,\dots ,j_m\}$ and, for $U\subset \{1,\dots ,T\}$, B(U) denotes the minimum of the linear program

$$\begin{aligned} \text {minimize}\quad&\sum _{i=1}^T b_i \nonumber \\ \text {s.t.}\quad&\alpha \sum _{i\in V_{t-1}{\setminus } U}b_i+ \sum _{i\in U\cap V_{t-1}}b_i + (T-|U\cap V_{t-1}|)b_{t} \ge 1,&t=1,\dots ,T\nonumber \\&b_t\ge 0,&t=1,\dots ,T, \end{aligned}$$

(8)

where $V_t=\{1,\dots ,t\}$. The following lemma refines [2, Lemma 5.2].

Lemma 2

$B(J) \ge B(\{T-m+1,T-m+2,\dots ,T\})$.

Proof

Fix $1\le r \le m$ and consider $q=j_r\in J$. We first show that $b_q \le b_{q+1}$ for some optimal solution to (8) with $U=J$. To this end, assume that this does not hold for some optimal solution $b=(b_1,\dots ,b_T)$. Then $\varepsilon := b_{q}-b_{q+1}> 0$. The constraints q and $q+1$ are

$$\begin{aligned} \alpha \sum _{i\in V_{q-1}{\setminus } J}b_i+ \sum _{i\in J\cap V_{q-1}}b_i + (T-r+1)b_{q} \ge 1;\\ \alpha \sum _{i\in V_{q}{\setminus } J}b_i+ \sum _{i\in J\cap V_{q}}b_i + (T-r)b_{q+1} \ge 1. \end{aligned}$$

Because $V_{q}{\setminus } J = V_{q-1}{\setminus } J$ and $J\cap V_{q} = (J\cap V_{q-1})\cup \{q\}$, the constraint $q+1$ is equivalent to

$$\begin{aligned} \alpha \sum _{i\in V_{q-1}{\setminus } J}b_i+ \sum _{i\in J\cap V_{q-1}}b_i + b_q + (T-r)b_{q+1} \ge 1. \end{aligned}$$

Therefore

$$\begin{aligned} \alpha \sum _{i\in V_{q-1}{\setminus } J}b_i+ \sum _{i\in J\cap V_{q-1}}b_i + (T-r+1)b_{q} \ge 1 + \varepsilon (T-r) > 1, \end{aligned}$$

which shows that the constraint q is not tight. Form a new solution $b'=(b'_1,\dots ,b'_T)$ by setting $b'_i=b_i$ for $1\le i \le q-1$, $b'_q = b_q - \varepsilon (T-r)/(T-r+1)$ and $b'_i = b_i + \varepsilon /(T-r+1)$ for $q+1 \le i \le T$. It is easy to check that $b'$ is feasible. Moreover,

$$\begin{aligned} b'_q - b'_{q+1}= b_q - \frac{\varepsilon (T-r)}{T-r+1} - b_{q+1} - \frac{\varepsilon }{T-r+1}=0 \end{aligned}$$

and

$$\begin{aligned} \sum _{i=1}^T b'_i = \sum _{i=1}^T b_i + \frac{\varepsilon (T-q)}{T-r+1} - \frac{\varepsilon (T-r)}{T-r+1}\le \sum _{i=1}^T b_i, \end{aligned}$$

because $r \le q$. Hence $b'$ is an optimal solution with $b'_q \le b'_{q+1}$.

Assume next that $q=j_r \in J$ and $q+1 \notin J$ for some r. Let $b=(b_1,\dots ,b_T)$ be a feasible solution to (8) with $U=J$, so that

$$\begin{aligned} \alpha \sum _{i\in V_{t-1}{\setminus } J}b_i+ \sum _{i\in J\cap V_{t-1}}b_i + (T-|J\cap V_{t-1}|)b_{t} \ge 1, \end{aligned}$$

(9)

for $1\le t \le T$. Assume also that $b_q \le b_{q+1}$. Let $J'=\{j_1,\dots ,j_{r-1},q+1,j_{r+1},\dots ,j_m\}$. We will show that b is a feasible solution to (8) with $U=J'$. Consider first $1\le t \le q$. Then $V_{t-1}{\setminus } J'=V_{t-1}{\setminus } J$ and $J'\cap V_{t-1}=J\cap V_{t-1}$, so

$$\begin{aligned} \alpha \sum _{i\in V_{t-1}{\setminus } J'}b_i+ \sum _{i\in J'\cap V_{t-1}}b_i + (T-|J'\cap V_{t-1}|)b_{t} \ge 1, \end{aligned}$$

by (9). Consider next $t=q+1$. Then $V_{t-1}{\setminus } J'=(V_{t-1}{\setminus } J)\cup \{q\}$ and $J'\cap V_{t-1}=(J\cap V_{t-1}){\setminus } \{q\}$. By (9) and using $b_q \le b_{q+1}$, we get

$$\begin{aligned} \alpha&\sum _{i\in V_{q}{\setminus } J'}b_i+ \sum _{i\in J'\cap V_{q}}b_i + (T-|J'\cap V_{q}|)b_{q+1} \\&=\alpha \sum _{i\in V_{q}{\setminus } J}b_i+\alpha b_q+ \sum _{i\in J\cap V_{q}}b_i-b_q + (T-|J\cap V_{q}|+1)b_{q+1}\\&\ge 1+\alpha b_q-b_q+b_{q+1}\ge 1. \end{aligned}$$

Finally, consider $t=q+k$ for $k \ge 2$. Then $V_{t-1}{\setminus } J'=((V_{t-1}{\setminus } J)\cup \{q\}){\setminus }\{q+1\}$ and $J'\cap V_{t-1}=((J\cap V_{t-1}){\setminus } \{q\})\cup \{q+1\}$. By (9) and using $b_q \le b_{q+1}$, we get similarly as above

$$\begin{aligned} \alpha&\sum _{i\in V_{q+k-1}{\setminus } J'}b_i+ \sum _{i\in J'\cap V_{q+k-1}}b_i + (T-|J'\cap V_{q+k-1}|)b_{q+k} \\&\ge 1+(b_{q+1}-b_q)(1-\alpha )\ge 1. \end{aligned}$$

This shows that b is a feasible solution to (8) with $U=J'$.

By combining the above results, we get

$$\begin{aligned} B(J) \ge B(J'). \end{aligned}$$

The proof of Lemma 2 is completed by repeating this argument sufficiently many times. $\square$

Lemma 2 and (7) now imply

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})} \ge B(\{T-m+1,T-m+2,\dots ,T\}). \end{aligned}$$

By the weak duality theorem, we get

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})}\ge \sum _{i=1}^T c^*_i, \end{aligned}$$

(10)

where $c^*=(c^*_1,\dots ,c^*_T)$ is an optimal solution to the dual problem of (8):

$$\begin{aligned} \text {maximize}\quad&\sum _{i=1}^T c_i \end{aligned}$$

(11)

$$\begin{aligned} \text {s.t.}\quad&Tc_t+\alpha \sum _{i=t+1}^T c_i\le 1,&1\le t \le T-m\end{aligned}$$

(12)

$$\begin{aligned}&(2T-m+1-t)c_t+\sum _{i=t+1}^T c_i\le 1,&T-m+1 \le t \le T\end{aligned}$$

(13)

$$\begin{aligned}&c_i\ge 0,&i=1,\dots ,T. \end{aligned}$$

(14)

Define the vector $c=(c_1,\dots ,c_T)$ by

$$\begin{aligned} c_t = {\left\{ \begin{array}{ll} \frac{1}{T}\left( 1-\frac{\alpha m}{T} \right) \left( 1-\frac{\alpha }{T}\right) ^{T-m-t}, &{} 1\le t \le T-m,\\ \frac{T-m}{(2T-m+1-t)(2T-m-t)}, &{} T-m+1 \le t \le T. \end{array}\right. } \end{aligned}$$

We will need the following two straightforward indentities:

$$\begin{aligned} \sum _{i=s}^{T-m} c_i&= \frac{1}{\alpha }\left( 1-\frac{\alpha m}{T} \right) \left( 1-\left( 1-\frac{\alpha }{T}\right) ^{T-m-s+1}\right) , \qquad 1 \le s \le T-m; \end{aligned}$$

(15)

$$\begin{aligned} \sum _{i=k}^T c_i&=\frac{T-k+1}{2T-m-k+1}, \qquad T-m+1 \le k \le T+1. \end{aligned}$$

(16)

Lemma 3

The vector c is a feasible solution to problem (11).

Proof

Consider first $1\le t \le T-m-1$. By (15) and (16),

$$\begin{aligned} \sum _{i=s}^T c_i = \sum _{i=s}^{T-m} c_i + \sum _{i=T-m+1}^{T} c_i=\frac{1}{\alpha }\left( 1-\frac{\alpha m}{T} \right) \left( 1-\left( 1-\frac{\alpha }{T}\right) ^{T-m-s+1}\right) +\frac{m}{T}, \end{aligned}$$

for $1 \le s \le T-m$. Hence

$$\begin{aligned} Tc_t+\alpha \sum _{i=t+1}^T c_i&=\left( 1-\frac{\alpha m}{T} \right) \left( 1-\frac{\alpha }{T}\right) ^{T-m-t}\\&\quad +\left( 1-\frac{\alpha m}{T} \right) \left( 1-\left( 1-\frac{\alpha }{T}\right) ^{T-m-t}\right) +\frac{\alpha m}{T}\\&=1, \end{aligned}$$

so $c_t$ satisfies the constraint (12).

By (16),

$$\begin{aligned} Tc_{T-m}+\alpha \sum _{i=T-m+1}^T c_i= \left( 1-\frac{\alpha m}{T} \right) +\frac{\alpha m}{T}=1, \end{aligned}$$

so $c_{T-m}$ also satisfies the constraint (12).

For $T-m+1 \le t \le T$, we get from (16) that

$$\begin{aligned} (2T-m+1-t)c_t+\sum _{i=t+1}^T c_i=1, \end{aligned}$$

so $c_t$ satisfies the constraint (13).

Finally, it is clear from the definition that each $c_t$ satisfies the constraint (14). This completes the proof of Lemma 3. $\square$

Lemma 3 and (10) imply

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})} \ge \sum _{i=1}^T c_i. \end{aligned}$$

Moreover, by (15) and (16),

$$\begin{aligned} \sum _{i=1}^T c_i = \frac{1}{\alpha }\left( 1-\frac{\alpha m}{T} \right) \left( 1-\left( 1-\frac{\alpha }{T}\right) ^{T-m}\right) + \frac{m}{T}=G(T,\alpha ,m), \end{aligned}$$

which yields the desired estimate

$$\begin{aligned} \frac{f(S_{gr})}{f(S_{opt})} \ge G(T,\alpha ,m) \end{aligned}$$

and completes the proof of (5).

We next show the tightness of $\widetilde{G}(T,\alpha ,n)$ by modifying the proof of [2, Theorem 5.4]. Let $1 \le T< n$ be any positive numbers. Pick any number $1\le r \le n/2$, let $X=\{a_1,\dots ,a_{r}, b_1,\dots , b_{n-r}\}$ and let $f:2^X\rightarrow \mathbb R_+$ be the set function

$$\begin{aligned} f(\{a_{i_1},\dots ,a_{i_s},b_{j_1},\dots , b_{j_u}\})= u+\left( 1-\frac{\alpha u}{T}\right) \sum _{k=1}^s\left( 1-\frac{\alpha }{T}\right) ^{i_k-1}, \end{aligned}$$

defined for all subsets $\{a_{i_1},\dots ,a_{i_s},b_{j_1},\dots , b_{j_u}\}\subset X$. Then $f(\emptyset )=0$. For any $S=\{a_{i_1},\dots ,a_{i_s},b_{j_1},\dots , b_{j_u}\}\subsetneq X$, where $s<r$ and $u\le n-r$, and $a_i\in X{\setminus } S$, we have

$$\begin{aligned} f(S\cup \{a_i\})-f(S)= \left( 1-\frac{\alpha u}{T}\right) \left( 1-\frac{\alpha }{T}\right) ^{i-1}\ge 0. \end{aligned}$$

For any $S=\{a_{i_1},\dots ,a_{i_s},b_{j_1},\dots , b_{j_u}\}\subsetneq X$, where $s\le r$ and $u< n-r$, and $b_j\in X{\setminus } S$, we have

$$\begin{aligned} f(S\cup \{b_j\})-f(S)= 1-\frac{\alpha }{T}\sum _{k=1}^s\left( 1-\frac{\alpha }{T}\right) ^{i_k-1} \ge 0. \end{aligned}$$

By recalling that a set function $g:2^X\rightarrow \mathbb R_+$ is submodular if and only if

$$\begin{aligned} g(S\cup \{x\})-g(S)\ge g(R\cup \{x\})-g(R), \end{aligned}$$

for all $S\subset R\subsetneq X$ and $x\in X{\setminus } R$ (e.g., [1]), these inequalities show that f is submodular and nondecreasing. Moreover,

$$\begin{aligned} \max \left\{ 1-\frac{f(X)-f(X{\setminus }\{x\})}{f(\{x\})}:x\in X, f(\{x\})\ne 0\right\} \\ =1-\frac{f(X)-f(X{\setminus }\{a_i\})}{f(\{a_i\})} =\alpha , \end{aligned}$$

for any $1\le i\le r$, so f has total curvature $\alpha$.

Consider next the case where $T> n/2$. Set $r=n-T$, so that $r<n/2<T$ and $n-r=T$. It is easy to verify that $S_{opt}=\{b_{1},\dots ,b_{T}\}$ is an optimal solution to problem (1) with $f(S_{opt})=T$. Since $f(\{a_1\})=f(\{b_j\})=1$, for any $1\le j \le T$, the greedy algorithm can choose the element $a_1$ at the first iteration. Assume next that the greedy algorithm has chosen $S_{t-1}=\{a_1,\dots , a_{t-1}\}$ for some $t \le n-T$. Using the fact

$$\begin{aligned} \sum _{k=1}^l \left( 1-\frac{\alpha }{T}\right) ^{k-1}=\frac{T}{\alpha }\left( 1-\left( 1-\frac{\alpha }{T}\right) ^l\right) \end{aligned}$$

it is easy to see that

$$\begin{aligned} f(S_{t-1}\cup \{a_t\})= f(S_{t-1}\cup \{b_j\})= \sum _{i=1}^t\left( 1-\frac{\alpha }{T}\right) ^{i-1}, \end{aligned}$$

so the greedy algorithm can choose $a_t$ at the tth iteration. We therefore can have $S_{gr}=\{a_1,\dots a_{n-T}, b_1,\dots , b_{2T-n}\}$. This solution has the value

$$\begin{aligned} f(S_{gr}) = \frac{T}{\alpha }\left( 1-\left( 1-\frac{\alpha m}{T}\right) \left( 1-\frac{\alpha }{T}\right) ^{n-T}\right) . \end{aligned}$$

The claim follows because $m=|S_{opt}\cap S_{gr}|=2T-n$, whence we obtain $n-T=T-m$.

The proof of case $T\le n/2$ is easier, so we omit its proof.