1 Introduction

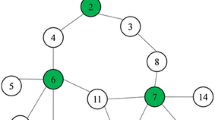
The dominating tree problem, discussed in this paper, has been recently introduced by Shin et al. in [13]. This problem is defined as follows: Let \(G=(V,E)\) be an undirected, connected, edge-weighted graph, where V denotes the set of vertices and E denotes the set of edges. To each edge \(e\in E\), a non-negative weight \(w_e\) is assigned. A tree \(T=(V(T), E(T))\) of graph G is called dominating if each vertex \(v\in V\) that is not in T is adjacent to a vertex in T. The weight of tree T is defined as \(\sum _{e\in E(T)}w_e\), i.e. as the sum of all edge weights in T. Now, the dominating tree problem (DTP) is to construct a dominating tree T of graph G with the minimal weight.

The DTP has several applications in network design and network routing. Multicasting is one example, given in [13], whose goal is simultaneous delivery of the same data to a group of destination computers. Servers are connected by a tree network structure T, and all other computers are one hop away from a server. If weights represent the cost, or energy to transmit data from one server to another, the sum of edge weights in T equals to overall cost to transmit data from one server to all others.

In [13] the DTP is proved to be NP-hard in the general case, and an approximation framework is provided. Due to the high runtime complexity of this approximation algorithm, the authors propose a polynomial time heuristic. They also propose an integer programming formulation of the DTP.

The first metaheuristic approaches for solving the DTP were proposed in [14], where the authors implemented two swarm inteligence techniques: artificial bee colony and ant colony optimization. The ant colony optimization algorithm produced better results on most of large instances, but it was slower than the artificial bee colony optimization algorithm.

Problems related to the DTP are: the connected dominating set problem (CDSP) [5, 11, 15, 16] and the tree cover problem (TCP) [1, 3, 4]. Subset D of vertices of graph G is a dominating set of G if each vertex of G is either in D or adjacent to a vertex in D. Now, the CDSP can be formulated as follows: For a given graph, find a minimum size connected dominating set. In some variants of this problem, vertices might have weights and the problem is formulated as to minimize the total weighted sum of the vertices that form a connected dominating set. Note that in the DTP weights are associated with edges and not with vertices.

On the other hand, the TCP considers a graph where each edge has a nonnegative weight. The problem is to find a tree T of graph G with the minimal weight that represents a vertex cover of G, i.e. every edge of G has at least one endpoint in T. In this case, the resulting tree represents an edge dominating set, contrary to the DTP, where the resulting tree is a vertex dominating set.

2 Variable neighborhood search for DTP

The variable neighborhood search (VNS) is a local search based metaheuristic proposed by Mladenović and Hansen [8] in 1997. The concept of the basic VNS can be outlined as follows: The main idea is to use more than one neighborhood structure and to proceed with their systematic change in search for a better solution. Given an incumbent solution, the shaking procedure generates randomly a feasible solution in the current neighborhood. Then, a local search is applied around the generated feasible solution in order to obtain a possibly better solution than the incumbent. If the local search gives a better solution, it becomes the new incumbent. Otherwise, the neighborhood is changed.

A detailed description of different VNS variants can be found in [6, 7]. An extensive computational experience with various optimization problems shows that the VNS often gives high-quality solutions in a reasonable time. In particular, we have shown that the VNS approach outperforms genetic algorithms in case of some NP-hard graph optimization problems [9, 10]. This experience motivated us to apply the VNS approach to the recently introduced dominating tree problem and to compare it with the existing swarm intelligence-based approaches: ant and bee colony optimization algorithms.

The main characteristics of the VNS metaheuristic applied to the DTP are the following. The feasible solution set X contains all permutations of vertex indices from graph G. To each permutation \(x\in X\), the corresponding dominating tree T of G is assigned and the objective function value of x is obtained as the sum of all edge weights from T. The neighborhood structures and the shaking step are defined in the usual way for searching in a set of permutations. The details of the VNS for the DTP are given in a pseudo-code in Fig. 1 and explained in more details below.

Fig. 1
figure 1

The VNS algorithm for DTP

Full size image

The feasible solution set To each vertex \(v \in V\) of graph G, let us assign an unique integer index number. The set of feasible solutions X is defined as the set of all permutations of vertex indices from graph G. To each permutation \(x\in X\), the corresponding dominating tree T of G is assigned by the procedure DominatingTree described in Fig. 2. The procedure first generates a dominating set B of vertices in graph G by including vertices one by one from the beginning of permutation x, until this set becomes a dominating set of G. If subgraph \(G_B\) of G induced by B is not connected, the procedure adds more vertices to set B using the order given by x, until \(G_B\) becomes connected. The procedure then finds MST(\(G_B\)) as the minimal spanning three T of \(G_B\), which represents a dominating tree of G, since it contains all vertices from dominating set B of G, and \(G_B\) is connected.

Fig. 2
figure 2

Procedure DominatingTree

Full size image

The objective function value The objective function value f(x) for a feasible solution \(x\in X\) is calculated as the sum of all edge weights of the corresponding dominating tree T, obtained by procedure DominatingTree.

The neighborhood structures For \(k\ge 2\) we define neighborhood \(N_k(x)\) of \(x\in X\) as a set of all permutations which differ from x in no more than k positions. During the search, the VNS uses neighborhood structures \(N_k, k=k_{\min },\ldots ,k_{\max }\), where \(k_{\min }\) and \(k_{\max }\) are given parameters.

Shaking step The shaking procedure chooses randomly a solution \(x'\) in neighborhood \(N_k(x)\) as follows. First, we choose k random numbers from \(\{1,\ldots ,|V|\}\), representing the positions in permutation x. Next, we permute at random the elements of x from these positions. The resulting vector is denoted by \(x'\).

The local search The local search is defined by procedure LocalSearch, given in Fig. 3. Starting from solution \(x'\), obtained by shaking, the procedure explores a small neighborhood of \(x'\), searching for a solution with smaller objective function value. The neighborhood which is explored consists of all solutions obtained from \(x'\) by swapping two of its elements, one from the corresponding dominating set B and the other from \(V{\setminus } B\). The first improvement strategy is used, i.e. as soon as the local search finds a solution with smaller objective function value, the search is continued from this solution. Scanning of the neighborhood is performed as follows: First, \(|V|-|B|\) neighbors are examined by swapping the first element of \(x'\) with elements of \(V{\setminus }B\), with indices \(|V|, |V|-1, \ldots , |B|+1\), respectively. If better solution is not found, we perform the same swapping procedure with elements of \(x'\) having indices \(2,3,\ldots ,|B|\). The local search stops when the whole neighborhood of the current solution is searched and no further improvement can be made. The best found solution is denoted as \(x''\).

Fig. 3
figure 3

Procedure LocalSearch

Full size image

After obtaining the solution \(x''\) by the local search, we have to compare it with the incumbent solution x in order to make a decision wether to accept it or not. In the basic VNS, a move to the new solution \(x''\) is made only if \(f(x'')<f(x)\), i.e. the objective function value of solution \(x''\) is smaller than the objective function value of solution x. Considering the permutation-based representation described above, there are different feasible permutations yielding the same objective function value. Moving from one to another such solution, we may diversify the search and explore different regions, increasing in this way the chance of finding a better solution. However, if we do this move every time, we could get trapped in a cycle. To avoid this problem, we use parameter p which represents the probability of moving from one to another solution with the same objective function value. Considering this, after the local search, we have three possibilities:

  • If \(f(x'')<f(x)\), we move to \(x''\) and continue the search with the same neighborhood \(N_k\) from \(x''\).

  • If \(f(x'')>f(x)\), we continue the search with the same x and the next neighborhood \(N_{k+1}(x)\).

  • If \(f(x'')=f(x)\), we move to \(x''\) with probability p and continue the search from \(x''\) with the same neighborhood and with probability \(1-p\) we continue the search with the same x and the next neighborhood \(N_{k+1}(x)\).

The stopping criterion Whenever \(k_{max}\) is attained, the search continues with the first neighborhood \(N_{k_{\min }}\). This is repeated until some stopping criterion is met. Possible stopping conditions can be the maximum CPU time allowed, the maximum number of iterations, the maximum number of iterations between two improvements, etc. In this VNS implementation, we use the following combination: the algorithm stops when either the maximum number of iterations \(iter_{\max }\) or the maximum CPU time \(t_{\max }\) is exceeded.

The initial solution The initial permutation can be generated randomly or by using special heuristics. In our implementation, we use the following heuristic approach. First, we construct a minimal spanning tree of G (MST(G)) and then remove all its leaves in order to obtain a tree T. Since all vertices of G are either in T or adjacent to some vertex in T, T is a dominating tree for G. Now, the initial permutation x is taken to be a permutation containing the indices of vertices from T followed by indices of the remaining vertices of G. The objective function value is equal to the sum of all edge weights in T. The described heuristic is implemented in the first three lines of the pseudo-code in Fig. 1.

During the whole VNS procedure, the minimal spanning tree problem is solved by the well known Prim’s algorithm [12].

Input parameters for the VNS are the minimum and the maximum number of neighborhoods that should be searched, \(k_{\min }\) and \(k_{\max }\), the maximum number of iterations \(iter_{\max }\), the maximum CPU time allowed \(t_{\max }\), and the probability p of moving from one solution to another with the same objective function value.

3 Experimental results

In this section, we present experimental results obtained by the proposed VNS algorithm for solving the DTP. The algorithm was implemented in C programming language. All computational experiments were performed on Intel Core I7-4702MQ 2.2 GHz with 4 GB RAM under Windows XP operating system.

The first group of experiments was performed in order to adjust the key VNS parameters and to analyze their influence on the VNS algorithm for the DTP. As it is well known, the most important parameters in VNS implementations are the values of \(k_{\min }\) and \(k_{\max }\), which determine the number of different neighborhood structures used during the search process. In our VNS implementation, value \(k_{\min }=2\) is a natural lower bound for k because neighborhood \(N_k(x)\) of \(x\in X\) is defined as the set of all permutations of vertex indices that differ from x in no more than k positions, which implies \(k \ge 2\). In order to find the most suitable values of \(k_{\max }\) and probability p for the VNS approach to the dominating tree problem, we have performed experiments with different values of \(k_{\max }\) and p on the set of benchmark instances from literature [14]. For each value of \(|V| \in \{50, 100, 200, 300, 400, 500\}\) there are three different test instances. The VNS has been run 20 times for each instance with the following stopping criterion: the algorithm stops when either the maximum number of iterations \(iter_{\max } = 1000\) or the maximum CPU time \(t_{\max } = 600s\) is exceeded.

The results of experiments are summarized in Table 1, organized as follows: In the first column Inst the instance name is given, containing the information about the number of nodes. For each \(p\in \{0, 0.1, 0.2, 0.5\}\) and \(k_{\max } \in \{10, 20, 30\}\), column named sol contains the best objective function value obtained by the VNS in 20 runs, while column \(sol_{avg}\) represents the average objective function value in 20 runs. For each instance the best values of sol and \(sol_{avg}\) are bolded. The analysis of the obtained results shows that values of \(k_{\max }\) and p influence the solution quality. For example, for instances 50_2 and 50_3, the best values of \(sol_{avg}\) are obtained for \(k_{\max }=10\) and \(p=0.1\), while for instance 300_3, the best \(sol_{avg}\) is for \(k_{\max }=20\) and \(p=0.5\). On the other hand, the best values of sol for instances 300_1, 400_2, 400_3 and 500_2 are obtained for combinations \(k_{\max }=30\) and \(p=0.5\), \(k_{\max }=30\) and \(p=0.1\), \(k_{\max }=20\) and \(p=0.5\), \(k_{\max }=30\) and \(p=0.5\), respectively. However, from Table 1 it follows that for combination \(k_{\max }=30\) and \(p=0\), the number of instances where the VNS achieved the best value for sol and \(sol_{avg}\) is 14 and 9, respectively. For all other combinations these numbers are smaller. This indicates that the best combination of parameters for this set of instances is \(k_{\max }=30\) and \(p=0\). Therefore, we used these values in all other experiments.

Table 1 Experiments with parameters \(k_{\max }\) and p
Full size table

In order to examine the average behavior of the VNS with parameters \(k_{\min }=2, k_{\max }=30, p=0, iter_{\max }=1000, t_{\max }=600s\), we constructed a set of randomly generated instances, which include graphs with different number of vertices and edges. The number of vertices vary from 10 to 300 and the number of edges from 15 to 1000. In the generation process, for each edge a randomly generated real number is selected from interval [1, 10] representing its weight. The adjacency matrix of a graph is randomly generated avoiding self-loops and more than one edge connecting the same two vertices. If a graph created in this way is not connected, the instance is ignored and a new instance is constructed. In order to achieve the diversity, for each graph size, a set of three different instances was generated with a different random seed. The generated instances can be found on http://poincare.matf.bg.ac.rs/~zdrazic/dtp.

Table 2 contains the VNS results on small size randomly generated instances. In order to verify the results we applied CPLEX to the integer linear programming formulation of the DTP, introduced in [13]. In the first column, Inst, the instance name is given, containing the information about its dimensions. For example, instance \(dtp\_10\_15\_2\) contains 10 vertices and 15 edges. The last number in the instance name represents the ordinal number of the instance of that size. The next two columns contain the information obtained with CPLEX: opt column contains the optimal objective function value and time column represents the running time used by CPLEX to finish its work. If CPLEX could not provide the result, the symbol “–” is written. In the following six columns, the information about the proposed VNS algorithm is given. The column named sol contains the best objective function value found by the VNS in 20 runs. If this value is equal to the optimal solution (from opt column), we mark it as opt. The next two columns \(sol_{avg}\) and \(\sigma \), contain the information on the average solution quality. Value \(sol_{avg}\) represents the average objective function value in 20 independent runs, while \(\sigma ^2\) is the corresponding mean squared error, i.e. \(\sigma ^2=\frac{1}{20}\sum _{i=1}^{20}(err_i-err)^2\), where \(err = \frac{1}{20} \sum _{i=1}^{20} err_i\), \(err_i = 100\times \frac{VNS_i - sol}{sol}\), and \(VNS_i\) is the VNS solution obtained in i-th run. Column ANDV contains the average number of vertices in the VNS solution for 20 runs. The last two columns contain the average execution time t, used to reach the best VNS solution and the average total execution time \(t_{tot}\).

Table 2 Experimental results on small size random instances
Full size table

As it can be seen in Table 2, the VNS quickly reaches optimal solutions obtained by CPLEX in all cases. In case of larger instances, dtp_20_30 and dtp_20_50, the VNS execution time values are from 1500 to 20,000 times smaller than CPLEX time values. Note that for instance \(dtp\_20\_50\_1 \) CPLEX failed to find any solution with “Out of memory” error message.

Table 3 contains results of the proposed VNS for large size randomly generated instances, which could be used as a base for future comparisons with other metaheuristic approaches. It is organized in a similar way as Table 2. Here we do not have columns regarding CPLEX because it was not able to solve these instances. The column \(t_{tot}\) is also omitted because, in all cases, the algorithm stops when time \(t_{\max }=600s\) is exceeded.

Table 3 Experimental results on large size random instances
Full size table

Table 4 presents a comparison of the proposed VNS approach with the results from [14], obtained by the artificial bee colony algorithm (ABC_DT) and the ant colony optimization algorithm (ACO_DT) on the set of instances from Table 1.

Table 4 Comparison with the existing methods
Full size table

In order to provide a fair comparison between these algorithms, we performed additional numerical experiments with the following stopping criterion: The algorithm stops when the maximum CPU time \(t_{\max }\) is exceeded, where \(t_{\max }\) is determined as follows. For each instance, \(t_{\max }\) is equal to the average execution time t of either ABC_DT or ACO_DT. We chose average execution time t of the algorithm which has obtained smaller value of sol. If both algorithms had the same value of sol, we chose the smaller t. Note that with such stopping criterion \(t_{\max }=t_{tot}\).

In Table 4, for each algorithm, the results are organized in the same way as in the previous tables. The additional last column, BSV, for each instance contains the overall best known objective function value arising from Tables 1 and 4.

From Table 4 it follows that the average objective function value \(sol_{avg}\), obtained by the VNS, is better than values \(sol_{avg}\) for both ABC_DT and ACO_DT in 7 out of 18 instances, including 5 out of 6 largest instances with 400 and 500 vertices. The VNS produced strictly better values of the best objective function value sol in 8 out of 18 cases, compared to ABC_DT and ACO_DT. The ABC_DT was strictly better than both the ACO_DT and the VNS in one case, and ACO_DT was never better than both ABC_DT and the VNS. In 4 cases all three algorithms obtained the same values of sol.

In order to verify the significance of the obtained computational results, we provide the statistical analysis with the best objective function values sol of ABC_DT, ACO_DT and VNS. Demšar [2] showed that when comparing the classifiers over multiple data sets, the non-parametric Friedman test should be preferred over ANOVA. It is easy to see that this statement can be extended to general metaheuristic approaches and not only to classifiers. The Friedman test showed that there was a statistically significant difference in the obtained computational results among three considered algorithms: \(p=0.034\) (\(<\)0.05). Post hoc Wilcoxon signed-rank test with Bonferroni adjustment showed that there is no statistical difference between ACO_DT and ABC_DT (\(p=0.345\)). Yet, there is a statistical difference between algorithm pairs: VNS and ABC_DT (\(p=0.016\)), VNS and ACO_DT (\(p=0.026\)). Based on this results, one can conclude that the VNS outperforms both compared algorithms, and that there is no significant difference between ABC_DT and ACO_DT.

Computational results in Tables 3 and 4 indicate that the VNS algorithm could be successfully applied to real-world large-scale networks. Namely, the average execution time t, used to reach high-quality VNS solutions does not increase rapidly with the size of the problem. For example, for instances 400_1 to 400_3 in Table 4, the average value of t is 397.89 s, while for instances 500_1 to 500_3 the average value of t is 556.24 s.

4 Conclusion

This paper is devoted to the recently introduced dominating tree problem. The problem is solved by the VNS algorithm that uses the set of vertex permutations in order to generate feasible solutions. The corresponding neighborhood structures allow an effective shaking procedure, which successfully diversifies the search process. For small dimensions, the VNS reaches optimal values obtained by CPLEX in all cases, while for large instances, it gives better results than the existing ant colony and bee colony approaches.

One possible extension of this research can be directed toward modifying this approach in order to solve similar dominating problems on graphs. The second extension could be a parallelization of the presented approach and its testing on powerful multiprocessor computers.