1 Introduction

The prediction of how evolves in time a phenomenon \({\mathcal {F}}\) of the real world, is of preminent human interest. To this scope, when the behaviour of \({\mathcal {F}}\) can be considered spatially homogeneous, a state vector\({\mathbf {U}}=(U_1,U_2, \cdots , U_n)^T\), with \(U_i(t),\,(i=1,2,\cdots , n)\), relevant parameters describing the state of \({\mathcal {F}}\) at time t, is introduced. Then, in order to model the behaviour of \({\mathcal {F}}\) via an O.D.Es system, the existence of a function \({\mathbf {F}}(t,{\mathbf {U}})\) such that

$$\begin{aligned} \displaystyle \frac{d{\mathbf {U}}}{dt}={\mathbf {F}},\qquad t\ge 0; \quad {\mathbf {U}}(0)={\mathbf {U}}_0, \end{aligned}$$
(1.1)

is established with \({\mathbf {U}}(0)\) assigned initial data [1].

Let \(\tilde{{\mathbf {U}}}\) denote a fixed solution of (1.1) and \({\mathbf {u}}={\mathbf {U}}-\tilde{{\mathbf {U}}}\) be the perturbation vector. Then the behaviour of \({\mathbf {u}}\) is governed by

$$\begin{aligned} \displaystyle \frac{d{\mathbf {u}}}{dt}=L{\mathbf {u}}+N{\mathbf {u}},\,\,\forall t>0,\,\, {\mathbf {u}}(0)={\mathbf {u}}_0, \end{aligned}$$
(1.2)

with \({\mathbf {u}}_0\) initial perturbation to \(\bar{{\mathbf {U}}}\) and \((N{\mathbf {u}})_{{\mathbf {u}}_0}={\mathbf {0}}\). We assume that

$$\begin{aligned} \bar{{\mathbf {U}}}=\text{ const. },\,\,L=\left\| a_{ij}\right\| ,\,\,i,j=1,2,\cdots , n,\,\,a_{ij}=\text{ const. }\in {\mathbb {R}} \end{aligned}$$
(1.3)

with \(a_{ij}\) independent of t. The stability/instability of \(\bar{{\mathbf {U}}}\) is called linear if it is evaluated via the linear system

$$\begin{aligned} \displaystyle \frac{d{\mathbf {u}}}{dt}=L{\mathbf {u}},\,\,\forall t>0,\,\, {\mathbf {u}}(0)={\mathbf {u}}_0, \end{aligned}$$
(1.4)

disregarding the nonlinear contribution \(N{\mathbf {u}}\).

In the present paper, we investigate the onset of instability via (1.4). Let \(\lambda _i,\,(i=1,2,\cdots , n)\), be the eigenvalues of the \(n\times n\) matrix \(\left\| a_{ij}\right\| \), i.e. the roots of the spectral equation

$$\begin{aligned} \det (a_{ij}-\lambda \delta _{ij})=0, \end{aligned}$$
(1.5)

with \(\delta _{ij}\) Kronecker numbers. Setting

$$\begin{aligned} R_e(\lambda )=\text{ real } \text{ part } \text{ of } \lambda ,\,\, \lambda ^*_i=R_e(\lambda _i),\,\,\lambda ^*=\max (\lambda ^*_1,\lambda ^*_2,\cdots , \lambda ^*_n), \end{aligned}$$
(1.6)

the basic property of the linear stability/instability is

if and only if all the eigenvalues have negative real part (\(\lambda ^*<0\)), \({\mathbf {u}}={\mathbf {0}}\)is linearly globally attractive and asymptotically exponentially stable. If\(\lambda ^*>0\), then\({\mathbf {u}}={\mathbf {0}}\)is unstable.

Denoting by \(\sigma (\lambda )\) the set \(\{\lambda _1,\cdots , \lambda _n\)), spectrum of L, it follows that

(a):

if and only if—in the complex plane—the spectrum is located in the left-hand side of the imaginary axis,\({\mathbf {u}}={\mathbf {0}}\)is linearly globally attractive and exponentially asymptotically stable;

(b):

the solution\({\mathbf {u}}={\mathbf {0}}\)is on the frontier of instability when\(\lambda ^*=0\), i.e. when exist zero and/or pure imaginary eigenvalues (all others having negative real part), since then any small variation of the coefficients\(a_{ij}\)can cause the passage to\(\lambda ^*>0\)and hence to instability;

(c):

if\(\lambda ^*=0\), at each\(\lambda ={\bar{\lambda }}=0\), (1.4) admits the constant (steady) solution\(\bar{{\mathbf {u}}}=(\bar{{\mathbf {u}}}_1,\bar{{\mathbf {u}}}_2,\cdots , \bar{{\mathbf {u}}}_n)^T\)with\(\bar{{\mathbf {u}}}\)given by

$$\begin{aligned} L\bar{{\mathbf {u}}}=0,\quad \det \left\| a_{ij}\right\| =0; \end{aligned}$$
(1.7)
(d):

if\(\lambda ^*=0\), at each\(\lambda =i\omega \), \((\omega >0)\), (1.4) admits the periodic (in time) complex solutions of frequency\(\omega \)and period\(\displaystyle \frac{2\pi }{\omega }\)given by\(\left\{ {\mathbf {u}}_1={\mathbf {k}}_1 e^{i\omega t},\quad {\mathbf {u}}_2={\mathbf {k}}_2e^{-i\omega t}\right\} \), with\({\mathbf {k}}_1=i\varvec{\Psi }, {\mathbf {k}}_2=-i\varvec{\Psi }\)corresponding eigenvectors, and exist two real solutions of type\(\left\{ \bar{{\mathbf {u}}}_1=\varvec{\Psi } \sin \omega t,\quad \bar{{\mathbf {u}}}_2=\varvec{\Psi } \cos \omega t\right\} \), with\(\varvec{\Psi }\)real vector;

(e):

if\(\lambda ^*=0\)and exists a null eigenvalue (all the others having negative real part), at the onset of instability the system passes from the (steady) solution\({\mathbf {u}}={\mathbf {0}}\)to the steady solution\(\bar{{\mathbf {u}}}\)given by (1.7) and this passage is calledsteady bifurcation;

(f):

if\(\lambda ^*=0\)and exists only one coupling pure imaginary eigenvalue\(\lambda =\pm i \omega \), with\(\omega =\hbox {const}.>0\)all the others having negative real part, at the onset of instability the system passes from the steady solution\({\mathbf {u}}={\mathbf {0}}\)to an unsteady periodic solution given by the linear combination\(\left\{ \bar{{\mathbf {u}}}= (a\sin \omega t+b\cos \omega t)\varvec{\Psi }\right\} \), withaandbreal constants and this passage is calledHopf (or rotatory) bifurcation;

(g):

if\(\lambda ^*=0\)and exist zero eigenvalues and a couple of pure imaginary eigenvalues\(\lambda =\pm i\omega \)(all the others having negative real part), then at the onset of instability, occurs a new state composed by steady solutions and a periodic solution and the bifurcation solution can be called Hopf–Steady (HS) bifurcation.

(h):

if\(\lambda ^*=0\)and exist two couples of pure imaginary eigenvalues\(\lambda _{1,2}=\pm i\omega _1,\, \lambda _{3,4}=\pm i\omega _2\)then an Hopf or an unsteady aperiodic bifurcation occurs according to\(\displaystyle \frac{\omega _1}{\omega _2}\)is or not a rational number.

At the onset of a bifurcation, a new scenario appears but the scenario produced by the Hopf bifurcations, letting the transition from a steady state to an unsteady state, is “less continuous” and more impressive from the physical point of view of the steady bifurcation. Our aim in the present paper is to furnish conditions necessary and/or sufficient for guaranteeing: (1) the existence of a unsteady bifurcations, periodic and aperiodic; (2) absence of unsteady bifurcations. Since the existence of bifurcations requires that the spectrum equation admits roots with zero real part, the starting point of our approach to the problem at stark is the looking for conditions necessary and/or sufficient to be satisfied by the characteristic values, coefficients of the spectral equation, for guaranteeing the existence of eigenvalues with zero real part.

The plan of the paper is the following. Section 2 is devoted to some Preliminaries. In the Sect. 2.1 the characteristic values of the spectral equation via the \(\left\| a_{ij}\right\| \) entries are furnished. Successively in 2.2 the Routh–Hurwitz criterion is recalled. Section 3 is devoted to the stability/instability conditions. Hopf bifurcations are investigated in Sects. 4, 5 and 6. The case of Hopf bifurcations depending on parameters is investigated in the subsequent Sect.7. Section 8 is devoted to the absence of Hopf bifurcations in symmetrizable systems, and conditions guaranteeing the symmetrizability are furnished. Applications of the results obtained are furnished in Sect. 9 while Sect. 10 is devoted to the discussion, final remarks and perspectives. The paper ends with an “Appendix” (Sect. 11) devoted to a necessary conditions for having eigenvalues with negative real part (Sect. 11.1) and the proof of the Routh–Hurwitz Criterion (Sect. 11.2). Sections 11.3 and 11.4 are respectively devoted to the eigenvalues of symmetric matrices and to the invariance of eigenvalues with respect to nonsingular transformations.

2 Preliminaries

2.1 Spectral equation

The spectrum equation (1.5) can be written

$$\begin{aligned} P(\lambda ){\mathop {=}\limits ^{def}}\displaystyle \prod _{i=1}^n(\lambda -\lambda _i) =\lambda ^n-\texttt {I}_1\lambda ^{n-1}+\texttt {I}_2\lambda ^{n-2} +\cdots +(-1)^n\texttt {I}_n=0, \end{aligned}$$
(2.1)

with \(\texttt {I}_i\) real constants given by

$$\begin{aligned} \texttt {I}_i=\displaystyle \sum \lambda _{r1}\lambda _{r2}\cdots \lambda _{ri},\qquad \left( \begin{array}{l} r_1+r_2+\cdots +r_i=i\in \{1,2,\cdots , n\}\\ r_1\ne r_2\ne \cdots \ne r_i \end{array}\right) . \end{aligned}$$
(2.2)

The coefficients \(\texttt {I}_i\) are the characteristic values of the spectrum equation and are invariants with respect to the nonsingular transformation \(\{\)see 11.1\(\}\) and govern the stability and the kind of instability occurring (bifurcations). These coefficients can be expressed via the entries of L. Precisely (1.5) implies that \(\texttt {I}_i\) is obtained by adding the principal minors of order i of \(\left\| a_{ij}\right\| \). In fact, \(P(\lambda )\), being a polynomial of n degree, can be written (Mac-Lauren)

$$\begin{aligned} P(\lambda )=\displaystyle \sum _{i=1}^n \displaystyle \frac{P(0)^{(i)}}{i!}\lambda ^i \end{aligned}$$
(2.3)

and it follows that

$$\begin{aligned} \texttt {I}_i=(-1)^i \displaystyle \frac{P(0)^{(i)}}{i!},\qquad i=1,2,\cdots , n \end{aligned}$$
(2.4)

with \(\texttt {I}_i\) obtained by adding the principal minors of order i. For the sake of simplicity, we verify (2.3) in the case \(n=3\). Then

$$\begin{aligned} P(\lambda )=\left| \begin{array}{c@{\quad }c@{\quad }c} a_{11}-\lambda &{}a_{12}&{}a_{13}\\ a_{21}&{}a_{22}-\lambda &{}a_{23}\\ a_{31}&{}a_{32}&{}a_{33}-\lambda \end{array}\right| , \end{aligned}$$
(2.5)

implies

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{d P}{d\lambda }&{}=-\left[ \left| \begin{array}{c@{\quad }c} a_{22}-\lambda &{}a_{23}\\ a_{32}&{}a_{33}-\lambda \end{array} \right| +\left| \begin{array}{c@{\quad }c} a_{11}-\lambda &{}a_{13}\\ a_{31}&{}a_{33}-\lambda \end{array} \right| + \right. \\ \\ &{}+\left. \left| \begin{array}{c@{\quad }c} a_{11}-\lambda &{}a_{12}\\ a_{21}&{}a_{22}-\lambda \end{array} \right| \right] ,\\ \\ \displaystyle \frac{d^2 P}{d\lambda ^2}&{}=2\left[ \left( a_{11}+a_{22}+a_{33}-3\lambda \right) \right] ,\,\, \displaystyle \frac{d^3 P}{d\lambda ^3}=-6 \end{array}\right. \end{aligned}$$

and hence

$$\begin{aligned} P(0)=\texttt {I}_3,\,\, P^\prime (0)=-\texttt {I}_2,\,\, P^{\prime \prime }(0)=2\texttt {I}_1,\,\, P^{\prime \prime \prime }(0)=-6. \end{aligned}$$

It follows that

$$\begin{aligned} P(\lambda )=-(\lambda ^3-\texttt {I}_1\lambda ^2+\texttt {I}_2\lambda -\texttt {I}_3) \end{aligned}$$
(2.6)

with

$$\begin{aligned} \texttt {I}_1=a_{11}+a_{22}+a_{33},\, \texttt {I}_2=\left| \begin{array}{c@{\quad }c} a_{11}&{}a_{12}\\ a_{21}&{}a_{22} \end{array} \right| + \left| \begin{array}{c@{\quad }c} a_{11}&{}a_{13}\\ a_{31}&{}a_{33} \end{array} \right| + \left| \begin{array}{c@{\quad }c} a_{22}&{}a_{23}\\ a_{31}&{}a_{33} \end{array} \right| ,\, \texttt {I}_3=\det \left\| a_{ij}\right\| . \end{aligned}$$
(2.7)

2.2 Routh–Hurwitz criterion

In order to determine the stability/instability of the unperturbed solution \({\mathbf {u}}\equiv {\mathbf {0}}\), one only needs to know if all roots of the spectrum equation (1.5) have or not negative real part: a direct evaluation of all roots is not needed. The equation (1.5) is an algebraic equation of n-th degree with real coefficients of type

$$\begin{aligned} \lambda ^n+a_1\lambda ^{n-1}+a_2\lambda ^{n-2}+\cdots +a_n=0. \end{aligned}$$
(2.8)

For (2.8), the following property holds \(\{\)see 11.1\(\}\).

Property 1

The conditions

$$\begin{aligned} a_i>0, \forall i \in \{1,2,\cdots , n\}, \end{aligned}$$
(2.9)

are necessary for all roots of (2.8) to have negative real part.

It remains to give a sufficient condition.

The problem of knowing if all the roots of (2.8)—without a direct evaluation of all roots—will have or not all negative real part, has been solved by Routh in 1877 (for \(n=4,5\)) and by Hurwitz in 1895, \(\forall n\in {\mathbb {N}}\), via different but equivalent procedures [2,3,4].

Following the Hurwitz procedure, let us introduce the \(n\times n\) (Hurwitz) matrix \(\left\| H_{ij}\right\| \) associated to (2.8). The first row, in a sequential array, contains the coefficients with odd indices of (2.8). The second row contains \(-1\) and the coefficients of (2.8) with even indices in a sequential array. The remaining entries of \(\left\| H_{ij}\right\| \) are given by

$$\begin{aligned} \left\{ \begin{array}{ll} H_{ij}=H_{2j}-1, &{} \text{ for } 0<2j-i\le n,\\ H_{ij}=0,&{} \text{ for } (2j-i)\notin ]0,n] \end{array}\right. \end{aligned}$$

and it follows that

$$\begin{aligned} \text{ Hurwitz } \text{ matrix }= \left\| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} a_{1}&{}a_3&{}a_5&{}\cdots &{}0\\ 1&{}a_2&{}a_4&{}\cdots &{}0\\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ 0&{}0&{}0&{}0&{}a_n \end{array}\right\| . \end{aligned}$$
(2.10)

The determinants \(\varDelta _i, (i=1,2,\cdots , n)\), of the principal diagonal minors of (2.10) are called Hurwitz determinants and are given by

$$\begin{aligned} \varDelta _1=a_1,\quad \varDelta _2=\left| \begin{array}{c@{\quad }c} a_1&{}a_3\\ 1&{}a_2 \end{array} \right| ,\quad \varDelta _3=\left| \begin{array}{c@{\quad }c@{\quad }c} a_1&{}a_3&{}a_5\\ 1&{}a_2&{}a_4\\ 0&{}a_1&{}a_3 \end{array} \right| ,\cdots \end{aligned}$$
(2.11)

Since \(a_1,a_2, \cdots , a_n\), are the entries of the principal diagonal of (2.10) and the entries of the last column except the last element \(a_n\) are all equal to zero, one has

$$\begin{aligned} \varDelta _n=a_n\varDelta _{n-1}. \end{aligned}$$
(2.12)

The following criterion holds \(\{\)see [2,3,4] and Sect. 11.2\(\}\).

Property 2

(Routh–Hurwitz criterion) If and only if

$$\begin{aligned} \varDelta _i>0,\quad \forall i\in \{1,2,\cdots , n\}, \end{aligned}$$
(2.13)

the roots of the algebraic equation (2.8) with real coefficients, have all negative real part.

In the case of the spectrum equation (2.1) one has

$$\begin{aligned} a_1=-\texttt {I}_1,\quad a_2=\texttt {I}_2, a_3=-\texttt {I}_3,\cdots , a_n=(-1)^n \texttt {I}_n \end{aligned}$$
(2.14)

and the Hurwitz matrix becomes

$$\begin{aligned} \text{ H-matrix }= \left\| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -\texttt {I}_1&{} -\texttt {I}_3&{} -\texttt {I}_5&{}\cdots &{}0\\ 1&{} \texttt {I}_2&{} \texttt {I}_4&{}\cdots &{}0\\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ 0&{}0&{}0&{}\cdots &{}(-1)^n\texttt {I}_n \end{array}\right\| . \end{aligned}$$
(2.15)

3 Stability conditions

3.1 RH stability conditions for binary ADS

The stability conditions for binary ADS are well known and are taken into account here only for the sake of completeness. In the case \(n=2\), (1.4) reduces to

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{du_1}{dt}=a_{11}u_1+a_{12}u_2,\\ \\ \displaystyle \frac{du_2}{dt}=a_{21}u_1+a_{22}u_2. \end{array}\right. \end{aligned}$$
(3.1)

The corresponding spectrum equation is

$$\begin{aligned} \lambda ^2-\texttt {I}_1 \lambda +\texttt {I}_2=0 \end{aligned}$$
(3.2)

with

$$\begin{aligned} \texttt {I}_1=\lambda _1+\lambda _2=a_{11}+a_{22},\quad \texttt {I}_2=\lambda _1\lambda _2=\det \left\| a_{ij}\right\| =a_{11}a_{22}-a_{12}a_{21}. \end{aligned}$$
(3.3)

The matrix (2.15) and the RH conditions are

$$\begin{aligned} \text{ Hurwitz } \text{ matrix }=\left\| \begin{array}{c@{\quad }c} -\texttt {I}_1&{}0\\ 1&{}\texttt {I}_2 \end{array}\right\| ,\quad \varDelta _1=-\texttt {I}_1>0,\quad \varDelta _2=-\texttt {I}_1\texttt {I}_2>0. \end{aligned}$$
(3.4)

Therefore

  1. (i)

    if and only if

    $$\begin{aligned} \texttt {I}_1=a_{11}+a_{22}<0,\quad \texttt {I}_2=a_{11}a_{22}-a_{12}a_{21}>0, \end{aligned}$$
    (3.5)

    \({\mathbf {u}}\equiv {\mathbf {0}}\)is asymptotically stable and globally attractive;

  2. (ii)

    if even only one of (3.3) is reversed, there exist eigenvalues with positive real part and instability occurs.

3.2 RH stability conditions for ternary ADS

In the case \(n=3\), (1.4) and the corresponding spectrum equation reduce respectively to

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{du_1}{dt}=a_{11}u_1+a_{12}u_2+a_{13}u_3,\\ \\ \displaystyle \frac{du_2}{dt}=a_{21}u_1+a_{22}u_2+a_{23}u_3,\\ \\ \displaystyle \frac{du_3}{dt}=a_{31}u_1+a_{32}u_2+a_{33}u_3 \end{array}\right. \end{aligned}$$
(3.6)

and to

$$\begin{aligned} \lambda ^3-\texttt {I}_1\lambda ^2+\texttt {I}_2\lambda -\texttt {I}_3=0, \end{aligned}$$
(3.7)

with

$$\begin{aligned} \texttt {I}_1=\lambda _1+\lambda _2+\lambda _3,\,\texttt {I}_2=\lambda _1 (\lambda _2+\lambda _3)+\lambda _2\lambda _3,\, \texttt {I}_3=\lambda _1\lambda _2\lambda _3, \end{aligned}$$
(3.8)

given in terms of the coefficients \(a_{ij}\) by (2.7). The Hurwitz matrix (2.15) and the corresponding RH conditions are

$$\begin{aligned} \left\| \begin{array}{c@{\quad }c@{\quad }c} -\texttt {I}_1&{}-\texttt {I}_3&{}0\\ 1&{}\texttt {I}_2&{}0\\ 0&{}-\texttt {I}_1&{}-\texttt {I}_3 \end{array} \right\| \end{aligned}$$
(3.9)

and

$$\begin{aligned} \varDelta _1=-\texttt {I}_1>0,\varDelta _2=-(\texttt {I}_1\texttt {I}_2-\texttt {I}_3)>0, \varDelta _3=-\texttt {I}_3\varDelta _2>0. \end{aligned}$$
(3.10)

Therefore

  1. (iii)

    if and only if

    $$\begin{aligned} \texttt {I}_1<0,\quad \texttt {I}_1\texttt {I}_2-\texttt {I}_3<0,\quad \texttt {I}_3<0, \end{aligned}$$
    (3.11)

    \({\mathbf {u}}\equiv {\mathbf {0}}\)is asymptotically stable and globally attractive (stable in the large);

  2. (iv)

    if even only one of (3.11) is reversed, there exist eigenvalues with positive real part and instability occurs.

We remark that (3.11) \(\Rightarrow \texttt {I}_2>0\).

3.3 RH stability conditions for quaternary ADS

In the case \(n=4\), the spectrum equation is

$$\begin{aligned} P(\lambda , n=4)=\lambda ^4-\texttt {I}_1\lambda ^3+\texttt {I}_2\lambda ^2-\texttt {I}_3\lambda +\texttt {I}_4=0.\end{aligned}$$
(3.12)

The Hurwitz matrix and the RH stability conditions are respectively given by

$$\begin{aligned} \left\| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -\texttt {I}_1&{}-\texttt {I}_3&{}0&{}0\\ 1&{}\texttt {I}_2&{}\texttt {I}_4&{}0\\ 0&{}-\texttt {I}_1&{}-\texttt {I}_3&{}0\\ 0&{}1&{}\texttt {I}_2&{}\texttt {I}_4 \end{array}\right\| \end{aligned}$$
(3.13)

and by

$$\begin{aligned} \left\{ \begin{array}{l} \varDelta _1=-\texttt {I}_1>0,\,\,\varDelta _2=-\texttt {I}_1\texttt {I}_2+\texttt {I}_3>0,\\ \varDelta _3=-\texttt {I}_3\varDelta _2-\texttt {I}_1^2\texttt {I}_4>0,\,\,\varDelta _4=\texttt {I}_4\varDelta _3>0. \end{array}\right. \end{aligned}$$
(3.14)

One easily verifies that (3.14) can be reduced to

$$\begin{aligned} \texttt {I}_1<0,\quad \texttt {I}_2>0,\quad \texttt {I}_3<0,\quad \texttt {I}_4>0,\quad \varDelta _3>0. \end{aligned}$$
(3.15)

In fact

$$\begin{aligned} \left\{ \begin{array}{l} (\texttt {I}_4>0,\varDelta _3>0)\Rightarrow \varDelta _4>0,\\ \left\{ \begin{array}{l} \varDelta _3>0\\ \texttt {I}_3<0,\texttt {I}_4>0 \end{array}\right\} \Rightarrow \varDelta _3+\texttt {I}^2_1\texttt {I}_4=-\texttt {I}_3\varDelta _2>0\Rightarrow \varDelta _2>0 \end{array} \right. \end{aligned}$$

In view of

$$\begin{aligned} -\texttt {I}_3\varDelta _2=\texttt {I}_1\texttt {I}_2\texttt {I}_3-\texttt {I}_3^2-\texttt {I}_1^2\texttt {I}_4, \end{aligned}$$

the RH stability conditions become

$$\begin{aligned} \left\{ \begin{array}{l} \texttt {I}_1<0,\quad \texttt {I}_3<0,\quad \texttt {I}_4>0,\\ \texttt {I}_1\texttt {I}_2\texttt {I}_3-\texttt {I}_3^2-\texttt {I}_1^2\texttt {I}_4>0. \end{array}\right. \end{aligned}$$
(3.16)

We remark that (3.16) implies \(\texttt {I}_2>0\) and that, in view of property 1 and (3.12), \(\texttt {I}_2>0\) is necessary for \(\lambda ^*<0\).

4 Unsteady bifurcations in binary ADS

4.1 Hopf bifurcations in binary ADS

Property 3

In binary ADS the Hopf bifurcations occur if and only if

$$\begin{aligned} \texttt {I}_1=a_{11}+a_{22}=0,\quad \texttt {I}_2=a_{11}a_{22}-a_{12}a_{21}>0, \end{aligned}$$
(4.1)

and have \(\omega =\sqrt{\texttt {I}_2}\) frequency (Table 1).

Proof

(4.1) are necessary. In fact the spectrum equation is given by (3.2) with

$$\begin{aligned} \texttt {I}_1=\lambda _1+\lambda _2,\quad \texttt {I}_2=\lambda _1\lambda _2. \end{aligned}$$
(4.2)

If the Hopf bifurcation occurs, then exists a positive \(\omega \) such that

$$\begin{aligned} \lambda _1=i\omega ,\,\,\lambda _2=-i\omega ,\,\,\texttt {I}_1=0,\,\,\texttt {I}_2=\omega ^2. \end{aligned}$$
(4.3)

Vice-versa (4.1) are sufficient. In fact (4.1) reduces to (4.2) to

$$\begin{aligned} \lambda ^2+\texttt {I}_2=0 \,\,\Leftrightarrow \,\,\lambda =\pm i \sqrt{\texttt {I}_2}. \end{aligned}$$
(4.4)

\(\square \)

Table 1 Bifurcation in binary DS
Full size table

5 Hopf bifurcations in ternary ADS

Property 4

In ternary ADS the Hopf bifurcations occur if and only if

$$\begin{aligned} \texttt {I}_1<0,\,\,\texttt {I}_2>0,\,\,\texttt {I}_3=\texttt {I}_1\texttt {I}_2 \end{aligned}$$
(5.1)

and are periodic in time with period \(\displaystyle \frac{2\pi }{\omega }\) and frequency \(\omega =\sqrt{\texttt {I}_2}= \sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\).

Proof

(5.1) is necessary. In fact, let \(\lambda _{1,2}=\pm i\omega \). Then (3.8)\(_1\) gives \(\lambda _3=\texttt {I}_1<0\) and (3.7) can be written

$$\begin{aligned} (\lambda -\texttt {I}_1)(\lambda ^2+\omega ^2)=\lambda ^3-\texttt {I}_1\lambda ^2+\omega ^2\lambda -\texttt {I}_1\omega =0, \end{aligned}$$
(5.2)

i.e.

$$\begin{aligned} \texttt {I}_2=\omega ^2,\,\,\,\texttt {I}_3=\texttt {I}_1\omega ^2=\texttt {I}_1\texttt {I}_2. \end{aligned}$$
(5.3)

The sufficiency of (5.1) is easily obtained. In fact (5.1) reduces (3.7) to

$$\begin{aligned} \lambda ^3-\texttt {I}_1\lambda ^2+\texttt {I}_2\lambda -\texttt {I}_1\texttt {I}_2=(\lambda -\texttt {I}_1)(\lambda ^2+\texttt {I}_2)=0,\end{aligned}$$
(5.4)

and one has

$$\begin{aligned} \lambda _{1,2}=\pm i\sqrt{\texttt {I}_2},\quad \lambda _3=\texttt {I}_1 \end{aligned}$$
(5.5)

and the Hopf bifurcation occurs with period \(\displaystyle \frac{2\pi }{\omega }\) and frequency \(\omega =\sqrt{\texttt {I}_2}\). \(\square \)

Property 5

In ternary ADS the Hopf–Steady bifurcations occur if and only if

$$\begin{aligned} \texttt {I}_1=0,\,\,\texttt {I}_2>0,\,\,\texttt {I}_1\texttt {I}_2=\texttt {I}_3=0 \end{aligned}$$
(5.6)

and have period \(\displaystyle \frac{2\pi }{\omega }\) and frequency \(\omega =\sqrt{\texttt {I}_2}\) (Table 2).

Proof

In fact, let

$$\begin{aligned} \lambda _{1,2}=\pm i\omega ,\qquad \lambda _3=0. \end{aligned}$$
(5.7)

Then

$$\begin{aligned} \texttt {I}_1=\lambda _1+\lambda _2+\lambda _3=0,\,\, \texttt {I}_2=\lambda _1\lambda _2=\omega ^2,\,\, \texttt {I}_3=\lambda _1\lambda _2\lambda _3=0=\texttt {I}_1\texttt {I}_2. \end{aligned}$$
(5.8)

Vice-versa (5.6) reduces (3.7) to

$$\begin{aligned} \lambda (\lambda ^2+\texttt {I}_2)=0. \end{aligned}$$
(5.9)

\(\square \)

Table 2 Bifurcation in ternary ADS
Full size table

6 Hopf bifurcations in quaternary ADS

Property 6

In quaternary ADS the Hopf bifurcations occur if and only if

$$\begin{aligned} \texttt {I}_1<0,\,\,\texttt {I}_3<0,\,\,\texttt {I}_4>0,\,\, \texttt {I}_3(\texttt {I}_1\texttt {I}_2-\texttt {I}_3)=\texttt {I}^2_1\texttt {I}_4 \end{aligned}$$
(6.1)

and occur with period \(\displaystyle \frac{2\pi }{\omega }\) and frequency \(\omega =\sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\).

Proof

Let \(\lambda _{1,2}=\pm i\omega \) and let \(\lambda _2,\lambda _3\) have negative real parts. Then the spectral equation is

$$\begin{aligned} (\lambda ^2+\omega ^2)(\lambda -\lambda _3)(\lambda -\lambda _4)=0, \end{aligned}$$
(6.2)

i.e.

$$\begin{aligned} \lambda ^4-(\lambda _3+\lambda _4)\lambda ^3+(\omega ^2+\lambda _3\lambda _4)\lambda ^2-\omega ^2 (\lambda _3+\lambda _4)\lambda + \omega ^2\lambda _3\lambda _4=0 \end{aligned}$$
(6.3)

and one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \texttt {I}_1=\lambda _3+\lambda _4<0,\,\texttt {I}_2=\omega ^2+\lambda _3\lambda _4>0,\,\, \texttt {I}_3=\omega ^2(\lambda _3+\lambda _4)<0,\,\,\texttt {I}_4=\omega ^2\lambda _3\lambda _4,\\ \\ \texttt {I}_1\texttt {I}_2-\texttt {I}_3=(\lambda _3+\lambda _4)(\omega ^2+\lambda _3\lambda _4)-\omega ^2(\lambda _3+\lambda _4)=(\lambda _3+\lambda _4)\lambda _3\lambda _4,\\ \\ \displaystyle \frac{\texttt {I}^2_1\texttt {I}_4}{\texttt {I}_3}=\displaystyle \frac{(\lambda _3+\lambda _4)^2\omega ^2\lambda _3\lambda _4}{\omega ^2(\lambda _3+\lambda _4)}= (\lambda _3+\lambda _4)\lambda _3\lambda _4=\texttt {I}_1\texttt {I}_2-\texttt {I}_3,\,\,\omega ^2=\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}, \end{array}\right. } \end{aligned}$$
(6.4)

i.e. (6.1) holds. Vice-versa, let (6.1) holds. Then \(\lambda =\pm i\sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\) is solution of (3.12). In fact, for \(\lambda =\pm i\sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\) one has

$$\begin{aligned} \texttt {I}_1\lambda ^3+\texttt {I}_3\lambda =\lambda \left( -\texttt {I}_1 \displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}+\texttt {I}_3\right) =0 \end{aligned}$$
(6.5)

and (3.12) reduces to

$$\begin{aligned} \lambda ^4+\texttt {I}_2\lambda ^2+\texttt {I}_4=0. \end{aligned}$$
(6.6)

In view of (6.1)\(_4\), (6.6) becomes

$$\begin{aligned} \lambda ^4+\texttt {I}_2\lambda ^2+\displaystyle \frac{\texttt {I}_3(\texttt {I}_1\texttt {I}_2-\texttt {I}_3)}{\texttt {I}^2_1}=0, \end{aligned}$$
(6.7)

verified by \(\lambda =\pm i \sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\). \(\square \)

6.1 Hopf–Steady bifurcations in quaternary ADS

The spectrum equation (3.12) reduces to

$$\begin{aligned} \lambda (\lambda ^3-\texttt {I}_1\lambda ^2+\texttt {I}_2\lambda -\texttt {I}_3)=0, \end{aligned}$$
(6.8)

in the case

$$\begin{aligned} \texttt {I}_4=0, \end{aligned}$$
(6.9)

to

$$\begin{aligned} \lambda ^2(\lambda ^2-\texttt {I}_1\lambda ^2+\texttt {I}_2)=0, \end{aligned}$$
(6.10)

in the case

$$\begin{aligned} \texttt {I}_3=\texttt {I}_4=0 \end{aligned}$$
(6.11)

and to

$$\begin{aligned} \lambda ^4+\texttt {I}_2\lambda ^2+\texttt {I}_4=0, \end{aligned}$$
(6.12)

in the case

$$\begin{aligned} \texttt {I}_1=\texttt {I}_3=0. \end{aligned}$$
(6.13)

In view of the results of Sect. 5, the following property holds.

Property 7

In quaternary ADS the Hopf–Steady bifurcations occur if and only if

$$\begin{aligned} \texttt {I}_1<0,\,\,\texttt {I}_2>0,\,\,\texttt {I}_3=\texttt {I}_1\texttt {I}_2,\,\, \texttt {I}_4=0, \end{aligned}$$
(6.14)

or

$$\begin{aligned} \texttt {I}_1=0,\,\,\texttt {I}_2>0,\,\,\texttt {I}_3=\texttt {I}_4=0 \end{aligned}$$
(6.15)

and the bifurcating solution has period \(\displaystyle \frac{2\pi }{\omega }\) with \(\omega =\sqrt{\texttt {I}_2}\).

6.2 Double-Hopf and unsteady bifurcations in quaternary ADS

We call Double-Hopf bifurcation the case

$$\begin{aligned} \lambda _{1,2}=\pm i\omega _1,\quad \lambda _{3,4}=\pm i \omega _2,\quad \omega _1\ne \omega _2. \end{aligned}$$
(6.16)

The following property holds.

Property 8

In quaternary ADS, Double-Hopf bifurcations occur if and only if

$$\begin{aligned} \texttt {I}_1=\texttt {I}_3=0,\,\,\texttt {I}_2>0,\,\,\texttt {I}_4>0,\,\,\texttt {I}^2_2\ge 4\texttt {I}_4 \end{aligned}$$
(6.17)

and the bifurcating solution is time dependent and periodic in time in the case

$$\begin{aligned} \displaystyle \frac{-\texttt {I}_2+\sqrt{\texttt {I}^2_2-4\texttt {I}_4}}{-\texttt {I}_2-\sqrt{\texttt {I}^2_2-4\texttt {I}_4}}=\displaystyle \frac{p^2}{q^2},\,\,\,\, p,q\in {\mathbb {N}}. \end{aligned}$$
(6.18)

Proof

(6.17)–(6.18) are necessary. In fact, let (6.16) holds. Then (3.12) can be written

$$\begin{aligned} (\lambda ^2+\omega ^2_1)(\lambda ^2+\omega ^2_2)=0, \end{aligned}$$
(6.19)

and hence

$$\begin{aligned} \lambda ^4+(\omega ^2_1+\omega ^2_2)\lambda ^2+\omega ^2_1\omega ^2_2=0. \end{aligned}$$
(6.20)

In view of

$$\begin{aligned} (\omega ^2_1+\omega ^2_2)^2-4\omega ^2_1\omega ^2_2=(\omega ^2_1-\omega ^2_2), \end{aligned}$$
(6.21)

easily (6.17) follows. Vice-versa, in view of (6.17), (6.19) reduces to (6.12) and one has (6.16) with

$$\begin{aligned} \omega ^2_1=\displaystyle \frac{-\texttt {I}_2+\sqrt{\texttt {I}^2_2-4\texttt {I}_4}}{2},\,\,\, \omega ^2_2=\displaystyle \frac{-\texttt {I}_2-\sqrt{\texttt {I}^2_2-4\texttt {I}_4}}{2}. \end{aligned}$$
(6.22)

The bifurcating solution is composed by two periodic solutions of period \(\displaystyle \frac{2\pi }{\omega _1}\) and \(\displaystyle \frac{2\pi }{\omega _2}\) and Hopf bifurcation occurs if

$$\begin{aligned} \displaystyle \frac{\omega _1}{\omega _2}=\displaystyle \frac{p_1}{p_2},\qquad \text{ with } p_i\in {\mathbb {N}}, i=1,2, \end{aligned}$$
(6.23)

with the period given by \(T=\displaystyle \frac{2\pi p_1}{\omega _1}=\displaystyle \frac{2\pi p_2}{\omega _2}\) and frequency \(\omega =\displaystyle \frac{\omega _1}{p_1}=\displaystyle \frac{\omega _2}{p_2}\). Is an unsteady aperiodic bifurcation when (6.23) does not hod. \(\square \)

Remark 1

In the case

$$\begin{aligned} \texttt {I}_1=\texttt {I}_2=\texttt {I}_3=0,\quad \texttt {I}_4>0, \end{aligned}$$
(6.24)

(6.12) reduces to \(\lambda ^4+\texttt {I}_4=0\) and one has \(\lambda =\sqrt{\pm i}(\texttt {I}_4)^\frac{1}{4}\). Since \(\{\sqrt{i}=\pm \displaystyle \frac{1+i}{\sqrt{2}},\, \{\sqrt{-i}=\pm \displaystyle \frac{1-i}{\sqrt{2}}\}\), two eigenvalues have positive real part and hence the zero solution is unstable (Table 3).

Table 3 Bifurcation in quaternary ADS
Full size table

7 Hopf bifurcations parameter depending

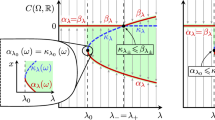
Let \(a_{ij}, (i,j=1,2,\cdots , n)\), depend continuously on a positive parameter R and let exists a positive value \(R_C\) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} R<R_C\,\,\Rightarrow \,\, \varDelta _i>0,\,\,\forall i\in \{1,2,\cdots , n\},\\ \\ R>R_C\,\,\Rightarrow \,\,\varDelta _i<0,\,\, \text{ for } \text{ at } \text{ least } \text{ one } i\in \{1,2,\cdots , n\}, \end{array}\right. } \end{aligned}$$
(7.1)

with \(\varDelta _i\) Hurwitz determinants. \(R_c\) is the critical value of R since it is the instability threshold and \(R=R_C\) implies the existence of eigenvalues (at least one) \(\lambda _{ci}\), with zero real part. Let

$$\begin{aligned} {\left\{ \begin{array}{ll} R_{CS}=\displaystyle \min _{R\in {\mathbb {R}}^+} R: \texttt {I}_n=0,\\ \\ R_{CH}=\displaystyle \min _{R\in {\mathbb {R}}^+} R: P(e^{i\omega })=0 \end{array}\right. } \end{aligned}$$
(7.2)

with \(\omega \) real positive number and let \(e^{i\omega t}\) root of the spectrum equation (2.1). Then, since \(\lambda =0\Leftrightarrow \texttt {I}_n=0\), it follows that Hopf bifurcations occur if and only if

$$\begin{aligned} R_{CH}<R_{CS}, \end{aligned}$$
(7.3)

and one has \(R_C=R_{CH}\). Setting

$$\begin{aligned} R_r=\displaystyle \min _{R\in {\mathbb {R}}^+} R: \texttt {I}_r=0,\quad r=1,2,\cdots , n, \end{aligned}$$
(7.4)

one has

$$\begin{aligned} R_n=R_{CS} \end{aligned}$$
(7.5)

and if and only if

$$\begin{aligned} R_n=R_{CS}<R_{CH}, \end{aligned}$$
(7.6)

steady bifurcations occur. In the sequel of this section, we assume that \(\texttt {I}_r(R)\) is a non-decreasing or a non-increasing function of R according too r be odd or even.

7.1 Hopf bifurcations parameter depending in binary ADS

Property 9

Let

$$\begin{aligned} {\left\{ \begin{array}{ll} n=2,\,\,\texttt {I}_1(R_1)=0,\,\, R_1<R_2,\\ \\ \texttt {I}_1<0,\,\,\texttt {I}_2>0,\qquad \forall R\in ]0,R_1[. \end{array}\right. } \end{aligned}$$
(7.7)

Then instability occurs at \(R=R_1\) via Hopf bifurcation associated to the eigenvalues \(\lambda =\pm i\sqrt{\texttt {I}_2}\).

Proof

In fact, at \(R=R_1\) the spectrum equation reduces to \(\lambda ^2+\texttt {I}_2=0\). \(\square \)

7.2 Hopf bifurcations parameter depending in ternary ADS

Property 10

If and only if

$$\begin{aligned} 0<R_{12}=\displaystyle \min (R_1,R_2)<R_3=R_{CS}, \end{aligned}$$
(7.8)

Hopf bifurcation occurs and occurs at \({\bar{R}}<R_{12}\) lowest positive root of \(\texttt {I}_1\texttt {I}_2-\texttt {I}_3=0\) and the frequency of the bifurcating solution is \(\sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\).

Proof

In fact, (7.8) is obviously necessary. Vice-versa, since (7.8) implies

$$\begin{aligned} \texttt {I}_1<0,\,\texttt {I}_2>0,\,\texttt {I}_3<0,\, \texttt {I}_1\texttt {I}_2-\texttt {I}_3<0,\,\,\text{ at } R=0 \end{aligned}$$
(7.9)

and

$$\begin{aligned} \left\{ \begin{array}{ll} (\texttt {I}_1\texttt {I}_2)=0,&{}\\ &{}\text{ at } R=R_1R_2 \\ \texttt {I}_1\texttt {I}_2-\texttt {I}_3=-\texttt {I}_3>0&{} \end{array} \right. \end{aligned}$$
(7.10)

it follows that \(\texttt {I}_1\texttt {I}_2-\texttt {I}_3=0\) has roots for \(R\in ]0, R_{12}[\). Let \({\bar{R}}\) be the lowest root. Then at \(R={\bar{R}},\,\texttt {I}_1\texttt {I}_2-\texttt {I}_3=0\) and at \(R={\bar{R}}\)

$$\begin{aligned} \lambda ^3-\texttt {I}_1\lambda ^2+\texttt {I}_2\lambda -\texttt {I}_3=0, \end{aligned}$$
(7.11)

reduces to

$$\begin{aligned} \lambda ^3- \texttt {I}_1\lambda ^2+\texttt {I}_2\lambda -\texttt {I}_1\texttt {I}_2=0, \end{aligned}$$
(7.12)

i.e. to

$$\begin{aligned} (\lambda -\texttt {I}_1)(\lambda ^2+\texttt {I}_2)=0 \end{aligned}$$
(7.13)

and one has

$$\begin{aligned} \lambda _1=\texttt {I}_1<0,\,\,\lambda _{2,3}=\pm i \sqrt{\texttt {I}_2}=\pm i \sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_2}}. \end{aligned}$$
(7.14)

\(\square \)

7.3 Hopf bifurcations parameter depending in quaternary ADS

Property 11

If and only if

$$\begin{aligned} 0<R_{123}=\min (R_1,R_2,R_3)<R_4=R_{CS}, \end{aligned}$$
(7.15)

Hopf bifurcation occurs and occurs at \({\bar{R}}<R_{123}\) lowest positive root of

$$\begin{aligned} (\texttt {I}_1\texttt {I}_2-\texttt {I}_3)=\texttt {I}_1^2\texttt {I}_4, \end{aligned}$$
(7.16)

with the frequency \(\omega =\left( \sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\right) _{(R={\bar{R}})}\).

Proof

(7.15) is obviously necessary. Vice-versa since, at \(R=0\), (7.15) implies

$$\begin{aligned} \texttt {I}_1<0,\,\,\texttt {I}_2>0\,\,\texttt {I}_3<0,\,\, (\texttt {I}_1\texttt {I}_2-\texttt {I}_3)-\texttt {I}_1^2\texttt {I}_4>0 \end{aligned}$$
(7.17)

and at \(R=R_{123}\)

$$\begin{aligned} {\left\{ \begin{array}{ll} \texttt {I}_1\texttt {I}_2\texttt {I}_3=0,\\ \\ (\texttt {I}_1\texttt {I}_2-\texttt {I}_3)\texttt {I}_3-\texttt {I}_1^2\texttt {I}_4=-\texttt {I}_3^2-\texttt {I}_1^2\texttt {I}_4<0, \end{array}\right. } \end{aligned}$$
(7.18)

it follows that (7.16) has roots for \(R\in ]0, R_{123}[\). Let \({\bar{R}}\) be the lowest root. Then, at \(R={\bar{R}}\) one has

$$\begin{aligned} \lambda ^4-\texttt {I}_1\lambda ^3+\texttt {I}_2\lambda ^2-\texttt {I}_1\lambda +\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1^2}(\texttt {I}_1\texttt {I}_2-\texttt {I}_3)=0. \end{aligned}$$
(7.19)

For \(\lambda =\pm i \left( \sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\right) _{(R={\bar{R}})}\), in view of \(\{\)see (6.5)\(\}\)

$$\begin{aligned} (\texttt {I}_1\lambda ^3+\texttt {I}_3\lambda )_{(R={\bar{R}})}=0, \end{aligned}$$
(7.20)

(6.12) at \(R={\bar{R}}\) reduces to

$$\begin{aligned} \lambda ^4+\texttt {I}_2\lambda ^2+\texttt {I}_4=0 \end{aligned}$$
(7.21)

and is verified \(\{\)see (6.7)\(\}\) by \(\lambda =\pm i \left( \sqrt{\displaystyle \frac{\texttt {I}_3}{\texttt {I}_1}}\right) _{(R={\bar{R}})}\). \(\square \)

Remark 2

If the entries depend on two positive parameters, \(R,{\mathcal {T}}\), then, \(\forall n\in {\mathbb {N}}\), one has that \(R_{CS}\) and \(R_{CH}\) depend on \({\mathcal {T}}\) and the Hopf bifurcations occur only for the values of \({\mathcal {T}}\) such that \(R_{CH}<R_{CS}\).

8 Absence of unsteady bifurcations in ADS

The present section is devoted to the ADS in which Hopf bifurcations are totally absent. This happens when \(L=\left\| a_{ij}\right\| \) is a symmetric or symmetrizable \(n\times n\) matrix. In fact, when

$$\begin{aligned} a_{ij}=a_{ji},\quad i\ne j \end{aligned}$$
(8.1)

as it is well known (see “Appendix A3”), the eigenvalues are all real numbers and the frontier of instability is given by null eigenvalues. The eigenvalues of \(L=\left\| a_{ij}\right\| \) are all real numbers also when (8.1) does not hold but L is symmetrizable according to the following property.

Property 12

Let exists a non singular transformation \({\mathbf {u}}={{\tilde{L}}}{\mathbf {V}}\) such that

$$\begin{aligned} {\mathcal {L}}=({\tilde{L}})^{-1}\cdot L\cdot {\tilde{L}}=\left\| b_{ij}\right\| , \end{aligned}$$
(8.2)

be symmetric. Then L is said symmetrizable and its eigenvalues are all real.

Proof

By virtue of the invariance principle \(\{\)see 11.4\(\}\), L and \({\mathcal {L}}\) have the same eigenvalues (all real). \(\square \)

8.1 Binary symmetrizable systems

Let

$$\begin{aligned} n=2,\qquad a_{12}a_{21}>0. \end{aligned}$$
(8.3)

Then Lis symmetrizable.

In fact, let \(\mu \ne 0\) be a scaling to be determined and set

$$\begin{aligned} {\mathbf {u}}=\tilde{{\mathcal {L}}}\cdot {\mathbf {V}},\quad \text{ with } \quad \tilde{{\mathcal {L}}}=\left\| \begin{array}{c@{\quad }c} 1&{}0\\ 0&{}\mu \end{array}\right\| . \end{aligned}$$
(8.4)

Then \(\tilde{{\mathcal {L}}}\) is non-singular and (8.4) implies \(\{ u_1=V_1, u_2=\mu V_2\}\) and

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{du_1}{dt}=a_{11}u_1+a_{12}u_2\\ \displaystyle \frac{du_2}{dt}=a_{21}u_1+a_{22}u_2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \displaystyle \frac{dV_1}{dt}=a_{11}V_1+\mu a_{12}V_2\\ \displaystyle \frac{dV_2}{dt}=\displaystyle \frac{a_{21}}{\mu }V_1+a_{22}V_2. \end{array} \right. \end{aligned}$$
(8.5)

Therefore

$$\begin{aligned} \mu a_{12}=\displaystyle \frac{a_{21}}{\mu }\quad \Rightarrow \quad \mu ^2=\displaystyle \frac{a_{21}}{a_{12}} \end{aligned}$$
(8.6)

and (8.5)\(_2\) becomes

$$\begin{aligned} \displaystyle \frac{d{\mathbf {V}}}{dt}={\mathcal {L}}{\mathbf {V}},\quad {\mathcal {L}}=\left\| \begin{array}{c@{\quad }c} a_{11}&{}\sqrt{a_{12}a_{21}}\\ \sqrt{a_{12}a_{21}}&{}a_{22} \end{array}\right\| \end{aligned}$$
(8.7)

8.2 Ternary symmetrizable systems

Let

$$\begin{aligned} n=3,\,\, a_{ij}\ne a_{ji}, a_{ij}a_{ji}>0,\,\, i\ne j,\,\, a_{12}a_{23}a_{31}=a_{21}a_{32}a_{13}. \end{aligned}$$
(8.8)

Then Lis symmetrizable.

In fact, let \(\mu \ne 0,\delta \ne 0\) be scalings to be determined and set

$$\begin{aligned} {\mathbf {u}}=\tilde{{\mathcal {L}}}\cdot {\mathbf {V}},\quad \tilde{{\mathcal {L}}}=\left\| \begin{array}{c@{\quad }c@{\quad }c} 1&{}0&{}0\\ 0&{}\mu &{}0\\ 0&{}0&{}\delta \end{array}\right\| . \end{aligned}$$
(8.9)

Then \(\tilde{{\mathcal {L}}}\) is non-singular and (8.9) implies \(\{u_1=V_1, u_2=\mu V_2, u_3=\delta V_3\}\) and

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{d u_1}{dt}=a_{11}u_1+a_{12}u_2+a_{13}u_3\\ \displaystyle \frac{d u_2}{dt}=a_{21}u_1+a_{22}u_2+a_{23}u_3\\ \displaystyle \frac{d u_3}{dt}=a_{31}u_1+a_{32}u_2+a_{33}u_3 \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} \displaystyle \frac{d V_1}{dt}=a_{11}V_1+a_{12}\mu V_2+a_{13}\delta V_3\\ \displaystyle \frac{d V_2}{dt}=\displaystyle \frac{a_{21}}{\mu }V_1+a_{22}V_2+\displaystyle \frac{\delta }{\mu } a_{23}V_3\\ \displaystyle \frac{d V_3}{dt}=\displaystyle \frac{a_{31}}{\delta }V_1+\displaystyle \frac{\mu }{\delta } a_{32}V_2+a_{33}V_3 \end{array}\right. \end{aligned}$$
(8.10)

Therefore

$$\begin{aligned} a_{12}\mu =\displaystyle \frac{a_{21}}{\mu },\quad a_{13}\delta =\displaystyle \frac{a_{31}}{\delta },\quad a_{23}\displaystyle \frac{\delta }{\mu }=\displaystyle \frac{\mu }{\delta }a_{32}, \end{aligned}$$
(8.11)

require

$$\begin{aligned} \mu ^2=\displaystyle \frac{a_{21}}{a_{12}},\quad \delta ^2=\displaystyle \frac{a_{31}}{a_{13}},\quad \left( \displaystyle \frac{\delta }{\mu }\right) ^2=\displaystyle \frac{a_{32}}{a_{23}}. \end{aligned}$$
(8.12)

The consistency of (8.12), in view of

$$\begin{aligned} \left( \displaystyle \frac{\delta }{\mu }\right) ^2=\displaystyle \frac{a_{32}}{a_{23}},\quad \displaystyle \frac{\delta ^2}{\mu ^2}=\displaystyle \frac{a_{31}}{a_{13}}\displaystyle \frac{a_{12}}{a_{21}}, \end{aligned}$$

is guaranteed by the assumption

$$\begin{aligned} a_{12}a_{23}a_{31}=a_{21}a_{32}a_{13}\,\,\Leftrightarrow \,\,\displaystyle \frac{a_{32}}{a_{23}}=\displaystyle \frac{a_{31}a_{12}}{a_{21}a_{13}}.\end{aligned}$$
(8.13)

In view of

$$\begin{aligned} a_{12}\mu =\displaystyle \frac{a_{21}}{\mu }=\sqrt{a_{12}a_{21}},\,\, a_{13}\delta =\displaystyle \frac{a_{31}}{\delta }=\sqrt{a_{13}a_{31}},\,\, a_{23}\displaystyle \frac{\delta }{\mu }=\displaystyle \frac{\mu }{\delta }a_{32}=\sqrt{a_{23}a_{32}},\end{aligned}$$
(8.14)

(8.10)\(_2\) becomes

$$\begin{aligned} \displaystyle \frac{d{\mathbf {V}}}{dt}={\mathcal {L}}{\mathbf {V}},\quad {\mathcal {L}}=\left\| \begin{array}{c@{\quad }c@{\quad }c} a_{11}&{}\sqrt{a_{12}a_{21}}&{}\sqrt{a_{13}a_{31}}\\ \sqrt{a_{12}a_{21}}&{}a_{22}&{}\sqrt{a_{23}a_{32}}\\ \sqrt{a_{13}a_{31}}&{}\sqrt{a_{23}a_{32}}&{}a_{33} \end{array}\right\| \end{aligned}$$
(8.15)

If \(a_{12}a_{21}=0\), (8.13)\(_1\) holds and \(\left\{ \delta ^2=\displaystyle \frac{a_{31}}{a_{13}},\,\left( \displaystyle \frac{\delta }{\mu }\right) ^2=\displaystyle \frac{a_{32}}{a_{23}}\right\} \Leftrightarrow \delta ^2=\displaystyle \frac{a_{31}}{a_{13}},\,\mu ^2=\displaystyle \frac{a_{31}a_{23}}{a_{13}a_{32}}\) and

$$\begin{aligned} \displaystyle \frac{d{\mathbf {U}}}{dt}={\mathcal {L}} {\mathbf {U}},\quad {\mathcal {L}}=\left\| \begin{array}{c@{\quad }c@{\quad }c} a_{11}&{}0&{}\sqrt{a_{13}a_{31}}\\ 0&{}a_{22}&{}\sqrt{a_{23}a_{32}}\\ \sqrt{a_{13}a_{31}}&{}\sqrt{a_{23}a_{32}}&{}a_{33} \end{array}\right\| . \end{aligned}$$

8.3 Quaternary symmetrizable systems

Let

$$\begin{aligned} \left\{ \begin{array}{l} n=4,\,\,a_{ij}a_{ji}>0,\,\,i\ne j,\, a_{12}a_{23}a_{31}=a_{21}a_{32}a_{13},\\ a_{12}a_{24}a_{41}=a_{21}a_{42}a_{14},\,\,a_{13}a_{34}a_{41}=a_{31}a_{43}a_{14}. \end{array}\right. \end{aligned}$$
(8.16)

Then Lis symmetrizable and

$$\begin{aligned} \displaystyle \frac{d{\mathbf {u}}}{dt}=L{\mathbf {V}} \,\, \text{ is } \text{ equivalent } \text{ to }\,\,\displaystyle \frac{d{\mathbf {V}}}{dt}={\mathcal {L}}{\mathbf {V}}, \end{aligned}$$

with

$$\begin{aligned} {\mathcal {L}}=\left\| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{11}&{}\sqrt{a_{12}a_{21}}&{}\sqrt{a_{13}a_{31}}&{}\sqrt{a_{14}a_{41}}\\ \sqrt{a_{12}a_{21}}&{}a_{22}&{}\sqrt{a_{23}a_{32}}&{}\sqrt{a_{24}a_{42}}\\ \sqrt{a_{13}a_{31}}&{}\sqrt{a_{23}a_{32}}&{}a_{33}&{}\sqrt{a_{34}a_{43}}\\ \sqrt{a_{14}a_{41}}&{}\sqrt{a_{24}a_{42}}&{}\sqrt{a_{34}a_{43}}&{}a_{44} \end{array}\right\| \end{aligned}$$
(8.17)

Proof

The proof is obtained following step by step the procedure given in 8.2. \(\square \)

Remark 3

Following step by step the previous procedure, for any \(1<m\le n\), one finds the requests on the entries \(a_{ij}\) to be added to \(\{a_{ij}a_{ji}>0, i, j=1,2,\cdots ,m\}\) in order to guarantee the symmetrizability of a \(m\times m\) matrix L.

9 Applications

9.1 Cournot triopoly game

Oligopoly theory studies the competitions between firms producing the same good [5]. Starting from the pioneering works of Cournot [6], this theory is one of the most intensively areas of mathematical economy. We refer to [7] for the general setting of the theory and the many contributions existing in the international literature. We confine ourselves to the basic setting of the theory.

Let G be the good and let be \(F_k,\,(k=1,2,\cdots , n)\), the firms producing G;  \(x_k\), the output quantity of \(F_k\);  p, the price (inverse demand) of G; \(C_k=c_kx^2_k\), \(c_k=\)positive constant, the cost function of \(F_k\); \(\varPi _k=px_k-C_k\), the profit of \(F_k\) and assume that:

  1. (1)

    the price p depends on all the good products

    $$\begin{aligned} p=f(Q),\qquad Q=\displaystyle \sum _{k=1}^n x_k; \end{aligned}$$
    (9.1)
  2. (2)

    p is a linear non-increasing function of Q

    $$\begin{aligned} p=a-bQ, \end{aligned}$$
    (9.2)

    with a, b positive constants;

  3. (3)

    the profit \(\varPi _k\) of \(F_k\) be given by

    $$\begin{aligned} \varPi _k=px_k-C_k=px_k-c_kx^2_k=x_k(p-c_kx_k)=x_k\left[ a-b\displaystyle \sum _{j=1}^n x_j-c_kx_k\right] .\nonumber \\ \end{aligned}$$
    (9.3)

The value of outputs maximizing the profit is

$$\begin{aligned} x_k=r_k(x_j)=\max _{x_k}\varPi _k\Leftrightarrow {\left\{ \begin{array}{ll} \displaystyle \frac{\partial \varPi _k}{\partial x_k}=a-b\displaystyle \sum _{j=1,j\ne k}^nx_j-2bx_k-2c_kx_k=0,\\ \displaystyle \frac{\partial ^2\varPi _k}{\partial x_k^2}=-2(b+c_k)<0 \end{array}\right. } \end{aligned}$$
(9.4)

It is easily found that

$$\begin{aligned} x_k=\displaystyle \frac{1}{2(b+c_k)}\left( a-b\displaystyle \sum _{j=1, j\ne k}^n x_j\right) . \end{aligned}$$
(9.5)

The expectations are said to be homogeneous when the firms (players) use the same strategy to decide their outputs in the market; heterogeneous when the firms use different strategies to decide their outputs in the market.

Let \(n=3\) (triopoly game) and let the players use different strategies.

  1. (1)

    The first player \(F_1\) does not have a complete knowledge of the demand function of the market and builds his output on the basis of the expected marginal profit \(\displaystyle \frac{\partial \varPi _k}{\partial x_k}\).

Then the discrete dynamical equation of \(F_1\) is

$$\begin{aligned} x_1(t+1)-x_1(t)=\alpha x_1\displaystyle \frac{\partial \varPi _1}{\partial x_1}, \end{aligned}$$
(9.6)

with \(\alpha \) positive parameter (relative speed adjustment), based on a bounded rationality. It follows that

$$\begin{aligned} x_1(t+1)-x_1(t)=\alpha x_1[a-2(b+c_1)x_1-b(x_2+x_3)]. \end{aligned}$$
(9.7)

Assuming that the second players \(F_2\) thinks with adaptive expectation i.e. he computes his outputs with weights between his last output and his reaction function \(r_2(x_1,x_3)\), one has

$$\begin{aligned} x_2(t+1)-x_2(t)=-\nu x_2+\displaystyle \frac{\nu }{2(b+c_2)}[a-b(x_2+x_3)], \end{aligned}$$
(9.8)

\(\nu \in [0,1]\) speed adjustment of the adaptive player.

Finally let \(F_3\) be a “naive player” i.e. he computes his outputs using the reaction function (9.4) (without introducing any speed of adjustment)

$$\begin{aligned} x_3(t+1)-x_3(t)=-x_3(t)+\displaystyle \frac{1}{2(b+c_3)}[a-b(x_1+x_2)]. \end{aligned}$$
(9.9)

Then the discrete triopoly game model is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1(t+1)-x_1(t)=\alpha x_1 \left[ a-2(b+c_1)x_1-b(x_2+x_3)\right] ,\\ x_2(t+1)-x_2(t)=-\nu x_2 +\displaystyle \frac{\nu }{2(b+c_2)}\left[ a-b(x_1+x_3)\right] ,\\ x_3(t+1)-x_3(t)=-x_3 +\displaystyle \frac{1}{2(b+c_3)}\left[ a-b(x_1+x_2)\right] \end{array}\right. } \end{aligned}$$
(9.10)

and the continuous triopoly game model is given by the ternary ADS of ODE

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{dx_1}{dt}=\alpha x_1 \left[ a-2(b+c_1)x_1-b(x_2+x_3)\right] ,\\ \displaystyle \frac{dx_2}{dt}=-\nu x_2 +\displaystyle \frac{\nu }{2(b+c_2)}\left[ a-b(x_1+x_3)\right] ,\\ \displaystyle \frac{dx_1}{dt}=-x_3 +\displaystyle \frac{1}{2(b+c_3)}\left[ a-b(x_1+x_2)\right] \end{array}\right. } \end{aligned}$$
(9.11)

The equilibrium points of (11.11) [and (11.10)] are

$$\begin{aligned} E_1=\left( 0, \displaystyle \frac{a(b+2c_3)}{3b^2+4b(c_2+c_3)+4c_2c_3},\displaystyle \frac{a(b+2c_2)}{3b^2+4b(c_2+c_3)+4c_2c_3}\right) \end{aligned}$$
(9.12)

and the Nash equilibrium—in which each firm has the expected profit

$$\begin{aligned} {\left\{ \begin{array}{ll} E_2=\left( \displaystyle \frac{a[b^2+2b(c_2+c_3)+4c_2c_3]}{{\mathcal {A}}}, \displaystyle \frac{a[b^2+2b(c_1+c_3)+4c_1c_3]}{{\mathcal {A}}},\right. \\ \left. \displaystyle \frac{a[b^2+2b(c_1+c_2)+4c_1c_2]}{{\mathcal {A}}}\right) \end{array}\right. } \end{aligned}$$
(9.13)

with

$$\begin{aligned} {\mathcal {A}}=2[2b^3+3b^2(c_1+c_2+c_3)+4b(c_1c_2+c_2c_3+c_1c_3)+4c_1c_2c_3] \end{aligned}$$
(9.14)

Setting

$$\begin{aligned} x_i={\bar{x}}_i+Y_i \end{aligned}$$
(9.15)

(11.11) gives

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{dY_1}{dt}=\alpha ({\bar{x}}_1+Y_1) [a-2(b+c_1)({\bar{x}}_1+Y_1)-b({\bar{x}}_2+{\bar{x}}_3)-b(Y_2+Y_3)],\\ \\ \displaystyle \frac{dY_2}{dt}=-\nu ({\bar{x}}_2+Y_2)+\displaystyle \frac{\nu }{2(b+c_2)}[a-b({\bar{x}}_1+{\bar{x}}_3)-b(Y_1+Y_3)],\\ \\ \displaystyle \frac{dY_3}{dt}=-({\bar{x}}_3+Y_3)+\displaystyle \frac{1}{2(b+c_3)}[a-b({\bar{x}}_1+{\bar{x}}_2)-b(Y_1+Y_2)] \end{array}\right. } \end{aligned}$$
(9.16)

Linearizing, one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{dY_1}{dt}=\alpha {\bar{x}}_1 [a-2(b+c_1)({\bar{x}}_1+Y_1)-b({\bar{x}}_2+{\bar{x}}_3)-b(Y_2+Y_3)]+\\ \\ +\alpha Y_1[a-2(b+c_1){\bar{x}}_1-b({\bar{x}}_2+{\bar{x}}_3)],\\ \\ \displaystyle \frac{dY_2}{dt}=-\nu Y_2+\displaystyle \frac{\nu }{2(b+c_2)}[a-b(Y_1+Y_3)],\\ \\ \displaystyle \frac{dY_3}{dt}=-Y_3+\displaystyle \frac{1}{2(b+c_3)}[-b(Y_1+Y_2)] \end{array}\right. } \end{aligned}$$
(9.17)

9.1.1 Linear stability of \(E_1\)

Setting

$$\begin{aligned} {\mathbf {X}}=E_1+{\mathbf {Y}},\qquad E_1=(0,{\bar{x}}_1, {\bar{x}}_2), \end{aligned}$$
(9.18)

one has

$$\begin{aligned} \displaystyle \frac{d{\mathbf {Y}}}{dt}=L{\mathbf {Y}}, \end{aligned}$$
(9.19)

with

$$\begin{aligned} L=\left( \begin{array}{c@{\quad }c@{\quad }c} \alpha [a-b({\bar{x}}_2+{\bar{x}}_3)]\,\,&{}\,\,0\,\,&{}\,\,0\,\,\\ -\displaystyle \frac{\nu b}{2(b+c_2)}\,\,&{}\,\,-\nu \,\,&{}\,\,-\displaystyle \frac{\nu b}{2(b+c_2)}\,\,\\ -\displaystyle \frac{b}{2(b+c_3)}\,\,&{}\,\,-\displaystyle \frac{b}{2(b+c_3)}\,\,&{}\,\,-1\,\, \end{array}\right) \end{aligned}$$
(9.20)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \texttt {I}_1=\alpha [a-b({\bar{x}}_2+{\bar{x}}_3)-(1+\nu )],\\ \texttt {I}_2=-\alpha [a-b({\bar{x}}_2+{\bar{x}}_3)](1+\nu )+\nu \displaystyle \frac{3b^2+4b(c_2+c_3)+4c_2c_3}{4(b+c_2)(b+c_3)},\\ \texttt {I}_3=\alpha \nu [a-b({\bar{x}}_2+{\bar{x}}_3)]\displaystyle \frac{3b^2+4b(c_2+c_3)+4c_2c_3}{4(b+c_2)(b+c_3)} \end{array}\right. } \end{aligned}$$
(9.21)

Since

$$\begin{aligned} a-b({\bar{x}}_2+{\bar{x}}_3)=a\displaystyle \frac{b^2+2b(c_2+c_3)+4c_2c_3}{3b^2+4b(c_2+c_3)+4c_2c_3} \end{aligned}$$
(9.22)

one has

$$\begin{aligned} \texttt {I}_3>0\,\,\,\Leftrightarrow \,\,\, E_1 \text{ is } \text{ unstable }\,\,\forall (a.b.c_1,c_2,c_3,\alpha , \nu ). \end{aligned}$$
(9.23)

9.1.2 Linear stability of (Nash) equilibrium point \(E_2\)

Setting

$$\begin{aligned} {\mathbf {X}}=E_2+{\mathbf {Z}} \end{aligned}$$
(9.24)

one has

$$\begin{aligned} \displaystyle \frac{d{\mathbf {Z}}}{dt}=L{\mathbf {Z}} \end{aligned}$$
(9.25)

with

$$\begin{aligned} L=\left( \begin{array}{c@{\quad }c@{\quad }c} -2\alpha (b+c_1)\bar{{\bar{x}}}_1\quad &{}-\alpha b\bar{{\bar{x}}}_1\quad &{}-\alpha b\bar{{\bar{x}}}_1\\ -\displaystyle \frac{\nu b}{2(b+c_2)}\quad &{}-\nu \quad &{}-\displaystyle \frac{\nu b}{2(b+c_2)}\\ -\displaystyle \frac{b}{2(b+c_3)}\quad &{}-\displaystyle \frac{b}{2(b+c_3)}\quad &{}-1 \end{array} \right) , \end{aligned}$$
(9.26)

one easily verifies that

$$\begin{aligned} {\left\{ \begin{array}{ll} a_{ij}a_{ji}>0,\\ a_{12}a_{23}a_{31}=a_{13}a_{21}a_{32}. \end{array}\right. } \end{aligned}$$
(9.27)

Hence: \(L(E_2)\) is symmetrizable, the eigenvalues are real numbers and steady bifurcation occurs at\(\texttt {I}_3=0\), with \(\texttt {I}_3\) given by

$$\begin{aligned} \texttt {I}_3= & {} \alpha b^2\nu \left[ \displaystyle \frac{1}{2(b+c_3)}\left( \displaystyle \frac{b}{2(b+c_2)}+1\right) + \displaystyle \frac{1}{2(b+c_2)}\left( 1-\displaystyle \frac{b}{2(b+c_3)}\right) \right] \bar{{\bar{x}}}_1\nonumber \\&+ -2\alpha \nu (b+c_1)\bar{\bar{ x}}_1\left( 1-\displaystyle \frac{b^2}{4(b+c_2)(b+c_3)}\right) \end{aligned}$$
(9.28)

9.2 Hopf bifurcations in rotatory thermal hydrodynamic

The linear stability of the thermal conduction in a horizontal layer \(\texttt {L}\) heated from below, rotating uniformly about a vertical axis—in the free-free boundary case—is governed by the stability of the zero solution of the ternary ADS [8]

$$\begin{aligned} \displaystyle \frac{d}{dt} \left( \begin{array}{l} X_1\\ X_2\\ X_3 \end{array}\right) =L\left( \begin{array}{l} X_1\\ X_2\\ X_3 \end{array}\right) \end{aligned}$$
(9.29)

with

$$\begin{aligned} L=\left( \begin{array}{c@{\quad }c@{\quad }c} -P_r(a^2+\pi ^2)&{} \displaystyle \frac{P_r{\mathcal {T}}}{a^2+\pi ^2}&{}\displaystyle \frac{a^2P_r R}{a^2+\pi ^2}\\ -P_r{\mathcal {T}}\pi ^2&{}-P_r(a^2+\pi ^2)&{}0\\ R&{}0&{}-(a^2+\pi ^2) \end{array}\right) \end{aligned}$$
(9.30)

with \(a^2, P_r, R, {\mathcal {T}}\) non-negative parameters [9,10,11].

The spectral equation is

$$\begin{aligned} \lambda ^3-\texttt {I}_1\lambda ^2+\texttt {I}_2\lambda -\texttt {I}_3=0, \end{aligned}$$
(9.31)

with the invariants \(\texttt {I}_{r}, (r=1,2,3)\), given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \texttt {I}_{1}=-(2P_r+1)\xi ,\,\texttt {I}_{2}=\displaystyle \frac{a^2P_r}{\xi } \left[ \displaystyle \frac{(2+P_r)\xi ^3+P_r{\mathcal {T}}^2\pi ^2}{a^2}\right] ,\\ \\ \texttt {I}_{3}=a^2P_r\left[ R^2-\displaystyle \frac{\xi ^3+{\mathcal {T}}^2 \pi ^2}{a^2}\right] ,\,\xi =a^2+\pi ^2 \end{array}\right. } \end{aligned}$$
(9.32)

and, via the Hurwitz criterion, setting

$$\begin{aligned} {\left\{ \begin{array}{ll} R_{2}=\displaystyle \min _{a^2\in {\mathbb {R}}^+}\displaystyle \frac{(2+P_r)(a^2+\pi ^2)^3+P_r{\mathcal {T}}^2\pi ^2}{a^2},\\ \\ R_{3}=\displaystyle \min _{a^2\in {\mathbb {R}}^+}\displaystyle \frac{(a^2+\pi ^2)^3+{\mathcal {T}}^2\pi ^2}{a^2} \end{array}\right. } \end{aligned}$$
(9.33)

the conditions

$$\begin{aligned} R^2-R_{2}<0,\quad R^2-R_{3}<0, \end{aligned}$$
(9.34)

are necessary stability conditions while

$$\begin{aligned} R^2-R_{2}<0,\quad R^2-R_{3}<0,\quad R^2-R_{4}<0, \end{aligned}$$
(9.35)

with \(R_{4}\) lowest \(R^2\) such that \(\texttt {I}_1\texttt {I}_2-\texttt {I}_3=0\), and

$$\begin{aligned} R^2<\min (R_{2}, R_{3}) \end{aligned}$$
(9.36)

is necessary for the stability. On the other hand \(R^2=R_{3}\Leftrightarrow \texttt {I}_3=0\) and \(\texttt {I}_3=0\) implies the existence of a zero solution of (9.31). then it follows that \(R_{3}<R_{2}\) implies steady bifurcation at \(R^2=R_{3}\) and Hopf bifurcation can occur only for \(R_{2}<R_{3}\) at \(R^2<R_{2}\). One easily verifies that \(P_r<1\) is necessary for \(R_{2}<R_{3}\) and that, setting

$$\begin{aligned} F_2=(2+P_r)\xi ^3+P_r{\mathcal {T}}^2\pi ^2,\,\,F_3=\xi ^3+{\mathcal {T}}^2\pi ^2, \end{aligned}$$
(9.37)

one has [8]

$$\begin{aligned} {\left\{ \begin{array}{ll} F_2-F_3\le 0\,\,\Leftrightarrow \,\,\xi ^3\le \xi ^3_*=\displaystyle \frac{1-P_r}{1+P_r}{\mathcal {T}}^2\pi ^2,\\ \\ \displaystyle \frac{d(F_2-F_3)}{d\xi ^3}=1+P_r>0. \end{array}\right. } \end{aligned}$$
(9.38)

In view of

$$\begin{aligned} (F_2-F_3)_{(\xi =\xi _*)}=0 \end{aligned}$$
(9.39)

and (9.38)\(_2\), it follows that

$$\begin{aligned} (F_2-F_3)_{(a^2=0)}<0. \end{aligned}$$
(9.40)

Then (9.39)–(9.40) are necessary and sufficient for having \(R_{C_2}<R_{C_3}\). One easily verifies that the bifurcation number, i.e. the threshold that \({\mathcal {T}}^2\) has to cross for the onset of Hopf bifurcation, is given by

$$\begin{aligned} {\mathcal {T}}_c=\displaystyle \frac{1+P_r}{1-P_r}\pi ^4 \end{aligned}$$
(9.41)

and one has that: The thermal conduction i the rotating layer\(\texttt {L}\):

a):

can be stable only if \(R^2<(R_{2}, R_{3})\);

b):

the inequality \(R_{2}<R_{3}\) is equivalent to

$$\begin{aligned} {\mathcal {T}}^2>{\mathcal {T}}_c>0 \end{aligned}$$
(9.42)
c):

instability occurs via Hopf bifurcation if and only if (9.42) holds and occurs at \(R^2<R_{2}\) given by the lowest positive root of \(\texttt {I}_1\texttt {I}_2-\texttt {I}_3=0\)

d):

instability occurs via steady bifurcation at \(R^2=R_{3}\) for

$$\begin{aligned} P_r\ge 1 \end{aligned}$$
(9.43)

and for

$$\begin{aligned} P_r<1,\quad {\mathcal {T}}\le {\mathcal {T}}_c. \end{aligned}$$
(9.44)

As concerns the critical value of \(a^2\) at which the Hopf bifurcation occurs, being

$$\begin{aligned} {\left\{ \begin{array}{ll} \texttt {I}_1\texttt {I}_2=\texttt {I}_3\,\Leftrightarrow \, 2P_rR^2=\displaystyle \frac{(1+P_r)(a^2+\pi ^2)^3-(1-P_r){\mathcal {T}}^2\pi ^2}{a^2},\\ \\ \displaystyle \frac{d(2P_rR^2)}{da^2}=0\,\Leftrightarrow \, 2(a^2+\pi ^2)^3-3\pi ^2(a^2+\pi ^2)^2+\displaystyle \frac{1-P_r}{1+P_r}{\mathcal {T}}^2\pi ^2=0 \end{array}\right. } \end{aligned}$$
(9.45)

one has that the Hopf bifurcation occurs at

$$\begin{aligned} R^2=R_{4}= \displaystyle \frac{1}{2P_r}\displaystyle \frac{(1+P_r)(a^2_{c4}+\pi ^2)^3-(1-P_r){\mathcal {T}}^2\pi ^2}{a^2_{c4}}, \end{aligned}$$
(9.46)

with \(a^2_{c4}\) lowest positive root of the cubic equation

$$\begin{aligned} 2(a^2+\pi ^2)^3-3\pi ^2(a^2+\pi ^2)^2+\displaystyle \frac{1-P_r}{1+P_r}{\mathcal {T}}^2\pi ^2=0. \end{aligned}$$
(9.47)

10 Discussion, final remarks and perspectives

  1. (i)

    The paper concerns the onset of bifurcations in binary, ternary and quaternary ADS;

  2. (ii)

    Conditions necessary and sufficient for the onset of Hopf bifurcations, in closed form, are furnished;

  3. (iii)

    Hopf–Steady, Double-Hopf and unsteady aperiodic bifurcations are taken into account;

  4. (iv)

    Conditions guaranteeing steady bifurcations, via symmetrizability of ADS, are furnished;

  5. (v)

    Continuous triopoly Cournot game ADS of mathematical economy is taken into account and its symmetrizability is found;

  6. (vi)

    Hopf bifurcations in rotatory thermal hydrodynamic, are characterized via the Taylor number instability threshold;

  7. (vii)

    Although conditions guaranteeing the onset of Hopf bifurcations have been furnished in many ADS {see, for instance, [9,10,11]}, as far as we know, the general analysis furnished in the present paper, appears new in the existing literature and could be generalized to multicomponent (\(n>4\)) ADS. In particular, in the case \(n>4\), when bifurcations depend on a parameter R, in view of (7.2)–(7.6) and properties 9–11, the following result holds:

    If and only if

    $$\begin{aligned} R<R_{12....n-1}=\displaystyle \min (R_1,R_2,\cdots , R_{n-1})<R_n, \end{aligned}$$
    (10.1)

    Hopf bifurcation occurs and occurs at\({\bar{R}}<R_{12\cdots {n-1}}\), lowest positive root of (7.2)\(_2\);

  8. (viii)

    If and how the results obtained in the present paper can be generalized to ADS of PDEs, is the scope of works in progress.