1 Introduction

In this paper we shall investigate the process of Turing pattern selection for the FitzHugh–Nagumo model (FN) that, in the adimensionalized form, writes as:

$$\begin{aligned} \frac{\partial u}{\partial t}= & {} \varGamma [-u^3+u-v]+\nabla ^2u, \end{aligned}$$
(1.1)
$$\begin{aligned} \frac{\partial v}{\partial t}= & {} \varGamma [\beta (u-\alpha v)]+d\nabla ^2v. \end{aligned}$$
(1.2)

In the above system \(u(\mathbf{x},t)\) and \(v(\mathbf{x},t)\) represent the densities of two species, being \(\mathbf{x}\in \varOmega \subset {\mathbb {R}}^n\). In the present paper we shall consider the cases \(n=1,2\), \(\varOmega \) being either a bounded interval or a rectangular domain. We shall impose homogeneous Neumann boundary conditions:

$$\begin{aligned} \mathbf{n}\cdot \nabla u(\mathbf{x},t)= \mathbf{n}\cdot \nabla v(\mathbf{x},t)=0 \qquad \text{ when }\quad \mathbf{x}\in \partial \varOmega , \end{aligned}$$

where \( \mathbf{n}\) is the outward normal of \(\partial \varOmega \).

The parameter \(\beta \) is the ratio of the characteristic time scales of the two species, \(\alpha \) controls the relative position and the number of intersections of the nullclines, d is the ratio between the diffusion coefficients of the two species, and the constant \(\varGamma \) regulates the domain size. All parameters are non negative.

The FN equations were initially derived as a mathematical simplification of the Hodgkin-Huxley model to describe the flow of an electric current through the surface membrane of a nerve fiber [14, 23]. In the resulting reaction–diffusion system u represents the electric potential, v a recovery variable and the diffusion term appears only in the equation for u (therefore \(d=0\)).

More recently, the FN system has appeared in the modeling of population dynamics. In [33] it has been shown that the local dynamics of phytoplankton and zooplankton can be described with a simple ODE model having a mathematical structure analogous to the FN kinetics. In [5, 8, 34] the FN model has been employed to describe the excitable character of the dynamics in a predator–prey interaction. In the framework of population modeling diffusion of both species must be considered (therefore \(d>0\)), with the consequence that the diffusion term appears in both equations of the FN system.

In this paper we shall be mainly concerned with the pattern forming properties of the FN equations. Reaction–diffusion systems, with diffusion and cross-diffusion terms, have been largely adopted to describe the spontaneous formation of inhomogeneous structures in many contexts [3, 7, 10, 12, 15, 21, 27]; however the capability of the FN equations to generate, through Turing bifurcation, coherent structures, has been addressed only recently, see [41], where the driving mechanism is classical diffusion, and [24], where super-diffusive effects are considered. In [24, 41] the authors consider the degenerate case, namely when the bifurcation occurs through a multiple eigenvalue, and derive the amplitude equations corresponding to the resonance of three active modes. This produces the occurrence of striped, hexagonal or mixed structure patterns, which are widely studied and often observed in many reaction–diffusion systems. Stationary squares are rarely found in experiments and simulations and are usually unstable; however, square aggregates, during the last 10/15 years have been experimentally found in a variety of systems, starting from fluid dynamics, but also in reaction–diffusion systems [26, 36, 37]. The aim of this paper is to show that the FN system on a planar domain supports a wider scenario of stationary extended structures than found in [24, 41]: we first consider the case when the instability is degenerate non-resonant and demonstrate that the pattern selection process can yield stable square patterns. We also derive the amplitude equations for mixed-mode and super-square patterns, which we prove to be unstable. Secondly, we investigate the pattern formation process when the initial datum is a localized circularly symmetric perturbation of the uniform state and derive the evolution equation of the outcoming target pattern.

The paper is organized as follows: in Sect. 2 we concisely derive the conditions for diffusion driven instability and, through a weakly nonlinear (WNL) analysis, derive the normal form of the bifurcation on a one dimensional spatial domain. In Sect. 3 the analysis focuses on 2D rectangular domains: the amplitude equations are derived when the bifurcation is degenerate non resonant and the emergence of target patterns is addressed through a matched asymptotic expansion. For the reader’s convenience, an Appendix has been added where the details of the 2D WNL analysis are reported.

2 Instability analysis and one dimensional patterns

In this section we derive the conditions for the onset of Turing instability for the system (1.1)–(1.2). If \(\alpha < 1\), the system admits a unique steady state solution \({\bar{E}}\equiv (0, 0)\). Linearizing the system (1.1)–(1.2) around the steady state \({\bar{E}}\), we get:

$$\begin{aligned} \frac{\partial \mathbf {w}}{\partial t}={\mathcal {L}}\mathbf {w}, \qquad {\mathrm{with}}\qquad \mathbf {w}=\left( \begin{array}{c} u\\ v \end{array}\right) , \end{aligned}$$
(2.1)

and:

$$\begin{aligned} {\mathcal {L}}=\varGamma K\mathbf {w}+D\nabla ^2,&\qquad K=\left( \begin{array}{cc} 1&{}\quad -1\\ \beta &{}\quad -\alpha \beta \end{array}\right) ,&\qquad \quad D=\left( \begin{array}{cc} 1&{}\quad 0\\ 0&{}\quad d \end{array}\right) . \end{aligned}$$
(2.2)

Looking for solutions of the form \(e^{\lambda t+ikx}\) leads to the following dispersion relation:

$$\begin{aligned} \lambda ^2+g\left( k^2\right) \lambda + h\left( k^2\right) =0, \end{aligned}$$
(2.3)

where:

$$\begin{aligned} h\left( k^2\right)= & {} \det (D)k^4-\varGamma (K_{11}D_{22}+K_{22}D_{11})k^2+\varGamma ^2\det (K)\nonumber \\= & {} dk^4+\varGamma (\alpha \beta -d)k^2+\varGamma ^2(\alpha \beta -1), \end{aligned}$$
(2.4)
$$\begin{aligned} g\left( k^2\right)= & {} k^2{\mathrm{tr}}(D)-\varGamma {\mathrm{tr}}(K)\nonumber \\= & {} k^2(1+d)+\varGamma (\alpha \beta -1). \end{aligned}$$
(2.5)

The conditions for diffusion driven instability require that the steady state solution must be linearly stable with respect to uniform-in-space perturbations and unstable with respect to non-homogeneous perturbations, namely \(\mathfrak {R}(\lambda (k))>0\) for some \(k\ne 0\). Choosing the diffusion coefficient d as the bifurcation parameter and imposing the marginality condition

$$\begin{aligned} \min h(k^2)=0, \end{aligned}$$

one finds the following values for the bifurcation parameter \(d_c\) and the critical wave number \(k_c\):

$$\begin{aligned} d_c=\beta \left( 2\sqrt{1-\alpha }+2-\alpha \right) , \qquad k_c^2=-\frac{\varGamma (\alpha \beta -d)}{2\det (D)}. \end{aligned}$$
(2.6)

It is straightforward to prove the following

Theorem 1

(Turing instability) Let \(\alpha < 1\) and let \(\beta >{1}/{\alpha }\), then the steady state \({\bar{E}}=(0, 0)\) exhibits a Turing bifurcation at \(d=d_c\).

Notice how Theorem 1 implies, for the destabilization of the homogeneous equilibrium, the classical condition on the diffusion parameter \(d>1\).

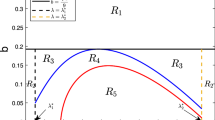
In Fig. 1a we report, for different values of \(\alpha \), the Turing instability region: notice that the effect of increasing \(\alpha \) is to enlarge the Turing region.

Theorem 1 gives the necessary conditions for the system (1.1)–(1.2) to admit a finite k pattern-forming Turing instability, but they do not guarantee the emergence of spatial patterns. The pattern in fact will emerge only if the parameter \(\varGamma \) is large enough so that there exists at least one integer n so that \(k_1^2<\left( \frac{n}{2}\right) ^2<k_2^2\), where \(k_1\) and \(k_2\) are the roots of \(h(k^2)\) and \(n/2 \, (n\in {\mathbb {N}})\) are the modes allowed by the Neumann boundary condition on the interval \([0,2\pi ] \subset {\mathbb {R}}\).

In what follows we shall perform a WNL expansion based on the method of multiple scales aimed to predict the solution to the system (1.1)–(1.2) near criticality. The method of multiple scales is used to transform the original system into its normal form near the threshold [22, 30] and, when the bifurcation is supercritical, an asymptotic approximation, uniformly approximating the solution of the original system [28], is thus generated. We recast the system (1.1)–(1.2), separating the linear and the nonlinear terms, in the following form:

$$\begin{aligned} \frac{\partial \mathbf {w}}{\partial t}={\mathcal {L}}\mathbf {w}+{\mathcal {N}}\left( \mathbf {w}\right) , \qquad \text {where } \qquad {\mathcal {N}}\left( \mathbf {w}\right) =-\varGamma \left( \begin{array}{c} u^3\\ 0 \end{array}\right) , \end{aligned}$$
(2.7)

and \({\mathcal {L}}\) is the linear operator defined in (2.2). Introducing the control parameter \(\varepsilon ^2 =(d-d_c)/d_c\), we expand the solution \({\mathbf {w}}\):

$$\begin{aligned} \mathbf {w}= & {} \varepsilon \mathbf {w}_1+\varepsilon ^2\mathbf {w}_2+\varepsilon ^3\mathbf {w}_3+\varepsilon ^4\mathbf {w}_4+\varepsilon ^5\mathbf {w}_5+{\mathcal {O}}(\varepsilon ^6). \end{aligned}$$
(2.8)

Next to the threshold the instability evolves on a slow time scale, so that we define:

$$\begin{aligned} \begin{array}{cccc} T_1=\varepsilon t,&T_2=\varepsilon ^2 t,&T_3=\varepsilon ^3 t,&\ldots \end{array} \end{aligned}$$
(2.9)

Substituting the expansions (2.8) and (2.9) into the system (2.7), a sequence of equations for the coefficients \(\mathbf {w}_i\), one at each order in \(\varepsilon \), are obtained. The \(O(\varepsilon )\) linear problem is:

$$\begin{aligned} {\mathcal {L}}_c\mathbf {w}_1=0, \end{aligned}$$
(2.10)

where \({\mathcal {L}}_c\) is the linear operator \({\mathcal {L}}\) in (2.2) evaluated at \(d=d_c\). The solution to the problem (2.10) satisfying the Neumann boundary conditions is given by:

$$\begin{aligned} \mathbf {w}_1=A(T_1,T_2,\ldots )\varvec{\varrho }\cos (k_cx),\qquad \quad \varvec{\varrho }\in Ker\left\{ \varGamma K-k_c^2D^{(c)}\right\} , \end{aligned}$$
(2.11)

where \(A(T_1, T_2, \ldots )\) is still unknown and \({\varvec{\varrho }}=\left( 1,(\varGamma -k_c^2)/\varGamma \right) ^t\). The compatibility condition at \(O(\varepsilon ^2)\) is automatically satisfied imposing \(T_1=0\) and the corresponding problem at this order admits the solution \({\mathbf {w}}_2=0\).

Imposing the Fredholm alternative at \(O(\varepsilon ^3)\), one obtains the following Stuart–Landau equation, which regulates the time evolution of the amplitude A:

$$\begin{aligned} \frac{\partial A}{\partial T_2}=\sigma A- LA^3, \end{aligned}$$
(2.12)

where:

$$\begin{aligned} \sigma =\frac{{\text {d}}^{(2)}k_c^2\left( \varGamma ^2-k_c^4\right) }{\varGamma ^2\left( k_c^4-\beta \right) }, \qquad L=\frac{\frac{3}{4}\varGamma ^3\beta }{\beta \varGamma ^2-\left( \varGamma -k_c^2\right) ^2}. \end{aligned}$$
(2.13)

Proposition 2.1

(Supercritical Bifurcation) Under the hypotheses of the Theorem 1, L is positive and the Turing bifurcation is always supercritical.

Proof

Showing that \(L>0\) is equivalent to prove that:

$$\begin{aligned} \beta \varGamma ^2-\left( \varGamma -k_c^2\right) ^2>0. \end{aligned}$$
(2.14)

Substituting the value of the critical wave number \(k_c^2=-\frac{\varGamma \left( \alpha \beta -d_c\right) }{2d_c}\), into the inequality (2.14), it reduces to:

$$\begin{aligned} d_c^2+\alpha ^2\beta ^2+2\alpha \beta d_c-4\beta d_c^2<0. \end{aligned}$$
(2.15)

Using the hypotheses of Theorem 1, the following estimate is obtained:

$$\begin{aligned} d_c^2+\alpha ^2\beta ^2+2\alpha \beta d_c-4\beta d_c^2<d_c^2+d_c^2+2 d_c^2-4\beta d_c^2=4d_c^2\left( 1-\beta \right) . \end{aligned}$$
(2.16)

Moreover, from \(\alpha < 1\) it follows that \(\beta >1\), which completes the proof. \(\square \)

Since the Turing branch of stationary nonhomogeneous solutions bifurcates supercritically from the uniform steady state, the asymptotic amplitude of the arising pattern is predicted by the following Theorem:

Theorem 2

(Asymptotic Solution) Under the hypotheses of Proposition 2.1, and assume the distance from the bifurcation threshold to be small enough so that \({\bar{E}}\equiv (0,0)\) is unstable only to modes corresponding to the critical wave number \(k_c\). Then the emerging pattern solution of the system (1.1)–(1.2) writes:

$$\begin{aligned} {\mathbf {w}}=\varepsilon {\varvec{\varrho }}A_{\infty }\cos \left( k_cx\right) , \end{aligned}$$
(2.17)

where \( A_{\infty }=\sqrt{\frac{\sigma }{L}} \) is the stable equilibrium of the Stuart–Landau equation (2.12).

In Fig. 1b the comparison between the solution predicted by the WNL analysis and the numerical solution of the full system computed using spectral methods is shown, displaying a very good agreement of the two solutions.

Fig. 1
figure 1

a The Turing instability region in which we have fixed \(\alpha =0.5\) (light grey), \(\alpha =0.6\) (grey) and \(\alpha =0.7\) (dark grey). b Comparison between the numerical solution (solid line) of the reaction–diffusion system (1.1)–(1.2) and the solution predicted by the WNL analysis (dotted line). The parameters are chosen as \(\alpha =0.5\), \(\beta =2.1\), \(\varGamma =9.6567\), \(\varepsilon =0.1\)

Full size image

If the domain size is large with respect to the characteristic length of the pattern, one can observe the phenomenon of propagation of the pattern as a travelling wave along the physical domain. Taking into account in our analysis also the slow modulation of the spatial variable, we obtain that the time evolution of the envelope of the propagating pattern is described by the following real Ginzburg-Landau equation:

$$\begin{aligned} \frac{\partial A}{\partial T}=\sigma A-LA^3+\nu \frac{\partial ^2A}{\partial X^2}, \end{aligned}$$
(2.18)

where the \(\sigma \) and L are as in (2.13) and:

$$\begin{aligned} \nu =\frac{\varGamma ^2\left( \beta +d_c\right) \left( 1+2k_c\right) -d_ck_c^2\left( 2k_c^3+5k_c^2+4\varGamma \right) }{\varGamma ^2\beta +\varGamma ^2-k_c^4}. \end{aligned}$$
(2.19)

3 Two dimensional patterns

In this Section, performing a WNL analysis, we will investigate the existence and stability of Turing patterns on a rectangular domain \(\varOmega =[0, L_x] \times [0, L_y]\). The solutions to the linearized system in \(\varOmega \) are:

$$\begin{aligned}&{\mathbf {w}}=\sum _{m,n\in {\mathbb {N}}}\mathbf {f}_{mn}e^{\lambda (k^2_{mn})t}\cos \left( \phi x\right) \cos \left( \psi y\right) , \end{aligned}$$
(3.1)
$$\begin{aligned}&{\mathrm{with}}\qquad \phi =\frac{m\pi }{L_x},\quad \psi =\frac{n\pi }{L_y},\qquad {\mathrm{and}}\ m, n\, \, {\mathrm{integers}}, \end{aligned}$$
(3.2)

where \(\phi \) and \(\psi \) have the expressions in (3.1) in order to satisfy the Neumann boundary conditions, \(\mathbf {f}_{mn}\) are the Fourier coefficients of the initial conditions, and \(\lambda (k^2_{mn})\) are the eigenvalues derived by the dispersion relation (2.3) (see [29]). The value of the critical wavenumber \(k_c\) is obtained via linear stability analysis as in (2.6), however once substituted the expression (3.1) in the system (2.1), in a two dimensional domain we obtain that the following condition should be satisfied:

$$\begin{aligned} k^2_{c}=\phi ^2+\psi ^2. \end{aligned}$$
(3.3)

We will assume \(\varGamma \) such that there exists only one unstable wavenumber admissible for the Neumann boundary conditions. Depending on whether there exists one or two pairs of integers (m, n) such that the condition (3.3) holds, the Turing bifurcation is respectively regular or degenerate and the following characterization of supported patterns can be made [17]:

  1. (i)

    rolls and square-rhombic patterns when the bifurcation is regular;

  2. (ii)

    rolls, square and mixed-mode patterns when the bifurcation is degenerate and the non resonant conditions hold;

  3. (iii)

    rolls and hexagonal patterns when the bifurcation is degenerate and the resonant conditions hold.

Since the classification in (iii) has been already obtained in [24, 41], here we will deal with the cases (i) and (ii).

3.1 Regular bifurcation

If there exists a unique pair of integers (m, n) such that the condition (3.3) holds, the WNL analysis is quite similar to the 1D case described in Sect. 2, therefore we skip the details and give the following result:

Theorem 3

If:

  1. (i)

    there exists a unique pair of integers (m, n) such that (3.3) is satisfied;

  2. (ii)

    the coefficient L of the Stuart–Landau equation (2.12) is positive;

then the emerging pattern solution of the system (1.1)–(1.2) is:

$$\begin{aligned} {\mathbf {w}}=\varepsilon A_{\infty }{\varvec{\varrho }}\cos \left( \phi x\right) \cos \left( \psi y\right) , \end{aligned}$$
(3.4)

where \(A_{\infty }\) is the stable equilibrium of (2.12).

The patterns in (3.4) are rhombic structures, reducing to rolls, when \(\phi \) or \(\psi \) is zero, and square, when \(\phi =\psi \).

In the numerical test shown in Fig. 2a, we choose the parameters in such a way that \(k_c^2=25\). In the rectangular domain \([0,2\sqrt{2}\pi ]\times [0,2\pi ]\) the only pair satisfying the condition (3.3) is (0, 10). Since the Stuart–Landau equation admits a stable equilibrium, the emerging solution of the system (1.1)–(1.2) starting from a random periodic perturbation of \({\bar{E}}\) is the roll pattern in Fig. 2a. The square pattern in Fig. 2b corresponds to the choice of the system parameters such that \(k_c^2=32\) and (4, 4) is the only couple satisfying condition (3.3) in the domain \([0,\pi ]\times [0,\pi ]\).

Fig. 2
figure 2

a Rolls. The parameters are chosen as \(\alpha =0.9\), \(\beta =1.5\), \(\varGamma =104.06\), \(\varepsilon =0.01\). b Squares. The parameters are chosen as \(\alpha =0.1\), \(\beta =11\), \(\varGamma =65.731\), \(\varepsilon =0.1\)

Full size image

In the numerical test given in Fig. 3, the parameters are chosen in such a way that \(k_c^2=4\). In the domain \(L_x=L_y=16\sqrt{2}\pi \) the unique pairs of integers which satisfies the condition (3.3) is \((m,n)\equiv (32,32)\). Giving, as initial condition, a radially symmetric perturbation at the center of the domain, one can observe a transient where the perturbation radially spreads as a wave; when the pattern wave meets the boundary, square structures begin to emerge at the corner to subsequently invade the whole domain. The emerging solution is the square pattern predicted by the WNL analysis.

Fig. 3
figure 3

Square patterns invading the whole domain. The parameters are chosen as \(\alpha =0.5\), \(\beta =2.1\), \(\varGamma =9.6568542499\), \(\varepsilon =0.001\). The solution of the system (1.1)–(1.2) is shown at: a\(t=0\), b\(t=4000\), c\(t=8000\), d\(t=12000\), e\(t=19200\), f\(t=40000\)

Full size image

3.2 Non resonant degenerate bifurcation

Let us assume that the bifurcation is degenerate as two mode pairs \((m_i,n_i)\) satisfy the condition in (3.3). Moreover, the following non resonant conditions hold:

$$\begin{aligned} \begin{array}{lll} \phi _i+\phi _j\ne \phi _j&{} \mathrm{or\ }\psi _i-\psi _j\ne \psi _j\\ &{}\mathrm{and}\\ \phi _i-\phi _j\ne \phi _j&{} \mathrm{or\ }\psi _i+\psi _j\ne \psi _j. \end{array} \end{aligned}$$
(3.5)

Performing the WNL analysis (the details are given in Appendix A), at \(O(\varepsilon ^3)\) the compatibility condition leads to the following two coupled Stuart–Landau equations for the amplitudes \(A_i\) of the pattern:

$$\begin{aligned} \begin{aligned} \frac{d A_1}{d T}&=\sigma A_1-L_1A_1^3+\varOmega _1A_1A_2^2,\\ \frac{d A_2}{d T}&=\sigma A_2-L_2A_2^3+\varOmega _2A_1^2A_2, \end{aligned} \end{aligned}$$
(3.6)

where the explicit expressions of the coefficients \(\sigma \), \(L_i\) and \(\varOmega _i\) are given by (A.1) in Appendix A.

Theorem 4

Suppose the following hypotheses are satisfied:

  1. (i)

    the equilibrium \({\bar{E}}\) is unstable to modes corresponding to a unique eigenvalue \(k_c\);

  2. (ii)

    there exist two couples of integers \((m_i,n_i)\) such that (3.3) is satisfied;

  3. (iii)

    the corresponding \(\phi _i\) and \(\psi _i\) satisfy the non resonant conditions (3.5);

  4. (iv)

    the system (3.6) admits at least one stable equilibrium;

then the emerging pattern solution of the system (1.1)–(1.2) is:

$$\begin{aligned} {\mathbf {w}}=\varepsilon \left( A_{1\infty }{\varvec{\varrho }}\cos \left( \phi _1x\right) \cos \left( \psi _1y\right) +A_{2\infty }{\varvec{\varrho }}\cos \left( \phi _2x\right) \cos \left( \psi _2y\right) \right) , \end{aligned}$$
(3.7)

where \((A_{1\infty }, A_{2\infty })\) is the stable equilibrium of (3.6).

The system (3.6) admits the equilibria:

$$\begin{aligned} \begin{aligned}&P_1^\pm \equiv \left( \pm \sqrt{\frac{\sigma }{L_1}},0\right) ,\qquad P_2^\pm \equiv \left( 0,\pm \sqrt{\frac{\sigma }{L_2}}\right) , \\&P_3^{\pm ,\pm }\equiv \left( \pm \sqrt{\frac{\sigma \left( L_1+\varOmega _2\right) }{L_1L_2-\varOmega _1\varOmega _2}},\pm \sqrt{\frac{\sigma \left( L_2+\varOmega _1\right) }{L_1L_2-\varOmega _1\varOmega _2}}\right) , \end{aligned} \end{aligned}$$
(3.8)

which exist stable if:

$$\begin{aligned} P_1^\pm&:\ {\mathrm{if}}\, L_1>0\, {\mathrm{and}}\ L_1+\varOmega _2<0; \qquad P_2^\pm :\ {\mathrm{if}}\, L_2>0 \, {\mathrm{and}}\, L_2+\varOmega _1<0;\\ P_3^\pm&: \, {\mathrm{if}}\, L_1L_2-\varOmega _1\varOmega _2>0, L_1+\varOmega _2>0, L_2+\varOmega _1>0\\&\quad {\mathrm{and}}\, L_1\varOmega _1+L_2\varOmega _2+2L_1L_2<0. \end{aligned}$$

Notice that if \(P_1^\pm \) or \(P_2^\pm \) is stable the emerging pattern (3.7) has the rhombic structure described in the previous Sect. 3.1. If \(P_3^\pm \) is stable, the solution (3.7) is a mixed-mode pattern. From the expressions of the coefficients \(\sigma \), \(L_i\) and \(\varOmega _i\) in (A.1) it is easy to show that if \(P_1^\pm \) and \(P_2^\pm \) exist they are always stable, on the contrary if \(P_3^{\pm ,\pm }\) exists it is always unstable. Therefore, from the formula (3.7) it follows that only rhombic patterns can be supported by the system in this case and no mixed mode patterns can arise.

In Fig. 4, we show the evolution of the system starting from a random perturbation of the homogeneous steady state \({\bar{E}}\). Choosing the parameters as in the caption of Fig. 4, in the square domain \(L_x=L_y=4\pi \) the only unstable mode is \(k_c^2=13\) and there exists two couples of integers \(\left( m_1,n_1\right) \equiv \left( 8,12\right) \) and \(\left( m_2,n_2\right) \equiv \left( 12,8\right) \) satisfying the condition (3.3). According to the WNL prediction both \(P_1^\pm \) and \(P_2^\pm \) are stable and the expected solutions are the following square patterns:

$$\begin{aligned} {\mathbf {w}}^{(1)}=\varepsilon \left( A_{1\infty }{\varvec{\varrho }}\cos \left( 4x\right) \cos \left( 6y\right) \right) \quad {\mathrm{or}}\, {\mathbf {w}}^{(2)}=\varepsilon \left( A_{2\infty }{\varvec{\varrho }}\cos \left( 6x\right) \cos \left( 4 y\right) \right) . \end{aligned}$$
(3.9)

Which one of the above solutions is reached depends on the initial conditions. In the numerical test given in Fig. 4 the emerging solution is \({\mathbf {w}}^{(2)}\) in (3.9).

Fig. 4
figure 4

Emerging square patterns. The parameters are fixed as \(\alpha =0.2\), \(\beta =5.1\), \(\varGamma =27.535\), \(\varepsilon =0.01\). The numerical solution of the system (1.1)–(1.2) is shown at different times: a\(t=0\), b\(t=500\), c\(t=1000\), d\(t=2000\), e\(t=4000\), f\(t=10000\)

Full size image

In Fig. 5 the system parameters are chosen such that \(k_c^2=80\) is the most unstable mode, therefore in the square domain \(L_x=L_y=2\pi \), the homogeneous equilibrium \({\bar{E}}\) is unstable to the mode pairs \(\left( m_1,n_1\right) \equiv \left( 8,16\right) \) and \(\left( m_2,n_2\right) \equiv \left( 16,8\right) \). The WNL analysis predicts that the equilibria \(P_1^+\) and \(P_2^+\) exist stable, and the equilibrium \(P_3^+\) exists unstable, see Fig. 5c. The solution corresponding to the point \(P_3^+\):

$$\begin{aligned} {\mathbf {w}}= & {} \varepsilon {\varvec{\varrho }}\left( A_{1\infty }\cos \left( 4x\right) \cos \left( 8y\right) +A_{2\infty }\cos \left( 8x\right) \cos \left( 4 y\right) \right) \end{aligned}$$
(3.10)

is a particular mixed mode pattern called supersquare. Choosing as initial condition the supersquare pattern (3.10), in our simulation the emerging solution of the system (1.1)–(1.2) is the square pattern with amplitude given by the equilibrium \(P_2^+\).

Fig. 5
figure 5

The solution of the system (1.1)–(1.2), starting from the predicted unstable supersquare in a, evolves to the predicted stable square pattern in b. c The phase portrait of the amplitude system (3.6) shows the basin of attraction of the equilibria \(P_i^+ i=1,2\) corresponding to the square patterns. The parameters are \(\alpha =0.3\), \(\beta =3.5\), \(\varGamma =175.618\), \(\varepsilon =0.05\)

Full size image

3.3 Target patterns

In the numerical test shown in Fig. 3 we have observed that, until the effect of the boundary is not relevant, giving a small perturbation of the homogeneous equilibrium at the center of a square domain as initial condition, a concentric wave radially propagates from the center of the domain. Let us investigate the formation of this type of axisymmetric patterns, known as target patterns, see Fig. 6.

Fig. 6
figure 6

Target pattern. a Axisymmetric initial datum. b Target solution at \(t=10\). c Profile of the solution at \(t=10\). The parameters are: \(\alpha =0.5\), \(\beta =2.1\), \(\varGamma =9.6568542499\), \(\varepsilon =0.1\) and \(L_x=L_y=16\pi \)

Full size image

Target patterns are characterized by an amplitude in the core of the domain significantly larger than the one far from the core. This is due to two main reasons: the region of the physical domain close to the initial perturbation is more affected by the perturbation itself; moreover, close to the core, the effects of the curvature of the wave are not negligible. Introducing the radial coordinate \(r=\sqrt{x^2+y^2}\) and assuming radially symmetric solution, we perform the WNL analysis to approximate the solution close to the threshold. Being the domain size large with respect to the characteristic length of the pattern, we need to consider the slow modulation of the spatial variable \(R=\varepsilon r\). In this way, following a standard procedure, we recover the following Ginzburg-Landau equation for the amplitude A:

$$\begin{aligned} \frac{\partial A}{\partial t}=\nu \left( \frac{\partial ^2 A}{\partial R^2}+\frac{1}{R}\frac{\partial A}{\partial R}-\frac{A}{4R^2}\right) +\sigma A-LA^3 \end{aligned}$$
(3.11)

and the solution at the leading order can be written as:

$$\begin{aligned} {\mathbf {w}}=\varepsilon {\mathbf {w}}_{1}A \cos \left( k_c r\right) +{\mathcal {O}}\left( \varepsilon ^2\right) . \end{aligned}$$
(3.12)

At the center of the pattern the curvature of the solution can not be neglected and the Eq. (3.11) does not hold. It is well known that the solution at the core of the pattern is proportional to the zeroth-order Bessel function of the first kind and, through a linear analysis [20, 31] we get the following inner solution:

$$\begin{aligned} {\mathbf {w}}_I=C {\mathbf {w}}_{1}A J_0\left( k_c r\right) , \end{aligned}$$
(3.13)

where C is a constant which has to be determined. When \(r\rightarrow +\infty \) the following approximation holds:

$$\begin{aligned} J_0\left( k_c r\right) =\frac{1}{\sqrt{\pi k_c r}}\cos \left( k_cr\right) , \end{aligned}$$
(3.14)

thus the inner solution, when \(r\rightarrow +\infty \) should match to the solution (3.12). This means that C has to be of order \(\varepsilon ^{\frac{1}{2}}\) confirming that the amplitude of the solution at the core is larger than the amplitude far from it.

4 Conclusions

In this paper we have investigated the process of pattern formation in the FN reaction–diffusion model showing that the emerging pattern-forming solution can be successfully predicted by the amplitude equation formalism.

Here it follows some of the topics that, in the present paper, we have not addressed and we believe to be of interest. First we recall that the FN model also exhibits Hopf bifurcation: to get a better understanding of the FN dynamics it would be crucial to investigate the competition between the Turing and the Hopf instability, as done in [18]; in fact, a detailed study in a small neighborhood of the codimension-2 Turing–Hopf bifurcation point could reveal the emergence of non stationary patterns and chaotic behaviour [1, 4, 6, 13, 19, 35]. Second, we mention that, in some numerical tests, we have detected the formation of localized solutions, which have been found to be stationary or oscillatory [9, 25]. This, particularly for an excitable dynamic system like FN, is a very relevant topic, and a rigorous analysis of these phenomena will be the subject of future work. Third to study the wave instability arising in the FN model, the corresponding hyperbolic reaction–diffusion system [2, 12, 39] will be investigated. Finally, the effect of cross-diffusion [11, 16, 32, 38, 40] on pattern formation will be addressed.