1 Introduction

Investigations on nanoscale magnetic materials devoted to the design of high-performance spintronic devices have increased significantly in the last decades. Today, applications range from biosensors to microwave emitters and receivers, from logic devices to data storage media [1,2,3,4,5,6,7,8,9,10,11,12,13]. In particular, the possibility of controlling the propagation of magnetic domain walls (DWs) in ferromagnetic nanostrips has been receiving a lot of interest from both theoretical and technological viewpoints [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

DWs are local deformations of the magnetization which originate between two uniformly and oppositely magnetized regions. Under the action of external driving sources, such as magnetic fields or electric currents, a domain may undergo an expansion at expenses of the other that causes, in turn, the shift of the DW location along the nanostrip axis. However, the DW motion along single-layer nanostructures encounters some difficulties. Among them, the DW displacement is not always reproducible, the depinning from a thermally stable position is difficult and the maximum achievable velocity (in the low field or current regime) is limited by structural instability, generally referred to as Walker breakdown. A strategy recently used to overcome these problems consists of exploiting the combined effects of spin-transfer-torque (STT) and spin-orbit-torque (SOT) that have been found to simultaneously occur in trilayer systems heavy-metal/ferromagnet/metal-oxide traversed by a longitudinal electric current [11]. The STT originates when a spin-polarized current crosses a DW and transfers its angular momentum to the internal structure of the DW, thereby pushing it along the direction of the current flow [17,18,19].

On the other hand, spin-orbit interactions are caused by structural inversion asymmetry (SIA) and may give rise to different phenomena, such as Rashba and spin-Hall effects. In detail, the Rashba effect takes place when electrons flowing through a ferromagnet experience an electric field generated by an asymmetric crystal-field potential profile that originates when the ferromagnetic film is sandwiched between nonmagnetic high-Z metals (such as Pt, Au, or Pd) and a metal oxide (such as MgO or AlOx). From the reference frame of the electrons, this electric field translates into a magnetic field (the so-called Rashba field) due to relativistic effects. The Rashba field creates a non-equilibrium spin density of conduction electrons in the ferromagnet that, via exchange interactions, couples with the magnetic moment generating a torque.

The Spin-Hall effect originates when unpolarized electrons, flowing through a material characterized by a very high spin-orbit coupling (such as a heavy metal), undergo a separation across the thickness of the layer according to the direction of spin-polarization. Such a phenomenon, that leads to an accumulation of spins of opposite signs on opposing lateral boundaries, implies the conversion of a charge current into a transverse spin current. The absorption of this spin current by the adjacent ferromagnetic layer results in an additional transfer of spin-torque to the ferromagnet [9,10,11,12,13].

The capability of manipulating DW structures in trilayers with SIA has several advantages: facilitated depinning, higher stability and wider high-mobility regime. However, while these results have been proved experimentally [11], very few analytical results are available in literature [20]. In fact, the complexity of the governing Extended Landau–Lifshitz–Gilbert (ELLG) equation [14,15,16, 21, 22] generally prevents the possibility of obtaining exact analytical solutions. Therefore, the problem is generally tackled by using semi-analytical approaches [20] and/or numerical simulation tools [23].

The purpose of this work is to investigate analytically the DW dynamics in the abovementioned trilayer systems with SIA in order to provide an explicit (even though approximate) expression for the key quantities involved into the two characteristic dynamical regimes of DW motion, steady and precessional, taking place at low and high values of the external driving sources, respectively.

In our approach we make use of several simplifying hypotheses: the DW motion is one-dimensional and takes place along the major nanostrip axis; the Rashba effect gives rise to a field-like term and a spin-torque-like term whereas the Spin-Hall effect enters the equation via a spin-torque term only; the amplitudes of both Rashba and Spin-Hall effects are conceived to be small in such a way that the classical Walker solution is recovered [24] and, at the same time, the DW width is treated as a constant; effects arising from external magnetic fields and magnetoelastic interactions are neglected; dissipative effects are taken into account via a classical linear Gilbert damping term and a nonlinear rate-independent dry-friction term. In particular, this latter contribution allows the characterization of realistic magnetic devices as it mimics pinning effects arising from structural disorder (such as inhomogeneities, impurities, dislocations and crystallographic defects) [14,15,16, 25].

The manuscript is organized as follows.

In Sect. 2 we build up a 1D model based upon the ELLG equation for the description of the current-driven DW motion occurring in a thin ferromagnetic layer sandwiched between a heavy metal and a metal oxide. Particular emphasis is given to the role played by the abovementioned STT and SOT effects in both steady and precessional regimes.

In Sect. 3, we address numerical investigations in order to enable a direct comparison with literature data and to gain more insights into the observed DW dynamics.

Some concluding remarks are addressed in the last section.

2 The mathematical 1D micromagnetic model

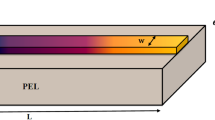
Let us consider a ferromagnetic (FM) nanostrip integrated in a trilayer structure exhibiting SIA, as sketched in Fig. 1. The sizes of the ultrathin elongated FM layer, length L, width w and thickness d, satisfy the constraint \(L>>w>\) d. This layer is traversed by an electric current density J that flows along the major axis \(\mathbf {e}_{x}\) and is assumed to be constant in time and uniform in space. The proximity of the FM with a heavy metal also generates a high perpendicular magnetocrystalline anisotropy which favors an out-of-plane magnetization configuration. As a consequence of that, we assume that two magnetic domains pointing along \(\pm \,\mathbf {e}_{z}\) are nucleated at the edges of the FM layer and the position of the resulting Bloch-type DW can be shifted along the nanostrip axis \(\mathbf {e}_{x}\) via the electric current (because of the geometrical confinement, we do not expect any variation along \(\mathbf {e}_{y}\) and \(\mathbf {e}_{z}\)). In other words, denoting with \(\mathbf {m}\) the unit magnetization vector, we look for solutions of the form:

$$\begin{aligned} \begin{aligned}\mathbf {m}= & {} \mathbf {m}(x,t) \\ \lim _{x\rightarrow \pm \infty }\mathbf {m}= & {} \mp \mathbf {e}_{z} \end{aligned} \end{aligned}$$
(1)

where x is the nanostrip axis coordinate and t is the time.

Fig. 1
figure 1

Schematics of the trilayer system consisting of a thin ferromagnetic nanostrip placed between a heavy metal and a metal oxide. Reference axes and geometrical sizes are also depicted

Full size image

To model the overall effects of the electric current on the magnetization, we thus consider a 1D model based upon the Landau–Lifshitz–Gilbert equation that includes, besides the usual precessional and damping terms, the current-induced STT and SOT contributions [14,15,16, 20,21,22]:

$$\begin{aligned} \overset{\bullet }{\mathbf {m}}\mathbf {=t}^{\textit{PRE}}+\mathbf {t}^{\textit{DISS}}+\mathbf {t} ^{\textit{STT}}+\mathbf {t}^{\textit{SOT}} \end{aligned}$$
(2)

where the over-dot denotes the partial time derivative.

The first term on the right-hand side of (2), \(\mathbf {t}^{\textit{PRE}}\), defines the undamped precessional torque induced by the effective magnetic field which, in turn, accounts for the contributions arising from demagnetizing \(\mathbf {h}^{\textit{dmg}}\), exchange \(\mathbf {h}^{\textit{exc}}\) and perpendicular magneto-crystalline anisotropy \(\mathbf {h}^{\textit{ani}}\) fields:

$$\begin{aligned} \mathbf {t}^{\textit{PRE}}=\gamma \left( \mathbf {h}^{\textit{dmg}}+\mathbf {h}^{\textit{exc}}+\mathbf {h} ^{\textit{ani}}\right) \wedge \mathbf {m} \end{aligned}$$
(3)

where \(\gamma = M_{S}\mu _{0}\gamma _{e}\) is a constant expressed in terms of saturation magnetization \(M_{S}\), magnetic permeability of the vacuum \(\mu _{0}\) and gyromagnetic ratio \(\gamma _{e}=ge/m_{e}\), being g the Landè factor, e the electron charge and \(m_{e}\) the electron mass. The fields appearing in (3) can be written as:

$$\begin{aligned} \begin{aligned} \mathbf {h}^{\textit{dmg}}&=-N_{x}\left( \mathbf {m} \cdot \mathbf {e}_{x}\right) \mathbf {e} _{x}-N_{y}\left( \mathbf {m} \cdot \mathbf {e}_{y}\right) \mathbf {e}_{y}-N_{z}\left( \mathbf {m} \cdot \mathbf {e}_{z}\right) \mathbf {e}_{z}\\ \mathbf {h}^{\textit{exc}}&=A\frac{\partial ^{2}\mathbf {m}}{\partial x^{2}} \\ \mathbf {h}^{\textit{ani}}&=\beta \left( \mathbf {m} \cdot \mathbf {e}_{z}\right) \mathbf {e} _{z} \end{aligned} \end{aligned}$$
(4)

where:

$$\begin{aligned} N_{x}+N_{y}+N_{z}=1{, \quad \quad \ }A=\frac{2A_{ex}}{\mu _{0}M_{S}^{2}} {, \quad \quad }\beta =\frac{2k_{u}}{\mu _{0}M_{S}^{2}} \end{aligned}$$
(5)

being \(N_{x},\) \(N_{y}\) and \(N_{z}\) the demagnetizing factors, whereas \( A_{ex} \) and \(k_{u}\) represent the exchange and the anisotropy constants of the material, respectively. In this model, we do not take into account effects arising from magnetostriction and external magnetic fields, because they do not contribute to SOT effects. An analysis of domain wall dynamics driven by these latter fields can be found in Refs. [8, 14,15,16].

The second term in (2), \(\mathbf {t}^{\textit{DISS}}\), accounts for the intrinsic dissipative phenomena. As widely discussed in previous works [14,15,16, 25], it includes the classical Gilbert damping torque [22] augmented by a non linear contribution arising from a rate-independent dry friction, namely:

$$\begin{aligned} \mathbf {t}^{\textit{DISS}}=\alpha _{G}\left( {\mathbf {m}\wedge \overset{\bullet }{ \mathbf {m}}}\right) +\mathbf {m}\wedge \left( \gamma \alpha _{D}|\overset{ \bullet }{\mathbf {m}}|^{-1}{\overset{\bullet }{\mathbf {m}}}\right) \end{aligned}$$
(6)

where the phenomenological dimensionless parameters \(\alpha _{G}\) and \( \alpha _{D}\) describe the strength of linear and nonlinear dissipation, respectively.

The third term appearing in (2), \(\mathbf {t}^{\textit{STT}}\), accounts for the classical spin-transfer torque generated by the current flow. Even in the case of negligible interfacial effects, \(\mathbf {t}^{\textit{STT}}\) includes adiabatic and non-adiabatic contributions responsible for the DW distortion and motion, respectively [17, 18]. It reads:

$$\begin{aligned} \mathbf {t}^{\textit{STT}}=\left( -\frac{\partial \mathbf {m}}{\partial x}-\eta \frac{ \partial \mathbf {m}}{\partial x}\wedge \,\mathbf {m}\right) u_{0}J \end{aligned}$$
(7)

with \(u_{0}=g\mu _{B}P/\left( 2eM_{s}\right) \), being \(\eta \) the phenomenological non-adiabatic parameter, \(\mu _{B}\) the Bohr magneton and P the polarization factor of the current.

The last term in (2), \(\mathbf {t}^{\textit{SOT}}\), describes the two spin-orbit coupling mechanisms (Rashba and Spin-Hall) which take place in such structures [9,10,11,12,13, 23]:

$$\begin{aligned} \mathbf {t}^{\textit{SOT}}=\gamma J\text { }\left[ \widetilde{\alpha }_{\textit{RA}}\left( \mathbf {e}_{y}\wedge \mathbf {m}\right) +\left( \eta \text { } \widetilde{\alpha }_{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) \mathbf {m}\,\wedge \left( \mathbf {m}\wedge \mathbf {e}_{y}\right) \right] \end{aligned}$$
(8)

where:

$$\begin{aligned} \widetilde{\alpha }_{\textit{RA}}=\frac{\alpha _{R}P}{\mu _{0}\mu _{B}M_{S}^{2}}{ ,\quad \quad }\widetilde{h}_{\textit{SH}}=\frac{\mu _{B}\theta _{\textit{SH}}}{\gamma eM_{S}d \text { }} \end{aligned}$$
(9)

In detail, the Rashba effect enters the governing equation both as a field-like term and as a spin-transfer-torque-like term, whereas the Spin-Hall effect acts as a spin-transfer-torque-like term only. In (9), \(\alpha _{R}\) is the parameter that measures the strength of the Rashba spin-orbit-torque and \(\theta _{\textit{SH}}\) represents the spin-Hall angle which parameterizes the ratio between the spin current and the charge current [23].

To analytically gain insight into the 1D motion of domain walls in such a nanostrip, we substitute the explicit expressions of the above defined torques into the Landau–Lifshitz–Gilbert equation (2) which, in polar coordinates, becomes:

$$\begin{aligned}&\sin \theta \overset{\bullet }{\varphi }-\left[ \alpha _{G}+\gamma \alpha _{D}\left( \overset{\bullet }{\theta }^{2}+\sin ^{2}\theta \overset{\bullet }{\varphi }^{2}\right) ^{-1/2}\right] \overset{\bullet }{\theta }\text { }\nonumber \\&\quad =\gamma \left\{ -A\frac{\partial ^{2}\theta }{\partial x^{2}}+A\sin \theta \cos \theta \left( \frac{\partial \varphi }{\partial x}\right) ^{2} \nonumber \right. \\&\qquad \left. -\,\widetilde{\alpha }_{\textit{RA}}J\cos \theta \sin \varphi +\left( \beta +N_{x}\cos ^{2}\varphi +N_{y}\sin ^{2}\varphi -N_{z}\right) \sin \theta \cos \theta \right. \nonumber \\&\qquad \left. -\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { }\widetilde{h} _{\textit{SH}}\right) J\cos \varphi \right\} -u_{0}J\sin \theta \frac{\partial \varphi }{\partial x}+\eta u_{0}J\frac{ \partial \theta }{\partial x} \nonumber \\&\quad \left[ \alpha _{G}+\gamma \alpha _{D}\left( \overset{\bullet }{\theta } ^{2}+\sin ^{2}\theta \overset{\bullet }{\varphi }^{2}\right) ^{-1/2}\right] \sin \theta \overset{\bullet }{\varphi }+\overset{\bullet }{\theta }\text { }\nonumber \\&\quad =\gamma \bigg \{ A\sin \theta \frac{\partial ^{2}\varphi }{\partial x^{2}} +2A\cos \theta \frac{\partial \theta }{\partial x}\frac{\partial \varphi }{ \partial x}\nonumber \\&\qquad + \left( N_{x}-N_{y}\right) \sin \theta \cos \varphi \sin \varphi -\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) J\cos \theta \sin \varphi +\widetilde{\alpha }_{\textit{RA}}J\cos \varphi \bigg \} \nonumber \\&\qquad -\,\eta u_{0}J\sin \theta \frac{\partial \varphi }{\partial x}-u_{0}J\frac{ \partial \theta }{\partial x} \end{aligned}$$
(10)

where \(\theta \) and \(\varphi \) are the polar and azimuthal angles, respectively, so that the unit magnetization vector \(\mathbf {m}\) is expressed as \(\mathbf {m}=(\cos \varphi \sin \theta ,\sin \varphi \sin \theta ,\cos \theta )\).

It is known that DW dynamics in a nanostrip can be classified into two regimes, steady and precessional, occurring, respectively, below and well above a given critical value of the driving source [referred to as Walker Breakdown (WB)]. Such a WB condition also delineates the stability of the wall structure [26]. For the sake of clarity, we will analyze these regimes separately.

2.1 The steady regime

This dynamical regime is characterized by a steady motion of the DW along the nanostrip axis \(\mathbf {e}_{x}\) with constant velocity v. Because of that, let us introduce a travelling wave ansatz for the polar angle \(\theta =\theta \left( x-vt\right) \) whereas the azimuthal angle is assumed to be constant in time and uniform in space \( \varphi =\varphi _{0}\) [24].

Under these assumptions, the system (10) reduces to:

$$\begin{aligned}&\left[ \alpha _{G}v-\eta u_{0}J\right] \theta ^{\prime }+\widehat{\alpha _{D} }=\gamma \Big \{ -A\theta ^{\prime \prime }-\widetilde{\alpha }_{\textit{RA}}J\cos \theta \sin \varphi _{0}+ \nonumber \\&\quad -\,\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { }\widetilde{h} _{\textit{SH}}\right) J\cos \varphi _{0}+\sin \theta \cos \theta \left[ \beta +N_{x}\cos ^{2}\varphi _{0}+N_{y}\sin ^{2}\varphi _{0}-N_{z}\right] \Big \} \nonumber \\&\left( u_{0}J-v\right) \theta ^{\prime }=\gamma \left\{ \widetilde{\alpha } _{\textit{RA}}J\cos \varphi _{0}-\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { } \widetilde{h}_{\textit{SH}}\right) J\cos \theta \sin \varphi _{0}\right. \nonumber \\&\quad \left. +\left( N_{x}-N_{y}\right) \sin \theta \cos \varphi _{0}\sin \varphi _{0}\right\} \end{aligned}$$
(11)

where the prime denotes the derivative with respect to the travelling wave variable \(\xi =x-vt\) and \(\widehat{\alpha _{D}}=\gamma \alpha _{D}\)sign\( \left( v\theta ^{\prime }\right) \). We recast Eq. (11)\(_{2}\) as:

$$\begin{aligned} \theta ^{\prime }=\varGamma \left( \sin \theta +\widetilde{\varGamma }\cos \theta + \widehat{\varGamma }\right) \end{aligned}$$
(12)

with:

$$\begin{aligned} \varGamma= & {} \frac{\gamma }{u_{0}J-v}\left( \frac{N_{x}-N_{y}}{2}\right) \sin 2\varphi _{0} \end{aligned}$$
(13)
$$\begin{aligned} \widetilde{\varGamma }= & {} -\frac{\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { } \widetilde{h}_{\textit{SH}}\right) }{\left( N_{x}-N_{y}\right) \cos \varphi _{0}}J=- \widetilde{\widetilde{\varGamma }}J \end{aligned}$$
(14)
$$\begin{aligned} \widehat{\varGamma }= & {} \frac{\widetilde{\alpha }_{\textit{RA}}}{\left( N_{x}-N_{y}\right) \sin \varphi _{0}}J=\widehat{\widehat{\varGamma }}J \end{aligned}$$
(15)

where \(\varGamma ^{-1}\) has the dimension of length whereas \(\widetilde{\varGamma } \) and \(\widehat{\varGamma }\) are dimensionless quantities (\(\widetilde{ \widetilde{\varGamma }}\) and \(\widehat{\widehat{\varGamma }}\) are \(\left( \text {current densities}\right) ^{-1}\)).

Then, inserting (12) into (11)\(_{1}\), after some algebra, we end up with the following trigonometric equation:

$$\begin{aligned} P\sin \theta +Q\cos \theta +R\sin \theta \cos \theta +S\sin ^{2}\theta +T=0 \end{aligned}$$
(16)

where:

$$\begin{aligned} \begin{aligned} P=&\varGamma \left( \alpha _{G}v-\eta u_{0}J\right) -\gamma A\varGamma ^{2}\widehat{ \varGamma }\widetilde{\varGamma } \\ Q=&\varGamma \widetilde{\varGamma }\left( \alpha _{G}v-\eta u_{0}J\right) +\gamma \left( A\varGamma ^{2}\widehat{\varGamma }+\widetilde{\alpha }_{\textit{RA}}J\sin \varphi _{0}\right) \\ R=&\gamma \left[ A\varGamma ^{2}\left( 1-\widetilde{\varGamma }^{2}\right) -\beta +N_{z}-N_{y}\sin ^{2}\varphi _{0}-N_{x}\cos ^{2}\varphi _{0}\right] \\ S=&-2\gamma A\varGamma ^{2}\widetilde{\varGamma } \\ T=&\varGamma \widehat{\varGamma }\left( \alpha _{G}v-\eta u_{0}J\right) +\widehat{ \alpha _{D}}+\gamma \left[ A\varGamma ^{2}\widetilde{\varGamma }+\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) J\cos \varphi _{0} \right] \end{aligned} \end{aligned}$$
(17)

The expression of the DW width is given by \(\delta =\varGamma ^{-1}\) and, in agreement with some previous results [14,15,16], it is obtained by imposing the condition \(R=0\). It leads to:

$$\begin{aligned} \delta ^{2}=\varGamma ^{-2}=\frac{A\left( 1-\widetilde{\varGamma }^{2}\right) }{ \beta +N_{x}\cos ^{2}\varphi _{0}+N_{y}\sin ^{2}\varphi _{0}-N_{z}} \end{aligned}$$
(18)

Comparing (18) with the expression found in [16], we notice that the presence of Rashba and Spin-Hall contributions reduces, via the coefficient \(\widetilde{\varGamma }\), the DW width.

A meaningful solution of Eq. (12) satisfying the symmetry condition \(\theta (0)=\pi /2\) can be obtained if the dimensionless quantities \( \widehat{\varGamma }\) and \(\widetilde{\varGamma }\) verify the constraint \(\left( \widehat{\varGamma }^{2}-\widetilde{\varGamma }^{2}\right) <1\). Under such hypotheses, the solution can be expressed as:

$$\begin{aligned} \theta \left( \xi \right) =2\arctan \frac{f_{2}K\exp \left( \varGamma \sqrt{1+ \widetilde{\varGamma }^{2}-\widehat{\varGamma }^{2}}\xi \right) -f_{1}}{K\exp \left( \varGamma \sqrt{1+\widetilde{\varGamma }^{2}-\widehat{\varGamma }^{2}}\xi \right) -1} \end{aligned}$$
(19)

with:

$$\begin{aligned} \begin{aligned} K&=\frac{1+\left( \widehat{\varGamma }-\widetilde{\varGamma }\right) \left( 1- \widetilde{\varGamma }\right) -\left( \widehat{\varGamma }-\widetilde{\varGamma } +1\right) \sqrt{1+\widetilde{\varGamma }^{2}-\widehat{\varGamma }^{2}}}{\left( \widehat{\varGamma }-\widetilde{\varGamma }\right) \left( \widehat{\varGamma } +1\right) } \\ f_{1}&=\frac{-1+\sqrt{1+\widetilde{\varGamma }^{2}-\widehat{\varGamma }^{2}}}{ \widehat{\varGamma }-\widetilde{\varGamma }},\quad f_{2}=\frac{-1-\sqrt{1+ \widetilde{\varGamma }^{2}-\widehat{\varGamma }^{2}}}{\widehat{\varGamma }-\widetilde{ \varGamma }} \end{aligned} \end{aligned}$$
(20)

In the limit \(\left| \widetilde{\varGamma }\right| \rightarrow 0,\left| \widehat{\varGamma }\right| \rightarrow 0\), we recover the classical Walker solution representing a 180\( {{}^\circ } \) Bloch DW with \(\theta \left( \xi \right) \simeq \pi \) for \(\xi \rightarrow +\infty \) and \(\theta \left( \xi \right) \simeq 0\) for \(\xi \rightarrow -\infty \) [24]. For this reason, hereafter we consider the assumptions \(\left| \widetilde{\varGamma }\right| \simeq 0\) and \( \left| \widehat{\varGamma }\right| \simeq 0\) that can be easily achieved by using realistic parameter values. Consequently, the DW width (18) can be safely approximated by \(\delta =\varGamma ^{-1} \approx \left[ A/\left( \beta +N_{x}\cos ^{2}\varphi _{0}+N_{y}\sin ^{2}\varphi _{0}-N_{z}\right) \right] ^{1/2}\), namely its value will only depend on exchange constant, perpendicular anisotropy and demagnetizing factors. We therefore assume the DW width to be independent of SOT effects, as usual in literature [11, 14,15,16, 20, 23].

To derive the expression of the steady DW velocity, we average the equation (16) over the range \(0\le \theta \le \pi \), taking into account that the coefficients P,Q,S and T (17) do not depend on \(\theta \). We obtain:

$$\begin{aligned} v=\frac{\widehat{\widehat{\varGamma }} \left( \pi \delta \eta u_{0}-2\gamma A \widetilde{\widetilde{\varGamma }}\right) J^{2}+\left[ 2\eta u_{0} -\pi \delta \gamma \cos \varphi _{0}\left( \eta \widetilde{\alpha } _{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) \right] \delta J-\pi \delta ^{2} \widehat{\alpha _{D}}}{ \alpha _{G}\delta \left( 2+\pi \widehat{\widehat{\varGamma }}J\right) } \end{aligned}$$
(21)

From a direct inspection of (21), we notice that, owing to the presence of dry-friction (proportional to \(\widehat{\alpha _{D}}\)), the DW velocity does not cross the origin of the \(J-v\) plane: this feature allows to take into account the above-mentioned pinning effects due to crystallographic disorder. We also point out that the source of nonlinearity between DW velocity v and electric current J lies in the Rashba effect only. In fact, in the absence of this contribution \(\left( \widehat{\widehat{\varGamma }} =0\right) \), the Spin-Hall effect would not lead to any nonlinearity:

$$\begin{aligned} v=\frac{2\eta u_{0} -\pi \delta \gamma \cos \varphi _{0}\text { }\widetilde{h} _{\textit{SH}}}{2\alpha _{G} }J-\frac{\pi \delta }{2\alpha _{G} } \widehat{\alpha _{D}} \end{aligned}$$
(22)

and the DW would shift along the nanostrip axis with a spin-Hall-dependent mobility \(\partial v/\partial J=\left( 2\eta u_{0} -\pi \delta \gamma \cos \varphi _{0}\widetilde{h}_{\textit{SH}}\right) /2\alpha _{G} \).

However, if we also neglected the spin-Hall effect \(\left( \widetilde{h}_{\textit{SH}}=0\right) \), the sign of the DW mobility (which determines the direction of DW motion), the value of the propagation threshold (also referred to as depinning threshold) and the upper limit of the steady motion (the Walker breakdown) would be fixed by the geometrical sizes and the chemical composition of the materials, making quite hard the process of optimization of steady DW dynamics. On the contrary, applications nowadays ask for the possibility to manipulate the direction of motion, to reduce the depinning thresholds and to achieve larger propagation velocities. As proven by experiments [11], SOT effects contribute significantly in this direction, since they provide additional degrees of freedom (the parameters \(\widetilde{\alpha }_{\textit{RA}}\) and \(\widetilde{h}_{\textit{SH}}\)) which can be suitably designed for these purposes. Moreover, the inspection of (21), (22) reveal that different scenarios may occur depending also on the value of the azimuthal angle \( \varphi _{0}\) which, as it will be shown, plays a fundamental role in such dynamics.

To analyze it in more detail, let us consider two representative cases: \(0<\varphi _{0}<\pi /2\) and \(\pi /2<\varphi _{0}<\pi \). In addition, hereafter we will assume the difference \(N_{x}-N_{y}\) to be positive and, for simplicity, we will also consider a positive current polarity (\(J>0\)) only. Let us notice that, if \(0<\varphi _{0}<\pi /2\) (\(\pi /2<\varphi _{0}<\pi \)), the denominator of (21) is positive (negative), so that the direction of steady DW motion is entirely ruled by the sign of the numerator (the opposite sign of the numerator). By inspecting the solutions of the quadratic function at the numerator of (21), we get:

$$\begin{aligned} J_{1,2}= & {} \bigg \{ \gamma \pi \delta \cos \varphi _{0}\left( \eta \widetilde{\alpha } _{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) -2\eta u_{0} \nonumber \\&\pm \left[ \left( \gamma \pi \delta \cos \varphi _{0}\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) -2\eta u_{0} \right) ^{2}+4\pi \delta ^{2} \widehat{\alpha _{D}}\widehat{\widehat{ \varGamma }} \left( \eta \pi \delta u_{0}-2\gamma A \widetilde{\widetilde{ \varGamma }}\right) \right] ^{1/2}\bigg \} \nonumber \\&\times \left[ 2\widehat{\widehat{\varGamma }} \left( \eta \pi \delta u_{0}-2\gamma A \widetilde{\widetilde{\varGamma }}\right) \right] ^{-1} \end{aligned}$$
(23)

By reminding the hypothesis on the smallness of the quantities \(\widetilde{\widetilde{\varGamma }} \) and \(\widehat{\widehat{\varGamma }}\), we conclude that the two roots (23) are always real and distinct. Let us introduce the depinning threshold as \(J^{\textit{DEP}}=\)max\(\left( J_{1},J_{2}\right) \). This quantity reflects the physical constraint that a net DW motion cannot originate if the amplitude of the electric current does not allow to overcome the pinning effect due to the static friction, i.e. \(v=0\) for \(J\le J^{\textit{DEP}}\). We can therefore summarize the steady DW dynamics obtained for \(J>J^{\textit{DEP}}\) as follows:

(24)

being \(h^{*}=\left[ \eta \pi \delta u_{0}\left( N_{x}-N_{y}\right) \cos \varphi _{0}\right] /\left( 2\gamma A\right) \). In such an analysis, we remind that the spin-Hall angle, and thus \( \widetilde{h}_{\textit{SH}}\), may assume negative values. On the contrary, the Rashba contribution \(\widetilde{\alpha }_{\textit{RA}}\) is always positive.

The upper bound of the range in which a steady motion occurs, the WB current, can be deduced from (13) and leads to the following restrictions to the DW velocity:

$$\begin{aligned} u_{0}J\mathbf {-}\frac{\gamma \delta }{2}\left( N_{x}-N_{y}\right) \le v\le u_{0}J+\frac{\gamma \delta }{2}\left( N_{x}-N_{y}\right) \end{aligned}$$
(25)

Therefore, by comparing (21) with (25), we deduce the WB values for current density:

$$\begin{aligned} J^{WB}= & {} \delta \left\{ 2\pi \delta \gamma \cos \varphi _{0}\left( \eta \widetilde{\alpha } _{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) \pm \pi \delta \alpha _{G}\gamma \widehat{ \widehat{\varGamma }}\left( N_{x}-N_{y}\right) -4u_{0} \left( \eta -\alpha _{G}\right) \pm \right. \nonumber \\&\pm \left\{ \left[ 2\pi \delta \gamma \cos \varphi _{0}\left( \eta \widetilde{ \alpha }_{\textit{RA}}+\text { }\widetilde{h}_{\textit{SH}}\right) \pm \pi \delta \alpha _{G}\gamma \widehat{\widehat{\varGamma }}\left( N_{x}-N_{y}\right) -4u_{0} \left( \eta -\alpha _{G}\right) \right] ^{2}\right. \nonumber \\&\left. +16 \widehat{\widehat{\varGamma }}\left[ \pi \widehat{\alpha _{D}} \pm \alpha _{G}\gamma \left( N_{x}-N_{y}\right) \right] \left[ \pi \delta u_{0}\left( \eta -\alpha _{G}\right) -2\gamma A \widetilde{\widetilde{ \varGamma }}\right] \right\} ^{1/2}\nonumber \\&\times \left\{ 4 \widehat{\widehat{\varGamma }}\left[ \pi \delta u_{0}\left( \eta -\alpha _{G}\right) -2\gamma A \widetilde{\widetilde{\varGamma }}\right] \right\} ^{-1} \end{aligned}$$
(26)

where the plus (minus) sign holds for forward (backward) motion.

As it can be noticed from (23), (24), (26), Rashba and spin-Hall effects affect the direction of motion, the depinning threshold and the Walker breakdown, so confirming that current-induced SOT effects may be properly used to manipulate and to optimize the overall steady dynamical regime.

2.2 The precessional regime

Let us now investigate the regime of precessional dynamics observed far above the WB condition. As known, this regime takes place for very large values of the driving source [violating condition (25)] and is characterized by a periodic oscillation of the DW structure between Bloch and Neel configurations so that the corresponding DW velocity can be only expressed in terms of an average velocity over the period of precession.

To describe such dynamics analytically, we assume that the precession occurs at microwave frequency with a constant angular speed \(\overset{\bullet }{ \varphi }=\omega _{0}\) and that the traveling wave profile given by (19) is unchanged [26].

To deduce an approximate expression of the DW velocity, we evaluate all the quantities at the center of the DW (\(\theta =\frac{\pi }{2}\)). The equations (10) can be rewritten in the form:

$$\begin{aligned}&\omega _{0}+\left[ \alpha _{G}+\gamma \alpha _{D}\left( \frac{v^{2}}{\delta ^{2}}\left( 1+\widehat{\widehat{\varGamma }}\right) ^{2}+\omega _{0}^{2}\right) ^{-1/2}\right] \frac{v}{\delta } \left( 1+\widehat{\widehat{\varGamma }}J\right) \nonumber \\&=-\,\gamma J\left[ \frac{A}{\delta ^{2}}\widetilde{\widetilde{\varGamma }}\left( 1+\widehat{ \widehat{\varGamma }}J\right) +\left( \eta \widetilde{\alpha }_{\textit{RA}}+\text { } \widetilde{h}_{\textit{SH}}\right) \cos \varphi \right] + \frac{\eta u_{0}J}{\delta } \left( 1+\widehat{\widehat{\varGamma }}J\right) \nonumber \\&\left[ \alpha _{G}+\gamma \alpha _{D}\left( \frac{v^{2}}{\delta ^{2}}\left( 1+ \widehat{\widehat{\varGamma }}\right) ^{2}+\omega _{0}^{2}\right) ^{-1/2}\right] \omega _{0}-\frac{v}{\delta } \left( 1+\widehat{\widehat{\varGamma }}J\right) \nonumber \\&=\gamma \left[ \left( N_{x}-N_{y}\right) \sin \varphi +\widetilde{\alpha } _{\textit{RA}}J\right] \cos \varphi -\frac{u_{0}J}{\delta } \left( 1+\widehat{\widehat{ \varGamma }}J\right) \end{aligned}$$
(27)

Then, by performing the average of the equations (27) over a period of precession, under the further (physical) restriction \(\overline{v}/\delta <<\) \(\omega _{0}\), we deduce:

$$\begin{aligned}&\delta \omega _{0}+ \alpha _{G}\overline{v}-\eta u_{0}J=0 \nonumber \\&\overline{v}-u_{0}J =\left( \alpha _{G}\omega _{0}+\gamma \alpha _{D}\right) \delta \end{aligned}$$
(28)

which leads to the following expression for the average DW velocity in the precessional regime:

$$\begin{aligned} \overline{v}=\frac{\left( 1+\alpha _{G}\eta \right) u_{0}}{1+\alpha _{G}^{2}} J+\frac{\gamma \delta \alpha _{D}}{ 1+\alpha _{G}^{2} } \end{aligned}$$
(29)

As it can be noticed, differently from the steady regime, SOT effects do not formally alter the structure of the classical solution as well as do not modify the DW mobility, in agreement with some previous results [16, 20]. For this reason, no further investigations will be addressed in this regime.

3 An illustrative comparison with literature data

The analytical results derived in the previous section are now evaluated numerically in order to enable a direct comparison with data extracted from literature. To this aim, we consider the setup proposed in [23], where the roles of Rashba and Spin-Hall effects were investigated by integrating numerically the governing equation (2) via a finite-differences tool [27]. In detail, the ferromagnetic layer of such a heterostructure has length \(L= 2.1\,\upmu \)m, width \(w=120\) nm and thickness \(d=\) 3 nm so that the constraint \(L>>w>d\) is satisfied. The parameters used to describe DW dynamics are: saturation magnetization \( M_{S}=3\times 10^{5}\) A/m, exchange constant \(A_{ex}=1\times 10^{-11}\) J/m, dimensionless Gilbert damping constant \(\alpha _{G}=0.5\), dry-friction coefficient \(\alpha _{D}=0.01\), demagnetizing factors \(N_{x}=0.9091\), \( N_{y}=\ 0.0021\) and \(N_{z}=0.0888\), current polarization factor \(P=0.5\), non-adiabatic coefficient \(\eta =0.04\), Rashba parameter \(\alpha _{R}\) \( =10^{-31}\) Jm. According to this set of parameters, the DW width is \(\delta =\varGamma ^{-1}\approx 7\) nm.

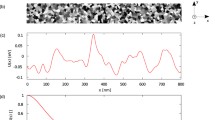
Firstly, we analyze the travelling wave profile in order to preliminarily verify the consistency of our previous assumptions. In particular, in Fig. 2a we depict the dimensionless parameters \(\widetilde{\varGamma }\) and \( \widehat{\varGamma }\), defined in (14)–(15), for a fixed value of the spin-Hall angle: \(\theta _{\textit{SH}}=0.05\). As it can be noticed, these quantities satisfy the required constraint \( \left( \widehat{\varGamma }^{2}-\widetilde{\varGamma }^{2}\right) <1\) and also approximate sufficiently well the limit \(\left| \widetilde{\varGamma }\right| \simeq 0,\left| \widehat{\varGamma }\right| \simeq 0\). By using the parameter values extracted from such a figure, we can compute the traveling wave profile \(\theta \left( \xi \right) \) for two different values of the input current density (\(J=0.5\) A/\(\upmu \hbox {m}^{2}\) and \(J=2.5\) A/\(\upmu \hbox {m}^{2}\)). Results shown in Fig. 2b denote that the analytical solution approximates satisfactorily well the classical Walker profile in both cases. This confirms the validity of our approach and allows us to get more insights into DW dynamics.

Fig. 2
figure 2

a Dependence of the dimensionless quantities \(\widetilde{\varGamma }\) (dashed line) and \(\widehat{\varGamma }\) (solid line) on current density J, for a fixed value of the spin-Hall angle \(\theta _{\textit{SH}}=0.05\). b Travelling wave profile obtained for \(J=0.5\) A/\(\upmu \hbox {m}^{2}\) (solid line) and \(J=2.5\) A/\(\upmu \hbox {m}^{2}\) (dashed line) by using the parameters values extracted from (a)

Full size image
Fig. 3
figure 3

a Steady DW velocity v as a function of the input current density J for different values of the Spin-Hall angle \(\theta _{\textit{SH}} \). Symbols denote results of numerical finite-differences simulations, whereas lines represent analytical results. b Dependence of the azimuthal angle \(\varphi _{0}\) as a function of the Spin-Hall angle \(\theta _{\textit{SH}}\). Symbols denotes the numerical data whereas the dash-dotted line represents the best linear fit. The linear fit crosses the value \(\varphi _{0}=\pi /2\) at \(\theta _{\textit{SH}}^{*}\simeq 0.13\) that separates the regime of forward motion from the backward one

Full size image

In particular, we now focus our attention on the results reported in Fig. 3a of [23] which depict the steady DW velocity obtained by fixing the Rashba field and varying the spin-Hall angle. In more detail, those numerical results indicate that the direction of DW propagation may undergo an abrupt reversal if the spin-Hall angle exceeds a critical value. Our analysis aims at providing a mathematical, and physical, justification of the mechanisms governing this phenomenon.

The comparison between analytical results and numerical data arising from micromagnetic simulations is summarized in Fig. 3a. Such an analysis reveals that, for \(\theta _{\textit{SH}}=0\), no DW motion takes place because the depinning threshold (related to dry-friction) is beyond the range of current density here considered. For \(\theta _{\textit{SH}}=0.05\) and 0.10 , the DW velocity is negative, which reflects a backward propagation (along the \(-\,\mathbf {e}_{x}\) axis), i.e. a DW motion against the electron flow. Moreover, the increase of the spin-Hall angle leads to an overall increase (in absolute value) of the DW mobility. At \(\theta _{\textit{SH}}=0.15\) the DW velocity has undergone an abrupt transition towards positive values. In this case, the DW moves forward (along the \(+\,\mathbf {e}_{x}\) axis), i.e. the DW propagates in accordance with the electron flow.

It is interesting to notice that our analytical approach (solid lines) is able to capture qualitatively well the behavior reported by such micromagnetic simulations (symbols). Moreover, we may also reproduce the above-mentioned abrupt transition by considering a correlation between the azimuthal angle \(\varphi _{0}\) and the spin-Hall angle \(\theta _{\textit{SH}}\). This assumption is consistent with the fact that the increase of the spin-Hall strength tilts the magnetization away from its equilibrium direction and pushes it towards the \(\mathbf {e}_{y}\) axis [see Eq. (8)]. Interestingly, results of our investigations reported in Fig. 3b reveal that the azimuthal angle depends almost linearly upon the spin-Hall angle and crosses the value \(\pi /2\) at \(\theta _{\textit{SH}}^{*}\) which falls within the interval [0.10, 0.15], in agreement with the numerical simulations [23]. In other words, from the analytical viewpoint, it implies that dynamics observed for \(\theta _{\textit{SH}}<\theta _{\textit{SH}}^{*}\) (\(\theta _{\textit{SH}}>\theta _{\textit{SH}}^{*}\)) correspond to the case II (IV) described in Eq. (24). Through a linear fit of the data, we extract the relationship \(\varphi _{0}=0.21\pi +2.25\pi \theta _{\textit{SH}}\) which may be therefore considered as the mechanism responsible for the reversal of propagation direction.

Finally, let us comment on the discrepancies resulting from the comparison between numerical and analytical data. As it can be noticed from Fig. 3a, once the Spin-Hall coefficient \(\theta _{\textit{SH}}\) is fixed, numerical data indicate a linear dependence of velocity v on current density J, whereas analytical results report a nonlinear behavior. We believe that the origin of such a partial disagreement could arise from the too restrictive assumption that, in the presence of SOT effects, the analytical solution still satisfies the classical Walker-like travelling-wave profile. In fact, when SOT effects become non-negligible, the equilibrium configuration close to the boundaries of the nanostrip deviates away from the \(\mathbf {e}_{z}\) axis and, at the same time, the magnetization within the DW region exhibits variations along the \(\mathbf {e}_{y}\) axis that cannot be included into the present 1D model (as also mentioned in [23]).

4 Conclusions

The propagation of a magnetic DW in a thin ferromagnetic layer interposed between a heavy metal and a metal oxide has been here analyzed in the framework of the Extended Landau–Lifshitz–Gilbert equation. The geometry under investigation exhibits structural inversion asymmetry and allows to combine two current-induced effects, the spin-transfer-torque and the spin-orbit-torque, the latter being in turn associated to Rashba and Spin-Hall effects.

In order to describe the DW dynamics observed in both steady and precessional regimes, some simplifying assumptions have been taken into account. Among the most significant ones, we recall: (i) owing to the thin and elongated geometry, the magnetization is assumed to vary along the nanostrip axis only and, thus, a 1D model is developed; (ii) the strengths of Rashba and Spin-Hall effects are considered to be so small that the constraint \(\left| \widehat{\varGamma }^{2}-\widetilde{\varGamma } ^{2}\right| <1\) holds true, the classical Walker-like solution is still valid and the DW width is independent of SOT effects; (iii) the presence of crystallographic defects is modelled via an additional dry-friction damping torque term.

These hypotheses have allowed to deduce approximate analytical expressions for the key physical quantities involved in such dynamics: DW velocity and mobility, direction of propagation, depinning threshold and Walker breakdown. In particular, their functional dependence on the strength of both SOT effects has been pointed out. To the best of our knowledge, such an investigation has been so far undertaken via numerical simulation tools only.

Our results have shown that, in the absence of SOT effects, the DW velocity exhibits the expected linear dependence on the driving source (the electric current). However, while this dependence is not altered by the sole Spin-Hall effect, it can be made nonlinear via Rashba contribution. In both cases, SOT terms introduce additional degrees of freedom which can be efficiently used to control and to optimize the DW dynamics occurring within the steady dynamical regime, whereas they play no role in the precessional one.

Finally, by enabling a direct comparison between analytical and numerical data, we have been able to gain more insights into such SOT-driven DW dynamics. In particular, our investigation has allowed to establish a possible linear relationship between the azimuthal angle \(\varphi _{0}\) and the spin-Hall angle \(\theta _{\textit{SH}}\) which could justify the reversal of propagation direction observed at the critical value \(\theta _{\textit{SH}}^{*}\).