Introduction

The integration of brain science and brain-like intelligence can guide developments in the fields of information science and artificial intelligence. A bio-brain has self-adaptive abilities, such as self-learning (Luo et al. 2021), self-organization (Kim et al. 2018) and self-repair (Dale et al. 2018). Learning from the advantages of bio-brains, a brain-like model that more conforms to bio-interpretability can enhance the information processing abilities of a model and promote the development of brain-like intelligence. However, the bio-interpretability of brain-like models is still insufficient. The spiking neural networks (SNNs) represents the latest generation of artificial neural networks (Liu et al. 2021), which is a kind of brain-like model that can reflect the electrophysiological activity of the nerves. An SNN with neuronal dynamics and synaptic weight dynamics has been necessary theory and model foundation of computational neuroscience (Li et al. 2020; Nobukawa et al. 2020; Kim and Lim 2021). Three elements of constructing an SNN are the topological structure, the neuron model and the synaptic plasticity model.

The network topology reflects the forms of connections among neurons. Many biological studies have indicated that a functional brain network has scale-free property and/or small-world property based on fMRI, PET, EEG, and so on. Hodkinson et al. (2019) investigated the resting-state fMRI signal related to spontaneous neural activity. They discovered that the network had a scale-free property, and its scaling exponent correlated with regional metabolic demands of a brain. Kate et al. (2018) investigated the gray matter networks of cognitively normal elderly based on PET data. Their results indicated that the brain networks of these elderly all had small-world property, but these small-world property declined with age, which were related to the influence of amyloid plaques in the precuneus. Bin et al. (2021) established function brain networks of alcohol addicts and healthy people based on EEG data, and found that these networks presented scale-free property and small-world property. And compared with healthy people, two properties of alcohol addicts declined through the analysis of clustering coefficient and proportion of nodes with high degree. According to the theory of complex networks, networks include regular networks, ER random graphs, and complex networks from the perspective of network topology (Barthelemy 2018). The regular networks are characterized by high average clustering coefficient and long average path length (Li et al. 2018). Whereas, the characteristics of ER random graphs are opposite to those of the regular networks (Habibulla 2020). The complex networks include small-world networks and scale-free networks. The small-world networks, combining the advantages of regular networks and ER random graphs, have high average clustering coefficient and short average path length (Watts and Strogatz 1998). This indicates that the small-world networks have more compactness of local connection and higher efficiency of information transmission. The degree of a scale-free network follows a power-law distribution (Barrat et al. 2004). This indicates that scale-free networks have strong fault tolerance due to the unevenness of the degree distribution. Furthermore, research into SNNs with a topology of complex network has been carried out. Zeraati et al. (2021) investigated the self-organized criticality of an SNN with scale-free property. They found that dynamics of the SNN self-organized to the critical state of synchronization through the change of the degree distribution regulated by a temporally shifted soft-bound spike timing dependent plasticity (STDP) rule. Gu et al. (2019) studied the dynamics of the small-world SNN (SWSNN) driven by noise. Compared with a regular-lattice network, they found that the activity of the SWSNN was perturbed along the continuous attractor and gave rise to the diffusive waves, which provided insights into the understanding of the generation of wave patterns. A brain-like network with only a single topological property is still insufficient in information processing ability. Inspired by structural characteristics of functional brain networks, the brain-like network with a topology of complex network has not only strong fault tolerance but also compactness of local connection and high efficiency of information transmission.

The neuron model is a mathematical model with dynamic process of spiking firing in SNN. Scholars in neural computing have carried out works on spiking neuron models. The Hodgkin-Huxley model (Hodgkin and Huxley 1952), as fourth-order partial differential equation, conforms to biological neurons in characteristics of neuronal firing. However, its inherent computational complexity imposes a high computational cost. In contrast, the Leaky Integrate-and-Fire model (Brette and Gerstner 2005) is first-order linear differential equation. Although it has a low computational complexity, it cannot closely conform to the firing characteristics of biological neurons. The Izhikevich neuron model (Izhikevich 2003), as a second-order nonlinear differential equation, strikes a good balance between computational complexity and the firing characteristics of biological neurons, which has been applied in constructing a large-scale neural network.

Synapses are considered to be the basis of learning and regulation in the nervous system (Xu et al. 2020). Tang et al. (2019) investigated an SNN based on excitatory synapses, and found that this synapse model could accelerate the inference speed during the unsupervised learning process. Biological researches (Du et al. 2016; Dargaei et al. 2019) have shown that inhibitory synaptic plasticity can dynamically regulate the information transmission in the aspects of speed, sensitivity, and stability. The joint regulation of excitatory and inhibitory synapses forms the foundation of information transmission and processing in a brain (Koganezawa et al. 2021). Lin et al. (2019) constructed an SNN which combined excitatory and inhibitory synapses, and found that the excitatory neurons facilitated synchronization by promoting oscillation mode switching, and the inhibitory neurons suppressed synchronization by delaying neuronal excitement. In our previous work (Guo et al. 2020), we constructed a scale-free SNN (SFSNN) with excitatory and inhibitory synapses, and verified the specificity of neural information coding under different kinds of stimuli from intra-class similarity and inter-class differences by algorithms. Biological researches (Swadlow 1985, 1988, 1992) have shown that a time-delay of chemical synapse is in the dynamic range 0.1–40 ms, and the time-delay varies randomly within this range on synapses of the rabbit brain cortex. Poo (2018) pointed out that synaptic time-delays can improve the information processing abilities of the nervous system, which are an important factor related to the formation of brain cognitive functions. Lammertse et al. (2020) investigated STXBP1 encephalopathy in mice, and found that synaptic time-delay was reduced due to decreasing stability of impaired mutant protein, which was considered the main underlying pathogenetic mechanism of intellectual disability and epilepsy. Li et al. (2021) investigated the synapses of Aldh1a1 neurons in Alzheimer’s mice, and found that the synaptic time-delay was changed due to the decrease in the binding rate of neurotransmitter and receptor under blue laser light at 473nm, which could improve self-control skills in decision. Research into brain-like networks with synaptic time-delay has been carried out. Shafiei et al. (2019) investigated the effect of synaptic time-delay on the pattern of the Izhikevich neuron network, where there were two types of time-delay in synaptic models: one was fixed time-delay, and the other was none time-delay. They observed that the network could switch between synchronous and asynchronous states by adjusting the ratio of two kinds of synaptic models, which helped to understand the information processing of an SNN. Wang and Shi (2020) investigated the electrical activities of memristive Hindmarsh-Rose neurons in H-R neuron network with synaptic fixed time-delay under white Gaussian noise, where its synapse was the coupling of magnetic flux. The results showed that multiple modes in electrical activities of the neuron could be observed by changing the size of time-delay, and appropriate time-delay could induce coherent resonance in electrical activities of the neuron, which could be associated with memory effect and self-adaption in neurons. Yu et al. (2020) constructed a cortical neuronal network with synaptic fixed time-delay, where its synapses were chemical synapse models. They discovered that the multiple stochastic resonances reached a peak when synaptic fixed time-delay was at integer multiples of the period of input signal, which was conducive to understanding the ability of brain-like networks to handle weak input signals. It can be concluded that synaptic time-delay has an important influence on the dynamic characteristics of a brain-like network. However, the time-delay of chemical synapse is randomly distributed in the range of 0.1–40 ms from biological experiments, and the time-delay is not fixed. Therefore, the synaptic plasticity models with time-delay still lack bio-interpretability. In our previous work (Liu et al. 2020), we investigated the anti-interference ability of an SFSNN under the magnetic field stimulation. However, our SFSNN was regulated by the synaptic plasticity including excitatory and inhibitory synapses without time-delay. On this basis, the purpose of this study is to construct a brain-like model with more bio-interpretable synaptic time-delay to evaluate its information processing abilities based on the anti-interference function. Therefore, combining excitatory and inhibitory synapses, we constructed a complex spiking neural network (CSNN) with synaptic random time-delay, in which the topology had scale-free property and small-world property, and the nodes were represented by an Izhikevich neuron model. Then, we comparatively investigated the information processing abilities of CSNNs with different types of synaptic time-delay based on the anti-interference function under different interference, and discussed the mechanism of this function. The main contributions of our work are as follows.

  1. (1)

    To improve bio-interpretability of brain-like models, we construct an CSNN with synaptic random time-delay, in which the topology has scale-free property and small-world property, and the nodes are represented by Izhikevich neurons.

  2. (2)

    Using two indicators of the anti-interference function and three kinds of noise, our simulation results consistently verify an CSNN with synaptic random time-delay outperforms an CSNN with synaptic fixed time-delay, which in turn outperforms an CSNN with synaptic none time-delay. This implies that brain-like networks with more bio-interpretable synaptic time-delay have stronger information processing abilities.

  3. (3)

    Our discussion indicates that synaptic plasticity is the intrinsic factor of the anti-interference function of CSNNs with different types of synaptic time-delay. The synaptic random time-delay makes an CSNN present better topological characteristics, which can improve the information processing ability of a brain-like network. It implies that synaptic time-delay is a factor that affects the anti-interference function at the level of performance.

The rest of this paper is organized as follows: “Construction of CSNNs” section provides a method to construct CSNNs with synaptic time-delay. “Anti-interference function of CSNNs with synaptic time-delay” section investigates the information processing abilities of CSNNs with different types of synaptic time-delay. “Discussion” section discusses the neural information processing in CSNNs under interference. Finally, the conclusion is presented in “Conclusion” section.

Construction of CSNNs

The CSNNs are constructed, in which the topology is a topology of complex network involving scale-free property and small-world property, the nodes are represented by Izhikevich neurons, and the edges are represented by synaptic plasticity with time-delay including excitatory and inhibitory synapses.

Generation of a topology of complex network

A topology of complex network with scale-free property and small-world property is generated based on the Barrat-Barthelemy-Vespignani (BBV) algorithm.

1. Theory and methodology

(i) BBV algorithm

The BBV algorithm (Barrat et al. 2004) models the dynamic growth of the local edge weights by adding new nodes during the generation of a network. An improved BBV algorithm (Wang and Jin 2012) not only yields the performance of the original BBV algorithm but also can adjust the clustering coefficients over a larger range. According to the improved BBV algorithm, the probability of adding a new node in the network is p, where \( p\in (0,1] \). The networks with different topological characteristics can be obtained by adjusting p.

(ii) Scale-free property

The research (Barrat et al. 2004) has shown that the degree distribution of a scale-free network follows a power-law distribution, and power-law exponent \( \gamma \) is between two and three. The probability that a node is connected to other k nodes is defined as follows:

$$\begin{aligned} P(k)\sim {k^{-\gamma }} \end{aligned}$$
(1)

(iii) Small-world property

Combining the advantages of regular networks and ER random graphs, a network presents the small-world property when the average clustering coefficient is high, and the average shortest path length is short (Watts and Strogatz 1998). The small-world property \( \sigma \) can be quantitatively analyzed as follows:

$$\begin{aligned} \sigma =\dfrac{C_{real}/C_{random}}{L_{real}/L_{random}} \end{aligned}$$
(2)

where \( C_{real} \) and \( C_{random} \) are the average clustering coefficient of the real network and its corresponding random network, respectively; \( L_{real} \) and \( L_{random} \) are the average shortest path length of the real network and its corresponding random network, respectively. When \( \sigma >1 \), the network presents the small-world property.

The average clustering coefficient C reflects the compactness of connection in the network, which is defined as follows:

$$\begin{aligned} C=\dfrac{1}{N}\sum _{i=1}^{N}\frac{2u_{i}}{e_{i}(e_{i}-1)} \end{aligned}$$
(3)

where \( e_{i} \) is the degree of node i; \( u_{i} \) is the number of connected edges between node i and its adjacent nodes; and N is the total number of nodes.

The average shortest path length L reflects the efficiency of information transmission of the network, which is defined as follows:

$$\begin{aligned} L=\dfrac{1}{N(N-1)}\sum _{i,j\in {V}, i\ne {j}}d_{ij} \end{aligned}$$
(4)

where \( d_{ij} \) is the shortest path length between node i and node j.

2. Parameters setting and simulation results

In the BBV algorithm, an appropriate selection of the parameter p is required for our topology of complex network by observing scale-free property and small-world property. To select p, we performed simulations of the network characteristics for different p. p was increased from 0.1 to 1.0 with steps of 0.1. For each p , we performed five realizations since the network generated by the BBV algorithm was stochastic in the form of connection under different probabilities of adding a new node p . Thus, we presented the averages of five simulation results in this paper. The power-law exponent \( \gamma \) and the small-world property \( \sigma \) of these networks were calculated according to Equations 1 and 2, respectively. The averages and standard deviations of five results are shown in Table 1.

Table 1 Topological property of complex networks for different p
Full size table

Biological studies (Eguiluz et al. 2005; He et al. 2010) reported that the power-law exponent was about two for a functional brain network of humans. From Table 1, the power-law exponent \( \gamma =2.15 \) is most consistent with biological conclusions, and the network has small-world property \( \sigma =1.2032 \) when \( p=0.3 \). However, we also observe that the network has the highest small-world property \( \sigma =1.3954 \) when \( p=0.8 \). Furthermore, we consider the anti-interference function as an indicator to select an appropriate p. According to the simulation results, CSNNs with \( p=0.3 \) outperform CSNNs with \( p=0.8 \) in terms of the anti-interference function. The detailed simulations can be seen in “Anti-interference function with different probabilities of adding a node” section. Thus, we select \( p=0.3 \) for our study.

Izhikevich neuron model

In this study, we use Izhikevich (Izhikevich 2003) neuron model as the nodes of the network concerning its advantages of good bio-interpretability and low computational complexity. The model can be described as follows:

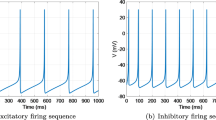
$$\begin{aligned} \begin{aligned}&\frac{dv}{dt}=0.04v^2+5v+140-u+I_{ext}+I_{syn} ,\\&\frac{du}{dt}=a(bv-u) ,\\&if\ v\ge 30, \, \ then {\left\{ \begin{array}{ll} v\leftarrow c\\ u\leftarrow u+d \end{array}\right. } \end{aligned} \end{aligned}$$
(5)

where v represents the neuronal membrane potential; u represents the recovery variable for the membrane voltage; \( I_{ext} \) represents external current; \( I_{syn} \) represents the sum of synaptic currents; and a, b, c, and d are four dimensionless parameters. Each neuron can be modeled as excitatory or inhibitory by controlling these dimensionless parameters. In this study, we use regular spiking (RS) and low-threshold spiking (LTS) firing patterns as the excitatory and inhibitory neurons in our CSNNs, respectively (Izhikevich 2004). For excitatory neuron: \( a=0.02 \), \( b=0.2 \), \( c=-65 \), and \( d=8 \). For inhibitory neuron: \( a=0.02 \), \( b=0.25 \), \( c=-65 \), and \( d=2 \). The different firing patterns of the neurons are shown in Fig. 1.

Fig. 1
figure 1

Firing patterns for Izhikevich neurons. a Excitatory firing pattern. b Inhibitory firing pattern

Full size image

Synaptic plasticity model with time-delay

Combining excitatory and inhibitory synapses, a chemical synaptic plasticity model with time-delay is introduced. The model can be described as follows:

$$\begin{aligned} \begin{aligned}&I_{syn}=g_{syn}r(V_{syn}-V_{post}) ,\\&\frac{dr}{dt}=\alpha T(1-r)-\beta r ,\\&T=\frac{1}{1+exp(-V_{pre}(t-\tau ))} \end{aligned} \end{aligned}$$
(6)

where \( I_{syn} \) is the synaptic current; \( g_{syn}(t) \) is the synaptic conductance; \( V_{post} \) is the membrane potential of the postsynaptic neuron; \( V_{syn} \) is the reversible synaptic potential; \( V_{pre} \) is the membrane potential of the presynaptic neuron; r is the fraction of receptor binding; T is the concentration of the neurotransmitter; \( \alpha \) and \( \beta \) are the forward and reverse rate constants of neurotransmitter binding, respectively; and \( \tau \) is the time-delay in synaptic transmission. The excitatory and inhibitory synaptic plasticity regulate the information transmission among neurons through synaptic conductance, for which the rules are as follows:

(i) If a postsynaptic neuron j does not receive the action potential of a presynaptic neuron i, the excitatory and inhibitory synaptic conductance is exponentially decreased as follows:

$$\begin{aligned} \tau _{ex}\frac{dg_{ex}}{dt}=-g_{ex}, \tau _{in}\frac{dg_{in}}{dt}=-g_{in} \end{aligned}$$
(7)

where \( g_{ex} \) and \( g_{in} \) are the synaptic conductance; and \( \tau _{ex} \) and \( \tau _{in} \) are the decay constants of the synaptic conductance.

(ii) If a postsynaptic neuron j receives the action potential of a presynaptic neuron i, the excitatory and inhibitory synaptic conductance is generated by STDP modification as follows:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} &{}{g_{ex}(t)}\rightarrow {g_{ex}(t)}+{{\bar{g}}_{ex}}\\ &{}{\bar{g}}_{ex}\rightarrow {w_{ij}}*g_{max} \end{array}\right. } \end{aligned}, \begin{aligned} {\left\{ \begin{array}{ll} &{}g_{in}(t)\rightarrow g_{in}(t)+{\bar{g}}_{in}\\ &{}{\bar{g}}_{in}\rightarrow {m_{ij}}*g_{max} \end{array}\right. } \end{aligned} \end{aligned}$$
(8)

where \(\bar{g}_{ex}\) and \(\bar{g}_{in}\) are the increments of the synaptic conductance, respectively; \( g_{max} \) is the upper limit on the synaptic weight; \( w_{ij} \) and \( m_{ij} \) are the synaptic correction functions as follows:

$$\begin{aligned} w_{ij}= & {} {\left\{ \begin{array}{ll} A_+\exp \! (\Delta t/\tau _+) , \, \Delta t<0\\ -A_-\exp \! (\Delta t/\tau _-), \, \Delta t\ge 0 \end{array}\right. },\nonumber \\ m_{ij}= & {} {\left\{ \begin{array}{ll} -B_+\exp \! (\Delta t/\tau _+) , \, \Delta t<0\\ B_-\exp \! (\Delta t/\tau _-), \, \Delta t\ge 0 \end{array}\right. } \end{aligned}$$
(9)

where \( \Delta t \) is the neuronal firing interval; \( \tau _+ \) and \( \tau _- \) are the time interval of neuron firing before and after synaptic strengthening and synaptic weakening, respectively; \( A_+ \) and \( A_- \) are the maximum and minimum correction values of the excitatory synaptic conductance, respectively; and \( B_+ \) and \( B_- \) are the maximum and minimum correction values of the inhibitory synaptic conductance, respectively. In our simulation, we use the total correction value divided by the logarithm to determine the parameters (Song et al. 2000): \( A_{+}=0.1 \), \( A_{-}=0.105 \), \( B_{+}=0.02 \), \( B_{-}=0.03 \), and \( \tau _+=\tau _-=20 \) ms.

Biological researches showed that the dynamic range of the synaptic time-delay is 0.1–40 ms (Swadlow 1985, 1988, 1992). Hence, the synapses with random time-delay are introduced into our synaptic plasticity model, in which random time-delay follows a Poisson distribution. The details are presented in “Anti-interference function of CSNNs with synaptic random time-delay” section.

Construction process of CSNNs

The construction and analysis of CSNNs were carried out on a PC with a 2.50 GHz CPU and 8 GB RAM. The construction process was as follows.

  1. 1.

    We constructed CSNNs with 500, 800, and 1000 nodes, and investigated their anti-interference function. Our simulation results showed that their anti-interference function was almost the same. Thus, we selected a complex network with 500 nodes as the topology of our CSNNs.

  2. 2.

    We constructed an CSNN using 500 excitatory or inhibitory Izhikevich neuron models as the nodes, and they were randomly distributed according to the ratio 4:1 from the biological result (Vogels et al. 2011).

  3. 3.

    We introduced random time-delay into the synaptic plasticity model which combined excitatory and inhibitory synapses, and this model represented the edges of connected nodes.

Anti-interference function of CSNNs with synaptic time-delay

The information processing abilities of CSNNs with different types of synaptic time-delay are evaluated based on the anti-interference function under different interference.

External interference and indicators of the anti-interference function

Three kinds of external interference are introduced to verify the anti-interference function. Two indicators of the anti-interference function are introduced to evaluate the anti-interference function.

External interference

We use three kinds of noise including white Gaussian noise, impulse noise, and electric field noise to verify the anti-interference function of CSNNs.

1. White Gaussian noise

The amplitude of white Gaussian noise follows a Gaussian distribution, which is described as follows:

$$ f(x) =\frac{1}{\sqrt{2\pi }\sigma }exp{-\frac{(x-\mu )^2}{2\sigma ^2}} $$
(10)

In our simulation, this noise as current interference was applied to all of neuronal current \( I_{ext} \) according to Equation 5 throughout the simulation.

2. Impulse noise

Impulse noise is an irregular and discontinuous signal composed of impulse peaks, which is described as follows:

$$ s(t)= {\left\{ \begin{array}{ll} A_{s}, \, t\in {[T_{0}, T_{0}+T]}\\ 0, \, else \end{array}\right. } $$
(11)

In our simulation, this noise as current interference was applied to all of neuronal current \( I_{ext} \) according to Equation 5 throughout the simulation.

3. Electric field noise

An external low-frequency alternating electric field is described as follows:

$$\begin{aligned} \triangle {V(t)}=\psi \dfrac{A}{\omega }sin({\omega }t) \end{aligned}$$
(12)

In our simulation, this noise as voltage interference was applied to all of neuronal membrane potential v according to Equation 5 throughout the simulation.

Indicators of the anti-interference function

We use two indicators of the relative change in the firing rate and the correlation between membrane potentials to evaluate the anti-interference function of CSNNs.

1. The relative change in the firing rate

The firing rate refers to the firing frequency per unit time of a neuron. The relative change in the firing rate represents the degree of change in the firing rate before and after interference. The mean relative change in the firing rate across the network \( \delta \) is defined as:

$$\begin{aligned} \delta \%=\frac{\mid f_{q}-f_{p}\mid }{f_{p}}*100\% \end{aligned}$$
(13)

where \( f_{p} \) and \( f_{q} \) represent the mean firing rates in the network before and after interference, respectively. The smaller the value of \( \delta \), the smaller the change in the neuronal firing rate before and after interference, and the stronger the anti-interference ability of the network.

2. The correlation between membrane potentials

The correlation between membrane potentials reflects the similarity between the membrane potentials of the neurons before and after interference. The mean correlation between membrane potentials across the network \( \rho \) is defined as:

$$\begin{aligned} \rho (\tau )=\frac{\sum \limits _{t=t_1}^{t_2-\tau +1}x_p(t)x_q(t+\tau )}{\sqrt{\sum \limits _{t=t_1}^{t_2-\tau +1}x_p^2(t) \sum \limits _{t=t_1}^{t_2-\tau +1}x_q^2(t+\tau )}} \end{aligned}$$
(14)

where \( x_{p} \) and \( x_{q} \) are the mean membrane potentials of neurons in the network before and after interference, respectively; \( [t_{1}, t_{2}] \) is the experimental period. The larger the value of \( \rho \), the smaller the change in the membrane potential before and after interference, and hence the stronger the anti-interference ability of the network.

Anti-interference function of CSNNs with synaptic random time-delay

The anti-interference function of CSNNs with synaptic random time-delay are investigated based on two indicators. And the optimal mean of random time-delay distribution \( \lambda \) and an appropriate probability of adding a node p are obtained through comparative analysis.

Anti-interference function with different means of random time-delay distribution

We investigate the anti-interference function of CSNNs with different means of random time-delay distribution under different interference based on two indicators \( \delta \) and \( \rho \) for the probability of adding a node \( p=0.3 \).

1. Anti-interference function based on \( \delta \)

Concerning that the dynamic range of biological synaptic time-delay is 0.1–40 ms, we investigate the anti-interference function of CSNNs, in which synaptic random time-delay follows a Poisson distribution, and its mean is represented by the parameter \( \lambda \) ranged from 5 to 35 ms with steps of 5 ms. Three kinds of noise with different intensities were applied to CSNNs: the intensity range of white Gaussian noise was [0, 24] dBW with steps of 3dBW, the amplitude range of impulse noise was [0, 8] mA with steps of 1mA, and the strength range of electric field noise was [0, 48] mV with steps of 6mV. The averages of five results for \( \delta \) of CSNNs with different \( \lambda \) under different interference within 1000 ms are shown in Fig. 2.

Fig. 2
figure 2

Comparison of \( \delta \) for CSNNs with different \( \lambda \) under different interference. a White Gaussian noise. b Impulse noise. c Electric field noise

Full size image

We analyze the simulation results shown in Fig. 2 from two perspectives.

  1. (i)

    From the perspective of noise intensity, we can see that the values of \( \delta \) gradually increase as the intensities of three kinds of noise gradually increase. When the intensity of white Gaussian noise is in the range [0, 6] dBW, the impulse amplitude is in the range [0, 3] mA, and the strength of electric field is in the range [0, 24] mV, the values of \( \delta \) for different CSNNs are less than 20%. When the intensities of three kinds of noise exceed the above ranges, the values of \( \delta \) increase quickly. These results indicate that CSNNs with different \( \lambda \) have their own anti-interference function against different interference, which decrease gradually with an increase in the noise intensity.

  2. (ii)

    From the perspective of the distribution of synaptic random time-delay, when the \( \lambda \) of an CSNN with synaptic time-delay is 20 ms, the \( \delta \) is lower than those of the other six CSNNs with their corresponding \( \lambda \) under three kinds of noise. This indicates that an CSNN with \( \lambda =20 \) ms can yield the best performance in the anti-interference function. In addition, the more the \( \lambda \) is far from 20 ms, the larger the \( \delta \) is, the anti-interference function of CSNNs is correspondingly worse.

2. Anti-interference function based on \( \rho \)

Fig. 3
figure 3

Under the same simulation conditions as \( \delta \), the averages of five results for \( \rho \) of CSNNs with different \( \lambda \) under different interference are shown in Fig. 3. Comparison of \( \rho \) for CSNNs with different \( \lambda \) under different interference. a White Gaussian noise. b Impulse noise. c Electric field noise

Full size image

We also analyze the simulation results shown in Fig. 3 from two perspectives.

  1. (i)

    From the perspective of noise intensity, we can see that the values of \( \rho \) show downward trend as the intensities of three kinds of noise gradually increase. When the intensity of white Gaussian noise is in the range [0, 12] dBW, the impulse amplitude is in the range [0, 6] mA, and the strength of electric field is in the range [0, 6] mV, the values of \( \rho \) for different CSNNs are larger than 0.7. When the intensities of three kinds of noise exceed the above ranges, the values of \( \rho \) decrease quickly. These results indicate that CSNNs with different \( \lambda \) have their own anti-interference function against different interference, which decrease gradually with an increase in the noise intensity.

  2. (ii)

    From the perspective of the distribution of synaptic random time-delay, when the \( \lambda \) of an CSNN with synaptic time-delay is 20 ms, the \( \rho \) is larger than those of the other six CSNNs with their corresponding \( \lambda \) under three kinds of noise. This indicates that an CSNN with \( \lambda =20 \) ms can yield the best performance in the anti-interference function. In addition, the more the \( \lambda \) is far from 20 ms, the smaller the \( \rho \) is, the anti-interference function of CSNNs is correspondingly worse.

According to the analysis of \( \delta \) and \( \rho \) above, it can be concluded that an CSNN with \( \lambda =20 \) ms has the best anti-interference performance. Hence, an CSNN with \( \lambda =20 \) ms is the optimal in this study.

Anti-interference function with different probabilities of adding a node

We have analyzed the probabilities of adding a node p in “Generation of a topology of complex network”, and shown that the scale-free property of an CSNN conforms to biological conclusions when \( p=0.3 \), and the small-world property of an CSNN is highest when \( p=0.8 \). Here, we further investigate an appropriate p based on the anti-interference function. Under the same simulation conditions as \( \delta \) and \( \lambda =20 \) ms, the averages and standard deviations of five results of \( \delta \) and \( \rho \) of CSNNs with \( p=0.3 \) and \( p=0.8 \) under different interference are shown in Tables 2, 3, and 4.

Table 2 Comparison of the anti-interference function of CSNNs with different p under white Gaussian noise
Full size table
Table 3 Comparison of the anti-interference function of CSNNs with different p under impulse noise
Full size table
Table 4 Comparison of the anti-interference function of CSNNs with different p under electric field noise
Full size table

From Tables 2, 3, and 4, under different interference, the values of \( \delta \) in CSNNs with synaptic random time-delay for \( p=0.3 \) are smaller than that for \( p=0.8 \). The values of \( \rho \) in CSNNs with synaptic random time-delay for \( p=0.3 \) are larger than that for \( p=0.8 \). These results indicate that an CSNN with \( p=0.3 \) outperforms an CSNN with \( p=0.8 \) in terms of the anti-interference function. Hence, a complex network with \( p=0.3 \) is an appropriate topology of CSNNs in this study.

Anti-interference function of CSNNs with different types of synaptic time-delay

Three types of synaptic time-delay including random time-delay, fixed time-delay, and none time-delay are introduced to further investigate the effect of synaptic time-delay on the anti-interference function in our study.

1. Anti-interference function based on \( \delta \)

The probabilities of adding a node of all CSNNs with different types of synaptic time-delay are \( p=0.3 \). The \( \lambda \) of synaptic random time-delay of an CSNN is 20 ms, the synaptic fixed time-delay of an CSNN is 20 ms, and an CSNN is without synaptic time-delay. Under the same simulation conditions as \( \delta \) above, the averages of five results for \( \delta \) of CSNNs with different types of synaptic time-delay under different interference are shown in Fig. 4.

Fig. 4
figure 4

Comparison of \( \delta \) for CSNNs with different types of synaptic time-delay. a White Gaussian noise. b Impulse noise. c Electric field noise

Full size image

We analyze the simulation results shown in Fig. 4 from two perspectives.

  1. (i)

    From the perspective of noise intensity, we observe that the values of \( \delta \) gradually increase as the intensities of three kinds of noise gradually increase. When the intensity of white Gaussian noise is in the range [0, 6] dBW, the impulse amplitude is in the range [0, 3] mA, and the strength of electric field is in the range [0, 30] mV, the values of \( \delta \) for different CSNNs are less than 20%. When the intensities of three kinds of noise exceed the above ranges, the values of \( \delta \) increase gradually. These results indicate that CSNNs with different types of synaptic time-delay have their own anti-interference function against different interference, which decrease gradually with an increase in the noise intensity.

  2. (ii)

    From the perspective of different types of synaptic time-delay, the \( \delta \) of an CSNN with synaptic random time-delay is lower than that of an CSNN with synaptic fixed time-delay under three kinds of noise, and the \( \delta \) of an CSNN with synaptic fixed time-delay is lower than that of an CSNN with synaptic none time-delay. These results indicate that an CSNN with synaptic random time-delay outperforms an CSNN with synaptic fixed time-delay, which in turn outperforms an CSNN with synaptic none time-delay in terms of the anti-interference performance.

2. Anti-interference function based on \( \rho \)

Under the same simulation conditions as \( \delta \), the averages of five results for \( \rho \) of CSNNs with different types of synaptic time-delay under different interference are shown in Fig. 5.

Fig. 5
figure 5

Comparison of \( \rho \) for CSNNs with different types of synaptic time-delay. a White Gaussian noise. b Impulse noise. c Electric field noise

Full size image

We analyze the experimental results shown in Fig. 5 from two perspectives.

  1. (i)

    From the perspective of noise intensity, we can see that the values of \( \rho \) show downward trend as the intensities of three kinds of noise gradually increase. When the intensity of white Gaussian noise is in the range [0, 9] dBW, the impulse amplitude is in the range [0, 5] mA, and the strength of electric field is in the range [0, 12] mV, the values of \( \rho \) are larger than 0.7. When the intensities of three kinds of noise exceed the above ranges, the values of \( \rho \) decrease gradually. These results indicate that CSNNs with different types of synaptic time-delay have their own anti-interference function against three kinds of noise, which decrease gradually with an increase in the noise intensity.

  2. (ii)

    From the perspective of different types of synaptic time-delay, the \( \rho \) of an CSNN with synaptic random time-delay is larger than that of an CSNN with synaptic fixed time-delay, and the \( \rho \) of an CSNN with synaptic fixed time-delay is lower than that of an CSNN with synaptic none time-delay. These results indicate that an CSNN with synaptic random time-delay outperforms an CSNN with synaptic fixed time-delay, which in turn outperforms an CSNN with synaptic none time-delay in terms of the anti-interference performance.

From the simulation results from “Anti-interference function of CSNNs with synaptic time-delay” section, our simulations using two indicators and three kinds of noise consistently verify that: (1) The optimal \( \lambda \) is 20 ms, and an appropriate p is 0.3 for our study. (2) All CSNNs with synaptic plasticity have the anti-interference function. (3) An CSNN with synaptic time-delay outperforms an CSNN with synaptic none time-delay in terms of the anti-interference function. (4) An CSNN with synaptic random time-delay that conforms to the characteristics of distribution of biological synaptic time-delay has the best anti-interference function. It implies that synaptic time-delay with bio-interpretability can improve information processing abilities. Also, we verify biological conclusions in reverse from the perspective of a brain-like model.

Discussion

To explore the mechanism by which synaptic time-delay affects information processing ability, we discuss the neural information processing in CSNNs under an example of white Gaussian noise, which involves the evolution of neuronal firing rate, synaptic weight, and topological characteristics.

Firing rate

To analyze the effect of external noise on the firing rate of neurons, we reveal the changes of firing rate of a single neuron and the evolution process of the entire CSNN under external noise.

Firing rate under white Gaussian noise with 12dBW

White Gaussian noise with 12dBW as an example is applied to CSNNs, and the firing sequences of a neuron after interference are shown in Fig. 6.

Fig. 6
figure 6

Firing sequences of Izhikevich neurons under interference. a Excitatory firing. b Inhibitory firing

Full size image

Compared Fig. 6 with Fig. 1, we can see that the interspike intervals of neurons are obviously changed under interference, which indicates that noise affects the firing activity of neurons. The average firing rate of an CSNN within a time window of 100 ms is taken to represent the firing rate at a given moment. According to the averages of five results, the evolution of the average firing rate in CSNNs with different types of synaptic time-delay with the simulation time from 100 to 1000 ms with steps of 100 ms is shown in Fig. 7.

Fig. 7
figure 7

Evolution of the average firing rate

Full size image

It can be seen from Fig. 7 that the evolution of average firing rate in CSNNs with different types of synaptic time-delay is different. However, three CSNNs show similar evolutionary trends. In the first 200 ms, the average firing rate of CSNNs with different types of synaptic time-delay decreases significantly. The reason is that noise interference strongly affects neuronal firing at the beginning of the simulation. After 200 ms, the average firing rate gradually stabilizes due to the regulation of CSNNs.

Note that: Actually, we run all the simulations for 1400 ms. However, the simulation results during [1000, 1400] ms remain almost unchanged. Thus, all simulation results during [0, 1000] ms are presented in this paper.

Evolution of firing rate and its change under different intensities of white Gaussian noise

To reveal the effect of different intensities of noise on the firing rate and its \( \delta \) of CSNNs, we simulate the evolution process of firing rate and its \( \delta \) of an CSNN with synaptic random time-delay under different intensities of white Gaussian noise, and present the averages of five results in Fig. 8. The \( \lambda \) of synaptic random time-delay of an CSNN is 20 ms. The intensity range of white Gaussian noise was [0, 24] dBW with steps of 6dBW. The duration of the simulation was 1000 ms. The simulation results during [0, 1000] ms are presented.

Fig. 8
figure 8

The evolution of the average firing rate and its \( \delta \). a Average firing rate. b \( \delta \)

Full size image

It can be seen from Fig. 8a that the evolution of all average firing rate shows the same trend. In the first 200 ms, the average firing rate of an CSNN decreases significantly. After 200 ms, the average firing rate gradually stabilizes. Also, we can observe the average firing rate increases as the increase of noise intensity during the stable phase of [300, 1000] ms. It can be seen from Fig. 8b that the evolution of all \( \delta \) shows the same trend. In the first 200 ms, the \( \delta \) increases intensely. After 200 ms, the \( \delta \) gradually stabilizes. Also, we can observe the \( \delta \) decreases as the increase of noise intensity during the stable phase of [300, 1000] ms.

Synaptic weight

The changes in neuronal firing rate can cause changes in synapse weight according to Equation 8, in which \( \triangle {t} \) relies on the neuronal firing rate of the presynaptic and postsynaptic. The average synaptic weight is the mean of the weights of all synapses in CSNNs. According to the averages of five results, the evolution of the average synaptic weight in CSNNs with different types of synaptic time-delay under white Gaussian noise is shown in Fig. 9.

Fig. 9
figure 9

Evolution of the average synaptic weight

Full size image

It can be seen from Fig. 9 that the evolution of average synaptic weight in CSNNs with different types of synaptic time-delay is different. However, three CSNNs show similar evolutionary trends. In the first 400 ms, the average synaptic weight of CSNNs with different types of synaptic time-delay decreases significantly. After 400 ms, the average synaptic weight gradually stabilizes. Fig. 9 presents the regulation process of synaptic plasticity.

Relationship between the synaptic plasticity and the anti-interference function

To explore the mechanism of information processing abilities of brain-like models, we conduct an association analysis to establish the relationship between the regulation of synaptic plasticity and the anti-interference function.

Evolution of the anti-interference function

Under the interference of white Gaussian noise with 12dBW, the evolution of the anti-interference function including \( \delta \) and \( \rho \) within 1000 ms based on the averages of five results is shown in Fig. 10.

Fig. 10
figure 10

Evolution of the anti-interference function. a Evolution of \( \delta \). b Evolution of \( \rho \)

Full size image

It can be seen from Fig. 10 that an CSNN with synaptic random time-delay outperforms an CSNN with synaptic fixed time-delay, which in turn outperforms an CSNN with synaptic none time-delay in terms of the anti-interference function from an evolutionary perspective, which is consistent with the conclusions of “Anti-interference function of CSNNs with different types of synaptic time-delay” section. However, three CSNNs show similar evolutionary trends. In the first 300 ms, the values of \( \delta \) and \( \rho \) in CSNNs with different types of synaptic time-delay increase significantly. After 300 ms, the stable anti-interference function is gradually formed.

Correlation analysis based on the Pearson correlation coefficient

We establish the relationship between the regulation of synaptic plasticity and the anti-interference function of CSNNs with different types of synaptic time-delay using a Pearson correlation. The Pearson correlation coefficient can reveal a statistical correlation between two samples X and Y. The correlation coefficient \( r_{XY} \) is defined as follows:

$$\begin{aligned} r_{XY}=\frac{\sum \limits _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{(X_i-\overline{X})^2}\sqrt{(Y_i-\overline{Y})^2}} \end{aligned}$$
(15)

The degree of correlation is significant when the absolute value of coefficient is close to one, and the opposite is the case when it is close to zero.

A t-test is used to determine the significance of a sample r and the totality, which is defined as follows:

$$\begin{aligned} t=\frac{r}{\sqrt{(1-r^2)/(n-2)}} \end{aligned}$$
(16)

If the significance level is 0.05, it is marked with “*” ; if the significance level is 0.01, it is marked with “**”.

In this study, X represents the averages of five results of the average synaptic weight in CSNN, recorded every 100 ms, Y represents the averages of five results of \( \delta \) or \( \rho \), recorded every 100 ms, \( n=10 \) represents the total number of samples, and the duration of the simulation was 1000 ms. The results of the correlation analysis between the average synaptic weight and the values of \( \delta \) or \( \rho \) of CSNNs with different types of synaptic time-delay within 1000 ms are shown in Table 5.

Table 5 Pearson correlation coefficients for the average synaptic weight, \( \delta \) and \( \rho \) for CSNNs
Full size table

From Table 5, it can be seen that the average synaptic weight and the values of \( \delta \) and \( \rho \) are significantly correlated at the level of 0.01 (two-sided t-test) for all CSNNs with different types of synaptic time-delay. Our simulation results indicate a significant correlation between the regulation of synaptic plasticity and the anti-interference function. This implies that the synaptic plasticity is the intrinsic factor of the anti-interference function of CSNNs with different types of synaptic time-delay.

Effect of synaptic time-delay on the information processing ability

We further investigate the effect of different types of synaptic time-delay on the information processing abilities of CSNNs under interference using the analysis of topological characteristics. Our CSNNs present scale-free property and small-world property in which the degree distribution follows a power-law distribution with power-law exponent \( \gamma =2.15 \), and small-world property is related to the average clustering coefficient and the average shortest path length. During the dynamic process of simulation, the degree distribution maintains a power-law distribution, while the average clustering coefficient and the average shortest path length vary with time.

The clustering coefficient \( \tilde{C_{i}} \) in a weighted network (Barrat et al. 2004) is defined as follows:

$$\begin{aligned} \tilde{C_{i}}=\frac{1}{s_i(k_i-1)}\sum _{j,k}\frac{(w_{ij}+w_{ik})}{2}a_{ij} a_{jk} a_{ki} \end{aligned}$$
(17)

where \(g_{ij}\) and \(g_{ik}\) are the synaptic weights; \(k_i\) and \(s_i\) are the degree and strength of the node i, respectively; and \(a_{ij}\) is the adjacency matrix. The average clustering coefficient can be used to describe the clustering coefficients of all the neurons in CSNNs.

The shortest path length \( L_{ij} \) in a weighted network (Antoniou and Tsompa 2008) is defined as follows:

$$\begin{aligned} L_{ij}=\underset{\Upsilon (i,j)\in {\Gamma (i,j)}}{min}\left[ \sum _{m,n\in {\Upsilon (i,j)}}\dfrac{1}{g_{mn}}\right] \end{aligned}$$
(18)

where \( g_{mn} \) is the synaptic weight. The average shortest path length can be used to describe the shortest path length all between pairs of nodes in CSNNs.

From Eqs. 17 and 18, the changes of synaptic weight can lead to changes in topological characteristics of the network. According to the averages of five results, the evolution of the average clustering coefficient and the average shortest path length in CSNNs with different types of synaptic time-delay under white Gaussian noise with 12dBW is shown in Fig. 11.

Fig. 11
figure 11

Evolution of topological characteristics. a Average clustering coefficient. b Average shortest path length

Full size image

It can be seen from Fig. 11 that CSNNs with different types of synaptic time-delay have different evolution of topological characteristics under noise interference. Fig. 11a shows that the average clustering coefficient of an CSNN with synaptic random time-delay is higher than that of an CSNN with synaptic fixed time-delay, which in turn is higher than an CSNN with synaptic none time-delay. Fig. 11b shows that the average shortest path length of an CSNN with synaptic random time-delay is shorter than that of an CSNN with synaptic fixed time-delay, which in turn is shorter than an CSNN with synaptic none time-delay. It implies that time-delay is a factor that affects the anti-interference function at the level of performance. According to the theory of complex networks, a network with high average clustering coefficient and short average shortest path length can yield the advantages of more compactness of local connection and higher efficiency of information transmission. Therefore, our simulation results indicate that the synaptic time-delay that more conforms to bio-interpretability can improve the information processing ability of a brain-like network.

Conclusion

The CSNNs with neuronal dynamics regulated by chemical synaptic plasticity were constructed, in which the topology was a topology of complex network including the scale-free property and small-world property, the nodes were represented by an Izhikevich neuron model, and the edges were represented by a synaptic plasticity model with time-delay including excitatory and inhibitory synapses. The information processing abilities of CSNNs with different types of synaptic time-delay were investigated based on the anti-interference function under interference, and the mechanism of this function was discussed. Using two indicators of the anti-interference function and three kinds of noise, our simulation results consistently verify that: (i) From the perspective of anti-interference function, an CSNN with synaptic random time-delay outperforms an CSNN with synaptic fixed time-delay, which in turn outperforms an CSNN with synaptic none time-delay. The results imply that brain-like networks with more bio-interpretable synaptic time-delay have stronger information processing abilities. (ii) The relationship between the regulation of synaptic plasticity and the anti-interference function is established using a Pearson correlation. Our simulation results indicate that the synaptic plasticity and the anti-interference function are significant correlation. It implies that synaptic plasticity is the intrinsic factor of the anti-interference function of CSNNs with different types of synaptic time-delay. (iii) Using the analysis of topological characteristics, our simulation results show that an CSNN with synaptic random time-delay outperforms an CSNN with synaptic fixed time-delay, which in turn outperforms an CSNN with synaptic none time-delay, which has more compactness of local connection and higher efficiency of information transmission. This indicates that synaptic time-delay that more conforms to the bio-interpretability can improve the information processing ability of a brain-like network. Also, it implies that synaptic time-delay is a factor that affects the anti-interference function of a brain-like network at the level of performance. Our founding indicates that brain-like networks with more bio-interpretable synaptic time-delay have stronger information processing abilities. Thus, we verify biological conclusions in reverse from the perspective of a brain-like model. Our research results can improve the ability of a brain-like model to process complex temporal-spatial information, and provide a theoretical foundation to develop computing power of the artificial intelligence. In this study, we comparatively investigate the effects of different types of synaptic time-delay on the information processing abilities of SNNs with the same type of topology based on the anti-interference function. In our future work, we will further investigate the effects of different types of topologies on the information processing abilities of SNNs with synaptic random time-delay. In addition, we will further investigate the effects of bio-rationally distributed Izhikevich neurons with different parameters on the information processing abilities of SNNs.