Spatially constrained adaptive rewiring in cortical networks creates spatially modular small world architectures

Abstract

A modular small-world topology in functional and anatomical networks of the cortex is eminently suitable as an information processing architecture. This structure was shown in model studies to arise adaptively; it emerges through rewiring of network connections according to patterns of synchrony in ongoing oscillatory neural activity. However, in order to improve the applicability of such models to the cortex, spatial characteristics of cortical connectivity need to be respected, which were previously neglected. For this purpose we consider networks endowed with a metric by embedding them into a physical space. We provide an adaptive rewiring model with a spatial distance function and a corresponding spatially local rewiring bias. The spatially constrained adaptive rewiring principle is able to steer the evolving network topology to small world status, even more consistently so than without spatial constraints. Locally biased adaptive rewiring results in a spatial layout of the connectivity structure, in which topologically segregated modules correspond to spatially segregated regions, and these regions are linked by long-range connections. The principle of locally biased adaptive rewiring, thus, may explain both the topological connectivity structure and spatial distribution of connections between neuronal units in a large-scale cortical architecture.

Introduction

Small-world networks, i.e. networks that are highly clustered but at the same time integrated, are remarkably prevalent, both in nature and in man-made systems. Small-worlds have been observed in contexts such as protein networks (Atilgan et al. 2004), amino acids (Vendruscolo et al. 2001), social networks (Travers and Milgram 1969), metabolic networks (Wagner and Fell 2001), ecological networks such as food webs (Montoya and Solé 2002), and in the commonly studied neural network of Caenorhabditis elegans (Achacoso and Yamamoto 1991). Also, the mental lexicon has small-world structure, according to the graph of co-occurrences of words in sentence contexts (Ferrer i Cancho and Solé 2001). The properties of this structure influence the speed of retrieval from the mental lexicon for recognition (Chan and Vitevitch 2009) and production of spoken word (Chan and Vitevitch 2010), as well as long and short term memory retrieval (Vitevitch et al. 2012).

The observation that small-world characteristics are pervasive in mental representation raises the issue of whether this property is a consequence of the architecture underlying information processing. Most importantly in this respect, such networks have recently been observed in the anatomical and functional connectivity of the human brain (He et al. 2007; Sporns 2011; Bullmore and Bassett 2011; Gallos et al. 2012). In addition, the latter has a modular topology (Rubinov et al. 2009b). This topology describes a small-world network that may be partitioned into a community structure in which distinct regions can be distinguished as having dense intraconnections and sparse interconnections. Such a structure supports dynamics that facilitate information processing (Latora and Marchiori 2001); whereas segregation facilitates independent processing within modules, integration allows for the fast propagation of information between them.

Segregation in small-world networks is expressed by a high value of the average clustering coefficient, $C$, a quantity which measures the degree of local connectedness around individual nodes. Integration is expressed by a low value of average shortest path length, $L$. This measure describes the efficiency with which all nodes of a network are interconnected, and is therefore a measure of global connectedness. To qualify as a small-world network the value of average clustering coefficient must be considerably greater than that for a corresponding (similar or equal number of nodes and connections) random network, such that $C \gg C_{\text {random}}$, whereas the value of average shortest path length must be relatively close to the value of that for a corresponding random network, such that $L \gtrsim L_{\text {random}}$.

In order to understand the principle by which modular small-world structure is formed in the brain, before developing realistic and therefore complex model processes, very simple, idealised ones are sometimes helpful. They allow us to understand which features are robust to variations in the specifics of the model process. Let us therefore consider whether some popular procedures for generating small-world structures would qualify as simple models of the evolving networks in the brain.

Consider first Watts and Strogatz’ (WS) widely known algorithm for obtaining topological small-world networks (Watts and Strogatz 1998). It starts from an initially regular-type lattice on the circle, which has a high clustering coefficient and high average path length—the network has local connectedness but is without global connectedness. The algorithm selects each edge once, and rewires at random with probability p. This type of rewiring results in phase transitions of these two network characteristics. As the probability for random rewiring increases from zero to one, there is firstly a gain of global connectedness, and secondly a loss of local connectedness. Within the interval between the two transitions a small-world network exists since it has both properties of global and local connectedness.

Despite its elegance, the WS algorithm cannot qualify as a principle of how brain network structure is formed. The assumed initial regular structure in the WS algorithm is not supported by physiological evidence (Innocenti and Price 2005). Furthermore, although the resulting network structure is clustered, it is not modular. In addition, brain structure is not fixed after a few rewirings, but is evolving continuously. In the WS algorithm, continued rewiring would create a fully random network. Finally, whereas in the WS algorithm, the rewiring affects arbitrarily and randomly chosen nodes, in brains rewiring is not arbitrary but adaptive: the creation and elimination of synapses is a result of patterns of neural activity (Zhang and Poo 2001).

A simple model process that satisfies the requirements of random initial structure and adaptive rewiring was initially proposed a decade ago by Gong and van Leeuwen (2004). It shares with the WS algorithm the robustness of structure and reliability of the self-organization process that yields a network with a small-world topology. The process begins from a network of randomly coupled nodes; the probability of a connection between pairwise nodes is uniform. The dynamics of nodes are governed by identical nonlinear maps operating in a chaotic regime. Connections are then iteratively rewired according to what can be regarded as a realisation of the principle that neurons which “fire together, wire together”, as proposed by Hebb (1949); adaptive rewiring according to the degree of temporal pairwise synchrony of activity between pairs of nodes. Repeatedly pruning connections between asynchronous nodes, while establishing new connections between synchronous ones gradually shapes the network into a modular small-world (Rubinov et al. 2009b).

In order to address the universality of the model, subsequent developments have relaxed some of the original constraints on the adaptive rewiring process, which improved the functioning of the model process. Instead of using coupled maps, model neurons have been introduced (Kwok et al. 2007), resulting in more realistic patterns of activity, including transient bursting observed in developing neuronal architectures (Nakatani et al. 2003). Network size and connectivity density—the number of nodes and the number of connections relative to the maximum possible number of connections, respectively—were not required to be constant, but were allowed to increase by random attachment (Gong and Leeuwen 2003). This resulted in networks that have, in addition to small-world, scale-free characteristics (Barabási et al. 1999). The psychological relevance of this property is clearly in evidence in the mental lexicon (Ferrer i Cancho and Solé 2001; Vitevitch et al. 2012).

The robustness of the adaptive rewiring process was previously investigated under changes of the network size and connectivity density (van den Berg et al. 2012). The process of forming small-worlds has a critical lower boundary with respect to the neural connectivity. If connections become too sparse, no small-world network results. However, the critical boundary was only a small scaling factor above the percolation threshold for random networks. This implies that the process is close to optimality with respect to efficiency of connection usage. In addition, the behaviour of the network at or below this critical threshold was related to some important characteristics of brain diseases such as schizophrenia (van den Berg et al. 2012), including phenomena such as intermittent recovery and hyperglobality (Rubinov et al. 2009a). Above this critical lower boundary, small-world emergence has been shown to be robust with respect to network size $n={300,400,\ldots ,1,000}$.

Despite these developments, there remains an important limitation to the applicability of adaptive rewiring as a model of real, biological cortices: adaptive rewiring is missing any notion of metric space. Embedding this process into a metric space may allow models to incorporate realistic characteristics of cortical networks, such as metabolic cost and wiring length (Laughlin et al. 1998; Cherniak 1994).

The unit sphere is chosen as the space in which to embed our adaptively rewiring networks. The sphere serves as a highly idealized representation of the sheet-like structure of the cortex that, in combination with the nodes being distributed as evenly as possible over its surface, leads to a spatial embedding with maximal symmetry and isotropy. These properties serve to minimize any biases due to the spatial embedding on the rewiring dynamics of individual nodes.

We then incorporate the cost of spatial distance into the adaptive rewiring process. Our choice of distance cost functions is motivated by the relative abundance of short-range corticocortical connections over long-range ones (He et al. 2007; Bullmore and Bassett 2011; Watts and Strogatz 1998). Accordingly, we use cost functions which penalise long-range connections and encourage short-range connections. We consider three monotonically increasing cost functions of distance: linear, concave up, and concave down. The linear cost function accumulates cost uniformly over distance while the concave up function accumulates cost more rapidly at longer distances, and vice versa for the concave down function. Thus, relative to the linear cost function, concave up provides an increased penalty for long-range connections, whilst concave down provides a reduced penalty on long-range connections.

We consider the effect, as seen by simulation study, that these different cost functions of distance have on the evolution of the network in space under an adaptive rewiring process. In Materials and Methods we describe the spatially biased rewiring process, define spatially adaptive rewiring functions, and introduce topological and spatial measures of network structure. In the Results section we present measures of the evolution of the topological and spatial structure of networks obtained from simulations of the spatially biased rewiring processes along with the non-spatial one. This is repeated for changes in connectivity density. In the Discussion the outcomes of the results are summarised. The “Appendix” includes our method for generating evenly distributed points on a sphere and verification of its accuracy, along with formal definitions of network measures.

Materials and methods

The evolving networks we study in this paper have $n=500$ nodes and $E$ undirected edges, with $E=\kappa \frac{n(n-1)}{2}$ where $\kappa \in (0,1]$ is the connection density; $\kappa$ takes the value of 0.1, i.e. 10 % connectivity density, except for our study of dependence on connection density where it ranges from 2.5 to 5 %. Previous non-spatial implementations of the adaptive rewiring process with $\kappa =0.1$ were found to yield small-world structure (Gong and van Leeuwen 2004; Berg and Leeuwen 2004).

The $n$ nodes of the network are assigned positions on a unit sphere that are approximately evenly distributed over the surface with sufficient accuracy for our purpose. To distribute the $n$ points on a sphere, we use a simple iterative algorithm based on repulsion. Beginning from an initial set of points drawn randomly from a uniform distribution over the sphere, on each iteration the point “most central” is selected, all other points are then repelled by a linearly dampening force function. See “Appendix 1” for details of implementation. Individual approximations of evenly distributed points on the sphere are used for independent runs.

As reference points for network structure, we also apply network measures to a random network and a regular type network on the sphere, with the same $n$ and $\kappa$ as our evolving networks. The random graph is generated by selecting $E$ pairs of vertices uniformly at random from all possible pairs and connecting each pair with an edge (Newman 2010). Note that the graph will (with very high probability) be connected if $E\gg \frac{\log {(n})}{n}$ (Bollabas 1985), which is the case for all networks we study here. The regular type network is constructed such that each node is connected to its $k=\kappa n$ nearest neighbours on the unit sphere. Note that, unlike the ring-like regular networks used by Watts and Strogatz (1998), it is not the case that $L_{\text {regular}}\gg L_{\text {random}}$ for our regular networks because of the spherical geometry and the relatively high connectivity density of our networks.

Dynamics and rewiring rule

The dynamics upon which rewiring is based is a well-established class of dynamical systems, that of coupled maps (Kaneko 1993; Atmanspacher and Scheingraber 2005). On these networks, the nodes are assigned identical nonlinear maps $f:[-1,1] \rightarrow [-1,1]$. The states of the nodes are updated iteratively using the following diffusive coupling scheme:

$$\begin{aligned} x_i(t+1) = f(x_i(t)) + \frac{\epsilon }{| \mathcal {N}_i |} \sum _{j \in \mathcal {N}_i} [f(x_j(t))-f(x_i(t))], \end{aligned}$$

(1)

for $i = 1,2,\ldots ,n$, $\epsilon$ is the coupling strength, $\mathcal {N}_i$ denotes the set of neighbours of node $i$, i.e. the set of all nodes that connect to node $i$, and $| \mathcal {N}_i |$ is the cardinality of the set $\mathcal {N}_i$, i.e. the number of neighbours to node $i$. Connections are undirected, i.e. $i$ connects to $j$ if and only if $j$ connects to $i$. Function $f$ is the logistic map

$$\begin{aligned} f(y) = 1 -\alpha y^2 \end{aligned}$$

with parameter $\alpha \in [0,2]$. As demonstrated in Figure 2 of Rubinov et al. (2009b), the logistic map can be considered as a reduced model, constructed using a Poincaré section, of a chaotic model of neuronal population activity (Breakspear et al. 2003). Since we are interested in population activity, this map was preferred as a model over others, such as Rulkov (2002), that represent individual neuron spiking activity. It is easy to verify that for $\epsilon \in [0,1]$, $x(0) = (x_1(0),\ldots , x_n(0)) \in [-1,1]^n$ implies $x(t) \in [-1,1]^n$ for all $t \ge 0$ so the dynamics are well-defined in forward time. The parameters used in this study are $\alpha = 1.7$, for which the dynamics $y(t+1) = f(y(t))$ are chaotic, and $\epsilon = 0.4$ which previous studies have shown to yield modular small-world structure in non-spatial networks of this size (van den Berg et al. 2012).

The network rewiring procedure uses a cost function so as to favour edges of low cost over edges of high cost when rewiring. This cost function,

$$\begin{aligned} R(i,j,t)=\gamma _{ij}(t)S(d_{ij}), \end{aligned}$$

is the product of an activation cost $\gamma _{ij}(t)$ and a spatial cost function $S(d_{ij})$ . The activation cost, $\gamma _{ij}(t)$, is the distance between the states of two nodes $i$ and $j$ at time $t$.

$$\begin{aligned} \gamma _{ij}(t)=\vert x_{i}(t)-x_{j}(t)\vert . \end{aligned}$$

The spatial cost, $S(\cdot )$, is a monotonic function of $d_{ij}$, the distance between nodes $i$ and $j$ defined as the length of the shortest arc on the sphere connecting $i$ and $j$. We consider the following spatial cost functions:

$$\begin{aligned} S(D) = \left\{ \begin{array}{ll} D &{} \text { linear}\\ \exp (D) -1 &{} \text { exponential}\\ &{} \text { (concave up)}\\ \log \left( \frac{D}{D_{\min }} + 1 \right) &{} \text { logarithmic}\\ &{} \text { (concave down)}\\ \end{array}\right. \end{aligned}$$

for $D_{\min } = \min _{i,j \in \mathcal {N}, i \ne j} d_{ij}$, the minimal pairwise distance amongst all nodes on the sphere. We will refer to the adaptive rewiring function, and the corresponding process of rewiring, by the spatial cost function used, e.g. logarithmic cost function will refer to the adaptive rewiring function with a logarithmic cost function of distance. Likewise, logarithmic rewiring process will refer to the rewiring process equipped with a logarithmic cost function.

For ease of comparison, Fig. 1 is presented with $S$ scaled such that the ranges of the spatial cost functions are equal. The ordering of node pairs induced by $R$, and hence the outcomes of Steps 2.2 and 2.3 described in the following procedure, are invariant to scaling of the image of $S$.

For $\mathcal {N}=\lbrace 1,2 ,\ldots ,n\rbrace$ the set of nodes, $R:\mathcal {N} \times \mathcal {N} \rightarrow \mathbb {R}_{0^{+}}$, ($\mathbb {R}_{0^{+}}$ the set of non-negative real numbers), we define the following rewiring process:

• Step 0: Generate a random graph with $n$ nodes and $E$ edges.

• Step 1: Take $x(0) \in [-1,1]^n$ randomly from a uniform distribution and iterate the dynamics (1) for $t=0,1,2,\ldots ,T-1$.

• Step 2: Rewiring:

  • 1. select a pivot node $p \in \mathcal {N}$ randomly from a uniform distribution

  • 2. determine the rewiring candidate $c = \mathrm{arg\,min }_{j\in \mathcal {N}\backslash \{ p\}} R(p,j,T)$

  • 3. go to Step 3 if $c \in \mathcal {N}_p$. If $c \notin \mathcal {N}_p$, update the graph by creating an edge between $p$ and $c$ and removing the edge between $p$ and $\overline{c} = \mathrm{argmax }_{j\in \mathcal {N}_p} R(p,j,T)$.

• Step 3: Repeat from Step 1 until $3\times 10^{5}$ iterates have been reached.

In the case of ties in Steps 2.2 and 2.3, i.e. multiple candidates to rewire to or disconnect from, the rewiring candidate is chosen at random.

A minimal number of time steps $T$ is needed in order to minimise the effect of initial transient activity after rewiring; $T$ needs to be sufficiently large such that the choice of $x(0)$ has minimal bias on the results. The relation between dynamics and structure during the rewiring stage is thus, effectively, independent of initial conditions. The value of $T=1,000$ as used in this study has previously shown to be sufficient for this purpose (Rubinov et al. 2009b).

For comparison we include as a baseline the previously mentioned rewiring process of Gong and van Leeuwen (2004), i.e. the non-spatial cost function in which spatial distance has no influence on the costs of rewiring and thus $S(D)$ is constant. Without loss of generality we take $S(D)\equiv 1$.

Across all versions of the method, in so far rewiring is based on non-spatial preferences, it was conceived in analogy to Hebbian learning. Hebbian learning relies on two mechanisms; the first is that synapses are strengthened according to correlated deviations from the mean firing rate (Sejnowski and Tesauro 1989). The second is that synaptic plasticity is competitive, where some synapses are strengthened, others are weakened (Song et al. 2000). Our rewiring function uses similar mechanisms. The mechanism for rewarding synchrony is the activation cost $\gamma _{ij}(t)$. Even though, rather than synchrony over a window of time, this mechanism follows instantaneous synchrony, it was shown in Rubinov et al. (2009b) that according to this mechanism, the evolving architecture reflects the long-term patterns of activity. The method of conservative rewiring then allows for competition among nodes.

Fig. 1

Cost functions of spatial distance: linear in blue, exponential in green, logarithmic in red. (Color figure online)

Measures of network structure

Here we describe the measures used to characterize network structure. Formal definitions are given in “Appendix 2”. All measures (except the network wiring cost) are discussed in (Rubinov and Sporns 2010) and implemented using the MATLAB scripts they provide. We first describe measures based solely on the topological structure of the network, then measures which quantify the spatial organisation.

Clustering coefficient ($C$) provides a measure of network segregation. Denote as a candidate triangle pivoting on node $i$ each pair of nodes adjacent to $i$, and as an actual triangle pivoting on $i$ each pair of nodes adjacent to $i$ that are themselves connected. The clustering coefficient $C_{i}$ for vertex $i$ is then the ratio of the number of actual triangles pivoting on $i$ to the number of candidate triangles pivoting on $i$. The clustering coefficient $C$ for the network is the average of $C_{i}$ over $i$.

Average shortest path length ($L$) provides a measure of network integration. A path of length $l$ connecting two given nodes $i$ and $j$ is a sequence of vertices $i=i_0,i_1,\ldots ,i_l=j$ with edges $\{i_k,i_{k+1}\}$ connecting successive pairs of vertices. The average shortest path length of the network is the average over all pairs $i$ and $j$ ($i \ne j$) of the length of the shortest path connecting $i$ and $j$. For disconnected pairs of nodes the path length is infinite. Such pairs are excluded from calculation of the average shortest path length. However, the connectivity densities we have used are above the corresponding percolation threshold and thus guarantee that all vertices belong to a single connected component.

Modularity ($Q$) provides a means of identifying community structure in a network. $Q$ measures the extent to which a given partition of a network into non-overlapping communities (or modules) of nodes has more intramodular connections and less intermodular connections than expected for a random network with the same degree distribution (Newman 2006). An optimal community structure for a given network can then be defined as one that maximises $Q$. Various algorithms have been suggested for finding optimal or near-optimal partitions. We use Newman’s community structure detection algorithm (Newman 2004). $Q$ is always strictly less than one. For a random network the maximal $Q$ is close to zero, while a $Q$ close to one can be obtained if the network can be partitioned into many modules of similar size with many intramodular connections and few intermodular ones. A $Q$ above about 0.3 is a generally good indicator that genuine modular structure has been found (Newman 2004). However, a regular lattice graph can give a $Q$ above 0.3 even though it has no genuine module structure: it admits many, very different partitions that are equally good (see “Spatial modularity” section).

Edge betweenness (EB) provides a measure of the centrality of a given edge in a network. Each edge is assigned a value equal to the fraction of all shortest paths in the network that include that edge. High betweenness edges have a considerable effect on the integration of the network through their effect on the average shortest path length. We will find it useful to look at edge betweenness in relation to spatial distance, in order to investigate to what extent spatially long-range edges contribute towards network integration.

Small-worldness ($\Sigma$) provides a single value involving both clustering coefficient and average shortest path length. The measure of small-worldness is calculated as the normalised ratio of clustering coefficient and average shortest path length, where $C$ and $L$ are normalised by the values of clustering coefficient $C_{\text {rand}}$ and average shortest path length $L_{\text {rand}}$ calculated for a random network. The measure of small-worldness was proposed by Humphries and Gurney (2008) as a method for determining network canonical equivalence; however, this measure has been criticised by Rubinov and Sporns (2010) for yielding false positives with highly segregated but poorly integrated networks. However, in combination with other measures, we can safely use this simple measure.

Network wiring cost ($M$) provides a measure of spatial localisation of edges. It is calculated as the normalised average edge length. Small $M$ corresponds to high spatial localisation and vice versa.

Weighted clustering coefficient ($C^{w}$) provides a measure of spatial segregation (also referred to here as spatially localised clustering or spatial clustering) by combining spatial distance with clustering. It uses a weighted adjacency matrix in which the weight of an edge is a linearly decreasing function of edge lengths in $[0,\pi ]$ normalised to the range $[0,1]$. The weighted clustered coefficient $C^{w}_{i}$ for vertex $i$ is calculated as the sum over all triangles centred on $i$ of the geometric mean of the three edge weights, divided by the number of candidate triangles pivoting on $i$. The weighted clustering coefficient $C^{w}$ for the network is the average of $C^{w}_{i}$ over $i$.

Results

The network measures are reported for rewiring processes under the given cost functions. The network structure is sampled every 500 iterations of the process, starting from the initial random network and ending after $3\times 10^{5}$ iterations. We conduct five such runs for each cost function (linear, exponential, logarithmic, and non-spatial). Independent instances of the random and regular type networks are constructed for each of the five runs.

This section is organised as follows: First we discuss obtained topological structure and show all rewiring processes to yield small-world architecture in “Topological small-worldness” section, then the effect of cost functions on spatial localisation of edges and clustering in “Spatial localization” section. This is followed by an examination of the relationship between edge betweenness and edge length in “Edge betweenness and distance relationship” section. Then we report on the degree of spatial modularity of the emergent small-world network in “Spatial modularity”. Finally, we report on the dependence of small-world emergence on connectivity density in “Dependence of small-world emergence on connection density” section.

Topological small-worldness

Figure 2a, b show the evolution of the clustering coefficient $C$ and average shortest path length $L$ for the non-spatial and spatial rewiring processes averaged over five runs. As shown in Fig. 2a, the non-spatial and all spatially constrained adaptive rewiring processes yield a network that is clustered: for the final network structure, adaptive rewiring processes yield values of $C$ that are greater than that of the regular lattice. Figure 2b shows that the values of $L$ for final network structure for the non-spatial and spatially constrained adaptive rewiring processes are less than that of the regular lattice, whilst exhibiting a modest increase over that of the random network. There is, on the whole, little difference between the final $C$ and $L$ values for the non-spatial and spatial processes. We may therefore conclude that, like the non-spatial rewiring process, the spatially biased rewiring ones successfully reach small-world topology. Furthermore, considering the evolution of the average values of $C$ and $L$, the linear and exponential rewiring processes show faster initial rates of increase than the non-spatial and logarithmic ones. This suggests that factoring in specific spatial constraints of a linear or exponential type may facilitate reaching a small-world topology in the system.

Figure 3a, b show the evolution of $C$ and $L$ for individual runs of the rewiring processes. The linear and exponential cost functions lead to rewiring processes that exhibit less variability between runs than the logarithmic and non-spatial ones throughout the full course of rewiring. Factoring in spatial constraints of a linear or exponential type therefore enhances the consistency of the small-world construction.

Fig. 2

Evolution of a the clustering coefficient values $C$ averaged over five runs; and b the average shortest path length values $L$ averaged over five runs; for the non-spatial and spatial rewiring processes, regular lattice on the sphere, and random network

Fig. 3

Evolution of a the clustering coefficient; and b the average shortest path length; for the non-spatial and spatial rewiring processes, regular lattice on the sphere, and random network. Individual runs in blue and their average value in red. (Color figure online)

Spatial localization

Figure 4a, b show the evolution of the spatially-weighted clustering coefficient $C^{w}$ and the network wiring cost $M$ for the non-spatial and spatial rewiring processes averaged over the five runs. We see from Fig. 4a that all spatially biased rewiring processes yield values of $C^{w}$ for final network structure that are well above the value of the non-spatial process, which in turn is still considerably greater than the random network on the sphere. In particular, the linear and exponential rewiring processes yield values of $C^{w}$ for final network structure that are greater than the regular lattice and, thus, yield small-worlds with higher degrees of spatial clustering than the regular lattice. The final value of $C^{w}$ for the logarithmic rewiring process, however, is slightly less than that of the regular lattice. In Fig. 4b, as one would expect, since connections in a regular lattice are optimal for spatial localisation, the regular lattice has the lowest value of $M$ amongst all the spatial rewiring processes. However, those of the linear and exponential rewiring processes are close to that of the regular lattice. On the other hand, the logarithmic rewiring process yields values of $M$ for final network structure that are well above the values for linear and exponential ones. The value of $M$ for the non-spatial process is approximately equal to that of the random one, and corresponds to an average edge length of $\frac{\pi }{2}$, as one would expect, this being the average distance between randomly chosen points on the sphere.

Spatially biased rewiring processes that have a linear or exponential cost function of distance, therefore, facilitate spatial localisation and spatial clustering better than ones with a logarithmic cost function. Furthermore, considering the evolution of the average value of $C^{w}$ and $M$, the linear and exponential rewiring processes exhibit similar initial rates of change and drive the network to a spatial small-world more rapidly than the logarithmic one.

Figure 5a, b show the evolution of $C^{w}$ and $M$ for individual runs of the rewiring process. Similar to Fig. 3a, b, the linear and exponential rewiring processes exhibit less variation for values of $C^{w}$ and $M$ than the logarithmic and non-spatial ones. Therefore, arguably the linear and exponential rewiring processes are most consistent in reaching a spatially localised and spatially clustered small-world topology.

We may conclude that spatially biased rewiring processes with linear or exponential cost functions produce spatially localised and clustered small-world topologies and achieve this more effectively, quickly, and consistently that the logarithmic-based process.

Fig. 4

Evolution of a the spatially-weighted clustering coefficient vaues $C^{w}$ averaged over five runs; and b the network wiring cost values $M$ averaged over five runs; for the non-spatial and spatial rewiring processes, regular lattice on the sphere, and random network

Fig. 5

Evolution of a the spatially-weighted clustering coefficient values $C^{w}$; and b the network wiring cost values $M$; for the non-spatial and spatial rewiring processes, regular lattice on the sphere, and random network. Individual trials in blue and averaged value of five runs in red. (Color figure online)

Edge betweenness and distance relationship

To investigate the relation between topological and spatial structure of the network, we focused on the evolving relationship between edge betweenness and spatial distance.

Figure 6a shows the linear correlation coefficients $\rho$ between edge betweenness and edge length for all edges generated by our models. For the non-spatial rewiring process, as one would expect, there is no correlation between edge betweenness and spatial distance. As for the spatially biased rewiring processes, the linear and exponential cost functions yield similar time-courses for $\rho$ throughout the full course of rewiring. The time-course shows an initial peak followed immediately by a trough and then a plateau. For the logarithmic rewiring process the correlation between edge betweenness and distance is much weaker and even exhibits a slightly negative trough prior to a gradual increase to a small positive value.

Scatter plots of edge betweenness and spatial distance at selected rewiring iterations reveal in more detail the evolving relation between topological and spatial structure. We uniformly randomly selected 4 % of the nodes from the combined five runs and plotted for all of their connections their values of edge betweenness against spatial distance at five different moments during the rewiring process: the initial moment; the moment when the peak occurs for the linear and exponential rewiring processes; the moment when the trough occurs for the linear and exponential rewiring processes; at the start of the plateau of the linear and exponential rewiring processes; and the final moment. The 2nd, 3rd, and 4th moments sampled are indicated in Fig. 6b by vertical lines.

In Fig. 7:

• Row 1 depicts the initial random structure.

• In Row 2 the linear and exponential rewiring processes exhibit a positive slope in their scatter plots whilst the non-spatial and logarithmic rewiring processes do not; all rewiring processes show the emergence of a small number of edges with somewhat higher values of edge betweenness.

• In Row 3 edges of even higher betweenness appear; for the linear and exponential rewiring processes, predominantly the short-range edges yield the greatest values of betweenness, while for the non-spatial and logarithmic rewiring processes, edges with high betweenness are present over the full range of edge lengths.

• In Row 4 the linear and exponential rewiring processes show what appears to be a newly emerged order; edges of still higher betweenness appear that are long-range, while long-range edges that are of low betweenness disappear. For the non-spatial and logarithmic rewiring processes, edges with high betweenness mostly remain of random edge length. (An apparent excess of high betweenness edges at mid-range lengths for the non-spatial process is merely because, given the geometry of the sphere, such distances are most common).

• In Row 5 the scatter plots show a strong resemblance to those in Row 4. Only the logarithmic rewiring process shows noticeable change: there are now more long-range high betweenness edges but still many short-range ones, and still many long-range edges of low betweenness.

We see that for the non-spatial case, there is, as one would expect, no trend in the correlation between edge betweenness and edge length. The linear and exponential rewiring processes show that after the initial trough, edges of high betweenness and large distance are present throughout the remaining course of rewiring (but not necessarily the same edges throughout). For the linear and exponential rewiring processes the network is strongly affected by the spatial constraint and quickly comprises mostly short-range edges of low betweenness along with a few long-range edges of high betweenness. By contrast, in the logarithmic rewiring process, network structure is not affected by spatial constraints to such an extent and spatial localisation proceeds more slowly.

Fig. 6

Linear correlation coefficient $\rho$ between edge betweenness and spatial distance averaged over five runs versus rewiring iterations. a The full course of rewiring; and b early course of rewiring

Fig. 7

Scatter plots of edge betweenness versus spatial distance. Betweenness values presented here were obtained by uniformly randomly selecting 4 % of nodes from the combined five runs and plotting the betweenness values of all their connections. Rows top to bottom for rewiring steps, $1,\; 0.75\times 10^{3},\; 1.5\times 10^{4},\; 5\times 10^{4},\; 3\times 10^{5}$, columns are for different rewiring processes

Spatial modularity

We now examine the degree of modularity in our networks and the spatial organisation of the modules.

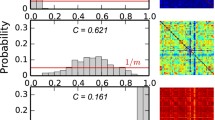
Figure 8a, b show the evolution of the modularity values $Q$ for the non-spatial and spatial rewiring processes averaged over five runs, and for individual runs, respectively. As shown in Fig. 8a, all rewiring processes yield a highly modular network. The spatially biased rewiring processes yield values of $Q$ for final network structure that are greater than that of the non-spatial one. In addition, the initial rates of $Q$ for the linear and exponential rewiring processes are greater than those of the non-spatial and logarithmic ones. Figure 8b shows the evolution of $Q$ for individual runs of the rewiring processes. As with previous measures we see that the linear and exponential rewiring processes exhibit less variability than the non-spatial and logarithmic ones. Linear or exponential cost functions therefore provide a mechanism that achieves a modular network structure to a greater extent, more rapidly, and with less variability compared to the non-spatial or logarithmic rewiring processes.

Fig. 8

Evolution of the value of the modularity $Q$. a The average of five runs; and b the individual runs; for the non-spatial and spatial rewiring processes, regular lattice on the sphere, and random network. Individual runs in blue and their average values in red. (Color figure online)

Figure 9 shows the adjacency matrices of the final network structure when columns and rows are permuted such that the connections between nodes within the same module are represented as blocks along the diagonal. We see that for all cases a modular network structure emerges: densely connected subsets of nodes and a sparse connectivity between those subsets. For individual runs, both the linear and exponential rewiring processes are more consistent between runs than the non-spatial and logarithmic ones. For all spatial rewiring processes, but more so for linear and exponential than for logarithmic ones, there exist more modules and there is less variation between the sizes of modules, compared to the non-spatial rewiring process.

Fig. 9

Permuted adjacency matrices that correspond to the module structure of the non-spatial, linear, exponential, and logarithmic rewiring processes. A point with coordinates $(i',j')$ is white if $i',j'$ are are the permuted indices of nodes $i$, $j$ that are connected; otherwise it is black

To show how the modular structure corresponds to the spatial organisation of the network, Figs. 10 and 11 represent typical networks resulting from the linear and logarithmic rewiring processes with nodes coloured according to the module they belong to. The exponential case yields results very similar to the linear one, hence for illustration we only present the case of the linear rewiring process. For the case of the linear rewiring process we see very little spatial overlap of communities of nodes. This is contrasted with the logarithmic rewiring process where modules are less clearly separated. Therefore, for the linear and exponential rewiring processes, modular topology indeed corresponds to a spatially modular structure, while this is not so clear cut for the logarithmic one.

These results show that the linear and exponential rewiring processes give rise to spatially modular small-worlds, while the logarithmic small-worlds are less spatially modular. We remark that the modularity algorithm (Newman 2004) does not always find the partition into modules that maximises $Q$. However we trust the modularity results for the rewiring processes because, as Fig. 9 shows, the adjacency matrices have a clear block-diagonal structure. In addition, we used an alternative algorithm for modularity, the Louvain algorithm (Blondel et al. 2008), and obtained similar results. A case where the algorithm (Newman 2004) performs poorly, however, is the regular graph. While the algorithm consistently gave a modularity value of around 0.3610, calculation of $Q$ using spatially modular partitions shown in Fig. 9b, c gave values of 0.4538 and 0.4219 respectively for the regular graph; substantially higher than the value of 0.3610 found by the algorithm.

Fig. 10

Final community structure of one run of the linear rewiring process. a, b Opposite hemispheres. Nodes are coloured according to the module to which they belong

Fig. 11

Final community of the logarithmic rewiring process. a, b Opposite hemispheres. Nodes are coloured according to the module to which they belong

Dependence of small-world emergence on connection density

Edge density had been found in non-spatial networks to have a critical threshold; as edge density falls below this threshold the development of a high clustering coefficient becomes first unreliable and then fails altogether (van den Berg et al. 2012). Since adding spatial constraints was shown to reduce the variability of the rewiring process, we hypothesize that the localizing tendency of the spatial cost functions shall reduce this threshold by promoting spatially localised clusters as occurs in the regular network limiting case. Accordingly, we investigated the dependence of rewiring processes on the parameter of edge density.

We performed simulations of the linear, exponential, and non-spatial rewiring processes with connectivity densities in the set $\{2.5,2.75,3,\ldots ,5\}$, using the same procedure as previous. The minimum, maximum, and average values of $C$ and $L$ after $3\times 10^{5}$ rewiring iterations are presented in Fig. 12 as functions of connectivity density.

For non-spatial rewiring, a connectivity density threshold of approximately 4 % was required for networks of this size to achieve self-organised clustering (Fig. 12a). Below this, the clustering coefficient drops off, until, at a connectivity density of approximately 3 %, it reaches that of a random network. This result confirms what was previously observed (Rubinov et al. 2009b). The average shortest path length increases gradually as edge density decreases and at the same rate as that of the random network but offset to a somewhat higher level. Below 3 % the non-spatial rewiring process remains, essentially random (Fig. 12b).

On the other hand, the linear and exponential rewiring processes share a threshold for self-organised clustering that is considerably lower than the non-spatial one. Similarly, reduced threshold is also observed for the average shortest path length of the linear and exponential rewiring processes (Fig. 12c–f); at 2.5 % connectivity these processes still yield small-world networks. Furthermore, preliminary data for $\kappa \in \{0.01,0.0125,0.015,\ldots ,0.025\}$ indicates that $C$ for the linear and exponential rewiring processes decreases gradually while remaining above that of the random network; there is no sudden phase transition of network structure toward random structure. Therefore, the linear and exponential adaptive rewiring processes yield small-world architecture for connectivity densities well below that required by the non-spatial adaptive rewiring process.

For $\kappa =0.1$, our small-world networks differed from the classic small-world example of WS based on the ring lattice in that it was not the case that $L_{\text {regular}}\gg L_{\text {random}}$. However as $\kappa$ approaches 0.025 we have $L_{\text {regular}}\gg L \gtrsim L_{\text {random}}$ since $L_{\text {regular}}/L_{\text {random}}$ increases more than $L/L_{\text {random}}$, and hence our small-world networks more resemble the classic example of WS.

This point is illustrated in Fig. 13 by the small-worldness measure $\Sigma$, as a function of connectivity density. The initial trend of $\Sigma$ for the three rewiring processes for decreasing connectivity density is the same with $\Sigma$ increasing. However, below a connectivity density of 4.25 %, the value of $\Sigma$ for the linear and exponential rewiring processes continues to increase while that for the non-spatial rewiring process begins to decrease until it reaches the value of one, that of the random network. In sum, for locally biased rewiring, the small-world effect is more pronounced in sparser networks. The critical threshold of edge density for self-organised clustering in a non-spatial adaptive rewiring regime is indeed reduced when adaptive rewiring becomes locally biased.

Fig. 12

Clustering coefficient, $C$, and average shortest path length $L$, for a, b non-spatial; c, d linear; and e, f exponential cost functions as function of edge density. Maximum, average, and minimum values from the five independent runs are shown, along with values for the corresponding random and regular graphs

Fig. 13

Small-worldness measure $\Sigma$ averaged over five runs for non-spatial, linear, and exponential rewiring processes as a function of edge density

Discussion

We are aiming to understand the principles whereby the large-scale information processing architecture of the cortex takes shape in particular, the observation that this structure consists of a large number of efficiently connected clusters: a modular small-world. In the cortex, this architecture exists within an essentially sheet-like structure, in which the modules are spatially segregated, and their links are long-range connections. We propose that this network structure, and its spatial layout, take shape in a process through which neural connections are rewired in response to the patterns of dynamic synchronization in ongoing neural activity. In a highly simplified model of the functional architecture, starting from a random initial network structure, a modular small world network gradually emerges when connections are attached and detached, depending on the presence or absence of pairwise synchrony between activity in the nodes.

Previous adaptive rewiring models have considered synchrony as the only rewiring criterion irrespectively of the information processing architecture of the brain (Gong and van Leeuwen 2004; Kwok et al. 2007; Berg and Leeuwen 2004). Here we consider networks endowed with metrics, a definition of distance between nodes, and study the effect on the outcome of adaptive rewiring. We study the effect of local bias on the rewiring of connections in a highly simplified model process. Doing so allows us to consider the effect of biological constraints such as metabolic costs and wiring length. Factoring in a preference for spatially local rewiring is cause for the modular small world structure to be reached with greater robustness, compared to rewiring based on synchrony alone. The resulting network, moreover, consists of spatially segregated modules, in which within-module connections are predominantly of short range and their interconnections are of long range. The spatially biased rewiring process, therefore, might be considered as a principle for how the large-scale architecture of the cortex is formed.

In our current, highly abstract model, a locally biased Hebbian-like adaptive rewiring process is applied to a network consisting of 500 nodes evenly distributed on a sphere. Rewiring depended on the factors of synchrony between pairwise unit activity and the spatial distance between nodes. The procedure extends the adaptive dynamical rewiring process of Gong and van Leeuwen (2004) with a function that biases rewiring such that spatially local connections are more likely. We considered three functions to specify the costs of a given wiring length: logarithmic, linear, and exponential.

For 10 % connectivity, all versions of the locally biased rewiring process preserve the phenomenon of small-world emergence found in the non-spatial one. Furthermore, the linear and exponential ones yielded networks that are spatially organised such that topologically segregated regions correspond to spatially segregated regions, with these regions being linked by long-range connections; that is to say, a spatially modular small-world.

Locally biased adaptive rewiring improves the robustness of network evolution from random to small-world topology. Non-spatial adaptive rewiring processes are subject to a minimum connectivity density threshold, below which the rewiring process does not achieve self-organised clustering (Rubinov et al. 2009b). Locally biased adaptive rewiring processes that have a linear or exponential cost function, however, achieve self-organised clustering for connectivity densities considerably lower than this threshold.

The measure of edge betweenness in relation to spatial distance enables us to relate hub nodes—nodes that participate in a relatively high proportion of shortest paths—with connections that are spatially long-range (since hub nodes can be inferred from high betweenness edges). Previously, anatomical network hub nodes appeared random in functional networks due to observed disparity between structural and functional connectivity (Rubinov et al. 2009b). Now, however, we see hub nodes connect spatially distant regions.

We conclude that a locally biased adaptive rewiring function equipped with a linear or exponential cost function is capable of generating a spatially modular small-world network. Thus, spatially constrained adaptive rewiring schemes are sufficient to explain both the emergence of topological connectivity structure and spatial distribution of large-scale cortical architecture.

For further study, we hope to provide analytical results that predict changes of network structure and which will complement the simulation study we have presented.

Appendices

Appendix 1: Evenly distributed points on a sphere

There does not yet exist a solution to evenly distribute points on a sphere for any number of points.

We thus devised the following iterative algorithm to approximate an even distribution of 500 points on the sphere.

• Step 0: Initialise points at positions drawn randomly from a uniform distribution on the unit sphere, with coordinate vectors $\mathbf {x}_i\in \mathbb {R}^{3}$, $i=1,\ldots ,n$, and $\Vert \mathbf {x}_{i}\Vert =1$.

• Step 1: Define the crowdedness around a point $i$ as $K_{i}=(\sum _{j\ne i} \Vert \mathbf {x}_{i}-\mathbf {x}_{j} \Vert )^{-1}$. Choose the most crowded point $j$ such that $K_{j}=\max _{i}{K_{i}}$.

• Step 2: Given point $j$, each other point $k$ moves away from $j$ in the direction of the vector $\mathbf {x}_{k}-\mathbf {x}_{j}$, by an amount determined by a linearly dampening function

  $$\begin{aligned} F_{jk}=\frac{\alpha }{c}\exp {( -\beta \Vert \mathbf {x}_{j}-\mathbf {x}_{k}\Vert )} \end{aligned}$$

  where $\beta =5$ determines how $F_{jk}$ decreases over distance; large $\beta$ means repelling force acts over a small spatial distance and vice versa. A systematic trial and error search found $\beta =5$ to be most successful. The dampening coefficient $\alpha$ decreases linearly with $\alpha (t)=1-\frac{t}{T}$ for $t=0,\ldots ,T-1$. The coefficient $c=\sqrt{\frac{n}{2}} \max _{k\ne j}{\left( \exp ^{\left( -\beta \Vert \mathbf {x}_{j}-\mathbf {x}_{k}\Vert _{1}\right) }\right) }$ normalises $F$ so that $F\in \left( 0,\alpha \sqrt{\frac{2}{n}}\right)$, where $\frac{2}{\sqrt{n}}$ is the approximate distance between nearest neighbours among an evenly distributed set of points on the sphere.

• Step 3: Project each point back onto the sphere: $\frac{\mathbf {x}_{k}-\mathbf {x}_{j}}{\Vert \mathbf {x}_{k}\Vert }$.

• Step 4: Repeat from Step 1 until $\frac{n(n-1)}{2}$ iterates have been reached.

For a set of finitely many evenly distributed points on the sphere, the cumulative number of points when moving in the azimuthal angle is a discrete approximation to the surface integral with respect to the azimuthal angle. Thus, we measure the accuracy of the approximated even distribution of points on the sphere as the absolute error between the cumulative number of points (normalised to unity) and the surface integral (normalised to unity). This is calculated for each point. Figure 14 shows the average value of absolute error for all points at the same azimuthal angle as a function of azimuthal angle.

We see in Fig. 14 that the average absolute error is always less than 0.35 %. Since $n=500$, a 0.4 % error is equal to $\frac{2}{n}$ and hence corresponds to approximately 2 points more or less than the expected cumulative number of points at any given azimuthal angle given a uniform distribution.

Fig. 14

Average value of absolute error between the cumulative number of points (normalised to unity) and the surface integral (normalised to unity) as a function of azimuthal angle

Appendix 2: Network measures

Measures of clustering coefficient, average shortest path length, weighted clustering coefficient, and edge betweenness are taken from (Rubinov and Sporns 2010).

Clustering coefficient

Let $a_{ij}$ be the entries of the adjacency matrix, i.e. $a_{ij}=1$ if $i$ connects to $j$, and $a_{ij}=0$ otherwise. The degree of a node with undirected connections is calculated as

$$\begin{aligned} k_{i}=\sum _{j=1}^{n}a_{ij}. \end{aligned}$$

The number of triangles pivoting on node $i$—pair nodes adjacent to node $i$ that are themselves connected—is calculated as

$$\begin{aligned} t_{i}=\frac{1}{2}\sum _{j,h\in \mathcal {N}}a_{ij}a_{ih}a_{jh}. \end{aligned}$$

Thus the clustering coefficient can be determined as,

$$\begin{aligned} C=\frac{1}{n}\sum _{i\in \mathcal {N}}C_{i}=\frac{1}{n}\sum _{i\in \mathcal {N}}\frac{2t_{i}}{k_{i}(k_{i}-1)} \end{aligned}$$

(2)

Average shortest path length

A path of length $l$ between nodes $i$ and $j$ is a sequence of vertices $\eta _{i\leftrightarrow j}=(i=i_0,\ldots ,i_l=j)$ with $a_{i_{k,k+1}}=1$. Let $l_{ij}$ be the length of the shortest path between $i$ and $j$. The average shortest path length is the mean value over all pairwise nodes, calculated as

$$\begin{aligned} L=\frac{1}{n(n-1)}\sum _{i\in \mathcal {N}}\sum _{j\in \mathcal {N}_{i}}l_{ij}. \end{aligned}$$

(3)

For disconnected pairs of nodes $l_{ij}$ is undefined, however, such pairs are excluded in the MATLAB program computation to allow a result.

Modularity

Let $\Theta =\lbrace \theta _1,\theta _2,\ldots \rbrace$ be a partition of the nodes of the network into modules, i.e. the subsets of nodes that form non-overlapping communities. Let $\Pi _{\theta _i\theta _j}$ denote the fraction of all edges in the network that connect nodes in module $\theta _i$ to nodes in module $\theta _j$. Then the modularity for this set of modules is calculated as

$$\begin{aligned} Q=\sum _{\theta _i\in \Theta }\left[ \Pi _{\theta _i\theta _i}-\left( \sum _{\theta _j\in \Theta }\Pi _{\theta _i\theta _j}\right) ^{2}\right] . \end{aligned}$$

(4)

Edge betweenness centrality

Calculated for each edge as the fraction of shortest paths in the network which pass through the edge. Let $H_{uv}$ be the number of shortest paths that connect nodes $u$ and $v$, and let $H_{uv}(i,j)$ be the number of shortest paths between nodes $u$ and $v$ that includes the edge between $i$ and $j$.

Then, the edge betweenness value for the edge between $i$ and $j$ is calculated as

$$\begin{aligned} \mathrm {EB} = \sum _{\begin{array}{c} u,v\in \mathcal {N}\\ u\ne v\\ \end{array}}\frac{H_{uv}(i,j)}{H_{uv}}. \end{aligned}$$

(5)

Small-worldness

Calculated as the normalised ratio of the clustering coefficient to the average shortest path length:

$$\begin{aligned} \Sigma =\frac{C/C_{\text {rand}}}{L/L_{\text {rand}}}, \end{aligned}$$

(6)

for $C$ the clustering coefficient and $L$ average shortest path length of a network, normalised respectively by the corresponding quantities $C_{\text {rand}}$ and $L_{\text {rand}}$ for a corresponding random network.

Weighted clustering coefficient

A weighted triangle is determined as the cubic root of the product of the three weighted edges that make a triangle centred on a given node. The sum of all triangles pivoting on a given node $i$ is

$$\begin{aligned} t_{i}^{w}=\frac{1}{2}\sum _{j,h\in \mathcal {N}}{(w_{ij}w_{ih}w_{jh})}^{1/3} \end{aligned}$$

for edge weights $w_{ij}$, defined by the linear relation

$$\begin{aligned} w_{ij}=\left\{ \begin{array}{ll} 1-\frac{d_{ij}}{\pi } &{} \text { if }\quad a_{ij}=1 \\ 0 &{} \text { otherwise} \end{array}\right. \end{aligned}$$

Zero distance corresponds to a weight of 1 and the maximum distance $\pi$ corresponds to a zero weight. Thus, the weighted clustering coefficient is calculated as

$$\begin{aligned} C^{w}=\frac{1}{n} \sum _{i\in \mathcal {N}} {C_{i}^{w}} = \frac{1}{n} \sum _{i\in \mathcal {N}} \frac{\sum _{j,h\in \mathcal {N}}2t_{i}^{w}}{k_{i}(k_{i}-1)} \end{aligned}$$

(7)

Network wiring cost

The normalised average edge length for all edges of the network is

$$\begin{aligned} M=\frac{1}{\pi \sum _{i\in \mathcal {N}}{k_{i}}}\sum _{i\in \mathcal {N}}\sum _{j\in \mathcal {N}_{i}}{d_{ij}}, \end{aligned}$$

(8)

where $\pi$ is the maximum edge length that connects two nodes on the shortest arc along the great circle for the network embedded on a unit sphere. A network wiring cost value of 1 indicates an average edge length of $\pi$, of zero indicates an average edge length of zero, and of $\frac{1}{2}$ indicates the expected value for randomly distributed edge lengths.